Abstract
Hydropower is the most important source of electricity in Brazil. It is subject to the natural variability of water yield. One building block of the proper management of hydropower assets is the short-term forecast of reservoir inflows as input for an online, event-based optimization of its release strategy. While deterministic forecasts and optimization schemes are the established techniques for short-term reservoir management, the use of probabilistic ensemble forecasts and multi-stage stochastic optimization techniques is receiving growing attention. The present work introduces a novel, mass conservative scenario tree reduction in combination with a detailed hindcasting and closed-loop control experiments for a multi-purpose hydropower reservoir in a tropical region in Brazil. The case study is the hydropower project Três Marias, which is operated with two main objectives: (i) hydroelectricity generation and (ii) flood control downstream. In the experiments, precipitation forecasts based on observed data, deterministic and probabilistic forecasts are used to generate streamflow forecasts in a hydrological model over a period of 2 years. Results for a perfect forecast show the potential benefit of the online optimization and indicate a desired forecast lead time of 30 days. In comparison, the use of actual forecasts of up to 15 days shows the practical benefit of operational forecasts, where stochastic optimization (15 days lead time) outperforms the deterministic version (10 days lead time) significantly. The range of the energy production rate between the different approaches is relatively small, between 78% and 80%, suggesting that the use of stochastic optimization combined with ensemble forecasts leads to a significantly higher level of flood protection without compromising the energy production.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Hydropower is the most important source of electricity in Brazil. During recent years, it has accounted for 60% to 70% of the total electrical power supply (EPE, 2014). The remaining electricity is provided mostly by thermal power plants using biomass, coal, natural gas, and nuclear power, but generally at higher costs. A nationwide transmission network allows for integrated management of the energy production. This management is done by a central organization called Operador Nacional do Sistema (ONS), whose objective is to optimize electricity production by increasing production at plants with lower operation costs and decreasing it at plants where these costs are higher. Operational costs of hydropower are lower than for thermal power plants; therefore, there is a strong economic reason to maximize the proportion of energy generated from hydropower (Hamlet et al. 2002). On the other hand, hydropower is dependent on weather and climate, which are naturally variable, leading to risks of power production shortage.
In such a complex system, benefits of reservoir inflow forecasts include the following: (1) spillage can be minimized; (2) reservoirs can operate with larger head for longer periods due to more reliable release schedules; (3) more energy can be generated at times when energy prices are higher; (4) more energy can be produced at hydropower plants that have the higher inflow forecasts (Faber and Stedinger 2001; Yeh et al., 1982; Hamlet et al. 2002; Maurer 2002). Forecast errors influence decision-making, leading to sub-optimal operation when water is released unnecessarily from reservoirs, or when thermal power plants are activated needlessly.
ONS uses a chain of optimization models for the management of the Brazilian power system (Maceira and Damázio 2005; Pereira and Pinto 1991). Two of the optimization models are meant for long-term operational planning (5 to 10 years) and for seasonal operational planning (12 months). These optimization models use stochastically generated inflow scenarios, and no actual forecasts. The third optimization model used by ONS is applied to make operational decisions up to 14 days in advance, and uses forecasts of inflows to more than two hundred reservoirs. Until less than a decade ago, all of the inflow forecasts were provided by periodic auto-regressive moving average (PARMA) models (Maceira and Damázio,). In 2005, ONS started to test inflow forecasting based on rainfall-runoff models with the input of quantitative precipitation forecasts. The forecasting models tested used precipitation forecasts generated by the Brazilian Weather Forecasting Center (Centro de Previsão de Tempo e Estudos Climáticos – CPTEC), primarily from the regional atmospheric Eta model (Chou et al. 2002). An assessment of results by Guilhon et al. (2007) showed that the new forecasting methods that included quantitative precipitation forecasts outperformed auto-regressive forecasting models based on inflow time series input only. As a result, forecasting models and methods that use quantitative precipitation forecasts are gradually replacing PARMA models in the Brazilian electric energy optimization chain (Guilhon et al. 2007). However, until now, mostly medium range (14 days) forecasts are deterministic, i.e. generated considering only one possible future.
In Brazil, the use of Ensemble Streamflow Forecasts (ESF) for both floods and reservoir inflow predictions is still starting (Fan et al. 2014). The aim of ESF is to account for uncertainties. They are usually produced by forcing hydrological models with meteorological forecasts which include multiple possible future trajectories of atmospheric variables (Cloke and Pappenberger 2009), although some others strategies to generate ESF such as the use of uncertainty of initial conditions and model parametrization are present in the literature (Demirel et al. 2013). The first examples of ESF for Brazilian cases are shown by Tucci et al. (2003 and 2008), who showed results of hindcasting experiments of seasonal streamflow forecasts for the rivers Uruguay and Grande. More recently, Calvetti and Pereira (2014), Collischonn et al. (2013) and Meller (2013) described experiments of short- to medium-range ensemble flood forecasting. Fernández Bou et al. (2015) showed the development of a methodology for 1-month flood forecasting in the upper region of the Uruguay River basin, at the Itá Hydroelectric Power Plant (HPP) reservoir. Finally, Fan et al. (2014, 2015a b) showed the assessment of ESF within operational forecasting systems.
While ESF are not yet widely used operationally in Brazil for medium-range hydropower optimization and planning (use of ensembles can be considered generally at a research level), a number of studies worldwide have shown the benefits of the use of ESF for reservoir operation. Selected recent works are cited as follows.
In the study of Zhao et al. (2011), synthetic experiments of ESF were applied to real-time reservoir operation and were compared with deterministic forecasts. Through the hypothetical example of a single-objective real-time reservoir operation model, the results illustrated that forecast uncertainty exerts significant effects. Results showed that, in general, the benefit from the reservoir operation using ensembles was nearly as high as the one obtained with a perfect forecast. Zhao et al. (2012) demonstrated with synthetic tests that we may have an effective forecast horizon where the forecast is useful for operational purposes, which is the horizon where uncertainties do not excessively compromise the forecast quality.
Boucher et al. (2012) quantified the economic benefits of employing the forecasts in a stochastic decision-making assistance tool for hydroelectricity production during a flood event on the Gatineau River, Canada. According to the authors, this allowed for the comparison between different types of forecasts according to their value in terms of energy, spillage and storage in a reservoir. ESF exhibited excellent performances when compared to observations and were also satisfying when involved in the operational management of electricity production.
Liu et al. (2015) investigated how the sources of uncertainty impact the process of reservoir flood control based on forecasts, using a case study from the Ankang Reservoir, Han River, China. Based on the results of a series of synthetic tests, authors shed light on how different uncertainties can affect the operation of reservoirs while anticipating floods. Anvari et al. (2014) tested optimization models in the Zayandeh-Rud reservoir system in Iran, aiming to investigate uncertainty-based optimal operation of this multipurpose water reservoir system. Authors also assessed the effect of Ensemble Streamflow Predictions (ESP) that were generated by artificial neural networks in the application. Results for the case study demonstrated that some of the specific approaches that were tested could be useful for real-time reservoir operation.
Ficchì (2015) presented a study where authors aimed to investigate the improvement of a four-reservoir operation system in the Seine River basin, France, using an ensemble of weather forecasts and a real-time control approach. In the proposed system, a model predictive control (MPC) optimization technique was used, and it was modified to a version that incorporated uncertainties in the form of a tree-based model predictive control (TB-MPC) approach in order to account for deterministic and ensemble forecasts, respectively. The management system was assessed by the simulation of historical events. Simulation results showed that the proposed real-time control system largely outperforms a no-forecasts management strategy based on rule curves, and that explicitly considering forecast uncertainty through ensembles compensated for the loss in performance due to forecast inaccuracies.
Focusing more on operational aspects (not using forecasts), Che and Mays (2015) developed and tested a methodology for determining reservoir release schedules before, during, and after an extreme flood event in real time. The problem was formulated as a real-time optimal control problem in which reservoir releases represent the decision variables, similar to the methodology adopted in the present work.
The present paper presents one of the first hindcasting experiments with multi-stage stochastic reservoir optimization on the basis of medium-range ESF for a tropical study case in Brazil. It is a follow-up of a previous study presented by Schwanenberg et al. (2015a) which used a similar approach, but restricted for a single-event simulation. The novel components of the present paper are: (i) the closed loop experiment of the stochastic optimization in application to a real-world case study and (ii) a novel, mass conservative scenario tree generation with a detailed comparison of the forecast skill of the ensemble against the reduced scenario tree.
2 Methodology
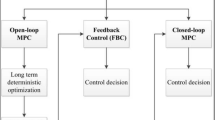
The proposed methodology here does not intend to reduce forecast uncertainties, but, instead, is focused in the usage of these uncertainties for better decision making by a short-term reservoir optimization approach.
The short-term reservoir optimization considers a discrete time-dynamic system according to
where x, y, u, d are the state, dependent variable, control and disturbance vectors, respectively, and f( ), g( ) are functions representing an arbitrary water resources model. Equation (1) is used to predict future trajectories of the state x and dependent variable y over a finite time horizon represented by k = 1, …, N time instants to determine the optimal set of control variables u by optimization. For a known disturbance d over the time-horizon, for example the inflows into the reservoir system, the deterministic optimization setup becomes
where J( ) is a cost function associated with a state transition and h( ) includes hard constraints on control variables and states. The notation x * refers to a subset of state variables which is used in the hard constraints and which therefore become independent optimization variables. In this case, the related process model becomes an equality constraint of the optimization problem.
The stochastic version of the above optimization problem is obtained by replacing the deterministic forecast d k by a forecast ensemble d k j , where j is the ensemble index. The objective function in Eq. (2) is reformulated by computing the probability-weighted sum of the objective function terms of the individual ensemble members. This can be expressed as
where p j is the probability of the ensemble member j and m are the number of ensembles.
The features of the stochastic optimization are determined by the choice of u k j . In its simplest form, the control trajectory is identical in all ensemble members according to u k j = u k. In this case, the optimization tries to find a trajectory which minimizes the objective function on average over all ensemble members. If we assume that the reservoir release is the typical control variable in a reservoir management application, this means that the variability in the reservoir inflow recurs as a variation of the forebay elevation of the reservoir. This can lead to infeasibility if the inflow variability is larger than the reservoir storage over the forecast horizon.
A more advanced formulation is achieved by the use of a scenario tree for the control trajectory and all other variables. Raso et al. (2013) and Schwanenberg et al. (2015a) applied this methodology to the multi-stage stochastic optimization of reservoirs. In this approach, the control adapts to the resolution of the forecast uncertainty. The scenario tree is defined by a tree nodal partition matrix P(j, k) ∈ ℤM × N. It assigns the control at time step k of scenario j to the control vector u. An example for a nodal partition matrix for a simple tree with two scenarios and one branching point at the second time step is presented in Eq. (3) by
The key to the method is the derivation of the scenario tree from an ensemble by a scenario tree reduction. We revised existing tree reduction techniques and found that most existing methods (Heitsch & Rőmisch 2003; Raso et al. 2013 among others) do not preserve the probability-weighted sum of a quantity of the original ensemble ∑ m j = 0 p j u k j due to a complete deletion of ensembles and an allocation of their probability to the closest remaining one. This is a drawback for reservoir management applications, since the probability-weighted inflow volumes change with the tree reduction techniques and their parameters.
The purpose in this study is to define an efficient and robust scenario tree reduction technique which i) keeps probability-weighted quantities constant in the tree reduction process; ii) leads to a constant number of branches in the tree (to keep the optimization effort roughly the same); and iii) preserves other properties of the original ensemble as much as possible.
Numerical experiments led to the refinement of the scenario tree reduction techniques for binary trees in Schwanenberg et al. (2015a, b). They are summarized as follows:
-
1.
The number of ensemble members is reduced to 2x, e.g. 2, 4, 8, 16, by deleting m − 2x members with the closest distance to remaining members by means of the distance matrix dis(i, j) = ∑ n k = 1 ‖d k i − d k j ‖. The probability of a deleted member is added to the closest remaining one. Next, the remaining member is replaced by the probability-weighted sum of the deleted and remaining members.
-
2.
A number of x branching points are distributed in equidistant steps along the forecast horizon.
-
3.
All ensemble members up to the first branching point get aggregated into a single branch. From this point on, the ensemble members get classified into two groups according to their remaining inflow volume.
-
4.
Step 3 is repeated at all other branching points for each of the previously generated subsets and split into two again.
-
5.
Optional smoothing is applied over a number of time steps after the branching point to reduce the negative impact of large, unphysical inflow steps on the optimization.
An example of a generated scenario tree is presented in Fig. 1.
For the performance assessment of the ensemble forecast and the derived scenario trees, three performance metrics were selected: Mean Absolute Error (MAE), Mean Continuous Ranked Probability Score (Mean CRPS, usually referred to as CRPS), and Brier Score (BS). A brief description about these metrics is provided below. For more information, we recommend Wilks (2006), Brown et al. (2010), Bradley and Schwartz (2011), and Jolliffe and Stephenson (2012):
-
Mean Absolute Error (MAE): this metric is the absolute difference between two values, in this case, between observations and forecasts at each lead time. In the case of ensemble forecasts. The MAE of a perfect model would be zero.
-
Mean Continuous Ranked Probability Score (CRPS): the CRPS is a score that summarizes the quality of a probability forecast into a number by comparing the integrated square difference between the cumulative distribution function of forecasts and observations. Lower CRPS values correspond to more accurate results.
-
Brier Score: the BS measures the average square error of a probability forecast for a dichotomous event, defined, for example, by a flow threshold exceedance. A perfectly sharp set of forecasts would show a BS value of zero.
3 Test Case Description
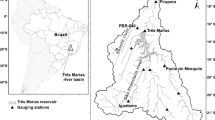
The case study of the present paper is the Três Marias reservoir, located in southeastern Brazil (Fig. 2). The reservoir is operated with two main objectives: (i) hydroelectricity generation and (ii) flood control at the downstream city of Pirapora. The main threat there is that floods in Pirapora occur due to the outflow at Três Marias and the Abaeté River tributary. In this case, an optimized operation must account for the reservoir inflow forecast and the incremental downstream flow contributions.
Três Marias HPP is operated by CEMIG (Companhia Elétrica de Minas Gerais). During low and medium flows, CEMIG follows rules defined by ONS to operate the HPP. However, during flood events, CEMIG operators take over the control of the reservoir turbines and spillways to mitigate downstream floods and without compromising future energy generation.
This case has already been the object of several recent studies. In the research of Fan et al. (2014), a first version of an ensemble forecasting system based on the MGB-IPH (Collischonn et al. 2007) hydrological model and on GEFS v2 meteorological forecasts (Hamill et al. 2013) was shown. Subsequently, Fan et al. (2015a) presented a second version of the ensemble forecasting system coupled with Delft-FEWS software shell (Werner et al. 2013) and tested it using multiple ensemble rainfall forecasts from the TIGGE database (Bougeault et al. 2010) and in comparison to other Brazilian basins. Finally, Schwanenberg et al. (2015a) developed a reservoir optimization system by coupling the MGB-IPH hydrological model, ECMWF rainfall forecasts (Buizza et al. 2007) and the RTC-Tools (Real-Time Control Tools) software (Schwanenberg et al. 2015b) to suggest optimum operations of the Três Marias HPP dam.
In the tests presented by Schwanenberg et al. (2015a) that developed system were applied to the reservoir’s operation during a single flood event, comparing results from perfect forecasts (e.g. observations), deterministic forecasts, and ensemble forecasts (stochastic optimization). Results showed that ensemble forecasts coupled with stochastic optimization were as good as perfect forecasts to the operation of the reservoir for the tested single event. The present paper extends the analysis to a more representative period of two consecutive years using optimum decisions to control the reservoir’s release. This means that the impact of medium-range forecasts to the long-term operation of the reservoir is also evaluated.
Hydrological forecasts are produced using the MGB-IPH model (Collischonn et al. 2007; Paz et al. 2007; Fan et al. 2014), forced by historical rainfall forecasts from the ECMWF global meteorological Bougeault et al. 2010). Both deterministic (fc) and probabilistic ensemble forecasts (pf) are used. The system runs in the Delft-FEWS software shell (Werner et al. 2013). This hydrological forecasting framework is the same one presented by Fan et al. (2015a), and forecasts used in the experiments shown here are the same as presented by Fan et al. (2015a).
The tested period is from July 2011 until March 2013, comprising two dry seasons (May to October) and two rainy seasons (November to March). Figure 3 presents the Três Marias HPP inflow hydrograph for the hindcast period and the Abaeté River hydrograph at the confluence with the São Francisco River at the Ponte BR-040 (PBR-040) river gauge. The hydrographs indicate two high inflows, the second of which reaches more than 6000 m3/s at Três Marias HPP in January 2012. When this second inflow occurred, Três Marias HPP operators had to deal with the large reservoir inflow and corresponding high flows in Abaeté River to avoid flooding in the city of Pirapora.
Operational constraints of the Três Marias HPP are:
-
1.
The minimum flow requirement is 460m3/s;
-
2.
Reservoir elevations must be between seasonally-dependent lower and upper bounds;
-
3.
The forebay elevation should be close to a requested forebay elevation at each time-step given by a guide cuve;
-
4.
Spillage must be avoided as much as possible;
-
5.
A discharge of 2000m3/s at the city of Pirapora must be avoided as much as possible to prevent inundating small islands along the river;
-
6.
If it is not possible to accomplish constraint 5, a discharge of 3800m3/s at the city of Pirapora must be avoided as much as possible to prevent severe inundations; and
-
7.
Changes in outflow should be as smooth as possible.
All of these constraints are included in the RTC-Tools model to optimize the operation of Três Marias HPP for the test period. Constraints 1 and 2 are considered hard constraints. The others are implemented as soft constraints by penalizing their violation in the objective function.
Weighting factors are adjusted under the supervision of CEMIG to represent the current operation of the Três Marias HPP. Under low flow conditions, operation of the Três Marias HPP must follow a guideline curve defined by ONS. Under high flow conditions, operation is focused on avoiding floods at the city of Pirapora while also protecting the dam’s integrity.
The hindcast experiments consider five different configurations, most of which are tested with different forecast horizons:
-
Configuration 01: perfect knowledge of the future (using observed discharges), at different total lead times (2, 3, 5, 7, 10, 15, 30, and 60 days);
-
Configuration 02: perfect knowledge of future rainfall is used to generate discharges of the hydrological model with different total lead times (2, 3, 5, 7, 10, 15, 30, and 60 days);
-
Configuration 03: deterministic future rainfalls obtained from ECMWF (ECMWF-fc) are used to generate discharges with the hydrological model, at different lead times (2, 3, 5, 7, and 10 days);
-
Configuration 04: ensemble mean of future rainfalls obtained from ECMWF (ECMWF-pf mean) are used to generate discharges within the hydrological model for different lead times (2, 3, 5, 7, 10, and 15days); and
-
Configuration 05: ensemble of future rainfalls obtained from ECMWF (ECMWF-pf) are used to generate discharges within the hydrological model, with a lead time of 15 days.
Results of these experiments are showed and discussed in the following section.
4 Results and Discussions
4.1 Evaluation of Hydrological Forecasts and Derived Scenario Trees
Evaluation results of deterministic and probabilistic hydrological forecasts and derived decision trees with 8 (8B) and 32 (32B) branches are shown in Fig. 4, 5 and 6.
MAE metric results (Fig 4) indicate that deterministic forecasts (ECMWF-fc) and ensemble forecasts (ECMWF-pf) perform very similarly until a lead time of 96 h, with errors increasing from 60 m3/s (0 h) to 170 m3/s (96 h). For higher lead times, the ensemble forecasts show smaller errors (198 m3/s at 240 h) than the deterministic ones (220 m3/s at 240 h). Figure 4 also demonstrates that the computed MAE of the decision trees 8B and 32B have the same value than the full ensemble. This is expected since the scenario tree reduction generation process supposes that the mean value of the distribution must be maintained. Hence, the test confirms the expected feature of the tree reduction.
CRPS metric results (Fig 5) indicate a similar performance to the deterministic forecasts (ECMWF-fc) and the ensemble forecasts (ECMWF-pf) until a lead time 48 h, with errors varying from 60 m3/s (0 h) to 115 m3/s (96 h). For higher lead times, the ensemble forecasts have smaller errors (151 m3/s at 240 h) than the deterministic ones (220 m3/s at 240 h). The CRPS of the scenario trees are between the deterministic forecasts and the ensemble. The tree with 8 branches (8B) has slightly higher error values than the 32B tree.
Another important feature noticed on Fig 5 is that for decision trees the mean CRPS values have “steps” along lead times. This happens due to the branching process. The trees have a lower number of branches for shorter lead times, whereas the number of branches increases for larger lead times. This property makes the decision tree more similar to a deterministic forecast at smaller lead times and more alike the probabilistic forecast for higher lead times. As such, the CRPS of the trees propagates from the deterministic forecasts to the probabilistic forecasts.
BS metric results (Fig 6) indicate that the performance of the deterministic forecasts (ECMWF-fc) is similar to the ensemble forecasts’ (ECMWF-pf) performance until a lead time of 120 h, with BS values varying from 0.01 (0 h) to 0.04 (120 h). For higher lead times, the ensemble forecasts show smaller BS values (0.035 at 240 h) than the deterministic forecasts (0.048 at 240 h).
As it was also observed in the CRPS analysis, the performance of the scenario trees is between the ones of the deterministic forecasts and the ensemble. Trees with 8 branches have slighter higher errors than trees with 32 branches. Both trees almost converge to the values of the full ensemble for high lead times, with a slightly better performance of the larger (32B) tree.
For MAE, CRPS and BS metrics it is visible that the lead time 100 h has critical importance. This lead time is when the uncertainties related to meteorological forecasts start to be more expressive in the basin and results start to differ more substantially, what is accused by the visible “split” between metrics results between different forecasting techniques (deterministic, full ensemble, or ensemble trees).
The metrics assessment results indicate two main conclusions. The first is that the ensemble forecasts have a better performance than the deterministic ones. This has been already reported in the broader analysis of Fan et al. (2015a) and recurs in the optimization results. Second, the generated scenario trees reveal a performance in between the deterministic forecast and the full ensemble. Usually, results are more similar to the ensemble at greater lead times when decision trees have more branches. At initial lead times, trees are more similar to the deterministic forecasts due to the smaller number of branches. This last fact is not a problem, because deterministic and probabilistic forecasts are usually close for smaller lead times; thus, the overall performance loss of the trees is small.
From the exclusive perspective of the tree metrics, the best option for the optimization is the use of a tree with 32 branches. However, a pre-assessment of the CPU time of the optimization shows an increase by a factor of 7 when increasing the number of branches from 8 to 32 in the multi-stage stochastic optimization. From this perspective, the metrics differences between these two trees are considered too small to justify the much longer processing time in an operational setup of the daily operation of the Três Marias HPP. Therefore, further analysis is based on the 8B tree only.
4.2 Optimization Results
Figure 7 shows the peak flow at the city of Pirapora for configurations 01-05. Lower values indicate a better performance. Thresholds are given by two horizontal lines at 2000 m3/s (start of small-scale inundation) and 3800 m3/s (start of large-scale inundation in the city). Results from optimizations using a perfect inflow forecast (“Perfect”) show that a forecast horizon of 3 days is not sufficient to avoid peak flows over 3800 m3/s. The peak flow decreases with a longer horizon and reaches the lower threshold of 2000 m3/s for a forecast horizon of 30 days. This indicates that it is all but impossible to avoid any flooding in a practical setting.
The “ForecastOBS” configuration uses perfect rainfall observations as forcing of the hyrological model. Once again, the performance increases with longer forecast horizons. However, the decrease in the peak flow is significantly less than the one in the “Perfect” configuration. This reflects the negative impact of the relatively sparse gauging network as well as the error introduced by the hydrological model.
The results obtained with the deterministic forecasts (ECMWF-fc) and the ensemble mean (ECMWF-pf mean) are very similar until forecast horizons of 10 days. Peak flows decrease with longer horizons, but stay above 3800 m3/s in all cases. For the horizon of 15 days, the remaining optimization with the ensemble mean (ECMWF-pf mean) shows a peak flow of 3500 m3/s and performs similarly to the ForecastOBS result. This shows the added value of the extra lead time of the ensemble mean (15 days) over the deterministic forecast (10 days).
The use of the 8B scenario tree in the multi-stage stochastic optimization significantly improve the performance at a horizon of 15 days by reducing the peak flow from 3500 m3/s (ECMWF-pf mean) to 2900 m3/s (ECMWF-pf). This clearly shows the benefit of the full tree in the stochastic setup versus the averaging of the ensemble and application of a deterministic optimization.
At Fig. 7 there are no values reported below the lower threshold. This happens because there is no motivation to have values below the lower threshold, once the objective of the optimization is to keep values discharges equal or below 2000m3/s., and values equals to 2000m3/s are the ones that guarantee the maximum flood protection without breaking the constrain.
Figure 8 shows the reservoir inflow and outflow as well as the obtained hydrographs at Pirapora for the optimization run using the stochastic optimization.
Figure 9 shows the total volume of water (hm3) above the lower inundation threshold of 2000 m3/s at the city of Pirapora during the entire simulated period. Lower values indicate a better performance with the optimum value of zero. For all configurations, a longer forecast horizon Greater observed values in this case indicate worse situations because the water level was higher and/or the flood lasted longer.
A general analysis of Fig. 9 indicates that for all studied circumstances increasing lead times in the optimization procedure results in decreasing volumes above 2000m3/s threshold. The lowest observed values were obtained for perfect inflows, culminating in zero values for horizons of 30 days and greater. The performance of the configurations of practical relevance decrease from 1450 hm3 for the deterministic ECMWF-fc run of 10 days to a value of 1250 hm3 for the run of 15 days with the ensemble mean and the deterministic optimization (ECMWF-pf mean) and to 650 hm3 for the stochastic optimization with the 8B tree (ECMWF-pf). The latter shows the same performance as the deterministic run with the perfect inflow forecast (Perfect).
Figure 10 summarizes the total energy production at the Três Marias HPP. It is provided as the percentage of the maximum energy generation that could have been generated at the HPP had the inflow for the entire 2-year test period been completely turbined. Therefore, higher values show a better performance.
The analysis of Fig. 10 indicates that the fluctuation in the total energy generated is relatively small among the different configurations and for different forecast horizons; it is between 78% and 80% for the forecast horizon of 15 days. Longer lead times do not necessarily lead to a higher energy production. This is due to the fact that the optimization becomes more flood-aware with longer horizons and probably deploys lower hydropower generation to achieve better flood mitigation. The cases of practical relevance are again the runs ECMWF-fc (10 days), ECMWF-pf mean (15 days) and ECMWF-pf (15 days). In all of these runs, the energy generation is between 79.5% and 80%, which can be considered as an almost identical performance. This means that the added value in the flood mitigation objectives does not jeopardize the generation efficiency.
5 Conclusions
In this study, deterministic and probabilistic forecasts force a short-term optimization model to operate the Três Marias HPP reservoir over a 2-years test period. Main focus is the assessment of the added value of probabilistic forecast, the novel mass-conservative scenario tree reduction technique and multi-stage-stochastic optimization in comparison to their deterministic counterparts.
Main conclusions are:
-
The skill of the scenario trees, measured by several performance metrics, tends to decrease with a decreasing number of branches, while the computational performance increases with a decreasing number of branches.
-
A larger lead time improves the skill of optimized reservoir operation in terms of flood protection. If forecasts were perfect, the required lead time to accomplish the best operation in terms of flood mitigation would be approximately 30 days.
-
In forcing the deterministic and probabilistic ECMWF forecasts into the deterministic optimization (by using the ensemble average), the main benefit is achieved by the longer lead time of the probabilistic forecast. Little benefit can be explained by the higher skill of the probabilistic forecast average.
-
The use of probabilistic forecasts in combination with the stochastic optimization (15 days lead time) outperforms the deterministic version (10 days lead time) significantly.
-
The range of the energy production rate between the different approaches is relatively small, between 78% and 80%. This means that the flood protection improvement of the probabilistic / stochastic approach is achieved without compromising the energy generation.
Since early 2016, the presented approach is being used in the operational flow forecasting and decision support system of CEMIG for the operation of six single reservoirs at different locations and climates. Future studies are intended to address the extension of this approach to reservoir systems, to analyze alternate scenario tree reduction techniques and to assess additional meteorological and hydrological models.
References
Anvari S, Mousavi SJ, Morid S (2014) Sampling/stochastic dynamic programming for optimal operation of multi-purpose reservoirs using artificial neural networks-based ensemble streamflow predictions. J Hydroinf 16(4):907–921. doi:10.2166/hydro.2013.236
Boucher M-A, Tremblay D, Delorme L, Perreault L, Anctil F (2012) Hydroeconomic assessment of hydrological forecasting systems. J Hydrol 416–417:133–144
Bougeault P, Toth Z, Bishop C, Brown B, Burridge D, Chen DH, Ebert B, Fuentes M, Hamill TM, Mylne K, Nicolau J, Paccagnella T, Park Y, Parsons D, Raoult B, Schuster D, Dias PS, Swinbank R, Takeuchi Y, Tennant W (2010) The THORPEX interactive grand global ensemble. Bull Am Meteorol Soc 91(8):1059–1072
Bradley AA, Schwartz SS (2011) Summary verification measures and their interpretation for ensemble forecasts. Mon Weather Rev 139(9):3075–3089
Brown JD, Demargne J, Seo D-J, Liu Y (2010) The ensemble verification system (EVS): a software tool for verifying ensemble forecasts of hydrometeorological and hydrologic variables at discrete locations. Environ Model Softw 25(7):854–872
Buizza R, Bidlot J-R, Wedi N, Fuentes M, Hamrud M, Holt G, Vitart F (2007) The new ECMWF VAREPS (Variable Resolution Ensemble Prediction System). Q. J. R. Meteorol Soc 133:681–695
Calvetti L, Pereira FAJ (2014) Ensemble hydrometeorological forecasts using WRF hourly QPF and TopModel for a middle watershed. Adv Meteorol 2014:1–12
Che D, Mays LW (2015) Development of an optimization/simulation model for real-time flood-control operation of river-reservoirs systems. Water Resour Manag 29(11):3987–4005. doi:10.1007/s11269-015-1041-8
Chou SC, Tanajura CA, Xue Y, Nobre CA (2002) Validation of the coupled ETA/SSiB model over South America. J Geophys Res 107(D20):80–88
Cloke HL, Pappenberger F (2009) Ensemble flood forecasting: a review. J Hydrol 375(3–4):613–626
Collischonn W, Allasia DG, Silva BC, Tucci CEM (2007) The MGB-IPH model for large scale rainfall-runoff modeling. Hydrol Sci J 52:878–895
Collischonn W, Meller A, Fan FM, Moreira DS, Silva DPL, Buarque DC, Bravo JM (2013) Short-term ensemble flood forecasting experiments in Brazil. Geophys Res Abstr 15:11910
EPE - Empresa de Pesquisa Energética (2014) Statistical Yearbook of Eletricity. http://www.epe.gov.br/. Accessed 12 Dec 2015
Demirel MC, Booij MJ, Hoekstra AY (2013) Effect of different uncertainty sources on the skill of 10 day ensemble low flow forecasts for two hydrological models. Water Resour Res 49:4035–4053. doi:10.1002/wrcr.20294
Faber BA, Stedinger JR (2001) Reservoir optimization using sampling SDP with ensemble streamflow prediction (ESP) forecasts. J Hydrol 249:113–133
Fan FM, Collischonn W, Meller A, Botelho LCM (2014) Ensemble streamflow forecasting experiments in a tropical basin: The São Francisco river case study. J Hydrol. doi:10.1016/j.jhydr
Fan FM, Schwanenberg D, Collischonn W, Weerts A (2015a) Verification of inflow into hydropower reservoirs using ensemble forecasts of the TIGGE database for large scale basins in Brazil. J Hydrol Reg Stud 4:196–227. doi:10.1016/j.ejrh.2015.05.012
Fan FM, Collischonn W, Quiroz KJ, Sorribas MV, Buarque DC, Siqueira VA (2015b) Flood forecasting on the Tocantins River using ensemble rainfall forecasts and real-time satellite rainfall estimates. J Flood Risk Manag. doi:10.1111/jfr3.12177
Fernández Bou AS, De Sá RV, Cataldi M (2015) Flood forecasting in the upper Uruguay river basin. Nat Hazards 79(2):1239–1256
Ficchì A, Raso L, Dorchies D, Pianosi F, Malaterre P, Van Overloop P, ay-Allemand M (2015) Optimal operation of the multireservoir system in the seine river basin using deterministic and ensemble forecasts. J Water Resour Plan Manag. doi:10.1061/(ASCE)WR.1943-5452
Guilhon LGF, Rocha VF, Moreira JC (2007) Comparison of forecasting methods for natural inflows in hydropower developments. Brazilian J Water Resour RBRH 12(3):13–20
Hamill TM, Bates GT, Whitaker JS, Murray DR, Fiorino M, Galarneau TJJ, Zhu Y, Lapenta Y (2013) NOAA's second-generation global medium-range ensemble reforecast data set. Bull Am Meteorol Soc 94:1553–1565. doi:10.1175/BAMS-D-12-00014.1
Hamlet AF, Huppert D, Lettenmaier DP (2002) Economic value of longlead streamflow forecasts for Columbia river hydropower. J Water Resour Plan Manag 128(2):91–101
Heitsch H, Rőmisch W (2003) Scenario reduction algorithms in stochastic programming. Comput Optim Appl 24:187–206
Jolliffe IT, Stephenson DB (2012). Forecast Verification: A Practitioner’s Guide in Atmospheric Science, second ed
Liu Z, Guo Y, Wang L, Wang Q (2015) Streamflow forecast errors and their impacts on forecast-based reservoir flood control. Water Resour Manag 29(12):4557–4572
Maceira MEP, Damázio JM (2005) Periodic auto-regressive streamflow models applied to operation planning for the Brazilian hydroelectric system. Regional Hydrological Impacts of Climatic Change – Impact Assessment and Decision Making. IAHS Publ. 295
Maurer EP (2002) Predictability of runoff in the Mississipi River basin, Water Resour. Ser. Tech. Rep. 172, Univ. of Wash., Seattle
Meller A (2013) Short-range ensemble flood forecasting. Phd Thesis. (In portuguese) Instituto de Pesquisas Hidráulicas. Universidade Federal do Rio Grande do Sul – Brazil
Paz AR, Collischonn W, Tucci CEM, Clarke RT, Allasia DG (2007) Data assimilation in a large-scale distributed hydrological model for medium-range flow forecasts. Proceedings of Symposium HS2004 at IUGG2007. IAHS Press, Wallingford, pp 471–478
Pereira M, Pinto L (1991) Multi-stage stochastic optimization applied to energy planning. Math Program 52(1–3):359–375
Raso L, Van De Giesen N, Stive P, Schwanenberg D, Van Overloop PJ (2013) Tree structure generation from ensemble forecasts for real time control. Hydrol Process 27:75–82
Schwanenberg D, Fan FM, Naumann S, Kuwajima JI, Montero RA, Assis Dos Reis A (2015a) Short-term reservoir optimization for flood mitigation under meteorological and hydrological forecast uncertainty. Water Resour Manag. doi:10.1007/s11269-014-0899-1
Schwanenberg D, Becker BPJ, Xu M (2015b) The open RTC-tools software framework for modeling real-time control in water resources systems. J Hydroinf 17(1):130–148. doi:10.2166/hydro.2014.046
Tucci CEM, Dias PLS, Clarke RT, Sampaio GO, Collischonn W (2003) Long-term flow forecasts based on climate and hydrologic modeling: Uruguay river basin. Water Resour Res 39(7):31–311. doi:10.1029/2003WR002074
Tucci CEM, Collischonn W, Clarke RT, Paz AR, Allasia D (2008) Short- and long-term flow forecasting in the Rio Grande watershed (Brazil). Atmos Sci Lett 9:53–56
Werner M, Schellekens J, Gijsbers P, Van Dijk M, Van Den Akker O, Heynert K (2013) The Delft-FEWS flow forecasting system. Environ Model Softw 40:65–77. doi:10.1016/j.envsoft.2012.07.010
Wilks D (2006) Statistical methods in the atmospheric sciences. Academic, Cambridge
Yeh WW-G BECKERL, ZETTLEMAOYER R (1982) Worth of inflow forecast for reservoir operation. J Water Resour Plann Manag 108(WR3):257–269
Zhao TTG, Cai XM, Yang DW (2011) Effect of streamflow forecast uncertainty on real-time reservoir operation. Adv Water Resour 34:495–504. doi:10.1016/j.advwatres.2011.01.004
Zhao T, Yang D, Cai X, Zhao J, Wang H (2012) Identifying effective forecast horizon for real-time reservoir operation under a limited inflow forecast. Water Resour Res. doi:10.1029/2011WR010623
Acknowledgments
The first author would like to acknowledge the Brazilian funding agency CAPES for the scholarship received during the work development period. Also, authors would like to thank Sheila Ball from Deltares, the Netherlands, for English language review.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Fan, F.M., Schwanenberg, D., Alvarado, R. et al. Performance of Deterministic and Probabilistic Hydrological Forecasts for the Short-Term Optimization of a Tropical Hydropower Reservoir. Water Resour Manage 30, 3609–3625 (2016). https://doi.org/10.1007/s11269-016-1377-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11269-016-1377-8