Enhancing Knowledge in Water Distribution Networks via Data Assimilation

Abstract

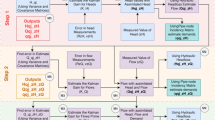
This paper deals with uncertainty estimation and knowledge enhancement in water distribution networks (WDNs). A new three steps data assimilation approach is introduced, which in combination with multi-objective optimization, allows selecting effective and affordable monitoring networks. An innovative cascade of Ensemble Kalman Filters is used to assimilate the information deriving from sensors measuring pressure heads, flow in pipes and demands, with the objective of increasing knowledge while preserving at the same time the structural relationships among state variables. Selection of the most appropriate and economically affordable measurement network, is then based on the derivation of a Pareto front using the NSGA-II algorithm in conjunction with the data assimilation approach. The front is obtained by compromising between the overall sensors cost and the uncertainty reduction (or knowledge enhancement), which is expressed as a function of the Total Variance of state variables. The operational use of the proposed data assimilation approach as well as the effectiveness of the chosen observation network is also demonstrated by showing the reduction of uncertainty deriving from successive assimilations of real-time observations.

Appendix

H :

nodal pressure heads vector

H ₀ :

known nodal pressure heads vector

Q :

pipe flows vector

q :

nodal demands vector

q _j :

nodal demands ensemble based on prior assumptions

${\mathbf{H}}_{\left|{\mathbf{q}}_j\right.},{\mathbf{Q}}_{\left|{\mathbf{q}}_j\right.}$ :

the value of state vectors H and Q given q _j

${\mathbf{H}}_{\left|{\mathbf{q}}_j,{\mathbf{z}}_H\right.},{\mathbf{Q}}_{\left|{\mathbf{q}}_j,{\mathbf{z}}_H\right.},{\mathbf{q}}_{\left|{\mathbf{q}}_j,{\mathbf{z}}_H\right.}$ :

the value of state vectors H, Q and q given q _j and measures z _H

${\mathbf{H}}_{\left|{\mathbf{q}}_j,{\mathbf{z}}_H,{\mathbf{z}}_Q\right.},{\mathbf{Q}}_{\left|{\mathbf{q}}_j,{\mathbf{z}}_H,{\mathbf{z}}_Q\right.},{\mathbf{q}}_{\left|{\mathbf{q}}_j,{\mathbf{z}}_H,{\mathbf{z}}_Q\right.}$ :

the value of state vectors H, Q and q given q _j and measures z _H and z _Q

${\mathbf{H}}_{\left|{\mathbf{q}}_j,{\mathbf{z}}_H,{\mathbf{z}}_Q,{\mathbf{z}}_q\right.},{\mathbf{Q}}_{\left|{\mathbf{q}}_j,{\mathbf{z}}_H,{\mathbf{z}}_Q,{\mathbf{z}}_q\right.},{\mathbf{q}}_{\left|{\mathbf{q}}_j,{\mathbf{z}}_H,{\mathbf{z}}_Q,{\mathbf{z}}_q\right.}$ :

the value of state vectors H, Q and q given q _j and measures z _H , z _Q and z _q

A ₁₁ :

diagonal matrix defined as in Todini and Pilati (1988)

A ₁₂, A ₂₁, A ₁₀ :

(0,1) topological incidence matrices defined as in Todini and Pilati (1988)

${\boldsymbol{\upmu}}_H,{\boldsymbol{\upmu}}_Q,{\boldsymbol{\upmu}}_Q^{\hbox{'}}$ :

vectors of means of ${\mathbf{H}}_{\left|{\mathbf{q}}_j\right.},{\mathbf{Q}}_{\left|{\mathbf{q}}_j,{\mathbf{z}}_H\right.},{\mathbf{Q}}_{\left|{\mathbf{q}}_j,{\mathbf{z}}_H,{\mathbf{z}}_Q\right.}$ estimation errors

${\mathbf{P}}_H,{\mathbf{P}}_Q,{\mathbf{P}}_Q^{\hbox{'}}$ :

variance-covariance matrices of ${\mathbf{H}}_{\left|{\mathbf{q}}_j\right.},{\mathbf{Q}}_{\left|{\mathbf{q}}_j,{\mathbf{z}}_H\right.},{\mathbf{Q}}_{\left|{\mathbf{q}}_j,{\mathbf{z}}_H,{\mathbf{z}}_Q\right.}$ estimation errors

${\mathbf{K}}_H,{\mathbf{K}}_Q,{\mathbf{K}}_Q^{\hbox{'}}$ :

Kalman Gain matrices for state vectors ${\mathbf{H}}_{\left|{\mathbf{q}}_j\right.},{\mathbf{Q}}_{\left|{\mathbf{q}}_j,{\mathbf{z}}_H\right.},{\mathbf{Q}}_{\left|{\mathbf{q}}_j,{\mathbf{z}}_H,{\mathbf{z}}_Q\right.}$

z _H  , z _Q  , z _q :

vectors of measures relevant to state vectors H, Q and q

M _H  , M _Q  , M _q  :

(0,1) topological matrices relating z _H to H, z _Q to Q and z _q to q

${\overset{-}{\mathbf{v}}}_{{\mathbf{z}}_H},{\overset{-}{\mathbf{v}}}_{{\mathbf{z}}_Q},{\overset{-}{\mathbf{v}}}_{{\mathbf{z}}_q}$ :

vectors of mean of measurement errors for state vectors H, Q and q

${\mathbf{R}}_{{\mathbf{z}}_H},{\mathbf{R}}_{{\mathbf{z}}_Q},{\mathbf{R}}_{{\mathbf{z}}_q}$ :

variance-covariance matrices of measurement errors for state vectors H, Q and q