Abstract
This study presents the state-of-the-art understanding of the data-scarce and hydrogeologically complex groundwater system of Lake Naivasha, Kenya, with the particular aim of exploring the influence groundwater abstractions have on Lake Naivasha’s water level. We developed multiple alternative but plausible parameterizations for a MODFLOW groundwater model, based on literature, existing models and available data, while trying not to over-complicate the model. In doing so, we illustrate a possible strategy of going about data-scarce regions in modelling in general. Processes encountered in the calibrated parameterizations show groundwater flows laterally from the escarpments to the valley floor and axially from the lake along the Rift, with a larger portion flowing out southward than northward. Extraction of groundwater interrupts the flow from the northwestern highlands to the lake, leading to a lake stage reduction of 0.7–7.5 cm due to abstractions at our target farm (Flower Business Park) or an implied 7–75 cm due to total groundwater abstractions in the area. Although this study demonstrates our understanding of Naivasha’s groundwater system remains fragile and the current model cannot be embedded in operational water management yet, it (i) reflects the contemporary understanding of the local groundwater system, (ii) illustrates how to go about modelling in data-scarce environments and (iii) provides a means to assess focal areas for future data collection and model improvements.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
When in a certain place at a certain time water demand exceeds water availability, water scarcity lures. Especially in arid and semi-arid basins in developing countries, climate change, population growth and economic development add to water scarcity risks (Millenium Ecosystem Assessment 2005). Water resources managers aiming to streamline supply and demand often rely on numerical models as useful water management tools (Johnston and Smakhtin 2014).
However, complex and highly non-linear processes and data scarcity may challenge hydro(geo)logical modelling (Rödiger et al. 2014). Concerted data collection efforts usually lack in developing countries, especially when it comes to groundwater systems. Recent groundwater modelling studies with a focus on semi-arid basins encountered difficulties in estimating recharge (Candela et al. 2013; Rödiger et al. 2014), abstractions (Le Page et al. 2012) and the effect of faults and fractures on hydrogeologically complex flow systems (Bense et al. 2013) or in defining a plausible, appropriate conceptual model of the aquifer system at hand (Ayenew and Tilahun 2008).
In an effort to do justice to stratigraphic heterogeneity, modelers tend to go beyond what available data endorses in conceptualizing the system at hand (e.g., Owor (2000), Yihdego and Becht (2013)). Subsequently applied mainstream methods of dealing with model uncertainty – such as Monte Carlo analyses or functional zoning (Li et al. 2015; Zekri et al. 2015) – may prove too sophisticated for data limited environments. Other options in modelling groundwater that are adaptable to data-scarcity need to be investigated too (Candela et al. 2013).
Lake Naivasha Basin is such a data-scarce region in Kenya’s semi-arid Rift Valley. Frugal understanding of the (ground)water system forms a major inhibiting factor for effective water management, even though previous, often quite detailed modelling efforts have been made (Becht et al. 2005; van Oel et al. 2013). Water authorities and modelers alike suffer from the fact that data on virtually all groundwater system variables is either absent, scarce, of mediocre or debatable quality and internally inconsistent (WRMA 2010). Water management based on such models may have unintended or even detrimental consequences.
This study’s aim is twofold. First, we aim to present our state-of-the-art understanding of Naivasha’s groundwater system and determine the influence groundwater abstractions have on Lake Naivasha’s water level, by developing a model based on literature, existing models and data that are available. Second, through our methodology we aim to illustrate a possible strategy of going about modelling data-scarce regions. This study therefore contributes to contemporary discussions (as raised by e.g., Johnston and Smakhtin (2014) and Candela et al. (2013)) concerning dealing with and reporting about data-scarce modelling efforts in water management.
2 Groundwater System of Lake Naivasha Area
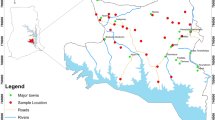
Lake Naivasha Basin in Kenya’s Rift Valley is an endorheic catchment with a central lake carrying the same name (Fig. 1). The area’s ecological functions are recognized by its designation as a Ramsar site (Ramsar 2012). Around the lake a prominent and thriving horticulture industry emerged over the last decades, which to date claims a significant share in Kenya’s GDP and employs around 30 000 people (WWF 2011). The flower farms depend on surface and – more and more – on groundwater for meeting their irrigation requirements, with largely unknown effects on the water system (van Oel et al. 2013).
The water system of Lake Naivasha has been subject of study for over a century, mainly because the lake is fresh but has no surface outlet to remove salts and chemicals. Hence, consensus seems to have emerged on the existence of a subsurface outlet from the lake to groundwater (Beadle (1932); Nilsson (1932); Sikes (1936); Thompson and Dodson (1963); Gaudet and Melack (1981); Åse et al. 1986; Darling et al. (1990); Clarke et al. (1990); Ojiambo et al. (2001); Becht and Nyaoro (2006)). Water balance terms, directions and magnitudes of flow of groundwater, however, are ambiguous. A synthesis of water balance studies by McCann (1974), Clarke et al. (1990) and Becht et al. (2006) suggests water is flowing out of Lake Naivasha vertically into deep geothermal layers and horizontally through shallower layers.
The lake is located on the culmination of the Rift’s valley floor – an up-warping of the earth’s crust where the African tectonic plate divides (Baker and Wohlenberg 1971). The floor consists of extensively faulted tuffs, welded tuffs and ignimbrites, assembling a complex stratigraphy of volcanic and fluvio-lacustrine deposits (Thompson and Dodson 1963). An intensive faulting zone with near vertical attitude can be found in the center of the valley (step-faulting), which parallels the escarpments (Richardson and Richardson 1972). Faults and fractures created numerous small groundwater compartments and may form either barriers or conduits to flow (Thompson and Dodson 1963). Further complicating hydrostratigraphy are possible interconnections between surface and groundwater bodies and geothermal activity. Given the fact that conclusive data are scarce, it is no surprise undisputed aquifer mapping is absent.
Recent extensive groundwater abstractions are believed to affect the natural flow system as well. The large-scale abstractions by the area’s horticultural industry are reflected by lake and groundwater level decline and water quality deterioration (Becht et al. 2005). A Water Abstraction Survey issued by the local Water Resource Management Authority (WRMA) showed groundwater abstractions around the lake amount to approximately 40 Mm3/yr, equivalent to ~20 % of annual river inflow into the lake (De Jong 2011). Consequently, along the transect from the lake to the northwest, according to some authors (e.g., Becht and Nyaoro (2006)) the cone of depression caused a flow direction reversal – from a southwesterly flow feeding the lake, to a northwesterly flow from the lake now feeding the aquifer upon abstractions (Fig. 2).
2.1 Groundwater Models for Lake Naivasha Area
The first attempt to numerically model Naivasha’s water system to acquire insight into its behavior was by Becht and Harper (2002). Their cascade water balance model has been updated and improved by van Oel et al. (2013). Using precipitation and evapotranspiration as stressors to the lake, water is dynamically routed from the lake cascade to a groundwater cascade or vice versa, based on their respective heads and one conductance parameter separating the two cascades. The model functions well to illustrate the different effects of abstractions taken from either surface or groundwater.
More sophisticated spatially explicit regional groundwater models have been developed by Owor (2000), Legese Reta (2011) and Yihdego and Becht (2013). These models adopt a multi-layered system, where an unconfined permeable sedimentary aquifer overlies one or more confined volcanic aquifers that are less permeable. Sparsely available data (see below), however, cannot endorse the conceptualizations made in these mdoels. Moreover, none of the models is validated for performance. Finally, after submitting them to a thorough assessment, the Legese Reta (2011) and Yihdego and Becht (2013) models proved to contain structural errors and omissions that render them defective for future application (for more details on this quality assessment, see Hogeboom (2013)). For all three models it was concluded that they to a large extent fail to account for data ambiguity and that model results are speculative. Such modelling could be seen as a best attempt and may even prove right. Given the minimal database, however, the models currently give the impression the system is much better understood that it actually is.
3 Methods and Data
Amongst the horticulture farms that have mushroomed in the direct vicinity of the lake during the last decennia is the Flower Business Park (FBP) (Becht and Nyaoro 2006). Abstractions drawn at the FBP which is located some 7 km northwest of the lake (Fig. 1), are taken as a test case for exploring the effect of these abstractions on lake levels. FBP is one of the largest farms, accounting for approximately 10 % of total groundwater abstractions, while providing the only reliable abstraction data by commercial farms available (De Jong 2011; FBP 2013).
3.1 Conceptual Model on Historical Data
An extensive analysis of available data and literature has been carried out. Primary data sources for stratigraphy, piezometer recordings and hydrogeologic parameters are handwritten borehole completion records dating back to colonial times. Additional sources include geodetic surveys and field work reports by visiting students and small scale monitoring output by the local water authorities (WRMA). If available, data was usually of low quality: wells are known to have penetrated multiple water-bearing layers, thereby aggregating pressures; geographic coordinates can be off by several hundreds of meters on the surface and tens of meters in elevation; time series, revealing seasonal or annual variations, are generally absent altogether; fragmented database management introduces additional, unknown uncertainties; recharge is poorly understood.
A synthesis of available borelogs endorses the complexity of the area’s hydrogeology and shows a highly heterogeneous subsurface composition, consisting of both volcanic and sedimentary deposits. While isotope studies may provide some clarity on such a complex hydrostratigraphic system (Bretzler et al. 2011), no conclusive data could be retrieved. We conclude the limited data for now only support a coarse conceptual model. Hence, a one layer system is postulated under confined conditions with a thickness of 100 m throughout the study area. This layer is composed of an aggregation of undifferentiated sedimentary and volcanic deposits. The thickness and condition is determined on a general conception of the available borelogs.
Boundary conditions are set based on the Geological Map (GKMEGS 1988) and historical groundwater contours, which have been interpolated from 76 retrieved head recordings taken between 1939 and 1980, i.e., roughly the period before larger scale development commenced. These 76 records are highly error-prone due a number of reasons, e.g., feet-to-meter conversion errors, uncertain exact location and elevation of boreholes and errors in the digitizing process of handwritten records. Boundaries conditions are therefore inconclusive as well and should be treated as best estimates.
The Mau escarpment to the east and the Kinangop divide to the west are assumed no flow boundaries, as is the Eburru volcanic complex north of the lake (Fig. 1). The base of the valley floor underlying the aquifer is taken as a physical no-flow boundary based on the assumption that below 250 m conductivity approaches zero by Clarke et al. (1990) and for lack of a better alternative. To the north, a specified head boundary at 1850 masl is assumed at the latitude of Gilgel town based on head recordings. Here, water is assumed to leave the Naivasha study area to re-emerge in Lake Elmenteita up north. Water with Lake Naivasha’s isotopic signature has been detected in springs and seeps south of Lake Elmenteita (Darling et al. 1990; Becht et al. 2006). Likewise to the south, a specified head boundary at 1800 masl is assumed along Hells Gate. Darling et al. (1996) suggest considerable southerly outflow through this section in their analysis of stable isotope composition of fumaroles in the southerly area. Given these boundaries, the modelled area encompasses approximately 1400 km2 (see Fig. 3).
The modelled area. Constant head boundaries (CHB) form boundary conditions along northern and southern transects. All other borders are no-flow boundaries. Colors indicate surface elevation. Grid cell size increases from 100 m squared at FBP to 500 m squared toward fringes. The cross-section is taken along the red line
The water balance of the groundwater system is poorly understood. The more prominently researched lake balance therefore serves as a partial basis to determine groundwater budget terms. Table 1 provides a literature overview of the lake water balance. Outflow from the lake is taken as input to the groundwater in Table 2 (lake seepage). The overview does not account for the effects of faults, which may route water to deep geothermal layers, nor evapotranspiration of groundwater in shallower regions. Although both terms are likely to have their share in the water balance, it is judged that the associated uncertainty does not justify the added complexity.
3.2 Numerical Model
The conceptual model is translated into a numerical MODFLOW 2005 model (Harbaugh 2006). The effect of FBP groundwater abstractions on water balances, flow patterns and lake levels is explored with reference to the historical, pre-development situation, i.e., prior to roughly 1980. Lack of time series of heads inhibited development of a transient model.
Based on a digitized version of the simplified surface geological map (GKMEGS 1988), and following a study by Legese Reta (2011), 26 zones of hydraulic conductivity have been identified. The calibrated horizontal hydraulic conductivity values by Legese Reta are taken as starting values for this model. Horizontal conductivity is assumed isotropic. As a rule of thumb, vertical conductivity is taken as 10 % of horizontal conductivity (Freeze and Cherry 1979).
Contrary to a recent suggestion by Yihdego and Becht (2013), recharge is virtually unknown. In order to obtain a first estimate, recharge has been estimated using the simple water balance method proposed by Simmers et al. (1997). Five sub-regions are delineated based on surface altitude, for each of which monthly average potential evapotranspiration is subtracted from monthly precipitation data from Meins (2013). Average annual precipitation ranges from 650 mm around Lake Naivasha to 1250–1500 mm in the Mau and Aberdare escarpments, while potential evapotranspiration ranges from 1500 mm in the scarps to 1900 mm around the lake. This led to recharge estimates of 86 mm from Kinangop Plateau till the Aberdares, 112 mm in Mau, 121 mm around Eburru, none around the lake and 40 mm between the lake and Mau. Zones roughly follow elevation contours (Fig. 1).
Lake Naivasha Basin is drained by the ephemeral Karati and perennial Malewa and Gilgil rivers, all of which discharge into Lake Naivasha. While Karati’s contribution is negligible and hence left out, Malewa and Gilgil Rivers are schematized in the River Package. Discharges for Malewa and Gilgil Rivers are 4.9, and 0.8 m3/s, respectively (Everard et al. 2002). Riverbed conductance is set to 0.3 m/d, based on fieldwork by Kibona (2000).
Lake Naivasha’s water levels show significant temporal variability. Over the past millennium, the lake has known periods of significantly higher water levels than at present, but it has gone dry as well (Verschuren et al. 2000). The main lake’s depth averages 4–6 m in present times (MOWD 1982). The lake is schematized with the Lake Package. The initial stage of the lake is set to the average lake level during the period 1939–1980, i.e., 1887.0 masl (MOWD 1982). The water balance assigned to the Lake Package is based on the middle of the range Table 1 and the area of the lake at 1887 masl levels (i.e., 116 km2). Runoff includes river and overland fluxes into the lake. A digital elevation model, integrated with a bathymetry map and calibrated against field geodetic measurements is taken from Legese Reta (2011).
Following model calibration for natural conditions, abstractions were included. Abstraction rates were set through the Well Package. The gross rate at FBP is set to 3.5 Mm3/yr, which is the average rate over the period 2008–2012 (FBP 2013). Following measurements by Mpusia (2006), the net consumption in FBP greenhouses is 2.5 Mm3/yr. The difference – i.e., the return flow – is assumed to become surface runoff and is accounted for by adding the amount (which equals 1 Mm3/yr) to lake inflow.
The aforementioned contour map based on 76 interpolated pre-development head observations has been taken to provide initial heads. Convergence was achieved and considered successful as soon as a head change between subsequent iterations became less than 0.01 m.
3.3 Calibration and Validation
The uncertainty in and scarcity of data qualifies multiple model parameters for estimation during calibration. To both underscore the indeterminacy of the underlying database concerning system variables and to illustrate ways of going about data-limited modelling, we hypothesize that the large number of degrees of freedom in the model will allow for multiple, non-unique parameter sets to emerge from calibration. The hypothesis was tested by assuming – a priori – two distinct values for the lakebed leakance parameter. This parameter largely governs lake-aquifer interaction – and thus also the effect abstractions have on lake levels – but lacks even prudent estimation. Hence, in one model scenario bed leakance is set 0.215 d-1, which represents a rather leaky lakebed of 1 m thick composed of sandy/silty material and which coincides with the calibrated outcome of the Owor (2000) model. A counterbalancing scenario was defined with a bed leakance of 0.01 d-1 to represent a rather sealed lakebed consisting of clayey material. Given these lakebed leakance values, the model is calibrated by adapting hydraulic conductivity of 26 aforementioned zones so that simulated heads match observed heads in the natural situation (i.e., 1939–1980). The low number of observations in fringe – i.e., mountain – zones led us to focus on 13 mainly interior zones, where also the FBP is located. This implies conductivities found for the remaining (13) fringe zones are somewhat arbitrary and should be treated with caution.
Automated calibration is performed in UCODE_2005 through USGS’s ModelMate (Banta 2011). It uses the powerful Gauss-Newton inverse modelling algorithm to adjust the value of user selected input parameters in an iterative procedure. The objective function minimizes the squared differences between observed and simulated heads. Manual adjustments of automated calibration output had to ensure lake balance closure and physically sound output. Observations located in the fixed zones (16 observations in total) have been excluded from the residual calculation in order to focus on the effects in the area of interest. This left 60 observations recorded prior to 1980 to contribute to the residual analysis.
The calibrated steady state models could only be validated to a limited extent. The physically measured groundwater levels that accompany the FBP abstraction rate, however, provide a means of verification: if the same rate is abstracted in the model, the resulting drawdown should be comparable to the measured drawdown. More qualitative validation is sought in identifying similar system behavior that occurs in both parameterizations. Judgement of whether the fit between model and reality is good enough is a subjective one and any verification effort should be considered only a partial one (Małloszewski and Zuber 1992).
4 Results
4.1 Calibration
The resulting hydraulic conductivity values for the high and low bed leakance parameterizations are shown in Fig. 4. In general, conductivity is low in the escarpments and increases towards the valley floor. For both bed leakance parameterizations, valley floor sediments show hydraulic characteristics equivalent to well sorted sand and gravel or highly fractured rocks (Freeze and Cherry 1979). Table 3 shows Root Mean Squared error (RMS) and Mean Absolute Error (MAE) metrics for the calibrated residuals. Eight of 60 observations were by far the most deviant in both calibration sets, with – irreconcilable – residuals over 20 m. Since no reason was found to remove them from the dataset altogether – other than a general error-proneness of each recorded head – RMS and MAE are calculated including (60 observations) and excluding (52 observations) them. Both calibrated parameterizations seem equally plausible.
4.2 Flow Patterns and Water Balances Under Natural Conditions
The calibrated steady state groundwater model is run for both bed leakance values. Simulated groundwater contour maps for pre-development times of both parameterizations indicate groundwater flows laterally from the escarpments to the valley floor with relatively steep gradients and axially from Lake Naivasha to the north and south with a smaller drop (Fig. 5a, b). Outflow from the lake occurs to the north and south, while inflow takes place in the east and west. The high bed leakance model shows smaller gradients towards the north than its low bed leakance equivalent.
Model results. Groundwater contours [m asl] for the natural situation in a high and b low bed leakance model; groundwater contours if abstraction takes place at FBP in the c high and d low bed leakance model (note the cone of depression at FBP) and; water particles pumped at FBP traced back to their point of origin in the e high bed leakance model (sharp edges in some paths are due to high hydraulic conductivity contrast between adjacent zones) and f low bed leakance model
Considering the groundwater budget, outflow from the groundwater system is on the high end of the estimated spectrum in literature (Table 2). The percentages of northerly and southerly outflow are 33 % and 67 % for the high leakance model, respectively, and 21 % and 79 % for the low leakance model.
Considering the lake water balance, it can be seen that although net outflow is similar as postulated in literature, there is inflow from groundwater into the lake as well (Table 1).
Groundwater levels at FBP are above the lake stage in both instances. Depths to groundwater are 17 and 13 m for the high and low leakance model, respectively. Head recordings in the close vicinity and the presence of an old hand-dug well at FBP confirm the feasibility of such simulated depths.
4.3 Flow Patterns and Water Balances Under Abstractions at FBP
To assess the effect of groundwater abstractions on lake levels, the model is run including abstractions at FBP and results are compared to the reference run of the natural situation. Simulated groundwater contour maps in case of abstractions in both parameterizations show flow patterns similar to the natural situation in most parts of the study area, except around FBP (Fig. 5c, d). The cone of depression generated by the abstractions here is clearly seen. The high leakance model shows a slightly larger spatial extent than its low counterpart, which in turn is modestly distorted westward.
Considering the groundwater budget, the amounts flowing out of the modelled region to the north and south – and by implication their split – do not significantly differ from the natural situation, for both leakance models (Table 2). In the lake budget, differences do occur (Table 1): less water is flowing from groundwater into the lake upon pumping at FBP (from 11.3 to 10.8 and from 8.6 to 7.3 Mm3/yr in the high and low bed leakance model, respectively). These differences in budget terms result in a lake stage reduction. In the high bed leakance model the new equilibrium lake levels are 0.7 cm lower and in the low leakance model 7.5 cm.
Groundwater levels at FBP are below the lake stage in both instances. Depths to groundwater are 56 and 52 m for the high and low leakance model, respectively. These values compare well with the measured depths – i.e., approximately 58 m (FBP 2013) – and increase confidence in the model.
In order to assess the place of origin of the water pumped at FBP and each source’s relative contribution, particles are traced back to their points of origin (Fig. 5e, f). The high bed leakance model showed 96 % of FBP water originates from the Kinangop highland area to the west and 4 % from Malewa River; the low leakance equivalent draws all water from Kinangop. The fraction ascribed to the Malewa is to a great extent governed by the conductance assigned to the river bed sediments. Since this value is highly uncertain, the fraction of water pumped at FBP may very well be higher or lower.
5 Discussion
5.1 Data and Modelling Method
Wherever data is scarce, the tendency is to either not model altogether, or to develop an overly sophisticated model. In the former case, abstractions will continue despite proper understanding of the implications remaining absent. In the latter case, claims can be made that are unsubstantiated by data or that neglect data ambiguity – with all unintended or detrimental consequences for management it may have. We tried to illustrate how in data-scarce regions one can balance these tendencies, by defining multiple, distinct yet plausible conceptualizations of the groundwater system in parallel.
That being said, one of the drawbacks of the current methodology is that error-prone data points can still significantly influence the perception of the system. For instance, regarding the boundary condition that governs whether or not outflow can occur underneath the Eburru volcanic complex. The geological map (GKMEGS 1988) does not indicate such a possibility, but the younger geological age of the complex than early lake sediments would make such a view conceivable (Thompson and Dodson 1963).
Limited data availability also impeded the development of a multi-layer model – which would do more justice to the known complexity of the groundwater system. An important intention, however, of opting for a single layer model was to prevent speculation on unknown system characteristics. Such sophisticated characteristics can by no modelling effort be retrieved save further data is gathered.
5.2 Discussion of Results
Calibrated conductivities and resulting water balances are deemed plausible for both parameterizations, thereby illustrating the aforementioned indistinctiveness of our understanding. Conductivity of the zone underlying the lake assumes a rather high value of 615 m/d in the high leakance model – equivalent to well sorted sand and gravel or highly fractured rocks. A suggestion why this value is found is that the aggregated aquifer incorporates the effects of non-modelled hydraulically active faults and fractures, which ease flow in especially a north–south direction. Both the geological features and this orientation are known to prevail in the area (GKMEGS 1988).
The model portrays an average miss of heads of 5 – 7 m. Although this seems significant, lake levels have fluctuated more than 6 m over the time span of the dataset, i.e., 1939–1980. Observations are hence subject to significant natural variability. Furthermore, adjacent head recordings sometimes differed substantially, dwindling calibration. Finally, uncertainty of exact borehole location, altitude or aggregate pressure heads in this mountainous region have led to measurement errors in the order of tens of meters (see section 2.1)
Both parameterizations of the schematization of the area endorse the view held in literature (Clarke et al. 1990; Becht et al. 2006) of groundwater flowing laterally from the escarpments to the valley floor at large gradients and axially along the valley floor to the north and south at a shallower drop, as well of the percentages of flow – 21–33 % to the north and 67–79 % to the south. The fact that total modelled (i.e., shallow) outflow is on the high end of its reported range may indicate shallow outflow is somewhat overestimated to the detriment of deeper outflow neglected by the model.
Becht and Nyaoro (2006) postulate that upon abstractions the southwesterly flow toward the lake is reversed (Fig. 2). This view is supposedly based on the assumption that the cone of depression generated by (FBP) pumping reaches to the lake, thereby drawing water from it. Although this still may be the case in reality, where all abstractions are contributing to flow patterns instead of just FBP’s, it is contradicted by both parameterizations of the model (Fig. 5e, f). The model suggests longitudinal flow from Kinangop – originating from recharge – toward and about to feed the lake is prematurely abstracted in favor of FBP’s horticulture.
Concerning the difference between lake level reductions in the two parameterizations – 0.7 cm (leaky lakebed) and 7.5 cm (sealed lakebed) – it appears that the balance between in- and outflow terms in equilibrium is less sensitive to disturbances such as pumping in the former than in the latter parameterization. In the leaky lake model, the better conducting aquifer underlying the lake may level out disturbances over a large area, thereby mitigating the effect of disturbances on the new equilibrium stage. Due to the steeper gradients encountered in the proximity of the lake in the low leakance model, a similar disturbance has a more profound impact here. Another part of the explanation is the ineluctable closure error (Table 1) of the lake balance in the high bed leakance parameterization.
The water balance model developed by van Oel et al. (2013) showed lake levels are lowered by about 1 m due to all known groundwater abstractions. Since FBP accounts for 10 % of total groundwater abstractions (De Jong 2011), a linear extrapolation implies a comparable estimated 7–75 cm lowering of lake levels by this study. Further research however is needed to more accurately assess the effect total combined abstractions have on lake levels.
6 Conclusions
This study first set out to present the state-of-the-art understanding of the groundwater system of Lake Naivasha, in order to explore the influence of groundwater abstractions on Lake Naivasha’s water level.
Results of multiple model parameterizations led to a better understanding when compared to simpler water balance models, while at the same time preventing unsubstantiated claims about system behavior as is the case in more complex models of previous studies.
Simulations show that under natural conditions groundwater flows laterally from the escarpments to the valley floor with relatively steep gradients and axially from Lake Naivasha to the north and south with a smaller drop. Outflow from the lake occurs to the north (one-third) and south (two-thirds), while inflow takes place in the east and west, showing that the lake is not merely draining water to groundwater (longitudinally), but also receives significant inflow from (lateral) recharge.
In the natural situation, water stemming from recharge at Kinangop flows towards the lake and feeds it. Extraction of groundwater interrupts and reduces this flow, resulting in a lake level lowering of 0.7–0.75 cm due to pumping at FBP or 7–75 cm due to total groundwater abstractions in the area. This view is contrary to a previous understanding of the flow system (Becht and Nyaoro 2006).
In order to prevent overly sophisticated modelling while at the same time building upon available data and literature, our strategy involved defining multiple, distinct yet plausible conceptualizations of the groundwater system in parallel. This approach to developing a spatially-explicit groundwater model illustrates how one can go about data limited modelling.
Although this study demonstrates our understanding of Naivasha’s groundwater system remains fragile and the current model cannot be embedded in operational water management yet, it (i) reflects the contemporary understanding of the local groundwater system, (ii) illustrates how to go about modelling in data-scarce environments and (iii) provides a means to assess focal areas for future data collection and model improvements.
References
Åse LE, Sernbo K, Syren P (1986) Studies of Lake Naivasha, Kenya and its drainage area. Forskningsrapport, vol 63. Naturgeografiska Institutionen, Stockholm University, Stockholm
Ayenew T, Tilahun N (2008) Assessment of lake-groundwater interactions and anthropogenic stresses, using numerical groundwater flow model, for a Rift lake catchment in central Ethiopia. Lakes Reserv Res Manag 13(4):325–343. doi:10.1111/j.1440-1770.2008.00383.x
Baker BH, Wohlenberg J (1971) Structure and evolution of the Kenya Rift Valley. Nature 229(5286):538–542. doi:10.1038/229538a0
Banta ER (2011) ModelMate -A graphical user interface for model analysis, vol 6-E4, U.S. Geological Survey Techniques and Methods. U.S. Geological Survey Techniques and Methods, USA
Beadle LC (1932) Scientific results of the Cambridge Expedition to the East African Lakes, 1930–1.—4. The waters of some East African Lakes in relation to their fauna and flora. J Linn Soc Lond Zool 38(258):157–211. doi:10.1111/j.1096-3642.1932.tb00699.x
Becht R, Harper DM (2002) Towards an understanding of human impact upon the hydrology of Lake Naivasha, Kenya. Hydrobiologia 488(1–3):1–11. doi:10.1007/978-94-017-2031-1_1
Becht R, Nyaoro JR (2006) The influence of groundwater on lake-water management: the Naivasha Case. ITC, Enschede
Becht R, Odada O, Higgins S (2005) Lake Naivasha : experience and lessons learned brief. Managing lakes and basins for sustainable use, a report for lake basin managers and stakeholders. Kusatsu, Kenya
Becht R, Mwango R, Muno FA (2006) Groundwater links between Kenyan Rift Valley lakes. ITC, Enschede
Bense VF, Gleeson T, Loveless SE, Bour O, Scibek J (2013) Fault zone hydrogeology. Earth Sci Rev 127:171–192. doi:10.1016/j.earscirev.2013.09.008
Bretzler A, Osenbrück K, Gloaguen R, Ruprecht JS, Kebede S, Stadler S (2011) Groundwater origin and flow dynamics in active rift systems - A multi-isotope approach in the Main Ethiopian Rift. J Hydrol 402(3–4):274–289. doi:10.1016/j.jhydrol.2011.03.022
Candela L, Elorza FJ, Tamoh K, Jiménez-Martínez J, Aureli A (2013) Groundwater modelling with limited data sets: the Chari-Logone area (Lake Chad Basin, Chad). Hydrol Process 28(11):3714–3727. doi:10.1002/hyp.9901
Clarke MCG, Woodhall DG, Allen D, Darling G (1990) Geological, volcanological and hydrogeological controls on the occurrence of geothermal activity in the area surrounding Lake Naivasha, Kenya. Ministry of Energy, Nairobi
Darling WG, Allen DJ, Armannsson H (1990) Indirect detection of subsurface outflow from a Rift Valley Lake. J Hydrol 113(1–4):297–305. doi:10.1016/0022-1694(90)90180-6
Darling WG, Gizaw B, Arusei MK (1996) Lake-groundwater relationships and fluid-rock interaction in the East African Rift Valley: isotopic evidence. J Afr Earth Sci 22(4):423–431. doi:10.1016/0899-5362(96)00026-7
De Jong T (2011) Water abstraction survey in Lake Naivasha Basin, Kenya. Internship report. University of Wageningen, Wageningen
Everard M, Vale JA, Harper DM, Tarras-Wahlberg H (2002) The physical attributes of the Lake Naivasha catchment rivers. Hydrobiologia 488(1–3):13–25. doi:10.1023/A:1023349724553
FBP (2013) Groundwater data flower business park. ITC, Enschede
Freeze RA, Cherry JA (1979) Groundwater, 1st edn. Prentice-Hall, Inc., Englewood Cliffs
Gaudet JJ, Melack JM (1981) Major ion chemistry in a tropical African lake basin. Freshw Biol 11(4):309–333. doi:10.1111/j.1365-2427.1981.tb01264.x
GKMEGS (1988) Geological map of Longonot Volcano, the greater Olkaria and Eburru volcanic complexes, and adjacent areas. Government of Kenya Ministry of Energy Geothermal Section (GKMEGS), Nairobi
Harbaugh AW (2006) MODFLOW-2005, The U.S. Geological survey modular ground-water model—the ground-water flow process. U.S. Geological Survey - Techniques and Methods, USA
Hogeboom HJ (2013) On the influence of groundwater abstractions on lake levels. University of Twente, Enschede. http://essay.utwente.nl/64413/
Johnston R, Smakhtin V (2014) Hydrological modeling of large river basins: How much is enough? Water Resour Manag 28(10):2695–2730. doi:10.1007/s11269-014-0637-8
Kibona SRU (2000) Temporal and spatial varation of groundwater level north of Lake Naivasha, Kenya (Analysed using Modflow). ITC, Enschede
Le Page M, Berjamy B, Fakir Y, Bourgin F, Jarlan L, Abourida A, Benrhanem M, Jacob G, Huber M, Sghrer F, Simonneaux V, Chehbouni G (2012) An integrated DSS for groundwater management based on remote sensing. The case of a semi-arid aquifer in Morocco. Water Resour Manag 26(11):3209–3230. doi:10.1007/s11269-012-0068-3
Legese Reta G (2011) Groundwater and Lake water balance of Lake Naivasha using 3-D transient groundwater model. ITC, Enschede
Li F, Zhao Y, Feng P, Zhang W, Qiao J (2015) Risk assessment of groundwater and its application. Part I: risk grading based on the functional zoning of groundwater. Water Resour Manag 29(8):2697–2714. doi:10.1007/s11269-015-0964-4
Małloszewski P, Zuber A (1992) On the calibration and validation of mathematical models for the interpretation of tracer experiments in groundwater. Adv Water Resour 15(1):47–62. doi:10.1016/0309-1708(92)90031-v
McCann DL (1974) Hydrogeologic investigation of Rift Valley catchments. United Nations - Kenya Government Geothermal Exploration Project, Nairobi
Meins FM (2013) Evaluation of spatial scale alternatives for hydrological modelling of the Lake Naivasha basin, Kenya. University of Twente, Enschede
Millenium Ecosystem Assessment (2005) Ecosystems and human well-being: general synthesis. Washington DC
MOWD (1982) Lake Naivasha water level variations. Kenya Ministry of Water Development (MOWD) Directorate of Public Works, Nairobi, Kenya
Mpusia PTO (2006) Comparison of water consumption between greenhouse and outdoor cultivation. ITC, Enschede
Nilsson E (1932) Quaternary glaciations and Pluvial Lakes in Britisch East Africa. Stockholm Hogskola, Stockholm
Ojiambo BS, Poreda RJ, Lyons WB (2001) Ground water/surface water interactions in Lake Naivasha, Kenya, using δ18O, δD, and 3H/3He age-dating. Ground Water 39(4):526–533. doi:10.1111/j.1745-6584.2001.tb02341.x
Owor M (2000) The long-term interaction of groundwater with Lake Naivasha, Kenya: a numerical simulation of the relationship between groundwater and lake allowing for fluctuating lake levels. ITC, Enschede
Ramsar (2012) Ramsar report for Lake Naivasha, Site NO. 724, Wetlands International Site Reference No. 1KE002, Designation date 10-04-1995.
Richardson JL, Richardson AE (1972) History of an African Rift Lake and its climatic implications. Ecol Monogr 42(4):499–534. doi:10.2307/1942169
Rödiger T, Geyer S, Mallast U, Merz R, Krause P, Fischer C, Siebert C (2014) Multi-response calibration of a conceptual hydrological model in the semiarid catchment of Wadi al Arab, Jordan. J Hydrol 509:193–206. doi:10.1016/j.jhydrol.2013.11.026
Sikes HJ (1936) Notes on the hydrology of Lake Naivasha. J East Afr Uganda Nat Hist Soc 13:73–89
Simmers I, Hendrickx JMH, Kruseman GP, Rushton KR (1997) Recharge of Phreatic Aquifers in (Semi-) Arid Areas, vol 19. International Association of Hydrogelologists. A.A. Balkema, Rotterdam
Thompson AO, Dodson RG (1963) Geology of the Naivasha area. Government of Kenya, Ministry of Commerce and Industry Geological Survey of Kenya, Nairobi
van Oel PR, Mulatu DW, Odongo VO, Meins FM, Hogeboom RJ, Becht R, Stein A, Onyando JO, van der Veen A (2013) The effects of groundwater and surface water use on total water availability and implications for water management: the case of Lake Naivasha, Kenya. Water Resour Manag 27(9):3477–3492. doi:10.1007/s11269-013-0359-3
Verschuren D, Laird KR, Cumming BF (2000) Rainfall and drought in equatorial east Africa during the past 1,100 years. Nature 403(6768):410–414. doi:10.1038/35000179
WRMA (2010) Water allocation plan - Naivasha Basin. Water Resources Management Authority - Republic of Kenya, Naivasha
WWF (2011) Shared risk and opportunity in water resources: seeking a sustainable future for Lake Naivasha, vol 2. World Wildlife Fund, Gland
Yihdego Y, Becht R (2013) Simulation of lake–aquifer interaction at Lake Naivasha, Kenya using a three-dimensional flow model with the high conductivity technique and a DEM with bathymetry. J Hydrol 503:111–122. doi:10.1016/j.jhydrol.2013.08.034
Zekri S, Triki C, Al-Maktoumi A, Bazargan-Lari MR (2015) An Optimization-Simulation Approach for Groundwater Abstraction under Recharge Uncertainty. Water Resour Manag 1–15. doi:10.1007/s11269-015-1023-x
Acknowledgments
This study was partly funded by NWO/WOTRO Science for Global Development, The Netherlands. Furthermore, we are thankful to Sarah Higgins of the Lake Naivasha Riparian Association and James Waweru of the Flower Business Park for providing us with essential data.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Hogeboom, R.H.J., van Oel, P.R., Krol, M.S. et al. Modelling the Influence of Groundwater Abstractions on the Water Level of Lake Naivasha, Kenya Under Data-Scarce Conditions. Water Resour Manage 29, 4447–4463 (2015). https://doi.org/10.1007/s11269-015-1069-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11269-015-1069-9