Abstract
State-of-the-art applications of short-term reservoir management integrate several advanced components, namely hydrological modelling and data assimilation techniques for predicting streamflow, optimization-based techniques for decision-making on the reservoir operation and the technical framework for integrating these components with data feeds from gauging networks, remote sensing data and meteorological weather predictions. In this paper, we present such a framework for the short-term management of reservoirs operated by the Companhia Energética de Minas Gerais S.A. (CEMIG) in the Brazilian state of Minas Gerais. Our focus is the Três Marias hydropower reservoir in the São Francisco River with a drainage area of approximately 55,000 km and its operation for flood mitigation. Basis for the anticipatory short-term management of the reservoir over a forecast horizon of up to 15 days are streamflow predictions of the MGB hydrological model. The semi-distributed model is well suited to represent the watershed and shows a Nash-Sutcliffe model performance in the order of 0.83-0.90 for most streamflow gauges of the data-sparse basin. A lead time performance assessment of the deterministic and probabilistic ECMWF forecasts as model forcing indicate the superiority of the probabilistic model. The novel short-term optimization approach consists of the reduction of the ensemble forecasts into scenario trees as an input of a multi-stage stochastic optimization. We show that this approach has several advantages over commonly used deterministic methods which neglect forecast uncertainty in the short-term decision-making. First, the probabilistic forecasts have longer forecast horizons that allow an earlier and therefore better anticipation of critical flood events. Second, the stochastic optimization leads to more robust decisions than deterministic procedures which consider only a single future trajectory. Third, the stochastic optimization permits to introduce advanced chance constraints for refining the system operation.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
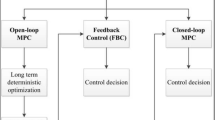
Reservoirs are important hydraulic infrastructure for water use and allocation. Among the main uses are hydropower generation and flood control, often in a multi-purpose way. In those water systems operation, optimal centralized control can be achieved by employing Model Predictive Control (MPC) (Ackermann et al. 2000; van Overloop 2006). Key elements of MPC are (Morari and Lee 1999): (1) a model of the physical process to predict future trajectories of the controlled variables over a finite horizon, (2) the calculation of a control sequence that optimizes an objective function, and (3) a receding horizon strategy. The receding horizon strategy means that, at each forecast time and control instant T0, the operator applies the first signal of the control sequence and shifts the forecast horizon ahead in time. Constraints on inputs, states and outputs are explicitly considered (Schwanenberg et al. 2012).
Contrary to conventional reservoir operation strategies, where operating rules are calculated offline, MPC considers the online solution of an online optimization problem at every time step. Available disturbance forecasts, i.e. reservoir inflows and laterals in downstream river reaches, are used directly in the control scheme, resulting in advantages and threats. The main advantage is that the control strategy becomes anticipatory or proactive (Zavala et al. 2009). Before the realization of a forecasted disturbance, the control sequences set the system to a state optimal to accommodate it, for example by lowering the water elevation in a reservoir before an expected flood event occurs. However, use of forecasts can also jeopardize the control robustness (Bemporad and Morari 1999), if MPC is applied in a deterministic mode and forecast uncertainty is high. In this case, the approach runs the risk of suggesting decisions in anticipation of expected events that eventually do not occur. To increase the robustness of MPC, enhancements of the approach take into account ensemble forecast and appropriate transformation into scenario trees, as shown by Raso et al. (2013), to extend the deterministic to a multi-stage stochastic optimization.
In contrary to long-term reservoir management approaches, in which streamflow forecasts are often generated by Ensemble Streamflow Predictions (ESP) based on climatology, short-term applications primarily rely on Quantitative Precipitation Forecasts (QPF) from multiple members of a Numerical Weather Prediction (NWP) model. In this approach, it is expected that the uncertainty related to the meteorological portion of the forecasting system is sampled and thus permits better decision-making (Cloke and Pappenberger 2009; Ramos et al. 2013). Although meteorological ensembles do not sample all uncertainties in the forecasting system (for example, uncertainties in the hydrological model are not considered), the meteorological forecast are usually the ones which introduce the highest amount of uncertainty to the system. This method for generating hydrological ensemble forecasts is actually broadly applied and has been showing better performance than deterministic forecasts in terms of performance metrics (Renner et al. 2009; Velázquez et al. 2009; Jaun and Ahrens 2009), decision making assessments (Boucher et al. 2011; Ramos et al. 2013), and also more recently to reservoirs operation assessments (Mccollor and Stull 2008; Zhao et al. 2011; Boucher et al. 2012; Raso et al. 2013).
On reservoir operation using ensembles, Boucher et al. (2012) reports the possibility to achieve better results for hydropower reservoirs operation by the use of ensemble forecasts in comparison to a high-resolution deterministic one. The authors as well show that results depend on the forecast skill (ensemble forecasts are not always better than the deterministic ones), and that the lead-time performance metrics not necessarily match with the best reservoir operation. Other examples include the work of Mccollor and Stull (2008), that presented an assessment of short-range ensemble precipitation forecasts of 24h to operate a hydroelectric reservoir at the Jordan River (Canada). The authors describe that employing the full ensemble or the ensemble average is better than using a single deterministic model or climatology data for the presented scenarios. Furthermore, Zhao et al. (2011) present a hypothetical example of how a single-objective real-time reservoir operation benefits from the streamflow uncertainty information. The authors also highlight that the operation efficiency, measured by a utility function, decreases as the forecast uncertainty increases and its magnitude depends on the skill of the forecast products.
Between the few studies found in literature on the assessment of short-term reservoir operation using ensembles, the usual consensus is that it is possible to have better operational results than using deterministic approaches, although the results are dependent on the forecast skill. Also, among the techniques applied, there are no further studies focused on the use of stochastic MPC methods except for a first discussions by Raso et al. (2013), who developed a scenario tree reduction technique to consider ensemble forecasts in MPC. These trees start with a single control trajectory in the first phase of the forecast horizon in which future system states are still uncertain. When uncertainty gets resolved over the forecast horizon, for example by the observation of precipitation and streamflow, branching points get introduced into the tree. This makes the reservoir management adaptive to the resolution of forecast uncertainty.
In this context, we see one important contribution of this paper in the use of a novel scenario tree reduction technique in application to an ensemble forecast. Different from Raso et al. (2013), we use precipitation-dependent distance metrics for the tree generation to generate streamflow trees for the stochastic optimization. This allows us to consider lag time between precipitation and reservoir inflow in larger river basins under the hypothesis that most forecast uncertainty gets resolved when forecasted precipitation is observed and the hydrological model uncertainty is smaller than the meteorological one. Another contribution of our work is the novel application of multi-stage stochastic optimization for flood control by a multi-purpose reservoir. Whereas existing work considers only single-stage setups (Boucher et al. 2012), the introduction of multiple stages at branching points of the scenario tree makes the management more adaptive to the resolution of uncertainty and should lead to a better performance.
2 Material and Methods
2.1 Case Description
The Três Marias hydropower reservoir is located in the São Francisco River in the center of Minas Gerais state, Brazil (Fig. 1). It has a drainage area of approximately 55,000 km. The region of interest in this case extends to Pirapora city, located 120 km downstream of the reservoir. The operation of Três Marias reservoir is responsible for flood control and mitigating flood inundation in Pirapora.
The Três Marias dam was built during the 1950s. Its reservoir has a total capacity of 19.5×109m3, with strategic importance for Brazil. It serves multiple purposes: hydropower generation, flood control, navigation, municipal and industrial water supply and irrigation. For Brazilian standards, the Três Marias is a watershed covered by a dense network of meteorological and fluviometric gauges. Many of them include telemetry with real-time data available from the National Water Agency (Agência Nacional de Águas ANA) and CEMIG.
The short-term management of the Três Marias reservoir during flood events is conducted by CEMIG. It implements the following components:
-
Spill is undesired and its volume should be minimized to indirectly increase the turbine flow and power generation.
-
A time-dependent maximum forebay elevation constraint limits the forebay elevation either to the reservoir’s maximum operating limit or an operational limit due to the allocation of flood control storage during the wet season.
-
Two flow thresholds at the downstream gauge of Pirapora Ponte exist at 2000 and 4000 m3/s. The lower one represents the flow at which the operators need to take first measures and small-scale inundation starts. The higher threshold indicates the start of large-scale inundation at the city of Pirapora causing significant flood damage.
-
Large outflow gradients from Três Marias reservoir are undesired.
2.2 Model Predictive Control
For the representation of an arbitrary water resources system, we consider a discrete time dynamic system according to
where x, y, u, d are respectively the state, dependent variable, control and disturbance vectors, and f(),g() are functions representing an arbitrary linear or nonlinear water resources model.
If being applied in Model Predictive Control (MPC), Eq. 1 is used to predict future trajectories of the state x and dependent variable y over a finite time horizon represented by k=1,...,N time instants, to determine the optimal set of control variables u by an optimization algorithm. Under the hypothesis of knowing the realization of the disturbance d over the time-horizon, for example the inflows into the reservoir system, a so-called multiple-shooting version (Diehl 2001) of the nonlinear MPC becomes
where J() is a cost function associated with each state transition, E() is an additional cost function related to the final state condition, and h() are hard constraints on control variables and states, respectively. The notation x ∗ refers to a subset of state variables which become independent optimization variables. In this case, the related process model becomes an equality constraint of the optimization problem in Eq. 4 such as in a simultaneous or collocated optimization setup. A simulation model computes the remaining state variables as well as the dependent variables according to Eq. 1 corresponding to a sequential or single-shooting optimization setup. Xu and Schwanenberg (2012) compare pros and cons of both methods from the perspective of control efficiency, constraints handling and scaling in application to a storage reservoir.
The extension of the deterministic to a multi-stage stochastic optimization is achieved by replacing the single-trace forecast by a forecast ensemble \(\left \{{\xi ^{j}_{k}}\right \}\), with j = 1,...,M, k = 1,...,N and computing the objective function values J and E as the probability-weighted sum of the objective function terms of the individual ensemble branches or scenarios. This lead to a reformulation of Eq. 2 as
where p j is the probability of the scenarios j = 1,,M and M is the total number of scenarios. Whereas the disturbance d as well as the model states x and outputs y are treated independently in each scenario, the control variable u is the key to the properties of the stochastic optimization approach. The most general formulation results from the use of scenario trees. One way for its definition is the scenario tree nodal partition matrix P(j, k) (Dupaèová et al. 2003) with the dimensions m × n. The matrix assigns the control at time step k of scenario j to the control vector u. This enables us to define a common control trajectory for all scenarios at the beginning of the forecast horizon when future system states are still uncertain and a single decision should cover all future trajectories.
When uncertainty gets resolved over the forecast horizon, for example when a forecasted precipitation is finally observed, we introduce branching points to receive an independent control in each scenario at the end of the forecast horizon. Equation 6 presents an example of a nodal partition matrix for a simple tree with two scenarios and a branching point at the second time step.
The introduction of multiple branching points at several time steps leads to a multi-stage stochastic optimization; check (Raso et al. 2013) for details. From a technical perspective, the solution of the multi-stage stochastic optimization (Eq. 5) is very similar to the solution of the deterministic setup of Eq. 2. The main difference is the number of dimensions of the optimization problem. According to our experience, it is larger by a factor of 5-20, if we derive a suitable scenario tree from a meteorological or hydrological ensemble forecast.
2.3 Scenario Tree Generation
A scenario tree is a rooted tree with the unique vertex at the first time step designated as the root of the tree. At this initial stage, all future trajectories are possible. When uncertainty gets resolved, we introduce branching points. At every branching point, the sample space of the original branch splits into at least two subsets.
Methods for generating a proper tree-structure from complete scenario ensembles are discussed in Sutiene et al. (2010), showing an empirical method to bundle scenarios based on the k-means technique. In Raso et al. (2012), an approach is introduced which takes into account the variety of variables the controller is able to observe along the forecasting horizon as well as the level of resolution. In this paper we refer to Gröwe-Kuska et al. (2003). The construction of the scenario tree is based on a simultaneous backward reduction strategy, applied in every time step of the ensemble forecasts prediction horizon.
The criterion to terminate the reduction is defined in various ways. A scenario tree with fixed structure can be created by determination of a predefined number of reductions for any time step in the prediction horizon. In a second approach, we apply the maximal reduction strategy to determine a reduced probability distribution of the stochastic process represented by the ensemble forecast. To trade off the scenario probabilities and the distances of scenario values we use the Kantorovich distance as a probability distance and limit it to a tolerance level 𝜖(t). For discrete probability distributions the Kantorovich distance is the optimal value of a linear transportation problem. The reduction algorithm stops if inequality (7) is violated for the first time.
fwhere \(c(\xi _{i},\xi _{j})={\sum }_{\tau =1}^{t}\left |\xi _{i}(\tau )-\xi _{j}(\tau )\right |\), with t ∈ {1,...,N} and |.| denotes a norm on \(\mathbb {R}^{n}\). J is the set of preserved scenarios.
The tolerance 𝜖(t) was calculated in 5 different ways. We considered 𝜖 exponentially or linear growing in t, constant or finally 𝜖(t) recursively defined by Eq. 8.
where t ∈ {1,...,N − 1}, q ∈ (0, 1) and 𝜖 = 𝜖 r e l ∗𝜖 m a x . Here 𝜖 m a x is the best possible Kantorovich distance of the original probability distribution of the ensemble forecast concerning its scenarios endowed with unit mass. The relative tolerance 𝜖 r e l ∈ (0, 1) can be modified.
If a scenario i is reduced in time step t, it will be added to the sample space of a scenario j. For ensemble forecasts resulting from a stochastic process with steady domain, the following approach is applicable. Instead of keeping the original ensemble member in the scenario tree, it is possible to choose a branch consisting of the average over the ensemble members from the sample space of the trajectory j. In every branching point one possible realization bifurcates into two or more branches. This branching results in an abrupt change of the scenario values. To avoid this sudden and physical unrealistic change of values we smooth the skip in new branches over a given number of time steps.
2.4 Ensemble Forecast Data
Quantitative Precipitation Forecasts (QPF) of the global Ensemble Prediction System (EPS) provided by the European Centre for Medium-range Weather Forecasts ECMWF (Molteni et al. 1996; Buizza et al. 2005) are used as meteorological forcing of the hydrological forecasting model. The data of this assessment is obtained from The Observing System Research and Predictability Experiment (THORPEX) Interactive Grand Global Ensemble (TIGGE) project portals (Bougeault et al. 2010). In comparison to the NWP of NOAA and CPTEC, the ECMWF forecast has the best skill for the Três Marias river basin (Fan et al. 2014).
The ECMWF-EPS forecasts consist of 50 members of perturbed precipitation of 0.5 degrees resolution for the whole globe considering initial uncertainties by using singular vectors and model uncertainties due to physical parameterizations by a stochastic scheme (Buizza et al. 2007). The data becomes available twice a day at 00:00 UTM and 12:00 UTM with a forecast horizon of 15 days and time steps of 6 hours. For the use in the hydrological model, it is spatially downscaled to the watershed by Thiessen polygons and disaggregated to hourly time steps. As a reference and comparison between deterministic and probabilistic results, we also consider the deterministic forecast provided by ECMWF. It is also available in the TIGGE portal.
We do not apply bias correction to the NWP rainfall. The most important restriction for bias correction in the present case was the data availability. Good observations from the telemetric network are only available recently starting in the year 2005, and data from the NWP models is only available from October 2006, making the periods too short for an adequate analysis. Also, we believe that results obtained for the NWP performance within the hydrological model, showed below in the present paper, do not clearly request for bias correction, and eventual differences do not affect our objectives and conclusions of this study.
The skill of the hydrological ensemble forecasts of the Três Marias inflow is assessed by six performance metrics. The consensus forecast ensemble is evaluated by the Mean Absolute Error (MAE). Regarding the ensemble distribution, we compute the Mean Continuous Ranked Probability Score (Mean CRPS) and Rank Histograms. To evaluate errors relative to discrete events, i.e. threshold crossings, computed the Brier Score (BS). For the BS, we adopt the exceedance of 1400m3/s, which corresponds to the Q10 of the inflow (exceedance probability of 10 %).
The same metrics (except rank histograms) are also assessed for the deterministic forecasts and, as a basis for verification, to the perfect forecasts obtained using the observed rainfall in the forecast horizon. Details about metrics interpretation are available in the Appendix Further descriptions of the metrics computation and its mathematical basins can be found in Wilks (2006), Brown et al. (2010), Bradley and Schwartz (2011), Hersbach (2000), and Jolliffe and Stephenson (2012).
2.5 Hydrological and Hydraulic Modeling
We use the MGB-IPH (Modelo de Grandes Bacias Instituto de Pesquisas Hidráulicas) model (Collischonn et al. 2005, 2007; Paz et al. 2007; Paiva et al. 2013) to conduct streamflow forecasts based on the meteorological forcing. The MGB-IPH model is a conceptual hydrological model developed for large-scales river basins. In its most recent version, it is applied using a distributed, sub-basin based spatial discretization of the main river basin (Paiva et al. 2013). The soil type and land uses within catchments are categorized by Hydrological Response Units (HRU) (Kouwen et al. 1993). The evapotranspiration in the model relies on the Penman-Monteith equation and flow propagation through the drainage network is implemented by the Muskingum-Cunge method. If applied for operational forecasting, the model time step is one hour, and the execution includes a Data Assimilation (DA) procedure presented by Paz et al. (2007). The DA uses the difference between observed and simulated streamflow to compute a correction factor and updates the state variables of the model at each time step.
The MGB-IPH model computes the inflow into Três Marias reservoir and the laterals of the downstream routing reach. From an optimization point-of-view, these are disturbances of the optimum control problem. In contrary, the routing model of the river reach downstream of the dam is executed as an internal models in the optimization to predict future system states, i.e. the discharge at gauge Pirapora. Since the reservoir operation can introduce high flow gradients into the downstream river reach, the required model should be able to correctly propagate these gradients to Pirapora. Furthermore, it should be computationally efficient enough to run in the optimization. Our model assessment we conduct for clarification of the proper model approach includes a full dynamic hydraulic model in SOBEK (Stelling and Duinmeijer 2003), a kinematic wave model as well as an integrator-delay model, the last two implemented in the RTC-Tools package (Schwanenberg et al. 2014), as well as the MGB-internal Muskingum-Cunge method.
3 Results
3.1 Model Uncertainty
The model uncertainty of the rainfall runoff simulation with the hourly MGB-IPH model is presented in Table 1. It provides an overview about performance indicators at 3 representative gauges in the basin and the inflow into Três Marias reservoir for a calibration period from December 2006 till June 2011 and a validation period from June 2000 till June 2006. The gauges Iguatama and Ponte do Mesquita are located upstream of the reservoir; gauge PBR040 measures the flow in the most important tributary of the downstream river reach. Gauge PBR040 and the reservoir inflow are boundary conditions of the routing models and of major importance.
The model calibration in the streamflow gauges shows an acceptable performance for the data-sparse basin. The Nash-Sutcliffe model efficiency (NSE) are above 0.7 for all gauges. Bias and Mean Average Error (MAE) are considered low in comparison to the mean flow. This performance do not drop significant in the validation period. For the inflow into Três Marias reservoir, NSE metrics shows a performance that can be considered adequate for forecasting purposes. MAE and Bias are larger at this point than in the gauging stations, mainly because flow at this point is also larger. Part of this error is also related to the fact that the inflow data is back-calculated by the reservoir’s mass balance, leading to noisy data.
The routing model between Três Marias reservoir and the gauge Pirapora propagates outflow from the reservoir to the downstream inundation area. It is essential for the decision-support on flood mitigation measures in the short-term optimization approach. The performance indicators in Table 2 summarize the performance of the different routing approaches.
The MGB model shows a relatively poor performance in the downstream routing reach. This primarily results come from the overestimation of inflow from tributaries in this reach. Furthermore, a visual inspection of observed and simulated flow data at the gauge Pirapora shows an inaccurate flow propagation with too much damping of flow gradients. Good performance is achieved with the full dynamic SOBEK model on a fine computational grid we introduce as a reference. Although its good performance, a direct integration in the optimization is not possible due to high computational costs and the absence of an adjoint model.
A coarser and finer simplified kinematic wave model shows a good model performance. However, a visual inspection of the simulated data shows too high damping of large flow gradients. A spatial and temporal refinement improves results, but increases the computational costs. The best combination of accuracy and computational performance is obtained by the integrator delay model. The integration of time lags and nonlinear reservoirs enables a fine tuning of the flow propagation even on a coarse grid with hourly time steps.
3.2 Forecast Uncertainty
We conduct the lead-time performance analysis for a five-years period between July 2008 and July 2013 including five wet seasons in the Três Marias basin. The wet season occurs during the austral summer (November to April) whereas the dry season takes place during austral winter (May to October).
The lead-time performance assessment of the hydrological forecasts for the Três Marias inflow is presented in Figs. 2, 3, 4 and 5. The MAE (Fig. 2) shows no significant difference between the deterministic and probabilistic ECMWF-based forecasts and the perfect forecast up to a lead-time of 48h. In this period, the forecast primarily depends on observed rainfall and streamflow. From a lead-time of 48h, the MAE using the ECMWF forcing starts to diverge from the perfect forecast error. Until a lead-time of 100h, the error between the deterministic NWP model and the mean of the ensemble is still similar. From a lead-time of 100h, the error of the ensemble mean gets significantly smaller than the error of the deterministic forecast indicating a higher skill of the consensus forecast.
The CRPS performance assessment (Fig. 3) confirms the similarities between forecasts until lead-times to 48h, when the results starts to diverge. From here, the results of the ensemble forecast shows a better performance than the deterministic one. Also, it is noteworthy that the ensemble forecast outperforms the perfect forecast until a lead-time of 260h. In our perception and experience, this mainly suggests problems related to the sparse rainfall gauge availability in the basin, and it is not uncommon that some rainfall events are not observed by the existing telemetry.
Rank Histograms (Fig. 4) of the ensemble forecasts predominately have a U-shaped form. This indicatives of lack of spread in the forecasts, but also results from the noisy, back-calculated inflows. The shape is more distinct until a lead-time of 48h because of the small spread in the ensembles. This is a common characteristic of hydrological ensemble forecasting systems that only relies on meteorological uncertainty and do not cover model uncertainty. However, in the present case, a lack of spread is also present for larger lead-times, indicating a general underestimation of uncertainty by the actual system. This aspect will probably trigger future research, however, for the scope of this study, the consideration of incomplete forecast uncertainty in the stochastic optimization should still outperform the deterministic approach.
Finally, the BS assessment (Fig. 5) for a threshold of 1400m3/s shows again close similarities between forecasts results until a lead-time of 48h. From here, the ensemble forecast performs always better than the deterministic one. In comparison to the perfect forecast, the ensembles show very similar results until a lead-time of 250h and become worse afterwards.
In general, the probabilistic forecast seems to have a clear added value above the deterministic forecast. First, all indicator show higher skills of the probabilistic forecast in comparison to the deterministic one. Second, the probabilistic forecast offers an additional 5 days of lead-time. Third, the ensemble spread will become a valuable input of the stochastic optimization for more robust decision-making. Also, ensemble results are close (or even better in terms of CRPS) to results obtained by using ’perfect’ forecasts with observed rainfall. Although we believe that the observed precipitation of the gauges is not very accurate, this is a noteworthy result.
3.3 Scenario Tree Generation
Figure 6a presents an ensemble inflow forecast to the Três Marias reservoir and one of the generated scenario trees (Fig. 6b). The forecast was issued on December 27, 2011, and shows a forecast for one of the major flood events of the last ten years.
The scenario tree is built with a fixed binary structure of maximum size. First, the number of ensemble members is reduced to the next smaller power of two. Then, branching points of the tree are introduced at equidistant time steps over the forecast horizon. The tree is constructed by reducing the number of the remaining ensemble members at every branching point, starting with the last branching point. The 32 resulting branches are averaged over their sample spaces and the transition to new branches is smoothed over 10 time steps.
Additionally, we construct a set of 118 scenario trees by using different tolerance levels. The comparison of the constructed trees to the corresponding ensemble forecast shows no bias of the probability weighted average of the scenarios, i.e. the MAE of both are identical. To compare the tree quality, we evaluate the error of the branches compared to its sample space in every time step of the prediction horizon and summed it up over the time and all branches in the tree. The worst case for this absolute quality measure occurs for a tree with only one branch. The relation between the absolute quality measure and the worst case of the quality measure helps to estimate the tree quality, i.e. the closer the relative quality measure is to zero the better is the accordance to the original ensemble forecast. We observe a direct dependence between the relative quality measure and the size of the tree. For the example in Fig. 6, the quality measure for the tree with averaged branches is below the quality measure of trees with original branches, while the size of the tree is constant.
3.4 Optimization Performance
Figure 7 presents deterministic and stochastic optimization results for the total outflow, spill and forebay elevation of the Três Marias reservoir as well as the flow at the gauge Pirapora Ponte for a forecast time of December 27, 2011. Deterministic results base upon perfect forecasts with a forecast lead time of 10 and 15 days. Therein, the streamflow forecast of the hydrological model is replaced by observed data. Another deterministic optimization uses the MGB streamflow forecast forced with the deterministic ECMWF forecast of 10 days. The stochastic optimization relies on the scenario tree of 32 final branches with a lead time of 15 days as presented in Fig. 6b.
Deterministic results with a lead time of 10 days show similar results. Since they do not include the peak inflow beyond Day 10, the forebay elevation increases faster and flow at the downstream gauge is lower than in the optimization runs with a lead time of 15 days. The latter detect the peak and foresee an average flow at the downstream gauge larger than the first threshold of 2000 m3/s. The least-square penalty motivates the optimization to prefer a constant flow at Pirapora Ponte by choosing an appropriate reservoir outflow under consideration of the flow propagation to the gauge and lateral inflows from downstream tributaries.
The stochastic optimization takes into account forecast uncertainty and propagates it through the decision-making process. It shows a more conservative allocation of reservoir storage, i.e. a lower forebay elevation compared to the deterministic optimization. On the other hand, the total reservoir outflow is larger from the beginning. The reason for this is the forebay elevation hard constraint. While the deterministic run fulfills the constraint only for the most probable scenario (without considering forecast uncertainty), the control trajectory of the stochastic optimization meets the constraint for all 32 branches of the scenario tree. In the operational context, this leads to a much higher chance to meet the constraint for a range of potential future inflows. An alternative and less conservative approach is the formulation of the forebay elevation bound as a chance constraint. In this case, the optimization accepts a limited probability of a forebay elevation violation.
4 Conclusions
The use of probabilistic forecasts in combination with the multi-stage stochastic optimization in comparison to a deterministic approach has a number of advantages in the short-term reservoir management. One is that probabilistic forecasts often show a better skill and are available for longer lead times, in our case 15 days compared to 10 days for the NWP of ECMWF. This leads to an earlier detection of critical events and its better anticipation by earlier decisions. Another one is the propagation of forecast uncertainty through the decision-making process and its visualization for the stakeholder.
Our suggestion for the correct representation of forecast uncertainty, in our case approximated by an ensemble forecast, in a multi-stage stochastic optimization is based on scenario tree generation. We propose a novel method which derives the tree structure from precipitation data to generate a streamflow tree. This takes into account time lags between the observed precipitation, i.e. the time when most of the meteorological uncertainty gets resolved, and streamflow forecasts in large-scale river basins. Furthermore, the applied sample space averages in the tree generation lead to identical MAE by definition between the ensemble and the tree representation in comparison to standard tree reduction approaches which only deletes branches and aggregates the probabilities.
The extension of the deterministic optimization towards a multi-stage sto-chastic optimization approach results in a number of conceptual advantages. An important one is the option to take risk-based decisions by considering the forecast uncertainty in the optimization. This will probably lead to more robust decisions. Furthermore, the sampling of control trajectories facilitates the integration of non-linearity and constraints.
So far, our assessment has been based on few individual flood events. One direction of future research will be the application of the framework to a more representative number of cases including a better-founded assessment of the skill and benefit of the stochastic technique in comparison to the deterministic method. A sideline will be the improvement of the hydrological framework by the integration of additional observation, for example by adding remote sensing data, to reduce the model uncertainty and put more focus on the forecast uncertainty. Finally, related to the optimization framework, chance constrains are an interesting feature for the conceptual improvement of the optimization setup.
References
Ackermann T, Loucks D, Schwanenberg D, Detering M (2000) Real-time modeling for navigation and hydropower in the river Mosel. Water Resour Plan Manag 126(5):298–303
Bemporad A, Morari M (1999) Robust model predictive control: a survey. Robustness in identification and control. Springer, London
Bradley AA, Schwartz SS (2011) Summary verification measures and their interpretation for ensemble forecasts. Mon Weather Rev 139:3075–3089
Brown JD, Demargne J, Seo D-J, Liu Y (2010) The ensemble verification system (EVS): a software tool for verifying ensemble forecasts of hydrometeorological and hydrologic variables at discrete locations. Environ Model Softw 25:854–872
Buizza R, Houtekamer PL, Toth Z, Pellerin G, Wei M, Zhu Y (2005) A comparison of the ECMWF, MSC, and NCEP global ensemble prediction systems. Mon Weather Rev 133:1076–1097
Buizza R, Bidlot J-R, Wedi N, Fuentes M, Hamrud M, Holt G, Vitart F (2007) The new ECMWF VAREPS (variable resolution ensemble prediction system). Q J R Meteorol Soc 133(624):681–695
Boucher MA, Anctil F, Perreault L, Tremblay D (2011) A comparison between ensemble and deterministic hydrological forecasts in an operational context. Adv Geosci 29(29):85–94
Boucher M-A, Tremblay D, Delorme L, Perreault L, Anctil F (2012) Hydroeconomic assessment of hydrological forecasting systems. J Hydrol 416–417:133–144
Bougeault P, Toth Z, Bishop C, Brown B, Burridge D, Chen DH, Ebert B, Fuentes M, Hamill T M, Mylne K, Nicolau J, Paccagnella T, Park Y, Parsons D, Raoult B, Schuster D, Dias PS, Swinbank R, Takeuchi Y, Tennant W (2010) The THORPEX interactive grand global ensemble. Bull Amer Meteorol Soc 91(8):1059–1072
Cloke H, Pappenberger F (2009) Ensemble flood forecasting: a review. J Hydrol 375:613–626
Collischonn W, Tucci CEM, Haas R, Andreolli I (2005) Forecasting river Uruguay flow using rainfall forecasts from a regional weather-prediction model. J Hydrol (Amsterdam) 305:87–98
Collischonn W, Allasia DG, Silva BC, Tucci CEM (2007) The MGB-IPH model for large scale rainfall-runoff modeling. Hydrol Sci J 52:878–895
Diehl M (2001) Real-time optimization for large scale nonlinear processes [dissertation]. University of Heidelberg, Heidelberg, Germany
Dupaèová J, Gröwe-Kuska N, Römisch W (2003) Scenario reduction in stochastic programming. Math Program 95(3):493–511
Fan F, Schwanenberg D, Kuwajima J, Assis dos Reis A, Collischonn W (2014) Ensemble streamflow predictions in the Trs Marias Basin, Brazil. EGU2014-14191, Vienna
Gröwe-Kuska N, Heitsch H, Römisch W (2003) Scenario reduction and scenario tree construction for power management problems. Power tech conference proceedings. IEEE, Bologna
Hersbach H (2000) Decomposition of the continuous ranked probability score for ensemble prediction systems. Weather Forecast 15:559–570
Jaun S, Ahrens B (2009) Evaluation of a probabilistic hydrometeorological forecast system. Hydrol Earth Syst Sci 13:1031–1043
Jolliffe IT, Stephenson DB (eds) (2012) Forecast verification: a practitioners guide in atmospheric science, 2nd edn
Kouwen N, Soulis ED, Pietroniro A, Donald J, Harrington RA (1993) Grouped response units for distributed hydrologic modeling. J. Water Resour Plan Manag 119:289–305
Mccollor D, Stull R (2008) Hydrometeorological short-range ensemble forecasts in complex terrain. Part II: economic evaluation. Weather Forecast 23:557–574
Molteni F, Buizza R, Palmer TN, Petroliagis T (1996) The ECMWF ensemble prediction system: methodology and validation. Q J R Meteorol Soc 122:73–119
Morari M, Lee JH (1999) Model predictive control: past, present and future. Comput Chem Eng 23:667–682
van Overloop PJ (2006) Model predictive control on open water systems [dissertation]. Delft University of Technology, Delft, The Netherlands
Paiva RCD, Buarque DC, Collischonn W, Bonnet M-P, Frappart F, Calmant S, Bulhões Mendes CA (2013) Large-scale hydrologic and hydrodynamic modeling of the Amazon River basin. Water Resour Res 49:1226–1243
Paz AR, Collischonn W, Tucci C, Clarke R, Allasia D (2007) Assimilation in a large-scale distributed hydrological model for medium range flow forecasts, vol 313. IAHS Press, IAHS Publication, pp 471–478
Ramos MH, Van Andel SJ, Pappenberger F (2013) Do probabilistic forecasts lead to better decisions? Hydrol Earth Syst Sci 17:2219–2232
Raso L, van de Giesen N, Stive P, Schwanenberg D, van Overloop PJ (2013) Tree structure generation from ensemble forecasts for real time control. Hydrol Process 27:75–82
Raso L, van Giesen N, Schwanenberg D (2012) Tree structure generation from ensembel forecasts for short-term reservoir optimization. AGU General Assembly 2012. San Francisco, USA. Control ID: 1487220, vol 15
Renner M, Werner M, Rademacher S, Sprokkereef E (2009) Verification of ensemble flow forecasts for the River Rhine. J Hydrol 376:463–475
Schwanenberg D, Sheret I, Rauschenbach T, Galelli S, Vieira JM, Pinho JL (2012) Adjoint modelling framework. In: 10th international conference on hydroinformatics. Hamburg, Germany
Schwanenberg D, Xu M, Ochterbeck T, Allen C, Karimanzira D (2014) Short-term management of hydropower assets of the Federal Columbia River power system. J Appl Water Eng Res 2(1):25–32
Schwanenberg D, Becker B, Xu M (2014) The open RTC-Tools software framework for modeling real-time control in water resources systems, submitted to Journal of Hydroinformatics. http://www.iwaponline.com/jh/up/jh2014046.htm
Sutiene K, Makackas D, Pranevius H (2010) Multistage k-means clustering for scenario tree construction. Informatica 21(1):123–138
Stelling GS, Duinmeijer SPA (2003) A staggered conservative scheme for every Froude number in rapidly varied shallow water flows. Int J Numer Methods Fluids 43 (12):1329–1354
Velázquez JA, Petit T, Lavoie A, Boucher M-A, Turcotte R, Fortin V, Anctil F (2009) An evaluation of the Canadian global meteorological ensemble prediction system for short-term hydrological forecasting. Hydrol Earth Syst Sci 13:2221–2231
Wilks d (2006) Statistical methods in the atmospheric sciences. Academic Press
Xu M, Schwanenberg (2012) Comparison of sequential and simultaneous model predictive control of reservoir systems. In: 10th international conference on hydroinformatics. Hamburg, Germany
Zavala VM, Constantinescu EM, Krause T, Anitescu M (2009) On-line economic optimization of energy systems using weather forecast information. J Process Control 19(10):1725–1736
Zhao TTG, Cai XM, Yang DW (2011) Effect of streamflow forecast uncertainty on real-time reservoir operation. Adv Water Resour 34:495–504
Acknowledgments
We conduct this research in the scope of the HyProM project (Short-Term Hydropower Production and Marketing Optimization) sponsored by the Bonneville Power Administration (BPA), Companhia Energética de Minas Gerais S.A. (CEMIG), Deltares and Fraunhofer IOSB-AST. The project team includes staff of the sponsors, the Brazilian research institute LACTEC, and researchers from the academic sector. Main focus is the short-term management of hydropower reservoir systems under the explicit consideration of forecast uncertainty as well as the integrated management of hydropower production and marketing. This paper presents results of the Brazilian case with a focus on flood management to mitigate downstream flood risks. Check Schwanenberg et al. (2014) for an application of the framework to the Federal Columbia River Power System in the USA.
Open Access
This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
-
Mean Absolute Error (MAE): For ensemble forecasts, the MAE is computed by i) averaging the ensemble members at each lead-time, ii) calculating the absolute difference between this average, also refered to as consensus forecast, and the corresponding observation. The MAE of a perfect model is equal to zero.
-
Mean Continuous Ranked Probability Score (CRPS): The CRPS is a score that summarizes the quality of a continuous probability forecast by comparing the integrated square difference between the cumulative distribution function of forecasts and observations. The average CRPS across all pairs of forecasts and observations leads to the Mean CRPS. It is usually considered the probabilistic equivalent of the MAE, since it reduces to the mean absolute error for deterministic forecasts, and allows the comparison of probabilistic and deterministic forecasts. Lower values of the mean CRPS correspond to better results.
-
Rank Histogram (RH): The RH consists in a simple counting of the percentage of cases where observed value are placed between the ensemble forecast members within all forecasts and lead-times. Each position between each forecast member is denominated a bin, and the number of bins is equal to the number of members in the ensemble forecast plus one. In the end, the resulting histograms give a measure of the forecast spread. A perfectly reliable with perfect spread set of forecasts would produce a flat uniform RH. High probabilities in both tails (U shape) of the rank histogram are an indicative of lack of spread. An inverted U shape rank histogram is an indicative of excessive spreading. Other formats may be indicative of biases in the set of ensembles.
-
Brier Score (BS): The BS measures the average square error of a probability forecast for a dichotomous event, defined by a flow threshold exceedance, for example. Error units are given in probabilities. A perfectly sharp set of forecasts would have resulting BS values equal to zero.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Schwanenberg, D., Fan, F.M., Naumann, S. et al. Short-Term Reservoir Optimization for Flood Mitigation under Meteorological and Hydrological Forecast Uncertainty. Water Resour Manage 29, 1635–1651 (2015). https://doi.org/10.1007/s11269-014-0899-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11269-014-0899-1