Abstract
In this research, temporal trends of reference evapotranspiration (ET0) values were investigated in arid regions of Iran. For this purpose, meteorological observations collected from 11 high quality meteorological sites over a 41-year period (1965–2005) were used and statistically significant ET0 trends in the monthly, seasonal and annual time basis were detected using nonparametric Mann-Kendall (MK) and Spearman’s Rho (SR) tests at the 5% significant level. To eliminate the effect of serial correlation on the test results, the Trend Free Pre-Whitening (TFPW) approach was applied. The results of this study indicated that the ET0 trends for some cities were increasing (positive) however, for some sites, they showed decreasing (negative) trends. The most number of significant ET0 trends on a monthly time scale occurred at Birjand but no significant trend was observed at the Bandarabbas, Sabzevar and Semnan sites. On the annual time scale, Mashhad revealed the highest positive trend (7.5 mm per year). On the other hand, Esfahan showed the highest decreasing (negative) ET0 trend of about −6.38 mm per year. In general, the performances and abilities of the MK and SR tests were consistent at the verified significant level.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
A lot of scientists have concluded that the earth surface air temperature increased during the 20th century. Human emissions of greenhouse gases caused most of the warming during the latter half of the century (IPCC 2001). Almost all the processes in the biosphere are influenced in some way by climate change phenomena and in this respect a major concern are the climate change impacts on the environment and water resources (Abdul Aziz and Burn 2006). Evapotranspiration is the most important variable for revealing the climate change and temporal-spatial patterns of variables influencing the eco-hydrological processes, which control the evolution of the surface ecosystem. This type of inquiry is fundamental to understand the coupling existing between ecosystem dynamics and the water cycle, in particular in arid and semi-arid environments, where water is an important limiting resource not only for its scarcity but also for its intermittency and unpredictable presence (Liu et al. 2008). Furthermore, investigation of climate change effects on the variables of evapotranspiration (ET) can be effective in determining appropriate adaptation strategies for mitigating the probable damage from these effects.
Many tests for the detection of significant trends in hydro-climatologic time series can be classified as parametric and non-parametric methods (Zhang et al. 2006; Chen et al. 2007). Parametric trend tests are more powerful than non-parametric ones, but they require data to be independent and normally distributed. In comparison, non-parametric trend tests require only that the data be independent and can tolerate outliers in the data. On the other hand, they are insensitive to the type of data distribution. (Hamed and Rao 1998; Yue et al. 2002a; Chen et al. 2007). The Mann-Kendall (MK) and Spearman’s Rho (SR) tests are examples of non-parametric tests that are applied for the detection of trends in many studies such as: Gellens 2000; Kahya and Kalayci 2004; Gadgil and Dhorde 2005; Li et al. 2008; Yaning et al. 2009; Daniel (1978); and Yue et al. (2002a). A comparison of the power of the MK and SR tests and their results showed the same power in detecting monotonic trends (Yue and Wang 2004; Novotny and Stefan 2007).
Recent studies of climate change have focused mainly on long-term variability of temperature and precipitation. ET, as the third most important climatic factor controlling energy and mass exchange between terrestrial ecosystems and the atmosphere, has received less attention (Chen et al. 2006).
Bandyopadhyay et al. (2009) used the MK test to analyze the temporal trend of reference evapotranspiration (ET0) which was estimated by the Penman Monteith FAO 56 (PMF 56) method for 133 selected stations in India. Their results showed a significant decreasing trend in ET0 all over India during the study period, which was mainly caused by a significant increase in the relative humidity and a consistent significant decrease in the wind speed throughout the country. An evaporation trend investigation in Canada revealed significant trends for June, July, August, October, and the warm season that were mainly decreasing (Burn and Hesch 2007). Palle and Butler (2001) reported a decreasing trend in sunshine hours and an increasing trend in cloudiness at four sites in Ireland. In the great plains of the United States, Garbrecht et al. (2004) analyzed trends in precipitation (P), stream flow, and ET. They showed that an upward trend in P over the last two decades of the 20th century led to a disproportionately large increase in stream flow and comparatively smaller increase in ET.
In another study that related to 150 meteorological stations in the Changjiang catchment (Yangtze River) in China during 1960–2000, Xu et al. (2006) reported downward trends for annual ET0 and pan evaporation. They concluded that the trends are mainly caused by a significant decrease in the net total radiation and to a lesser extent by a significant decline in the wind speed over the catchment.
In trend analysis over central Europe, Zaninović and Gajić-Čapka (2000) found a significant increase in potential evapotranspiration (ETp) and a decrease in runoff and soil water content for annual and warm season values during the 20th century. Dongsheng et al. (2007) have shown, using the linear regression and MK methods, an increasing tendency in the mean annual temperature, mean annual P, ETp and moisture index during 1961–2004 in northeastern China.
Tabari et al. (2011) examined the annual, seasonal and monthly trends in the PMF-56 ET0 at 20 meteorological stations during 1966–2005 in the western half of Iran using the MK test and linear regression. The annual analysis of the ET0 series indicated a positive trend in 70% of the stations according to the MK test and in 75% of the stations according to the linear regression. On a seasonal scale, stronger increasing trends were identified in ET0 data in winter and summer compared with those in autumn and spring. Meanwhile, the highest number of stations with significant trends was found in the monthly ET0 series in February, while the lowest number of stations with significant trends was observed in November. In another study, Tabari and Marofi (2011) analyzed changes of observed pan evaporation for 12 stations in Hamedan province, western Iran, from 1982 to 2003. The trend analysis was carried out using the MK test and the linear regression method. Significantly increasing pan evaporation was observed in 67% of the stations at the 95% and 99% confidence levels.
The goal of this study was to investigate the temporal trends on ET0 time series over arid regions of Iran, which were analyzed by the trend free pre-whitening (TFPW) approach (Yue et al. 2002b), using the MK and SR tests. The slope magnitude of the significant trends was also identified by the Thiel-Sen method (Thiel 1950; Sen 1968). The evaluation (performance of trend detection) of the test used was another aim of the study.
2 Materials and Methods
2.1 Site Location and Data
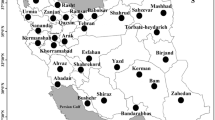
In this study, the effect of climate change on ET0 was considered for 11 synoptic stations in arid regions of Iran (Fig. 1). The 41-years (1965–2005) monthly meteorological data of mean air temperature, precipitation, atmospheric relative humidity, pressure, actual vapor pressure, net solar radiation, and wind speed were obtained from the stations. Based on the aridity index (AI), stations in arid regions (0.05 < AI < 0.20) were selected. A summary of the geographic information of the stations is presented in Table 1. The following relationship is used for the aridity index calculation (AI), by the international associations (UNESCO 1977; UNEP 1992):
where ET P is the annual mean of ET P and P is annual mean of precipitation.
2.2 Penman-Monteith FAO 56 (PMF-56)
In this study, the PMF-56 standard method was used for estimation of ET0 (Allen et al. 1998). The model equation is as follows:
where R n is the net radiation at the crop surface (MJ m−2 day−1), T is the mean daily air temperature at 2 m height (°C), U 2 is the wind speed at 2 m height (ms−1), Δ is the slope of the vapor pressure curve (kPa °C−1), G is the soil heat flux density (MJ m−2 day−1), γ is the psychrometric constant (kPa °C−1), and e a and e d are the saturation and actual vapor pressures (kPa), respectively.
2.3 Statistical Tests
In this study, in order to detect the significant trends of the considered ET0 time series of the selected stations, the MK and SR tests were used. Before any analysis, the TFPW approach was to eliminate the influence of the serial correlation of the time series. The Thiel-Sen method was applied in order to determine the slope value of the significant trends. The methods used are described as follows:
2.3.1 The MK Test
This is a rank nonparametric test that was developed by Mann (1945) and Kendall (1975), and it is superior for detecting linear or non-linear trends (Hisdal et al. 2001; Wu et al. 2008). In this test, the null (H0) and alternative hypotheses (H1) are equal to the non-existence and existence of a trend in the time series of the observational data, respectively. The related equations for calculating the MK test statistic S and the standardized test statistic Z MK are as follows:
where X i and X j are the sequential data values of the time series in the years i and j, n is the length of the time series, t p is the number of ties for the pth value, and q is the number of tied values. Positive values of Z MK indicate increasing trends, while negative Z MK values indicate decreasing trends in the time series. When \( \left| {{Z_{{MK}}}} \right| > {Z_{{1 - \alpha /2}}} \), the null hypothesis is rejected and a significant trend exists in the time series. Z 1-α/2 is the critical value of Z from the standard normal table, for 5% significant level the value of Z 1-α/2 is 1.96.
2.3.2 The SR Test
This is similar to the MK method and is a non-parametric test. The SR test is a simple method with uniform power for linear and non-linear trends and is commonly used to verify the absence of trends (Dahmen and Hall 1990; Tonkaz et al. 2007). In this test, the null hypothesis (H0) is that all the data in the time series are independent and identically distributed, while the alternative hypothesis (H1) is that increasing or decreasing trends exist (Yue et al. 2002a). The SR test statistic D and the standardized test statistic Z SR are expressed as follows:
where R i is the rank of ith observation X i in the time series and n is the length of the time series. Positive values of Z SR indicate upward trends, while negative Z SR indicate downward trends in the time series. When \( \left| {{Z_{{SR}}}} \right| > {t_{{(n - 2,1 - \alpha /2)}}} \), the null hypothesis is rejected and a significant trend exists in the time series. t (n-2,1-α/2) is the critical value of t from the t-student table, for 5% significant level. The value of t (n-2,1-α/2) for n = 41 (the sample size in this study) is 2.02.
2.4 Thiel-Sen Approach
This approach (Thiel 1950; Sen 1968) was used for estimating the magnitude of the slope of the identified trends (by the MK and SR methods). The advantage of this method is that it limits the influence of the outliers on the slope in comparison with linear regression.
where X i and X j are the sequential data values of the time series in the years i and j, and β is the estimated magnitude of the trend slope in the data series.
2.5 TFPW Approach
The data must be serially independent in the case of the non-parametric tests. Based on the performed studies, the existence of serial correlation will increase the probability for significant trend detection. This leads to a disproportionate rejection of the null hypothesis of non trend, whereas the null hypothesis is actually true. Therefore, the influence of serial correlation must be eliminated (Yue et al. 2002b). In this regard, different methods such as pre-whitening, variance correction (Hamed and Rao 1998), and TFPW (Yue et al. 2002b) have been proposed. The TFPW procedure presented here provides a better assessment of the significance of the trends for serially correlated data than the other approaches (Yue et al. 2002b; Yue et al. 2003; Zhang and LU 2009) and several researchers (Burn et al. 2004; Abdul Aziz and Burn 2006; Novotny and Stefan 2007; Leclerc and Ouarda 2007; Wu et al. 2008; Xu et al. 2008; Zhang and Lu 2009; Kumar et al. 2009) have used this procedure.
In this study, the TFPW procedure was applied to the time series with significant autocorrelation (at 5% significant level) to remove the effect of serial correlation on both tests (MK and SR).
3 Results and Discussion
3.1 Monthly Analysis
The results of the application of the MK and SR tests for trend identification of monthly ET0 were similar, and they are summarized in Table 2. As shown, the ET0 had a mixture of increasing and decreasing monthly and yearly trends. The trend tests revealed no statistically significant trends at Bandarabbas, Sabzevar and Semnan stations. Significant trends at Birjand station were a decreasing trend during the months of January, March and May as well as August to December. Esfahan station had a significant decreasing trend in June to September and in December and a decreasing trend for Kerman station occurred from June to October. At Mashhad station, the monthly ET0 were increasing in the months of July, October, and November over the period of analysis. In other stations, significant trend occurred for a few months of the year. Figure 2 shows the spatial distribution of monthly ET0 trends for each month in Iran during the period of 1965–2005.
The results for the slope magnitude of significant trends (in monthly scales) indicated that the observed trends in Esfahan, Birjand, Kerman, and Mashhad stations were more rapid in comparison with other places. The maximum values of increasing (1.00 mm/month) and decreasing (1.54 mm/month) slopes of the significant trends in the monthly ET0 data were observed in Mashhad (in July) and in Esfahan (in August), respectively. The trends of the monthly ET0 for the above mentioned stations are presented in Fig. 3. Analysis of the impact of climatic variables on the significant increasing trend in monthly ET0 shows that the increasing trend is mainly caused by a significant increase in air temperature and wind speed during the study period. Also decreasing trend of ET0 is mainly due to a significant decrease in wind speed.
3.2 Annual and Seasonal Analysis
The MK and SR tests were also applied in order to study trends in the annual and seasonal ET0 over the study period (1965–2005). Table 3 shows the MK and SR tests results for trend significance, which were similar for both tests in tested time series. Significant trends were increasing or decreasing trend (Table 3). Among the study stations, Ahvaz, Bandarabbas, Kashan, Sabzevar and Semnan stations did not exhibited any significant trend in the annual and seasonal time series. The ET0 trend at Birjand and Esfahan stations decreased in the annual and seasonal scales except winter. At Kerman Station, the monthly ET0 decreased during summer and autumn and at Bushehr Station, the decrease occurred in the annual, winter and autumn time series. Shiraz station in the autumn encountered with with a decreasing significant trend. Increasing trends were only present at Mashhad station. The annual, autumn and summer time series were characterized by significant positive trends at Mashhad station. Figure 4 shows the spatial distribution of annual and seasonal ET0 trends in Iran during the period of 1965–2005.
In the present study among the investigated stations, Mashhad station showed a maximum increasing trend of annual ET0 with an increase of 7.50 mm/year, while Esfahan station had a decreasing trend with a slope of 6.38 mm/year. Figure 5 shows the magnitude of the variations in annual ET0 for stations with significant trend during the study period.
The results of the seasonal investigations (Table 3) demonstrated that in agreement with the monthly results, the number and percent of significant cases for upward and downward trends were observed mainly in autumn and summer, respectively. On the other hand, these seasons showed more sensitivity to changes in the trend of ET0. Analysis of the impact of climatic variables on the significant increasing trend in annual and seasonal ET0 shows that the increasing trend is mainly due to a significant increase in air temperature and wind speed during the study period. Also decreasing trend of ET0 is mainly caused by a significant decrease in wind speed.
In the analysis of climate change effects in India (Bandyopadhyay et al. 2009) and China (Xu et al. 2006), decreasing trends of ET0 were confirmed while regions in Central Europe reported a significant increase in potential evapotranspiration and evapotranspiration (Zaninović and Gajić-Čapka 2000) and the annual potential evapotranspiration showed an increasing trend by itself in Northeastern China (Dongsheng et al. 2007). In the western half of Iran, annual, seasonal and monthly analysis of the ET0 series indicated a positive trend during 1966–2005 (Tabari et al. 2011)
3.3 Comparison of the MK and SR Tests for Detection of Trend Existence
The results obtained using both tests indicate that the analogous values of MK and SR tests (ratio of significant cases to total tested cases) for detections of trend in ET0 were 26% and 25%, respectively. Therefore, these tests had similar performance at the 5% significant level for analysis of trends. In cases where the detection of significance by means of the two tests was different, values of significant level of trend acceptance exhibited low difference. Yue et al. (2002a) also confirmed similar performance of MK and SR tests for analysis of trends.
4 Conclusions
In this study, temporal trends in ET0 data for 11 main stations in arid regions were analyzed. The results showed that increasing and decreasing tends were found for monthly ET0. The annual trends at Birjand, Bushehr, Esfahan, Mashhad, and Sabzevar stations were significant at the 5% significant level. The highest numbers of significant trends were found in the summer and autumn series, respectively. Results using MK and SR tests demonstrated the agreement of performance for the two tests in detection of the trend for the ET0 variable. There was a small difference in detection of the significant trend by the two tests for tested cases but in these cases, the difference in values of significant level of trend acceptance were low. Finally, the results of this study emphasize the need for more analysis on the effects of climate change on the study variable, especially in arid climate.
References
Abdul Aziz OI, Burn DH (2006) Trends and variability in the hydrological regime of the Mackenzie River Basin. J Hydrol 319:282–294
Allen RG, Pereira LS, Raes D, Smith M (1998) Crop Evapotranspiration: Guidelines for Computing Crop Water Requirements. FAO Irrigation and Drainage, Paper No. 56. FAO, Rome, Italy. pp 300
Bandyopadhyay A, Bhadra A, Raghuwanshi NS, Singh R (2009) Temporal trends in estimates of reference evapotranspiration over India. J Hydrol Eng 14(5):508–515
Burn DH, Hesch NM (2007) Trends in evaporation for the Canadian Prairies. J Hydrol 336:61–73
Burn DH, Cunderlik DH, Pietroniro A (2004) Hydrological trends and variability in the Liard River Basin. Hydrolog Sci J 49(1):53–67
Chen SB, Liu YF, Thomas A (2006) Climatic change on the Tibetan plateau: potential evapotranspiration trends from 1961–2000. Climatic Change 76:291–319
Chen H, Guo S, Xu CY, Singh VP (2007) Historical temporal trends of hydro-climatic variables and runoff response to climate variability and their relevance in water resource management in the Hanjiang basin. J Hydrol 344:171–184
Dahmen ER, Hall MJ (1990) Screening of hydrological data: tests for stationarity and relative consistency. ILRI, The Netherlands, p 58, Publication #49
Daniel WW (1978) Applied Nonparametric Statistics, Boston
Dongsheng Z, Zheng D, Shaohong W, Zhengfang W (2007) Climate changes in northeastern china during last four decades. Chin Geogr Sci 17:317–324
Gadgil A, Dhorde A (2005) Temperature trends in twentieth century at Pune, India. Atmos Environ 39:6550–6556
Garbrecht J, Van Liew M et al (2004) Trends in precipitation, streamflow, and evapotranspiration in the Great Plains of the United States. J Hydrol Eng 9(5):360–367
Gellens D (2000) Trend and correlation analysis of k-day extreme precipitation over Belgium. Theor Appl Climatol 66:117–129
Hamed KH, Rao AR (1998) A modified Mann-Kendall trend test for autocorrelated data. J Hydrol 204:182–196
Hisdal H, Stahl K, Tallaksen LM, Demuth S (2001) Have streamflow droughts in Europe become more severe or frequent. Int J Climatol 21:317–333
Intergovernmental Panel on Climate Change (IPCC) (2001) In: Houghton JT et al (eds) The Third Assessment Report of Working Group I of the Intergovernmental Panel on Climate Change (IPCC). Cambridge Univ. Press, New York, p 881
Kahya E, Kalayci S (2004) Trend analysis of streamflow in Turkey. J Hydrol 289:128–144
Kendall MG (1975) Rank correlation methods. Griffin, London
Kumar S, Merwade V, Kam J, Thurner K (2009) Streamflow trends in Indiana: effects of long term persistence, precipitation and subsurface drains. J Hydrol 374:171–183
Leclerc M, Ouarda TBMJ (2007) Non-stationary regional flood frequency analysis at ungauged sites. J Hydrol 343:254–265
Li ZL, Xu ZX, Li JY, Li ZJ (2008) Shift trend and step changes for runoff time series in the Shiyang River Basin, Northwest China. Hydrol Process 22:4639–4646
Liu Q, Yang Z, Cui B (2008) Spatial and temporal variability of annual precipitation during 1961–2006 in Yellow River Basin, China. J Hydrol 361:330–338
Mann HB (1945) Nonparametric tests against trend. Econometrica 13:245–259
Novotny EV, Stefan HG (2007) Stream flow in Minnesota: indicator of climate change. J Hydrol 334:319–333
Palle E, Butler CJ (2001) Sunshine records from Ireland: cloud factors and possible link to solar activity and cosmic rays. Int J Climatol 21:709–729
Sen PK (1968) Estimates of the regression coefficient based on Kendall’s tau. J Amer Statistical Assoc 63:1379–1389
Tabari H, Marofi S (2011) Changes of pan evaporation in the West of Iran. Water Resour Manag 25(1):97–111
Tabari H, Marofi S, Aeini A, Talaee PH, Mohammadi K (2011) Trend Analysis of Reference Evapotranspiration in the Western Half of Iran. Agr Forest Meteorol 151(2):128–136 [Available online 20 October 2010]
Thiel H (1950) A rank-invariant method of linear and polynomial regression analysis, Part 3. Proceedings of Koninalijke Nederlandse Akademie van Weinenschatpen A 53:1397–1412
Tonkaz T, Çetin M, Kâzım T (2007) The impact of water resources development projects on water vapor pressure trends in a semi-arid region, Turkey. Climatic Change 82:195–209
UNEP (1992) World Atlas of Desertification. United Nations Environment Programme (UNEP). London
UNESCO (1977) World Map of Desertification. United Nations Conference on Desertification. A/Conf., 74/2
Wu H, Soh LK, Samal A, Chen XH (2008) Trend analysis of streamflow drought events in Nebraska. Water Resour Manage 22:145–164
Xu C, Gong L, Jiang T, Chen D, Singh VP (2006) Analysis of spatial distribution and temporal trend of reference evapotranspiration and pan evaporation in Changjiang (Yangtze River) catchment. J Hydrol 327:81–93
Xu J, Yang D, Yi Y, Lei Z, Chen J, Yang W (2008) Spatial and temporal variation of runoff in the Yangtze River basin during the past 40 years. Quatern Int 186:32–42
Yaning C, Changchun X, Xingming H, Weihong L, Yapeng C, Chenggang Z, Zhaoxia Y (2009) Fifty-year climate change and its effect on annual runoff in the Tarim River Basin, China. Quatern Int 208:53–61
Yue S, Wang CY (2004) The Mann–Kendall test modified by effective sample size to detect trend in serially correlated hydrological series. Water Resour Manage 18:201–218
Yue S, Pilon P, Cavadias G (2002a) Power of the Mann-Kendall and Spearman’S rho tests for detecting monotonic trends in hydrological series. J Hydrol 259:254–271
Yue S, Pilon P, Phinney B, Cavadias G (2002b) The influence of autocorrelation on the ability to detect trend in hydrological series. Hydrol Process 16:1807–1829
Yue S, Pilon P, Phinney B (2003) Canadian streamflow trend detection: impacts of serial and cross correlation. Hydrol Sci J 48(1):51–63
Zaninović K, Gajić-Čapka M (2000) Changes in components of the water balance in the Croatian Lowlands. Theor Appl Climatol 65:111–117
Zhang S, Lu XX (2009) Hydrological responses to precipitation variation and diverse human activities in a mountainous tributary of the lower Xijiang, China. Catena 77:130–142
Zhang Q, Liu C, Xu CY, Xu YP, Jiang T (2006) Observed trends of water level and streamflow during past 100 years in the Yangtze River basin, China. J Hydrol 324:255–265
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Shadmani, M., Marofi, S. & Roknian, M. Trend Analysis in Reference Evapotranspiration Using Mann-Kendall and Spearman’s Rho Tests in Arid Regions of Iran. Water Resour Manage 26, 211–224 (2012). https://doi.org/10.1007/s11269-011-9913-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11269-011-9913-z