Skip to main content
SpringerLink
Log in

Two-Dimensional Horizontal Numerical Model of Open Flow over a Bed with Obstacles

  • Hydrophysical Processes
  • Published:
Water Resources Aims and scope Submit manuscript

Abstract

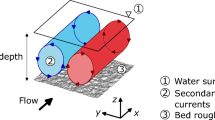
An explicit numerical algorithm for solving two-dimensional system of shallow-water equations is presented. The algorithm is based on the control volume method with recording mass and momentum fluxes through the faces of the volume with the use of an approximate solution of the Riemann problem. A numerical solution is compared with analytical solutions for a flow over a bottom step and with data of laboratory experiments in a flume with a sloped bed or a bed with an obstacle.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

REFERENCES

  1. Veksler, A.B., Ivashintsov, D.A., and Stefanishin, D.V., Nadezhnost’, sotsial’naya i ekologicheskaya bezopasnost’ gidrotekhnicheskikh ob’‘ektov: otsenka riska i prinyatie reshenii (Reliability and Social and Environmental Safety of Hydraulic-Engineering Structures: Risk Assessment and Decision Making), St. Petersburg, 2002.

  2. Girgidov, A.A., Modeling of Oil Spreading after a Failure of Oil Storage, Tr. V mezhdunar. konf. “Akvaterra” (Proc. V Intern. Conf. “Aquaterra”), St. Petersburg, 2002, pp. 45–46.

  3. Klimovich, V.I. and Prokof’ev, V.A., Numerical Modeling of Interaction between Open Flows and Obstacles, Tr. Mezhdunar. konf. “Vodnye problemy-2001” (Proc. Intern. Conf. “Water Problems”), Yerevan, 2001, pp. 413–416.

  4. Kulikovskii, A.G., Pogorelov, N.V., and Semenov, A.Yu., Matematicheskie voprosy chislennogo resheniya giperbolicheskikh sistem uravnenii (Mathematical Problems of Numerically Solving Hyperbolic Systems of Equations), Moscow: Fizmatlit, 2001.

    Google Scholar 

  5. Prokof’ev, V.A., Modern Numerical Schemes for Modeling Rapid Flows and Dam-Break Waves Based on the Control Volume Method, Gidrotekh. Stroit., 2002, no. 7, pp. 22–29.

  6. Prokof’ev, V.A., Modeling the Consequences of Hydrodynamic Accidents: Numerical Algorithm and Software Implementation, Tr. V mezhdunar. konf. “Akvaterra” (Proc. V Intern. Conf. Aquaterra), St. Petersburg, 2002, pp. 118–119.

  7. Alcrudo, F. and Benkhaldoun, F., Exact Solutions to the Riemann Problem of the Shallow Water Equations with Bottom Step, Computers Fluids, 2001, vol. 30, pp. 643–671.

    Article  Google Scholar 

  8. Atzeni, A., Balzano, A., Falconer, R.A., et al., Comparison of Shallow Water Flow Models with Accurate Treatment of Flooding and Drying, Proc. XXIX IAHR Congr., Peking, 2000, pp. 211–222.

  9. Aureli, F., Mignosa, P., and Tomirotti, M., Dam-Break Flows in Presence of Abrupt Bottom Variations, Proc. XXVIII IAHR Congr., Graz, 1999, pp. 163–171.

  10. Aureli, F., Mignosa, P., and Tomirotti, M., Numerical Simulation and Experimental Verification of Dam-Break Flows with Shocks, J. Hydraulic Res., 2000, vol. 38, no.3, pp. 197–200.

    Google Scholar 

  11. Delis, A.I., Skeels, C.P., and Ryrie, S.C., Evaluation of Some Approximate Riemann Solvers for Transient Open Channel Flows, J. Hydraulic Res., 2000, vol. 38, no.3, pp. 217–231.

    Google Scholar 

  12. Nujic’, M., Efficient Implementation of Non-Oscillatory Schemes for the Computation of Free-Surface Flows, J. Hydraulic Res., 1995, vol. 33, no.1, pp. 101–111.

    Google Scholar 

  13. Sanders, B.F., High Resolution and Non-Oscillatory Solution of the St.Venant Equations in Non-Rectangular and Non-Prismatic Channels, J. Hydraulic Res., 2001, vol. 39, no.3, pp. 236–244.

    Google Scholar 

  14. Zuhua, C., Guangqian, W., and Zhishi, W., Numerical Solution of the Two-Dimensional Unsteady Depth-Averaged Flow and Solute Transport, Proc. XXIX IAHR Congr., Peking, 2000, pp. 192–205.

Download references

Author information

Authors and Affiliations

  1. All-Russia Research Institute of Hydraulic Engineering, ul. Gzhatskaya 21, St. Petersburg, 195220, Russia

    V. A. Prokof’ev

Authors
  1. V. A. Prokof’ev
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

__________

Translated from Vodnye Resursy, Vol. 32, No. 3, 2005, pp. 282–294.

Original Russian Text Copyright © 2005 by Prokof’ev.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Prokof’ev, V.A. Two-Dimensional Horizontal Numerical Model of Open Flow over a Bed with Obstacles. Water Resour 32, 252–264 (2005). https://doi.org/10.1007/s11268-005-0034-z

Download citation

  • Received:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11268-005-0034-z

Keywords

Search

Navigation