1 Introduction

A key limitation of today’s successful ANN algorithms is that they cannot operate autonomously in a closed-loop dynamic environment the way biological creatures can. The ANNs typically work in batch mode with single sensory modality; ANNs are principally restricted to classifying audio or visual patterns, one at a time but do not contribute to any further action based on classification result nor does the classification result influence future classification. In contrast, biological creatures decide and act based on active real-time, multi-modal perception, and fusion of sensory inputs. Another limitation of current ANN models is that they have poor and ad-hoc mechanisms for multiple-timescale sequence processing and memory. The brain, in contrast, has evolved to select, process, and memorize streaming information over many inherent time scales. This capability enables the amazing time coordinated motor performance of, for instance, a table tennis player.

It is clear that current deep learning technology is very useful, but it also suffers from problems with potential technical usability impact. Firstly, it relies almost exclusively on supervised learning, which requires classification and labeling of training examples by humans. In contrast, biological brains are designed for unsupervised learning from abundantly available unlabeled data and on reinforcement learning with only very coarse global feedback from the environment.

Secondly, the prominently featuring learning algorithm is error back-propagation, which is more competent than biological Hebbian forms of synaptic plasticity and learning, but also quite dubious from a neurobiological perspective. It requires very detailed error information to follow error gradients. This requirement for high precision is why most ANN hardware accelerators are focusing on the inference and not on the learning side of the network. Correlation-based learning methods are employed in the brain and are thus provably robust enough to function well with very noisy and imprecise computing substrate, such as real neurons and synapses. The BCPNN is proven to be able to function using lower precision. In the work done by Vogginger et al. [1], it was shown that the BCPNN could work with precision as low as 22bits.

Thirdly, there is a prominent architectural difference between the predominantly feed-forward wired deep learning networks compared to the brain networks dominated by recurrence. A typical cortical area receives about 10% of its synapses from lower-order structures. The rest are lateral and top-down, mostly recurrent connections from other cortical areas, thought to be involved in among other things associative memory, constraint-satisfaction for perceptual segmentation and reconstruction, as well as top-down selective control of attention [2].

To achieve brain-like cognitive capability, we need to adopt biologically plausible brain models with a proven function, e.g., efficient associative memory [3,4,5,6]. In this paper, we have adopted the Bayesian Confidence Propagation Neural Network (BCPNN) as the candidate biologically plausible model. This model has, for a long time, been used for simulation of cortical associative memory processes, recently also of working memory, which is a key determinant of human intelligence and advanced cognitive function [7, 8]. It has further been used to model sequence learning and serial recall [5], olfactory perception [6], and decision making in basal ganglia [7, 8]. Recently it has been evaluated in a typical machine learning classification benchmark, i.e., MNIST handwritten digit recognition using unsupervised learning of hidden layer representations [9, 10]. It achieved 97.5% correct on the unseen test set, which is only 1% less than a corresponding back-propagation network [11].

The details on how BCPNN can help to achieve brain-like cognition and its functions are outside the scope of this paper, where we focus on its efficient architectural design. However, BCPNN also provides the benefit of a more compact solution in terms of its algorithmic architecture, compared to other biologically plausible models. Typically, these spiking neural networks (SNNs) use Leaky Integrate and Fire (LIF) neurons and Spike Time-Dependent Plasticity (STDP) learning rule. The LIF-STDP type of networks closely emulates the behavior of individual neurons. The use of single neurons as the basic elements makes them extremely large and impractical for larger-scale models, such as the human cortex. The BCPNN, on the other hand, is composed in terms of coarse-grained atomic neuronal units that model cortical columns. This makes BCPNN more compact and practical to emulate the human scale cortex.

This work builds on our previous work on implementing eBrain [12] and presents three novel contributions that differentiate it from the previous work:

  1. 1.

    We present a semi-formal method to co-explore the algorithm and architecture design space for an extremely demanding biologically plausible model of the cortex, that requires 162tflop/s of computations and 200 tb/s of memory bandwidth.

  2. 2.

    We introduce a novel custom 3d-dram design with a BCPNN specific addressing scheme.

  3. 3.

    We benchmark against a GPU implementation and a best-effort estimate implementation on spinnaker-2. We also analyze the results to show what makes eBraiII, non-incrementally more efficient, compared to GPU and spinnaker-2.

2 The BCPNN Model

The BCPNN model features Hebbian-Bayesian synaptic plasticity for spiking neurons [13]. Next, we introduce the computational model of BCPNN and justify the lazy evaluation model and derive its computational, storage, and spiking bandwidth requirements. Finally, we discuss the parallelism in BCPNN. These details then become the basis for the design and dimensioning of eBrainII in the next section 3.

2.1 BCPNN Overview

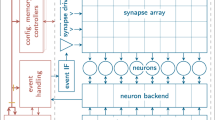
The atomic neuronal unit in the BCPNN is Mini-Column Unit (MCU) that mimics 100 neurons in a cortical column whose outputs are strongly correlated. The dimensions we state here are for human-scale BCPNN. Hyper Column Units (HCUs) encapsulate 100 MCUs. In every time step, the MCUs inside each HCU compete in a soft winner take all fashion. The winning MCU, if any, then generates an output spike. Each HCU has 10,000 possible inputs. These inputs are connected to the output of MCUs in the same or other HCUs.

A human-scale BCPNN has 2 million HCUs. Each HCU can receive, on average 10,000 incoming pre-synaptic spikes/s coming from MCUs in other or the same HCU. Each HCU can produce 100 outgoing post-synaptic spikes/s. Each such outgoing post-synaptic spike is fanned out to 100 HCUs, effectively creating 10,000 output spikes/s/HCU.

2.1.1 Synaptic Weights of BCPNN

In this section, we explain the basis for the synaptic weights of BCPNN, see Fig. 1a. The MCUs are modeled as leaky integrators. The input and output spikes, Si and Sj, respectively, are low pass filtered in three stages to generate traces called Zi, Ei, Pi, and Zj, Ej, Pj, see Fig. 2. Each of the traces has a different time constant, namely τz, τe, and τp, as shown in Fig. 2. The index i represents one of the 10,000 inputs to HCU at which the input spike arrives, see Fig. 1. Similarly, the index j represents one of the 100 outputs of the HCU that emits spikes. The i traces are stored in an i-column vector, and the j traces are stored in a j-row vector. The correlation of i and j traces for Z, E, and P traces are stored in the ij-matrix. The P traces, Pi, Pj, and Pij, represent the estimated posterior Bayesian probabilities and forms the basis for calculating the weights {wij}, which are also stored in the matrix. Lastly, the bias bj of each MCU, representing its prior activation, is derived from the trace pj. This bias plus the sum of weights from incoming spikes determines the activation-potential of each target MCU. These activation potentials are the basis for a soft winner take all competition to decide with MCU(s) will fire.

Figure 1
figure 1

HCU structure and computations in a human scale BCPNN.

Full size image
Figure 2
figure 2

The BCPNN Computational Model in terms of a cascade of traces and their differential equations.

Full size image

2.1.2 Computation Model of BCPNN

The original computational model of BCPNN is called periodic computational model. In this model, the whole synaptic matrix of each HCU has to be fetched and updated every millisecond (ms); 1 ms is the simulation step in BCPNN. The leaky aspect of MCUs implies that each synaptic trace is decayed every ms irrespective of input or output spikes. The presence of an input or an output spike triggers the reinforcement of the related traces. The equations in the red or blue boxes in Fig. 2 are invoked, depending on the existence of an input or output spike. The updated activation-potentials of MCUs then compete, every ms, to decide if an output spike(s) is/are generated or not.

The periodic update model is extremely expensive in terms of the required bandwidth because it requires a) updating the entire synaptic weight matrices, rows, and columns every ms for decaying. Additionally, it requires updating the volume of data equivalent to all synaptic weights (matrices, rows, and columns) twice per second Once for updating the rows in response to 10,000 input spikes/s. The second time for updating the column in response to 100 output spikes/s. Note that, in both cases, there is a high spatio-temporal locality. This means that the same row/column could be updated in rapid succession.

To avoid this massive bandwidth requirement, a lazy evaluation scheme has been proposed and implemented in [14]. In the lazy evaluation scheme, each cell in the synaptic storage and spike is time stamped. Rather than updating the synaptic storage every ms for decay, the decay is integrated for the time lapsed between the spike’s emission/arrival and the time when the cell was the last accessed and updated.

figure a

The lazy evaluation scheme requires additional computation for the integration and storage of time stamps. However, compared to the energy saved in accessing the entire synaptic storage every ms, these overheads are trivial, as analyzed in [14].

The BCPNN implementation reported in this paper is based on the lazy evaluation scheme [14]. A pseudocode describing the execution process of the BCPNN is presented in Algorithm 1. Algorithm 1 is using the keyword parbegin and parend to describe the parallelism of the BCPNN. The code—blocks inside the parbegin/parend can be executed in parallel and independent from each other. In the lazy evaluation scheme, computations are divided into three categories. Two of these, the row and the column updates are based on lazy evaluation, and the third, the support update, remains periodic.

  1. 1.

    Row update: on an average 10,000 spikes/s or 10 spikes/ms are received by each hcu. These spikes address specific rows in an hcu. The row corresponding to each input spike is fetched. The integrated decay for each synaptic trace is calculated, as described above, and is applied to it. The synaptic trace is then updated according to the equations shown in the red box in fig. 2 and is stored back.

  2. 2.

    Column update: if an output spike is generated by an mcu, its corresponding column is fetched. The integrated delay is calculated and applied, similar to the row update. The synaptic trace is then updated according to the equations shown in the blue box in Fig. 2 and stored back.

  3. 3.

    Support update: at every ms, the support vector is updated to decide which, if any, of the 100 mcus has fired to generate the output spike. The support update has to be periodic since it is the one that calculates the existence (or not) of an output spike. In essence, the support update is what drives the BCPNN network, by activating the hcu and generating the spikes.

Many ANNs and scientific applications are modeled as a matrix or vector multiplications. Inner loops of such applications are efficiently handled by GPUs. However, the kernel operations in BCPNN are far more complex. The operations that are carried out during the lazy evaluation update of a synaptic cell can be seen in Eq. 1–5. The customization of eBrainII synaptic storage and computational logic targets vectorizing such complex operations. This customization, elaborated in the following sections, is what gives eBrainII its 3 orders superior energy-delay product compared to GPU and SpiNNaker-2.

$$ {Z}_j={Z}_j\cdotp {e}^{-{k}_{z_j}\cdotp pdt} $$
(1)
$$ {Z}_i={Z}_i\cdotp {e}^{-{k}_{z_i}\cdotp pdt} $$
(2)
$$ {E}_{ij}=\left({E}_{ij}+{Z}_i\cdotp {Z}_j\cdotp {k}_n\right)\cdotp {e}^{-{k}_E\cdotp pdt}-{Z}_i\cdotp {Z}_j\cdotp {k}_n\cdotp {e}^{-{k}_f\cdotp pdt} $$
(3)
$$ {P}_{ij}=\left({P}_{ij}+{E}_{ij}\cdotp {k}_1+{Z}_i\cdotp {Z}_j\cdotp {k}_2-{Z}_i\cdotp {Z}_j\cdotp {k}_3\right){e}^{-{k}_P\cdotp pdt}-\left(\left({E}_{ij}\cdotp {k}_1+{Z}_i\cdotp {Z}_j\cdotp {k}_2\right)\cdotp {e}^{k_E\cdotp pdt}-{Z}_i\cdotp {Z}_j\cdotp {k}_3\cdotp {e}^{k_4\cdotp pdt}\right) $$
(4)
$$ {W}_{ij}= wgain\cdotp \Big(\mathit{\log}\left(\frac{\left({P}_{ij}+{eps}^2\right)}{\left({P}_i+ eps\right)\cdotp \left({P}_j+ eps\right)}\right) $$
(5)

2.1.3 Bandwidth for Spike Propagation

The bandwidth for spike propagation in BCPNN is modest, 200 GBs/s. Figure 3 shows the fields of BCPNN spike and the calculation for aggregate spike propagation bandwidth. The spikes themselves are not stored in the main memory, but they are directly generated and consumed by the HCUs. Some fields are beyond the scope of this paper and are used during the structural plasticity phase of training. Two of the three remaining fields are obvious, i.e., Destination HCU and Row. The third field, Delay, is used to emulate biological delay required for a spike to propagate from source HCU to the destination HCU.

Figure 3
figure 3

BCPNN Spike components and bandwidth.

Full size image

We note here that while the conceptual BCPNN spike is just a pulse, the spike in eBrainII is not binary. The eBrainII spike requires 10 bytes, as illustrated in Fig. 3, to hold the necessary information required by the BCPNN learning rule.

The BCPNN spikes are associated with propagation delay corresponding to the physical distance between emitting and receiving HCUs. This delay is used to emulate biological delay. Spike propagation in electronic systems is nearly instantaneous compared to the ms standards of biology. For this reason, when an input spike arrives at an HCU, it is first stored in a delay queue. Once the delay is elapsed, they are moved to an active queue.

2.1.4 Summary of BCPNN Requirements

We summarize the above discussion with the requirements of the lazy evaluation model in Table 1. The j-vector, being sufficiently small, is stored locally and excluded from the bandwidth requirement to synaptic storage. The computational requirements are calculated directly from the operations required by the BCPNN equations. The number of times these equations are invoked is based on BCPNN requirements that on an average 10,000 row updates and 100 column updates happen every second. Since we know the equations involved in row and column updates, we are in a position to know the number of computational operations and also the storage access.

Table 1 Requirements for Lazy Evaluation model of human scale BCPNN containing 2 million HCUs.
Full size table

2.2 The Parallelism in BCPNN

BCPNN computation is embarrassingly parallel and deeply hierarchical, as shown in Fig. 4a. Each of the 2 million HCUs are independent threads with their own synaptic weight storage; there is no memory consistency problem.

Figure 4
figure 4

Parallelism options in BCPNN, a) illustrate the deep hierarchy of parallelism in BCPNN, and b) presents the parallelism of execution threads in the BCPNN.

Full size image

Each HCU thread, in turn, has three concurrent threads for a) row computation in response to the input spikes, red box in Fig. 2, b) column computation in response to the output spikes, blue box in Fig. 2, and c) the support computation that is periodically performed every ms, see Fig. 4b. Though these three categories of threads are concurrent, each row and column update have to be atomic. The two operations cannot be interleaved because the two threads share the same storage; this is conceptually also shown by the overlap of red and blue boxes in Fig. 2. However, multiple row and column computations can be done in parallel, as these computations do not share data. The support computation, in contrast, is independent and can be carried in parallel to both row and column computations.

Each row and column computation threads can themselves be split into embarrassingly parallel computations. Each cell in the row or column can be updated independently. Finally, the computation for each cell involves numeric solutions to a) the differential equations shown in Eq. 1–5, and b) integrated decay update. These computations are fairly complex and have a deep arithmetic flow graph with rich potential for arithmetic level parallelism (ALP). This observation also applies to support computation.

3 eBrainII: Design & Dimensioning

The design space for implementing the BCPNN is spanned by the dimensions corresponding to the parallelism options discussed in section 2.2., and shown in Fig. 4a. The valid solutions in this space are the ones that fulfill the BCPNN requirements shown in Table 1 and the ones that the different technology options permit. Figure 4b illustrates the parallelism of execution inside each HCU. Each HCU thread services row-computation, column-computation, and periodic support-vector computation as atomic sub-threads, see sections 2.1.2. An HCU can have more than one of these threads running in parallel, apart from the support computation has to be executed only once per ms. Each of these three threads can be further parallelized to sub-threads that update the synaptic traces of a single cell. These sub-threads use their own computational units and FSM and are exposed to arithmetic level parallelism. In this section, we discuss the design and technology space for eBrainII and how we systematically made the design and dimensioning decisions.

3.1 eBrainII’s Hierarchical Organization

The requirements for a human scale BCPNN, as listed in Table 1, are obviously beyond a single chip solution for any technology available today. For this reason, eBrainII will be implemented as multiple chips called Brain Computation units (BCUs). The hierarchical organization of the eBrainII can be seen in Fig. 5. Each BCU has resources to implement Pmax HCUs. A BCU can be split in M memory vaults, each one of them servicing P HCUs, Pmax = P × M. There are two extreme options for how the resources for these HCUs can be organized.

Figure 5
figure 5

The hierarchical organization of eBrain.

Full size image

One extreme is to cluster the synaptic weights for all HCUs in a single storage unit, one vault, accessed over a single shared channel for Pmax non-deterministically concurrent HCU processes. The non-determinism makes it hard to dimension the shared channel and would require over-dimensioning it. The second extreme option is to have Pmax vaults, each serving a single HCU. Since each HCU requires only 25 MBs, this would compromise the efficiency of the storage unit because the area of peripheral circuitry would overwhelm the area for bits. The optimal size of the vault, as usual, is somewhere in between, where each vault integrates P < Pmax HCUs. This would give sufficiently small DRAMs to have the benefit of high speed and low energy and acceptable overhead of the peripheral circuits. We call these vaults as H-Cubes. In each H-Cube, there are P parallel threads, each with its own R floating-point units (FPUs), control, and scratchpad resources.

3.2 The Design Flow for Dimensioning eBrainII

The design flow to dimension eBrainII in terms of the order of dimensioning decisions, functional and technology constraints, and their dependencies is shown in Fig. 6. The process starts by factoring in the real-time constraint on the worst-case number of input spikes that must be handled in each ms. The worst-case number of spikes that must be dealt with in each ms are derived from the BCPNN specification that the average input spike rate is 10 spikes/ms and that they are Poisson distributed, see Fig. 7. The worst-case number of spikes, in turn, decides the worst case requirement on the bandwidth to 3D-DRAM and computational load.

Figure 6
figure 6

The Design flow for dimensioning eBrainII.

Full size image
Figure 7
figure 7

The probability of dropping spikes as a function of queue size to deal with the max number of spikes/ms and its impact on Computational Load and Bandwidth.

Full size image

The second aspect of eBrainII that must be dimensioned is the synaptic storage system. In section 5, we defend the choice of using custom 3D DRAM for the synaptic storage and how the P′ and M parameters are decided partly based on design space exploration, and partly based on prevalent standards and pragmatics, like improving yield. The channel width has been customized for the BCPNN weight matrix cell and the frequency adjusted to cover the worst-case bandwidth. Additionally, the DRAM row/page size has been customized to be of the same size as the BCPNN weight matrix row size, and the data organization and memory controller are also customized for BCPNN. Both customizations, the channel width, and the DRAM dimensions improve utilization and lower the energy consumed by the synaptic storage subsystem.

The third and the last aspect of dimensioning concerns the logic that implements the BCPNN computation. The computation core has to fulfill the worst-case computational load (0.5 MFlop/ms) and the area and frequency constraint imposed by the decision on the P′ parameter while dimensioning the synaptic storage. Concretely, the logic for P′ HCUs cannot exceed the footprint of the synaptic storage for P′ HCUs, the two together form an H-Cube. The H-Cube logic should also have a frequency that is compatible with the DRAM frequency and sufficiently fast to meet the worst-case computational load. The frequency, in turn, decides the number of FPUs, the R parameter. The micro-architecture for the logic core is customized for BCPNN.

In the next three sections, we elaborate the dimensioning of spike queue, synaptic storage, and computational core for eBrainII.

4 Spike Queue Dimensioning

One of the reasons for having the spike queue is used to absorb the worst-case burst of spikes. Theoretically, one needs an infinite size queue to ensure no spikes would ever be dropped; the tail of Poisson distribution approaches zero asymptotically. However, in practice, we dimension a queue size that ensures an acceptable drop rate. To find an acceptable spike drop rate, we assumed that the spikes arrive at each HCUs with Poisson distribution with a mean value (λ) of 10 input spikes/ms. This assumption is based on BCPNN specifications. Next, we plotted the complement of the cumulative Poisson distribution, Eq. 6. The complement of the cumulative probability depicts the probability of dropping spikes and is plotted in Fig. 7.

$$ P\left(x,\lambda \right)=1-{\sum}_{k=0}^{x-1}\frac{e^{-\lambda }{\lambda}^{x-1}}{k!} $$
(6)

This plot shows the probability of having x-or-more, i.e., x + spikes/ms. The leftmost value is 0+ spikes, and that has a probability of 1, whereas the probability of having 10+ spikes is ~0.5 as expected. As can be seen, the probability reduces to near 0, after 22+ spikes.

The x + values can also be interpreted as the queue-size. For instance, if we have a queue-size of 10, in each ms, there is a 50% chance that more than 10 spikes will arrive, and spikes will be dropped. If instead, we have a queue size of 22, there will be very few ms(s) in which more than 22 spikes will arrive. Based on these arguments, we selected the queue size to be 36 to reduce the probability of dropping spikes to near zero per ms; this implies a 30% probability of dropping spike once in a month. An acceptable spike drop-rate decides the size of the spike queue, and this, in turn, provides a constraint on computational load and the bandwidth to 3D DRAM, also shown in Fig. 7.

Delay Queue Dimensioning: As discussed in section 2.1.3, there is a need to emulate biological delay. The queue dimensioning above is when the spike delay has been counted down to zero. We also need a spike for the delay to elapse that we call as delay queue. The delay queue dimension is derived from the active queue dimension by multiplying it by the average biological delay. For the human scale BCPNN, the average delay is 4 ms, which means that on an average, a spike in the delay queue will persist for 4 ms time slots before being moved to active queue. For this reason, we need the delay queue to be four times as large as the active queue.

4.1 Constraints on Synaptic Storage Access and Computation

An important implication of dimensioning the spike queue is that it sets the worst-case bandwidth and computation load constraints. As discussed above, the worst-case number of input spikes that eBrainII will deal with is 36. This implies that eBrainII should be dimensioned to do the following in this worst-case ms: a) Do the support update including storage access for read/write, b) Potentially do the column update, read-compute-write, in case support update results in an output spike and c) Do row updates, again read-compute-write, corresponding to the 36 input-spikes.

An early design decision that we can easily make is that since periodic update happens irrespective of input or output spikes every ms and the data needed for it is modest 3.2 KB, it can be stored locally and not clog the bandwidth for the main synaptic weight matrix. Based on this, worst case bandwidth and computational load requirements are as follows: 640 MBs/HCU/ms and 0.5 MFlop/ms.

5 Synaptic Weights Storage Subsystem

The synaptic storage and bandwidth requirements are the dominant requirements in Table 1. We note here that the sole purpose of the 3D DRAM is to store the synaptic traces and weights, as illustrated in Fig. 1a. The 3D DRAM has to be optimized in such a way that the fetching and storing of the synaptic traces and weights, during the row and column update, is done as efficiently as possible. The spikes are not stored in the 3D DRAM, and they are directly generated, distributed, and consumed by the HCUs. Local queues in the logic die are used to buffer the spikes before consumption, see section 4. The size of the spike queues is 1000x smaller than the synaptic matrix, that is stored in the DRAM.

In this section, we justify the technology choice of custom 3D DRAM, the dimensioning and architecture for the 3D DRAM, and how did we customize the data organization and memory control to optimize the channel bandwidth.

5.1 The Case for Custom 3D-DRAM

There are many emerging memory technologies with attractive attributes like non-volatility, low energy, and high density, etc. [15]. However, DRAM still has the best combination of density, speed, endurance, write energy, and manufacturing maturity, including 3D integration. The maturity of the technology and its design methods provide us with accurate circuit-level parametric design capability to customize the design and know its cost accurately. In the past, we have also used custom 3D DRAM for bioinformatics applications as well [16].

Given the large storage and bandwidth requirements, 50 TB, and 200 TBs/s, 3D integrated DRAM is an obvious choice. There are two competing standards for 3D integrated DRAM: Hybrid Memory Cube (HMC) and High Bandwidth Memory (HBM) [17, 18]. However, both options have a limited number of channels/links. The HMC has a maximum of four links, and HBM has a maximum of eight channels. Thus, targeting very large shared data of 1 to 2 GB over a high bandwidth shared channel/link. BCPNN is embarrassingly parallel at a much finer granularity; each HCU needs 25 MBs. To use HMC and HBM, would imply packing synaptic storage for 32 to 64 non-deterministically concurrent HCUs in a large memory over a shared channel. Shared channel for non-deterministically concurrent HCU processes could result in over-dimensioning the channel cope with peak traffic and underutilization when there is slack in the traffic. Finally, these memories cannot be custom dimensioned to match the dimensions of the BCPNN data structure to improve access efficiency. These considerations motivated us to settle for a custom 3D DRAM. Additionally, to fully exploit the high available bandwidth of through-silicon vias (TSVs), the custom 3D-DRAM is implemented using fine-grained rank-level partitioning and stacking architecture [19].

5.2 The H-Cube Dimension and Architecture

The H-Cube dimension decides the number of HCUs that share a channel to 3D DRAM vault, the P′ parameter in Fig. 5. The 3D DRAM vault stores the synaptic traces and weights of these P′ HCUs. A smaller value of P′ implies higher architectural efficiency because fewer HCUs would contend for the channel bandwidth. However, a smaller value of P′ implies a smaller DRAM partition, which in turn lowers the cell efficiency. Cell efficiency is defined as the percentage of the total area used by the storage cells to the total area, including the peripheral circuits like row buffer, sense amplifier, etc. The cell efficiency of commodity DRAMs is usually 45–55%. For this reason, we set the lower limit to be 40%. Thus, our exploration for 28 nm node resulted in 128 Mb memory tile per bank, see Fig. 8. This configuration provides a nearly optimum solution from the perspective of cell efficiency, vault area, and energy consumption for this application [19]. Eight DRAM layers add up to 1 Gb per vault that corresponds to synaptic storage for 5 HCUs, i.e., P′ = 5. Since the power of two simplifies addressing, we settled for P′ = 4, allowing us to also reserve some space for future extensions.

Figure 8
figure 8

The organization of BCU in terms of M H-Cubes.

Full size image

5.3 Dimensioning TSV Channel Width and Frequency

The HCU computations are in the granularity of one synaptic cell, 192 bits. Hence, the granularity of DRAM accesses is also set to 192 bits. This granularity imposes the channel burst length (BL) times the databus width (DQ) to be equal to 192 bits. The possible combinations of DQ and BL are (96, 2), (48, 4), (24, 8), etc. Higher values of DQ width results in proportionally higher channel bandwidth, while adversely affecting the power dissipation and TSV area. Since the aim of custom 3D DRAM is to have a high number of channels, we choose the midrange DQ count of 48 and burst length of 4 as a good tradeoff between TSV area and DRAM power dissipation.

Finally, to address the bandwidth constraints for the worst-case ms, the custom 3D-DRAM I/O frequency must be tuned to a minimum of 400 MHz. With the presented dimensions, the 3D-DRAM vault delivers an effective bandwidth of 4.35GB/s. This frequency not only achieves the bandwidth goal of 2.6GB/s, or 4 × 640 KB/ms but is in alignment with logic layer frequency of 200 MHz that we elaborate in section 6. In other words, the single-cycle data transaction granularity (192 bits) of an HCU is equivalent to two DRAM cycle burst transactions.

The row dimension was customized to be an exact multiple of synaptic weight matrix cell that requires 192 bits. This customization of the row dimension optimizes the memory access. Since there are 100 cells, see Fig. 1, the DRAM row size was dimensioned to be 100 × 192b. The logical weight matrix row size is matched with the physical row size in the vault.

5.4 Dimensioning the BCU

Each BCU has one logic die, and eight layers of stacked DRAM dies integrated with TSVs. The decision for 8 layers is based on what is possible in today’s manufacturing technology. BCUs are divided into M equal-sized partitions on each of the nine dies (8 DRAM +1 Logic) and aligned to create M H-Cubes. Each H-Cube has a memory vault that is private for the logic die underneath it, as shown in Fig. 8. A single tile per bank and single bank per die were chosen to reduce the overhead of peripheral circuits.

Given that each DRAM layer in a vault is 128 Mb, the present DRAM manufacturing norm suggests that we can either have 4Gb or 8Gb. In the interest of lower cost and higher yield, we have selected 4 Gb per layer. For eight layers, this adds up to 32Gb, thus allowing 32 H-Cubes. The timing, current, and area values of the presented custom 3D DRAM for the 28 nm process with the TSV pitch of 40 μm are extracted from DRAMSpec [20, 21], and the exact area dimension of each H-Cube is shown in Fig. 8.

5.5 BCPNN Specific Data Organization

While the previous section focused on dimensioning of the 3D-DRAM for BCPNN, in this section, we focus on the custom data organization for the BCPNN. This custom data organization is needed to optimize and achieve the desired bandwidth for the worst-case ms, as it was explained in section 4.

Row misses are the primary cause of the inadequate utilization of the maximum DRAM bandwidth that results in reduced performance, timing penalties, and increased DRAM energy. The optimization of the DRAM physical address mapping is one of the approaches to reduce the number of row misses. There are a few prevailing address mapping schemes, such as Bank Interleaving [22, 23], Permutation-Based Page Interleaving [24, 25], Bit-Reversal [26]. Apart from these general-purpose address mapping schemes, a few memory controllers employ an address mapping that is tailored for a particular application, for example, the Toggling Rate Analysis presented in [27, 28]. These Application-Specific Memory Controllers (ASMC) [29] are designed from the overall system perspective and effectively utilize the application knowledge to largely improve the memory system bandwidth and reduces the DRAM energy in contrast to general-purpose memory controllers. In our work, eBrainII, we have selected to implement such an ASMC.

A naive approach to store the big synaptic matrix of size 10,000 × 100 BCPNN cells is direct mapping. This addressing will allow every row of the synaptic matrix to be mapped to a single DRAM row in the same bank. This simple technique is very effective for accessing an entire row of the synaptic matrix. It allows all 100 cells of that row are continuously available on the DRAM data bus without any DRAM row misses. In contrast, the column access of the synaptic matrix deteriorates the DRAM performance due to a huge number of DRAM row misses, i.e., one row-miss per ij cell access. This mapping imposes a high penalty on available DRAM bandwidth utilization and energy consumption. Identifying the low DRAM performance or inappropriateness of the prevailing address mapping schemes mentioned above for the BCPNN application, this work proposed a novel application-specific address mapping called Row-Merge.

The Row-Merge technique divides the 10,000 rows of BCPNN synaptic matrix into equal groups, called as row-groups, each containing X rows. Every row is further divided into X equal blocks. All row-groups are rearranged to form new row-groups. The rearrangement is performed by placing the yth block of each row of an original row-group in the yth row of a new row-group. Figure 9a shows the rearrangement for X = 5, where block B1.3 in row 1, block 3, is moved to row 3, block 1. This method is similar to block-level interleaving in communication systems [30]. However, its use in DRAM is novel.

Figure 9
figure 9

The proposed row-merge scheme to minimize DRAM row misses.

Full size image

The row-Merge scheme maps the rearranged synaptic matrix row to a DRAM row, thus ensuring the BCPNN column access of X ij cells per DRAM row hit because these previous column cells have now been rearranged as row cells. However, it will also result in X DRAM row misses to access an entire synaptic matrix row. There are on an average 100 column updates and 10,000 row updates per second. To find the best value of X, we should first identify the overall DRAM row misses per second due to these accesses, and the X value that amounts to a minimum row misses is selected. The read/write of a synaptic matrix row or a column results in X or 100 × (100/X) DRAM row misses, respectively. The overall DRAM row misses per second is formulated, as shown by Eq. 7. The possible values of the X are the factors of 100, where X = 1 is nothing but a direct address mapping scheme. Figure 10 shows the number row misses per second for each value of X. As can be seen X = 10 is the best solution as gives the minimal number of row misses, which is 5 times less compared to direct mapping.

Figure 10
figure 10

DRAM row misses as a function of the number of blocks

Full size image

The rows of the rearranged synaptic matrix corresponding to each HCU of an H-cube are mapped to a DRAM row. They are row-wise banks interleaved across 4 DRAM banks to further improve the DRAM bandwidth due to bank-level parallelism, as shown in Fig. 9b. The above-mentioned Row-Merge scheme and bank mapping are implemented in ASMC using address translation.

$$ Rowmiss=10000\cdotp \left(X+\left(\frac{100}{X}\right)\right)\cdotp 2 $$
(7)

6 Dimensioning Computational Core

In this section, we explain how we designed and dimensioned the computational core to meet the worst-case computational load constraint of 0.5 MFlop/ms/HCU derived in section 4. This worst-case requirement is further constrained by the decisions made in the previous section 5: 4 HCUs per H-Cube, the area available is 2.582 mm2, and the bandwidth available is 4.35 GB/s.

We divide the dimensioning of the computational core in terms of the local SRAM based storage, timing, and computational resources required for the three types of updates in BCPNN, as introduced in section 2.1.2.

6.1 The Local SRAM Requirement

The BCPNN makes use of two different data-structures of different data sizes, namely synaptic columns and rows in Fig. 1. The synaptic columns are 100X bigger than rows in terms of data size. One row requires ~2.4 KBs, which is moderate, and it is reasonable to hold one or a few rows in scratchpad SRAM buffer(s). However, a BCPNN column will require an unreasonably large buffer to hold it. For this reason, column updates are split into 100 row sized updates. The periodic support-vector computation is relatively modest (11 KB) and is updated every ms. For this reason, the periodic update vector is not stored in DRAM but locally in an SRAM buffer.

6.2 Time Constraints for BCPNN Computation

The worst-case ms load of the BCPNN updates is formalized in Eq. 8, expressed in terms of the three types of updates. The factor of 36 in Eq. 8 is the worst-case number of incoming spikes per ms, as discussed previously. To explain in more detail, we describe each of the equation terms.

  1. 1.

    For 36 inputs spikes, 36 rows with 100 cells per row must be fetched, updated, and written back to the 3D-DRAM

  2. 2.

    For 1 output spike, 1 column with 10,000 cells must be fetched, updated, and written back to the 3D-DRAM

  3. 3.

    The periodic support vector computation must be performed; the data is stored locally in SRAM.

$$ {T}_{worst\_ case\_ ms}=36\cdotp {T}_{row}+{T}_{col}+{T}_{periodic}\le 1 ms $$
(8)
$$ {T}_{ro w}=\left(2-k\right)\cdotp \left({T}_{DRAM}+{T}_{ro{w}_{comp}}\right)\kern3.25em +\left(k-1\right)\cdotp \mathit{\operatorname{MAX}}\left({T}_{DRAM},{T}_{ro w\_ comp}\right) $$
(9)
$$ {T}_{row\_ comp}={T}_{init}+\frac{100\cdotp {T}_{cell}}{\# FPU\_ Sets} $$
(10)

Eq 9 models the timing required for a row update (Trow) with or without ping pong buffers. With ping pong buffer, the DRAM latency is masked, and without, the DRAM latency (TDRAM) adds to the row computation latency (Trow_comp). The factor k models the presence (k = 2) or absence (k = 1) of ping pong buffers. When k = 2, the first term disappears, and Trow is decided by the second term that selects the dominant latency between DRAM latency and the row computation latency. When k = 1, the second term disappears, and the first term decides Trow simply by the addition of DRAM and computation latencies.

The computational load for the row, column, and periodic updates for the worst-case ms is approximately 15 million Flop/s. For the k = 1, the non-ping-pong case, a significant portion of ms would be spent on DRAM access, making the task of fulfilling 15 MFlop/s more challenging. For this reason, we have opted for k = 2, which is having ping pong buffers to hide the DRAM access latency.

With k = 2 design decision made, the first term in Eq. 9 disappears, and Trow will be decided by the dominant latency between TDRAM and Trow_comp. The ideal design would balance them perfectly so that one does not starve the other. Since the design decision on the size of DRAM macro per H-Cube is already made, see section 5, the channel bandwidth, and the speed at which it operates is decided, i.e., TDRAM is decided. One of the constraints on the DRAM macro design is to ensure that the TDRAM is small enough to meet the constraint specified by Eq. 8. The DRAM speed requires us then to design the datapath for row computation such that Trow_comp matches TDRAM as closely as possible. The row and column computations are very similar and dominate the overall computational load, with the periodic support computation being trivially small in Eq. 8. Next, we explain how the computational resources were dimensioned to meet the timing constraints discussed in this section.

6.3 Computational Resources

Each HCU partition in an H-Cube exploits parallelism at two levels, as discussed in section 2.2. One is to update multiple cells in parallel, and the other is to have arithmetic level parallelism while updating each cell. First, we dimensioned the arithmetic level parallelism to update each cell, and then we decided how many such parallel datapaths are needed to meet the timing constraints specified by Eq. 8. The high-level synthesis was used to explore the design space for implementing Z, E, and P updates while using a different type of FPUs, as shown in Fig. 11.

Figure 11
figure 11

Design Space exploration for Arithmetic Level Parallelism in row/column cell computation.

Full size image

Each point in the design space plot shows the number (#) and type of FPUs used as a triplet <#multiplier, #adder, #exp.>. The log and divider are not included because one instance of them is needed for all cases. As expected, and seen in the plot, in general, increasing area reduces the latency for one cell update, Tcell in Eq. 10. The selected point is shown as a red triangle with a boxed legend. This design point was selected because increasing area further has little impact on latency.

Once we have decided the arithmetic level parallelism for a row/cell computation and its latency (Tcell), we can decide how many cells must be updated in parallel to satisfy the Eq. 8. The factor #FPU_sets in Eq. 10 captures this cell-level-parallelism. Each FPU_set is the set of FPUs corresponding to the selected design point in Fig. 11. To satisfy Eq. 8, we need to update two cells in parallel requiring two FPU_sets.

We next explain, why we cannot increase the cell parallelism arbitrarily: There is a delay associated with filling the register files with data from scratchpad buffer (SRAM) and is represented by Tinit in Eq. 10. Since the scratchpad buffers, have single read and write ports, the register files of each datapath are filled in sequentially. It puts a limit on how many cells can be updated in parallel before Tinit starts to dominate.

6.4 BCPNN Specific Infrastructure

Besides the custom computational core and synaptic storage for BCPNN, eBrainII also has BCPNN specific infrastructural resources. It includes custom concurrent finite state machines (FSMs) for managing computation, spike propagation, and interaction with custom 3D DRAM-based synaptic storage. These infrastructural operations, as we will show in section 8.1. degrade the GPU’s rated performance by 60%. The organization of these infrastructural resources, along with computational and local storage, is shown in Fig. 12a. We also have an aggressive power management policy to power down idle resources.

Figure 12
figure 12

Illustration of (a) detailed Schematic of an HCU Partition and (b) execution threads and data access to the buffers of each HCU. Each HCU executes the three sub-threads (Support update, row updates, and column updates in series). Each of the sub-thread is then fed with data for the ping-pong buffers (yellow arrows) and updates the synaptic cells using two threads; each cell thread uses the FPU set 0 and 1, respectively. The buffers are loaded from the DRAM (red arrows) before the execution of the update and stored back to the DRAM once it is completed.

Full size image

In each HCU partition, we use a hierarchy of FSMs to control the update of the synaptic weights. For the row and column updates, the control-FSM fetches data into one of the ping-pong buffers by requesting the DRAM-round-robin-scheduler. For the periodic update, the data is stored locally in the periodic-update-buffer and not fetched from DRAM.

From the ping-pong or the periodic-update buffers, depending on the update, data is repeatedly transferred for two cells at a time into the register file. The register file is connected to the FPU-sets via Mux/Demux logic. The FPU-sets are themselves controlled by a separate FSM that takes care of the weight update.

Figure 12b illustrates how the computation inside the HCU is done. The row, column, and support update computations are executing in series. Before each update, the data are loaded from the DRAM to one of the ping-pong buffers. Once the update for two cells is done, the data is written back to the same buffer from which it was read. In parallel, data for the next row or column fragment is loaded into the other ping-pong buffer to pipe-line the computation and DRAM access. After the update of all the cells inside the buffer has been completed, and before new data are loaded in the buffer, the updated data are stored back to the DRAM.

6.5 Spike Propagation Network

The spike propagation in eBrainII is also hierarchical, reflecting the overall hierarchy of the architecture, as shown in Fig. 5. Since H-Cube is intended to cluster only a few HCUs (P′ = 4), the spike propagation network and interface at the H-Cube level is a point to point with P′ spike in and out ports.

At the BCU level, the input spike distribution network is a pipe-lined hierarchical binary tree with a pipe-line stage at each node. It allows a regular log latency distribution and could be considered as a simple special-purpose hierarchical network on chip (NOC). The output spike distribution network is similar but reversed in its direction of the data flow. Since the spike generation/arrival have ms latency, whereas these networks operate at ns granularity, the need for deep buffering and complex flow control that is typical of multicore NOCs is absent. Instead, the buffered tree serves both the purpose of buffering for long electrical wires and serves as a spatially distributed queue. The generality and versatility of a full-blown NOC would be an overkill for the intra-BCU spike propagation. The inter-BCU spike propagation details have not been refined yet, but we argue that its impact on the overall cost will be trivially small because a) the total spike propagation requirement is 3 orders less (Giga vs. Tera) than the synaptic storage and computational requirements.

7 Implementation of eBrainII

In this section, we elaborate on the design methodology, the tool, and the libraries that were used to implement eBrainII. We explain the experimental basis for the area, energy, and performance numbers we claim. Table 2 presents the experimental setup. We then divide the presentation of the results into two sub-sections. The sub-section 7.1. details the major phases and sequence of the design flow, and sub-section 7.2. presents a detailed analysis of area, energy, and performance.

Table 2 Experimental Setup
Full size table

7.1 eBrainII Design Steps

eBrainII implementation was carried out in three major design phases, as described below. The objective of this sub-section is to give a feel for the sequence, and the effort involved in designing eBrainII.

7.1.1 Phase I: Component Implementation and Dimensioning

In this phase, we implemented the building blocks, characterized them, and dimensioned the eBrainII.

Floating Point Units: The floating-point units (FPUs) down to physical level and each floating point unit was characterized with exhaustive gate-level simulation back annotated with post-layout data to have sign-off quality assurance in the energy, area and latency numbers. The exponential unit was in the critical path and had 2× longer logic depth compared to other FPUs. For this reason, we created a pipe-lined and non-pipe-lined unit as the basis for design space exploration (DSE) done by the high-level synthesis (HLS) tool. An important outcome of the FPU synthesis was the decision on the frequency of operation. We used the largest logic depth of FPUs as the basis for the frequency of operation, i.e., 200 MHz.

HLS Based DSE: The BCPNN equations, the subset is shown in Eq. 1–5, were modeled in C for DSE using a public domain HLS tool [32]. The HLS library was populated with the synthesized FPUs. Note that the HLS tool was used only for DSE. The actual RTL implementation was done manually in Phase II.

Spike Queue Dimensioning: The spike queue was dimensioned, as explained in section 4.

3D-DRAM Macro Dimensioning – the P Factor: Using the DRAMsys design space exploration framework, design space for finding the optimal P factor, number of HCUs per H-Cube, was determined. As part of 3D DRAM macro size dimensioning, we also explored the data organization and how to optimize the channel bandwidth utilization. To achieve this, we created a stochastic model of BCPNN. This model did not have the actual computation but generated and absorbed spikes on a stochastic basis that mimicked the real BCPNN. This allowed us to generate a very large trace of DRAM access requests that were used to decide the data organization in DRAM and decide its dimensions.

Datapath Dimensioning: The datapath was dimensioned, as explained in section 6. This essentially decides a) if ping-pong buffers are to be used or not, k factor in Eq. 9, b) the optimal FPU set from the HLS design space exploration, and c) the number of parallel cells to be updated to satisfy Eq. 8.

7.1.2 Phase II: RTL Design and Verification

In this phase, we implemented the eBrainII hierarchy up to the BCU level in register-transfer level (RTL) hardware description language (HDL) and verified it.

RTL Design: For the H-Cube and HCU partitions for the specific dimensions that were decided in sections 5 and 6, including the refinement of the computational core, as shown in Fig. 12. The hierarchical spike propagation network for integrating the HCUs in a BCU was also implemented.

RTL Verification: for the above RTL was carried out using a SystemVerilog based verification environment in a bottom fashion against the golden BCPNN model in C++.

7.1.3 Phase III: Logic and Physical Synthesis

In this phase, we performed the logic and physical synthesis of the RTL design down to the physical level. The area, energy, and latency results reported in this paper are based on post-layout sign off quality design data and exhaustive gate-level simulation with back annotation of post layout data.

7.2 Quantification of eBrainII Implementation Results

In this section, we present the area, energy, and performance numbers of eBrainII (Table 3). The energy calculation for the ASIC implementation was done based on post-layout simulations. The design was synthesized down to the physical level in 40 nm technology. The numbers were scaled to 28 nm based on [31], i.e., area was scaled by 0.5 and power by 0.71. The SRAM energy numbers were based on memory compiler, and the DRAM numbers were extracted using the DRAMSys design space exploration framework [28].

7.2.1 eBrainII Energy Numbers

The energy numbers are for an average spike rate of 10 input spikes/ms as per BCPNN specification. Figure 13a shows the breakdown of energy in the form of a pie chart. As expected, the DRAM is the most dominant cost, despite a custom design and having minimal distance between DRAM and logic. The DRAM energy includes the core and I/O energy and that of the memory controller.

Figure 13
figure 13

Energy and Area breakdown of the eBrainII in 28 nm technology node.

Full size image

On the logic die, the computation and SRAM consume the bulk of energy, whereas infrastructure that includes the spike queues, their controllers, spike propagation network, and HCU master FSM only 3%. Note that the computation percentage includes FPUs, Register Files, Multiplexors, FSMs, and the wires; FSMs, again as expected, take a minuscule percentage and not shown as it would be invisible. The energy reported is for dynamic and static power consumption. When the logic is idle, as stated before, we power them down.

We report two power numbers, one for full activity at human scale level with 2 million HCUs, all working. This power is 15.3 kW, and it is artificial because it corresponds to every neuron firing at the same time. The activity in the biological brain is very sparse. However, since the neuronal unit in BCPNN is MCU, which itself is an aggregation of 100 neurons, we report a number for 20% activity, which should be considered as a highly active cortex, and this requires a modest 3 kW.

7.2.2 eBrainII Area Numbers

The area breakdown is shown in Fig. 13b. One can see that the infrastructure that had a small percentage of energy pie has a fairly large percentage of the area pie. It is because the spike queues are implemented using registers, and there are quite many FSMs. However, the number of cycles spent in infrastructure is very less, typically at ms boundaries when spikes arrive, whereas once triggered, the computational logic works at every 5 ns cycle until each spike has been serviced.

Table 3 Summary of the Experimental Results
Full size table

Since the DRAM area and logic area overlap, the pie chart gives a breakdown of the logic die. Note that the DRAM macro for each H-Cube takes approximately twice as much area as the logic that is needed to do the computation and manage spikes. It can be seen in Fig. 13b with the 38% unused part of the pie. To balance the footprint of synaptic storage and computational logic, we need a memory technology with a higher density than what 8 layers of 3D DRAM integration can provide.

Each H-Cube has a footprint of 2.58 mm2. Each BCU integrated 32 such H-Cubes making BCUs approximately 82.56 mm2. If one factor in additional infrastructural blocks for the clock, reset, and power supply and pads, the area will approach 100 mm2. For a human scale BCPNN, we would need 62.5 K BCUs. To reduce this number, one could consider increasing the size of the die and/or integrating 16 such BCUs on an interposer to create super-BCUs.

7.2.3 eBrainII Performance Numbers

The eBrainII design achieves real-time. For the worst-case ms when it needs to deal with 36 input spikes, all the necessary computation in Eq. 8 is achieved in 0.8 ms, and for the average case of 10 spikes/ms, the computation is achieved in 0.2 ms. We did not use DVFS to fulfill worst-case with less logic area because we have ample area under 3D-DRAM that is not utilized, i.e., we are not area constrained. This is the reason why we opted for the lowest voltage-frequency operating point, highest level parallelism, and power gating when idle as the most effective option.

7.3 Rodent Scale eBrainII

The eBrainII design was customized and optimized for human-scale BCPNN. The mice scale BCPNN has significantly lower requirements: 32 K HCUs, 1200 rows, and 70 columns. It is possible to map 16 rodent HCUs in each human scale H-Cube, even if such a mapping would underutilize some of the resources. With such a mapping, we would need 62 BCUs, the mice scale BCPNN would run in real-time and consume ~12 watts of power.

8 BCPNN on Other Platforms

In this section, we compare the BCPNN implementation on GPU and a best effort mapping of BCPNN to SpiNNaker-2 chip to eBrainII. We also briefly comment on why TrueNorth is not a suitable platform for BCPNN.

8.1 BCPNN on GPU

BCPNN is mapped to NVIDIA Tesla K80 GPU card with dual GK210 cores, each with 12 GBs of DRAM. We used one of the cores and mapped 400 HCUs on it because the synaptic storage of 400 HCUs requires 10 GBs. We used the CUDA framework to map BCPNN that was composed in terms of four kernels: row update, column update, periodic update, queue management.

Figure 14
figure 14

Human Scale BCPNN: eBrainII vs. GPU (GK210). 20% Sparse activity.

Full size image

The ms tick in hardware is emulated by the execution of a loop in CUDA. This ms loop includes the four kernels. Two of them, the row and the column, are triggered by the presence of spikes, and the other two, the queue management and the periodic support update are unconditionally executed.

When, as a result of the periodic update, an MCU triggers and generates an output spike, two actions happen. The first is that the column update kernel in source HCU is triggered, and the second is that the output spike is fanned out to the destination HCUs as input spikes by copying these spikes to their respective delay queues. The queue management kernel decrements the biological delay in each iteration, and when the delay reduces to zero, it triggers the row update kernels. This CUDA implementation was also verified against the golden C++ model of BCPNN.

To estimate power consumed by GK210, we used the in-built power measurement sensor to accurately know the power consumed and the CPU time was to know the time used and thereby energy. To find out how the energy was distributed among the major resource categories – storage, computation, and infrastructure, we profiled CUDA BCPNN implementation on a Jetson TK1 for which we could use an accurate energy model [33]. The profiling data was fed to this energy model to know the percentage distribution of power among the resource categories. This percentage distribution was then applied to total energy measured on GK210, see Fig. 14.

The key factors that degrade GPU’s efficiency vis-à-vis eBrainII are a) that the column access in GPU DRAM is poor compared to eBrainII’s custom 3D DRAM, see section 5, b) lack of custom concurrent FSMs that eBrainII has to manage infrastructure, computation, and DRAM access. All these functions in GPU are mapped to the same resources that also do the number-crunching. This sequentializes the execution and underutilizes the resources. Therefore, the GPU implementation achieves 2645 kJ energy-delay product that is 867 X worse off compared to eBrainII. Further, the GPU implementation delivers barely 23 GFlop/s vs. the rated spec of 4365 GLFOPs/s, i.e., only 5%.

8.2 BCPNN on SpiNNaker-2

We have also conceptually mapped BCPNN to the SpiNNaker-2 system that is the next-generation implementation of the SpiNNaker system. The SpiNNaker-2 architectural details are based on the early information available from [34] and email discussion with Prof. Stephen Furber at Univ. of Manchester, the principal architect of the system. The mapping is illustrated in Fig. 15. To maximize the utilization of the 144 cores and the 2GB available LPDDR4 DRAM, we propose mapping 72 HCUs to each SpiNNaker 2 chip. Each HCU’s worst-case ms load is divided into two cores to approximately balance the load among them. 72 HCUs also use 1.8 GB of DRAM.

Figure 15
figure 15

Conceptual Mapping of BCPNN to SpiNNaker-2.

Full size image

8.2.1 Best Effort Estimation Method

  1. 1.

    250 mhz operation and 1.95 instructions per cycle

  2. 2.

    BCPNN equations were compiled for cortex m4f and simulated through the ovp model [35].

  3. 3.

    the energy per instruction is based on measured values for cortex m4f [36] and scaled from 90 nm to 28 nm based on [31, 37].

  4. 4.

    the dram access latency is completely hidden by the dma transfer in the pipe-line with the computation.

  5. 5.

    lpddr4 bandwidth of 10 gb/s.

  6. 6.

    lpddr4 energy assumed to be 5 pj/bit based on [38]

Based on the above estimation method for a human scale BCPNN, the total energy consumption for sparse activity (20%) is 220 kJ, and it runs approximately 10× slower than real-time. It results in an energy-delay product of 2200 kJ·s, i.e., 721× worse compared to eBrainII.

  1. 1.

    Each floating-point operation in BCPNN equations results in an average of 7 instructions. It was found from the compilation results and simulation and is also consistent with the results reported in [36].

  2. 2.

    Spinnaker-2, based on cortexm4f, like any processor, needs fetch-decode-execute on a generic pipe-line through 3–4 stages. eBrain, in contrast, has a hard-wired fsm that executes these floating operations in a single cycle or, in some cases, two-three cycles for exp, log, and div operations.

  3. 3.

    Cortexm4f has floating-point operations but can only execute two of them in parallel (1.95 dmips/cycle). In contrast. eBrainII has 3 multipliers, 2 adders, 2 exponentials, 1 log, and 1 div fpus for updating each cell.

  4. 4.

    Cortexm4f implements exp and log functions in terms of primitive fp operations as library calls that further degrades the efficiency. eBrainII, in contrast, has custom hardware units for them.

  5. 5.

    Conceptual mapping of BCPNN to SpiNNaker-2

  6. 6.

    GPU, in comparison, has massive parallelism for many cells because that is the granularity of parallelism and exploits the large number of fpus available.

The energy and latency numbers reported does for the conceptual mapping of human scale BCPNN to SpiNNaker 2 did not include the Infrastructural operations, including queue management and co-ordination between Spike arrival, DRAM access, and computation. We draw the reader’s attention to the fact that in the case of GPU, the lack of custom concurrent FSMs that efficiently manages the infrastructural operations in eBrainII results in 60% degradation compared to the rated specs of the core. Further, we also ignore the Spike propagation cost. This is justified because, in BCPNN, it is proportionally insignificant compared to computation and synaptic weight storage. We have also given SpiNNaker 2 the benefit of the unknown in assuming that LPDDR4 that lacks the customization in dimension and data organization of eBrainII will be as efficient in accessing rows and columns.

8.3 BCPNN on TrueNorth and Other Platforms

TrueNorth [39] is a custom design to implement Neural Network models at a fine granularity of neuronal models that are much simpler than the BCPNN neuronal unit – the MCU. The computational and storage units in TrueNorth are dimensioned to deal with simple leaky integrator and fire models of neurons, whereas the BCPNN, especially the lazy evaluation model, involves the far more complex operation and requires multi-level traces as described in section 2.1. For this reason, we did not find any reasonable way to even conceptually map BCPNN to TrueNorth and compare the results.

BCPNN, in the past, has been mapped to CRAY and IBM BlueGene supercomputers, almost a decade ago. The energy-delay product is worse than what one can achieve with other platforms, and we do not see that comparing eBrainII to these machines would bring any added scientific value. There are analog platforms like FACETs that are so different from eBrainII that it is hard to make a fair comparison and would require an unreasonably large effort.

9 Conclusion & Future Work

In this paper, we have demonstrated that it is possible with modest engineering effort to do a custom ASIC design of a challenging biological plausible model of cortex like BCPNN stringent demands on real-time to attain 162 TFlop/s and 200 TBs/s bandwidth to access 50 TBs of storage. The resulting design was shown to be three orders better than GPUs and SpiNNaker designed around general-purpose RISC micro-controllers. Custom logic and 3D DRAM storage with novel mapping enabled to lower the power consumption enough for a rodent size biologically plausible cortex, 12 W, to be deployed as cognition engine of embedded systems, and the engineering effort is at least two orders less compared to ad hoc system on a chip (SOC) designs of comparable complexity.

In the future, we are planning eBrainIII that will have the following features:

  1. 1.

    It will use fixed-point representation with a maximum 22 bit for some traces. This will significantly reduce the storage and energy cost compared to eBrainII.

  2. 2.

    The BCPNN algorithm has been tweaked to eliminate the column updates and merge them with row updates. This not only halves the need to access to dram storage but also eliminate the more difficult part – the column access.

  3. 3.

    The input spikes in BCPNN have a strong spatio-temporal locality. We plan to exploit this to design a software-controlled cache to buffer the rows that have been fetched to avoid having to fetch them from drams. This and the previous point taken together are expected to significantly reduce the dominant cost of accessing dram in eBrainII.

  4. 4.

    As a more long-term plan, we plan to map the BCPNN computations to computation in memristors to fundamentally overcome the von-neumann bottleneck of separating computation and storage. We expect this approach to lower the power consumption of human-scale BCPNN to the order of 100 w.

While the above measures provide a path to significantly improved energy efficiency, engineering and manufacturing efficiencies remain a challenge. To address these challenges, we plan to adopt the Lego-inspired synchoros VLSI design style. The word synchoros is derived from the Greek word choros for space and is the spatial analog of the well-known concept of synchronicity. This work has been presented in [40] and used to design dedicated hardware for ANNs [41, 42], and wireless communication [43].

The synchoros VLSI design style is also called the SiLago (Silicon Lego) method and would involve building SiLago bricks for ordinary differential equations, queues, NOCs, memory controllers, and 3D DRAM vaults. For the inter-BCU communication, we plan to use the GRLS [44] protocol, which allows for latency insensitive data transfer. Such an architectural framework is expected to provide ASIC comparable efficiency and retain a fair degree of configurability to experiment with changes in BCPNN algorithms, degree of parallelism, etc. The SiLago method is in line with the proposed Moore’s EDA law [45]. This framework allows for automating synthesis from a higher level of abstraction. We have previously developed tools that enable synthesis for DSP applications [46], and grammar-based protocol synthesis [47]. We plan to further improve these tools to support the required structures of the eBrain.