Efficient Hardware Architectures for 1D- and MD-LSTM Networks

Abstract

Recurrent Neural Networks, in particular One-dimensional and Multidimensional Long Short-Term Memory (1D-LSTM and MD-LSTM) have achieved state-of-the-art classification accuracy in many applications such as machine translation, image caption generation, handwritten text recognition, medical imaging and many more. However, high classification accuracy comes at high compute, storage, and memory bandwidth requirements, which make their deployment challenging, especially for energy-constrained platforms such as portable devices. In comparison to CNNs, not so many investigations exist on efficient hardware implementations for 1D-LSTM especially under energy constraints, and there is no research publication on hardware architecture for MD-LSTM. In this article, we present two novel architectures for LSTM inference: a hardware architecture for MD-LSTM, and a DRAM-based Processing-in-Memory (DRAM-PIM) hardware architecture for 1D-LSTM. We present for the first time a hardware architecture for MD-LSTM, and show a trade-off analysis for accuracy and hardware cost for various precisions. We implement the new architecture as an FPGA-based accelerator that outperforms NVIDIA K80 GPU implementation in terms of runtime by up to 84× and energy efficiency by up to 1238× for a challenging dataset for historical document image binarization from DIBCO 2017 contest, and a well known MNIST dataset for handwritten digits recognition. Our accelerator demonstrates highest accuracy and comparable throughput in comparison to state-of-the-art FPGA-based implementations of multilayer perceptron for MNIST dataset. Furthermore, we present a new DRAM-PIM architecture for 1D-LSTM targeting energy efficient compute platforms such as portable devices. The DRAM-PIM architecture integrates the computation units in a close proximity to the DRAM cells in order to maximize the data parallelism and energy efficiency. The proposed DRAM-PIM design is 16.19 × more energy efficient as compared to FPGA implementation. The total chip area overhead of this design is 18 % compared to a commodity 8 Gb DRAM chip. Our experiments show that the DRAM-PIM implementation delivers a throughput of 1309.16 GOp/s for an optical character recognition application.

1 Introduction

In recent years, a wide variety of neural network accelerators [9, 26, 53] have been published that achieve higherperformance and higher energy efficiency compared to general purpose computing platforms. Many of these accelerators target feed-forward networks such as CNN, however far fewer investigations exist on efficient hardware implementations for Recurrent Neural Networks (RNNs), and Long Short-Term Memory (LSTM) in particular, especially under energy constraints.

Compared to feed-forward Neural Networks (NNs), efficient implementation of LSTM networks are especially challenging for the following reasons: first, LSTM, namely One-dimensional Long Short-Term Memory (1D-LSTM) has a recurrence along a time-axe in speech recognition or writing direction in Optical Character Recognition (OCR) that creates data dependence to previous steps, which forces sequentialization of the processing and affects the overall throughput of the compute architecture; second, the LSTM algorithm includes multiple non-linear activation functions in contrast to low-complexity rectified linear units common for CNN layers; third, LSTM networks have a large memory footprint, and a peak performance that is not computation bounded but limited by the external memory bandwidth [26]. The challenges are further augmented for Multidimensional Long Short-Term Memory (MD-LSTM) that has recurrent connections along multiple axes, e.g. two in image processing or three in volumetric imagining. Multidimensional recurrences further enlarge the memory footprint and required memory bandwidth, significantly reduce the potential for parallelization that extremely slows down the inference and training. Although, it has been shown that a size of a model based on MD-LSTM can be 3-11 times smaller than a CNN model with similar accuracy [38, 45], the best parallel implementation of a single layer of MD-LSTM has a computational complexity that is typically by one or two orders of magnitude higher than of a naive implementation of a convolutional layer [45]. These aforementioned reasons challenge the design of efficient hardware accelerators for LSTM networks.

In this work, we systematically address these challenges and propose efficient hardware accelerators for the inference of LSTM networks. We present two novel hardware architectures: first, an FPGA-based hardware architecture for MD-LSTM network targeting image segmentation and recognition problems. Second, a DRAM-based Processing-in-Memory (PIM) architecture for 1D-LSTM network targeting energy efficient compute platforms. To the best of our knowledge, our research is the first to propose a DRAM-based Processing-in-Memory (PIM) architecture for 1D-LSTM network and the first ever to propose a hardware architecture for MD-LSTM.

Excessive sequential execution of MD-LSTM is a bottleneck that significantly constrains efficiency of using massive parallelism of modern GPUs that prevents intensive research involving MD-LSTM in recent years. In this paper, we show that high flexibility of FPGAs that allows for custom pipelined datapath, and natural support of low bit-width operations provides an efficient solution to complex recurrent dataflow of MD-LSTM, when massive parallelism of GPUs ain’t enough to provide the necessary performance required by the application. An efficient implementation for inference is presented that opens a door for efficient training that can boost application of MD-LSTM. We elaborate on two vanilla MD-LSTM [19] based typologies, where one was trained to perform binarization of historical documents from DIBCO 2017 competition [44], and second to perform handwritten digits recognition task on MNIST dataset [30]. The former task was selected because it is a challenging problem that shows that the selected topology has a representative complexity and deals with a real world problem. Additionally, MNIST was chosen as a benchmark to have a fair comparison with existing FPGA-based implementations with respect to throughput and energy efficiency.

The PIM architecture focuses on integrating a binary weighted 1D-LSTM inference engine into a commodity DRAM architecture. The aim of the PIM architecture is to eliminate the memory bound (bandwidth and energy) issues that are associated with NN data and parameter access. It bridges the memory-computation gap by integrating the computation logic in the memory devices. The tight coupling of the memory and computational logic enables massive data parallelism and minimal data movement cost, which results in a much higher energy efficiency. The challenge in DRAM-based PIM architecture is the physical implementation of the computational logic that is constrained by factors like DRAM sub-array width, fine bit-line pitch and the limited number of available metal layers (e.g. three) in the DRAM process.

The novel contributions of this paper are:

• A novel hardware architecture of MD-LSTM neural network is presented.

• A systematic exploration of accuracy vs. hardware cost trade-off for MD-LSTM using challenging DIBCO 2017 and MNIST datasets is conducted. We investigate the effects of quantization of weights, input, output, recurrent, and in-memory cell activations on accuracy during training. In particular, we explore binarized weights and activation functions.

• We provide the first open source HLS implementation for parameterizable hardware architectures of MD-LSTM layers on FPGAs, which provides full-range precision flexibility, and allows for parameterizable performance scaling.¹

• An open-source implementation of MD-LSTM in Pytorch (http://pytorch.org/) for training and inference on GPU is provided.²

• We present a novel DRAM based 1D-LSTM-PIM architecture that is compatible with the existing commodity DRAM technology, strictly not modifying the DRAM sub-array design.

The paper is structured as follows: In Section 2 we review the basics of 1D- LSTM and MD-LSTM algorithms. This is followed by Section 3, which presents the details of the MD-LSTM accelerator. Section 3.1 gives an overview of the existing research on MD-LSTM. We describe the training setup and quantization techniques in Section 3.2 and Section 3.3, respectively. Section 3.4 provides the details of the novel hardware architecture of MD-LSTM. Section 3.5 presents the results with respect to implementation of MD-LSTM. Section 4 presents the details of the 1D-LSTM PIM accelerator. The prior-art on PIM accelerators is reviewed in Section 4.1 and followed by the basics of DRAM in Section 4.2. Section 4.3 presents DRAM based 1D-LSTM PIM architecture in detail. The results of the PIM implementation are discussed in Section 4.5. Finally, Section 5 concludes the paper.

2 Background

2.1 1D-LSTM

In this paper, as a showcase topology for the PIM architecture we selected a Bidi- rectional LSTM (Bi-LSTM) with Connectionist Temporal Classiffication (CTC) layer targeting OCR. Bidirectional Recurrent Neural Networks (RNNs) were proposed to take into account impact from both the past and the future status of the input signal by presenting the input signal forward and backward to two separate hidden layers both of which are connected to a common output layer that improves overall accuracy [20]. CTC is the output layer used with LSTM networks designed for sequence labelling tasks. Using the CTC layer, LSTM networks can perform the transcription task on a level of text-lines without requiring pre-segmentation into characters.

For the sake of clarity, we review the basic LSTM algorithm, earlier presented in [18, 22].

$$ \begin{array}{@{}rcl@{}} \boldsymbol{a}^{t} &=& \tanh(\boldsymbol{W}_{a} \boldsymbol{x}^{t} + \boldsymbol{R}_{a} \boldsymbol{y}^{t-1} + \boldsymbol{b}_{a})\\ \boldsymbol{i}^{t} &=& \sigma(\boldsymbol{W}_{i} \boldsymbol{x}^{t} + \boldsymbol{R}_{i} \boldsymbol{y}^{t-1} + \boldsymbol{b}_{i})\\ \boldsymbol{f}^{t} &=& \sigma(\boldsymbol{W}_{f} \boldsymbol{x}^{t} + \boldsymbol{R}_{f} \boldsymbol{y}^{t-1} + \boldsymbol{b}_{f})\\ \boldsymbol{o}^{t} &=& \sigma(\boldsymbol{W}_{o} \boldsymbol{x}^{t} + \boldsymbol{R}_{o} \boldsymbol{y}^{t-1} + \boldsymbol{b}_{o})\\ \boldsymbol{c}^{t} &=& \boldsymbol{i}^{t} \odot \boldsymbol{a}^{t} + \boldsymbol{f}^{t} \odot \boldsymbol{c}^{t-1}\\ \boldsymbol{y}^{t} &=& \boldsymbol{o}^{t} \odot \tanh(\boldsymbol{c}^{t}) \end{array} $$

(1)

The LSTM architecture is composed of a number of recurrently connected memory cells. Each memory cell is composed of three multiplicative gating connections, namely input, forget, and output gates (i, f, and o, in Eq. 1); the function of each gate can be interpreted as write, reset, and read operations, with respect to the cell internal state (c). The gate units in a memory cell facilitate the preservation and access of the cell internal state over long periods of time. The implemented LSTM cells have been implemented without peephole connections that are optional and according to some research even redundant [6]. There are recurrent connections from the cell output (y) to the cell input (a) and the three gates. Equation 1 summarizes formulas for LSTM network forward pass. Rectangular input weight matrices are shown by W, and square weight matrices by R. x is the input vector, b refers to bias vectors, and t denotes the time (and so t-1 refers to the previous timestep). Activation functions are point-wise non-linear functions, that is logistic sigmoid ($\frac {1}{1+e^{-x}}$) for the gates (σ) and hyperbolic tangent for input to and output from the node. Point-wise vector multiplication is shown by ⊙.

2.2 MD-LSTM

A MD-LSTM neural network was firstly proposed in [19] to extend the applicability of unidimensional counterpart for data with more than one spatio-temporal dimension like in image and video processing or volumetric medical imaging. Having recurrent connections along multiple axes, typically the x-axis and y-axis in image processing, allows MD-LSTM to capture long-term dependencies along all dimensions of the data that makes MD-LSTM very robust to local distortions along any combination of input dimensions. MD-LSTM provides state-of-the-art performance on most of benchmarks for offline Handwritten Text Recognition [38, 54]. They show advanced results in semantic segmentation [7] and medical imaging [14, 51].

Probably, MD-LSTM is one of the most controversial neural networks. While having high theoretical potential for learning, [19, 38, 45, 55] acknowledged that MD-LSTMs are in principle more powerful and more robust to distortions than CNNs, they suffer from lack of investigation due to slow training. Recently, there were a lot of discussions if MD-LSTM layers are needed at all. It was shown that in some scenarios, MD-LSTM layers can be replaced with CNN layers that can provide similar or higher accuracy at lower computational cost [45]. However, most recent research on handwritten text recognition [38] proofs that MD-LSTM interleaved with CNN layers and 1D-LSTM on the top provides a superior performance than pure CNN based topology or CNNs combined with 1D-LSTM in the case of more complex and challenging real-world datasets. That justifies research related to MD-LSTM.

As already said, MD-LSTM is a generalization of a recurrent neural network, which can deal with higher-dimensional data. In the following we restrict ourselves to the two-dimensional case, which is commonly used for handwriting and similar tasks. A 2D Long Short-Term Memory (2D-LSTM) scans the input image along horizontal and vertical axes and produces an output image of the same size following equations (Eq. 2) for each coordinate (i,j) in the input image x.

It is common to use parallel 2D-LSTM layers processing an input image in four directions (top-left origin, top-right origin, bottom-left origin and bottom-right origin) as it is depicted in Fig. 1 for top-left origin. The outputs from four directions are later combined (concatenated) so that a spatio-temporal context from all four directions is available at each position (pixel).

Figure 1

In the case of top-left origin: a the dependencies between each position (pixel), b the pixel-by-pixel processing order, c the diagonal-wise processing order.

For the sake of clarity, we review the basic 2D-LSTM algorithm. Equation 2 summarizes formulas for the network forward pass. Similar to unidimensional LSTM, 2D-LSTM architecture is composed of a number of recurrently connected memory cells. However, each memory cell is composed of four, rather than tree multiplicative gating connections, namely input, forget for the y-coordinate and x-coordinate, and output gates (k, f, g, and o). There are two square weight matrices, one for the y-coordinate (U) and one for x-coordinate (V). The rest is similar to the unidimensional case.

3 MD-LSTM

$$ \begin{array}{@{}rcl@{}} \boldsymbol{a}_{i,j} &=& \tanh(\boldsymbol{W}_{a} \boldsymbol{x}_{i,j} + \boldsymbol{U}_{a} \boldsymbol{y}_{i-1,j} + \boldsymbol{V}_{a} \boldsymbol{y}_{i,j-1} + \boldsymbol{b}_{a})\\ \boldsymbol{k}_{i,j} &=& \sigma(\boldsymbol{W}_{k} \boldsymbol{x}_{i,j} + \boldsymbol{U}_{k} \boldsymbol{y}_{i-1,j} + \boldsymbol{V}_{k} \boldsymbol{y}_{i,j-1} + \boldsymbol{b}_{k})\\ \boldsymbol{f}_{i,j} &=& \sigma(\boldsymbol{W}_{f} \boldsymbol{x}_{i,j} + \boldsymbol{U}_{f} \boldsymbol{y}_{i-1,j} + \boldsymbol{V}_{f} \boldsymbol{y}_{i,j-1} + \boldsymbol{b}_{f})\\ \boldsymbol{g}_{i,j} &=& \sigma(\boldsymbol{W}_{g} \boldsymbol{x}_{i,j} + \boldsymbol{U}_{g} \boldsymbol{y}_{i-1,j} + \boldsymbol{V}_{g} \boldsymbol{y}_{i,j-1} + \boldsymbol{b}_{g})\\ \boldsymbol{o}_{i,j} &=& \sigma(\boldsymbol{W}_{o} \boldsymbol{x}_{i,j} + \boldsymbol{U}_{o} \boldsymbol{y}_{i-1,j} + \boldsymbol{V}_{o} \boldsymbol{y}_{i,j-1} + \boldsymbol{b}_{o})\\ \boldsymbol{c}_{i,j} &=& \boldsymbol{f}_{i,j} \odot \boldsymbol{c}_{i-1,j} + \boldsymbol{g}_{i,j} \odot \boldsymbol{c}_{i,j-1} + \boldsymbol{a}_{i,j} \odot \boldsymbol{k}_{i,j}\\ \boldsymbol{y}_{i,j} &=& \boldsymbol{o}_{i,j} \odot \tanh(\boldsymbol{c}_{i,j}) \end{array} $$

(2)

This section presents a complete design methodology that starts from selecting a neural topology. Later training, refinement and selection of a full-precision model is done. Further, we train a model with quantized learning parameters to identify a search space of accuracy as a function of hardware cost for various precision points. In the following, a selection of a configuration with an optimal trade-off between accuracy and hardware cost using Pareto frontier is performed. As the main goal of the paper, we present a novel hardware architecture and provide implementation details. We perform a throughput scalability analysis to identify a configuration with the highest throughput that is used for comparison to the state-of-the-art with respect to accuracy, achieved throughput and energy efficiency.

3.1 Related work

In this section, we review related work on MD-LSTM with respect to its application, and earlier presented optimisation techniques for accelerating both inference and training. As there are no prior publications on hardware architectures for MD-LSTM, we review state-of-the-art architectures for recurrent neural networks, namely unidirectional LSTM.

3.1.1 Application

Afzal et al. [2] has proposed treating the image binarization as a sequence learning problem and modeled the image as a two-dimensional sequence. MD-LSTM was used to learn spatial dependencies in the two-dimensional image, the same as 1D-LSTM is used in temporal domain to learn temporal dependencies. In general the task was formulated as a semantic segmentation problem, where each pixel was classified either as text or non-text. The approach was evaluated on DIBCO 2013 dataset achieving comparable results with the state-of-the-art. Similar idea was applied by one of the participants at DIBCO 2017 [44] competition using Grid LSTM cells [27]. We use similar topology to Afzal et al. but with more memory cells to cope with increased complexity of DIBCO 2017 dataset. Graves et al. [19] could achieve accuracy comparable to state-of-the-art applying MD-LSTM on MNIST dataset without using any pre-processing or augmentation. They formulated the task as a semantic segmentation problem, where each pixel was classified according to the digit it belonged to. Our approach is different as we do not make prediction for each pixel but for the complete image based on all outputs from hidden layers taken together. We selected an alternative topology in order to explore more on architectural level, otherwise the architecture would be identical to the semantic segmentation one.

3.1.2 Optimization

There is a number of papers proposing to accelerate inference and training of MD-LSTM by new parallelization approaches or improving stability of the cells for faster convergence. Leifert et al. [31] has shown that MD-LSTM has a severe conceptual problem related to computational instability of a value of the memory state that grows drastically over time and can even become infinite. They proposed an improved version of a cell called Leaky − LP that overcomes the instability, while preserves the state over long period of time, however at the expense of more complex computational graph. In our research we use vanilla MD-LSTM cells, so to be able to evaluate all optimizations with respect to the original model.

MD-LSTM has constraints on computing order of the steps (pixels) due to recurrent dependencies between the pixels, see Fig. 1a. Each pixel is considered as one time step/position here. Each position requires an input from two neighboring ancestor positions, one located on the previous column, another on the previous row. The straightforward implementation follows a pixel-by-pixel processing order, one pixel is processed after another as it is shown in Fig. 1b. Voigtlaender et al. [54] and Oord et al. [41] proposed conceptually similar parallelization approaches. They have noticed that all pixels on the same diagonal can be computed in parallel because they are computationally independent from each other, the processing order is depicted in Fig. 1c. The diagonal-wise approach reduces the time complexity to process an image from $\mathcal {O}(W \cdot H)$ to $\mathcal {O}(W + H)$ because there are (W + H − 1) diagonals in an image with H rows and W columns. Our architecture is based on the pixel-by-pixel order of processing. In the case of GPU, we have implemented both approaches. Additionally, Wenniger et al. [55] proposed an efficient approach of packing samples in batches with low computational and memory overhead. The approach could achieve 6.6 times seed-up on word-based handwriting recognition by avoiding wasteful computation on padding. In the case of MNIST dataset, the padding is not necessary because all images are of the same size. For DIBCO dataset, the padding is negligible because we process big size images (up to 4M pixels) in small chunks (64 by 64 pixels). Our approach is orthogonal to all previously proposed, as we present a hardware acceleration on alternative computing platform, namely FPGA. Our approach potentially can be combined with previously presented ones.

3.1.3 Architecture

To the best of our knowledge, we are proposing the first hardware architecture of MD-LSTM. However, it is not the first architecture of RNNs. In [48] Rybalkin et al. gives a good overview of FPGA-based implementations. The most remarkable architectures providing the highest throughput are [48] and [21]. Where the later one operates on partially stored on-chip sparse model. However, in this paper we investigate influence of low precision on accuracy rather than sparsity, and keep our model dense. Furthermore, as it has been mentioned in Section 1, the MD-LSTM models are much more compact in comparison to other types of neural networks [38, 45] that makes them very appealing for on-chip implementation. In the following, we primary compare new architecture with [48] as it operates on a dense model stored completely on-chip. The new architecture has additional datapaths for recurrent dependencies along extra dimensions. We exploit a concept of interleaving data corresponding to different processing directions proposed in [49], and extend it to four processing directions (see Section 2). Interleaving in the case of RNNs enables to keep pipelined datapath always busy (see Section 3.4). We show that in the case of MNIST datatset, it is not necessary to align corresponding outputs from four processing directions that significantly reduces the required on-chip memory for intermediate computations. However, in the case of semantic segmentation problem, like in binarization, the alignment is necessary. We propose an architecture of an output layer operating on multidimensional buffer.

3.2 Training

In the following chapter, we give an overview of the selected applications and benchmarking datasets, namely MNIST and DIBCO. A complete training flow is presented in this section.

During training we experimented with a different number of MD-LSTM cells, precision and different hyper parameters. The quantized versions of the networks were trained de novo without full-precision pre-training. We trained the networks with quantized weights, biases, input, output, recurrent activatuions, and full-precision in-cell activations. A quantized LUT-based version of the in-cell activations was used during the test. It was found that gradient clipping can be necessary to achieve stable learning that is reasonable in the case of vanilla cells in particular [55]. We applied dropout between the 2D-LSTM layers and output layer for better generalization.

3.2.1 MNIST

We used a well-known MNIST dataset [30] of isolated handwritten digits to have a common benchmark to compare our hardware implementation to existing FPGA-based designs with respect to throughput and energy efficiency. The database consists of gray-scale images, each of which is 28 pixels high and 28 pixels wide depicting a single handwritten digit like in Fig. 2.

Figure 2

Sample images from the MNIST dataset.

MNIST has a training set with 60k images and a test set with 10k. We used 5% of the training set for validation. We report the best test accuracy of a model with the highest validation accuracy after at most 1000 epochs. We did not perform any pre-processing or augmentation on MNIST dataset. We used a threshold-based binarization on the input pixels in the case of quantized network and real-value pixels in the case of full-precision configuration. The architecture of 2D-LSTM network depicted in Fig. 3 has a single hidden layer that is separated into four independent LSTMs processing the input in four directions with N^H memory cells each. The red arrows in Fig. 3 indicate the direction of propagation during the forward pass. The input layer is of size (C) 1. The outputs from all hidden layers and from all pixels are concatenated and fed into the common output layer of size (N^O) 10 that is a number of classes (digits from 0 to 9). The LogSoftmax activation function was used at the output layer. We used a negative log likelihood loss criterion with Adam optimizer and a mini-batch size of 512 or 256 depending on a size of a model. We used larger batch size for training smaller models to fully utilize the GPU resources. The learning rate starts from 0.01 and reduced by a factor of 0.8 every 20 epochs. We used gradient clipping with a value of 100.

Figure 3

Image classification topology for MNIST dataset. The forward pass.

3.2.2 DIBCO 2017

Document image binarization is a process of separating text from images, where text consists of pixels of interest, thus we train a model to label every pixel as belonging to text of background. Binarization of document images is a common pre-processing step for the document image processing that enhances quality of the images. Document images, especially of historical documents, usually contain different types of degradation and noise, i.e. different artifacts, uneven background, and bleedthrough text like it is shown in Fig. 4.

Figure 4

Sample image with bleedthrough text between the lines and corresponding ground truth from the DIBCO 2017 dataset.

We considered a dataset that is used in DIBCO 2017 document image binarization contest to proof representability and correctness of our implementation. For training we used a combination of datatsets from DIBCO 2009 - 2016 competitions that gave us 86 images, where 10 of them were randomly chosen for validation. We report the highest test accuracy associated with the highest validation accuracy after at most 300 epochs. For testing we used a dataset from DIBCO 2017 [44] as the most challenging among all of them. The test datasets contains 10 printed and 10 handwritten documents. All datasets contain both color and gray-scale images with up to 4M pixels per image. We treated all images as 3-channel color images (C = 3). We did not perform any pre-processing or augmentation. The images are divided into patches of size n by n and are fed into the 2D-LSTM. We could achieve the best results with n = 64. The architecture of 2D-LSTM network depicted in Fig. 5 has a single hidden layer that is separated into four independent LSTMs processing the patches from all the four possible directions. Each LSTM consists of N^H memory cells. The values from each LSTM are concatenated with respect to corresponding pixels, and fed into a common output layer of size (N^O) 2. Now, the output has a context from four different directions of the image at each pixel. Each output value indicates the probability of each pixel to be either text or background. We used a negative log likelihood loss criterion with Adam optimizer with a mini-batch size of 128 or 96 patches depending on a size of a model. We used larger batch size for training smaller models to fully utilize the GPU resources. The learning rate starts from 0.01 and reduced by a factor of 0.7 every 10 epochs. We used gradient clip with a value of 10.

Figure 5

Document image binarization topology for DIBCO 2017 dataset. The forward pass.

3.3 Quantization

In this section, we present the approaches that have been used for quantizing learning parameters and activations of the networks during training.

Our quantization methods are based on those presented in [24, 46, 58]. For multi-bit weights and activations, we adopt Eq. 3a as a quantization function, where a is a full-precision activation or weight, a_q is the quantized version, k is a chosen bit-width, and f is a number of fraction bits. For multi-bit weights, the choice of parameters is shown in Eq. 3b. For multi-bit activations, we assume that they have passed through a bounded activation function before the quantization step, which ensures that the input to the quantization function is either x ∈ [0, 1) after passing through a logistic sigmoid function, or x ∈ [− 1,1) after passing through a tanh function. As for the quantization parameters, we use Eq. 3b after the tanh and Eq. 3c after the logistic sigmoid.

$$ \boldsymbol{a}_{\boldsymbol{q}} =clip(round(\boldsymbol{a} \cdot 2^{\boldsymbol{f}}) \cdot 2^{-\boldsymbol{f}},\min,\max), \text{where} $$

(3a)

$$ \begin{array}{@{}rcl@{}} \boldsymbol{f} = \boldsymbol{k}-1\\ \min=-(2^{(\boldsymbol{k}-\boldsymbol{f}-1)})=-1\\ \max=-\min-2^{-\boldsymbol{f}}=1-2^{-\boldsymbol{f}} \end{array} $$

(3b)

$$ \begin{array}{@{}rcl@{}} \boldsymbol{f} = \boldsymbol{k}\\ \min=0\\ \max=2^{\boldsymbol{k}-\boldsymbol{f}}-2^{-\boldsymbol{f}}=1-2^{-\boldsymbol{f}} \end{array} $$

(3c)

In the case of binarized activations a_b, we apply a sign function as the quantization function [46], as shown in Eq. 4. In the case of binarized weights w_b, on top of the sign function we scale the result by a constant factor that is a standard deviation calculated according to Glorot et al. [17]. Our motivation to use this scaling coefficient based on that we use Glorot initialization for the weights in the case of full-precision model. In the case of binarization, the weights are constrained to -1 and 1, thus it makes sense to scale them to the boundary limits of the full-precision weights.

$$ \boldsymbol{a_{b}}=sign(\boldsymbol{a}) $$

(4)

$$ \boldsymbol{w_{b}}=sign(\boldsymbol{a}) \cdot scaling\_factor $$

(5)

3.4 Architecture

This section presents a hardware architecture of 2D-LSTM and fully-connected layers. The main challenge to design an efficient architecture of an algorithm with feed-back loop comes from recurrency that becomes a throughput bottleneck. A next time step (pixel) can be calculated only if the previous step has been finished due to precedence constraint that makes pipeline part-time idle. An efficient solution is to make pipeline busy with calculations that do not have recurrent dependencies between each other. In the case of 2D-LSTM, the processing of the different directions (top-left origin, top-right origin, bottom-left origin and bottom-right origin) are independent. Being inspired with the idea presented in [49], we propose to interleave calculations corresponding to different directions. First, the architecture processes first pixel from each direction in a sequence, then second pixel, and so on. This approach keeps pipeline always busy without throughput penalties, if the number of sequentially processed LSTM cells is enough.

The architecture is parametrizable with respect to performance scaling. The parametrization allows to apply coarse-grained parallelization on a level of 2D-LSTM cells, and fine-grained parallelization on a level of dot-products. The former, indicated as PE_LSTM unrolling, while the latter, indicated as SIMD_INPUT and SIMD_RECURRENT unrolling factors for input data and recurrent paths, respectively. This flexibility allows for tailoring of parallelism according to the available resources on the target device. When PE unrolling is performed, the LSTM cell will be duplicated PE_LSTM times, generating for each clock cycle PE_LSTM output activations. When SIMD unrolling is applied, each gate will receive a portion of the input data, namely SIMD_INPUT and a portion of the recurrent state SIMD_RECURRENT in each clock cycle. The same is applied to the fully-connected layer with PE_FC and SIMD_FC unrolling factors.

In the following, we explain the functionality of each component of the 2D-LSTM accelerator depicted in Fig. 6.

• Mem2Stream core is responsible for DMA reads of input data from DRAM using AXI memory-mapped non-coherent interface, and converting each transaction into AXI stream. The input data (pixels) are concatenated into 64- or 128-bit words that correspond to a single bus transaction depending on a bus width. For simplicity, the pixels are quantized so that the bus width is a multiple of pixel width, so the pixels do not spread over several transactions, and no padding is required.

• The Data Width Converter splits each transaction into separate pixels and concatenates them according to SIMD_INPUT.

• The 2D-LSTM Hidden Layer core depicted in Fig. 7 implements all functionality according to Eq. 2 except the recurrent connections. All memory cells and corresponding dot-products are instantiated with respect to PE_LSTM, and SIMD_INPUT, SIMD_RECURRENT respectively. Computations corresponding to different memory cells and dot-products can be calculated with various degree of parallelization, but always in a sequence with respect to different directions. Sequential execution of computations corresponding to different directions instead of parallel execution allows to save hardware resources as we do not quadruple datapath and memory ports. Although it increases latency per image, it keeps pipeline always busy that results in a higher computational efficiency.

• The Recurrent Path X/Y-axis Data With Converter converts the output from the hidden layer that has a width that is a multiple of PE_LSTM into input with a width that is a multiple of SIMD_RECURRENT. The buffers are required to match the inputs and outputs from the corresponding directions. The X-axis buffer contains 4 × N^H recurrent values (y_i− 1,j) along x-axis, while the Y-axis buffer contains W × 4 × N^H recurrent values (y_i,j− 1) along y-axis.

• The Output Layer implements the output fully-connected layer with PE_FC = FULL and SIMD_FC equal to PE_LSTM of the previous hidden layer, so to match the throughput. The architecture of the core is depicted in Fig. 8. In the case of MNIST, the outputs from different directions do not need to be matched for the same pixels, thus there is no need for a large matching buffer. The results are accumulated in a single-value buffer instantiated for each output unit. Opposite for DIBCO, outputs from hidden layer corresponding to the same pixel processed from different directions have to be matched, thus there is a matching buffer of size (H × W) for each output unit shown in Fig. 8. The buffers are implemented with dual-port read-write memories that allow to read and write partial sums in a pipelined manner at each clock cycle. Due to pixel-by-pixel processing order and sequential computations corresponding to different directions, the read and write patterns never risk to address the same address (partial sum) in the buffer in the same clock cycle. The processing directions follow distinct access sequence that is encoded in Row offset and Column index buffers.

• The SoftMax core implements a simplified version of Softmax function. It finds a label with the maximum value among all outputs from the output layer in the case of MNIST, or among all outputs corresponding to the same pixel in the case of DIBCO.

• The Data Width Converter concatenates the labels into 64- or 128-bit words depending on bus width.

• The Stream2Mem writes the labels to DRAM using AXI memory-mapped non-coherent interface.

Figure 6

System-level view of the 2D-LSTM Accelerator.

Figure 7

Hardware Architecture of the Hidden Layer.

Figure 8

Hardware Architecture of the Output Layer.

3.5 Results

3.5.1 Full-Precision Accuracy

In the following, we are presenting accuracy achieved with a full-precision 2D-LSTM network on MNIST and DIBCO 2017 datasets.

3.5.2 MNIST

Table 1 presents classification accuracy achieved with the full-precision 2D-LSTM on MNIST dataset. Our full-precision version is approaching accuracy of the state-of-the-art network [29] without using any pre-processing or augmentation, and confidently outperforms the result of a similar approach presented in the original paper on MD-LSTM [19] (see Section 3.1). The network presented in [29] is based on three deep learning architectures working in parallel, namely fully-connected deep network, deep CNN and deep RNN. The top result was achieved using a combination of 30 deep learning models that by far exceeds the size and complexity of our network. The 2D-LSTM architecture with 20 memory cells shows accuracy comparable with the sate-of-the-art. This configuration has been selected for a trade-off analysis of accuracy and hardware cost for various precisions.

Table 1 Accuracy of a full-precision 2D-LSTM on MNIST and DIBCO 2017 datasets depending on a number of memory cells (N^H) in comparison to earlier approaches.

3.5.3 DIBCO

Table 1 presents accuracy (F-measure) achieved with the full-precision 2D-LSTM on DIBCO 2017 dataset in comparison with previous methods. Our implementation with the highest accuracy outperforms the similar approach (see Section 3.1) and loses only 2.8% in accuracy to the winner of the competition presented in [44] without using any pre-processing or augmentation of the dataset. The winner approach presented in [44] is based on U-Net [47] type of fully convolutional neural network and data augmentation during training. The 2D-LSTM architecture with 40 memory cells shows accuracy comparable with the sate-of-the-art. In the following experiments, this configuration has been used for a trade-off analysis of accuracy and hardware cost for various precisions.

3.5.4 Accuracy vs. Hardware Cost vs. Precision

In the following experiments we explore accuracy as a function of hardware cost for various precision. All hardware prototypes have been implemented on Xilinx Zynq UltraScale+ MPSoC ZCU102 board featuring a XCZU9EG device that contains (1) Quad-core ARM Cortex-A53 and (2) FPGA fabric. The HLS synthesis and place and route have been performed with Vivado Design Suite 2017.4.

Figures 9, 10, 11, 12 plot the achieved test accuracy over BRAM36k and LUT utilization for different precisions for MNIST and DIBCO 2017 datasets. All resources are given after post-placement and routing. Each point on the plots represents a configuration represented with a combination of number of bits used for inputs (x), weights (w_LSTM), biases (b_LSTM), output activation (y_LSTM) of the 2D-LSTM layer and weights (w_FC) and biases (b_FC) of the FC layer. In the experiments, the parallelism of the hardware accelerator has been kept constant, with a number of instances of the complete accelerator M= 1, PE_LSTM= 1, SIMD_INPUT=FULL, SIMD_RECURRENT=FULL, PE_FC=FULL and SIMD_FC= 1 with a target frequency that has been set to 300 MHz and 240 MHZ for accelerators running MNIST and DIBCO 2017 datasets, respectively. In order to identify a configuration with the lowest hardware cost and accuracy that satisfies chosen criteria, we find Pareto frontier for various precisions in a space of accuracy as a function of hardware cost. The Pareto frontier identifies the configurations with the best trade-off between accuracy and hardware cost.

Figure 9

Pareto frontier for accuracy against BRAMs for 2D-LSTM with N^H = 20 memory cells runing on MNIST dataset depending on precision of input activation (x), weights (w_LSTM), biases (b_LSTM), output activation (y_LSTM) of the 2D-LSTM layer, and precision of weights (w_FC) and biases (b_FC) of the FC layer.

Figure 10

Pareto frontier for accuracy against LUTs for 2D-LSTM with N^H = 20 memory cells runing on MNIST dataset depending on precision of input activation (x), weights (w_LSTM), biases (b_LSTM), output activation (y_LSTM) of the 2D-LSTM layer, and precision of weights (w_FC) and biases (b_FC) of the FC layer.

Figure 11

Pareto frontier for accuracy against BRAMs for 2D-LSTM with N^H = 40 memory cells runing on DIBCO 2017 dataset depending on precision of input activation (x), weights (w_LSTM), biases (b_LSTM), output activation (y_LSTM) of the 2D-LSTM layer, and precision of weights (w_FC) and biases (b_FC) of the FC layer.

Figure 12

Pareto frontier for accuracy against LUTs for 2D-LSTM with N^H = 40 memory cells runing on DIBCO 2017 dataset depending on precision of input activation (x), weights (w_LSTM), biases (b_LSTM), output activation (y_LSTM) of the 2D-LSTM layer, and precision of weights (w_FC) and biases (b_FC) of the FC layer.

3.5.5 MNIST

The full-precision configurations presented in Table 1 have achieved higher test accuracy with a higher value of dropout than quantized versions (0.8 vs. 0.7, respectively) that confirms observations that quantization has a regularization effect on neural network similar to dropout that prevents model overfitting [23, 56]. Furthermore, high dropout values mean that MD-LSTM has a strong tendency to overfitting that is also in accordance with earlier observations presented in [43] and [38]. Considering Figs. 9 and 10 in the following, a configuration with 2-bit weights is not depicted on the plots because it has shown bad convergence that is probably a result of imbalanced representation of negative and positive values in the case of 2-bit quantization, namely (-1.0, -0.5, 0, 0.5). We expect that ternarisation of the model will result in higher accuracy.

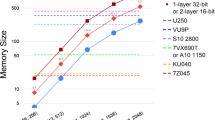
Configuration 1/1,1/1/1,1 demonstrates that binarization of activation causes stronger degradation of accuracy than binarization of the weights that can be explained by that we did not use scaling factor for binarized activation but weights and biases only. Some of the configurations with lower precision have higher test classification accuracy than some with higher precision that can mean that regularization that is brought by the quantization outperforms the negative effects of the lower precision. Moderate degradation in accuracy even for the configuration with binary weights means that the 2D-LSTM is an overkill for the MNIST problem. We constrained a selection of an optimal configuration with accuracy that is higher than the best test accuracy on MNIST dataset for existing FPGA-based implementations presented in Table 3. A hardware implementation of a multilayer perceptron presented in [42] with 98.92% of accuracy identifies the low bound. We selected a configuration 1/1,1/2/1,1 that is Pareto optimal with the lowest hardware cost and accuracy higher than the low bound for further throughput scalability analysis and comparison with existing FPGA implementations processing MNIST dataset.

3.5.6 DIBCO

Considering Sections 11 and 12 in the following, the results show a strong correlation between the precision of the operands and accuracy. Comparing configurations 8/4,4/4/8,8 and 8/4,8/4/8,8, we see that precision of a bias has a noticeable influence on accuracy with 1.31% gain in accuracy for the later one. Keeping higher precision for bias, while reducing precision for weights or activation can be an efficient approach for increasing accuracy at low hardware cost. The noticeable influence of biases on accuracy can be explained by higher contribution of biases to the final result in the case of smaller models. The full-precision versions presented in Table 1 could achieve higher accuracy with higher value of dropout than quantized versions (0.6 vs. 0.5, respectively). There is still a noticeable gap between train and test accuracy that can mean an overfitting of the model, however higher dropout values did not improve the accuracy. The gap in accuracy between training and test can be also explained by a different complexity between training and test datasets as DIBCO 2017 dataset is more challenging for binarization than previous additions. We constrained a selection of an optimal configuration with degradation in accuracy of less then 1% with respect to full-precision version. 1% degradation is an empirical value for fair trade-off between complexity and accuracy. According to Fig. 11 configurations 8/4,4/8/8,8 and 8/4,8/4/8,8 are Pareto optimal with accuracy higher than the low bound. However, in the case of LUT utilization, 8/4,4/8/8,8 is not a Pareto optimal configuration that makes 8/4,8/4/8,8 a selection for further investigation. The preference is given to Pareto optimal configurations with respect to LUT resources as the LUT utilization is the implementation bottleneck, see Table 2.

Table 2 Resource utilization for a baseline configuration (M= 1, PE_LSTM= 1, SIMD_INPUT=FULL, SIMD_RECURRENT=FULL, PE_FC=FULL and SIMD_FC=PE_LSTM) of the accelerator implemented on XCZU9EG for MNIST and DIBCO 2017 datasets.

3.5.7 Throughput Scalability

According to Eq. 2, a number of learnable parameters per single 2D-LSTM cell is 5 × (C + 2 × N^H + 1), where five comes from a number of gates including input to a memory cell. In the case of semantic segmentation problem, a single neuron of the output layer has (4 × N^H + 1) parameters, where 4 × N^H gives a number of concatenated outputs from the hidden layers. In the case of MNIST, a single unit of the output layer has (4 × N^H × H × W + 1) parameters. The number of operations of the 2D-LSTM layer per image is Op_LSTM = (2 × 5 × (C + 2 × N^H) + 11) × N^H × H × W × 4, where two comes from multiplication and addition counted as separate operations, eleven is a number of point-wise operations, and four is a number of possible processing directions. The same applies to the output layer: Op_FC = (2 × (4 × N^H) + 1) × N^O × H × W. We neglect a complexity of the rest of the network.

The resource utilization for selected configurations of the accelerator for MNIST and DIBCO 2017 datasets are presented in Table 2. In the case of design implemented for DIBCO dataset, a LUT utilization is a resource bottleneck that condition a selection of a Pareto optimal configuration with higher BRAM number but lower LUT utilization. The resource utilization of a baseline configuration (PE_LSTM = 1, SIMD_LSTM = FULL, PE_FC = FULL, SIMD_FC = PE_LSTM) allows to place more instances. The architecture allows to scale throughput by increasing a number of PE_LSTM or instantiating multiple (M) instances of the complete accelerator. The following Figs. 13 and 14 show a throughput scalability depending on a number of PE_LSTM with M = 1. The measured throughput scales near perfectly with respect to theoretical throughput with discrepancy that increases with a higher PE_LSTM number. The discrepancy can be explained by increased throughput penalty due to reduced number of sequentially executed cells that makes the pipeline partially idle. The theoretical throughput is calculated according to the following formula: (Op_LSTM + Op_FC) × F × (PE_LSTM×M)/L, where F is target frequency and L = N^H × 4 × H × W is a theoretical latency in clock cycles to process a single image without considering any architecture related features like depth of a pipeline. In the following experiments we aim to find a configuration with the highest throughput instantiating multiple (M> 1) accelerators with PE_LSTM> 1.

Sections 13 and 14 clearly show that instantiating multiple cells rather than multiple instances of the complete accelerator is more efficient because we avoid unnecessary replication of conversion cores and weights’ memory. In the case of instantiating multiple cells, although the design operates on the same model, there is still an increase in memory utilization that comes from more parallel ports required to supply higher throughput. The measured throughput shows near theoretical values with increased discrepancy over a number of PE_LSTM.

The configurations PE_LSTM= 5, M= 14 and PE_LSTM= 10, M= 2 for MNIST and DIBCO 2017 datasets, respectively, with the highest throughput are used for comparison with GPU and other FPGA implementations in Table 3. Configurations with higher PE_LSTM are not presented as they failed routing.

Table 3 Comparison to FPGA and GPU implementations processing MNIST, DIBCO 2017 datasets.

Figure 13

Throughput scalability depending on a number of PE_LSTM and a number of instances (M) of the complete accelerator for MNIST dataset.

Figure 14

Throughput scalability depending on a number of PE_LSTM and a number of instances (M) of the complete accelerator for DIBCO 2017 dataset.

3.5.8 Comparison

The host code runs on Cortex-A53 running Ubuntu 16.04.6 LTS. It reads test images from the SD card, stores them in the shared DRAM, starts the accelerator execution, measures runtime, and computes accuracy against the ground truth classifications. During processing, we perform two types of power measurements: P_board that is a power consumption of the complete board, in the case of FPGA measured using digital multimeter Voltcraft VC-870, and P_chip that has been acquired using Zynq UltraScale+ MPSoC Power Advantage Tool [1] for FPGA, and nvidia-msi for GPU.

As it is shown in Table 3, 2D-LSTM model provides the highest accuracy with respect to other FPGA-based implementations, while having one of the smallest models that confirms finding in the earlier works [38, 45] that MD-LSTM layers require less trainable parameters to achieve similar accuracy to other types of neural networks. Although, it has one of the smallest models, the number of operations is the highest that is also in alignment with the previous works, and this is the primary reason why other types of networks are preferred over MD-LSTM in the recent years.

Table 3 presents comparison with earlier FPGA implementations of multilayer perceptron processing MNIST datsaset, and our 2D-LSTM implementations for pixel-by-pixel (P) and diagonal-wise (D) approaches running on GPU for MNIST and DIBCO 2017 datasets. Our FPGA-based implementation processing MNIST dataset outperforms all reference FPGA implementations in accuracy, however it loses to implementations with similar precision in terms of throughput and energy efficiency due to several reasons. First of all, all other implementations use multilayer perceptron models that have much lower implementation complexity due to only feed-forward dataflow and low-complexity activation functions like ReLu or just a step function in the case of binarized models [53]. In contrast, 2D-LSTM has two recurrent paths and multiple non-linear activation functions, and has to process image in four directions. Additionally, the implemented architecture follows the pixel-by-pixel order of execution that has the highest time complexity. Nevertheless, it shows very promising results taking into account that we did not apply any of the orthogonal approaches for accelerating 2D-LSTM (Section 3.1).

Our FPGA-based implementation outperforms pixel-by-pixel and diagonal-wise approaches running on GPU in terms of throughput by 36-84× and 11-36×, and in terms of energy efficiency by 429-1238× and 180-756×, respectively. However, a difference in throughput between pixel-by-pixel and diagonal-wise GPU implementations is less than expected (H × W)/(H + W), due to overheard of picking up pixels from diagonals for diagonal-wise processing. Additionally, in the case of MNIST dataset, the batch size for pixel-by-pixel approach was larger than for diagonal-wise approach (2560 vs. 2048, respectively) due to lower memory overhead that also reduces the speedup of the later approach. In the case of DIBCO dataset, the batch size was the same for both implementations. Clearly there is a big room for optimization. However, even if we consider perfect speedup with respect to pixel-by-pixel approach, our FPGA-based implementation still outperforms the perfect diagonal-wise GPU implementation in terms of throughput and energy efficiency.

It has been shown that FPGA is a promising computing platform for deep-learning that achieves higher performance and energy efficiency in comparison to conventional platforms. However, even higher levels of efficiency can be achieved following emerging computing paradigms. In recent years, new computing approaches have been proposed targeting much higher energy efficiency and parallelism than ever before. One such technology is Processing-in-Memory (PIM).

4 1D-LSTM PIM

The peak performance and energy efficiency of many advanced neural network accelerators (e.g. LSTM) are constrained due to limited external memory bandwidth and high data access energy. PIM is an emerging computing paradigm that bridges the memory-computation gap by integrating the computation units inside the memory device. The tight coupling of memory and computation logic minimizes the data movement cost, enables the massive internal data parallelism and results in high energy efficiency. In this section, we present a novel DRAM based PIM hardware architecture for binary 1D-LSTM inference. As an initial step, this work only focuses on implementing of a 1D-LSTM inference model in a DRAM-based PIM that will be the base architecture for future variants of LSTM models, such as MD-LSTM.

4.1 Related Work

Recently, there are several research publications on CNN PIM accelerators that are based on RRAM [8, 10, 50, 57], SRAM [3, 5, 16, 28, 34] and DRAM [15, 25, 32, 52] devices. However, a limited number of publications have focused on RNN PIM accelerators. The authors of [37] and [35] propose a PIM accelerator for basic RNNs that are based on SRAM and RRAM, respectively. However, these works did not consider advanced networks, such as LSTMs. The authors of [36] extended the work of [35] for other advanced RNN networks such as LSTMs. The basic computation unit of this architecture is a vector multiplication unit that is realized using RRAM crossbar array. This architecture needs an area, power, and latency intensive 8-bit analog to digital converter (ADC) in the Sub-Array (SA). The ADCs increase the area of PIM SAs by 10 × compared to a standard RRAM SA. The ADCs consumed 43% of the total system power and 49% of the total chip area, respectively. Another issue of RRAM based PIM accelerators is the high process variation that affects the final computation results between the SAs/devices. Additionally, the RRAM process is not technologically as mature as SRAMs or DRAMs. On the other side, SRAM based accelerators have low memory density and are not suitable for networks with a large memory footprint.

Hence, this paper presents a DRAM based LSTM PIM accelerator.

4.2 DRAM Basics

In this section, we describe the DRAM architecture and its functionality in order to provide the required background to understand our PIM architecture. A DRAM device is organized as a set of banks that include memory arrays. Each bank consists of row and column decoders, Master Wordline Driver (MWLD), and Secondary Sense Amplifiers (SSAs) (see Fig. 15). The memory array is designed as an hierarchical structure of SAs (eg. 1024 × 1024 cells). To access the data from DRAM, an activate command (ACT) is issued to a specific row, which activates the associated MWLD and LocalWordline Drivers (LWDs). This initiates the charge sharing between the memory cells and the respective Local Bitlines (LBLs), the voltage difference on each of these LBLs is sensed by the Primary Sense Amplifiers (PSAs) (e.g. 1024 PSAs) integrated in each SA. The PSAs are integrated on either sides of a SA (half the number of PSAs on each side) and are shared between the two neighbouring SAs. The concurrently sensed data by the PSAs of all the SA in a block (i.e. row of SA) creates an illusion of a large row buffer or a page (e.g. Page size = 1 KB). After row activation, read (RD) or write (WR) commands are issued to specific columns of this logical row buffer to access the data via Master Datalines and SSAs. Each column of SAs (CSA) has a separate set of Master Datalines and SSAs (e.g. 8 per CSAs) that are shared. Reading or writing the data from/to the PSAs of a block (or page) is performed in a fixed granularity of I/O data width ×bursts length (e.g. 8 × 8 = 64 bit in DDR3/4) and equal amount of data is fetched (e.g. 8 bits for x8 device) from all the associated SA (e.g. 8 SAs) of a block. In order to activate a new row in the same bank, a precharge (PRE) command has to be issued to equalize the bitlines and to prepare the bank for a new activation.

Figure 15

DRAM architecture.

4.3 Architecture

This section presents the DRAM based 1D-LSTM PIM architecture in detail. One of the major goals of this architecture is to conserve the regular and repetitive structure of a DRAM bank to benefit from the high memory density. The computation units should not break this modularity. The aim is to maximize the data parallelism and minimize the data transfer cost by integrating the computation units close to the storage units without modifying the highly optimized commodity SA. Hence, the nearest possible location to integrate the computation units is at the output of the PSA where the data parallelism is maximum. However, the DRAM architecture and its process restrict the integration of logic units in this region i.e. at the output of the PSA due to the following reasons:

• PSA region has no clocking signals i.e. only combinational logic can be integrated.

• Among the three available metal layers in the DRAM process one metal layer in this region is utilized for the LBL of the neighboring SA due to PSA sharing. Hence, the computation logic will only have two metal layers, requiring more engineering efforts for floor planning and routing.

• The width (in μ m) of the computational logic is limited to the SA width in order to conserve the repetitive structure of a DRAM bank.

Contrarily, integrating the computation logic near the SSAs do not impose hard design constrains but compromises the parallelism. Hence, our new architecture partition the computation logic into basic computation units and secondary processing units (SPU) in order to attain a balance between parallelism and design constraints of the DRAM architecture and its process. Only, the basic computation units are integrated at the output of the PSA in each SA. The rest of the logic required to process the output of these basic units are in SPU that is integrated at the output of the SSAs. The computational hierarchy matches the memory hierarchy without affecting the structure of the DRAM bank. The basic computation units are explicitly built using combinational logic due to lack of clocking signals near the PSA.

In the following, we first elaborate the micro-architecture of a basic unit followed by the details of the overall architecture. The proposed architecture is for a state-of-the-art commodity 8 Gb x8 DDR4 DRAM device with 16 banks, 1024 × 1024 SA dimension, 16 SAs per block (8 per Half-Bank see Fig. 15.), 2 KB page size, 1024 PSAs per SA, 128 master bitlines (eight per SA), and 128 SSAs (eight per CSA). The architecture is scalable to other dynamic random access memory (DRAM)s and their technologies. This architecture targets a binary 1D-LSTM with 1 bit weight (i.e. $logic 0 \rightarrow +1$, $logic 1 \rightarrow -1$), 2 bit data and 2 bit activation. The authors of [24] and [48] have shown that the binary networks have negligible impacts on the accuracy as compared to full-precision networks for various applications such as OCR.

4.3.1 Basic Computation Unit

The basic computation unit (i.e. dot-product unit) consists of N multiplication units and an adder-tree as shown in Fig. 16. A single multiplication unit for a binary NN is realized using two XOR gates and a 2s complement converter (as shown in Fig. 17.). The 2s complement converter is a simple adder that adds logic 1 to the output of the XOR gates if the sign of the weight is negative.

Figure 16

Dot-Product Unit.

Figure 17

Basic unit at the PSAs.

The 3-bit output of the multiplication units is fed to an adder tree that outputs the dot-product result of two 1D-arrays of dimension N. The value of the N is crucial as it directly influences the size/depth of the adder-tree and can potentially blow up the design near the SA.. Hence, based on the architectural exploration the value of N is confined to 32 (i.e. 8-bit dot-product result), which also satisfies all the aforementioned physical implementation constraints.

The architecture specifically stores the weight array (i.e. W or R) and its corresponding data array (i.e. x^t or y^t− 1) in different rows of the same SA. felements of the weight array are aligned column-wise with the corresponding elements of the data array. For example, the element zero of weight array has been stored in the same columns of a SA as element zero of the data array. Hence, 1-bit weights are duplicated to align with 2-bit data in the column direction. Before the start of the dot-product computations, the weight array row is first activated and are accessed by the PSA. These weights are also buffered in shadow latch (SHL) by enabling the isolation (ISO) switch. Once the weights are latched in shadow-latches it is reused for several computations by changing only the corresponding data in PSAs (i.e. activation of a new row), refer Fig. 17.

A single SA of a DRAM bank is integrated with 16 basic computation units (i.e. dot-product units). Each of this unit can only compute the dot-product of the arrays whose dimension are less than or equal to 32. If the dimensions of the dot-product operation are larger than 32 then the dot-product operation is broken down to multiple smaller dot-products such that it could be mapped to the basic units. The 8-bit partial dot-product results computed by multiple basic units are transferred to the SSA region (i.e. same as read operation) where they are added in the SPU to obtain the final result of the large dot-product operation. The 8-bit width of the basic unit output also matches with the DRAM architecture since the master bitlines connecting a single SA to the SSAs are also 8-bit wide.

4.3.2 Overall Architecture

Figure 18 shows the architecture of a single bank that is enhanced with LSTM computation units. The architecture exploits different levels of parallelism (i.e SA parallelism, bank parallelism) available in DRAM to achieve high throughput. The computations of each LSTM cell are mapped to an individual CSA (refer Fig. 15) in a DRAM bank. Hence, the computations of each LSTM cell are executed in parallel. For example, a DRAM with 16 banks and 16 CSAs per bank executes a maximum of 256 LSTM cells in parallel. In our architecture, one bank, called as FC-bank, is reserved for the fully-connected layer computations. The remaining banks are used for LSTM cell computations. Hence, the maximum LSTM cells executed in parallel is 240. This architecture offers flexibility to configure any bank as FC-bank.

Figure 18

PIM bank architecture.

In an individual CSA, the dot-product operations of each gate of an LSTM cell are mapped to an individual SA or to a group of SAs. These SAs operate in a pipeline fashion i.e. while a particular SA is transferring the results of 16 basic units to the SPU unit, another SA belonging to the same CSA starts its computation by activating (i.e. ACT) the required rows of that sub-array. The transfer of basic unit output from the SA to the SSA region is similar to a read operation. The CSL lines that are used to select the required burst of data from the currently active row (in the PSAs) for a read/write operation are also used to select one of the 16 basic units outputs when a SA is operated in computation mode. The selected 8-bit data from a SA in each CSA is then transferred to the respective SSAs/SPU via the master bitlines. Figure 19 shows the block diagram of a SPU. The partial dot-product results computed in the basic computation unit are added using a sequential adder in the SPU to complete the summation operations of each LSTM gate (e.g. $\boldsymbol {W}_{a} \boldsymbol {x}^{t} +\boldsymbol {R}_{a} \boldsymbol {y}^{t-1} + \boldsymbol {b}_{a}$, see Eq. 1). The sequential adder and the transfer operations are executed in pipeline manner. Hence, adding only one clock cycle delay to the overall latency. The intermediate results of each LSTM gate are stored in a buffer. As the summation result corresponding to a gate for an instance t is finished, the dot-product done signal is set high and the result is transferred to an appropriate activation function (i.e. tanh or sigmoid). The non-linear activation functions are implemented as a piece-wise linear function similar to [40]. Figure 20. shows the comparison between the actual value and the hardware implemented piece-wise linear sigmoid function. Once the activation function outputs a^t, i^t, f^t and o^t are computed for a given instance, c^t and y^t computations are triggered.

Figure 19

SPU unit.

Figure 20

Actual vs the hardware implemented piece-wise linear sigmoid function.

Each of the SPU produces a 2-bit output corresponding to an LSTM cell. The 2-bit output of all concurrently executed LSTM cells are concatenated to form the y^t output array. If the LSTM cells are distributed across the banks, each bank broadcasts its 16 × 2-bit (i.e. 32-bit) result to all other banks including FC-bank. This architecture does not use an explicit bus for such broadcasting. It reuses the shared bus (i.e. 64 bit wide for DDR4) that is used to transfer the data from the banks to the interface and vice-versa. Once the y_t output array is available in all the banks, it is written back to the appropriate SAs that are responsible for the computations of the next instance in each CSA. Note that the writebacks are concurrent in all the CSAs. Since the y^t is applicable to all the gates of an LSTM cell, this y^t has to be written multiple time to all the memory locations that are responsible for the respective LSTM gate computations within the CSA. This writing of the same data multiple times within the CSA imposes a huge latency. Hence, the architecture enables multiple CSL lines instead of only 8 CSLs per CSA. This enables concurrent writes of the same data to multiple 8-bit word memory locations in each CSA but at the cost of increased load capacity of the write drivers. Since the LSTM cells have a maximum of four gates (including input to a memory cell), the concurrent write is limited to four memory locations in each CSA, which requires an increase in driver strength by 10-15% only.

Although the architecture considers each CSA as a parallel entity, the commodity DRAM bank architecture imposes a major restriction. All the SAs belonging to the same block (i.e. row of SAs) has to perform the same set of operations at any given time due to coupling of these SAs by the MWL and other control lines.

The basic unit computations require activation of rows and these commands in a DRAM bank corresponds to an entire block that activates the same row in each SA of that block. Similarly, transfer of data between the SA and SSAs involve read and write commands that are applicable for the entire block i.e. all the SAs in a block are concurrently in data transfer mode. However, the restriction that imposes dependency between the CSAs is addressed by mapping and executing the same processing steps of the respective LSTM cell in each CSA in a bank.

FC-bank stores the y^t results and performs the fully-connected operations of the previous instance (i.e t − 1) in parallel with the LSTM cell operations of the current instance (i.e. t). The same basic units and the sequential adder in the SPU are sufficient for the fully-connected layer. The final results of the fully-connected layer are also stored in the same bank. The number of dot-product operations per unit/neuron of the fully-connected layer is less than the LSTM cell i.e. LSTM cells are more computationally intensive. Hence, the FC-bank finishes its operations before the availability of y^t results of the next instance. This architecture only performs the operations corresponding to the input layer, hidden layer and fully-connected layer of the LSTM inference engine. The remaining processing steps like softmax and connectionist temporal classification (CTC) are assumed to be executed in an external processing unit.

4.4 Experimental Setup

This work investigated all the relevant DRAM circuits (e.g. PSAs) and the aforementioned PIM circuits using the DRAM architecture exploration tool DRAMSpec [39] and an adapted UMC 65 nm Low-Leakage CMOS bulk technology, respectively. The UMC 65 nm process technology was modified to emulate a 65 nm DRAM process by changing the transistor parameters, restricting the number of metal layers (three metal-layers only), and layout rules, such as the minimum metal pitch. The area, power, latency results of all the PIM circuitry are based on the exhaustive circuit level simulations and the full custom layout implementations that are done using Cadence Spectre and Virtuoso, respectively. To retain the modular and regular architecture of commodity DRAMs, the layout confines the total width of the PIM circuitry integrated near the SA to the width of the SA.

The rest of the DRAM architecture results, including SAs, SSAs, peripherals circuitry, row and column decoders, are evaluated with DRAMSpec. All the estimated results are for the DRAM core clock period of 3ns. The results obtained from DRAMSpec and the circuit-level simulations are substituted in the bit-true model of the proposed PIM architecture to calculate the total area, power consumption, and performance. Finally, the calculated total area in 65 nm technology is conservatively scaled to a 20 nm node to make a fair comparison with recent commodity DRAMs.

4.5 Results

This section presents the experimental results of our DRAM based PIM implementation. The system performance is evaluated using the inference of a Bi-LSTM model for OCR application adapted from [48]. The Bi-LSTM model is trained for 1-bit weight and 2-bit data/activation that achieves a classification accuracy of 94% for the same dataset as used in [48]. The inference of the Bi-LSTM model is also implemented on Xilinx Zynq UltraScale+ MPSoC ZCU102 board featuring a XCZU9EG device using the same architecture as in [48]. The FPGA implementation is used as a baseline for comparison in this paper.

4.5.1 Area

We implemented the PIM architecture and designed all necessary circuits in a 65 nm technology. The obtained die area results are conservatively scaled to 20 nm in order to compare it to a state-of-the-art 8 Gb commodity DRAM. Table 4 shows the calculated area results of a standard DRAM die and the PIM enhanced DRAM die for a 65 nm technology and for a scaled 20 nm technology. The scaled area of a standard DRAM die for 20 nm technology is comparable to 8 Gb commodity DRAM dice from various vendors. This shows the correctness of our estimation methodology.

Table 4 Area comparison of DRAM PIM vs Standard DRAMs

The presented area results for the PIM enhanced DRAM are evaluated for two architecture variants, (1) all DRAM SAs are enhanced with basic computation units (referred as all MAC rows) (2) limited number of blocks (four in this case) in each bank are enhanced with basic computation units (referred as 4 MAC rows). 4 MAC rows are sufficient to store all the parameters of the specified Bi-LSTM inference model. However, for the networks with larger parameter size, the parameters corresponding to initial timestamps are stored in the available space of 4 MAC rows. The parameters of the subsequent timestamps are overwritten on a timely basis that is stored in non-PIM SAs. Alternatively, a suitable architecture variants like 8 MAC rows or 16 MAC rows can be chosen at a cost of larger area.

The 4 MAC rows architecture variant is preferable as it achieves a high memory density, similar to a commodity DRAM chip. This architecture variant (i.e 4 MAC rows) enables the DRAM based PIM chips to be used as both a conventional memory device and an accelerator.

Such a PIM chip has a total area overhead of 18% compared to an 8 Gb commodity DRAM. All the evaluation results presented henceforth are only for the 4 MAC rows variant.

4.5.2 Power Consumption

The power overhead of NN circuits compared to total power consumption is only 10%. The remaining power consumption is due to the conventional DRAM operations required for the computation. The prime benefit of this architecture is the low power consumption. The total power of our PIM implementation is 0.384 W, while the FPGA implementation consumes a power of 19 W measured using Zynq UltraScale+ MPSoC Power Advantage Tool [1]. Only the FPGA core power is presented not the board power for a fair comparison.

4.5.3 Throughput and Energy Efficiency

The throughput of the proposed architecture for the aforementioned Bi-LSTM inference is 6329113 input layer columns per second that accounts to 1309.16 GOp/s. The same inference executed on an aforementioned FPGA results a throughput of 4000 GOp/s. Although, the FPGA based implementation achieves higher throughput, the goal of our new architecture is mainly to optimize the energy efficiency, i.e. performance per Watt. The PIM based implementation is 16.19 × more energy efficient compared to an FPGA based implementation. As there are no prior publications on DRAM based LSTM PIM, we show for the sake of completeness the results of this work against the results of the RRAM based implementation from [36] (Refer Table 5). Note that, both the systems are designed for different quantizations and the obtained results are for different applications. Hence, a fair comparison of these two works is not possible.

Table 5 Results of our work against RRAM based LSTM PIM

5 Conclusion

We presented two novel hardware architectures for inference of LSTM neural networks.

First, a hardware architecture for MD-LSTM neural network was presented. We conducted a systematic exploration of accuracy as a function of hardware cost for various precisions using Pareto frontier for DIBCO 2017 and MNIST datasets. It was demonstrated that MD-LSTM achieves an accuracy that is comparable with state-of-the-art for MNIST dataset with binary weights and 2-bit activation. It also approaches best results for DIBCO 2017 dataset with low bit-width weights and activation. Based on this new architecture we implemented an FPGA-based accelerator that outperforms NVIDIA K80 GPU implementation in terms of runtime and energy efficiency. At the same time, our accelerator demonstrates higher accuracy and comparable throughput in comparison to state-of-the-art FPGA-based implementations of multilayer perceptron for MNIST dataset.

Second, we proposed a DRAM based PIM architecture for 1D-LSTM with binary weights and 2-bit data/activation. This architecture is explicitly proposed for energy efficient computing and addressing the memory bound issues of LSTM networks. One of the major highlights of our architecture is retaining the regular and repetitive DRAM structure without compromising the memory density. The small area overhead (18 %) compared to an 8 Gb DDR4 DRAM qualifies this architecture to be embedded in upcoming DRAM devices. The results show that the PIM implementation is 16.19 × more energy efficient as compared to the FPGA based design. In the future, this work will be extended to different input data quantizations and weights, and to MD-LSTM.

We have shown that the new compute paradigm PIM, and FPGAs are very promising platforms for deep learning that can offer a solution in cases, where conventional platforms, such as GPU, fail to provide the necessary performance and energy efficiency required by the applications.