On the Performance Analysis of a Class of Transform-domain NLMS Algorithms with Gaussian Inputs and Mixture Gaussian Additive Noise Environment

Abstract

This paper studies the convergence performance of the transform domain normalized least mean square (TDNLMS) algorithm with general nonlinearity and the transform domain normalized least mean M-estimate (TDNLMM) algorithm in Gaussian inputs and additive Gaussian and impulsive noise environment. The TDNLMM algorithm, which is derived from robust M-estimation, has the advantage of improved performance over the conventional TDNLMS algorithm in combating impulsive noises. Using Price’s theorem and its extension, the above algorithms can be treated in a single framework respectively for Gaussian and impulsive noise environments. Further, by introducing new special integral functions, related expectations can be evaluated so as to obtain decoupled difference equations which describe the mean and mean square behaviors of the TDNLMS and TDNLMM algorithms. These analytical results reveal the advantages of the TDNLMM algorithm in impulsive noise environment, and are in good agreement with computer simulation results.

1 Introduction

Adaptive filters are widely used for filtering problems in which the statistics of the underlying signals are either unknown a priori, or in some cases, slowly-varying. Many adaptive filtering algorithms have been proposed and they are usually variants of the well known least mean square (LMS) [1] and the recursive least squares (RLS) [2] algorithms. An important variant of the LMS algorithm is the normalized least mean square (NLMS) algorithm [3], where the step size is normalized with respect to the energy of the input vector. Due to the numerical stability and computational simplicity of the LMS and the NLMS algorithms, they have been widely used in various applications [4, 5].

An important class of NLMS is the transform domain NLMS (TDNLMS) algorithms [6–11] where unitary transformations such as the discrete Fourier transform (DFT), the discrete cosine transform (DCT), and the wavelet transform (WT) are employed to pre-whiten the input signal. Prewhitening and element-wise normalization usually help to reduce the eigenvalue spread of the input autocorrelation matrix and hence significantly improve the convergence speed. Driven by the practical advantages of the TDNLMS family, there is also considerable interest in the performance analysis of these algorithms [8, 9]. Results concerning the performance behaviors of the TDNLMS algorithm were studied in [6–11].

In this paper, we study a more general TDNLMS algorithm, the TDNLMS algorithm with general error nonlinearity. The convergence performance of this algorithm in Gaussian inputs and additive Gaussian and impulsive noise environments are studied. The main novelty lies in handling the normalization, evaluating the expectations specific to this algorithm and dealing with the error nonlinearity. We study with particular emphasis on two special cases of this algorithm: the conventional TDNLMS algorithm with no nonlinearity, and the transform domain normalized least mean M-estimate (TDNLMM) algorithm [12], which is based on robust M-estimation [13, 14] and adaptive threshold selection (ATS) [12, 15]. These techniques have been successfully employed in the LMM [12], the recursive least M-estimate (RLM) [15] and the normalized LMM (NLMM) [16] algorithms for robust filtering in impulsive noise environment. The motivation of studying this algorithm is that the performance of the TDNLMS algorithm, which is based on LS estimation as in the LMS algorithm, will deteriorate considerably when the desired or the input signal is corrupted by impulsive noise. The mean and mean square convergence analysis for the TDNLMS algorithm with general error nonlinearity is treated in a single framework using the Price’s theorem [17] for Gaussian case and its extension [18] for contaminated Gaussian (CG) case. The finally obtained decoupled difference equations clearly interpret the convergence performance of all the studied algorithms. The validity of the analytical results is verified through extensive simulations and they are in good agreement with each other. The rest of this paper is organized as follows: In section 2, the TDNLMS and TDNLMM algorithms are reviewed and the TDNLMS algorithm with general error nonlinearity is formulated. Their convergence performance analysis is given in section 3. Computer simulations are conducted in section 4. Finally, conclusions are drawn in section 5.

2 TDNLMS Algorithm with General Error Nonlinearity and TDNLMM Algorithm

2.1 The TDNLMS Algorithm

Consider the adaptive system identification problem in Fig. 1 where an input signal x(n) is applied simultaneously to an adaptive transversal filter of order L with weight vector $W(n) = {\left[ {{w_1}(n),{w_2}(n), \cdots, {w_L}(n)} \right]^T}$ and an unknown system to be identified with an impulse response $W* = {\left[ {{w_1},{w_2}, \cdots, {w_L}} \right]^T}$. $X(n) = {\left[ {x(n),x\left( {n - 1} \right), \cdots, x\left( {n - L + 1} \right)} \right]^T}$ is the input vector and the superscript T denotes the transpose of a vector or a matrix. e(n) is the estimation error and d(n) is the desired signal of the adaptive filter, which may be corrupted by an additive noise η _o (n). Hence

Figure 1

Adaptive system identification.

$$ d(n) = {X^T}(n)W* + {\eta_o}(n) $$

(1)

The update equations for the TDNLMS algorithm can be written as:

$$ e(n) = d(n) - {W^T}(n){X_C}(n), $$

(2)

$$ W\left( {n + 1} \right) = W(n) + \mu \Lambda_C^{ - 1}{X_C}(n)e(n), $$

(3)

where μ is a constant step size parameter controlling the convergence rate and steady state error of the algorithm. ${X_C}(n) = CX(n) = {\left[ {{X_{C,1}}(n),{X_{C,2}}(n), \cdots, {X_{C,L}}(n)} \right]^T}$ is the transformed signal vector. C is an L × L transform matrix such as (DFT) or (DCT). $\Lambda_C^{ - 1} = {\hbox{diag}}\left[ {\varepsilon_1^{ - 1}(n),\varepsilon_2^{ - 1}(n), \cdots, \varepsilon_L^{ - 1}(n)} \right]$ which is an element-wise normalization matrix with ε _i (n) being the estimated power of the i-th signal component after transformation. Common methods for choosing ε _i (n) include ${\varepsilon_i} + X_{C,i}^2(n)$ and ${\varepsilon_i}(n) = \left( {1 - {\alpha_\varepsilon }} \right){\varepsilon_i}\left( {n - 1} \right) + {\alpha_\varepsilon }X_{C,i}^2(n)$, where ${\alpha_\varepsilon }$ is a positive forgetting factor smaller than one. ε _i is a small positive value used to avoid division by zero or it can be chosen as certain prior power estimate of the corresponding component. In the analysis to be presented in section 3, a form ${\varepsilon_i} + {\alpha_\varepsilon }X_{C,i}^2(n)$ similar to the above two choices will be chosen. In the simulation section, we shall introduce a method to approximately analyze the effect of this choice.

2.2 The TDNLMM Algorithm and TDNLMS Algorithm with General Error Nonlinearity

Many techniques have been proposed to combat the adverse effect of impulsive noise on adaptive filters. They include the median-filtering algorithms [19, 20], the nonlinear clipping approaches [21, 22], and approaches based on robust statistics [12, 15, 16]. The LMM [12] and the RLM [15] algorithms are two effective algorithms derived from robust M-estimation and their improved robustness in impulsive noise and performance comparison with other relevant algorithms were thoroughly discussed in [12] and [15].

In the TDNLMM algorithm [12], an M-estimate distortion measure ${J_\rho } = E\left[ {\rho \left( {e(n)} \right)} \right]$ is minimized, where ρ(e), as illustrated in Fig. 2 (a), is chosen as the modified Huber (MH) function:

$$ \rho (e) = \left\{ {\begin{array}{*{20}{c}} {{e^2}/2,} \hfill & {0 \leqslant \left| e \right| < \xi } \hfill \\{{\xi^2}/2,} \hfill & {\xi \leqslant \left| e \right|.} \hfill \\\end{array} } \right. $$

(4)

ξ is a threshold parameter used to suppress the effect of outlier when the estimation error e is very large. Other M-estimate function such as the Hampel’s three-part redescending function [14] can also be used. Notice that when $\rho (e) = {e^2}/2$ it reduces to the conventional mean square error (MSE) criterion. Like the LMS algorithm, ${J_\rho }$ is minimized by updating W(n) in the negative direction of the instantaneous gradient vector ${\hat{\nabla }_{{\mathbf{W}}\rho }}$. Therefore, the gradient vector, ${\nabla_{\mathbf{W}}}\left( {{J_\rho }} \right)$, is approximated by ${\hat{\nabla }_{{\mathbf{W}}\rho }} = - \partial \rho \left( {e(n)} \right)/\partial \mathbf{W} = - \psi \left( {e(n)} \right)\mathbf{X}(n)$, where $\psi (e) = \partial \rho (e)/\partial e$ is the score function, which is depicted in Fig. 2 (b). The following LMM algorithm can be obtained:

$$ \mathbf{W}\left( {n + 1} \right) = \mathbf{W}(n) - \mu {\hat{\nabla }_{{\mathbf{W}}\rho }} = \mathbf{W}(n) + \mu \psi \left( {e(n)} \right)\mathbf{X}(n). $$

(5)

Figure 2

a The MH function ρ(e); bψ(e), the MH score function of ρ(e).

It can be seen that when e(n) is smaller than ξ, ψ(e(n)) is equal to e(n) and (5) becomes identical to the LMS algorithm. When $\left| {e(n)} \right| > 1$, ψ(e(n)) will become zero. Thus the LMM algorithm can effectively reduce the adverse effect of large estimation error on updating the filter coefficients. In the adaptive threshold selection (ATS) method used in [12, 15], e(n) is assumed to be Gaussian distributed except being corrupted occasionally by additive impulsive noise and the following robust variance estimate is proposed

$$ \hat{\sigma }_e^2(n) = {\lambda_\sigma }\hat{\sigma }_e^2\left( {n - 1} \right) + {c_1}\left( {1 - {\lambda_\sigma }} \right){\hbox{med}}\left( {{A_e}(n)} \right), $$

(6)

where ${\lambda_\sigma }$ is a forgetting factor close to but smaller than one, c ₁ = 2.13 is the finite sample correction factor and N _w is the length of the data set. med(·) is the median operator and ${A_e}(n) = \left[ {{e^2}(n), \cdots, {e^2}\left( {n - {N_w} + 1} \right)} \right]$. Using (6), the following adaptive threshold ξ can be obtained:

$$ \xi = {k_\xi }{\hat{\sigma }_e}(n). $$

(7)

${k_\xi }$ is a constant used to control the suppression of impulsive interference. A reasonable value of ${k_\xi }$ is 2.576 and the window length N _w is usually chosen between 5 and 9 [12, 15].

If the step sizes for updating the coefficients are normalized according to the power of the corresponding transform signal components as in the TDNLMS algorithm, the following TDNLMM algorithm can be obtained from (5) [12]:

$$ e(n) = d(n) - {\mathbf{W}^T}(n){\mathbf{X}_C}(n), $$

(8)

$$ \mathbf{W}\left( {n + 1} \right) = \mathbf{W}(n) + \mu \Lambda_C^{ - 1}\psi \left( {e(n)} \right){\mathbf{X}_C}(n). $$

(9)

The convergence performance of the LMS algorithm with other nonlinearity than MH function can be found in literature. The LMS algorithm with error function nonlinearity was studied in [23]. A related algorithm is the dual-sign LMS [24] algorithm. The former concluded that the nonlinearity will slow down the convergence rate, while the latter is mainly introduced to reduce the implementation complexity. The robustness of this class of algorithms to impulsive outliers was later studied by Koike in [22, 25, 26], and in [21] using the clipping nonlinearity. On the contrary, in [12, 15] the threshold parameter ξ in the MH function is continuously updated as in (7), which greatly improves the convergence speed and steady state error.

3 Mean and Mean Square Convergence Analysis

In this section, the convergence performance analysis of the TDNLMS algorithm with general nonlinearity and particularly the TDNLMS and TDNLMM algorithms will be studied. The main contributions of the analysis include: i) the use of the Price’s theorem [17] to handle the nonlinearity for Gaussian noise case and its extension [18] for the CG noise case, and ii) introduction of new special functions and the evaluation of related expectations in order to obtain decoupled difference equations describing the mean and mean square behaviors of the algorithms. To simplify the analysis, we make the following assumptions:

Assumption 1

The input signal x(n) is an ergodic process which is Gaussian distributed with zero mean and autocorrelation matrix ${\mathbf{R}_{XX}} = E\left[ {\mathbf{X}(n){\mathbf{X}^T}(n)} \right]$.

Assumption 2

The additive noise η _o (n) is assumed to be a Gaussian noise (${\eta_o}(n) = {\eta_g}(n)$) for the analysis in section 3.1 below. For the analysis in section 3.2 below, η _o (n) is modeled as a CG noise [27] which is a frequently used model for analyzing impulsive noise. More precisely, it is given by:

$$ {\eta_o}(n) = {\eta_g}(n) + {\eta_{im}}(n) = {\eta_g}(n) + b(n){\eta_w}(n), $$

(10)

where η _g (n) and η _w (n) are both independent and identically distributed (i.i.d.) zero mean Gaussian sequences with respective variance $\sigma_g^2$ and $\sigma_w^2$. b(n) is an i.i.d. Bernoulli random sequence whose value at any time instant is either zero or one, with occurrence probabilities ${P_r}\left( {b(n) = 1} \right) = {p_r}$ and ${P_r}\left( {b(n) = 0} \right) = 1 - {p_r}$. The variances of the random processes η _im (n) and η _o (n) are then given by $\sigma_{im}^2 = {p_r}\sigma_w^2$ and $\sigma_{{\eta_o}}^2 = \sigma_g^2 + \sigma_{im}^2 = \sigma_g^2 + {p_r}\sigma_w^2$. The ratio ${r_{im}} = \sigma_{im}^2/\sigma_g^2 = {p_r}\sigma_w^2/\sigma_g^2$ is a measure of the impulsive characteristic of the CG noise. Accordingly, the probability distribution function (PDF) of this CG distribution is given by

$$ {f_{{\eta_o}}}\left( \eta \right) = \frac{{1 - {p_r}}}{{\sqrt {{2\pi \sigma_g^2}} }}\exp \left( { - \frac{{{\eta^2}}}{{2\sigma_g^2}}} \right) + \frac{{{p_r}}}{{\sqrt {{2\pi \sigma_\Sigma^2}} }}\exp \left( { - \frac{{{\eta^2}}}{{2\sigma_\Sigma^2}}} \right). $$

(11)

Assumption 3

W(n), x(n) and η _o (n) are statistically independent (the independent assumption [1]). Although this assumption is not completely valid in general applications, it is a good approximation for large value of L and is commonly used to simplify the convergence analysis of adaptive filtering algorithms. Moreover, we denote $\mathbf{W}* = R_{{X_C}{X_C}}^{ - 1}{P_{d{X_C}}}$, where ${P_{d{X_C}}} = E\left[ {d(n){\mathbf{X}_C}(n)} \right]$ is the ensemble-averaged cross-correlation vector between X _C (n) and d(n). W* is related to the optimal Wiener solution ${\mathbf{W}_{\rm{OPT}}} = \mathbf{R}_{XX}^{ - 1}{\mathbf{P}_{dX}}$ by W_OPT = CW*.

3.1 Mean and Mean Square Convergence Behaviors in Gaussian noise

3.1.1 Mean Behavior

From (9), the weight-error vector ${\mathbf{v}}(n) = \mathbf{W}* - \mathbf{W}(n)$ for the TDNLMS algorithm with general nonlinearity can be written as

$$ {\mathbf{v}}\left( {n + 1} \right) = {\mathbf{v}}(n) - \mu \Lambda_C^{ - 1}\psi \left( {e(n)} \right){X_C}(n), $$

(12)

where W* is the transformed optimal weight vector defined above and ψ(e(n)) is a general nonlinearity. When it is equal to e(n), (12) reduces to the conventional TDNLMS algorithm. Taking expectation over {v, X _C , η _g } on both sides of (12), one gets

$$ E\left[ {{\mathbf{v}}\left( {n + 1} \right)} \right] = E\left[ {{\mathbf{v}}(n)} \right] - \mu H, $$

(13)

where E[·] denotes the expectation over {v(n), X _C (n), η _g (n)} (also written as ${E_{\left\{ {{\mathbf{v}},{{\mathbf{X}}_C},{\eta_g}} \right\}}}\left[ \cdot \right]$ for clarity), and $H = {E_{\left\{ {{\mathbf{v}},{{\mathbf{X}}_C},{\eta_g}} \right\}}}\left[ {\Lambda_C^{ - 1}\psi \left( {e(n)} \right){X_C}(n)} \right]$. By dropping the time index of X _C (n), e(n), and η _g (n), one gets

$$ H = {E_{\left\{ {{\mathbf{v}},{{\mathbf{X}}_C},{\eta _g}} \right\}}}\left[ {\Lambda _C^{ - 1}\psi \left( e \right){X_C}} \right] = {E_{\left\{ {\mathbf{v}} \right\}}}\left[ {{H_1}} \right] $$

(14)

where ${H_1} = {E_{\left\{ {{X_C},{\eta_g}} \right\}}}\left[ {\Lambda_C^{ - 1}\psi (e){X_C}\left| v \right.} \right]$ and the second equation is obtained from the independence assumption of η _g (n), W(n) and x(n) in Assumption 3.

The i-th component of H ₁ is evaluated in Appendix A to be

$$ {H_{1,i}} \approx \overline {\psi \prime } \left( {\sigma_e^2(n)} \right){\alpha_i}e_i^T{R_{{X_C}{X_C}}}v(n), $$

(15)

where $\sigma_e^2(n) = E\left[ {{v^T}(n){R_{{X_C}{X_C}}}v(n)} \right] + \sigma_g^2$, $\overline {\psi \prime } \left( {\sigma_e^2} \right) = \int_{ - \infty }^\infty {\frac{{\psi \prime (e)}}{{\sqrt {{2\pi }} {\sigma_e}}}\exp \left( { - \frac{{{e^2}}}{{2\sigma_e^2}}} \right)de}$, ${\alpha_i} = \int_0^\infty {\exp \left( { - \beta {\varepsilon_i}} \right){{\left( {{g_i}\left( {\tilde{\beta }} \right)} \right)}^{ - 3/2}}d\beta }$, ${g_i}\left( {\tilde{\beta }} \right) = \left( {1 + 2\tilde{\beta }{R_{{X_C}{X_C}_ i,i}}} \right)$, ${R_{{X_C}{X_{C\_i,j}}}}$ is the (i, j)-th element of ${R_{{X_C}{X_C}}}$, e _i is a column vector with the i-th element equal to one and zero elsewhere. For a given ψ(e), $\overline {\psi \prime } \left( {\sigma_e^2} \right)$ can be evaluated analytically or numerically. Substituting (14), (15) into (13), the following mean weight-error vector update equation is obtained:

$$ E\left[ {v\left( {n + 1} \right)} \right] = \left( {I - \mu {A_\psi }\left( {\sigma_e^2(n)} \right){D_\alpha }{R_{{X_C}{X_C}}}} \right)E\left[ {v(n)} \right], $$

(16)

where ${D_\alpha } = {\hbox{diag}}\left( {{\alpha_1}, \ldots, {\alpha_L}} \right)$ is a diagonal matrix. For notation convenience, we write $\overline {\psi \prime } \left( {\sigma_e^2(n)} \right)$ as ${A_\psi }\left( {\sigma_e^2(n)} \right)$ and use $\sigma_e^2(n)$ and $\sigma_e^2$ interchangeably. Also we replace the approximate sign in (16) by the equality sign. Let $V(n) = D_\alpha^{ - 1/2}v(n)$, (16) can be simplified to

$$ E\left[ {V\left( {n + 1} \right)} \right] = \left( {I - \mu {A_\psi }\left( {\sigma_e^2(n)} \right){R_{{X_D}{X_D}}}} \right)E\left[ {V(n)} \right], $$

(17)

where ${R_{{X_D}{X_D}}} = D_\alpha^{1/2}{R_{{X_C}{X_C}}}D_\alpha^{1/2}$ is the correlation matrix of a scaled input vector ${X_D} = D_\alpha^{1/2}{X_C}$. Since it is symmetric, it can be written as the following eigenvalue decomposition (EVD): ${R_{{X_D}{X_D}}} = {U_{{X_D}}}{\Lambda_{{X_D}}}U_{{X_D}}^T$, where ${U_{{X_D}}}$ is certain orthogonal matrix and ${\Lambda_{{X_D}}}{\hbox{ = diag}}\left( {\lambda_1^\prime, \lambda_2^\prime, \cdots, \lambda_L^\prime } \right)$ contains the corresponding eigenvalues. Pre-multiplying both sides of (17) with $U_{{X_D}}^T$ gives

$$ E\left[ {{V_D}\left( {n + 1} \right)} \right] = \left( {I - {A_\psi }\left( {\sigma_e^2(n)} \right){\Lambda_{{X_D}}}} \right)E\left[ {{V_D}(n)} \right], $$

(18)

where $E\left[ {{V_D}(n)} \right] = U_{{X_D}}^TE\left[ {V(n)} \right]$. This is equivalent to the following L scalar first order finite difference equations:

$$ E{\left[ {{V_D}\left( {n + 1} \right)} \right]_i} = \left( {1 - {A_\psi }\left( {\sigma_e^2(n)} \right)\lambda_i^\prime } \right)E{\left[ {{V_D}(n)} \right]_i}, $$

(19)

where $E{\left[ {{V_D}(n)} \right]_i}$ is the i-th element of the vector $E\left[ {{V_D}(n)} \right]$ for $i = 1,2, \cdots, L$.

Remarks

• (R-A1): The TDNLMS algorithm

For conventional TDNLMS algorithm, ψ(e) = e and $\overline {\psi \prime } \left( {\sigma_e^2} \right) = {A_\psi }\left( {\sigma_e^2} \right) = 1$. The algorithm will converge if

$$ \begin{array}{*{20}{c}} {\left| {1 - \mu \lambda_i^\prime } \right| < 1,} \hfill & {for\,all\,i,} \hfill \\\end{array} $$

(20)

where $\lambda_i^\prime$ is the i-th eigenvalue of ${R_{{X_D}{X_D}}}$. The corresponding maximum step size for convergence should satisfy

$$ \begin{array}{*{20}{c}} {{\mu_{\max }} < 2/\lambda_{\max }^\prime, } \hfill & {for\,all\,i,} \hfill \\\end{array} $$

(21)

where $\lambda_{\max }^\prime$ is the maximum eigenvalue of ${R_{{X_D}{X_D}}}$. Let us examine the eigenvalues of ${R_{{X_D}{X_D}}}$. We note that ${R_{{X_D}{X_D}}} = D_\alpha^{1/2}\left( {C{R_{XX}}{C^T}} \right)D_\alpha^{1/2}$. It can be shown that ${\alpha_i} = \frac{1}{{2{\alpha_\varepsilon }{R_{{X_C}{X_C}_ i,i}}}}\exp \left( {\frac{1}{2}{\varepsilon_i}\alpha_\varepsilon^{ - 1}R_{{X_C}{X_C}_ i,i}^{ - 1}} \right) \cdot {E_{3/2}}\left( {\frac{1}{2}{\varepsilon_i}\alpha_\varepsilon^{ - 1}R_{{X_C}{X_C}_ i,i}^{ - 1}} \right),$where ${E_n}(x) = \int_1^\infty {\frac{{\exp \left( { - \beta x} \right)}}{{{\beta^n}}}d\beta }$. The i-th diagonal element of ${R_{{X_D}{X_D}}}$ is

$$ {R_{{X_D}{X_D}_ i,i}} = {\alpha_i}{R_{{X_C}{X_C}_ i,i}} = \frac{1}{{2{\alpha_\varepsilon }}}\exp \left( {\frac{1}{2}{\varepsilon_i}\alpha_\varepsilon^{ - 1}R_{{X_C}{X_C}_ i,i}^{ - 1}} \right) \times {E_{3/2}}\left( {\tfrac{1}{2}{\varepsilon_i}\alpha_\varepsilon^{ - 1}R_{{X_C}{X_C}_ i,i}^{ - 1}} \right) = {\hat{\lambda }_i}. $$

(22)

It can be seen that ${R_{{X_D}{X_D}_ i,i}}$ has the same order as ${R_{{X_C}{X_C}_ i,i}}$. Therefore, the order of the elements in ${R_{{X_C}{X_C}}}$ after scaling, i.e. ${D_\alpha }{R_{{X_C}{X_C}}}{D_\alpha }$, is preserved. If ε _i is simply chosen as $R_{{X_C}{X_C}_ i,i}^{ - 1}$ with ${\alpha_\varepsilon } = 0$, i.e. perfect power estimation, then ${\alpha_i} = R_{{X_C}{X_C}_ i,i}^{ - 1}$, and hence ${\hat{\lambda }_i} = 1$ for all i.

If C diagonalizes R _XX , then ${R_{{X_D}{X_D}}}$ becomes the identity matrix. The eigenvalue spread is equal to one and it will significantly speed up the convergence of the algorithm, especially for situations with large eigenvalue spread.

Usually C only approximately diagonalizes R _XX and the detailed analysis becomes rather difficult. Here we try to study the eigenvalue and obtain bounds for their values using the Gershgorin circle theorem (GCT). For orthogonal transformation, the eigenvalues of R _XX and ${R_{{X_C}{X_C}}} = C{R_{XX}}{C^T}$ are the same. From the GCT, we have

$$ \left| {{\lambda_i} - {R_{{X_C}{X_C}_ i,i}}} \right| \leqslant \sum\limits_{\mathop {{j \ne i}}\limits^{1 \leqslant j \leqslant L} } {\left| {{R_{{X_C}{X_C}_ i,j}}} \right|} = \sum\limits_{\mathop {{j \ne i}}\limits^{1 \leqslant j \leqslant L} } {\left| {{{\left( {{R_{{X_C}{X_C}_ i,i}}{R_{{X_C}{X_C}_ j,j}}} \right)}^{1/2}}{\rho_{{X_C}{X_C}_ i,j}}} \right|}, $$

where ${\rho_{{X_C}{X_C}_ i,j}}$ is the normalized correlation coefficients. Similarly, the eigenvalues of ${R_{{X_D}{X_D}}}$ satisfy

$$ \left| {\lambda_i^\prime - {\alpha_i}{R_{{X_C}{X_C}_ i,i}}} \right| \leqslant \sum\limits_{1 \leqslant j \ne i \leqslant L} {\left| {{{\left( {{\alpha_i}{\alpha_j}} \right)}^{1/2}}{R_{{X_C}{X_C}_ i,j}}} \right|} . $$

Since ${\alpha_i} = {\left( {{R_{{X_C}{X_C}_ i,i}}} \right)^{ - 1}}{\hat{\lambda }_i}$, we have $\left| {\lambda_i^\prime - {{\hat{\lambda }}_i}} \right| \leqslant \sum\limits_{1 \leqslant j \ne i \leqslant L} {\left| {{{\left( {\frac{{{{\hat{\lambda }}_i}{{\hat{\lambda }}_j}}}{{{R_{{X_C}{X_C}_ i,i}}{R_{{X_C}{X_C}_ j,j}}}}} \right)}^{ - 1/2}}{R_{{X_C}{X_C}_ i,j}}} \right|}$. If ${R_{{X_C}{X_C}}}$ is diagonal-dominant, then the off-diagonal elements ${\rho_{XX_ i,j}}$, i ≠ j will be small and all the eigenvalues of ${R_{{X_D}{X_D}}}$ will be close to one with a tight bound. ${\hat{\lambda }_i}$ can therefore be viewed as the estimated eigenvalues of ${R_{{X_D}{X_D}}}$. The corresponding estimated eigenvalue spread for diagonal-dominant ${R_{{X_C}{X_C}}}$ is

$$ \frac{{{{\hat{\lambda }}_{i \in \max }}}}{{{{\hat{\lambda }}_{i \in \min }}}} = \frac{{\exp \left( {\frac{1}{2}{\varepsilon_i}\alpha_\varepsilon^{ - 1}R_{{X_C}{X_C}_ i,i \in \max }^{ - 1}} \right){E_{3/2}}\left( {\frac{1}{2}{\varepsilon_i}\alpha_\varepsilon^{ - 1}R_{{X_C}{X_C}_ i,i \in \max }^{ - 1}} \right)}}{{\exp \left( {\frac{1}{2}{\varepsilon_i}\alpha_\varepsilon^{ - 1}R_{{X_C}{X_C}_ i,i \in \min }^{ - 1}} \right){E_{3/2}}\left( {\frac{1}{2}{\varepsilon_i}\alpha_\varepsilon^{ - 1}R_{{X_C}{X_C}_ i,i \in \min }^{ - 1}} \right)}}, $$

(23)

which is close to one for a relatively wide range of ${R_{{X_C}{X_C}_ i,i}}$ and ${R_{{X_C}{X_C}_ j,j}}$. This explains the speed-up in convergence rate of the TDNLMS algorithm even if sub-optimal transformations are used. It was also shown that [9], pp.219] the performance of the TDNLMS algorithm can never be worse than its conventional LMS counterpart and the degree of improvement achieved depends on the distribution of the signal powers at transformed outputs.

• (R-A2): TDNLMS algorithm with general nonlinearity and the TDNLMM algorithm

For general nonlinearity other than ψ(e) = e, (18) or (19) becomes a set of nonlinear difference equations. A general solution is rather difficult to obtain because the term ${A_\psi }\left( {\sigma_e^2} \right)$ is dependent on MSE.

For $C = {D_\alpha } = I$, we obtain the LMS algorithm with general nonlinearity. (19) agrees with the result for the LMS algorithm with dual-sign nonlinearity [23]. (18) also agrees with the result in [22] for the LMS algorithm with error function nonlinearity. The case for LMS and NLMM algorithms with general nonlinearity was studied in [30]. For most M-estimate functions, ψ(e) = q(e)e, where q(e) is equal to 1 when |e| is less than a certain threshold ξ and will gradually decrease to reduce its sensitivity to impulses with large amplitude. Hence, $0 \leqslant \psi \prime (e) \leqslant 1$ and ψ′(e) ≈ 1 when |e| < ξ. For MH nonlinearity, it can be shown that ${A_{\rm{MH}}}\left( {\sigma_e^2} \right) = {A_{\rm{MH}}}\left( {\sigma_e^2} \right) = \frac{2}{{\sqrt {{2\pi }} }}\int_0^{\xi /{\sigma_e}} {\exp \left( { - \frac{{{u^2}}}{2}} \right)du} - \frac{{2\xi }}{{\sqrt {{2\pi }} {\sigma_e}}}\exp \left( { - \frac{{{\xi^2}}}{{2\sigma_e^2}}} \right)$ with $\mathop {{\lim }}\limits_{\sigma_e^2 \to 0} {A_{\rm{MH}}}\left( {\sigma_e^2} \right) \to 1$ and $\mathop {{\lim }}\limits_{\sigma_e^2 \to \infty } {A_{\rm{MH}}}\left( {\sigma_e^2} \right) \to 0$. For sufficiently small step size μ, the algorithm will converge and $\sigma_e^2$ will decrease. If ${A_{\rm{MH}}}\left( {\sigma_e^2} \right)$ is not made adaptive, an inappropriately chosen ξ may suppress the signal component, instead of the outliers. This will cause ${A_{\rm{MH}}}\left( {\sigma_e^2} \right)$ to increase gradually and lead to slow adaptation. For the TDNLMS algorithm, ξ is chosen as a multiple of the estimated σ _e as shown in (7). This helps to maintain a fairly stationary ${A_{\rm{MH}}}\left( {\sigma_e^2} \right)$ so as to avoid significant signal suppression since ${A_{\rm{MH}}}\left( {\sigma_e^2} \right) \approx {\hbox{erf}}\left( {\frac{{{k_\xi }}}{{\sqrt {2} }}} \right) = {A_{\rm{C}}}$ (if $\hat{\sigma }_e^2 \approx \sigma_e^2$) is approximately constant and slightly less than one. The degradation in convergence over its TDNLMS counterpart is therefore minimal. Though the maximum possible step size is in general difficult to obtain, a sufficient condition for the algorithm to converge is $\left| {1 - \mu {A_\psi }\left( {\sigma_e^2} \right)\lambda_i^\prime } \right| < 1$, for all i. If $\overline {\psi \prime } \left( {\sigma_e^2} \right)$ is bounded above by a constant ${A_{\psi \_\max }}$, then a conservative maximum step size is

$$ {\mu _{\max }} < 2/\left( {{A_{\psi \_\max }}\lambda _{\max }^\prime } \right), $$

(24)

which yields good estimates in practical algorithms. ${A_\psi }\left( {\sigma_e^2} \right)$ for some commonly used error nonlinearities are summarized in Table 1.

Table 1 List of ${A_\psi }\left( {\sigma_\varepsilon^2} \right)$, ${B_\psi }\left( {\sigma_\varepsilon^2} \right)$ and ${C_\psi }\left( {\sigma_\varepsilon^2} \right)$ for three related algorithms.

3.1.2 Mean Square Behavior

Post-multiplying (12) by its transpose and taking expectation over {v, X _C , η _g } gives

$$ \Xi \left( {n + 1} \right) = \Xi (n) - {M_1} - {M_2} + {M_3}, $$

(25)

where $\Xi (n) = E\left[ {v(n){v^T}(n)} \right]$,

$$ {M_1} = \mu {E_{\left\{ {\mathbf{v}} \right\}}}\left[ {{E_{\left\{ {{\mathbf{X}},{\eta_g}} \right\}}}\left[ {\Lambda_C^{ - 1}\psi (e){X_C}|v} \right]{v^T}} \right]{\kern 1pt} = \mu {E_{\left\{ {\mathbf{v}} \right\}}}\left[ {H{v^T}} \right]\,{\kern 1pt} \approx \mu {A_\psi }\left( {\sigma_e^2} \right){D_\alpha }{R_{{X_C}{X_C}}}\Xi (n), $$

(26)

$$ {M_2} = M_1^T = \mu {E_{\left\{ v \right\}}}\left[ {v{H^T}} \right] \approx \mu {A_\psi }\left( {\sigma_e^2} \right)\Xi (n){R_{{X_C}{X_C}}}{D_\alpha }, $$

(27)

and

$$ {M_3} = {E_{\left\{ {v,{X_C},{\eta_g}} \right\}}}\left[ {{{\left( {\mu \psi (e)} \right)}^2}\Lambda_C^{ - 1}{X_C}X_C^T\Lambda_C^{ - 1}} \right] = {\mu^2}{E_{\left\{ v \right\}}}\left[ {{s_3}} \right], $$

(28)

where ${s_3} = {E_{\left\{ {X,{\eta_g}} \right\}}}\left[ {{\psi^2}(e)\Lambda_C^{ - 1}{X_C}X_C^T\Lambda_C^{ - 1}\left| v \right.} \right]$. Note, the final expressions in (26) and (27) are obtained by using our previous result in (15). The (i, j)-th element of s ₃ is evaluated in Appendix B to be:

$$ {s_{3,i,j}} = {C_\psi }\left( {\sigma_e^2} \right)\left[ {s_{ij}^{(0)}{{\left( {{r_{{X_C}{X_C}_ i}}} \right)}^T}v{v^T}{r_{{X_C}{X_C}_ j}} + s_{ij}^{(1)}{{\left( {{r_{{X_C}{X_C}_ j}}} \right)}^T}v{v^T} \cdot {r_{{X_C}{X_C}_ j}} + s_{ij}^{(2)}{{\left( {{r_{{X_C}{X_C}_ i}}} \right)}^T}v{v^T}{r_{{X_C}{X_C}_ i}} + s_{ij}^{(3)}{{\left( {{r_{{X_C}{X_C}_ i}}} \right)}^T}v{v^T}{r_{{X_C}{X_C}_ j}}} \right] + {B_\psi }\left( {\sigma_e^2} \right)\sum\limits_{m = 0}^\infty {\alpha_{i,j}^{(m)}\left( {{4^m}} \right)} \left( {\begin{array}{*{20}{c}} { - \frac{3}{2} + m - 1} \\m \\\end{array} } \right)R_{{X_C}{X_C}_ i,j}^{\left( {2m + 1} \right)}. $$

(29)

where

$$ \begin{array}{*{20}{c}} {s_{ij}^{\left( 0 \right)} = 2\sum\limits_{m = 0}^\infty {\left( {\begin{array}{*{20}{c}} { - \frac{5}{2} + m - 1} \\ m \\ \end{array} } \right){{\left( { - 4{R_{{X_C}{X_C}\_j,i}}} \right)}^m}\alpha _i^{\left( {m,\left( {3 + 2m} \right)/2} \right)}\alpha _j^{\left( {m,\left( {3 + 2m} \right)/2} \right)}} ,} \\ {s_{ij}^{\left( 1 \right)} = \frac{1}{2}\sum\limits_{m = 0}^\infty {\left( {\begin{array}{*{20}{c}} { - \frac{5}{2} + m - 1} \\ m \\ \end{array} } \right){{\left( { - 4{R_{{X_C}{X_C}\_i,j}}} \right)}^{m + 1}}\alpha _i^{\left( {m,\left( {3 + 2m} \right)/2} \right)}\alpha _j^{\left( {m + 1,\left( {5 + 2m} \right)/2} \right)}} ,} \\ {s_{ij}^{\left( 2 \right)} = \frac{1}{2}\sum\limits_{m = 0}^\infty {\left( {\begin{array}{*{20}{c}} { - \frac{5}{2} + m - 1} \\ m \\ \end{array} } \right){{\left( { - 4{R_{{X_C}{X_C}\_i,j}}} \right)}^{m + 1}}\alpha _i^{\left( {m + 1,\left( {5 + 2m} \right)/2} \right)}\alpha _j^{\left( {m,\left( {3 + 2m} \right)/2} \right)}} ,} \\ {s_{ij}^{\left( 3 \right)} = \frac{1}{2}\sum\limits_{m = 0}^\infty {\left( {\begin{array}{*{20}{c}} { - \frac{5}{2} + m - 1} \\ m \\ \end{array} } \right){{\left( { - 4{R_{{X_C}{X_C}\_i,j}}} \right)}^{m + 2}}\alpha _i^{\left( {m + 1,\left( {5 + 2m} \right)/2} \right)}\alpha _j^{\left( {m + 1,\left( {5 + 2m} \right)/2} \right)}} .} \\ {\alpha _{i,j}^{(k)} = \int_0^\infty {\int_0^\infty {{{\left( {{{\tilde{\beta }}_1}{{\tilde{\beta }}_2}} \right)}^k}{{\left( {{g_i}\left( {{{\tilde{\beta }}_1}} \right){g_j}\left( {{{\tilde{\beta }}_2}} \right)} \right)}^{ - \left( {2k + 3} \right)/2}}\exp \left( { - \left( {{\beta _1}{\varepsilon _i} + {\beta _2}{\varepsilon _j}} \right)d{\beta _2}d{\beta _1} = \alpha _i^{\left( k \right)}\alpha _j^{\left( k \right)}} \right)} } ,} \\ \end{array} $$

where $\alpha_i^{(k)} = \int_0^\infty {\int_0^\infty {{{\left( {\tilde{\beta }} \right)}^k}{{\left( {{g_i}\left( {\tilde{\beta }} \right)} \right)}^{ - \left( {2k + 3} \right)/2}}\exp \left( { - \beta {\varepsilon_i}} \right)d\beta } }$, $\alpha_i^{\left( {m,n} \right)} = \int_0^\infty {{{\tilde{\beta }}^m}\exp \left( { - \beta {\varepsilon_i}} \right)/{{\left( {1 + 2\tilde{\beta }{R_{{X_C}{X_C}_ i,i}}} \right)}^n}} d\beta$,${B_\psi }\left( {\sigma_e^2} \right) = \int_{ - \infty }^\infty {\frac{{{\psi^2}(e)}}{{\sqrt {{2\pi }} {\sigma_e}}}\exp \left( {\frac{{ - {e^2}}}{{2\sigma_e^2}}} \right)de}$, ${C_\psi }\left( {\sigma_e^2} \right) = \frac{d}{{d\sigma_e^2}}E\left[ {{\psi^2}(e)} \right]$, and ${\left( {{r_{{X_C}{X_C}_ i}}} \right)^T}$ is the i-th row of ${R_{{X_C}{X_C}}}$. For a given nonlinearity ψ(e), the above two integrals can be computed analytically or numerically.

Substituting (26–29) into (25) gives

$$ \Xi \left( {n + 1} \right) = \Xi (n) - \mu {A_\psi }\left( {\sigma_e^2} \right){D_\alpha }{R_{{X_C}{X_C}}}\Xi (n) - \mu {A_\psi }\left( {\sigma_e^2} \right)\Xi (n){R_{{X_C}{X_C}}}{D_\alpha } + {\mu^2}{C_\psi }\left( {\sigma_e^2} \right)\left[ {{S^{(0)}} \circ \left( {{R_{{X_C}{X_C}}}\Xi (n){R_{{X_C}{X_C}}}} \right) + {S^{(1)}}{D_\sigma } + {D_\sigma }{S^{(2)}} + {S^{(3)}} \circ \left( {{R_{{X_C}{X_C}}}\Xi (n){R_{{X_C}{X_C}}}} \right)} \right] + {\mu^2}{B_\psi }\left( {\sigma_e^2} \right){\Gamma_\alpha }, $$

(30)

where ${D_\sigma }$ is a diagonal matrix with its i-th element ${\left[ {{D_\sigma }} \right]_{i,i}} = {\left( {{r_{{X_C}{X_C}_ i}}} \right)^T}\Xi (n){r_{{X_C}{X_C}_ i}}$, ${\left[ {{S^{(k)}}} \right]_{i,j}} = s_{ij}^{(k)}$ and ${\left[ {{\Gamma_\alpha }} \right]_{ij}} = \sum\limits_{m = 0}^\infty {\alpha_{i,j}^{(m)}\left( {{4^m}} \right)} \left( {\begin{array}{*{20}{c}} { - \frac{3}{2} + m - 1} \\m \\\end{array} } \right)R_{{X_C}{X_C}_ i,j}^{\left( {2m + 1} \right)}.$

Let $\Phi (n) = D_\alpha^{ - 1/2}\Xi (n)D_\alpha^{ - 1/2}$, (30) can be further simplified to

$$ \Phi \left( {n + 1} \right) = \Phi (n) - \mu {A_\psi }\left( {\sigma_e^2} \right)D_\alpha^{1/2}{R_{{X_C}{X_C}}}D_\alpha^{1/2}\Phi (n) - \mu {A_\psi }\left( {\sigma_e^2} \right)\Phi (n)D_\alpha^{1/2}{R_{{X_C}{X_C}}}D_\alpha^{1/2} + {\mu^2}{C_\psi }\left( {\sigma_e^2} \right)\left\{ {\left[ {\left( {{S^{(0)}} + {S^{(3)}}} \right) \circ \left( {D_\alpha^{ - 1/2}R_{{X_C}{X_C}}D_\alpha^{1/2}\Phi (n)D_\alpha^{1/2}{R_{{X_C}{X_C}}}D_\alpha^{ - 1/2}} \right)} \right] + D_\alpha^{ - 1/2}{S^{(1)}}D_\alpha^{ - 1/2}{D_\sigma } + {D_\sigma }D_\alpha^{ - 1/2}{S^{(2)}}D_\alpha^{ - 1/2}} \right\} + {\mu^2}{B_\psi }\left( {\sigma_e^2} \right)D_R^{ - 1/2}{\Gamma_\alpha }D_R^{ - 1/2}, $$

(31)

where ${\left[ {{D_\sigma }} \right]_{i,i}} = {\left( {D_\alpha^{1/2}{r_{{X_C}{X_C}_ i}}} \right)^T}\Phi (n)\left( {D_\alpha^{1/2}{r_{{X_C}{X_C}_ i}}} \right)$.

Since $D_\alpha^{1/2}{R_{{X_C}{X_C}}}D_\alpha^{1/2}$ is symmetric, it can be diagonalized as ${U_{{X_D}}}{\Lambda_{{X_D}}}U_{{X_D}}^T$. Again, let $\Psi (n) = U_{{X_D}}^T\Phi (n){U_{{X_D}}}$, (31) yields

$$ \begin{gathered} \Psi \left( {n + 1} \right) = \Psi (n) - \mu {A_\psi }\left( {\sigma_e^2} \right){\Lambda_{{X_D}}}\Psi (n) - \mu {A_\psi }\left( {\sigma_e^2} \right)\Psi (n){\Lambda_{{X_D}}} + {\mu^2}{C_\psi }\left( {\sigma_e^2} \right)\left\{ {U_{{X_D}}^T\left[ {\left( {{S^{(0)}} + {S^{(3)}}} \right) \circ \left( {D_\alpha^{ - 1}{U_{{X_D}}}{\Lambda_{{X_D}}}\Psi (n){\Lambda_{{X_D}}}U_{{X_D}}^TD_\alpha^{ - 1}} \right)} \right]{U_{{X_D}}} + U_{{X_D}}^TD_\alpha^{ - 1/2}{S^{(1)}}D_\alpha^{ - 1/2}{D_\sigma }{U_{{X_D}}} + U_{{X_D}}^T{D_\sigma }D_\alpha^{ - 1/2}{S^{(2)}}D_\alpha^{ - 1/2}{U_{{X_D}}}} \right\} \hfill \\+ {\mu^2}{B_\psi }\left( {\sigma_e^2} \right)U_{{X_D}}^TD_\alpha^{ - 1/2}{\Gamma_\alpha }D_\alpha^{ - 1/2}{U_{{X_D}}}. \hfill \\\end{gathered} $$

(32)

Since ${\left[ {{D_\sigma }} \right]_{i,i}} = {\left( {D_\alpha^{1/2}{r_{{X_C}{X_C}_ i}}} \right)^T}{U_{{X_D}}}\Psi (n)U_{{X_D}}^T\left( {D_\alpha^{1/2}{r_{{X_C}{X_C}_ i}}} \right)$ is a scalar, after taking the vec(·) operation we have the following:

$$ {\left[ {{{\mathbf{D}}_\sigma }} \right]_{i,i}} = {\left( {D_\alpha^{1/2}{r_{{X_C}{X_C}_ i}}} \right)^T} \otimes {\left( {D_\alpha^{1/2}{r_{{X_C}{X_C}_ i}}} \right)^T}\left( {{U_{{X_D}}} \otimes {U_{{X_D}}}} \right){\hbox{vec}}\left( {\Psi (n)} \right) = \left( {{\Delta_i}} \right) \cdot {\hbox{vec}}\left( {\Psi (n)} \right). $$

Hence,

$$ {\hbox{vec}}\left( {{D_\sigma }} \right) = {\left[ {{{\left( {{{\mathbf{D}}_\sigma }} \right)}_{1,1}},0, \ldots, 0,0,{{\left( {{{\mathbf{D}}_\sigma }} \right)}_{2,2}},0, \ldots, 0, \cdots, 0, \ldots, 0,{{\left( {{{\mathbf{D}}_\sigma }} \right)}_{L,L}}} \right]^T} = \Delta \cdot {\hbox{vec}}\left( {\Psi (n)} \right), $$

(33)

where the $\left[ {\left( {i - 1} \right)L + i} \right] - {\hbox{th}}$ row of Δ is equal to Δ _i and zero elsewhere. Let $\Theta (n) = {\hbox{vec}}\left( {\Psi (n)} \right)$. (32) can be rewritten as

$$ \Theta \left( {n + 1} \right) = {\Gamma_1}(n)\Theta (n) + {\Gamma_2}(n), $$

(34)

where ${\Gamma_1}(n) = I - \mu {A_\psi }\left( {\sigma_e^2} \right)\left( {{\mathbf{I}} \otimes {\Lambda_{{X_D}}}} \right) - \mu {A_\psi }\left( {\sigma_e^2} \right)\left( {{\Lambda_{{X_D}}} \otimes {\mathbf{I}}} \right) + {\mu^2}{C_\psi }\left( {\sigma_e^2} \right)\left\{ {\left( {U_{{X_D}}^T \otimes U_{{X_D}}^T} \right)\left( {{S^{(0) + (3)}}} \right)\left[ {\left( {D_\alpha^{ - 1}{U_{{X_D}}}} \right) \otimes \left( {D_\alpha^{ - 1}{U_{{X_D}}}} \right)} \right] \cdot \left( {{\Lambda_{{X_D}}} \otimes {\Lambda_{{X_D}}}} \right) + \left( {U_{{X_D}}^T \otimes U_{{X_D}}^T} \right)\left[ {I \otimes \left( {D_\alpha^{ - 1/2}S_D^{(1)}D_\alpha^{ - 1/2}} \right) + \left( {D_\alpha^{ - 1/2}S_D^{(2)T}D_\alpha^{ - 1/2}} \right) \otimes I} \right]\Delta } \right\}$, ${\Gamma_2}(n) = {\mu^2}{B_\psi }\left( {\sigma_e^2} \right){\hbox{vec}}\left( {U_{{X_D}}^TD_\alpha^{ - 1/2}{\Gamma_\alpha }D_\alpha^{ - 1/2}{U_{{X_D}}}} \right)$, and ${S^{(0) + (3)}} = {\hbox{diag}}\left( {{S^{(0)}} + {S^{(3)}}} \right)$.

The algorithm will converge if ${\left\| {I - {\Gamma_1}(n)} \right\|_2} < 1$. Using triangular inequality, we have

$$ \begin{gathered} {\left\| {I - {\Gamma_1}(n)} \right\|_2} = {\left\| {\mu {A_\psi }\left( {\sigma_e^2} \right)\left( {I \otimes {\Lambda_{{X_D}}}} \right) + \mu {A_\psi }\left( {\sigma_e^2} \right)\left( {{\Lambda_{{X_D}}} \otimes I} \right) - {\mu^2}{C_\psi }\left( {\sigma_e^2} \right)\left\{ {\left( {U_{{X_D}}^T \otimes U_{{X_D}}^T} \right){S^{(0) + (3)}}\left[ {\left( {D_\alpha^{ - 1}{U_{{X_D}}}} \right) \otimes \left( {D_\alpha^{ - 1}{U_{{X_D}}}} \right)} \right] \cdot \left( {{\Lambda_{{X_D}}} \otimes {\Lambda_{{X_D}}}} \right) + \left( {U_{{X_D}}^T \otimes U_{{X_D}}^T} \right)\left[ {I \otimes \left( {D_\alpha^{ - 1}S_D^{(1)}D_\alpha^{ - 1}} \right) + \left( {D_\alpha^{ - 1}S_D^{(2)T}D_\alpha^{ - 1}} \right) \otimes I} \right]\Delta } \right\}} \right\|_2} \hfill \\\leqslant 2\mu {A_\psi }\left( {\sigma_e^2} \right)\lambda_{\max }^\prime + {\mu^2}{C_\psi }\left( {\sigma_e^2} \right){\left( {\lambda_{\max }^\prime } \right)^2}\alpha \prime < 1, \hfill \\\end{gathered} $$

where $\alpha \prime = s_{\max }^{(0) + (3)} + {\left( {\lambda_{\max }^\prime } \right)^{ - 2}}\left( {s_{\max }^{(2)} + s_{\max }^{(1)}} \right){\Delta_{\max }}$.

Therefore the algorithm converges if

$$ \left| {1 - 2\mu {A_\psi }\left( {\sigma_e^2} \right)\lambda_{\max }^\prime + {\mu^2}{C_\psi }\left( {\sigma_e^2} \right){{\left( {\lambda_{\max }^\prime } \right)}^2}\alpha \prime } \right| < 1 \Leftrightarrow \left| {\left( {1 - \mu {{\left( {r_0^\prime } \right)}^{ - 1}}} \right)\left( {1 - \mu {{\left( {r_1^\prime } \right)}^{ - 1}}} \right)} \right| < 1 $$

where $r_{0,1}^\prime = \lambda_{\max }^\prime \left( {{A_\psi }\left( {\sigma_e^2} \right)\pm \sqrt {{A_\psi^2\left( {\sigma_e^2} \right) - {C_\psi }\left( {\sigma_e^2} \right)\alpha \prime }} } \right)$. Hence, the maximum possible step size for mean square convergence is

$$ {\mu_{\max }} < {\left( {r_1^\prime } \right)^{ - 1}} = {\left[ {\lambda_{\max }^\prime \left( {{A_\psi }\left( {\sigma_e^2} \right) + \sqrt {{A_\psi^2\left( {\sigma_e^2} \right) - {C_\psi }\left( {\sigma_e^2} \right)\alpha \prime }} } \right)} \right]^{ - 1}}. $$

If the algorithm converges, we have from (34)

$$ {\kern 1pt} \Theta \left( \infty \right) = {\left( {I - {\Gamma_1}\left( \infty \right)} \right)^{ - 1}}{\Gamma_2}\left( \infty \right). $$

The excess mean square error (EMSE) at time instant n is ${\hbox{EMSE}}(n) = {\hbox{Tr}}\left( {\Xi (n){R_{{X_C}{X_C}}}} \right) = {\hbox{Tr}}\left( {\Psi (n){\Lambda_{{X_D}}}} \right)$. Hence

$$ {\hbox{EMSE}}\left( \infty \right) = {\hbox{Tr}}\left( {{\hbox{ve}}{{\hbox{c}}^{ - 1}}\left( {\Theta \left( \infty \right)} \right){\Lambda_{{X_D}}}} \right), $$

(35)

where vec⁻¹(·) is the inverse vec(·) operator. (35) is rather difficult to further simplify in general. We shall analyze the cases with small step size and uncorrelated transform output below.

Small step sizes

If μ is small enough, then we can drop the terms involving Ψ(n) and μ ², and (32) becomes

$$ \Psi \left( {n + 1} \right) \approx \Psi (n) - \mu {A_\psi }\left( {\sigma_e^2} \right){\Lambda_{{X_D}}}\Psi (n) - \mu {A_\psi }\left( {\sigma_e^2} \right)\Psi (n){\Lambda_{{X_D}}} + {\mu^2}{B_\psi }\left( {\sigma_e^2} \right){\hat{\Gamma }_{{\rm{UD}}_ \alpha }}, $$

(36)

where ${\hat{\Gamma }_{{\rm{UD}}_ \alpha }} = U_{{X_D}}^TD_\alpha^{ - 1/2}{\Gamma_\alpha }D_\alpha^{ - 1/2}{U_{{X_D}}}$. Let D _diag(K) be an operator which retains only the diagonal values of a square matrix K and setting the others to zero. When the algorithm converges, we have

$$ {D_{\rm diag}}\left( {\Psi (n)} \right) = \mu \frac{{{B_\psi }\left( {\sigma_e^2} \right)}}{{2{A_\psi }\left( {\sigma_e^2} \right)}}{D_{diag}}\left( {\Lambda_{{X_D}}^{ - 1}{{\hat{\Gamma }}_{{\rm{UD}}_ \alpha }}} \right), $$

(37)

Hence, (35) reduces to

$$ {\hbox{EMSE}}\left( \infty \right) = \frac{{\mu {B_\psi }\left( {\sigma_e^2\left( \infty \right)} \right)}}{{2{A_\psi }\left( {\sigma_e^2\left( \infty \right)} \right)}}{\hbox{Tr}}\left( {{{\hat{\Gamma }}_{{\rm{UD_ \alpha }}}}} \right) = \frac{{\mu {B_\psi }\left( {\sigma_e^2\left( \infty \right)} \right)}}{{2{A_\psi }\left( {\sigma_e^2\left( \infty \right)} \right)}}{\hbox{Tr}}\left( {{\Gamma_\alpha }D_\alpha^{ - 1}} \right) $$

(38)

Uncorrelated Case

If ${R_{{X_C}{X_C}}}$ is diagonal, then it can be shown that ${I_{1,i,i}} = 2{\left( {{v_i}{\lambda_i}} \right)^2}\tilde{\alpha }_i^{\left( { - 5/2} \right)}$, ${I_{2,i,i}} = {\lambda_i}\tilde{\alpha }_i^{\left( { - 3/2} \right)}$, and zero otherwise, where $\tilde{\alpha }_i^{(k)} = \int_0^\infty {\int_0^\infty {\exp \left( { - \left( {{\beta_1} + {\beta_2}} \right){\varepsilon_i}} \right){g_i}{{\left( {{{\tilde{\beta }}_1} + {{\tilde{\beta }}_2}} \right)}^{ - k}}d{\beta_2}d{\beta_1}} }$ and ${\lambda_i} = {R_{{X_C}{X_C}_ i,i}}$. Hence, (30) reduces to

$$ \Xi \left( {n + 1} \right) = \Xi (n) - \mu {A_\psi }\left( {\sigma_e^2} \right){D_\alpha }{R_{{X_C}{X_C}}}\Xi (n) - \mu {A_\psi }\left( {\sigma_e^2} \right)\Xi (n){R_{{X_C}{X_C}}}{D_\alpha } + 2{\mu^2}{C_\psi }\left( {\sigma_e^2} \right){R_{{X_C}{X_C}}}{D_{{{\tilde{\alpha }}^{ - 5/2}}}}{\hbox{diag}}\left( {\Xi (n)} \right){R_{{X_C}{X_C}}} + {\mu^2}{B_\psi }\left( {\sigma_e^2} \right){R_{{X_C}{X_C}}}{D_{{{\tilde{\alpha }}^{ - 3/2}}}} $$

which is equivalent to the following set of scalar equations:

$$ {\Xi_{i,i}}\left( {n + 1} \right) = {\Xi_{i,i}}(n) - 2\mu {A_\psi }\left( {\sigma_e^2} \right){\alpha_i}{\lambda_i}{\Xi_{i,i}}(n) + 2{\mu^2}{C_\psi }\left( {\sigma_e^2} \right)\lambda_i^2\tilde{\alpha }_i^{\left( { - 5/2} \right)}{\Xi_{i,i}}(n) + {\mu^2}{B_\psi }\left( {\sigma_e^2} \right){\lambda_i}\tilde{\alpha }_i^{\left( { - 3/2} \right)}. $$

(39)

Assuming the difference equation converges, the corresponding steady state value of ${\Xi_{i,i}}\left( \infty \right)$ can be obtained from (39) as

$$ {\Xi_{i,i}}\left( \infty \right) = \frac{{\mu {B_\psi }\left( {\sigma_e^2\left( \infty \right)} \right)\tilde{\alpha }_i^{\left( { - 3/2} \right)}}}{{2\left( {{\alpha_i}{A_\psi }\left( {\sigma_e^2\left( \infty \right)} \right) - \mu {C_\psi }\left( {\sigma_e^2\left( \infty \right)} \right){\lambda_i}\tilde{\alpha }_i^{\left( { - 5/2} \right)}} \right)}}. $$

(40)

The EMSE is then given by

$$ {\hbox{EMSE}}\left( \infty \right) = {\hbox{Tr}}\left( {{R_{{X_C}{X_C}}}\Xi \left( \infty \right)} \right) = \sum\limits_{i = 1}^L {{\lambda_i}{\Xi_{i,i}}\left( \infty \right)} . $$

(41)

Remarks

• (R-A3): TDNLMS algorithm

In this case, ${A_\psi }\left( {\sigma_e^2} \right) = {C_\psi }\left( {\sigma_e^2} \right) = 1$, ${B_\psi }\left( {\sigma_e^2} \right) = \sigma_e^2$. Since $\sigma_e^2(n) = {\hbox{EMS}}{{\hbox{E}}_{\rm{TDNLMS}}}(n) + \sigma_g^2$, the EMSE from the small step size result in (38) is

$$ {\hbox{EMS}}{{\hbox{E}}_{\rm{TDNLMS}}}\left( \infty \right) = \frac{{\frac{1}{2}\mu \sigma_g^2{\phi_{\rm{TDNLMS}}}}}{{1 - \frac{1}{2}\mu {\phi_{\rm{TDNLMS}}}}}, $$

(42)

where ${\phi_{\rm{TDNLMS}}} = Tr\left( {{\Gamma_\alpha }D_\alpha^{ - 1}} \right)$. Particularly, for the LMS algorithm, C = I, ${D_\alpha } = I$, and ${\Gamma_\alpha } = {R_{XX}}$. (42) will reduce to

$$ {\hbox{EMS}}{{\hbox{E}}_{\rm{LMS}}}\left( \infty \right) = \frac{{\frac{1}{2}\mu \sigma_g^2{\phi_{\rm{LMS}}}}}{{1 - \frac{1}{2}\mu {\phi_{\rm{LMS}}}}},{\phi_{\rm{LMS}}} = {\hbox{Tr}}\left( {{R_{XX}}} \right), $$

(43)

which agrees with the conventional result for the LMS algorithm.

For the uncorrelated case,

$$ {\hbox{EMS}}{{\hbox{E}}_{{\rm{TDNLMS_ U}}}}\left( \infty \right) = \frac{{\frac{1}{2}\mu \sigma_g^2{\phi_{{\rm{TDNLMS_ U}}}}}}{{1 - \frac{1}{2}\mu {\phi_{{\rm{TDNLMS_ U}}}}}}, $$

(44)

where ${\phi _{{\text{TDNLMS\_U}}}} = \sum\limits_{i = 1}^L {\frac{{\tilde{\alpha }_i^{\left( { - 3/2} \right)}{\lambda _i}}}{{\alpha {}_i - \mu {\lambda _i}\tilde{\alpha }_i^{\left( { - 5/2} \right)}}}}$. For perfect power estimation, ${\varepsilon_i} = \sigma_{{X_C}_ i}^2$ and ${\alpha_\varepsilon } = 0$, α _i  = ε _i ⁻¹, $\tilde{\alpha }_i^{\left( { - 3/2} \right)} = \tilde{\alpha }_i^{\left( { - 5/2} \right)} = \varepsilon_i^{ - 2}$ and $\mu {\varphi_{{\rm{TDNLMS_ U}}}} = \sum\limits_{i = 1}^L {\frac{{\left( {\mu /{\varepsilon_i}} \right){\lambda_i}}}{{1 - \left( {\mu /{\varepsilon_i}} \right){\lambda_i}}}} = \frac{{\mu L}}{{1 - \mu }}$, which reduces to the classical result of the LMS algorithm with an exact power normalized step size (μ/ε _i ). For stability, EMSE(∞) should be a finite quality and it gives the following two conditions on μ for stability:

$$ 0 < \mu < \alpha {}_i/\left( {{\lambda_i}\tilde{\alpha }_i^{\left( { - 5/2} \right)}} \right)\,and\,\sum\limits_{i = 1}^L {\frac{{\mu \tilde{\alpha }_i^{( - 4/2)}{\lambda_i}}}{{\alpha {}_i - \mu {\lambda_i}\tilde{\alpha }_i^{\left( { - 6/2} \right)}}}} \leqslant 2. $$

Following the approach in [30], one gets the approximate stepsize bound as

$$ {\mu_B} = \frac{2}{{\sum\limits_{i = 1}^L {{\lambda_i}\left( {2{d_i} + {c_i}} \right)} }}, $$

(45)

where ${c_i} = \frac{1}{{{\alpha_i}}}{\lambda_i}\tilde{\alpha }_i^{\left( { - 3/2} \right)}$ and ${d_i} = \frac{1}{{{\alpha_i}}}\mu {\lambda_i}\tilde{\alpha }_i^{\left( { - 5/2} \right)}$.

• (R-A4): The TDNLMS algorithm with general nonlinearity and the TDNLMM algorithm

For the TDNLMS algorithms with general nonlinearity, (38) or (42) is a nonlinear equation in EMSE(∞) since $\sigma_{\rm{e}}^2\left( \infty \right) = {\hbox{EMSE}}\left( \infty \right) + \sigma_{\rm{g}}^2$, general solution is difficult to obtain. In contrast, for the TDNLMM algorithm using MH nonlinearity and ATS, ${A_{\rm{MH}}}\left( {\sigma_e^2} \right) \approx {\hbox{erf}}\left( {\frac{{{k_\xi }}}{{\sqrt {2} }}} \right) - \frac{{2{k_\xi }}}{{\sqrt {{2\pi }} }}\exp \left( { - \frac{{k_\xi^2}}{2}} \right) = {A_{\rm{c}}}$, ${B_{\rm{MH}}}\left( {\sigma_e^2} \right) \approx \left( {{\hbox{erf}}\left( {\frac{{{k_\xi }}}{{\sqrt {2} }}} \right) - \frac{{2{k_\xi }}}{{\sqrt {{2\pi }} }}\exp \left( { - \frac{{k_\xi^2}}{2}} \right)} \right)\sigma_e^2 = {A_c}\sigma_e^2$, ${C_{\rm{MH}}}\left( {\sigma_e^2} \right) \approx {A_{\rm{c}}} - \left( {\frac{{k_\xi^3}}{{\sqrt {{2\pi }} }}} \right)\exp \left( { - \frac{{k_\xi^2}}{2}} \right) \cdot {\hbox{EMS}}{{\hbox{E}}_{\rm{TDNLMM}}}\left( \infty \right) \approx \frac{1}{2}\mu \sigma_e^2{\hbox{Tr}}\left( {{\Gamma_\alpha }D_\alpha^{ - 1}} \right)$. Solving for EMSE_TDNLMM(∞) gives

$$ {\hbox{EMS}}{{\hbox{E}}_{\rm{TDNLMM}}}\left( \infty \right) \approx \frac{{\frac{1}{2}\mu \sigma_g^2{\phi_{\rm{TDNLMM}}}}}{{1 - \frac{1}{2}\mu {\phi_{\rm{TDNLMM}}}}}, $$

(46)

where ϕ _TDNLMM = ϕ _TDNLMS.

For the LMM algorithm with MH nonlinearity, C = I, D _R = I, and ${\Gamma_\alpha } = {R_{XX}}$. (41) will reduce to

$$ {\hbox{EMS}}{{\hbox{E}}_{\rm{LMM}}}\left( \infty \right) \approx \frac{{\frac{1}{2}\mu \sigma_g^2{\phi_{\rm{LMM}}}}}{{1 - \frac{1}{2}\mu {\phi_{\rm{LMM}}}}},{\phi_{\rm{LMM}}} = {\phi_{\rm{LMS}}}, $$

(47)

which agrees with the result in [16] and is close to their LMS counterpart. ${B_\psi }\left( {\sigma_e^2} \right)$ and ${C_\psi }\left( {\sigma_e^2} \right)$ for some related algorithms are summarized in Table 1.

3.2 Convergence Behaviors in CG Noise

We now study the mean and mean square behaviors of the TDNLMS algorithm with general nonlinearity and particularly the TDNLMS and TDNLMM algorithms in CG noise environment. For most M-estimate functions which suppress outliers with large amplitude, the convergence rate will only be slightly impaired after employing ATS. We shall employ an extension of the Price’s theorem to Gaussian mixtures [18]. This extension was employed in the analysis of the LMS and NLMS algorithms with MH nonlinearity and CG noise in [16]. Similar techniques were also employed in analyzing the RLM and other related algorithms [15] for the MH nonlinearity. We shall show in the following that with the use of M-estimate function and ATS, the impulsive noise can be effectively suppressed and the EMSE is similar to the case where only Gaussian noise is present. On the other hand, the EMSE of the LMS-based algorithms will be substantially affected by the impulsive CG noise.

3.2.1 Mean Behavior

Since η _o is now a CG noise as defined in (11), it is a Gaussian mixture consisting of two components η _{o_1} and η _{o_2}, each with zero mean and variance $\sigma_1^2 = \sigma_g^2$ and $\sigma_2^2 = \sigma_\Sigma^2$, respectively. The occurrence probability of the impulsive noise is p _r . Accordingly,

$$ {E_{\left\{ {v,X,{\eta_o}} \right\}}}\left[ {f\left( {{\mathbf{X}}(n),e(n)} \right)} \right] = \left( {1 - {p_r}} \right){E_{\left\{ {v,X,{\eta_{o_ 1}}} \right\}}}\left[ {f\left( {X(n),e(n)} \right)} \right] + {p_r}{E_{\left\{ {v,X,{\eta_{o_ 2}}} \right\}}}\left[ {f\left( {X(n),e(n)} \right)} \right], $$

(48)

where $f\left( {X(n),e(n)} \right)$ is an arbitrary quantity whose statistical average is to be evaluated. Since X(n), η _{o_1}, and η _{o_2} are Gaussian distributed, each of the expectation on the right hand side can be evaluated using the Price’s theorem. Consequently, the results in section A can be carried forward to the CG noise case by firstly changing the noise power respectively to $\sigma_g^2$ and $\sigma_\Sigma^2$, and then combining the two results using (48).

Recall the relation of the mean weight-error vector in (13):

$$ E\left[ {v\left( {n + 1} \right)} \right] = E\left[ {v(n)} \right] - \mu H\prime, $$

(49)

where $H\prime = {E_{\left\{ {v,{X_C},{\eta_o}} \right\}}}\left[ {\Lambda_C^{ - 1}\psi \left( {e(n)} \right){X_C}(n)} \right] = \left( {1 - {p_r}} \right)H_1^\prime + {p_r}H_2^\prime$, $H_1^\prime$ and $H_2^\prime$ are respectively the expectation of the term inside the brackets above with respect to {v, X _C , η _{o_1}}, and {v, X _C , η _{o_2}}. From (16) and (17), we have $H_i^\prime \approx \overline {\psi \prime } \left( {\sigma_{{e_i}}^2} \right){D_\alpha }{R_{{X_C}{X_C}}}v\left( {n} \right)$, i = 1,2, where $\sigma_{{e_1}}^2(n) = \sigma_{{e_g}}^2(n) = E\left[ {{v^T}(n){R_{{X_C}{X_C}}}v(n)} \right] + \sigma_g^2$, $\sigma_{{e_2}}^2(n) = \sigma_{{e_\Sigma }}^2(n) = E\left[ {{v^T}(n){R_{{X_C}{X_C}}}v(n)} \right] + \sigma_\Sigma^2$. Hence

$$ H\prime \approx {\tilde{A}_\psi }(n){D_\alpha }{R_{{X_C}{X_C}}}v(n), $$

(50)

where ${\tilde{A}_\psi }(n) = \left( {1 - {p_r}} \right)\overline {\psi \prime } \left( {\sigma_{{e_g}}^2(n)} \right) + {p_r}\overline {\psi \prime } \left( {\sigma_{{e_\Sigma }}^2(n)} \right)$. Substituting (50) into (49) and using the transformation ${V_D}(n) = U_{{X_D}}^TD_\alpha^{ - 1/2}v(n)$, one gets

$$ E\left[ {{{\mathbf{V}}_D}\left( {n + 1} \right)} \right] = \left( {{\mathbf{I}} - \mu {{\tilde{A}}_\psi }(n){\Lambda_{{X_D}}}} \right)E\left[ {{V_D}(n)} \right]. $$

(51)

For simplicity, we have replaced the approximate symbol by the equality symbol. This yields the same form as (18), except for ${\tilde{A}_\psi }(n)$. Similar argument regarding the mean convergence in section 3.1 also applies to (51). A sufficient condition for the algorithm to converge is $\left| {1 - \mu {{\tilde{A}}_\psi }(n)\lambda_i^\prime } \right| < 1$, for all i. If $\overline {\psi \prime } \left( {\sigma_e^2} \right)$ is upper bounded and so is ${\tilde{A}_\psi }(n)$, say by ${\tilde{A}_{\psi \_\max }}$, then following the argument in part 3.1, the following conservative maximum step size is obtained:

$$ {\mu _{\max }} < 2/\left( {{{\tilde{A}}_{\psi \_\max }}\lambda _{\max }^\prime } \right). $$

Remarks:

• (R-B1): TDNLMS algorithm

In this case, ${\tilde{A}_\psi }(n) = 1$. Compared with the Gaussian case, the convergence rate remains unchanged. All the conclusions in (R-A1) apply.

• (R-B2): TDNLMS algorithm with general nonlinearity and TDNLMM algorithm:

For general nonlinearity without ATS, both $\sigma_{{e_g}}^2$ and $\sigma_{{e_\Sigma }}^2$ can be very large due to the large value of $\sigma_{{e_\Sigma }}^2$ and the slow decay of the EMSE $E\left[ {{v^T}(n){R_{{X_C}{X_C}}}v(n)} \right]$, as the gain ${\tilde{A}_\psi }(n) = \left( {1 - {p_r}} \right)\overline {\psi \prime } \left( {\sigma_{{e_g}}^2(n)} \right) + {p_r}\overline {\psi \prime } \left( {\sigma_{{e_\Sigma }}^2(n)} \right)$ can be very small initially. This leads to nonlinear adaptation and slow convergence. Near convergence, $E\left[ {{v^T}(n){R_{XX}}v(n)} \right]$ and ${\tilde{A}_\psi }(n)$ will become stable. The convergence is exponential and the convergence rate of the i-th mode is approximately $1 - \mu {\tilde{A}_\psi }\left( \infty \right)\lambda_i^\prime$, where ${\tilde{A}_\psi }\left( \infty \right)$ is the steady state value of ${\tilde{A}_\psi }(n)$. Normally, the second term ${p_r}\overline {\psi \prime } \left( {\sigma_{{e_\Sigma }}^2(n)} \right)$ will be much smaller than the first one due to the clipping property of the nonlinearity and the large variance of the impulsive noise $\sigma_\Sigma^2$. For the TDNLMM algorithm with ATS, the degradation in convergence rate is not so serious since if $\sigma_{{e_g}}^2 < < \sigma_{{e_\Sigma }}^2$, ${\tilde{A}_{\rm{MH}}} \approx \left( {1 - {p_r}} \right){A_c}$ is a constant close to one if p _r is not too large.

3.2.2 Mean Square Behavior

Using a similar approach, it can be shown that

$$ \Psi \left( {n + 1} \right) = \Psi (n) - \mu {\tilde{A}_\psi }(n){\Lambda_{{X_D}}}\Psi (n) - \mu {\tilde{A}_\psi }(n)\Psi (n){\Lambda_{{X_D}}} + {\mu^2}{\tilde{C}_\psi }(n)\left\{ {U_{{X_D}}^T\left[ {\left( {{S^{(0)}} + {S^{(2)}}} \right) \circ \left( {D_\alpha^{ - 1}{U_{{X_D}}}{\Lambda_{{X_D}}}\Psi (n){\Lambda_{{X_D}}}U_{{X_D}}^TD_\alpha^{ - 1}} \right)} \right]{U_{{X_D}}} + U_{{X_D}}^T{D_\sigma }D_\alpha^{ - 1/2}{S^{(1)}}D_\alpha^{ - 1/2}{U_{{X_D}}} + U_{{X_D}}^TD_\alpha^{ - 1/2}{S^{(3)}}D_\alpha^{ - 1/2}{D_\sigma }U_{{X_D}}^T} \right\} + {\mu^2}{\tilde{B}_\psi }(n)U_{{X_D}}^TD_\alpha^{ - 1/2}{\Gamma_\alpha }D_\alpha^{ - 1/2}{U_{{X_D}}}, $$

(52)

where ${\tilde{C}_\psi }(n) = \left( {1 - {p_r}} \right){C_\psi }\left( {\sigma_{{e_g}}^2(n)} \right) + {p_r}{C_\psi }\left( {\sigma_{{e_g}}^2(n)} \right)$ and ${\tilde{B}_\psi }(n) = \left( {1 - {p_r}} \right){B_\psi }\left( {\sigma_{{e_g}}^2(n)} \right) + {p_r}{B_\psi }\left( {\sigma_{{e_g}}^2(n)} \right)$.

Due to page limitation, we only summarize the result for the small step size case as:

$$ {\hbox{EMSE}}\left( \infty \right) \approx \mu \frac{{{{\tilde{B}}_\psi }\left( \infty \right)}}{{2{{\tilde{A}}_\psi }\left( \infty \right)}}{\hbox{Tr}}\left( {{\Gamma_\alpha }D_\alpha^{ - 1}} \right). $$

(53)

• (R-B3): TDNLMS algorithm

In these cases, ${\tilde{A}_\psi }(n) = {\tilde{C}_\psi }(n) = 1$, and ${\tilde{B}_\psi }(n) = \left( {1 - {p_r}} \right)\left( {\sigma_{\rm{excess}}^2(n) + \sigma_g^2} \right) + {p_r}\left( {\sigma_{\rm{excess}}^2(n) + \sigma_\Sigma^2} \right) = \sigma_{\rm{excess}}^2(n) + \sigma_{{\eta_o}}^2$ where $\sigma_{{\eta_o}}^2 = \left( {1 - {p_r}} \right)\sigma_g^2 + {p_r}\sigma_\Sigma^2$, $\sigma_{\rm{excess}}^2(n) = E\left[ {{v^T}(n){R_{{X_C}{X_C}}}v(n)} \right]$ is the EMSE. Hence

$$ {\hbox{EMS}}{{\hbox{E}}_{\rm{TDNLMS}}}\left( \infty \right) = \left. {\sigma_{\rm{excess}}^2\left( \infty \right)} \right) \approx \tfrac{1}{2}\mu \left( {\sigma_{\rm{excess}}^2\left( \infty \right) + \sigma_{{\eta_o}}^2{\hbox{Tr}}\left( {{\Gamma_\alpha }D_\alpha^{ - 1}} \right)} \right), $$

which gives

$$ {\hbox{EMS}}{{\hbox{E}}_{\rm{TDNLMS}}}\left( \infty \right) \approx \frac{{\frac{1}{2}\mu \sigma_{{\eta_o}}^2{\phi_{\rm{TDNLMS}}}}}{{1 - \frac{1}{2}\mu {\phi_{\rm{TDNLMS}}}}}, $$

(54)

It can be seen that the EMSE will be considerably increased over the Gaussian case by ${p_r}\mu \sigma_w^2{\phi_{\rm{TDNLMS}}}/\left( {1 - \mu {\phi_{\rm{TDNLMS}}}} \right)$, which increases with the probability of occurrence of the impulses and the difference in power between the impulsive and Gaussian components.

For the TDNLMM algorithm with MH nonlinearity and ATS, ${\tilde{A}_{\rm{MH}}}\left( \infty \right) \approx \left( {1 - {p_r}} \right){A_c}$, ${\tilde{B}_{\rm{MH}}}\left( \infty \right) \approx \left( {1 - {p_r}} \right)\sigma_{{e_g}}^2{\hbox{erf}}\left( {\frac{{{k_\xi }}}{{\sqrt {2} }}} \right) = \left( {1 - {p_r}} \right)\sigma_{{e_g}}^2{A_c}$, ${\tilde{C}_{\rm{MH}}}\left( \infty \right) \approx {\tilde{A}_{\rm{MH}}}\left( \infty \right) - \left( {1 - {p_r}} \right)\left( {\frac{{k_\xi^3}}{{\sqrt {{2\pi }} }}} \right)\exp \left( { - \frac{{k_\xi^2}}{2}} \right)$

$$ {\hbox{EMS}}{{\hbox{E}}_{\rm{TDNLMM}}}\left( \infty \right) \approx \frac{{\frac{1}{2}\mu \sigma_g^2{\phi_{\rm{TDNLMS}}}}}{{1 - \frac{1}{2}\mu {\phi_{\rm{TDNLMS}}}}}, $$

(55)

which is identical to the case with Gaussian noise only. This illustrates the robustness of the TDNLMM algorithm to impulsive noise.

For the LMM algorithm with the MH nonlinearity, D _R = I, and ${\Gamma_\alpha } = {R_{XX}}$. (55) will reduce to

$$ {\hbox{EMS}}{{\hbox{E}}_{\rm{LMM}}}\left( \infty \right) \approx \frac{{\mu \sigma_g^2{\text{Tr}}\left( {{R_{XX}}} \right)}}{{2 - \mu {\hbox{Tr}}\left( {{R_{XX}}} \right)}}, $$

(56)

which is also similar to its conventional LMS counterpart when the additive noise is Gaussian. This illustrates the robustness of the M-estimation based algorithms to impulsive noise.

4 Simulation Results

In this section, computer simulations on the system identification problem shown in Fig. 1 are conducted to evaluate the analytical results for the TDNLMS and TDNLMM algorithms obtained in section 3. The unknown system W* is a FIR filter with L = 8. Its coefficients are randomly generated and normalized to unit energy. The input signal x(n) is generated as a first-order AR process

$$ x(n) = ax\left( {n - 1} \right) + v(n), $$

(57)

where v(n) is a white Gaussian noise sequence with zero mean and variance $\sigma_v^2$. 0 < a < 1 is the correlation coefficient and in our experiment it is set to be 0, 0.5 and 0.9. DCT is employed due to its wide usage and efficiency in practice. The simulation results are averaged over K = 200 independent runs. Only impulses in the desired signal are considered. The locations of impulses are not fixed for each independent run and their amplitudes are varying. For the CG impulsive noise, we test p _r  = 0.005, 0.01 and 0.02; r _im  = 50, 100 and 200. ${\lambda_\sigma } = 0.95$, N _w  = 9, ${k_\xi } = 2.576$. For mean convergence, the norm of the mean square weight-error vector

$$ {\left\| {{v_A}(n)} \right\|_2} = \sqrt {{{{\sum\nolimits_{i = 1}^L {\left[ {\frac{1}{K}\sum\nolimits_{j = 1}^K {v_i^{(j)}(n)} } \right]} }^2}}}, i = 1, \cdots, L,\,j = 1, \cdots, K, $$

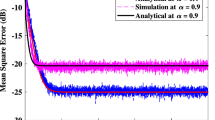
is used as the performance measure. ${\hbox{EMSE}}(n) = {\hbox{Tr}}\left( {\Xi (n){R_{XX}}} \right) = {\hbox{Tr}}\left( {\Phi (n)\Lambda } \right)$ is adopted as the mean square performance measure. The integrals α _i defined in (A-9b), $\alpha_i^{(k)}$ in (B-9) and $\alpha_i^{\left( {m,n} \right)}$ in (B-10) are evaluated numerically [28]. Figures 3 and 4 respectively depict the mean and mean square performance of the TDNLMS algorithm in Gaussian noise and the TDNLMM algorithm with CG noise. The theoretical results are computed respectively from (19), (30) and (51), (52). Different values of a, μ, $\sigma_g^2$, r _im and p _r are used as specified in respective figure caption. All these figures show a satisfactory agreement between the theoretical and simulation results. Since the results for the TDNLMM algorithm in Gaussian noise is similar to those in CG noise, they are omitted to save space. For the TDNLMS algorithm in CG noise, the mean weight vector can be considerably affected by the impulsive noise and the independent assumption in assumption 3 becomes less accurate. Since this case is of little interest, the simulation result is also omitted.

Figure 3

The mean and mean square convergence performance of the TDNLMS algorithm with Gaussian noise: a, b: α = 0, $\sigma_g^2 = {10^{ - 4}}$, c, d: α = 0.5, $\sigma_g^2 = {10^{ - 3}}$, e, f: α = 0.9, $\sigma_g^2 = {10^{ - 5}}$; Three step sizes are used: (1) μ = 0.01, (2) μ = 0.004, (3) μ = 0.002.

Figure 4

The mean and mean square convergence performance of the TDNLMM algorithm with CG noise: a, b: a = 0, $\sigma_g^2 = {10^{ - 4}}$, r _im  = 200, p _r  = 0.02. c, d: a = 0.5, $\sigma_g^2 = {10^{ - 3}}$, r _im  = 100, p _r  = 0.01. (e), (f): a = 0.9, $\sigma_g^2 = {10^{ - 5}}$, r _im  = 100, p _r  = 0.005; Three step sizes are used: (1) μ = 0.01, (2) μ = 0.004, (3) μ = 0.002.

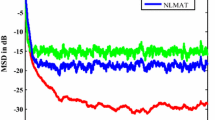
To study the effect of the recursive power estimation of the signal components in the normalization part of the TDNLMS algorithm, ${\varepsilon_i}(n) = \left( {1 - {\alpha_\varepsilon }} \right)\sigma_{{X_{C_ i}}}^2 + {\alpha_\varepsilon }X_{C,i}^2(n)$ is used, which allows us to approximately model the effect of prior knowledge of the signal power on the algorithms. This is valid when the recursive estimation of the signal power converges. The value of $\sigma_{{X_{C_ i}}}^2$ can be obtained from calculation or offline estimation. In our experiment, it is derived from (57) plus DCT operation and known parameters. Figure 5 illustrates that with the increase of ${\alpha_\varepsilon }$, the estimation accuracy slightly deteriorates. This verifies the efficiency of power normalization in TDNLMS algorithm.

Figure 5

Test of the effect of a priori knowledge of signal power in normalization part of the TDNLMS algorithm. μ = 0.01. (1) ${\alpha_\varepsilon } = 0.01$, $\sigma_g^2 = {10^{ - 3}}$, (2) ${\alpha_\varepsilon } = 0.25$, $\sigma_g^2 = {10^{ - 4}}$, (3) ${\alpha_\varepsilon } = 0.5$, $\sigma_g^2 = {10^{ - 5}}$, (4) ${\alpha_\varepsilon } = 0.75$, $\sigma_g^2 = {10^{ - 6}}$.

5 Conclusions

The convergence performance of the TDNLMS algorithm and its TDNLMM generalizations with Gaussian inputs and additive Gaussian and contaminated Gaussian noises is presented. Difference equations describing the mean and mean square convergence behaviors for these algorithms are derived. The analytical results reveal the advantages of the TDNLMM algorithms in impulsive noise environment, and they are shown to be in good agreement with computer simulation results.

Appendices

Appendix A

In this Appendix, ${H_1} = {E_{\left\{ {{X_C},{\eta_g}} \right\}}}\left[ {\Lambda_C^{ - 1}\psi \left( {e(n){X_C}(n)} \right)\left| v \right.} \right]$ is evaluated. For notational convenience, we shall drop the subscript C in X _C . An approach similar to [15, 29] is employed to evaluate this expectation. As η _g (n) and x(n) are assumed to be statistically independent, and X are jointly Gaussian with covariance matrix ${R_{{X_C}{X_C}}}$, the i-th element of the vector H ₁ is

$$ {H_{1,i}} = {C_R}\iint\limits_{L + 1{\rm{ fold}}} {\frac{{\psi (e){X_i}}}{{{\varepsilon_i} + {\alpha_\varepsilon }X_i^2}}}\exp \left( { - \frac{1}{2}{X^T}R_{{X_C}{X_C}}^{ - 1}X} \right){f_{{\eta_g}}}\left( {{\eta_g}} \right)d{\eta_g}dX, $$

(A-1)

where ${C_R} = {\left( {2\pi } \right)^{ - L/2}}{\left| {{R_{{X_C}{X_C}}}} \right|^{ - 1/2}}$ and ${f_{{\eta_g}}}\left( {{\eta_g}} \right)$ is the PDF of the Gaussian noise η _g . |·| denotes the determinant of a matrix. Similar to [17], let us consider the integral

$$ {F_i}\left( \beta \right) = {C_R}\iint\limits_{L + 1{\rm{ fold}}} {\frac{{\psi (e){X_i}\exp \left( { - \beta \left( {{\varepsilon_i} + {\alpha_\varepsilon }X_i^2} \right)} \right)}}{{{\varepsilon_i} + {\alpha_\varepsilon }X_i^2}}} \dot \exp \left( { - \frac{1}{2}{X^T}R_{{X_C}{X_C}}^{ - 1}X} \right){f_{{\eta_g}}}\left( {{\eta_g}} \right)d{\eta_g}dX $$

(A-2)

It can be seen that H _1,i = F _i (0). Differentiating (A-2) with respect to β, one gets

$$ \frac{{d{F_i}\left( \beta \right)}}{{d\beta }} = - \exp \left( { - \beta {\varepsilon_i}} \right){C_R}\iint\limits_{L + 1{\rm{ fold}}} {\psi (e){X_i}}\exp \left( { - \frac{1}{2}{X^T}B_i^{ - 1}X} \right){f_{{\eta_g}}}\left( {{\eta_g}} \right)d{\eta_g}dX, $$

(A-3)

where ${B_i} = {\left( {2\tilde{\beta }{e_i}e_i^T + R_{{X_C}{X_C}}^{ - 1}} \right)^{ - 1}}$, $\tilde{\beta } = {\alpha_\varepsilon }\beta$ and e _i is a column vector with its i-th element equal to one and zero elsewhere. Using the matrix inversion lemma, we get

$$ {B_i} = {\left( {2\tilde{\beta }{e_i}e_i^T + R_{{X_C}{X_C}}^{ - 1}} \right)^{ - 1}} = {R_{{X_C}{X_C}}}{G_i}, $$

(A-4)

where ${G_i} = \left( {{\mathbf{I}} - 2\tilde{\beta }{{\left( {{g_i}\left( {\tilde{\beta }} \right)} \right)}^{ - 1}}{E_i}} \right)$, ${g_i}\left( {\tilde{\beta }} \right) = 1 + 2\tilde{\beta }{R_{{X_C}{X_C}_ i,i}}$, ${R_{{X_C}{X_C}_ i,j}}$ is the (i, j)-th element of ${R_{{X_C}{X_C}}}$ and ${E_i} = {e_i}r_{{X_C}{X_C}_ i}^T$. $r_{{X_C}{X_C}_ i}^T$ is the i-th row of ${R_{{X_C}{X_C}}}$. The determinant of B _i is $\left| {{B_i}} \right| = \left| {{R_{{X_C}{X_C}}}} \right|\left| {{G_i}} \right| = \left| {{R_{{X_C}{X_C}}}} \right|{\left( {{g_i}\left( {\tilde{\beta }} \right)} \right)^{ - 1}}$. (A-3) can be rewritten as follows

$$ \frac{{d{F_i}\left( \beta \right)}}{{d\beta }} = - {\gamma_i}\left( \beta \right){C_{{B_i}}}\iint\limits_{L + 1{\rm{ fold}}} {\psi (e){X_i}} \cdot \exp \left( { - \frac{1}{2}{X^T}B_i^{ - 1}X} \right){f_{{\eta_g}}}\left( {{\eta_g}} \right)d{\eta_g}d\mathbf{X} = - {\gamma_i}\left( \beta \right){E_{\left\{ {X,{\eta_g}} \right\}}}\left[ {\psi (e){X_i}\left| v \right.} \right]\left| {_{E\left[ {X{X^T}} \right] = B{}_i} = - {\gamma_i}\left( \beta \right){L_{2,i}}} \right., $$

(A-5)

where ${C_{{B_i}}} = {\left( {2\pi } \right)^{ - L/2}}{\left| {{B_i}} \right|^{ - 1/2}}$,${\gamma_i}\left( \beta \right) = \exp \left( { - \beta {\varepsilon_i}} \right){\left( {{g_i}\left( {\tilde{\beta }} \right)} \right)^{ - 1/2}}$, and ${L_{2,i}} = {E_{\left\{ {X,{\eta_g}} \right\}}}\left[ {\psi (e){X_i}\left| v \right.} \right]\left| {_{E\left[ {X{X^T}} \right] = {B_i}}} \right.$ is the expectation of ψ(e)X _i conditioned on v when X _i , X _j ∈ X are jointly Gaussian with covariance matrix B _i . Since X and e are assumed to be jointly Gaussian in Assumption 3, the Price’s theorem [18] for X and e can be invoked to obtain the following,

$$ {L_{2,i}} = \overline {\psi \prime } \left( {\sigma_e^2} \right)b_i^Tv(n)\,. $$

(A-6)

b _i is the i-th column of B _i . Inserting (A-6) into (A-5) and integrating with respect to β yields

$$ \begin{array}{*{20}{c}} {{F_i}\left( \beta \right) = - \left( {\int^\beta {{\gamma_i}\left( \beta \right)\overline {\psi \prime } \left( {\sigma_e^2} \right)b_i^Td\beta } } \right) \cdot v(n),} \\{ \approx \overline {\psi \prime } \left( {\sigma_e^2} \right){\rm I}_i^T\left( \beta \right)v(n),} \\\end{array} $$

(A-7)

where $\overline {\psi \prime } \left( {\sigma_e^2} \right) = \int_{ - \infty }^\infty {\frac{{\psi \prime (e)}}{{\sqrt {{2\pi }} \sigma_e}}\exp \left( { - \frac{{{e^2}}}{{2\sigma_e^2}}} \right)de}$, ${\rm I}_i^T\left( \beta \right) = - \int^\beta {{\gamma_i}\left( \beta \right)b_i^Td\beta }$, and the constant of integration is equal to zero because of the boundary condition F _i (∞) = 0. Here, we have assumed that $\sigma_e^2(v)$ depends weakly on β and can be taken outside of the integral. This is a good approximation if the variation of $\overline {\psi \prime } \left( {\sigma_e^2} \right)$ is limited, such as in the TDNLMM algorithm with adaptive threshold selection or at the steady state of the algorithm. To evaluate ${\rm I}_i^T\left( \beta \right)$, we note from (A-4) that

$$ {\left[ {{B_i}} \right]_{i,j}} = {R_{{X_C}{X_C}_ i,j}} - 2\tilde{\beta }{\left( {{g_i}\left( {\tilde{\beta }} \right)} \right)^{ - 1}}{\left[ {{R_{X{}_C{X_C}}}{E_i}} \right]_{i,j}} = {\left( {{g_i}\left( {\tilde{\beta }} \right)} \right)^{ - 1}}{R_{{X_C}{X_C}_ i,j}}. $$

(A-8)

Hence,

$$ {\left[ {{\rm I}_i^T(0)} \right]_j} = \int_0^\infty {{\gamma_i}\left( \beta \right){{\left[ {{B_i}} \right]}_{i,j}}d\beta } = {\alpha_i}{R_{{X_C}{X_C}_ i,j}}, $$

(A-9a)

and

$$ {\rm I}_i^T(0) = {\alpha_i}r_{{X_C}{X_C}_ i}^T, $$

(A-9b)

where ${\alpha_i} = \int_0^\infty {\exp \left( { - \beta {\varepsilon_i}} \right){{\left( {{g_i}\left( {\tilde{\beta }} \right)} \right)}^{ - 3/2}}d\beta }$. Combining, we have the desired result

$$ {H_{1,i}} = {F_i}(0) \approx \overline {\psi \prime } \left( {\sigma_e^2} \right){\alpha_i}e_i^T{R_{{X_C}{X_C}}}v(n). $$

(A-10)

Appendix B

In this appendix, ${s_3} = {E_{\left\{ {{X_C},{\eta_g}} \right\}}}\left[ {{\psi^2}(e)\Lambda_C^{ - 1}{X_C}X_C^T\Lambda_C^{ - 1}\left| v \right.} \right]$ is evaluated. Similar to deriving H _i in Appendix A, the (i, j)-th element of s ₃ is given by

$$ {s_{3,i,j}} = {C_R}\iint\limits_{L + 1{\rm{ fold}}} {\frac{{{\psi^2}(e){X_i}{X_j}}}{{\left( {{\varepsilon_i} + {\alpha_\varepsilon }X_i^2} \right)\left( {{\varepsilon_j} + {\alpha_\varepsilon }X_j^2} \right)}}} \cdot exp\left( { - \frac{1}{2}{X^T}R_{{X_C}{X_C}}^{ - 1}X} \right){f_{{\eta_g}}}\left( {{\eta_g}} \right)d{\eta_g}dX, $$

(B-1)

Let us define

$$ {\overline F_{i,j}}\left( {{\beta_1},{\beta_2}} \right) = {C_R}\iint\limits_{L + 1{\rm{ fold}}} {\frac{{{\psi^2}(e){X_i}{X_j}exp\left( { - {\beta_1}\left( {{\varepsilon_i} + {\alpha_\varepsilon }X_i^2} \right) - {\beta_2}\left( {{\varepsilon_j} + {\alpha_\varepsilon }X_i^2} \right)} \right)}}{{\left( {{\varepsilon_i} + {\alpha_\varepsilon }X_i^2} \right)\left( {{\varepsilon_j} + {\alpha_\varepsilon }X_j^2} \right)}}} \dot \exp \left( { - \frac{1}{2}{X^T}R_{{X_C}{X_C}}^{ - 1}X} \right){f_{{\eta_g}}}\left( {{\eta_g}} \right)d{\eta_g}dX. $$

(B-2)

It can be seen that ${s_{3,i,j}} = {\overline F_{i,j}}\left( {0,0} \right).$ To evaluate ${\overline F_{i,j}}\left( {{\beta_1},{\beta_2}} \right)$, let’s differentiate (B-2) twice with respect to β ₁ and β ₂:

$$ \frac{{{\partial^2}{{\overline F }_{i,j}}\left( {{\beta_1},{\beta_2}} \right)}}{{\partial {\beta_1}\partial {\beta_2}}} = {C_R}exp\left( { - \left( {{\beta_1}{\varepsilon_i} + {\beta_2}{\varepsilon_j}} \right)} \right) \cdot \iint\limits_{L + 1{\rm{ fold}}} {{\psi^2}(e){X_i}{X_j}exp\left( { - \frac{1}{2}{X^T}B_{i,j}^{ - 1}X} \right){f_{{\eta_g}}}\left( {{\eta_g}} \right)d{\eta_g}dX} = {\gamma_{i,j}}\left( {{\beta_1},{\beta_2}} \right){L_{3,i,j}}, $$

(B-3)

where ${L_{3,i,j}} = {E_{\left\{ {X,{\eta_g}} \right\}}}{\left. {\left[ {{\psi^2}(e){X_i}{X_j}\left| v \right.} \right]} \right|_{E\left[ {X{X^T}} \right] = {B_{i,j}}}}$, ${B_{i,j}} = {\left( {2{{\tilde{\beta }}_1}{e_i}e_i^T + 2{{\tilde{\beta }}_2}{e_j}e_j^T + R_{{X_C}{X_C}}^{ - 1}} \right)^{ - 1}}$, ${\gamma_{i,j}}\left( {{\beta_1},{\beta_2}} \right) = \exp \left( { - \left( {{\beta_1}{\varepsilon_i} + {\beta_2}{\varepsilon_j}} \right)} \right){\left| {{B_{i,j}}} \right|^{1/2}}{\left| {{R_{{X_C}{X_C}}}} \right|^{ - 1/2}}$, and ${C_{{B_{i,j}}}} = {\left( {2\pi } \right)^{ - L/2}}{\left| {{B_{i,j}}} \right|^{ - 1/2}}$.

Using the matrix inversion formula, it can be shown that [30] the determinant of B _i,j and its (i, k)-th and (k, j)-th elements are respectively given by

$$ \left| {{B_{i,j}}} \right| = {\left( {{u_{i,j}}\left( {{{\tilde{\beta }}_1},{{\tilde{\beta }}_2}} \right)} \right)^{ - 1}}\left| {{R_{{X_C}{X_C}}}} \right|, $$

(B-4a)

$$ {\left[ {{B_{i,j}}} \right]_{i,k}} = {\left( {{u_{i,j}}\left( {{{\tilde{\beta }}_1},{{\tilde{\beta }}_2}} \right)} \right)^{ - 1}}{\phi_{i,j,i,k}}\left( {{{\tilde{\beta }}_2}} \right), $$

(B-4b)

$$ {\left[ {{{\mathbf{B}}_{i,j}}} \right]_{k,j}} = {\left( {{u_{i,j}}\left( {{{\tilde{\beta }}_1},{{\tilde{\beta }}_2}} \right)} \right)^{ - 1}}{\phi_{i,j,k,j}}\left( {{{\tilde{\beta }}_1}} \right), $$

(B-4c)

where ${u_{i,j}}\left( {{{\tilde{\beta }}_1},{{\tilde{\beta }}_2}} \right) = {g_i}\left( {{{\tilde{\beta }}_1}} \right){g_j}\left( {{{\tilde{\beta }}_2}} \right) - 4{\tilde{\beta }_1}{\tilde{\beta }_2}R_{{X_C}{X_C}_ j,i}^2$, ${\phi_{i,j,i,k}}\left( {{{\tilde{\beta }}_2}} \right) = \left[ {{R_{{X_C}{X_C}_ i,k}} + 2{{\tilde{\beta }}_2}\left( {{R_{{X_C}{X_C}_ j,j}}{R_{{X_C}{X_C}_ i,k}}{\kern 1pt} - {R_{{X_C}{X_C}_ i,j}}{R_{{X_C}{X_C}_ j,k}}} \right)} \right]$, ${\phi_{i,j,k,j}}\left( {{{\tilde{\beta }}_1}} \right) = \left[ {{R_{{X_C}{X_C}_ k,j}} + 2{{\tilde{\beta }}_1}\left( {{R_{{X_C}{X_C}_ k,j}}{R_{{X_C}{X_C}_ i,i}} - {R_{{X_C}{X_C}_ i,j}}{R_{{X_C}{X_C}_ k,i}}} \right)} \right]$, and

$$ {\left[ {{B_{i,i}}} \right]_{i,k}} = {R_{{X_C}{X_C}_ i,k}}{\left[ {1 + 2\left( {{{\tilde{\beta }}_1} + {{\tilde{\beta }}_2}} \right){R_{{X_C}{X_C}_ i,i}}} \right]^{ - 1}} $$

(B-4d)

Using (B-4), γ _i,j (β ₁, β ₂) is determined as follows

$$ {\gamma_{i,j}}\left( {{\beta_1},{\beta_2}} \right) = {\left( {{u_{i,j}}\left( {{{\tilde{\beta }}_1},{{\tilde{\beta }}_2}} \right)} \right)^{ - 1/2}}\exp \left( { - \left( {{\beta_1}\varepsilon {}_i + {\beta_2}{\varepsilon_j}} \right)} \right). $$

(B-5)

Using the Price’s theorem, L _3,i,j is evaluated to be [30]

$$ {L_{3,i,j}} \approx 2{C_\psi }\left( {\sigma_e^2} \right)b_i^Tv{v^T}{b_j} + {B_\psi }\left( {\sigma_e^2} \right){b_{i,j}}. $$

(B-6)

where b _i,j is the (i,j)-th element of B _i and ${\mathbf{}}{B_\psi }\left( {\sigma_e^2} \right) = E[{\psi^2}(e)] = \tfrac{1}{{\sqrt {{2\pi }} \sigma_e}}\int_{ - \infty }^\infty {{\psi^2}(e)\exp \left( { - \frac{{{e^2}}}{{2\sigma_e^2}}} \right)de}$, ${C_\psi }\left( {\sigma_e^2} \right) = \frac{d}{{d\sigma_e^2}}E\left[ {{\psi^2}(e)} \right]$. From (B-3) and (B-6), we have

$$ \frac{{{\partial^2}{{\overline F }_{i,j}}\left( {{\beta_1},{\beta_2}} \right)}}{{\partial {\beta_1}\partial {\beta_2}}} = 2{C_\psi }\left( {\sigma_e^2} \right){\gamma_{i,j}}\left( {{\beta_1},{\beta_2}} \right)b_i^Tv{v^T}{b_j} + {B_\psi }\left( {\sigma_e^2} \right){\gamma_{i,j}}\left( {{\beta_1},{\beta_2}} \right){b_{i,j}}. $$

(B-7)

Integrating (B-7) with respect to β ₁ and β ₂ yields

$$ {s_{3,i.j}} \approx {C_\psi }\left( {\sigma_e^2} \right){I_{1,i,j}} + {B_\psi }\left( {\sigma_e^2} \right){I_{2,i,j}}, $$

(B-8)

where ${I_{1,i,j}} = \int_0^\infty {\int_0^\infty {2{\gamma_{i,j}}\left( {{\beta_1},{\beta_2}} \right)b_i^Tv{v^T}{b_j}d{\beta_2}d{\beta_1}} }$ and ${I_{2,i,j}} = \int_0^\infty {\int_0^\infty {{\gamma_{i,j}}\left( {{\beta_1},{\beta_2}} \right){b_{i,j}}d{\beta_2}d{\beta_1}} }$.

To simplify the analysis, we shall assume that $\sigma_e^2$ depends weakly on β and is taken outside the integral (mean value theorem). Like ${A_\psi }\left( {\sigma_e^2} \right)$, this is a good approximation if the variations of ${B_\psi }\left( {\sigma_e^2} \right)$ and ${C_\psi }\left( {\sigma_e^2} \right)$ are limited. The integrals are evaluated below.

Evaluation of I _2,i,j .

From (B-5) and (B-8), we have

$$ {I_{2,i,j}} = {R_{{X_C}{X_C}_ i,j}}\int_0^\infty {\int_0^\infty {{{\left( {{u_{i,j}}\left( {{{\tilde{\beta }}_1},{{\tilde{\beta }}_2}} \right)} \right)}^{ - \frac{3}{4}}}} } \exp \left( { - \left( {{\beta_1}{\varepsilon_1} + {\beta_2}{\varepsilon_2}} \right)} \right)d{\beta_2}d{\beta_1} = \sum\limits_{m = 0}^\infty {\alpha_{i,j}^{(m)}\left( {{4^m}} \right)} \left( {\begin{array}{*{20}{c}} { - \frac{3}{2} + m - 1} \\m \\\end{array} } \right)R_{{X_C}{X_C}_ i,j}^{\left( {2m + 1} \right)}. $$

(B-9)

where $\alpha_{i,j}^{(k)} = \int_0^\infty {\int_0^\infty {{{\left( {{{\tilde{\beta }}_1}{{\tilde{\beta }}_2}} \right)}^k}{{\left( {{g_i}\left( {{{\tilde{\beta }}_1}} \right){g_j}\left( {{{\tilde{\beta }}_2}} \right)} \right)}^{ - \left( {2k + 3} \right)/2}}} } \cdot \exp \left( { - \left( {{\beta_1}{\varepsilon_i} + {\beta_2}{\varepsilon_j}} \right)} \right)d{\beta_2}d{\beta_1} = \alpha_i^{(k)}\alpha_j^{(k)}$, and $\alpha_i^{(k)} = \int_0^\infty {\int_0^\infty {{{\left( {\tilde{\beta }} \right)}^k}{{\left( {{g_i}\left( {\tilde{\beta }} \right)} \right)}^{ - \left( {2k + 3} \right)/2}}\exp \left( { - \beta {\varepsilon_i}} \right)d\beta } }$.

Evaluation of I _1,i,j .

Similarly from (B-5) and (B-8), we get

$$ \begin{array}{*{20}{c}} {{I_{1,i,j}} = 2\sum\limits_{k = 1}^L {\sum\limits_{l = 1}^L {{v_l}{v_k}} } \int_0^\infty {\int_0^\infty {{{\left( {{u_{i,j}}\left( {{{\tilde{\beta }}_1},{{\tilde{\beta }}_2}} \right)} \right)}^{ - 5/2}}\exp \left( { - \left( {{\beta _1}{\varepsilon _i} + {\beta _2}{\varepsilon _j}} \right)} \right)} } \cdot {\phi _{i,j,l,j}}\left( {{{\tilde{\beta }}_1}} \right){\phi _{i,j,i,k}}\left( {{{\tilde{\beta }}_2}} \right)d{\beta _1}d{\beta _2}} \\ { = 2\sum\limits_{k = 1}^L {\sum\limits_{l = 1}^L {{v_l}{v_k}} } \int_0^\infty {\int_0^\infty {{{\left( {{g_i}\left( {{{\tilde{\beta }}_1}} \right){g_j}\left( {{{\tilde{\beta }}_2}} \right)} \right)}^{ - 5/2}}\exp \left( { - \left( {{\beta _1}{\varepsilon _i} + {\beta _2}{\varepsilon _j}} \right)} \right)} } \cdot \left[ {\sum\limits_{m = 0}^\infty {\left( {\begin{array}{*{20}{c}} { - \frac{5}{2} + m - 1} \\ m \\ \end{array} } \right){{\left( { - 4{{\tilde{\beta }}_1}{{\tilde{\beta }}_2}R_{{X_C}{X_C}\_j,i}^2} \right)}^m}{{\left( {{g_i}\left( {{{\tilde{\beta }}_1}} \right){g_j}\left( {{{\tilde{\beta }}_2}} \right)} \right)}^{ - m}}} } \right] \cdot {\phi _{i,j,l,j}}\left( {{{\tilde{\beta }}_1}} \right){\phi _{i,j,i,k}}\left( {{{\tilde{\beta }}_2}} \right)d{\beta _1}d{\beta _2}} \\ \begin{gathered} = 2\sum\limits_{k = 1}^L {\sum\limits_{l = 1}^L {{v_l}{v_k}} } \sum\limits_{m = 0}^\infty {\left( {\begin{array}{*{20}{c}} { - \frac{5}{2} + m - 1} \\ m \\ \end{array} } \right){{\left( { - 4{R_{{X_C}{X_C}\_j,i}}} \right)}^m} \cdot \left( {{R_{{X_C}{X_C}\_l,j}}{R_{{X_C}{X_C}\_i,k}}\alpha _i^{\left( {m,\left( {3 + 2m} \right)/2} \right)}\alpha _j^{\left( {m,\left( {3 + 2m} \right)/2} \right)}} \right.} \hfill \\ - 2{R_{{X_C}{X_C}\_i,j}}{R_{{X_C}{X_C}\_j,k}}{R_{{X_C}{X_C}\_l,j}} \cdot \alpha _i^{\left( {m,\left( {3 + 2m} \right)/2} \right)}\alpha _j^{\left( {m + 1,\left( {5 + 2m} \right)/2} \right)} \hfill \\ \left. { - 2{R_{{X_C}{X_C}\_i,j}}{R_{{X_C}{X_C}\_l,i}}{R_{{X_C}{X_C}\_i,k}}\alpha _i^{\left( {m + 1,\left( {5 + 2m} \right)/2} \right)}\alpha _j^{\left( {m,\left( {3 + 2m} \right)/2} \right)} + 4R_{{X_C}{X_C}\_i,j}^2{R_{{X_C}{X_C}\_l,i}}{R_{{X_C}{X_C}\_j,k}}\alpha _i^{\left( {m + 1,\left( {5 + 2m} \right)/2} \right)}\alpha _j^{\left( {m + 1,\left( {5 + 2m} \right)/2} \right)}} \right), \hfill \\ \end{gathered} \\ \end{array} $$

(B-10)

where we have assumed that the matrix ${R_{{X_C}{X_C}}}$ is diagonal-dominant so that we can employ the binomial expansion and

$$ \alpha_i^{\left( {m,n} \right)} = \int_0^\infty {\frac{{{{\tilde{\beta }}^m}\exp \left( { - \beta {\varepsilon_i}} \right)}}{{{{\left( {1 + 2\tilde{\beta }{R_{{X_C}{X_C}_ i,i}}} \right)}^n}}}} d\beta . $$

In matrix form, we have

$$ {I_{1,i,j}} = s_{ij}^{(0)}{\left( {{{\mathbf{r}}_{{X_C}{X_C}_ i}}} \right)^T}v{v^T}{r_{{X_C}{X_C}_ j}} + s_{ij}^{(1)}{\left( {{r_{{X_C}{X_C}_ j}}} \right)^T}v{v^T}{r_{{X_C}{X_C}_ j}} + s_{ij}^{(2)}{\left( {{r_{{X_C}{X_C}_ i}}} \right)^T}v{v^T}{r_{{X_C}{X_C}_ i}} + s_{ij}^{(3)}{\left( {{r_{{X_C}{X_C}_ i}}} \right)^T}v{v^T}{r_{{X_C}{X_C}_ j}}, $$

where

$$ \begin{array}{*{20}{c}} {s_{ij}^{(0)} = 2\sum\limits_{m = 0}^\infty {\left( {\begin{array}{*{20}{c}} { - \frac{5}{2} + m - 1} \\m \\\end{array} } \right)} {{\left( { - 4{R_{{X_C}{X_C}_ j,i}}} \right)}^m}\alpha_i^{\left( {m,\left( {3 + 2m} \right)/2} \right)}\alpha_j^{\left( {m,\left( {3 + 2m} \right)/2} \right)},} \\{s_{ij}^{(1)} = \frac{1}{2}\sum\limits_{m = 0}^\infty {\left( {\begin{array}{*{20}{c}} { - \frac{5}{2} + m - 1} \\m \\\end{array} } \right)} {{\left( { - 4{R_{{X_C}{X_C}_ i,j}}} \right)}^{m + 1}}\alpha_i^{\left( {m,\left( {3 + 2m} \right)/2} \right)}\alpha_j^{\left( {m + 1,\left( {5 + 2m} \right)/2} \right)},} \\{s_{ij}^{(2)} = \frac{1}{2}\sum\limits_{m = 0}^\infty {\left( {\begin{array}{*{20}{c}} { - \frac{5}{2} + m - 1} \\m \\\end{array} } \right)} {{\left( { - 4{R_{{X_C}{X_C}_ i,j}}} \right)}^{m + 1}}\alpha_i^{\left( {m + 1,\left( {5 + 2m} \right)/2} \right)}\alpha_j^{\left( {m,\left( {3 + 2m} \right)/2} \right)},} \\{s_{ij}^{(3)} = \frac{1}{2}\sum\limits_{m = 0}^\infty {\left( {\begin{array}{*{20}{c}} { - \frac{5}{2} + m - 1} \\m \\\end{array} } \right)} {{\left( { - 4{R_{{X_C}{X_C}_ i,j}}} \right)}^{m + 2}}\alpha_i^{\left( {m + 1,\left( {5 + 2m} \right)/2} \right)}\alpha_j^{\left( {m + 1,\left( {5 + 2m} \right)/2} \right)}.} \\\end{array} $$