A Versatile Iterative Framework for the Reconstruction of Bandlimited Signals from Their Nonuniform Samples

Abstract

In this paper, we study a versatile iterative framework for the reconstruction of uniform samples from nonuniform samples of bandlimited signals. Assuming the input signal is slightly oversampled, we first show that its uniform and nonuniform samples in the frequency band of interest can be expressed as a system of linear equations using fractional delay digital filters. Then we develop an iterative framework, which enables the development and convergence analysis of efficient iterative reconstruction algorithms. In particular, we study the Richardson iteration in detail to illustrate how the reconstruction problem can be solved iteratively, and show that the iterative method can be efficiently implemented using Farrow-based variable digital filters with few general-purpose multipliers. Under the proposed framework, we also present a completed and systematic convergence analysis to determine the convergence conditions. Simulation results show that the iterative method converges more rapidly and closer to the true solution (i.e. the uniform samples) than conventional iterative methods using truncation of sinc series.

1 Introduction

According to the Shannon sampling theorem [1], a continuous-time (CT) signal can be exactly reconstructed from its uniform discrete-time (DT) samples if the signal is bandlimited and the sampling frequency is greater than twice the signal bandwidth. While a similar result for nonuniform samples exists, the operations involved are far more complicated than the uniform case. Conventionally, the reconstruction of the CT signal given its nonuniform samples is to first recover the uniform samples and then invoke the sampling theorem to reconstruct the original CT signal.

Nonuniform sampling appears in many applications such as signal, speech and video processing, high-speed data converters, and power spectral estimation, etc. For the special case of M-periodic nonuniform sampling, the uniform DT signal reconstruction is particularly important for the timing mismatch correction in time-interleaved (TI) analog-to-digital converters (ADCs) [2]. Conventionally, this problem is usually analyzed and represented using the concept of perfect reconstruction filter bank because of the periodic nonuniform sampling pattern [3–5]. However, when the sampling pattern changes during operation, say due to component variations, the synthesis filter bank has to be redesigned to compensate for the new pattern. To overcome this problem, sophisticated digital filters, namely multivariate polynomial impulse response time varying FIR filters, has been proposed to implement the tunable synthesis filter bank [6–8]. Since the response of the synthesis filter bank can be adjusted to cope with the changing pattern, online filter design is not required. However, this approach is only limited to small number of channels and small range of time-skew errors. Moreover, the design and implementation complexities of the tunable synthesis filter bank would grow rapidly with the number of channels.

On the other hand, alternate reconstruction methods that do not involve the filter bank structure exist for various classes of nonuniformly sampled signals. In general cases where the sampling pattern is nonperiodic, the filter bank structure cannot be applied directly, as it is only applicable to the periodic sampling case with fixed timing mismatch. Iterative methods such as [9–11] were commonly used for the recovery of nonperiodically sampled signals. However, the implementation complexities of these approaches are generally higher than those of filter banks because of its iterative nature and large number of multiplications involving all or a large batch of samples in order to achieve high reconstruction accuracy. This makes them less attractive in real-time applications such as TI ADCs. Another disadvantage of these approaches is the ill-conditioned system matrix formed by the truncated sinc series, which results in low convergence rate and thereby raising the implementation cost. Another interesting approach without using the filter bank structure was reported in [12]. Based on the Taylor series approximation of the nonuniform samples, a detailed analysis of the reconstruction error showed that the reconstruction performance can be improved by cascading several stages of approximation. This leads to a multi-stage differentiator-cascade multiplier (DMC) structure, which consists of linear-phase FIR differentiators and few time-varying multipliers. Two major advantages of this approach are that its implementation complexity is independent of the number of channels, and it is not restricted to signal reconstruction in periodic nonmuinform sampling, when comparing with conventional filter bank structures.

In the paper, we propose a versatile framework for the development of iterative methods and structures to solve the reconstruction problem of uniform samples from nonuniform samples of a bandlimited signal. As will be illustrated in Section 3, this problem can generally be viewed as solving a system of linear equations with infinite dimension. An important difference between the proposed approach and conventional iterative methods in [9–11] using the truncated sinc series is that the ideal response is only approximated in the frequency range of interest, i.e. the signal bandwidth. Consequently, the only mild assumption is that the signal is slightly oversampled. This approximation not only improves considerably the condition of linear system and convergence of iterations, but also leads naturally to practical implementation because the interpolation involving the sinc series can now be well approximated by a fractional delay digital filter (FDDF). Also, by exploiting the diagonal dominance of the linear system, an efficient iterative framework is developed to recover the uniform samples iteratively. The usefulness of the proposed framework is demonstrated by studying in detail an efficient iterative method called Richardson iteration (RI) [13]. Unlike the block-based iterative methods in [9–11], the proposed iterative method can be realized in a sample-by-sample manner so as to further reduce computational costs. Moreover, the proposed framework provides a general form for solving the reconstruction problem using iterative methods, which greatly extends the previous works in [9–11]. Based on this framework, extension to other iterative methods such as Jacobi iteration, Gauss-Seidel iteration and successive over relaxation algorithms is also possible. A preliminary study on the former two algorithms was briefly presented in [14]. For simplicity, only the RI is considered in this paper.

To ensure the convergence of the iterative algorithm, we studied in detail its convergence conditions and found that it is independent of the input signal spectrum. Therefore, bounds and conditions for convergence can be pre-determined numerically according to the given bounds of the timing mismatch errors. In most applications, these conditions should be readily satisfied. Design results show that the proposed iterative method closely converges to the true solution (i.e. the uniform samples) with faster convergence rate and higher accuracy than conventional iterative methods.

By further examining the structure of the linear system, we found that the operations involved can be viewed as processes of convolution and hence digital filtering. We also found that these processes can be efficiently implemented by the Farrow-based variable digital filter (VDF) [15, 16]. Important advantages of the proposed structure are that the VDF coefficients can be varied online cope with possibly changing timing jitters, and more importantly it can be implemented in hardware without any multiplications, apart from a limited number of multipliers required to implement the tuning variables [17].

Another interpretation of the proposed approach is that it measures the estimation error between the given nonuniform samples and those computed by VDF so as to iteratively recover the desired uniform samples. When it is applied to the timing mismatch correction in TI ADCs, more savings in hardware costs can be achieved over conventional filter bank methods [3–8], as the implementation complexity of the overall iterative procedure is independent of the number of channels. Compared to multivariate polynomial FIR filters in [6–8], the VDF has much lower dimensionality and hence implementation complexity since it is just a bivariate polynomial FIR filter. Apart from the important advantages of avoiding online filter design and multiplier-less realization, the proposed iterative algorithm is applicable to both periodic nonuniform sampling in TI ADCs, and general nonuniform sampling. Finally, we note that the approach in [12] can also be viewed as a simplified implementation of the proposed RI method. More specifically, the proposed approach provides a new framework for the development and convergence analysis of more efficient iterative reconstruction algorithms.

The paper is organized as follows: Section 2 describes sampling theorem and the problem of signal reconstruction for nonuniform sampling. The linear model and iterative framework for signal reconstruction from nonuniform samples are then presented in Section 3. Section 4 is devoted to the realization of the fractional delay operation in the linear model using VDFs. Efficient implementation of the iterative methods using Farrow structure is also discussed. The convergence conditions of the proposed iterative algorithm are studied in Section 5. Comparisons with other conventional methods are given in Section 6. Finally, conclusion is drawn in Section 7.

2 Background

Suppose that we have a bandlimted continuous-time (CT) signal x _c (t) with maximum frequency f _max. The sampling theorem states that x _c (t) can be exactly recovered from its uniform samples, x[n] = x _c (nT), if the sampling rate f _s is greater than the Nyquist rate 2f _max. More precisely, x _c (t) can be reconstructed from x[n] as follows

$$ {x_c}(t) = \sum\limits_{k = - \infty }^\infty {x\left[ k \right] \cdot {\hbox{sinc}}\left( {\frac{{t - kT}}{T}} \right)}, $$

(1)

where $T = 1/{f_s}$ is the sampling interval. Figure 1a shows the uniform sampling of x _c (t), where x[n] is obtained by sampling the signal at regular interval using an ADC. On the other hand, if x _c (t) is nonuniformly sampled as depicted in Figure 1b, where the discrete-time sequence y[n] is defined by y[n] = x _c (nT−α _n T) for $\left| {{\alpha_n}} \right| \leqslant 0.5$, it is desirable to reconstruct x[n] from y[n] since most processing algorithms and display systems are designed to work with uniformly spaced samples. While the solution of such reconstruction problem is not trivial, its reverse problem (i.e. to compute y[n] from x[n]) is frequently encountered and has been well studied in sampling rate conversion [17–19]. In what follows, we shall briefly review the reverse problem. Later, we shall show that the result so obtained can be employed to solve the original uniform sample reconstruction problem in an iterative manner.

Figure 1

Illustration of a uniform and b nonuniform sampling.

The nonuniform sequence y[n] can be expressed in terms of x[n] using (1) as follows

$$ y\left[ n \right] = {x_c}\left( {nT - {\alpha_n}T} \right) = \sum\limits_{k = - \infty }^\infty {x\left[ k \right] \cdot {\hbox{sinc}}\left( {n - {\alpha_n} - k} \right)}, \forall n. $$

(2)

If α _n is given, then y[n] can be seen to be a delayed version of the uniform sequence x[n]. From (2), the discrete-time impulse response of this fractional delay operation can be expressed as

$$ {h_{ideal}}\left[ {{n_0},\alpha } \right] = {\hbox{sinc}}\left( {{n_0} - \alpha } \right),{n_0} = ..., - 1,0,1,..., $$

(3)

and the discrete-time Fourier transform (DTFT) of h _ideal [n,α] is

$$ {H_{ideal}}\left( {{e^{j\omega }},\alpha } \right) = {e^{ - j\omega \alpha }},\omega \in \left[ { - \pi, \pi } \right]. $$

(4)

As seen in (3), it is impossible to realize this ideal delay operation since it has an impulse response with infinite length. Therefore, appropriate approximation to h _ideal [n ₀,α] has to be considered.

In [9–11], the infinite sinc series are truncated directly to approximate the ideal fractional delay operation in (3). However, due to the slow decay of the sinc function, the truncation error for the approximation would be substantial. As a common practice, it is usually assumed that the CT signal x _c (t) is slightly oversampled, and hence the DTFT of x[n] is zero for $\kappa \pi \leqslant \left| \omega \right| \leqslant \pi$, 0 < κ < 1. This assumption allows us to relax the specification of H _ideal [e   ^jω,α] to

$$ {H_{ideal}}\left( {{e^{j\omega }},\alpha } \right) = {e^{ - j\omega \alpha }},\omega \in \left[ { - \kappa \pi, \kappa \pi } \right]. $$

(5)

Let h[n ₀,α] be the corresponding approximation of the ideal impulse response h _ideal [n ₀,α]. Assume that the frequency response of h[n ₀,α] is designed to approximate H _ideal [e   ^jω,α] in the frequency band of interest, then Eq. 2 can be written as

$$ y\left[ n \right] \approx \sum\limits_{k = n - {N_{h2}}}^{n + {N_{h1}}} {x\left[ k \right] \cdot h\left[ {n - k,{\alpha_n}} \right]}, $$

(6)

where, N _h1 and N _h2 are positive integers. When both N _h1 and N _h2 are finite, h[n ₀,α] can be realized as a FIR filter parameterized by the fractional delay parameter α _n . On the other hand, if N _h1 and/or N _h2 are infinite, h[n ₀,α] may alternatively be realized as an IIR filter. For simplicity, we will mainly focus on the FIR case in the rest of the paper.

3 Versatile Iterative Framework for the Reconstruction of Signals from Nonuniform Samples

3.1 Linear Model for the Reconstruction of Uniform Signals

Consider the matrix form of (6):

$$ {\mathbf{y}} = {\mathbf{Ax}}, $$

(7)

where ${\mathbf{y}} = {\left[ {y\left[ { - \infty } \right], \cdots, y\left[ \infty \right]} \right]^T}$, ${\mathbf{x}} = {\left[ {x\left[ { - \infty } \right], \cdots, x\left[ \infty \right]} \right]^T}$ and ${\left[ {\mathbf{A}} \right]_{n,k}} = {a_{n,k}} = h\left[ {n - k,{\alpha_n}} \right]$, for $n,k = \cdots, - 1,0,1, \cdots$. The problem at hand is to recover the uniform sequence x, given its nonuniform counterpart y. In other words, we want to solve the system of linear equations in (7). For the sake of presentation, {y[n]} and {x[n]} are assumed to be discrete signals with finite and sufficiently large number of samples N for $n = 0,1, \cdots, N - 1$. Thus, y and x now become (N × 1) vectors and A is a (N × N) matrix. Also, h[n ₀,α _n ] is assumed to be noncausal. For practical implementation, it can be easily made causal by introducing appropriate delays.

From the discussion in Section 2, the following characteristics of the matrix A are readily observed: (i) With the assumption that α _n ∈(−0.5,0.5), A is nonsingular. (ii) A is effectively a banded matrix because h[n ₀,α _n ] is only nonzero for n ₀<−N _h1 and n ₀>N _h2. (iii) Since h[n ₀,α _n ] tends to zero as |n ₀| increases, the absolute values of diagonal elements of A are always greater than those of other off-diagonal elements. For small α _n , A may be a diagonally dominant matrix (i.e. $\left| {{a_{n,n}}} \right| > \sum\nolimits_{n \ne k} {\left| {{a_{n,k}}} \right|}$, for all n).

3.2 Iterative Framework for Solving the Linear System

For high-speed applications, directly inverting A to find x is undesirable due to very high arithmetic complexity. Because of the diagonally dominant nature of A, it is more efficient to determine x using iterative methods. A number of iterative methods have been studied in the literature (see [13] and references therein). For efficient implementation, methods that can be realized in a sample-by-sample manner are particularly attractive. Most of them take the form of

$$ {{\mathbf{x}}^{\left( {m + 1} \right)}} = {\mathbf{G}}{{\mathbf{x}}^{(m)}} + {\mathbf{f}}, $$

(8)

where G and f are derived from A and y, and x ^(m) denotes the solution in the m-th iteration. Eq. 8 provides the general form for solving the reconstruction problem using iterative methods, which greatly extends the previous works in [9–11]. The next step is to consider the partitioning of A to form G.

As an illustration, we define a simple decomposition as ${\mathbf{G}} = {\mathbf{I}} - \mu {\mathbf{A}}$ and f = μ y for some scalar μ. Then, an efficient iterative method can be written as:

$$ {x^{\left( {m + 1} \right)}}\left[ n \right] = {x^{(m)}}\left[ n \right] + \mu \left( {y\left[ n \right] - \sum\limits_{k = n - {N_{h2}}}^{n + {N_{h1}}} {{x^{(m)}}\left[ k \right] \cdot h\left[ {n - k,{\alpha_n}} \right]} } \right),n = 0, \cdots, N - 1, $$

(9)

which is known as Richardson iteration (RI). Alternatively, based on the versatile framework in (8), other iterative methods such as Jacobi iteration, Gauss-Seidel iteration and successive over relaxation can also be used. For simplicity, we only focus on the RI. Intuitively, it can be seen from the RI that the term inside the bracket represents the error between the given nonuniform samples and those computed by means of FDDF with delay α _n . This forms the basis for solving the reconstruction problem according to its inverse problem, where a signal is delayed digitally.

It should also be noted that the iterative method studied in [9–11] is similar to the RI, where the system matrix entries of A in (6) are otherwise given by ${a_{n,k}} = {\hbox{sinc}}\left( {n - k - {\alpha_n}} \right)$, $n,k = 0,1 \cdots, N - 1$. Consequently, the matrix entries would always be nonzero for α _n ≠ 0. In this case, multiplications with all samples or a large batch of samples are required to recover one uniform sample. Therefore, the implementation cost depends on the number of samples, making them less attractive in real-time applications such as TI ADCs. Another disadvantage of these approaches is the ill-behaved system matrix formed by truncating the sinc series, which results in lower convergence rate and thereby raising the implementation cost. A comparison with the approach in [9] will be given in Section 6. In next section, we shall illustrate how these problems can be tackled using variable FDDF (VFDDF), and describe its efficient implementation using the Farrow structure [15].

4 Realization of Fractional Delay Operation

4.1 Fractional Delay Digital Filters

In this subsection, we shall discuss common approaches to approximate the ideal fractional delay operation in (6) in order to improve the convergence behaviour and reduce the implementation complexity of the proposed approach. The fractional delay operation can be realized by a FIR FDDF with fixed coefficients. A number of design techniques such as windowing method [20, 21], and convex programming [22] are available in the literature. However, this approach may not be suitable for real-time applications because h[n ₀,α _n ] in general depends on the arbitrary delays α _n .

Another efficient approach, which is able to vary the characteristics of a digital filter online, is to employ so-called variable digital filters (VDFs). In the context of FDDF, it gives rise to a class of digital filters called VFDDFs, where the required samples at fractional sampling intervals can be computed by tuning a single parameter α, also known as tuning or spectral parameter [15, 16, 18, 23, 24]. The ideal response of the VFDDF is identical to (5), where in contrast to the case of fixed filter coefficients, the tuning parameter α is assumed to vary continuously in a finite interval, say (−0.5,0.5). The basic idea to design and realize the VFDDF is to represent its impulse response as a polynomial in α:

$$ h\left[ {{n_0},\alpha } \right] = \sum\limits_{l = 0}^{L - 1} {{h_l}\left[ {{n_0}} \right]} \cdot {\alpha^l},{n_0} = - {N_{h1}}, \cdots, 0, \cdots, {N_{h2}}, $$

(10)

where L is the number of subfilters and h _l [n ₀] is the impulse response of the l-th subfilter. For more details on design techniques of VFDDFs, see [18, 23, 24].

In particular, if N _h1=N _h2=N _h for some finite positive integer N _h and h[0,α] is chosen as the center of symmetry of the impulse response when α = 0, it can be verified that h[n ₀,α] exhibits the following coefficient symmetry

$$ h\left[ {{n_0},\alpha } \right] = h\left[ { - {n_0}, - \alpha } \right],{n_0} = - {N_h}, \cdots, 0, \cdots, {N_h}. $$

(11)

For VFDDFs, it can further be shown that the impulse responses of subfilters are either symmetric or anti-symmetric if Eq. 11 is satisfied. That is

$$ {h_l}\left[ {{n_0}} \right] = {\left( { - 1} \right)^l}{h_l}\left[ { - {n_0}} \right], $$

(12)

for ${n_0} = - {N_h}, \cdots, 0, \cdots, {N_h}$ and $l = 0, \cdots, L - 1$. As a result, the implementation complexities of VFDDF can be reduced approximately by a factor of two.

Furthermore, according to (10), the z-transform of the VFDDF can be expressed as:

$$ H\left( {z,\alpha } \right) = \sum\limits_{l = 0}^{L - 1} {{H_l}(z){\alpha^l}} = \sum\limits_{l = 0}^{L - 1} {\left[ {\sum\limits_{{n_0} = - {N_{h1}}}^{{N_{h2}}} {{h_l}\left[ {{n_0}} \right]{z^{ - n}}} } \right]} {\alpha^l}, $$

(13)

where H _l (z) is the z-transform of the l-th subfilters. This gives rise to the Farrow structure as shown in Figure 2. It can be seen that the Farrow structure consists of digital subfilters with fixed coefficients and a limited number of multipliers to implement the tuning parameter α. As the coefficients of the subfilters are fixed, they can be realized using sum-of-power-of-two (SOPOT) coefficients or canonical signed digit in stead of expensive general-purpose multipliers [17, 19]. In addition, if the subfilters are implemented as their transposed form, the redundancy in realizing the multiplications of these SOPOT coefficients can be significantly reduced by means of a multiplier-block technique [25], which gives rise to minimum adder realization. In this paper, we shall mainly focus on the approximation of fractional delay operation using VFDDFs, because of their numerous advantages mentioned above.

Figure 2

Farrow structure for implementing a VDF.

4.2 Efficient Implementation Using Farrow Structure

We now consider the efficient implementation of the RI using the Farrow structure mentioned above. First of all, we rewrite the RI in (9) as

$$ {x^{\left( {m + 1} \right)}}\left[ n \right] = {x^{(m)}}\left[ n \right] + \mu {e^{(m)}}\left[ n \right],\quad n = 0, \cdots, N - 1, $$

(14)

where ${e^{(m)}}\left[ n \right] = y\left[ n \right] - {y^{(m)}}\left[ n \right]$; ${y^{(m)}}\left[ n \right] = \sum\limits_{k = n - {N_{h2}}}^{n + {N_{h1}}} {{x^{(m)}}\left[ k \right]h\left[ {n - k,{\alpha_n}} \right]}$. It can be seen the major arithmetic complexity of the RI comes from the computation of y ^(m)[n], which can be implemented by means of digital filtering with input being x ^(m)[n]. According to (10) and (14), the input/output transfer function for x ^(m)[n] and y ^(m)[n] is a VDF H _RI (z,α) which is identical to H(z,α) in (13). More precisely, y ^(m)[n] can be viewed as the output of the VDF H _RI (z,α) with appropriate values of α _n :

$$ {y^{(m)}}\left[ n \right] = \sum\limits_{l = 0}^{L - 1} {\left( {{x^{(m)}} * {h_l}} \right)\left[ n \right] \cdot \alpha_n^l}, $$

(15)

where * denotes the DT convolution. The resulting VDF-based structure for implementing the m-th iteration of the RI-based reconstruction algorithm is shown in Figure 3. Moreover, it can be pipelined to increase the throughput of the system. From a digital signal processing point of view, the RI first delays the uniform sequence x ^(m)[n] by α _n samples using the VDF H _RI (z,α), and then calculates the error e ^(m)[n] between true and approximated samples. Finally, it updates x ^(m)[n] to obtain x ^(m+1)[n] until the error is sufficiently small or the maximum number of iterations is reached.

Figure 3

VDF-based corrector in the form of the m-th Richardson iteration.

5 Convergence Analysis

An important aspect of iterative method is the conditions for convergence. It is well known that the iteration in (8) converges for any f and x ⁽⁰⁾ iff the spectral radius of G, ρ(G), is less than one. However, due to large N and time-varying parameter α _n (and hence A) in general, it is difficult to derive a necessary and sufficient condition based on the spectral radius of G. Therefore, sufficient conditions that guarantee convergence will be considered below.

By using the fact that $\rho \left( {\mathbf{G}} \right) \leqslant \left\| {\mathbf{G}} \right\|$ for any matrix norm, it is sufficient to show that the RI-based algorithm converges for any f and x ⁽⁰⁾ iff $\left\| {\mathbf{G}} \right\| < 1$ [13]. To determine the conditions for the convergence of the RI, the infinity norm is considered below

$$ \begin{gathered} {\left\| {{{\mathbf{G}}_\mu }} \right\|_\infty } = {\left\| {{\mathbf{I}} - \mu {\mathbf{A}}} \right\|_\infty } \\= \mathop {{\max }}\limits_{0 \leqslant n \leqslant N - 1} \left\{ {\sum\limits_{k = 0}^{N - 1} {\left| {{\delta_{n,k}} - \mu \cdot {a_{n,k}}} \right|} } \right\} \\= \mathop {{\max }}\limits_{0 \leqslant n \leqslant N - 1} \left\{ {\sum\limits_{{n_0} = - {N_{h1}}}^{{N_{h2}}} {\left| {{g_\mu }\left[ {{n_0},{\alpha_n}} \right]} \right|} } \right\}, \\\end{gathered} $$

where ${g_\mu }\left[ {0,{\alpha_n}} \right] = 1 - \mu h\left[ {0,{\alpha_n}} \right]$ except ${g_\mu }\left[ {{n_0},{\alpha_n}} \right] = - \mu h\left[ {{n_0},{\alpha_n}} \right]$ for n ₀ ≠ 0. Therefore, it is natural to define the cost function representing the upper bound of ${\left\| {{{\mathbf{G}}_\mu }} \right\|_\infty }$ for a given maximum value of α _n :

$$ C\left( {\mu, {\alpha_{\max }}} \right) = \mathop {{\max }}\limits_{\left| \alpha \right| \leqslant {\alpha_{\max }}} \left\{ {\sum\limits_{{n_0} = - {N_{h1}}}^{{N_{h2}}} {\left| {{g_\mu }\left[ {{n_0},\alpha } \right]} \right|} } \right\}, $$

(16)

where α _max denotes the maximum absolute time-skew error given by $\max \left\{ {{ }\left| {{\alpha_n}} \right|{ }} \right\}$. To ensure the fastest convergence, we want to find μ for a given α _max such that C(μ,α _max) is minimized. Since the subfilter coefficients of a given VFDDF is pre-determined, the conditions for convergence can be analyzed numerically by considering the values of μ and α _max that minimize C(μ,α _max). Instead of directly evaluating the 2-D function in (16), we further define the following cost functions to simplify the analysis:

$$ {C_1}\left( \mu \right) = \mathop {{\min }}\limits_{{\alpha_{\max }}} \left\{ {C\left( {\mu, {\alpha_{\max }}} \right)} \right\}; $$

(17)

$$ {C_2}\left( {{\alpha_{\max }}} \right) = \mathop {{\min }}\limits_\mu \left\{ {C\left( {\mu, {\alpha_{\max }}} \right)} \right\}; $$

(18)

$$ {C_3}\left( {{\alpha_{\max }}} \right) = \arg \mathop {{\min }}\limits_\mu \left\{ {C\left( {\mu, {\alpha_{\max }}} \right)} \right\}. $$

(19)

Also, in order for the RI to converge, the upper bounds of C(μ,α _max), C ₁(μ) and C ₂(α _max) should be less than one. Using these results, we can obtain useful information regarding: (i) the range of μ that guarantees convergence according to (17), (ii) the smallest value of C ₂(α _max)(or more appropriately the fastest rate of convergence) for a given α _max according to (18), and (iii) the value of μ that ensures the fastest convergence for a given α _max according to (19).

As an illustration, suppose that a VFFDF have been designed using the approach in [18] with the following specifications: filter order ${N_{h1}} = {N_{h2}} = {N_h} = 35$, number of subfilters L = 4, ω∈[−0.9π,0.9π], and α∈[−0.2,0.2]. Since the maximum absolute timing offset α _max is typically small, a range of α∈[−0.2,0.2] is sufficient for most applications. For example, α _max is around few percents of the sampling period in the case of TI ADCs. Figure 4 shows the magnitude and group delay responses of the VFDDF, which approximates h[n ₀,α] for different values of α. Because of the real-valued filter coefficients, the responses are only shown for ω∈[0,π]. The corresponding maximum passband and group delay errors are respectively 6.04 × 10⁻⁵ and 1.14 × 10⁻³.

Figure 4

a Frequency and b group delay responses of a VFDDF. The design parameters are as follows: filter order 2N _h  = 70, number of subfilter L = 4, ω∈[−0.9π,0.9π], and α∈[−0.2,0.2].

Given the VFDDF designed earlier, Figure 5a–d show respectively the cost functions in (16–19) with μ∈[−3,3] and α _max∈[−0.2,0.2]. Note due to coefficient symmetry in (11), it suffices to consider α _max∈[0,0.2] only. In particular, Figure 5b reveals that ${\left\| {{{\mathbf{G}}_\mu }} \right\|_\infty }$ is smaller than one (i.e. the RI converges) if μ lies in the interval (0,2). Two cases μ = 0 and μ = 2 are excluded because ${\left\| {{{\mathbf{G}}_\mu }} \right\|_\infty } = 1$ in either case violates the sufficient condition. Figure 5c shows that faster rate of convergence is achieved for smaller α _max. Also, it can be seen that when α _max exceeds 0.16, the sufficient condition is violated because ${\left\| {{{\mathbf{G}}_\mu }} \right\|_\infty } \geqslant 1$. In this case, the RI may not converge. Finally, Figure 5d shows the value of μ for which the rate of convergence is the fastest. It can be seen that the best value of μ is very close to one.

Figure 5

Cost functions defined for the Richardson iteration with μ∈[−3,3] and α _max∈[0,0.2]: a C in (16), b C ₁ in (17), which determines the range of μ that guarantees convergence, c C ₂ in (18), which determines the fastest rate of convergence for a given α _max, and d C ₃ in (19), which determines the value of μ that ensures the fastest rate of convergence for a given α _max.

From the numerical results shown above, the convergence is guaranteed when α _max is less than 0.16 samples, although the VFDDF designed in this example is capable of supporting a fractional delay α up to ±0.2 samples. This illustrates the fact that the range of support for α is independent of that for α _max. With the help of computer simulations, the latter should relate to the passband width of the VFDDF and hence the amount of oversampling. Generally, the wider the passband width of the VFDDF, the smaller the value of α _max it can support. Therefore, for a smaller α _max, another VFDDF with wider bandwidth can be employed so that the amount of oversampling can be reduced.

6 Design Examples

To demonstrate the effectiveness of the proposed iterative algorithm, a test signal given by $\sum\nolimits_{k = 1}^{10} {\cos \left[ {nk\left( {0.09\pi } \right)} \right]}$, $n = 0,1 \cdots, N - 1$, is considered. The total number of samples is N = 1000. The VFDDF in Figure 4 is employed to implement the proposed iterative algorithms. The initial guess is set as the given nonuniform sequence, i.e. x ⁽⁰⁾ = y. The reconstruction performance is assessed using the signal to noise and distortion ratio (SNDR) as follows:

$$ SNDR = \frac{{{{\left\| {\mathbf{x}} \right\|}^2}}}{{{{\left\| {{\mathbf{x}} - {{\mathbf{x}}^{(m)}}} \right\|}^2}}}, $$

(20)

where $\left\| \cdot \right\|$ denotes the Euclidean norm. Note, to avoid the transient responses at either end of the sequences, only the middle 800 samples are used to evaluate SNDRs. The timing mismatch error α _n is randomly chosen in the interval (−α _max, α _max). The parameter μ in the RI is chosen as 1.05 according to the convergence analysis in Section 5. Figure 6a–c show the performances of the RI for α _max = 0.05, α _max = 0.1 and α _max = 0.15, respectively. It can be seen that the RI converges to slightly different SNDRs for different α _max because the error between the VFDDF and the ideal one in (5) depends on the values of frequency and tuning parameter.

Figure 6

a–c Performances of various iterative methods for the cases α_max = 0.05, α_max = 0.1 and α_max = 0.15, respectively. The proposed iterative algorithm is based on the VFDDF with α∈[−0.2,0.2].

Generally, the SNDR will improve with (i) increased filter order (ii) increased number of subfilters, (iii) reduced passband width, and (iv) reduced tuning range of the VFDDF. To illustrate the idea, we have designed another VFDDF with the same design parameters except that α∈[−0.1,0.1]. The corresponding maximum passband and group delay errors are 4.04 × 10⁻⁶ and 1.27 × 10⁻⁴, respectively. Repeating the experiments using the VFDDF so obtained, it can be seen from Figure 7a and b that the SNDR is improved by about 25 dB for α _max = 0.05 and α _max = 0.1. However, the range of support is reduced from α∈[−0.2,0.2] to α∈[−0.1,0.1].

Figure 7

Performances of various iterative methods for the cases a ϕ _max = 0.05 and b ϕ _max = 0.1. The proposed iterative algorithm is based on the VFDDF with ϕ∈[−0.1,0.1].

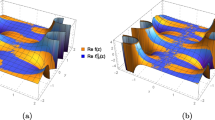
As a comparison, the iterative algorithm in [9] was considered. The above experiments are repeated and the corresponding SNDRs are shown as dash lines in Figures 6 and 7. In all cases, its SNDRs and the convergence rates are worse than the proposed algorithm. The poorer performance of the iterative algorithm in [9] is largely attributed to the ill-behaved system matrix formed by truncating the sinc series. Also, as mentioned in Section 2, its implementation complexity depends on the number of samples, which may be the reason why the conventional iterative algorithms are somehow overlooked in real-time applications. On the other hand, according to the above detailed discussions, several potential advantages of the proposed iterative algorithm over the conventional ones are summarized as follows. First, it works for infinite number of samples. Second, its implementation complexities in each iteration depend on the length of VFDDFs rather than the total number of samples. Third, it can be efficiently implemented using well known Farrow structure. Last but not least, their convergence conditions are well developed and can be pre-determined.

Besides, under the same experimental settings, we also carried out another comparison with the approach in [12], which employs a multi-stage differentiator-multiplier cascade (DMC) structure to perform reconstruction of nonuniformly sampled signals. In this approach, error samples are first approximated by Taylor series expansion of a given nonuniform signal, and are then used to refine the accuracy of the reconstructed uniform samples stage-by-stage. Also, the authors suggested that the order of Taylor series expansion should increase with the number of stages. It is worth mentioning that the DMC structure in the l-th stage can also be implemented using Farrow structure with (l + 1) subfilters [26]. The relation is given by ${H_k}(z) = {{{{\left[ { - G(z)} \right]}^k}} \mathord{\left/{\vphantom {{{{\left[ { - G(z)} \right]}^k}} {k!}}} \right.} {k!}}$, for $k = 0,1 \cdots, l$, where G(z) is a first-order differentiator, and the delay term is ignored for simplicity Eq. 11 in [26]. To make a fair comparison, a three-stage DMC structure considered in [12] is implemented using a FIR differentiator with a filter length of 101 and a cutoff frequency of 0.9π, and the VFDDF we used is derived by this differentiator according to [26] and consists of four FIR subfilters. Figure 8 shows the simulation results obtained using the proposed iterative algorithms and the three-stage DMC structure with α _max = 0.05, α _max = 0.1 and α _max = 0.15. We can see that the RI has higher reconstruction accuracy than the DMC structure. The reason is due to the fact that the DMC structure in principle uses a lower order Taylor series expansion at the earlier stages and hence more reconstruction error would be introduced. Moreover, after a careful examination, the DMC structure may be regarded as a simplification of the RI because the latter has a third-order Farrow structure in each iteration or stages and an additional convergence parameter μ. On the other hand, the DMC structure has a lower implementation complexity than the RI method at the expense of slightly reduced reconstruction accuracy. In summary, the proposed approach can be viewed as a generalization of the approach in [12], covering a more flexible and versatile basis for the extension of more efficient iterative reconstruction algorithms such as Jacobi iteration, Gauss-Seidel iteration and successive over relaxation. Interested readers are referred to [14] for a preliminary study of the former two algorithms. Also, thanks to the well developed theoretical results of the iterative methods, we can easily provide a more completed and systematic convergence analysis under the proposed framework.

Figure 8

Comparison with a three-stage DMC structure in [12].

7 Conclusion

A versatile iterative framework for the recovery of uniform samples from nonuniform samples of bandlimited signals has been presented. While extension to other iterative methods of similar form such as Jacobi iteration, Gauss-Seidel iteration and successive over relaxation is possible, the Richardson iteration has been studied in detail to illustrate how the uniform samples can be efficiently reconstructed by iteratively solving the system of linear equations with the mild assumption that the input signal is slightly oversampled. Moreover, since the proposed iterative method can be efficiently realized using Farrow-based variable digital filters, the entire iterative procedure can be implemented without any multiplications, apart from the limited number of multipliers in the Farrow structure. Furthermore, convergence conditions have been investigated, and they should be readily satisfied in most applications. Simulation results showed that the proposed method has better performance than conventional iterative methods. An important application of the proposed approach is the timing mismatch correction in TI ADCs.