Abstract
We propose a method for eliminating the temporal illumination variations in whisk-broom (point-scan) hyperspectral imaging. Whisk-broom scanning is useful for acquiring a spatial measurement using a pixel-based hyperspectral sensor. However, when it is applied to outdoor cultural heritages, temporal illumination variations become an issue due to the lengthy measurement time. As a result, the incoming illumination spectra vary across the measured image locations because different locations are measured at different times. To overcome this problem, in addition to the standard raster scan, we propose an additional perpendicular scan that traverses the raster scan. We show that this additional scan allows us to infer the illumination variations over the raster scan. Furthermore, the sparse structure in the illumination spectrum is exploited to robustly eliminate these variations. We quantitatively show that a hyperspectral image captured under sunlight is indeed affected by temporal illumination variations, that a Naïve mitigation method suffers from severe artifacts, and that the proposed method can robustly eliminate the illumination variations. Finally, we demonstrate the usefulness of the proposed method by capturing historic stained-glass windows of a French cathedral.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Over the last two decades, hyperspectral imaging has been gaining attention in the field of cultural heritage for studying artworks (Morimoto et al., 2008; 2010; Cucci and Casini 2020). Hyperspectral imaging provides a spectrum at each pixel in the image of a scene, providing rich color information of the scene. Much progress has been made in both hyperspectral imaging devices (Shmilovich et al. , 2020) and their applications, such as photogrammetry (Mathys et al. , 2019), pigment recognition (Cucci et al. , 2011), and painting analysis (Cucci et al. , 2013). Many of the applications require high spectral-resolution (2 nm bins or even shorter, according to (Cucci et al. , 2013). However, hyperspectral imaging requires a long measurement time with careful light calibration (Pillay et al. , 2019), which limits its applicability to on-site measurements of historic buildings and artifacts, particularly for challenging subjects, such as stained-glass windows (Babini et al. , 2020).
In this paper, we aim to achieve a high spectral-resolution hyperspectral imaging method under natural illumination for digital preservation and analysis of cultural assets, with a particular focus on stained-glass windows of cathedrals (Fig. 1). Some of these windows have been there since their establishments, while others are said to have been broken and later restored. Although 3-color RGB information is insufficient for distinguishing these differences, spectral information is expected to provide new clues for historians and archaeologists to inspect the windows and investigate the history of the cathedrals.
There are a few technical difficulties that arise in the hyperspectral measurement of stained-glass windows. Unlike paintings, stained-glass windows are transmissive, and their reflectances are weak and less informative than the transmittances. As with many other cultural heritages, they are firmly installed in a building; therefore it is undesirable to detach the windows from the building. These constraints restrict the measurement to be conducted from inside the building. On the other hand, the benefit is that natural sunlight can be utilized as an illumination source, which has a broad range of spectrum. Under this setting, it is preferred to use a snapshot approach, which can record a hyperspectral image in one shot, because it can neglect temporal illumination variations. Unfortunately though, existing snapshot approaches are limited in spatial resolution as they map three dimensional spatial-spectral information into a two-dimensional sensor array. Scanning-based approaches can address the issue of spatial resolution; however, they require lengthy measurement times, naturally suffer from the temporal illumination variations. Although capturing a reference object under the illumination during the scanning helps to compensate for the variations, direct measurement of the illumination spectrum is difficult from inside the building.
To overcome the problem of both spatial resolution and temporal illumination variations, this paper proposes a whisk-broom hyperspectral imaging method that compensates the unknown temporal illumination variations. Our method can capture a few thousand spectral channels with a spectral resolution of less than 1 nm for the visible and near-infrared bands (400–2500 nm) with angular (or spatial) resolution of \({0.010}^{\circ }\) at maximum. At the heart of the method, we propose the use of extra single scan that perpendicularly traverses the whisk-broom scans. We show that this extra scan allows us to infer the temporal illumination variations in the whisk-broom scans. In addition, we introduce a method for robustly eliminating the temporal illumination variations by exploiting the sparse structure in illumination spectra. As a result, our method allows capturing high spatial and spectral resolution images by effectively eliminating the temporal illumination variations during the scan. The chief contributions of this work are as follows:
-
We introduce a scanning strategy for eliminating the temporal illumination variations during the whisk-broom scanning for hyperspectral imaging with high spatial and spectral resolutions.
-
We develop a robust method against numerical instability caused by noise for eliminating the temporal illumination variations by exploiting the sparse structure of illumination spectra.
-
Effectiveness of the proposed method is demonstrated by recording the actual strained-glass windows in a French cathedral in addition to evaluation using a public dataset.
2 Related work
2.1 Hyperspectral imaging
Hyperspectral imaging devices are grouped into four main categories: Snapshot imaging spectrometers (Hagen & Kudenov, 2013), wavelength-scanning systems (Gat , 2000), point-scanning systems, and line-scanning systems.
Recent studies using diffractive optics have described snapshot approaches that are free from the effects of illumination changes. Baek et al. (2017) proposed a compact snapshot imaging system using a conventional digital single-lens reflex (DSLR) camera and a prism. This method exploits spectral information obtained from dispersion over edges in a scene and computationally reconstructs the full hyperspectral image of the scene. They demonstrated a reconstruction of a spectral cube with \(860\times 600\times 23\) spatial and spectral resolution in the 430–650 nm. Jeon et al. (2019) presented a compact, diffraction-based snapshot hyperspectral imaging method. They introduce a novel diffractive optical element (DOE) design that generates an anisotropic shape for the spectrally varying point-spread function (PSF), where the PSF shape rotates as the wavelength of light changes, while its size remains virtually unchanged. They also adopted an end-to-end network for spectral reconstruction. This method was able to perform hyperspectral imaging with \(1440\times 960\times 25\) spatial and spectral resolution with a fabricated DOE attached to a DSLR sensor. Hauser et al. (2020) presented a deep learning-based technique for the reconstruction of a spectral cube measuring \(256\times 256\times 29\) in the 420–700 nm visible spectral range from dispersed and diffused (DD) monochromatic snapshots captured by a single monochromatic camera equipped with a 2-D separable, binary phase diffuser. Dun et al. (2020) presented a joint learning algorithm with a diffractive achromats design and an image recovery neural network.
Spectral filters are also used for snapshot hyperspectral imaging. Hu et al. (2019) proposed a multispectral video acquisition method for dynamic scenes that uses a spectral-sweep camera, which is composed of a monochromatic camera and a synchronized liquid crystal tunable filter. Monakhova et al. (2020) proposed a lensless imaging system with a 64-channel spectral filter array spanning the 386–898 nm range and a randomized phase mask, allowing to recover close to the full spatial resolution of the sensor. This approach enables a flexible design in which either contiguous or noncontiguous spectral filters with user-selected bandwidths can be chosen; however, the spectral resolution fully depends on the spectral filter array and cannot achieve many, say thousands of, bands.
For compressive imaging architectures with coded aperture snapshot spectral imaging (CASSI) (Gehm et al. , 2007; Wagadarikar et al. , 2008; Lin et al. , 2014), hyperspectral image reconstruction algorithms using deep learning methods (Choi et al. , 2017; Miao et al. , 2019; Meng et al. , 2020) have been proposed. The above techniques can capture images with up to 100 channels, mostly at approximately 10 nm spectral resolution. There exists some limitations in the optics and sensors for obtaining the snapshot and they essentially result in a trade-off between spatial-spectral resolutions. Our study aims to capture a spectral image with thousands of channels at less than 1 nm resolution, which would be beneficial for pigment analysis (Cucci et al. , 2011). We captured a spectral cube with 1600 bands in 400–1100 nm spectral range from stained glasses.
Wavelength- and line-scanning systems use a scanning mechanism to capture additional dimensions. A typical wavelength-scanning system uses a tunable filter whose spectral transmission can be electronically controlled (Gat , 2000). It has many advantages in terms of cost, compactness, and operability; however, wavelength-scanning systems usually have coarse spectral resolutions (\(\sim \)10 nm) due to their broad bandwidth. Compressive sensing approaches have also been proposed for this architecture. Wang et al. (2018) proposed a coded aperture tunable filter spectral imager, which is capable of compressive sensing on both the spatial and spectral domains, and produced a reconstructed image with \(400\times 400\) spatial resolution and 170 spectral bands from a measurement with 25 different coded aperture patterns and 22 spectral bands for the 500–710 nm wavelength range. Although they also proposed a multichannel spectral coding method to decrease the number of measurements required while maintaining the reconstruction quality, it still requires multiple measurements. Oiknine et al. (2018) proposed a compressive sensing miniature ultra-spectral imaging camera, which multiplexes image spectra with a liquid crystal (LC) phase retarder and demonstrated a reconstructed image with \(700\times 700\) spatial resolution and 391 spectral bands in the 410–800 nm wavelength range from 32 spectrally multiplexed shots. Later, the same group also proposed a reconstruction algorithm using deep learning (Gedalin et al. , 2019). Recently, Saragadam and Sankaranarayanan (2019) adopted both spatial coding with a coded aperture and spectral coding with a combination of a diffractive grating and a single spatial light modulator to measure a low-rank approximation of a scene’s hyperspectral image. They demonstrated a \(560\times 500\times 256\) spectral cube for 400–700 nm with 2.9 nm spectral resolution from six spectral and six spatial measurements.
Many commercial systems adopt a line-scanning architecture, also known as push-broom imaging, in which a slit is equipped as the aperture and spatial 1-D and spectral axes are mapped onto a 2-D sensor. These systems capture a line in the scene with one shot and scan along the other spatial axis to capture a spectral cube. Similarly, point-scanning systems, utilizing so-called whisk-broom imaging, capture the spectrum at one point and scan the scene to fill the 2-D spatial axes. Push-broom imaging requires less time for scanning than whisk-broom imaging; however, the 2-D sensor limits the spatial and spectral resolutions, whereas whisk-broom imaging enables the best spectral resolution and a great degree of flexibility for spatial scanning.
These approaches enable the capture of an image with fine spatial and spectral resolutions; however, they suffer from temporally varying illumination when the measurements are conducted outside a controllable environment such, e.g. outdoors.
2.2 Illumination and reflectance spectra separation
Captured hyperspectral images are influenced by the illumination spectrum. A simple way to compensate for the illumination variations is the use of an ideal reference target such as a reflectance or transmittance standard to capture the illumination variations itself during the measurement. By employing a scanning approach, Wendel and Underwood (2017) recently addressed the problem of scanning an agricultural field under natural illumination by mounting a reference panel at the edge of the field of view of the camera. However, there is nowhere to place such a reference target that could be directly illuminated by the sunlight when measuring the illumination through a stained-glass window.
Decomposing a hyperspectral image into illumination and object spectra is referred to as the illumination and reflectance spectra separation problem. Chen et al. (2017) and Drew and Finlayson (2007) recovered the spectral reflectance of an object under varying illumination by reproducing the color constancy mechanism of human eyes. Ho et al. (1990) introduced linear models of low dimensionality into both the illuminance and reflectance spectra to separate these components in hyperspectral images. Additionally, Chang and Hsieh (1995) and Drew and Finlayson (2007) improved the accuracy and the speed of computation by applying constraints and introducing a logarithmic finite-dimensional model to the spectrum. Zheng et al. (2015) demonstrated that the separation problem could be modeled as low-rank matrix factorization, showing that the separation is unique up to an unknown scale under the standard assumption of low dimensionality of reflectivity and developing a scalable algorithm. Different from the above, Su et al. (2018) proposed a method for directly estimating the illumination component from specularities, where many methods assume Lambertian surfaces. These methods are effective in decomposing the captured spectra into the scene reflectance and the illumination; however, they do not suppose a temporally varying environment, as they assume that the hyperspectral image is captured under a constant illumination. As an extension of (Zheng et al. , 2015), Chen et al. (2017) relaxed the assumptions to a case of spatially varying illumination caused by multiple light sources by addressing the problem as a conditional random field (CRF) optimization task over local separations. However, this method is unable to compensate for the hyperspectral images captured by wavelength- and point-scanning systems under temporally varying illumination.
3 Proposed method
In this section, we propose a method for eliminating temporally varying illumination in whisk-broom hyperspectral imaging without a reference object, starting from the mathematical model of hyperspectral imaging. For the proposed method, we first introduce an extra single-column scan as reference for the mitigation. Then, we explain a Naïve mitigation method using the extra scan. Since there is no guarantee that the extra scan captures the “ideal reference target”, the method can result in the creation of artifacts. Finally, we propose a method to overcome the potential artifact problem by utilizing low dimensionality in the spectral aspect of illumination.
3.1 Notations and problem setting
A hyperspectral image, also known as spectral cube, has multiple channels along the spectrum. The image can be represented by a tensor \({\mathcal {I}} \in {\mathbb {R}}_+^{M \times N \times L}\), where M and N are the height and width of the image, respectively, and L is the number of spectral channels. We use \(m \in \left\{ 1, \ldots , M\right\} (\equiv {\mathcal {M}})\) and \(n \in \left\{ 1, \ldots , N\right\} (\equiv {\mathcal {N}})\) as indices for the pixel locations. We call the tube of this tensor at pixel location (m, n) a spectral vector denoted as \(\mathbf {i}_{m,n}\). The measured spectral vector \(\mathbf {i}_{m,n}\) is represented as
where \({\varvec{\rho }}_{m, n} \in {\mathbb {R}}^L_+\) is the reflectance (or transmittance) spectrum of the scene at point (m, n), \(\mathbf {l}\in {\mathbb {R}}^L_+\) is the incoming illumination spectrum, and \(\odot \) represents the Hadamard (element-wise) product. We assume that the scene is static during recording; therefore, \({\varvec{\rho }}_{m, n}\) is unchanged over time but is spatially varying.
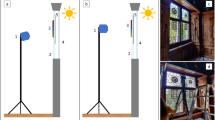
Our whisk-broom imaging device consists of a high spectral-resolution spectrometer and a two-dimensional mechanical scanning head, as shown in Fig. 2a. The spectrometer measures the spectral distribution of a single scene point, and the mechanical scanner head spatially sweeps the scene to form a hyperspectral image \({\mathcal {I}}\). The scan order is from left to right in each row, and row-by-row from top to bottom, as illustrated by the blue arrows in Fig. 2b. While our device can capture a hyperspectral image with thousands of spectral channels, it takes a long time to scan the whole scene, e.g., a few hours for megapixel resolution (Cucci et al. , 2016). Because the scanning time is non-negligible, we consider the illumination spectrum to vary over time during the scanning; thus, the illumination spectrum \(\mathbf {l}\) is considered a function of time t, or \(\mathbf {l}(t)\).
Given the measured hyperspectral image \({\mathcal {I}}\) affected by unknown variations in the illumination spectra, our goal is to recover a hyperspectral image unaffected by these variations. In other words, we wish to recover spectral vectors \(\{{\hat{\mathbf {i}}}_{m,n}\}\) under a reference illumination spectrum \(\mathbf {l}_{\mathrm {ref}}\) as follows:
In our setting, we treat both the illumination spectra \(\{\mathbf {l}(t)\}\) and the reflectance spectra \(\{{\varvec{\rho }}_{m,n}\}\) as unknowns. A reference illumination spectrum \(\mathbf {l}_{\mathrm {ref}}\) can be arbitrarily defined, e.g., it can be chosen from any of the illumination spectra in \(\{\mathbf {l}(t)\}\).
Row-wise constant illumination spectra assumption: Obviously, the problem stated above is ill-posed, because one can arbitrarily form the estimate of the spectral vectors \(\{{\hat{\mathbf {i}}}_{m,n}\}\) with unknown reflectance spectra \(\{{\varvec{\rho }}_{m,n}\}\) and the reference illumination spectrum \(\mathbf {l}_{\mathrm {ref}}\). To make the problem tractable, we assume that the illumination changes are negligible during the scanning of each single row in an image. In the interest of brevity, we denote the illumination spectrum of row m as \(\mathbf {l}_{m,:} \in {\mathbb {R}}_+^{L}\). As a result, Eq. (1) is rewritten as
The problem is still ill-posed, however, because each row of the hyperspectral image \({\mathcal {I}}\) is independently affected by changes in the illumination spectrum \(\{\mathbf {l}_{m,:}\}\).
Extra single-column scan as a constraint To solve this problem, we propose the use of an extra single-column scan in addition to the full row-wise scan, which corresponds to the red arrow in Fig. 2b. It is again assumed that the illumination variation during the single-column scan is negligible. The extra scan \(\mathbf {e}_{m,n'}\) at column \(n'\) is written as
where \(\mathbf {l}_{:,n'}\) is the corresponding illumination spectrum of the single column. Using the extra column scan, we develop a method for estimating the spectral vectors \(\{{\hat{\mathbf {i}}}_{m,n}\}\), in which the temporal variation of the illumination spectrum is eliminated.
In summary, our problem is stated as follows. Given the measured spectral vectors \(\{\mathbf {i}_{m,n}\}\) under unknown row-wise illumination spectrum \(\{\mathbf {l}_{m,:}\}\) and spatially varying, unknown but constant reflectance spectra \(\{{\varvec{\rho }}_{m,n}\}\), we estimate the spectral vectors \(\{{\hat{\mathbf {i}}}_{m,n}\}\) that are unaffected by the row-wise (temporal) variation in the illumination spectra using the extra-single column scan \(\mathbf {e}_{m,n'}\). We first discuss a Naïve approach to this problem, then develop a robust method for stably deriving better solutions.
3.2 The Naïve approach
In hyperspectral image coordinates, the pixels in column \(n'\), the site of the extra column scan, are associated with two sets of measured spectral vectors, i.e., \(\{\mathbf {i}_{m, n'} | m \in {\mathcal {M}}\}\) from the full row-wise scan and \(\{\mathbf {e}_{m, n'} | m \in {\mathcal {M}}\}\) from the extra single-column scan. The spectral vectors of the row-wise scan \(\{\mathbf {i}_{m, n'}\}\) suffer from the variation in the illumination spectrum over the rows, while those of the column scan \(\{\mathbf {e}_{m, n'}\}\) are free from these illumination variations. From this, we can compute vectors of spectrum coefficients \(\{\mathbf {c}_{m, n'} | m \in {\mathcal {M}} \}\) representing the variation in the illumination spectra as
where \(\oslash \) is element-wise division.
By multiplying the spectrum coefficients \(\mathbf {c}_{m, n'}\) by the measured spectrum vectors \(\mathbf {i}_{m, n}\) at other pixels \((m,n), n \ne n'\), we can normalize the illumination spectra to the column scan illumination spectrum \(\mathbf {l}_{:,n'}\) as follows:
where \(\hat{\mathbf {i}}_{m,n}\) is the reconstructed spectral vector in which the illumination variations are eliminated.
The Naïve method works well when the measurements are free from imaging and quantization noise and zero divisions do not occur. However, in practice, imaging and quantization noise are inevitable and are amplified due to the division operations in Eq. (5), particularly when the scene’s reflectance spectrum \({\varvec{\rho }}_{m, n'}\) is small. This causes unstable estimation of the spectrum coefficients \(\{\mathbf {c}_{m,n'}\}\), and as a result, the reconstructed spectral vectors \(\hat{\mathbf {i}}_{m,n}\) suffer from strong visible artifacts.
3.3 Solution based on robust principal component analysis
To stably estimate the spectrum coefficients \(\{\mathbf {c}_{m,n'}\}\), we exploit the observation that the illumination can be naturally assumed to have a low-dimensional spectral structure (Judd et al. , 1964; Drew and Finlayson , 2007). Based on this observation, we approximate the logarithm of the illumination spectrum \(\log \left( \mathbf {l}\right) \) by a linear combination of a small number of basis spectra \(\{\mathbf {b}_s\}, s \in \{1, \ldots , S\}\) as follows:
where S is the number of basis spectra, and \(w_{\cdot ,s} \in {\mathbb {R}}\) is the weighting factor associated with basis spectrum \(\mathbf {b}_s\). Using this low-dimensional approximation, we can rewrite Eq. (5) as
where \(\mathbf {L}\) is an \(L \times S\) matrix whose s-th column vector is \(\mathbf {b}_s\), and \(\mathbf {w}_{m,n'}=\left[ w_{n',1}-w_{m,1},\, \ldots ,\, w_{n',S}-w_{m,S}\right] ^\top \) is a weighting vector defined for the m-th row.
Now, let \(\mathbf {C}\) be an \(L \times M\) matrix composed of a stack of coefficient vectors \(\{\log \left( \mathbf {c}_{m, n'}\right) \}\) from Eq. (5). Its low-dimensional approximation can be written as
where \(\mathbf {W} = \left[ \mathbf {w}_{1,n'}, \ldots , \mathbf {w}_{M,n'}\right] \in {\mathbb {R}}^{S \times M}\). By assuming the number of basis spectra S to be smaller than either L and M, the coefficient matrix \(\mathbf {D}\) has a low-dimensional structure; however, the actual coefficient matrix \(\mathbf {C}\) obtained from Eq. (5) may not, due to outliers introduced by numerical instability. We therefore cast the problem as a low-rank matrix decomposition by explicitly accounting for the outliers \(\mathbf {E} \in {\mathbb {R}}^{L \times M}\) as
By assuming the outlier matrix \(\mathbf {E}\) is sparse and the low-dimensional coefficient matrix \(\mathbf {D}\) is smooth over m, meaning that the illumination change is temporally smooth, the problem can be solved by implementing the total variation-regularized low-rank matrix factorization (LRTV) method proposed by He et al. (2016) with regularization-weight factors \(\mu \) and \(\lambda \) as
where \(\mathbf {D}^*\) and \(\mathbf {E}^*\) are respectively the recovered coefficient and outliers matrices, \(\Vert \cdot \Vert _*,\, \Vert \cdot \Vert _1,\, \Vert \cdot \Vert _\mathrm {HTV}\) represent the nuclear norm, \(\ell _1\) norm, and the total variation along m, respectively. Note that \(\lambda \) is a hyperparameter that needs to be tuned, but it can be determined according to the size of matrix \(\mathbf {C}\), as proposed in (Candès et al. , 2011). Using the recovered coefficient matrix \(\mathbf {D}^* = \left[ \mathbf {d}^*_{1,n'}, \ldots , \mathbf {d}^*_{M,n'} \right] \), Eq. (6) can be rewritten as
by which the reconstructed spectrum vectors \(\{\hat{\mathbf {i}}_{m,n}\}\) have a constant illumination spectrum.
4 Experiments
We developed an imaging system comprising a single-point spectrometer and a scanning head. Figure 2a illustrates the composition of the system. The spectrometer is a Maya2000 Pro (Ocean Optics, Inc.), which outputs 2068 channels over a spectrum ranging from 199.50 to 1118.15 nm with a resolution of approximately 0.5 nm. The scanner is a RobotEye REHS25 (Ocular Robotics Ltd.), which scans with a spatial resolution up to 0.01\(^{\circ }\) for 360\(^{\circ }\) in the yaw direction and 70\(^{\circ }\) in the pitch direction. It enables to capture a wide spectral range, 400–2500 nm.[funa:Check] The devices are connected with an optical fiber. The effective field of view of the point scan depends on the size of the fiber core.Footnote 1 We chose 600 and 200 \(\upmu \hbox {m}\) fiber core for the experiment in Sects. 4.1 and 4.2, respectively.
4.1 Quantitative evaluation
Subject We captured two hyperspectral images of a ColorChecker Passport (X-Rite, Inc.) under temporally varying sunlight on a patly cloudy day, as shown in Fig. 3. One is a horizontally scanned image, which is the target image \(\mathbf {i}_{m, n}\) from which the illumination variations are going to be eliminated, and the other is a vertically scanned image whose one column is used as the extra scan \(\mathbf {e}_{m, n'}\).
Figure 4 depicts the RGB images synthesized by an open-source Python package for colour science (Mansencal et al. , 2020) from the horizontal scan, the vertical scan, and the results of the Naïve and the proposed methods. The scan times were 1099 s for the horizontal image and 4 s for one of the columns of the vertical image. Since the vertical image consists of 140 columns, the total scan time was 552 s.Footnote 2 The figure shows that the images scanned under natural sunlight are strongly affected by the temporal variation of the illumination, whereas the Naïve and the proposed methods are capable of mitigating this variation.
Figure 5 shows some of the mitigated results at several wavelengths. It can be seen that the Naïve method exhibits artifacts along the horizontal scanline, which could not be visually identified in Fig. 4. In contrast, the proposed method successfully suppresses such artifacts.
Figure 6 illustrates the low-dimensional structure extracted during the mitigation procedure by the proposed method. Here, the rank of \(\mathbf {D}\) was constrained to 3. The upper part of the figure shows the basis spectra \(\{\mathbf {b}_s\}\), and the lower left part shows the corresponding weights. The vertical axis for this latter part of the figure represents m and corresponds to the row shown on the right. \(\mathbf {w}_1\), drawn in blue, has the strongest impact on the coefficients. \(\mathbf {b}_1\) is smooth and flat along the wavelength axis, and thus it mainly represents the changes in terms of intensity. The figure shows that \(\mathbf {w}_1\) corresponds to the temporal changes in the illumination intensity during the horizontal scan shown on the right.
The other weight vectors \(\mathbf {w}_s\) are of lower amplitude, and the corresponding basis vectors \(\mathbf {b}_s\) have spectral dependencies. Thus, they are interpreted to be involved in mitigating the changes in a manner dependent on the spectrum. Each weight \(\mathbf {w}_s\) undergoes a sudden change when \(m=40,56,72\), at which the black-colored frames appear in the image. This artifact can be suppressed by making \(\mu \) in Eq. (12) sufficiently large; however, this would also suppress the effect of mitigation, e.g., the strong illumination around \(m=30\) would remain in the mitigated results. The best parameter \(\mu \) depends on the scan; thus, the proposed method requires hyperparameter tuning. It was set to 0.1 in this experiment.
Evaluation using a spectral library: We use the spectral library from (Myers , 2020) for quantitative evaluation. The values in the spectral cube depend on the illumination spectrum. Thus, we estimated the illumination spectrum by comparing the values with the reflectance in the spectral library and canceled it out from the cube. Since the spectral library has spectra ranging from 380–730 nm with 10 nm resolution, we preprocessed the spectral cubes as follows:
-
1.
Manually select a region of \(8\times 8\) pixels for each of 24 color patches.
-
2.
Select 36 spectral channels whose corresponding wavelengths are nearest to those in the library.
-
3.
For each wavelength, estimate the illumination amplitude in the cube using the \(8\times 8\times 24\) values within it and the reflectance of the corresponding 24 patches in the library.
-
4.
Cancel the estimated illumination spectrum from the cube to be comparable to that of the library.
Figure 7 shows the spectra of each color patch from the scans and the mitigated results. The spectra from both scans are different from those of the library since the temporal variation in the illumination affects the estimation of the illumination spectrum. Meanwhile, the results mitigated by both the Naïve and the proposed methods are much closer to the library’s spectra. However, the spectra of the Naïve method are noisier than those of the proposed method and the library.
The low-dimensional structure extracted from coefficient matrix \(\mathbf {C}\) when \(S=3\) and \(\mu =0.1\). The upper part of the figure shows the basis spectra \(\{\mathbf {b}_s\}\). The lower left part of the figure shows the weights of the bases. The vertical axis represents m and corresponds to the rows shown on the right
We then quantitatively evaluated these results using the root-mean-square error (RMSE) as the error metric. RMSE had been calculated over the entire spectral channels. Figure 8a–d display the error maps of the cubes, with the average RMSE shown beneath each panel. As expected from Fig. 7, both the horizontal and vertical scans produce large errors mainly from the illumination changes, while, the mitigated results have much smaller errors. Figure 8e presents a comparison of the error between the Naïve and proposed methods. The negative values, represented in blue, indicate that the Naïve method results in a larger error than the proposed method; that is, the proposed method outperforms the Naïve method in all regions.
Figure 9 illustrates the spectral distributions at a point (POI) and the corresponding reference point used for the mitigation. The Naïve method outputs a noisy spectrum with outliers affected by the selection of an unsuitable reference point from a ‘black’ patch, which has low reflectance. However, the proposed mitigation has less noise and no outliers.
Performance evaluation against column selection: The set of results presented above illustrate an example of the mitigation procedure; the results depend on the selection of the additional column. Therefore, we investigated the robustness of the methods against the selection of the column for the extra scan. Figure 10 shows the performance of the methods, evaluated as the mean error over all patches, with respect to the column selected for the extra scan. Both methods mitigate the temporal variability in the illumination well when the extra scan is performed on a suitable patch. However, the errors increase when the extra scan is performed close to or on a black frame, which has low intensity on all spectral channels irrespective of the illumination. Otherwise, the most difficult mitigation occurred over the ‘white’ patch when the extra scan was performed on a ‘black’ patch, corresponding to the results shown above. The proposed method always outperforms the Naïve method regardless of the column selected, even if the extra scan column contains dark elements. This analysis demonstrates the robustness of the proposed method.
Comparison of spectra in each color patch. The spectra in both the horizontal and vertical scans are different from the ones of the library due to illumination variations during the scanning. The spectra of the Naïve method are noisy. Meanwhile, the spectra of the proposed method is much closer to the ones (Color figure online)
The error maps of a the horizontal and b vertical scans and the mitigated results from c the Naïve and d the proposed methods. e Comparison of the errors from the mitigation methods. The blue values indicate that the Naïve method produces larger errors than the proposed method. The numbers below figures represent the spatial average of RMSEs (Color figure online)
Performance with respect to low rankness: The performance of the proposed method also depends on the selection of the rank S. Although the dimension representing the illumination variation was discussed in the literature (Ho et al. , 1990; Drew and Finlayson , 2007; Zheng et al. , 2015), we also conducted an analysis to investigate how S affects the performance of our method, as shown in Fig. 11. Similar to the results obtained in the literature, the performance was best when \(S=3\) and stably comparable when \(S\in [3,10]\), but worse for a very low dimensionality (for example, \(S=1,2\)) and for dimensionalities higher than 15.
4.2 Experiment in the wild
We captured images of stained-glass windows in a cathedral using the proposed system. As the scan speed of the RobotEye is 25 points/s, it takes a certain amount of time to capture a hyperspectral image, e.g., approximately 1 hour for a resolution of \(300\times 300\) pixels.
We conducted a horizontal raster scan and an extra single-column scan for three stained-glass windows. The spatial resolution and the time spent on the scans are summarized in Table 1. For each measurement, the raster scan took approximately 1 h, whereas the extra single-column scan took less than 20 s and was negligibly affected by changes in sunlight.
As in Sect. 4.1, we applied both mitigation methods to the hyperspectral images of the stained-glass windows. \(\mu \) was set to 0.3 in this experiment. Because these measurements were performed under natural sunlight, it was impossible to avoid the temporal changes in sunlight due to natural phenomena such as the movement of clouds and the sun. As we were unable to obtain a ground-truth hyperspectral image, we conducted only qualitative evaluations here.
Figure 12 shows the synthesized RGB images from the scan and the mitigated results. We also captured an RGB image using a Ricoh Theta for reference, which is shown in Fig. 12a. To visualize the mitigation effect, we also show the difference between the scan and the result of the proposed method in Fig. 12e. Compared with the scan, the mitigated result has a lower intensity in the blue areas of the difference image and a higher intensity in the red areas.
Some of the spectral channels in the scan and the mitigated results are shown in Fig. 13. The figures, especially at longer wavelengths, reveal that the scan images demonstrate gradual intensity changes. The Naïve mitigation results contain noticeable horizontal artifacts, similar to those seen in Fig. 5. On the other hand, the proposed method suppresses these artifacts and recovers smoother images.
Figure 14 also shows the spectral distributions at a point POI and the corresponding reference point. In Fig. 14, the spectrum of the Naïve method at POI is noisy and contains some outliers, while the spectrum of the proposed method is much more acceptable. These results indicate that the proposed method achieves a better mitigation effect than the Naïve method.
Figure 15 illustrates the low-dimensional structure extracted from the mitigation by the proposed method. As in Fig. 6, \(\mathbf {w}_1\) mostly corresponds to the temporal changes in the illumination intensity during the scan. We can also see that the extracted bases have similar forms but differ in their details. There is some room to improve the mitigation effects by optimizing the method to share the bases, but this remains the subject of future work.
Captured image and mitigation results from a field experiment in a cathedral. Each hyperspectral image was converted to an RGB image using (Mansencal et al. , 2020). a An RGB image photographed by a Ricoh Theta (Ricoh, Inc.), b a horizontal scan, c the result mitigated by the Naïve method, d the result mitigated by the proposed method, and e the difference between the horizontal scan and the mitigated result, which represents the intensity changes in the sunlight during the horizontal scan with respect to those during the single-column scan. f–i are, respectively, magnified images from the middle of images a–d. Note that the images have been adjusted for better visualization. Some areas that appear to be saturated are not in the actual hyperspectral images
5 Conclusion
We proposed a method for eliminating the temporal illumination variations in whisk-broom hyperspectral imaging by introducing an extra single-column scan. While the Naïve method suffers if the reference scan contains dark pixels, the proposed method successfully alleviates these artifacts thanks to the low-dimensional structure of the spectra of the resulting image. The proposed method allows the capture of a hyperspectral image of high spatial and spectral resolution under an environment containing temporal illumination variations with few extra measurements. Hence, it has a wide range of applications such as the measurement of historical assets in their own natural environment where lighting cannot be mastered. As an example, we measured historic stained-glass windows, which took approximately 1 hour for scanning. The proposed method is expected to mitigate the temporal illumination variations within tens of seconds. We believe our method serves for digitally preserving large cultural heritages with as high spatial resolution as time allows for the scanning.
Notes
Please refer to the REHS25 user manual for detailed description. https://www.ocularrobotics.com/wp-content/uploads/2016/11/RobotEye-REHS25-User-Manual.pdf, accessed 9 September, 2021.
Although the vertical image has the same spatial resolution as the horizontal image, the scanning times are different since the total lengths of the scanning paths differ.
References
Babini, A., George, S., & Lombardo, T. (2020). Potential and challenges of spectral imaging for documentation and analysis of stained-glass windows. London Imaging Meeting, 1, 109–113.
Baek, S. H., Kim, I., Gutierrez, D., & Kim, M. H. (2017). Compact single-shot hyperspectral imaging using a prism. Transactions on Graphics (TOG), 36(6), 1–12.
Candès, E. J., Li, X., Ma, Y., & Wright, J. (2011). Robust principal component analysis? Journal of ACM, 58(3), 1–37.
Chang, P. R., & Hsieh, T. H. (1995). Constrained nonlinear optimization approaches to color-signal separation. IEEE Transactions on Image Processing, 4(1), 81–94.
Chen, X., Drew, M. S., & Li, Z. N. (2017). Illumination and reflectance spectra separation of hyperspectral image data under multiple illumination conditions. IS&T Electronic Imaging, 18, 194–199.
Choi, I., Jeon, D. S., Nam, G., Gutierrez, D., & Kim, M. H. (2017). High-quality hyperspectral reconstruction using a spectral prior. Transactions on Graphics (TOG), 36(6), 1–13.
Cucci, C., & Casini, A. (2020). Chapter 3.8—hyperspectral imaging for artworks investigation. In Hyperspectral imaging, data handling in science and technology, vol 32 (pp. 583–604). Elsevier.
Cucci, C., Casini, A., Picollo, M., Poggesi, M., & Stefani, L. (2011). Open issues in hyperspectral imaging for diagnostics on paintings: when high-spectral and spatial resolution turns into data redundancy. In O3A: Optics for arts, architecture, and archaeology III, SPIE, vol. 8084 (pp. 57 – 66).
Cucci, C., Casini, A., Picollo, M., & Stefani, L. (2013). Extending hyperspectral imaging from Vis to NIR spectral regions: a novel scanner for the in-depth analysis of polychrome surfaces. In Optics for Arts, Architecture, and Archaeology IV, SPIE, vol. 8790 (pp. 53–61).
Cucci, C., Delaney, J. K., & Picollo, M. (2016). Reflectance hyperspectral imaging for investigation of works of art: Old master paintings and illuminated manuscripts. Accounts of chemical research, 49(10), 2070–2079.
Drew, M. S., & Finlayson, G. D. (2007). Analytic solution for separating spectra into illumination and surface reflectance components. Journal of the Optical Society of America (JOSA), 24(2), 294–303.
Dun, X., Ikoma, H., Wetzstein, G., Wang, Z., Cheng, X., & Peng, Y. (2020). Learned rotationally symmetric diffractive achromat for full-spectrum computational imaging. OSA Optica, 7(8), 913–922.
Gat, N. (2000). Imaging spectroscopy using tunable filters: a review. Wavelet Applications VII, SPIE, 4056, 50–64.
Gedalin, D., Oiknine, Y., & Stern, A. (2019). Deepcubenet: Reconstruction of spectrally compressive sensed hyperspectral images with deep neural networks. OSA Optics Express, 27(24), 35811–35822.
Gehm, M. E., John, R., Brady, D. J., Willett, R. M., & Schulz, T. J. (2007). Single-shot compressive spectral imaging with a dual-disperser architecture. OSA Optics Express, 15(21), 14013–14027.
Hagen, N. A., & Kudenov, M. W. (2013). Review of snapshot spectral imaging technologies. SPIE Optical Engineering, 52(9), 1–23.
Hauser, J., Zeligman, A., Averbuch, A., Zheludev, V. A., & Nathan, M. (2020). DD-Net: Spectral imaging from a monochromatic dispersed and diffused snapshot. OSA Applied Optics, 59(36), 11196–11208.
He, W., Zhang, H., Zhang, L., & Shen, H. (2016). Total-variation-regularized low-rank matrix factorization for hyperspectral image restoration. IEEE Transactions on Geoscience and Remote Sensing, 54(1), 178–188. https://doi.org/10.1109/TGRS.2015.2452812
Ho, J., Funt, B. V., & Drew, M. S. (1990). Separating a color signal into illumination and surface reflectance components: Theory and applications. Transactions on Pattern Analysis and Machine Intelligence (PAMI), 12, 966–977.
Hu, X., Lin, X., Yue, T., & Dai, Q. (2019). Multispectral video acquisition using spectral sweep camera. OSA Optics Express, 27(19), 27088–27102.
Jeon, D. S., Baek, S. H., Yi, S., Fu, Q., Dun, X., Heidrich, W., & Kim, M. H. (2019). Compact snapshot hyperspectral imaging with diffracted rotation. Transactions on Graphics (TOG), 38(4).
Judd, D. B., MacAdam, D. L., Wyszecki, G., Budde, H. W., Condit, H. R., Henderson, S. T., & Simonds, J. L. (1964). Spectral distribution of typical daylight as a function of correlated color temperature. Journal of the Optical Society of America (JOSA), 54(8), 1031–1040.
Lin, X., Liu, Y., Wu, J., & Dai, Q. (2014). Spatial-spectral encoded compressive hyperspectral imaging. Transactions on Graphics (TOG), 33(6).
Mansencal, T., Mauderer, M., Parsons, M., Shaw, N., Wheatley, K., Cooper, S., Vandenberg, JD., Canavan, L., Crowson, K., Lev, O., Leinweber, K., Sharma, S., Sobotka, TJ., Moritz, D., Pppp, M., Rane, C., Eswaramoorthy, P., Mertic, J., Pearlstine, B., Leonhardt, M., Niemitalo, O., Szymanski, M., Schambach, M., Huang, S., Wei, M., Joywardhan, N., Wagih, O., Redman, P., Goldstone, J., & Hill, S. (2020). Colour 0.3.16. https://doi.org/10.5281/zenodo.3757045
Mathys, A., Semal, P., Brecko, J., & Van den Spiegel, D. (2019). Improving 3d photogrammetry models through spectral imaging: Tooth enamel as a case study. PLoS ONE, 14(8), 1–33.
Meng, Z., Ma, J., & Yuan, X. (2020). End-to-end low cost compressive spectral imaging with spatial-spectral self-attention. In European conference on computer vision (ECCV) (pp. 187–204). Springer.
Miao, X., Yuan, X., Pu, Y., & Athitsos, V. (2019). lambda-net: Reconstruct hyperspectral images from a snapshot measurement. In IEEE/CVF international conference on computer vision (pp. 4058–4068).
Monakhova, K., Yanny, K., Aggarwal, N., & Waller, L. (2020). Spectral diffusercam: Lensless snapshot hyperspectral imaging with a spectral filter array. OSA Optica, 7(10), 1298–1307.
Morimoto, T., Mihashi, T., & Ikeuchi, K. (2008). Color restoration method based on spectral information using normalized cut. International Journal of Automation and Computing, 5(3), 226–233.
Morimoto, T., Tan, RT., Kawakami, R., & Ikeuchi, K. (2010). Estimating optical properties of layered surfaces using the spider model. In Computer vision and pattern recognition (CVPR) (pp. 207–214).
Myers, R. (2020). Spectral library, Chromaxion™. https://chromaxion.com/spectral-library.php.
Oiknine, Y., August, I., Farber, V., Gedalin, D., & Stern, A. (2018). Compressive sensing hyperspectral imaging by spectral multiplexing with liquid crystal. MDPI Journal of Imaging, 5(1), 3.
Pillay, R., Hardeberg, J., & George, S. (2019). Hyperspectral imaging of art: Acquisition and calibration workflows. Journal of The American Institute for Conservation, 58, 3–15.
Saragadam, V., & Sankaranarayanan, A. C. (2019). Krism—Krylov subspace-based optical computing of hyperspectral images. Transactions on Graphics (TOG). https://doi.org/10.1145/3345553
Shmilovich, S., Oiknine, Y., AbuLeil, M., Abdulhalim, I., Blumberg, D., & Stern, A. (2020). Dual-camera design for hyperspectral and panchromatic imaging, using a wedge shaped liquid crystal as a spectral multiplexer. Nature Scientific Reports, 10, 3455.
Su, T., Zhou, Y., Yu, Y., Cao, X., & Du, S. (2018). Illumination separation of non-Lambertian scenes from a single hyperspectral image. OSA Optics Express, 26(20), 26167–26178.
Wagadarikar, A., John, R., Willett, R., & Brady, D. (2008). Single disperser design for coded aperture snapshot spectral imaging. OSA Applied Optics, 47(10), B44–B51.
Wang, X., Zhang, Y., Ma, X., Xu, T., & Arce, G. R. (2018). Compressive spectral imaging system based on liquid crystal tunable filter. OSA Optics Express, 26(19), 25226–25243.
Wendel, A., & Underwood, J. (2017). Illumination compensation in ground based hyperspectral imaging. ISPRS Journal of Photogrammetry and Remote Sensing, 129, 162–178.
Zheng, Y., Sato, I., & Sato, Y. (2015). Illumination and reflectance spectra separation of a hyperspectral image meets low-rank matrix factorization. In Computer vision and pattern recognition (CVPR) (pp. 1779–1787).
Acknowledgements
We acknowledge Prof. Cédric Demonceaux (University of Burgundy) and Dr. Nicolas Ragot (ESIGELEC) for their support in executing the experiments in Amiens Cathedral, France. We also acknowledge Prof. Hongyan Zhang (Wuhan University) for providing us with an implementation of He et al. (2016).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Communicated by Takeshi Oishi.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This study is partly supported by JSPS and MAEDI under the Japan–France Integrated Action Program (SAKURA), JSPS KAKENHI JP20K21816, and Japan Science and Technology Agency CREST Grant No. JPMJCR1764.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Funatomi, T., Ogawa, T., Tanaka, K. et al. Eliminating Temporal Illumination Variations in Whisk-broom Hyperspectral Imaging. Int J Comput Vis 130, 1310–1324 (2022). https://doi.org/10.1007/s11263-022-01587-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11263-022-01587-8