Abstract
Discriminative Correlation Filters (DCF) have been shown to achieve impressive performance in visual object tracking. However, existing DCF-based trackers rely heavily on learning regularised appearance models from invariant image feature representations. To further improve the performance of DCF in accuracy and provide a parsimonious model from the attribute perspective, we propose to gauge the relevance of multi-channel features for the purpose of channel selection. This is achieved by assessing the information conveyed by the features of each channel as a group, using an adaptive group elastic net inducing independent sparsity and temporal smoothness on the DCF solution. The robustness and stability of the learned appearance model are significantly enhanced by the proposed method as the process of channel selection performs implicit spatial regularisation. We use the augmented Lagrangian method to optimise the discriminative filters efficiently. The experimental results obtained on a number of well-known benchmarking datasets demonstrate the effectiveness and stability of the proposed method. A superior performance over the state-of-the-art trackers is achieved using less than \(10\%\) deep feature channels.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Visual object tracking is one of the most popular topics in computer vision and machine intelligence, motivated by a wide spectrum of practical applications in robotics, medical image analysis, intelligent transportation and human-computer interaction. Given the initial state of a target in the first frame of a video sequence, a tracker aims to automatically locate the target in the subsequent frames. Typical visual object tracking algorithms include particle filters (Sanjeev 2002), support vector machine (Avidan 2004), subspace representations with sparse and low-rank constraints (Zhang et al. 2015), and deep neural networks (Bertinetto et al. 2016). They are invariably equipped with powerful image features such as histograms (Dalal and Triggs 2005), colour attributes (Weijer et al. 2009) and deep Convolutional Neural Network (CNN) features (Danelljan et al. 2017a). Despite the significant progress made in the tracking methodology and the ever improving results, the fast growing video data with practical challenges, e.g. occlusion, non-rigid deformation, blur and background clutter, imposes increasingly stricter requirements on the accuracy, speed and robustness of visual object tracking algorithms.
In order to mitigate the tension between the effectiveness and efficiency of traditional visual object tracking methods, the Discriminative Correlation Filters (DCF) tracking paradigm has been proposed and extensively studied (Henriques et al. 2012). The efficiency of its learning and localisation stages, involving all circularly augmented samples, is guaranteed by the property of the circulant matrix (Gray 2006). The learning of a correlation operator, formulated as the ridge regression problem, is accelerated by Discrete Fourier Transform (DFT) with closed-form solutions in the frequency domain (Henriques et al. 2015). Exploiting the advantage of this framework, the recent improvements focusing on spatial regularisation (Danelljan et al. 2015; Kiani Galoogahi et al. 2017) and deep neural networks (Danelljan et al. 2016, 2017a; Valmadre et al. 2017) have achieved superior performance on benchmarking datasets (Wu et al. 2013, 2015; Liang et al. 2015; Mueller et al. 2016) and in competitions (Kristan et al. 2015, 2016, 2017, 2018). In addition, it has been demonstrated that feature representation plays the most important role in boosting the performance of visual object tracking (Wang et al. 2015). Compared with other image descriptors, deep Convolutional Neural Network (CNN) features are more intuitive and effective. However, hundreds to thousands of channels of deep features, some of which may be redundant, are directly fused in the DCF paradigm. The relationships among multiple deep channels have not been explored. Motivated by this observation, we investigate the relevance of high dimensional multi-channel features in the learning framework to identify the group relationships between deep image features with the aim of adaptive channel selection.
To reflect the group character of multi-channel features, we impose an adaptive group elastic net regularisation on the DCF solution so as to simultaneously select relevant channels and enforce appearance model continuity across successive frames. A standard elastic net is the combination of \(\ell _1\)-norm and \(\ell _2\)-norm regularisation. It shrinks the variables towards the origin with a trade-off between bias and variance. In our proposal, we construct an adaptive elastic net by combining the \(\ell _1\)-norm regularisation, which induces group-independent sparsity, with an \(\ell _2\)-norm temporal smoothness constraint. It will be shown that this creates a combination of a group elastic net and an adaptive term which controls the shape of the net depending on the temporal smoothness of the estimated DCF. It will also be argued that our adaptive channel selection performs implicit spatial regularisation, in compliance with the principle of spatially regularised DCFs (Danelljan et al. 2015; Kiani Galoogahi et al. 2017).
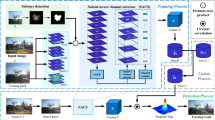
Overview of the proposed Discriminative Correlation Filter with embedded Adaptive Channel Selection. We construct our spatio-temporal appearance model (Blue rectangle) by taking into account the relevance and redundancy of multi-channel features. This is achieved by employing an adaptive group elastic net regularisation to perform group variable selection. Green rectangles show some multi-channel deep representations (ResNet-50). Orange rectangle visualises the learned discriminative filters with the selected channels (Red rectangles) activated. The DCF design based on the selected feature channels enhances both temporal smoothness and discrimination (Color figure online)
In this paper, we propose a new DCF-based tracking algorithm equipped with an adaptive channel selection mechanism (ACS-DCF). An overview of our ACS-DCF algorithm is depicted in Fig. 1. To the best of our knowledge, this is the first study introducing adaptive channel selection in the formulation of DCF-based visual object tracking. It reduces the number of feature channels by structured regularisation using an adaptive group elastic net, which tends to induce sparsity across channels and smoothness across frames. The proposed channel selection strategy suppresses the perturbations injected by non-informative channels, as well as reducing the number of filters. In the learning stage, the augmented Lagrangian method is used to achieve fast optimisation. The experimental results obtained on OTB100 (Wu et al. 2015), OTB2013 (Wu et al. 2013) and VOT2017/ VOT2018 (Kristan et al. 2017) demonstrate the effectiveness and robustness of the proposed adaptive channel selection framework, delivering superior performance over the state-of-the-art trackers. In addition, the stability of the proposed method is confirmed by experiments involving adding random noise to the learned filter model. The impact of varying the regularisation parameters is analysed in the paper. A notable improvement of the tracking performance is observed, especially for deep CNN features, in experiments covering a wide range of regularisation parameter settings.
The main contributions of the proposed ACS-DCF method are:
-
A new appearance model construction technique endowed with adaptive channel selection. Relevant channels are adaptively selected in the learning stage to reduce filter dimensionality as well as to enhance discrimination. Improved performance is achieved by our ACS-DCF even when only \(10\%\) deep feature channels are used for the DCF design.
-
A spatio-temporal group variable selection method using a novel adaptive group elastic net regularisation. Independent sparsity and temporal smoothness are combined in our tracking framework to realise a robust channel selection mechanism. Thanks to the convexity of the proposed formulation, we employ an iterative optimisation technique for efficient filter learning.
-
A deep analysis of the impact of each regularisation term as well as the channel selection ratio. The experimental results confirm the merits and effectiveness of the proposed adaptive channel selection strategy.
The rest of this paper is organised as follows. In Sect. 2, we briefly review related tracking techniques for constructing appearance models and extracting multi-channel features. The classical regularised DCF formulation is presented in Sect. 3. The proposed ACS-DCF method is introduced in Sect. 4 where an efficient optimisation scheme is developed. In Sect. 5, we present the details of the proposed tracking algorithm. The implementation details and experimental results are reported in Sect. 6, which also presents a component and stability analysis.
2 Related Work
In this section, we briefly review existing visual object tracking methods, focusing on the learning models and feature representation approaches. For a detailed account and comprehensive understanding of the visual object tracking literature the reader is referred to recent surveys (Wu et al. 2015; Kristan et al. 2016). The context of the DCF paradigm with its advanced improvements is also presented. We discuss high-dimensional multi-channel features and their common implementations in DCF-based trackers as a prerequisite to analysing their properties to provide supporting evidence and motivation for the approach proposed in this paper.
2.1 Learning Models
Learning models describe the mathematical framework underpinning the visual object tracking task. The most well-known learning concepts in the pioneering stages of visual object tracking include optical flow (Lucas and Kanade 1981) and mean-shift (Comaniciu et al. 2000). The key assumptions behind these approaches are brightness constancy and negligible appearance variations and as they are rarely satisfied, the methods invariably fail when processing challenging videos. To improve the tracking robustness, a particle filter was applied to visual object tracking (Sanjeev 2002) as a means of estimating the target posterior distribution. It is well known that more particles can achieve a better estimate, but only at the expense of growing computational complexity. As the particle filter paradigm is an external modelling framework, it has been successfully fused with other generative methods, e.g. sparse and low-rank subspace representations (Bao et al. 2012; Zhang et al. 2013, 2016, 2012, 2015). A change of paradigm was introduced by formulating visual object tracking as a target recognition problem. Various classification methods, such as support vector machine (Avidan 2004), multiple instance boosting (Babenko et al. 2011), and linear regression (Henriques et al. 2012) have been employed in constructing learning models, exploiting the discriminatory information between target region and its surroundings. However, a common weakness of the above trackers is their robustness, as they initialise the learning model in the first frame, when the information about the target is limited. More recently, deep Siamese networks (Tao et al. 2016; Valmadre et al. 2017; Song et al. 2017; Wang et al. 2018; Li et al. 2018a; Xu et al. 2020b; Wang et al. 2019b, a) have been successfully applied in visual object tracking. Taking the advantages of large visual datasets, deep structures and powerful Graphical Processing Units, Siamese networks achieve efficient visual object tracking by performing template matching in the feature space of high-level abstraction.
The DCF paradigm is the closest learning model that defines the baseline for the research presented in this paper. To achieve efficiency and adaptibility in visual object tracking, the DCF paradigm has been intensively studied in the recent years (Kristan et al. 2015, 2016). Almost all the top performing trackers in the recent VOT challenges are based on the DCF framework. The origins of the approach can be traced back to Bolme et al., who proposed the minimum output sum of squared error (MOSSE) filter (Bolme et al. 2010) to realise adaptive correlation filtering in the frequency domain. This fundamental work was then extended to kernel methods (Henriques et al. 2015) and theoretically interpreted in terms of the circulant structure (Henriques et al. 2012). Exploiting the basic formulation, Danelljan et al. realised effective tracking by learning spatially regularised discriminative correlation filters (SRDCF) (Danelljan et al. 2015). To emphasise colour information, Sum of Template and Pixel-wise Learners (Staple) (Bertinetto et al. 2016) was proposed to combine DCF with colour histograms. In addition, context-aware (Mueller et al. 2017) and background-aware (Kiani Galoogahi et al. 2017) correlation filters were proposed to explore relevant target surroundings to achieve enhanced discriminative capability of a DCF tracker. To further improve the tracking performance in accuracy, Danelljan et al. proposed sub-grid tracking by learning continuous convolution operators (C-COT) (Danelljan et al. 2016). Besides performing spatial regularisation with predefined energy distribution, Xu et al. proposed to learn adaptive discriminative correlation filters (LADCF) using spatial feature selection (Xu et al. 2019). In contrast, the proposed ACS-DCF method focuses on channel selection, improving the tracking performance by assigning discriminative attributes (feature channels) in each frame. In this paper, we improve the existing DCF framework by incorporating an adaptive channel selection mechanism to identify the most effective multi-channel features, including both hand-crafted features and advanced deep CNN features.
2.2 Feature Representation
Another important component of appearance modelling is target representation, which has been demonstrated to play the most essential role in high-performance visual object tracking (Wang et al. 2015; Gundogdu and Alatan 2018; Xu et al. 2020c). We roughly divide existing target representation approaches into three categories: Region of Interest (ROI-) based features, histogram-based features and multi-channel features.
Typical examples of ROI-based features include Scale-Invariant Feature Transform (SIFT) (Lowe 1999) and Speeded Up Robust Features (SURF) (Bay et al. 2006). Both of them are local representations that convey the information about the context of target visual appearance conveyed by the search region. As such, ROI-based features are designed to preserve the local pattern. They are suitable for videos with a stable content. However, their use is frequently invalidated by non-rigid deformations, 3D object motion and motion blur.
To extract deformation-invariant image features, histogram-based feature extraction methods have been proposed to capture the distribution of the characteristics adopted for modelling visual appearance inside an image patch. Specific examples include colour histograms, which have been shown to exhibite impressive performance in visual object tracking (Comaniciu et al. 2000; Sanjeev 2002; Lukezic et al. 2017). But histogram-based features are dependent only on the intensity values in the image patch, ignoring the shape and texture.
To simultaneously acquire local invariance and incorporate spatial context in visual object tracking, multi-channel features have been studied extensively. Histogram of Oriented Gradients (HOG) (Dalal and Triggs 2005), which has been also widely used in many other computer vision and pattern recognition applications, is the seminal representation for visual object tracking that re-arranges the gradient information into orientation bins, (Zhu et al. 2006; Feng et al. 2015, 2017). The Colour Names feature extraction method (CN) (Weijer et al. 2009) maps the original 3-channel RGB format patch to a 10-channel image feature representation, enhancing the discrimination among specific colour attributes. Recent deep learning architectures, e.g., AlexNet (Krizhevsky et al. 2012), VGG (Simonyan and Zisserman 2014), GoogLeNet (Szegedy et al. 2015) and ResNet (He et al. 2016), generate even more powerful multi-channel features for high-performance visual object tracking. These deep multi-channel features, learned from large image datasets, contain hundreds to thousands of channels, offering outstanding discrimination. However, for a specific target, many of these channels are irrelevant and they also retain a lot of redundancy. This deficiency has not been addressed in the visual object tracking research.
Although a promising performance has been achieved by combining the regularised DCF paradigm and powerful features (Danelljan et al. 2016; Xu et al. 2020a; Sun et al. 2019), existing studies usually consider feature channels as being equally important. In order to mitigate this shortcoming, Lukezic et al. (Lukezic et al. 2017) proposed the concept of channel reliability, where each channel is weighted by analysing the ratio of the first and second major mode in the response map. Sun et al. (Sun et al. 2018a), on the other hand, acknowledged reliability in terms of spatial masks. However, such channel-wise weighting strategies ignore the relevance of a channel in the context of other channels. Moreover, the diversity and redundancy of multi-channel features are not considered. In contrast, in our approach, we perform an adaptive channel selection of multi-channel features in the learning stage of DCF. The adaptive spatio-temporal group variable selection is achieved by imposing channel sparsity and temporal smoothness of the learned filters in successive video frames.
3 Regularised DCF
Given a training pair \(\{\mathcal {X},\mathbf {Y}\}\) in frame t, where \(\mathcal {X}\in \mathbb {R}^{N\times N\times C}\) and \(\mathbf {Y}\in \mathbb {R}^{N\times N}\) are the multi-channel features and corresponding labels in the form of a response map, the aim of visual object tracking is to distinguish the target from its background in the next frame. We follow the DCF paradigm (Henriques et al. 2015) to formulate our objective as a regularised least square problem that learns the multi-channel discriminative filters \( \mathcal {W}\in \mathbb {R}^{N\times N\times C}\) (frame index t is omitted for simplification):
where \(\circledast \) is the circular convolution operator (Henriques et al. 2012), \(\mathbf {X}^j \in \mathbb {R}^{N\times N}\) and \(\mathbf {W}^j \in \mathbb {R}^{N\times N}\) are the j-th channel feature map and the corresponding discriminative filter slice. \(\mathbf {Y}\) is the predefined desired response map in the form of 2D Gaussian shape (Henriques et al. 2012) that highlights the target’s centre. \(\mathcal {R}\left( \mathcal {W}\right) \) is the regularisation term corresponding to the prior assumptions constraining the filters. The conventional DCF paradigm employs the \(\ell _2\)-norm (Frobenius norm for a matrix, \(\sum _{j=1}^C\Vert \mathbf {W}^j\Vert ^2_F\)) constraint to formulate the main objective as a ridge regression problem. A closed-form solution can be directly obtained in the frequency domain (Henriques et al. 2015). Though the \(\ell _2\)-norm (\(\ell _F\)-norm) regularisation achieves computational efficiency, it sacrifices the parsimony of the discriminative filter. To achieve enhanced discrimination and parsimony in the regularised DCF formulation, we propose a group variable selection mechanism to realise adaptive spatio-temporal channel selection.
4 Adaptive Channel Selection
In this section, we introduce our proposed learning framework that achieves adaptive channel selection for a multi-channel feature representation. To be more specific, an adaptive group elastic net is proposed to implement the group variable selection. A unique characteristic of the proposed learning framework is that the relevance of spatial feature channels and their temporal smoothness are simultaneously enforced. To gain intuitive understanding of the proposed approach, we elaborate the potential properties of the selected channels from the perspectives of attribute selection and spatial unit selection. A qualitative evaluation is also carried out to provide supporting evidence for the asserted merit and effectiveness of the proposed adaptive channel selection method.
4.1 Spatio-temporal Adaptive Elastic Net
Motivated by the seminal work of variable selection (Yuan and Lin 2006; Zou and Hastie 2005; Nie et al. 2010), in the proposed approach, we embed adaptive channel selection in the learning framework by means of an adaptive group elastic net. First, the elements in \(\mathcal {W}\) are arranged to specific groups according to their third dimension (channel). Such a grouping operator forms natural clusters of variables for the high-dimensional filtering system. To fuse the information conveyed by each group, we need a balancing function \(\sigma ()\) to gauge its reliability. Here, we define the balancing function, \(\sigma ()\), as the Frobenius norm for each \(N\times N\) matrix \(\mathbf {W}^j\), i.e., \(\sigma ^j = \sigma \left( \mathbf {W}^j\right) = \left\| \mathbf {W}^j\right\| _F\). and form a balancing reliability vector \(\varvec{\sigma }=\left[ \sigma ^1,\sigma ^2,\ldots ,\sigma ^C\right] \) for use in the adaptive group elastic net to impose spatio-temporal regularisation.
Visualisation of the activated image pixels corresponding to the selected channels in sequence David and MotorRolling. The orange rectangle shows the original target as well as the surroundings, while the red solid and red dashed rectangles visualise the activated pixels from the selected channels and discarded channels, respectively (Color figure online)
To amplify spatial discrimination and impose temporal continuity for the selected channels, the filters are assumed to be sparse across channels and to be smooth across frames:
The first term in the above equation imposes independent sparsity for the balancing group reliability vector \(\mathbf {\sigma }\), focusing on the current training data pair to regularise the estimate centred at the origin. The second term in Eq. (2) promotes temporal smoothness forcing the newly learned filters \(\mathcal {W}\) to be close to the filter learned from the previous frame \(\mathcal {W}_{\text {t-1}}\), such that the estimate is robust to target appearance variations, with the selected channels being similar to those of the consecutive frame.
Expanding the second term on the right hand side of Eq. (2) and rearranging, we can write
Note that the two terms on the first line on the right of Eq. (3) define the standard elastic net regularisation. The impact on regularisation of the term on the second line on the right is adaptive. It will change depending on the relationship between \(\varvec{\sigma }\) and \(\varvec{\sigma }_{\text {t-1}}\). When \(\varvec{\sigma }_{\text {t-1}}=0\), as for instance at the beginning of tracking, the regularisation will revert to the standard group elastic net. When the balancing reliability vector in the current frame is equivalent to its previous frame counterpart, i.e. \(\varvec{\sigma }=\varvec{\sigma }_{\text {t-1}}\), the regularisation collapses to the \(\ell _1\)-norm process. In general, when, \(\varvec{\sigma }\ne \varvec{\sigma }_{\text {t-1}}\), the term on the second line on the right of Eq. (3) will pull the group elastic net towards the previous frame \(\varvec{\sigma }_{\text {t-1}}\).
2-D visualisation of the proposed adaptive elastic net in Eq. (2) with \(\varvec{\sigma }=\left( \sigma _1,\sigma _2\right) \), \(\mathcal {R}(\varvec{\sigma })=1\) and \(\alpha =0.5\). The state of \(\varvec{\sigma }_{t-1}\) controls the structured regularisation of the estimate. Compared with the original elastic net (\(\varvec{\sigma }_{t-1}=\left( 0,0\right) \)), the proposed adaptive elastic net guides the processing of variable selection. As \(\varvec{\sigma }_{t-1}\) moves away from the origin along the \(\sigma _1\)-axis, the model tends to select variables \(\sigma _1\)
As shown in Fig. 3, the proposed adaptive elastic net retains a similar structure compared with the standard group elastic net (\(\varvec{\sigma }_{\text {t-1}}=(0,0)\)). The adaptive group elastic net enhances the group effect (Zou and Hastie 2005) during group variable selection in \(\mathcal {W}\), improving the stability by selecting highly correlated variables.
The difference between the proposed adaptive elastic net and \(\ell _1\)-norm in inducing sparsity can be viewed to lie in assigning different priors: the Laplacian sparse distribution prior, and a combination of the Laplacian sparse distribution and Gaussian dense distribution prior, as well as an additional adaptive correction term. Note, the Gaussian dense distribution prior term, \(\left\| \mathbf {\sigma }\right\| _2^2\) in Eq. (3), relaxes the \(\ell _1\)-norm with strong convexity. Therefore, the adaptive group elastic net regularisation ensures the estimate is unaffected by noisy channels. Only the relevant information is used for advanced discrimination. Note that \(\alpha \) is the trade-off parameter for the proposed adaptive group elastic net.
4.2 Explicit Attribute Selection and Implicit Spatial Unit Selection
The circular convolution operator in Eq. (1) can be considered as being constituted by multiple inner-product operators. The channel selection assisted by the adaptive structured regularisation will identify non-informative channels, and suppress them by setting the associated DCF weights to zero. By virtue of the optimisation process, the informative, or in other words, the relevant channels, will be assigned non zero weights, that is larger values of balancing reliability. As each informative channel is tuned to respond to different image properties, it can be considered as selecting and representing specific attributes of the tracked target. The target appearance representation is then constituted by a set of the attributes identified by the selected channels. These attributes play an instrumental role in data fitting with parsimony and discrimination. It should be noted that within a channel, the target attribute will relate to specific spatial units, which exhibit the image characteristic picked up by the channel (e.g. a high frequency content). The spatial locations which do not contain the channel specific content will fail to respond, and the associated DCF weights will be close to zero. It follows, that even within informative channels with a relative large value of \(\sigma \), the contributions of individual spatial features to the channel reliability value will be diverse and spatially dependent. This shows that the explicit attribute selection achieved by channel weight regularisation will implicitly perform simultaneous spatial unit selection.
This notion of explicit attribute selection and implicit spatial unit regularisation is depicted in Fig. 2. The figure shows the result of implicit spatial regularisation effected by our adaptive channel selection for both hand-crafted and deep features. By feeding back the selected channels to the original input image patch we can identify the activation pattern of pixels producing the channel output. Clearly, channel selection can be considered as a method of selecting specific spatial pixel configurations. Fig. 2 also shows that deep features are more expert in configuring the relevant spatial information than hand-crafted features, resulting in more robust tracking performance, as confirmed in recent benchmarking competitions and challenges. The proposed adaptive group elastic net configures different channels for each frame in video to compose a joint spatial appearance representation of image content to maximise discrimination.
5 The Proposed ACS-DCF Tracker
5.1 Formulation
To combine the proposed adaptive elastic net into the DCF formulation (Eq. (1)), we embed the balancing function, \(\sigma ^j = \sigma \left( \mathbf {W}^j\right) = \left\| \mathbf {W}^j\right\| _F\), into Eq. (2) with reverse triangle inequality and obtain the following regularisation term:
Therefore, we aim to solve the following objective:
where \(\lambda _1=\alpha \lambda \), \(\lambda _2=\left( 1-\alpha \right) \lambda \), It should be noted that the internal balancing function \(\sigma \) maps each group in \(\mathcal {W}\) to a non-negative value, avoiding the problem of \(\ell _1\)-norm discontinuity at the origin.
5.2 Optimisation
We employ the augmented Lagrangian method (Lin et al. 2010) to optimise Eq. (1). Note that \(\mathcal {R}\left( \mathcal {W}\right) \) is channel-wise separable. We introduce the slack variable, \(\mathcal {W}^\prime =\mathcal {W}\), and reformulate the objective to minimise the following Lagrangian function:
where \(\varvec{\varGamma }\) is the Lagrangian multiplier sharing the same size as \(\mathcal {W}\), and \(\mu \) is the corresponding penalty.
5.2.1 Updating \(\mathcal {W}\)
To optimise \(\mathcal {W}\), we solve the following sub-problem in the frequency domain by employing the circulant structure (Henriques et al. 2015):
Note that the symbol \(\hat{}\) stands for Fourier representations in the frequency domain (Henriques et al. 2015). The closed-form solution of the above sub-problem can be obtained as (Petersen and Pedersen 2008):
where vector \(\hat{\mathbf {w}}\left[ m,n\right] =\left[ \hat{w}_{m,n}^1,\hat{w}_{m,n}^2, \ldots ,\hat{w}_{m,n}^C\right] \in \mathbb {C}^C\) denotes the m-th row n-th column units of \(\hat{\mathcal {W}}\) through all the C channels, and \(\mathbf {g} = \hat{\mathbf {x}}\left[ m,n\right] \hat{y}\left[ m,n\right] +\frac{\mu }{2} \hat{\mathbf {w}}^\prime \left[ m,n\right] +\lambda _2\hat{\mathbf {w}}_{\text {t-1}} \left[ m,n\right] -\frac{\hat{\varvec{\gamma }}\left[ m,n\right] }{2}\).
5.2.2 Updating \(\mathcal {W}^\prime \)
To optimise \(\mathcal {W}^\prime \), we need to minimise the following sub-problem similar to group lasso (Yuan and Lin 2006):
A closed-form solution with shrinkage operator can be derived as:
where \(\mathbf {H}^j = \mathbf {W}^j + \varvec{\varGamma }^j/{\mu }\).
5.2.3 Updating other variables
In each iteration, the penalty \(\mu \) and the multiplier \(\varvec{\varGamma }\) are updated as:
where \(\rho \) controls the strictness of the penalty in each iteration and \(\mu _{\max }\) is the maximal penalty value. A parameter K is used to control the maximum number of iterations. As each sub-problem is convex, the convergence of our optimisation is guaranteed (Boyd et al. 2010).

5.3 Learning and Tracking Details
We summarise the proposed ACS-DCF tracking method in Algorithm 1.
5.3.1 Tracking
In the tracking stage, we obtain the position and scale of a target simultaneously as proposed in fDSST (Danelljan et al. 2017b). To be more specific, given a new image in frame t and the predicted target state of frame \(t-1\) (target centre \(p_{t-1}\), the target width, \(w_{t-1}\), and height \(h_{t-1}\)), we extract a search window set \(\left\{ \varvec{I}_s\right\} \) centred around \(p_{t-1}\) with multiple scales, \(s=1,2,\ldots ,S\), where S is the number of search windows. For each scale s, the search window patch is centred around \(p_{t-1}\) with a size of \(a^N n^\prime \times a^N n^\prime \) pixels, where a is the scale factor and \(N=\lfloor \frac{2s-S-1}{2}\rfloor \). We resize each patch to the \(n\times n\) basic search window size. \(n^\prime \) is determined by the target size \(w_{t-1}\times h_{t-1}\) and the padding parameter, \(\varrho \) as: \(n^\prime =\left( 1+\varrho \right) \sqrt{w_{t-1}\times h_{t-1}}\). Then we extract multi-channel features of each search window with the scale of s as \(\varvec{\mathcal {X}}_s\in \mathbb {R}^{N\times N\times C}\). Given the filter model obtained from the previous frame, \(\mathcal {W}_{\text {t-1}}\), the response map \(\mathbf {R}_s\) can efficiently be calculated in the frequency domain as:
Suppose the maximal value in the multi-scale response maps \(\{\mathbf {R}_s\}\) corresponds to position \(p_t^*\) and scale \(s^*\). Then the final target centre \(p_t\) and scale \(w_t\times h_t\) of the target in the \(t^{th}\) frame is obtained as:
5.3.2 Learning
In the learning stage, we first extract the feature representation \(\mathcal {X}\) of the tracked target in frame t. Then the filter \(\mathcal {W}\) is optimised based on the detailed steps in Sect. 5.2.
5.3.3 Update
After the learning stage, the same updating strategy as in (Henriques et al. 2015) is adopted:
where \(\beta \) is the updating rate.
6 Experiments
6.1 Implementation
To evaluate the performance of the proposed tracker, we implement our ACS-DCF in MATLAB on an Intel i5 2.50 GHz CPU with a Nvidia GTX 960 GPU. The code is publicly available at GithubFootnote 1. The detailed settings for the parameters used in Sect. 5.3 are as follows. We set the basic window size \(n\times n = 240\times 240\) pixels, the padding parameter \(\varrho =4\), the scale factor and scale number as \(a=1.01\) and \(S=7\). To verify the generalisation capability of the proposed adaptive channel selection method, we equip ACS-DCF with three different feature configurations, i.e. hand-crafted features (ACS-DCF\(\_\text {HC}\)), deep CNN features (ACS-DCF\(\_\text {Deep}\)), and compound features using both feature types (ACS-DCF\(^*\)). The hand-crafted set includes HOG and Colour Names (CN) features, with 4 pixel cell size, \(\lambda _1=5\), \(\lambda _2=30\) and learning rate \(\beta =0.6\). Specifically, the HOG (31 channels) and CN (10 channels) features are concatenated along the channel dimension to obtain the final hand-crafted feature representation \(\varvec{\mathcal {X}}\_\text {HC}\in \mathbb {R}^{60\times 60\times 41}\). We use ResNet-50 (the output of layer 3 with 16 pixels stride) to extract deep feature representations using the MatConvNet toolboxFootnote 2 (Vedaldi and Lenc 2015). The learning rate for deep feature is set to \(\beta =0.06\), with \(\lambda _1=5\), \(\lambda _2=5\). The dimensionality of the ResNet-50 feature representation tensor is \(\varvec{\mathcal {X}}\_\text {Deep}\in \mathbb {R}^{15\times 15\times 1024}\). For ACS-DCF\(^*\), the filters for the hand-crafted and deep features are independently trained based on \(\varvec{\mathcal {X}}\_\text {HC}\) and \(\varvec{\mathcal {X}}\_\text {Deep}\), according to Algorithm 1. In the tracking stage, for each search scale s, the final response map \(\varvec{R}_s\) is constructed by adding the response maps obtained by the deep features \(\varvec{R}_s\_\text {Deep}\) and the hand-crafted features \(\varvec{R}_s\_\text {HC}\). Note that the response map produced by the deep features, \(\varvec{R}_s\_\text {Deep}\), is resized to the same spatial resolution as \(\varvec{R}_s\_\text {HC}\) for the additive operation.
6.2 Evaluation Metrics
We perform evaluation on three challenging benchmarks: OTB2013 (Wu et al. 2013), OTB100 (Wu et al. 2015) and VOT2017/VOT2018 (Kristan et al. 2017, 2018). For the first two datasets, we employ precision plot and success plot to evaluate the tracking performance (Wu et al. 2013). The precision plot measures the proportion of frames with the distance between the tracking results and the ground truth less than a certain number of pixels. The distance precision (DP) is defined by the corresponding value when the precision threshold is 20 pixels. Centre location error (CLE) measures the mean distance between the centres of the tracking results and the ground truth values. The success plot describes the percentage of successful frames with the threshold ranging from 0 to 1. The target in a frame is considered successfully tracked if the overlap of the two bounding boxes exceeds a given threshold. The overlap precision (OP) is defined by the corresponding value when the overlap threshold is 0.5. The area under curve (AUC) of the success plot quantifies the result in terms of overlap evaluation. For VOT2017/VOT2018, we use the expected average overlap (EAO), accuracy and robustness metrics for performance evaluation (Kristan et al. 2016).
We compare our method against recent state-of-the-art approaches, including VITAL (Song et al. 2018), STRCF (Li et al. 2018b), ECO (Danelljan et al. 2017a), C-COT (Danelljan et al. 2016), MCPF (Zhang et al. 2017), MetaTracker (Park and Berg 2018), CREST (Song et al. 2017), BACF (Kiani Galoogahi et al. 2017), CACF (Mueller et al. 2017), ACFN (Choi et al. 2017), CSRDCF (Lukezic et al. 2017), Staple (Bertinetto et al. 2016), SiamFC (Bertinetto et al. 2016), CFNet (Valmadre et al. 2017), SRDCF (Danelljan et al. 2015), DSST (Danelljan et al. 2017b) and KCF (Henriques et al. 2015). For VOT2017/VOT2018, we compare our ACS-DCF with the top trackers in VOT2017 and VOT2018, i.e., ECO, CFCF (Gundogdu and Alatan 2018), CFWCR (He et al. 2017), LSART (Sun et al. 2018b), UPDT (Bhat et al. 2018), SiamRPN (Zhu et al. 2018), MFT (Kristan et al. 2018) and LADCF (Xu et al. 2019), reported in (Kristan et al. 2017, 2018).
6.3 Ablation Studies
The purpose of the proposed adaptive channel selection method is to improve discrimination by enhancing the relevance of filters, as well as reducing information redundancy. As illustrated in Fig. 2, hand-crafted and deep features present different selection patterns. For each feature category, we first analyse the effect of each component in the proposed adaptive elastic net for ACS-DCF\(\_\text {HC}\) and ACS-DCF\(\_\text {Deep}\). The baseline method is the standard spatially regularised DCF tracker (Danelljan et al. 2015). Generally, the proposed adaptive elastic net as well as its corresponding components, i.e., temporal smoothness and channel sparsity, produce improvement for the baseline tracker. The results are reported in Table 1. Compared with the baseline method (Hand-crafted/Deep), the temporal smoothness significantly improves the performance in terms of AUC score by \(1.4\%\) and \(2.5\%\), respectively. Intuitively, connecting successive frames in the learning stage enables the learned filters to become more invariant to appearance variations. Channel sparsity also leads to improvement in the tracking performance, from \(62.3\% / 52.1\%\) to \(64.1\% / 59.7\%\), compared with the baseline method. In addition, the combination of both above components, using the proposed adaptive elastic net, achieves the best performance (\(65.5\% / 59.7\%\)) as compared with all the other configurations.
Besides, the impact of using different deep network feature layers is also reported in Table 2. Compared with the shallower layers (layer1 and layer2), layer 3 achieves a better AUC score, whereas the deepest layer, layer 4, exhibits a drastic drop in terms of tracking performance. In general, deep CNN features are more powerful than hand-crafted features as a target detector, but because of their low spatial resolution, their ability to localise the target is limited. Note that the resolution of the salient feature maps extracted from deep CNN layers is only 1/16 of the original input for layer-3 of VGG or ResNet, resulting in intrinsic centre location error (e.g., 8 pixels). Therefore, all the state-of-the-art DCF trackers use both shallow features and deep features jointly to achieve better performance in terms of accuracy.
To verify the sensitivity of the proposed regularisation model, we perform corresponding experiments for ACS-DCF\(*\) via varying \(\lambda _1\) from 0.1 to 100, and \(\lambda _2\) from 0.5 to 500, respectively. The results are shown in Fig. 4. Deep features benefit from the proposed group variable selection scheme, with the channel group sparsity parameter \(\lambda _1\) ranging from 1 to 50. However, a similar AUC score is achieved by the hand-crafted features with different \(\lambda _1\). These results demonstrate that deep features are highly redundant, and exhibit undesirable interference. As such, they offer a scope for dimensionality reduction by the proposed adaptive channel selection, leading to improvement in performance. While the hand-crafted features are extracted in a fixed manner, different attributes are considered for different channels. Therefore, only redundancy is alleviated by the proposed channel sparsity without increasing discrimination for handcrafted features. In addition, hand-crafted features present stable and smooth performance in terms of different \(\lambda _2\) ranging from 1 to 100. Improvement in the AUC score is achieved by deep features with \(\lambda _2\) ranging from 1 to 10. The above results demonstrate the effectiveness of the proposed adaptive elastic net in formulating a spatio-temporal appearance model, robust to varying regularisation parameters.
6.4 Comparison with State-of-the-art
6.4.1 Quantitative Performance
Precision plots and success plots on OTB100 and OTB2013 are presented in Fig. 5, with the DP and AUC scores reported in the figure legends respectively. The performance achieved by ACS-DCF\(*\) is superior to the state-of-the-art trackers in both criteria. On OTB100, the advantage of our ACS-DCF\(*\) is obvious, with a \(2.0\%\) in DP and \(0.8\%\) in AUC improvement compared with the second best, VITAL\(*\) and ECO\(*\), respectively. On OTB2013, ACS-DCF\(*\) achieves accurate tracking with \(96.1\%\) in DP. Compared to ECO\(*\), which can be considered the best of a class of DCF-based trackers, our performance is better. OP, CLE and AUC are presented in Tables 3 and 4, respectively. Compared with the other trackers with hand-crafted features, our ACS-DCF_HC achieves the best OP score and the second best in terms of CLE. In addition, for hybrid features, ACS-DCF\(*\) obtains accurate and robust tracking results on OTB2013 and OTB100, with the best OP/CLE, \(93.6\%/6.6\ pixels\) and \(88.4\%/7.8\ pixels\). We attribute our performance improvement to the adaptive integration of temporal smoothness and channel selection. The above performance is achieved using only about \(7\%\) of the deep channels available. By focusing on relevance and reducing redundancy in multi-channel deep feature representation, ACS-DCF\(*\) exhibits adaptive context awareness with an outstanding generalisation.
Illustration of the qualitative tracking results on challenging sequences (Left column top to down: Biker, Dragonbaby, Matrix, Singer2 and Soccer. Right column top to down: Bird1, Ironman, MotorRolling, Skiing and Shaking). The colour bounding boxes are the corresponding results of BACF, STAPLE_CA, CFNet\(*\), C-COT\(*\), ECO\(*\), CREST\(*\), MCPF\(*\), VITAL\(*\), MetaTracker\(^*\) and ACS-DCF\(*\), respectively (Color figure online)
In Table 5, we report the results obtained on VOT2017/VOT2018. As VOT consists of diverse challenging factors, all the top-performing trackers use deep CNN features. The proposed ACS-DCF method performs best under the EAO metric, achieving a relative gain of \(1.4\%\) compared to the second best, LADCF. For accuracy and robustness, ACS-DCF achieves comparable performance to the top-performing trackers.
Besides, in Table 6, we report the results of top DCF trackers, i.e., ECO, C-COT, LADCF, and the proposed ACS-DCF, using the same deep features extracted by the VGG network. The proposed ACS-DCF achieves favourable tracking performance compared with other spatial regularisation approaches, demonstrating the merit of the proposed adaptive channel selection strategy in the filter learning stage.
6.4.2 Qualitative Performance
Qualitative comparisons are presented in Fig. 6, which shows the intuitive tracking results of the state-of-the-art methods, i.e., BACF, STAPLE_CA, CFNet\(*\), C-COT\(*\), ECO\(*\), CREST\(*\), MCPF\(*\), VITAL\(*\), MetaTracker\(^*\) and ACS-DCF\(*\), on some challenging video sequences. The difficulties are posed by rapid changes in the appearance of targets as well as the surroundings. Our ACS-DCF\(*\) performs well on these challenges as it successfully identifies the pertinent spatial salience configurations. Sequences with deformations (MotorRolling, Dragonbaby) and out of view (Biker, Bird1) can be successfully tracked by our method without any failures. Videos with rapid motions (Biker, Matrix, Skiing, Ironman) also benefit from our strategy of exploring relevant deep channels to enhance discrimination. Specifically, ACS-DCF\(*\) is expert in solving in-plane and out-of-plane rotations (Biker, MotorRolling, Skiing), because the proposed adaptive channel selection approach provides a novel solution to the appearance information fusion from the central region and surroundings by implicit spatial regularisation.
6.4.3 The Performance on Challenging Attributes
The tracking performance evaluated on OTB100 in 7 challenging attributes (Wu et al. 2013), i.e., scale variation, occlusion, motion blur, in-plane rotation, out of view, background clutter and low resolution, is summarised in Fig. 7. For presentation clarity, only the trackers within the top ten in terms of overall performance on OTB100 are included. The results demonstrate that our ACS-DCF\(*\) outperforms the state-of-the-art trackers in out of view, in-plane rotation, motion blur and scale variations. Due to the implicit spatial regularisation performed by our adaptive channel selection for deep features, the spatio-temporal salience of the target incorporates the surroundings. Compared to C-COT\(*\) and ECO\(*\), the learning scheme of our ACS-DCF\(*\) only depends on the filter model \(\mathcal {W}_\text {t-1}\) and current appearance representation \(\mathcal {X}\), without gathering a historical appearance pool. Overall, the proposed ACS-DCF\(*\) deals with challenging video sequences in a superior manner.
6.5 Stability Analysis of ACS-DCF
To evaluate the robustness of the proposed ACS-DCF method, we investigate its stability using OTB100. Unlike using contaminated input, in our design, random Gaussian noise is added to the filter model \(\mathcal {W}_{\text {t-1}}\) in the learning stage, so that the intermediate variable \(\mathbf {g}\) in Eq. (8) becomes \(\mathbf {g} = \hat{\mathbf {x}}\left[ m,n\right] \hat{y}\left[ m,n\right] +\mu \hat{\mathbf {w}}^\prime \left[ m,n\right] -\mu \hat{\varvec{\gamma }}\left[ m,n\right] +\lambda _2 \hat{\mathbf {w}}_{\text {t-1}}\left[ m,n\right] +\lambda _2\hat{\mathbf {s}}\left[ m,n\right] \), where \(\mathbf {S}\in \mathbb {R}^{N\times N\times C}\) and \(s^j\left[ m,n\right] \sim \mathcal {N}\left( 0,\sigma ^2\right) \). The rest of the optimisation process remains unchanged. To analyse the impact of noise, we set \(\sigma \) to 5 levels, \(\left[ 0.01\ 0.1\ 1\ 10\ 100\right] \times \bar{w}\), where \(\bar{w}\) is the absolute mean value of \(\mathcal {W}_{\text {t-1}}\).
We run the experiment 10 times for each noise level. Table 7 gives the tracking performance on AUC using OTB100 in terms of the mean value and standard deviation. We can see that the introduction of the spatio-temporal appearance regularisations can achieve adaptive channel selection with high stability. More specifically, ACS-DCF\(\_\text {Deep}\) only drops \(1.4\%\) in mean value of AUC in the presence of level 100 noise, while ACS-DCF\(\_\text {HC}\) loses \(15\%\) of performance. Intuitively, deep features are more robust to noise than the hand-crafted features after channel selection. This can be explained by the fact that deep features achieve more decisive discrimination compared to hand-crafted features. The relevant discriminatory information is enhanced by eliminating redundancy. In addition, ACS-DCF\(\_\text {HC}\), ACS-DCF\(\_\text {Deep}\) and the hybrid ACS-DCF\(*\) all perform well under the first four noise levels, with the performance loss of less than \(0.6\%\). In summary, the proposed ACS-DCF method can provide robust appearance model, thereby leading to superior and stable performance in visual object tracking.
6.6 Channel Selection or Spatial Regularisation?
As shown in Fig. 4 and Table 7, the proposed channel selection strategy significantly improves the tracking performance with deep CNN features in terms of both accuracy and robustness. In contrast, hand-crafted features do not benefit much from such strategy besides reducing limited redundancy. Interestingly, the dimensionality reduction methods with spatial regularisation investigated in recent tracking methods, i.e., SRDCF (Danelljan et al. 2015), BACF (Kiani Galoogahi et al. 2017), ECO (Danelljan et al. 2017a), LADCF (Xu et al. 2019), achieve notable improvements for hand-crafted features, but do not seem to work so well with deep features, as they are very compact and convey information accumulated over an extensive set of pixels. Therefore, here we explore the possibility of improving the performance further by adopting an appropriate formulation for hand-crafted features, and combine the result with channel-based selection for deep CNN features.
We employ the formulation in LADCF for hand-crafted features and construct a fused tracker, coined as ACSDCF\(_\text {Deep}\)+LADCF\(_\text {HC}\). The experimental results on OTB100 are shown in Table 8. Compared with ACSDCF\(*\), the tracking performance is improved from \(69.9\%/93.8\%\) to \(70.8\%/94.5\%\) in terms of AUC/DP, with a significant additional gain of \(0.9\%/0.7\%\), respectively. The results demonstrate that we should treat different feature categories with different strategies, i.e., spatial regularisation for hand-crafted features while channel selection for deep features.
7 Conclusion
In this paper, we developed a novel tracking method featuring adaptive channel selection. The proposed ACS-DCF effectively handles target variations by adaptively selecting relevant discriminative deep channels. This approach is achieved by employing grouped elastic net regularisation to simultaneously identify spatial relevance and impose temporal smoothness on the DCF solution. Furthermore, the proposed ACS-DCF method realises implicit spatial regularisations, which confirms earlier findings about its importance reported in the tracking community. Qualitative and quantitative evaluations on several well-known benchmarking datasets demonstrate the effectiveness and robustness of our adaptive channel selection method with the comparison to the state-of-the-art trackers.
References
Avidan, S. (2004). Support vector tracking. IEEE transactions on pattern analysis and machine intelligence, 26(8), 1064–1072.
Babenko, B., Yang, M. H., & Belongie, S. (2011). Robust object tracking with online multiple instance learning. IEEE Transactions on Pattern Analysis and Machine Intelligence, 33(8), 1619–1632.
Bao, C., Wu, Y., Ling, H., Ji, H. (2012) Real time robust l1 tracker using accelerated proximal gradient approach. In: IEEE Conference on Computer Vision and Pattern Recognition, pp 1830–1837.
Bay, H., Tuytelaars, T., Van Gool, L. (2006) Surf: Speeded up robust features. In: European conference on computer vision, Springer, pp 404–417.
Bertinetto, L., Valmadre, J., Golodetz, S., Miksik, O., & Torr, P. H. S. (2016). Staple: Complementary learners for real-time tracking. IEEE Conference on Computer Vision and Pattern Recognition, 38, 1401–1409.
Bertinetto, Luca and Valmadre, Jack and Henriques, Joao, F. and Vedaldi, Andrea and Torr, Philip, H.S. (2016) Fully-convolutional siamese networks for object tracking. In: European conference on computer vision, Springer, pp 850–865.
Bhat, G., Johnander, J., Danelljan, M., Khan, F.S., Felsberg, M. (2018) Unveiling the power of deep tracking. arXiv preprint arXiv:180406833.
Bolme, D.S., Beveridge. J.R., Draper, B.A., Lui, Y.M. (2010) Visual object tracking using adaptive correlation filters. In: IEEE Conference on Computer Vision and Pattern Recognition, pp 2544–2550.
Boyd, S., Parikh, N., Chu, E., Peleato, B., & Eckstein, J. (2010). Distributed optimization and statistical learning via the alternating direction method of multipliers. Foundations and Trends in Machine Learning, 3(1), 1–122.
Choi, J., Jin Chang, H., Yun, S., Fischer, T., Demiris, Y., Young Choi, J. (2017) Attentional correlation filter network for adaptive visual tracking. In: Proceedings of the IEEE conference on computer vision and pattern recognition, pp 4807–4816.
Comaniciu, D., Ramesh, V., Meer, P. (2000) Real-time tracking of non-rigid objects using mean shift. In: IEEE Conference on Computer Vision and Pattern Recognition, pp 142–149.
Dalal, N., & Triggs, B. (2005). Histograms of oriented gradients for human detection. IEEE Conference on Computer Vision and Pattern Recognition, IEEE, 1, 886–893.
Danelljan, M., Hager, G., Khan, F.S., Felsberg, M. (2015) Learning spatially regularized correlation filters for visual tracking. In: IEEE International Conference on Computer Vision, pp 4310–4318.
Danelljan, M., Robinson, A., Khan, F.S., Felsberg, M. (2016) Beyond correlation filters: Learning continuous convolution operators for visual tracking. In: European conference on computer vision, pp 472–488.
Danelljan, M., Bhat, G., Khan, F.S., Felsberg, M. (2017a) Eco: Efficient convolution operators for tracking. In: IEEE Conference on Computer Vision and Pattern Recognition, pp 6931–6939.
Danelljan, M., Häger, G., Khan, F. S., & Felsberg, M. (2017b). Discriminative scale space tracking. IEEE transactions on pattern analysis and machine intelligence, 39(8), 1561–1575.
Feng, Z. H., Hu, G., Kittler, J., Christmas, W., & Wu, X. J. (2015). Cascaded collaborative regression for robust facial landmark detection trained using a mixture of synthetic and real images with dynamic weighting. IEEE Transactions on Image Processing, 24(11), 3425–3440.
Feng, Z.H., Kittler, J., Christmas, W., Huber, P., Wu, X.J. (2017) Dynamic attention-controlled cascaded shape regression exploiting training data augmentation and fuzzy-set sample weighting. In: IEEE Conference on Computer Vision and Pattern Recognition, pp 2481–2490.
Gray, R. M. (2006). Toeplitz and circulant matrices : a review. Foundations and Trends in Communications and Information Theory, 2(3), 155–239.
Gundogdu, E., & Alatan, A. A. (2018). Good features to correlate for visual tracking. IEEE Transactions on Image Processing, 27(5), 2526–2540.
He, K., Zhang, X., Ren, S., Sun, J. (2016) Deep residual learning for image recognition. In: IEEE conference on computer vision and pattern recognition, pp 770–778.
He, Z., Fan, Y., Zhuang, J., Dong, Y., Bai, H. (2017) Correlation filters with weighted convolution responses. In: Proceedings of the IEEE International Conference on Computer Vision, pp 1992–2000.
Henriques, J., o F, Caseiro, R., Martins, P., Batista, J. (2012) Exploiting the circulant structure of tracking-by-detection with kernels. In: European Conference on Computer Vision, pp 702–715.
Henriques, J. F., Rui, C., Martins, P., & Batista, J. (2015). High-speed tracking with kernelized correlation filters. IEEE Transactions on Pattern Analysis and Machine Intelligence, 37(3), 583–596.
Kiani Galoogahi, H., Fagg, A., Lucey, S. (2017) Learning background-aware correlation filters for visual tracking. In: Proceedings of the IEEE international conference on computer vision, pp 1135–1143.
Kristan, M., Pflugfelder, R., Matas, J., Leonardis, A., Felsberg, M., Cehovin, L., Fernandez, G., Vojir, T., Hager, G., Nebehay, G. (2015) The visual object tracking vot2015 challenge results. In: IEEE International Conference on Computer Vision Workshop, pp 564–586.
Kristan, M., Leonardis, A., Matas, J., Felsberg, M., Pflugfelder, R., Čehovin Zajc, L., et al. (2016). The visual object tracking vot2016 challenge results. : Springer.
Kristan, M., Leonardis, A., Matas, J., et al (2017) The visual object tracking vot2017 challenge results. In: IEEE International Conference on Computer Vision Workshops, pp 1949–1972.
Kristan, M., Leonardis, A., Matas, J., Felsberg, M., Pflugfelder, R., Cehovin Zajc, L., Vojir, T., Bhat, G., Lukezic, A., Eldesokey, A. et al. (2018) The sixth visual object tracking vot2018 challenge results. In: Proceedings of the European Conference on Computer Vision (ECCV).
Krizhevsky, A., Sutskever, I., Hinton, G.E. (2012) Imagenet classification with deep convolutional neural networks. In: Advances in neural information processing systems, pp 1097–1105.
Li, B., Yan, J., Wu, W., Zhu, Z., Hu, X. (2018a) High performance visual tracking with siamese region proposal network. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp 8971–8980.
Li, F., Tian, C., Zuo, W., Zhang, L., Yang, M.H. (2018b) Learning spatial-temporal regularized correlation filters for visual tracking. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp 4904–4913.
Liang, P., Blasch, E., & Ling, H. (2015). Encoding color information for visual tracking: Algorithms and benchmark. IEEE Transactions on Image Processing, 24(12), 5630–5644.
Lin, Z., Chen, M., Ma, Y. (2010) The augmented lagrange multiplier method for exact recovery of corrupted low-rank matrices. arXiv preprint arXiv:10095055.
Lowe, D.G. (1999) Object recognition from local scale-invariant features. In: Computer vision, 1999. The proceedings of the seventh IEEE international conference on, Ieee, vol 2, pp 1150–1157.
Lucas, B.D., Kanade, T. (1981) An iterative image registration technique with an application to stereo vision. In: International Joint Conference on Artificial intelligence, pp 674–679.
Lukezic, A., Vojir, T., Zajc, L.C., Matas, J., Kristan, M. (2017) Discriminative correlation filter with channel and spatial reliability. In: IEEE Conference on Computer Vision and Pattern Recognition, pp 4847–4856.
Mueller, M., Smith, N., Ghanem, B. (2016) A benchmark and simulator for uav tracking. In: European Conference on Computer Vision, Springer, pp 445–461.
Mueller, M., Smith, N., Ghanem, B. (2017) Context-aware correlation filter tracking. In: IEEE Conference on Computer Vision and Pattern Recognition, pp 1396–1404.
Nie, F., Huang, H., Cai, X., Ding, C.H. (2010) Efficient and robust feature selection via joint \(\ell _{2, 1}\)-norms minimization. In: Advances in neural information processing systems, pp 1813–1821.
Park, E., Berg, A.C. (2018) Meta-tracker: Fast and robust online adaptation for visual object trackers. arXiv preprint arXiv:180103049.
Petersen, K., Pedersen, M. (2008) The matrix cookbook. technical university of denmark. Technical Manual.
Sanjeev, M. (2002). A tutorial on particle filters online nonlinear/nongaussian bayesian tracking. IEEE transactions on signal processing, 50(2), 174–188.
Simonyan, K., Zisserman, A. (2014) Very deep convolutional networks for large-scale image recognition. arXiv preprint arXiv:14091556.
Song, Y., Ma, C., Gong, L., Zhang, J., Lau, R., Yang, M.H. (2017) Crest: Convolutional residual learning for visual tracking. In: IEEE International Conference on Computer Vision, pp 2555–2564.
Song, Y., Ma, C., Wu, X., Gong, L., Bao, L., Zuo, W., Shen, C., Lau, R., Yang, M.H. (2018) Vital: Visual tracking via adversarial learning. arXiv preprint arXiv:180404273.
Sun, C., Wang, D., Lu, H., Yang, M.H. (2018a) Correlation tracking via joint discrimination and reliability learning. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp 489–497.
Sun, C., Wang, D., Lu, H., Yang, M.H. (2018b) Learning spatial-aware regressions for visual tracking. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp 8962–8970.
Sun, Y., Sun, C., Wang, D., He, Y., Lu, H. (2019) Roi pooled correlation filters for visual tracking. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp 5783–5791.
Szegedy, C., Liu, W., Jia, Y., Sermanet, P., Reed, S., Anguelov, D., Erhan, D., Vanhoucke, V., Rabinovich, A. (2015) Going deeper with convolutions. In: Proceedings of the IEEE conference on computer vision and pattern recognition, pp 1–9.
Tao, R., Gavves, E., Smeulders, A.W. (2016) Siamese instance search for tracking. In: IEEE Conference on Computer Vision and Pattern Recognition, IEEE, pp 1420–1429.
Valmadre, J., Bertinetto, L., Henriques, J., Vedaldi, A., Torr, P.H. (2017) End-to-end representation learning for correlation filter based tracking. In: IEEE Conference on Computer Vision and Pattern Recognition, IEEE, pp 5000–5008.
Vedaldi, A., Lenc, K. (2015) Matconvnet: Convolutional neural networks for matlab. In: Proceedings of the 23rd ACM international conference on Multimedia, ACM, pp 689–692.
Wang, G., Luo, C., Xiong, Z., Zeng, W. (2019a) Spm-tracker: Series-parallel matching for real-time visual object tracking. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp 3643–3652.
Wang, N., Shi, J., Yeung, D.Y., Jia, J. (2015) Understanding and diagnosing visual tracking systems. In: IEEE International Conference on Computer Vision, IEEE, pp 3101–3109.
Wang, Q., Teng, Z., Xing, J., Gao, J., Hu, W., Maybank, S. (2018) Learning attentions: residual attentional siamese network for high performance online visual tracking. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp 4854–4863.
Wang, Q., Zhang, L., Bertinetto, L., Hu, W., Torr, P.H. (2019b) Fast online object tracking and segmentation: A unifying approach. In: Proceedings of the IEEE conference on computer vision and pattern recognition, pp 1328–1338.
Weijer, J. V. D., Schmid, C., Verbeek, J., & Larlus, D. (2009). Learning color names for real-world applications. IEEE Transactions on Image Processing, 18(7), 1512–23.
Wu, Y., Lim, J., Yang, M.H. (2013) Online object tracking: A benchmark. In: IEEE Conference on Computer Vision and Pattern Recognition, pp 2411–2418.
Wu, Y., Lim, J., & Yang, M. H. (2015). Object tracking benchmark. IEEE Transactions on Pattern Analysis and Machine Intelligence, 37(9), 1834–1848.
Xu, T., Feng, Z. H., Wu, X. J., & Kittler, J. (2019). Learning adaptive discriminative correlation filters via temporal consistency preserving spatial feature selection for robust visual object tracking. IEEE Transactions on Image Processing, 28(11), 5596–5609.
Xu, T., Feng, Z. H., Wu, X. J., & Kittler, J. (2020a). An accelerated correlation filter tracker. Pattern Recognition, 102, 107172.
Xu, T., Feng, Z.H., Wu, X.J., Kittler, J. (2020b) Afat: Adaptive failure-aware tracker for robust visual object tracking. arXiv preprint arXiv:200513708.
Xu, T., Feng, Z. H., Wu, X. J., & Kittler, J. (2020c). Learning low-rank and sparse discriminative correlation filters for coarse-to-fine visual object tracking. IEEE Transactions on Circuits and Systems for Video Technology, 30(10), 3727–3739.
Yuan, M., & Lin, Y. (2006). Model selection and estimation in regression with grouped variables. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 68(1), 49–67.
Zhang, T., Ghanem, B., Liu, S., Ahuja, N. (2012) Low-rank sparse learning for robust visual tracking. In: European conference on computer vision, Springer, pp 470–484.
Zhang, T., Ghanem, B., Liu, S., & Ahuja, N. (2013). Robust visual tracking via structured multi-task sparse learning. International Journal of Computer Vision, 101(2), 367–383.
Zhang, T., Liu, S., Ahuja, N., Yang, M. H., & Ghanem, B. (2015). Robust visual tracking via consistent low-rank sparse learning. International Journal of Computer Vision, 111(2), 171–190.
Zhang, T., Bibi, A., Ghanem, B. (2016) In defense of sparse tracking: Circulant sparse tracker. In: IEEE Conference on Computer Vision and Pattern Recognition, pp 3880–3888.
Zhang, T., Xu, C., Yang, M.H. (2017) Multi-task correlation particle filter for robust object tracking. In: Proceedings of the IEEE conference on computer vision and pattern recognition, pp 4335–4343.
Zhu, Q., Yeh, M. C., Cheng, K. T., & Avidan, S. (2006). Fast human detection using a cascade of histograms of oriented gradients. IEEE Conference on Computer Vision and Pattern Recognition, 2, 1491–1498.
Zhu, Z., Wang, Q., Li, B., Wu, W., Yan, J., Hu, W. (2018) Distractor-aware siamese networks for visual object tracking. In: Proceedings of the European Conference on Computer Vision (ECCV), pp 101–117.
Zou, H., & Hastie, T. (2005). Regularization and variable selection via the elastic net. Journal of the Royal Statistical Society, 67(2), 301–320.
Acknowledgements
This work was supported in part by the UK EPSRC Programme Grant (FACER2VM) EP/N007743/1, in part by the EPSRC/dstl/MURI Project EP/R018456/1, and in part by the National Natural Science Foundation of China (61672265, U1836218, 61902153, 61876072).
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Mei Chen.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Xu, T., Feng, Z., Wu, XJ. et al. Adaptive Channel Selection for Robust Visual Object Tracking with Discriminative Correlation Filters. Int J Comput Vis 129, 1359–1375 (2021). https://doi.org/10.1007/s11263-021-01435-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11263-021-01435-1