Abstract
Feature matching aims at generating correspondences across images, which is widely used in many computer vision tasks. Although considerable progress has been made on feature descriptors and fast matching for initial correspondence hypotheses, selecting good ones from them is still challenging and critical to the overall performance. More importantly, existing methods often take a long computational time, limiting their use in real-time applications. This paper attempts to separate true correspondences from false ones at high speed. We term the proposed method (GMS) grid-based motion Statistics, which incorporates the smoothness constraint into a statistic framework for separation and uses a grid-based implementation for fast calculation. GMS is robust to various challenging image changes, involving in viewpoint, scale, and rotation. It is also fast, e.g., take only 1 or 2 ms in a single CPU thread, even when 50K correspondences are processed. This has important implications for real-time applications. What’s more, we show that incorporating GMS into the classic feature matching and epipolar geometry estimation pipeline can significantly boost the overall performance. Finally, we integrate GMS into the well-known ORB-SLAM system for monocular initialization, resulting in a significant improvement.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Feature matching is one of the most fundamental problems in the computer vision community. It aims to generate correspondences across different views of an object or scene, which is widely used in many vision tasks such as structure-from-motion (Schonberger and Frahm 2016) and Visual SLAM (Davison et al. 2007; Mur-Artal et al. 2015). Typical solutions rely on feature detectors (Harris and stephens 1988), descriptors (Lowe 2004), and matchers (Muja and Lowe 2009) for generating putative correspondences. Then the selected correspondences are taken as input in a high-level task, where a RANSAC (Fischler and Bolles 1981) based estimator is often applied to fit a geometric model and remove outliers simultaneously. Although considerable progress has been made on features, matchers, and estimators, the overall performance is still limited by the false correspondences, i.e, they cause robust estimators to fail to find a correct model and true inliers. This problem is critical but received relatively less attention than other problems motioned above. More importantly, existing approaches are time-consuming (Lin et al. 2017), limiting their use in real-time applications. To address this gap, we propose a novel method termed (GMS) grid-based motion statistics for separating true correspondences from false ones at high speed.
GMS matching. Although Lowe’s ratio test (RT) can remove many false matches, generated by ORB (Rublee et al. 2011) features here, the results are still noisy (a) and degenerate RANSAC (Breiman 2001) based estimators in applications. To address this issue, we propose GMS, which further removes motion-inconsistent correspondences towards the high-accuracy matching (b)
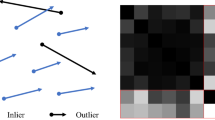
The proposed method relies on the motion smoothness constraint, i.e, we assume that neighboring pixels in one image would move together since they often land in one rigid object or structure. Although the assumption is not generally correct, e.g., violated in image boundaries, it suits to most regular pixels. This is sufficient for our purpose since we are not targeting a final correspondence solution but a set of high-quality correspondences for RANSAC-like approaches. The assumption causes that neighboring true correspondences in one image would also be close in other images, while false correspondences not. This allows us to classify a correspondence as true or false by just counting the number of its similar neighbors, the correspondences that are close to the reference correspondence in both images. Figure 2 shows an visualization for our assumption, and Sect. 3.2 presents the theoretical analysis.
The computational cost is critical to a false match removal method, since feature matching is often used in real-time applications such as Visual SLAM (Mur-Artal et al. 2015). We accelerate the calculation by proposing a grid-based framework in Sect. 3.3, where we divide images into non-overlap cells and process data at the cell level instead of at individual correspondence level. This avoids the distance comparison between correspondences, reducing the overall complexity from the plain \(O(N^2)\) to O(N). As a result, GMS takes only 1 or 2 milliseconds CPU time in a single thread to identify true correspondences, even when the number of matches reaches 50K, as shown in Fig. 11.
The basic grid framework suffers from significant image changes in scale and rotation. To address the issue, we propose multi-scale and multi-rotation solutions. Specifically, we define 5 relative scales and 8 relative rotations between image pairs for scale and rotation enhancement, respectively. Then we repeat the basic GMS algorithm at different settings and collect the best results. As no data dependence exists in different repeats, the proposed methods can be implemented using multi-thread programming. Theoretically, they can be as fast as the basic GMS algorithm, when 8 (or 5) CPU threads are available. This resource burden is affordable to a regular desktop or laptop.
We conduct a comprehensive evaluation of GMS, including the robustness to common image changes, the performance and efficiency with varying feature numbers, and the accuracy of retrieved correspondences. Moreover, we evaluate the proposed method on very recent FM-Bench (Bian et al. 2019) for exploring how it can contribute to epipolar geometry estimation. The results demonstrate the superiority of GMS against other state-of-the-art alternatives. Finally, we incorporate the proposed GMS into the well-known ORB-SLAM (Mur-Artal et al. 2015) for monocular initialization, and a clear improvement is shown. This paper is an extension of our preliminary version (Bian et al. 2017). We extend it in the following four aspects: (1) more straightforward and more intuitive presentation; (2) scale and rotation enhancements; (3) more comprehensive evaluation; (4) use in real-time applications.
2 Related Works
2.1 Relation to RANSAC
The proposed method attempts to remove false correspondence. Although it is related to RANSAC (Fischler and Bolles 1981) based algorithms, which fit a model from correspondences and remove outliers, note that GMS is not an alternative to the latter. The difference includes: (1) GMS cannot fit a model as RANSAC-based estimators; and (2) outliers are model-dependent and are not conceptually equivalent to false correspondences. For example, in the image based reconstruction problem where the static scene assumption is made, some correct correspondences would also be removed as outliers if they land in moving objects. Instead of replacing RANSAC, the goal of GMS is to provide high-quality correspondence hypotheses to the latter towards better overall performance, i.e., model fitting and inlier generation.
2.2 False Correspondence Removal
Lowe’s ratio test (Lowe 2004), referred as RT, is a widely used approach. It compares the distance of two nearest neighbors for identifying distinctive correspondences. However, due to lacking more powerful constraints, many false correspondences remain under challenging scenarios. An example is shown in Fig. 1, where applying GMS can further remove false correspondences. Other methods include KVLD (Liu et al. 2012) which uses constraints in both photometry and geometry, and VFC (Ma et al. 2014) which interpolates a vector field between two point sets and estimates the consensus set. Recently, CODE (Lin et al. 2017) leverages non-linear optimization for globally modeling the motion smoothness. Our method is inspired by it, but simpler and more efficient. LPM (Ma et al. 2019) explores the local structure of surrounding feature points, which makes more restrictive assumptions than GMS. LC (Yi et al. 2018) uses deep neural networks to find good correspondences by fitting an essential matrix. It is like an alternative to RANSAC (Fischler and Bolles 1981). However, the authors show that the predicted model is not as good as using RANSAC. They instead suggest using the method for finding good correspondences and then applying RANSAC for model fitting.
2.3 Successful Applications that use GMS
After the conference version of GMS was published, we notice that many recent works have used our method in their applications and achieved remarkable performances. For instance, (Causo et al. 2018) use GMS in an item picking system for the Amazon Robotics Challenge, and the system can pick all target items with the shortest amount of time; (Zhang et al. 2019) use GMS and extend the idea to tackle the tracking problem in dynamic scenes. The resultant solution produces one order of magnitude more accurate camera trajectory than ORB-SLAM2 (Mur-Artal et al. 2015) in the TUM benchmark (Sturm et al. 2012; Yoon et al. 2018) use GMS for point cloud triangulation in 3D their trajectory reconstruction system. Moreover, our implementation of GMS has been integrated into OpenCV library (Bradski 2000), and we encourage researchers to use and extend it in more real-time applications.
3 Grid-Based Motion Statistics
Given putative correspondences generated by feature detectors, descriptors, and matchers, our goal is to separate the true correspondences from false ones.
3.1 Motion Smoothness Assumption
To differentiate true and false correspondences, we assume that pixels those are spatially close in the image coordinates would move together. It is intuitive, i.e., imagine that neighboring pixels have a high probability of landing in one rigid object or structure and hence have similar motions. The assumption is not generally correct, e.g, it may be violated in image boundaries where neighboring pixels may land in different objects and these objects have independent motions. However, it suits regular pixels, which are overwhelmingly more than edges. Besides, as our goal is a set of high-quality correspondence hypotheses for further processing instead of a final correspondence solution, the assumption is sufficient for our purpose.
3.2 Motion Statistics
True correspondences are influenced by the smoothness constraints, while false correspondences are not. Therefore, true correspondences are often have more similar neighbors than false correspondences, as shown in Fig. 2, where the similar neighbors refer to the correspondences which are close to the reference correspondence in both images. We use the number of similar neighbors to identify good correspondences.
Formally, let C be all correspondences across image \(I_1\) and \(I_2\), \(c_i\) be one correspondence that connects the point \(p_i\) and \(q_i\) between two images. We define \(c_i\)’s neighbors as
and its similar neighbors as
where \(d(\cdot ,\cdot )\) refers to the Euclidean distance of two points, and \(r_1, r_2\) are thresholds. We term \(|S_i|\), the number of elements in \(S_i\), motion support for \(c_i\).
The motion support can be used as a discriminative feature to distinguish true and false correspondences. Modeling the distribution of \(|S_i|\) for true and false correspondence, we get:
where \(B(\cdot ,\cdot )\) refers to the binomial distribution. \(|N_i|\) refers to the number of neighbors for \(c_i\). t and \(\epsilon \) are the respective probabilities that a true and false correspondence are supported by one of its neighbors.
In Eq. 3, t is dominated by the feature quality, i.e., it is near to correct rate of correspondences. \(\epsilon \) is usually small because false correspondences are nearly random distributed in regular regions. Note that it would be larger in visually similar but geographically different regions, e.g, repetitive structures (Kushnir and Shimshoni 2014). Here we assume that features are sufficiently discriminating that their correspondence distribution is better than random and that caused by repetitive patterns, i.e., t is larger than \(\epsilon \).
We can derive \(|S_i|\)’s expectation:
and variance:
This allows definition of partionability between true and false correspondences as:
where \(P \propto \sqrt{|N_i|}\) and if \(|N_i|\rightarrow \infty \), \(P\rightarrow \infty \). This means that the separability of true and false matches based on \(|S_i|\) becomes increasingly reliable as the feature numbers are sufficiently large. This occurs even if t is only slightly greater than \(\epsilon \), making it possible to obtain reliable correspondence on difficult scenes by simply increasing the number of detected features. The similar results are shown in Lin et al. (2018), where ambiguous distributions are separated through large numbers of independent trials. Besides, it shows that improving feature quality (t) can also boost the separability.
The distinctive attributes permit us to classify \(c_i\) as true or false by simply thresholding \(|S_i|\), giving:
where \(\mathcal {T}\) and \(\mathcal {F}\) denote true and false correspondence sets, respectively. Based on Eq. 6, we set \(\tau _i\) to be:
where \(\alpha \) is a hyperparameter, and we empirically find that it results in good performance when \(\alpha \) ranges from 4 to 6.
3.3 Grid-Based Framework
The complexity of a plain implementation for computing \(S_i\) is O(N), where \(N = |C|\) is the number of all correspondences, since we need to compare \(c_i\) with all other correspondences. Therefore, the overall algorithm complexity is \(O(N^2)\). Although approximated nearest neighbor algorithms, like FLANN (Muja and Lowe 2009), can reduce the complexity to O(Nlog(N)), we show that using the proposed grid-based framework is faster (O(N)).
Figure 3 illustrates the framework, where we divide two images into non-overlap cells \(\mathcal {G}_1\) and \(\mathcal {G}_2\), respectively. Assume \(c_i\) be a correspondence that lands in the cell \(G_a\) and \(G_b\), like one of the red correspondences in Fig. 3. The neighbors of \(c_i\) are re-defined as:
and the similar neighbors are re-defined as:
where \(C_a\) are correspondences those land in \(G_a\), and \(C_{ab}\) are correspondences those land in \(G_a\) and \(G_b\) simultaneously. In other words, we regard correspondences those are in one cell as neighbors, and correspondences those are in one cell-pair as similar neighbors. This avoids the explicit comparison between correspondences. To obtain motion support for all correspondences, we only need to put them in cell-pairs. In this fashion, the overall complexity is reduced to O(N).
Note that correspondences those land in one cell-pair share the same motion support, so we only need classify cell-pairs instead of individual correspondences. Moreover, instead of determining all possible cell-pairs, we only check the best one cell-pair that contains most correspondences for each cell in the first image. For example, we only check \(G_{ab}\) and discard \(G_{ac}\), \(G_{ad}\) in Fig. 3. This operation significantly decreases the number of cell-pairs and early rejects a considerable amount of false correspondences.
3.4 Motion Kernel
Few neighbors would be considered, if the cell size is small. This degenerates the performance. However, if the cell size is big, inaccurate correspondences would be included. To address this issue, we set the grid size to be small for accuracy and propose motion kernel for considering more neighbors.
Figure 4 shows the basic motion kernel, where we consider additional eight cell-pairs (\(C_{a^1b^1},\ldots , C_{a^9b^9}\)) for classifying the original cell-pair (\(C_{ab}\)). Formally, let \(c_i\) land in \(C_{ab}\) again. We re-define its neighbors as
where
We re-define its similar neighbors as
where
The basic kernel assumes that the relative rotation between two images is small. For matching image pairs with significant rotation changes, we can rotate the basic kernel, as described in the next section.
3.5 Multi-scale and Multi-rotation
To deal with significant scale and rotation changes between two images, we propose the multi-scale and multi-rotation solutions in this section.
3.5.1 Multi-rotation Solution
We rotate the basic kernel for simulating different relative rotations, resulting in total 8 motion kernels, as shown in Fig. 5. The rotation is often unknown in real-world problems, so we run GMS algorithm using all motion kernels and collect the best results, i.e., we find the kernel that results in most correspondences retrieved. The efficacy of multi-rotation solution is demonstrated in Sect. 4.2.
3.5.2 Multi-scale Solution
The relative scale between two images can be simulated in our grid framework, i.e., we fix the cell size (cell numbers) of one image and vary that of the other image. Assume that both images are divided into \(n \times n\) cells. We change the cell number of the second image to be \((n\cdot \alpha ) \times (n\cdot \alpha )\). Here, we provide 5 candidates for \(\alpha \), including \(\{\frac{1}{2}, \frac{\sqrt{2}}{2}, 1, \sqrt{2}, 2\}\). Similarly, we run GMS using all pre-defined relative scales and collect the best results. Note that we provide only 5 relative scales to demonstrate that our solution is effective for solving the scale issue, which is efficient and sufficient for most scenes, as demonstrated in Sects. 4.2 and 4.4. However, for more significant scale changes, we can use more candidates or increase \(\alpha \).

3.6 Algorithm and Limitation
Algorithm 1 shows the GMS algorithm, which takes putative correspondences and the setting for scale and rotation as input and outputs selected matches. We use the basic motion kernel and the single equal scale for matching regular images, e.g., video frames. The multi-scale and multi-rotation solutions are used for images with significant changes in scale and rotation, respectively.
3.6.1 Implementation
We implement the algorithms using C++ with OpenCV library (Bradski 2000). A single CPU thread is used currently, but the multi-thread programming can be used for accelerating the multi-scale and multi-rotation solutions. We use \(20 \times 20\) cells as the default mode, and we vary the number of cells in the second image when activating the multi-scale solution. \(\alpha = 4\) in Eq. 8 is used for thresholding. The code has been integrated into the OpenCV library.
3.6.2 Limitation
The limitation of GMS lies in three aspects. First, as we assume that image motion is piece-wise smooth, the performance may degenerate in areas where the assumption is violated, e.g., image boundaries. This issue is not critical because regular pixels are overwhelmingly more than boundaries. Besides, as we are not targeting a final correspondence solution but a set of high-quality hypotheses, the assumption is sufficient for our purpose. To solve this problem, we will consider using edge detection (Liu et al. 2019) or image segmentation (Cheng et al. 2016; Liu et al. 2018) techniques in future work. Second, the performance is limited in visually similar but geographically different image regions. This issue often occurs in scenes that have heavy repetitive patterns. We leave the problem to global geometry estimation algorithms (Kushnir and Shimshoni 2014), as only local visual information is not sufficient to address that. Third, as we process data at the cell-pair level, inaccurate correspondences that lie the correct cell-pair will remain. These correspondences are useful in many applications which are not sensitive to matching accuracy such as Object Retrieval (Philbin et al. 2007). However, for accuracy-sensitive tasks, e.g., geometry estimation, they should be excluded. Therefore, we propose to run GMS on correspondences selected by RT instead of all putative correspondences for mitigating the issue. The efficacy of using RT as pre-processing can be seen in Fig. 7 and Table 4.
4 Experiments
We evaluate four aspects of GMS:
Comprehensive performance characterization on correspondence selection.
Matching challenging image pairs with significant relative scale and rotation changes.
Contribution to the overall performance of feature matching and epipolar geometry estimation.
Integration in real-time computer vision applications, i.e., Visual SLAM here.
4.1 GMS for Correspondence Selection
To comprehensively evaluate the performance of GMS, we experiment with different local features and varying feature numbers. We also examine the accuracy of retrieved correspondences using varying error thresholds. Two challenging datasets (Graffiti and Wall) selected from VGG (Mikolajczyk and Schmid 2005) are used for evaluation, which are well-known for significant viewpoint changes. Each dataset contains six images, where the ground truth homography between the first image to others is provided, resulting in five pairs with increasing difficulty for testing. Recall and Precision are used as evaluation metrics, where we regard correspondences those distances to the ground truth are smaller than 10 pixels as correct and others as wrong.
Results on pairs with gradually increasing viewpoint changes. “#” stands for the feature numbers. RT refers to Lowe’s ratio test (Lowe 2004). GMS and RT take all correspondences as input, while RT–GMS takes the results of RT as input. Therefore, the Recall of RT is the upper bound for RT–GMS
4.1.1 Results on Different Features
Figure 6 shows the results on Graffiti and Wall datasets, where SIFT (Lowe 2004) and ASIFT (Morel and Yu 2009) are used for generating correspondences, respectively. We test GMS on both all correspondences and the correspondences selected by Lowe’s ratio test. Here SIFT is not able to provide sufficient correct correspondences on very challenging pairs due to significant viewpoint changes, while ASIFT can. The results show that GMS gets high recall and precision on correspondences generated by ASIFT, while the recall degenerates on correspondences generated by SIFT. The reason is that ASIFT provide sufficient correspondences and GMS can translate the high feature numbers to high match quality, as indicated in Eq. 6, while SIFT correspondences are quite sparse. However, on SIFT correspondences, RT–GMS can achieve high performance, although they are sparse. Note that the Recall of RT is the upper bound of RT–GMS. This is because the performance of GMS is also related to the feature quality, as indicated in Eq. 6, and the quality of correspondences selected by RT is higher than that of initial correspondences in terms of precision. Compared with SIFT–RT, the most widely used feature matching method as we know, the proposed SIFT–RT–GMS can get similar recall (i.e., similar correspondence numbers) but higher precision. It has important implications for many computer vision applications. We show a comparison of both methods in Table 2, where the performance gap is wide on challenging wide-baseline datasets in terms of epipolar geometry estimation.
4.1.2 Accuracy of Correspondences
Figure 7 shows the results with varying error thresholds on Graffiti, where we use all correspondences in Graffiti (5 pairs) for evaluation. Note that regarding the number of correct correspondences, ALL is the upper bound for GMS, and RT is the upper bound for RT–GMS. The results show that ASIFT provides better correspondences than SIFT (see ALL for comparison). However, when RT or GMS is applied, the precision on SIFT correspondences is higher than that on ASIFT correspondences, especially when the error threshold is small, e.g., 1 or 2 pixels. This is because there are many correct but not accurate correspondences generated by ASIFT and selected by RT and GMS. These inaccurate correspondences are useful in many applications where the accuracy is not critical, e.g., Object Retrieval (Philbin et al. 2007). However, they limit the performance of accuracy-sensitive applications such as epipolar geometry estimation. Therefore, we suggest using SIFT–RT–GMS solution for high accuracy of matching. Note that using ASIFT is also possible and may lead to a higher performance, since ASIFT correspondences are generally better than SIFT correspondences. For example, Lin et al. (2017) uses ASIFT features and achieves the state-of-the-art performance in terms of camera pose estimation. However, it uses a highly complicated regression method, which consumes huge computational cost to remove inaccurate correspondences.
4.1.3 Performance with Varying Feature Numbers
Equation 6 indicates that the performance of GMS relies on feature numbers. To understand how feature numbers impact it, we randomly pick a subset of ASIFT features with varying maximum feature numbers for evaluation. Figure 8 shows the results on Graffiti dataset. It shows that GMS requires the most features, while the performance of RT is less sensitive to feature numbers. RT-GMS can reduce the number requirement of GMS and achieves the most accurate matching. Overall, we suggest users trying RT and RT-GMS in scenarios where feature numbers are limited. Besides, note that the performance of GMS is also related to feature quality. We show that with the same feature detector (i.e., the same feature numbers), using better descriptors could also improve the performance in Sect. 4.4.
Runtime of GMS in a single CPU thread. GMS-S and GMS-R repeat the basic GMS using different settings 5 and 8 times, respectively, so the runtime is linearly increased. GMS-SR, not shown in this figure, consumes 40 times more computational cost than the basic GMS. Note that the multi-scale and multi-rotation solutions could be accelerated by using multi-threshold programming, since no data dependence exists in different repeats
4.2 Robustness to Scale and Rotation Change
We use Semper and Venice datasets for testing the robustness of GMS to rotation and scale changes, respectively. Both datasets are selected from Heinly et al. (2012), which is an extension of VGG (Mikolajczyk and Schmid 2005) with the same data organization. We also use Boat dataset for testing, where image pairs have significant relative changes in both scale and rotation. Figure 9 shows the results, where we use SIFT feature (Lowe 2004) for generating putative correspondences and run GMS variants on correspondences selected by RT. It shows that the basic GMS is sensitive to large scale and rotation changes while using the multi-scale and multi-rotation solution can improve the performance significantly. Similar to previous results, the proposed method can achieve similar recall with RT and higher precision. We show visual results of GMS in Fig. 10, where the results on the most challenging pair of each dataset is illustrated. The scale invariance is critical in the unstructured environment, as the relative scale of images is unknown. We show that using the proposed multi-scale solution can significantly improve the performance for challenging wide-baseline scenarios in Table 4.
4.3 Runtime of GMS
We evaluate the runtime of GMS with varying feature numbers on Graffiti dataset using ASIFT features. Figure 11 shows the results, where GMS takes about only \(2\,ms\) in a single CPU thread, even when feature numbers reach 50, 000. The multi-scale (GMS-S) and multi-rotation (GMS-R) variants repeat the basic GMS with different pre-defined patterns 5 and 8 times, respectively. Therefore, their computational costs are linearly increased. We do not show GMS-SR in the figure for clarity. However, its time consuming is apparent, i.e., 40 times higher than the basic GMS. Note that both multi-scale and multi-rotation solutions have no data-dependent in different repeats, so they could be accelerated by using multi-thread programming. Theoretically, the multi-scale (or rotation) version could achieve the same speed with the basic GMS, when there are 5 (or 8) CPU threads available.
4.4 GMS for Epipolar Geometry Estimation
We evaluate the proposed method on FM-Bench (Bian et al. 2019), where correspondences selection methods are integrated into a classic feature matching and epipolar geometry estimation pipeline (i.e., SIFT, RANSAC, and the 8-point algorithm), and the overall performance is compared. The benchmark datasets, metrics, and baselines are described below.
4.4.1 Datasets
FM-Bench consists of 4 datasets, including TUM (Sturm et al. 2012), KITTI (Geiger and Lenz 2012), Tanks and Temples (T&T) (Knapitsch et al. 2017), and a Community Photo Collection (CPC) dataset (Wilson and Snavely 2014). The first two datasets are popular for Visual SLAM testing, which provide indoor and outdoor videos, respectively. The last two datasets are widely used for structure-from-motion evaluation, which provides wide-baseline scenarios. Especially, the CPC dataset is challenging, in which images are collected from the Internet and captured by tourists. 1000 matching image pairs per dataset are randomly picked by Bian et al. (2019) for testing. Table 1 summarizes the test dataset, and Fig. 12 shows sample images.
4.4.2 Baselines
We compare with three state-of-the-art correspondence selection methods, including CODE (Lin et al. 2017), LPM (Ma et al. 2019), LC (Yi et al. 2018) as strong baselines. CODE leverages the sophisticated non-linear optimization for finding correct correspondences, and it relies on a self-implemented GPU-ASIFT feature, which extracts several times more features than the standard ASIFT (Morel and Yu 2009). LPM explores neighborhood structures, and LC uses deeply trained neural networks. Both methods are independent of features and use SIFT (Lowe 2004) in the original paper. Note that the comparison is unfair to our method because CODE uses ASIFT features and a very complicated solution (\(1000\times \) slower than GMS).
4.4.3 Implementation Details
We use the DoG detector and SIFT descriptor (Lowe 2004) for generating putative correspondences. The implementation is from the VLFeat library (Vedaldi and Fulkerson 2010). We use the default parameters, which results in average 1082, 1751, 8133, and 7213 detected features in four datasets (as order in Fig. 12). The correspondences are pre-processed by using ratio test (RT), with the threshold being 0.8. Then we apply the evaluate methods (LPM, LC, and GMS) for good correspondence selection. We empirically find that using correspondences by RT results in better performance than using all correspondences for LC (Yi et al. 2018), although it uses the latter in the original paper. We use the basic GMS in the first two SLAM datasets and the multi-scale solution in the last two SfM datasets, as where images are more unstructured. The multi-rotation solution is not used since there is no significant image rotation in these datasets. For CODE (Lin et al. 2017), we directly evaluate the output correspondences since it is a highly integrated correspondence system. We use the publicly available implementation for all methods and use the pre-trained model by authors for LC.
4.4.4 Metrics
To compare the overall performance of different correspondence systems, we fed their correspondences into a RANSAC-based 8-point estimator (Fischler and Bolles 1981; Hartley 1997) to recover the FM, and then compare the estimated FM with the ground truth FM using normalized symmetric geometry distance (NSGD) (Bian et al. 2019). See the appendix for details. We then report the success ratio of FM estimation (%Recall), where the NSGD threshold is 0.05, and we also show the results with varying error thresholds. What’s more, we report the inlier rate (%Inlier) after RANSAC-based outlier removal for match quality comparison. Here inliers refer to matches those distances to the ground truth epipolar lines are smaller than \(\alpha * l\), where l stands for the length of image diagonal and \(\alpha = 0.003\). More details can be found in the appendix and Bian et al. (2019).
4.4.5 Experimental Results
Table 2 shows the recall of FM estimation. Figure 13 shows the results with varying error thresholds on two wide-baseline datasets. Table 3 reports the inlier rate. All the above results demonstrate that GMS can show better performance with LC (Yi et al. 2018) and LPM (Ma et al. 2019) using the same feature correspondences as input, i.e., SIFT–RT (Lowe 2004). However, our correspondence system is not as good as the powerful CODE (Lin et al. 2017) system. Compares with SIFT–RT, our approach can lead to significantly better results on T&T and CPC datasets, demonstrating the efficacy of GMS for high-accuracy matching. Concerning the runtime, CODE requires several seconds for correspondence selection, while GMS is more 1000 times faster. As the authors reported, LC needs 13 ms on GPU (or 25 ms on CPU) to find good correspondences from 2K putative matches, and LPM can identify false matches from 1000 putative correspondences in a few milliseconds. They are both slower than the proposed method (Fig. 11).
4.4.6 Effects of RT and Multi-scale
To understand how our multi-scale solution and using RT before GMS can benefit the overall performance, we conduct an ablation study by removing them respectively. The results are shown in Table 4. It shows that the performance is significantly decreased without RT. The reason is that inaccurate correspondences are included, and they limit the performance of geometry estimation. Besides, the results on wide-baseline matching datasets (T&T and CPC) demonstrate that using the proposed multi-scale solution can significantly improve the performance.
4.4.7 Paring with Deep Features
As Eq. 6 indicates that the performance of GMS is related to feature quality, we experiment with recently proposed deep learning based features, including the HardNet (Mishchuk et al. 2017) descriptor and HessAff (Mishkin et al. 2018) detector. Specifically, we use DoG (Lowe 2004) and HessAff for interest point detection, respectively. Then we use use HardNet to compute descriptors, resulting in two putative correspondence generation solutions. The powerful CODE is compared as the strong baseline. Instead of RANSAC, we use LMedS (Rousseeuw and Leroy 1987) based FM estimator here, as it shows better performance than the former in FM-Bench (Bian et al. 2019). Table 5 shows the results, where GMS with deep features can achieve a competitive performance with CODE (Lin et al. 2017). The results are remarkable and have important implications to real-time applications since these deep features are efficient, while CODE is several orders of magnitude slower.
4.5 GMS for Monocular SLAM Initialization
Monocular SLAM methods (Mur-Artal et al. 2015) have to initialize the system before tracking and mapping, where the initial 3D map is created by triangulating correspondences to recover depths. Robust initialization has important implications for a monocular SLAM system, and high-quality correspondence is the key to this step. As Visual SLAM systems have high requirements for the run-time of methods for the overall real-time performance, many advanced correspondence approaches can not be used in this scenario. Fortunately, GMS is sufficiently fast for this purpose. In this section, we show that GMS can be used in the popular ORB-SLAM system (Mur-Artal et al. 2015) for better initialization.
4.5.1 Integration
In the initializer of ORB-SLAM, we replace the original Bag-of-Words based matching with the brute-force nearest neighbor matching, and we apply GMS for selecting good correspondences. The selected matches are used to recover geometry and create the 3D map by triangulation. For system stability, we use the default feature detection parameters, i.e., detecting 4K well-distributed ORB features for initialization in KITTI-like images.
4.5.2 Dataset and Metrics
We evaluate methods on the sequence 00–10 of KITTI odometry dataset (Geiger and Lenz 2012). For each sequence, we crop it into non-overlap fragments, with each fragment containing 20 consecutive frames. The performance averaged over all fragments is reported In each fragment, we measure (1) whether the initialization is successful; (2) how quickly the system is initialized; and (3) how many 3D points are generated. Regarding (1), we compare the estimated camera pose with the ground truth, and those are recognized as successful if pose error is less than 5 degrees in both rotation and translation. Regarding (2), we report the order of the first successfully initialized image in each fragment.
4.5.3 Experimental Results
Table 6 shows the results, where we compare with the original initializer. It shows that the proposed initializer leads to a significantly higher success ratio, faster initialization, and denser 3D map. This has a huge impact on monocular SLAM systems, especially when they work on challenging environments where previous solutions fail to provide reliable correspondences for initialization. The proposed method can mitigate this issue and enable the use of SLAM systems in more real-world scenarios.
5 Conclusion
This paper presents a fast correspondence selection algorithm that we termed grid-based motion statistics (GMS). It can effectively separate true correspondences from false ones at high speed by leveraging the motion smoothness constraint. Comprehensive experimental results demonstrate its robustness in different environments. We also show that it advances the feature matching and geometry estimation. Moreover, we plug GMS into the Monocular ORB-SLAM system for initialization, demonstrating its great potential to real-time applications. The code has been released and integrated into the OpenCV library.
References
Bian, J., Lin, W.-Y., Matsushita, Y., Yeung, S.-K., Nguyen, T. D., & Cheng, M.-M. (2017). GMS: Grid-based motion statistics for fast, ultra-robust feature correspondence. In IEEE conference on computer vision and pattern recognition (CVPR) (pp. 4181–4190). IEEE.
Bian, J.-W., Wu, Y.-H., Zhao, J., Liu, Y., Zhang, L., Cheng, M.-M., et al. (2019). An evaluation of feature matchers for fundamental matrix estimation. In British machine vision conference (BMVC).
Bradski, G. (2000). The OpenCV library. Dr. Dobb’s Journal of Software Tools.
Breiman, L. (2001). Random forests. Machine Learning, 45(1), 5–32.
Causo, A., Chong, Z.-H., Luxman, R., Kok, Y. Y., Yi, Z., Pang, W.-C., et al. (2018). A robust robot design for item picking. In 2018 IEEE international conference on robotics and automation (ICRA) (pp. 7421–7426). IEEE
Cheng, M.-M., Liu, Y., Hou, Q., Bian, J., Torr, P., Hu, S.-M., et al. (2016). HFS: Hierarchical feature selection for efficient image segmentation. In European conference on computer vision (ECCV) (pp. 867–882). Springer.
Davison, A. J., Reid, I. D., Molton, N. D., & Stasse, O. (2007). Monoslam: Real-time single camera slam. IEEE Transactions on Pattern Recognition and Machine Intelligence, 29(6), 1052–1067.
Fischler, M. A., & Bolles, R. C. (1981). Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Communications of the ACM, 24(6), 381–395.
Geiger, A., Lenz, P., & Urtasun, R. (2012). Are we ready for autonomous driving? the kitti vision benchmark suite. In IEEE conference on computer vision and pattern recognition (CVPR) (pp. 3354–3361). IEEE.
Harris, C., & Stephens, M. (1988). A combined corner and edge detector. In Alvey vision conference (pp. 10–5244).
Hartley, R. I. (1997). In defense of the eight-point algorithm. IEEE Transactions on Pattern Recognition and Machine Intelligence, 19(6), 580–593.
Heinly, J., Dunn, E., & Frahm, J.-M. (2012). Comparative Evaluation of Binary Features. In European conference on computer vision (ECCV) (pp. 759–773).
Knapitsch, A., Park, J., Zhou, Q.-Y., & Koltun, V. (2017). Tanks and Temples: Benchmarking large-scale scene reconstruction. ACM Transactions on Graphics, 36(4), 78.
Kushnir, M., & Shimshoni, I. (2014). Epipolar geometry estimation for urban scenes with repetitive structures. IEEE Transactions on Pattern Recognition and Machine Intelligence, 36(12), 2381–2395.
Lin, W.-Y., Lai, J.-H., Liu, S., & Matsushita, Y. (2018). Dimensionality’s blessing: Clustering images by underlying distribution. In Proceedings of the IEEE conference on computer vision and pattern recognition (pp. 5784–5793).
Lin, W.-Y., Wang, F., Cheng, M.-M., Yeung, S.-K., Torr, P. H., Do, M. N., et al. (2017). Code: Coherence based decision boundaries for feature correspondence. IEEE Transactions on Pattern Recognition and Machine Intelligence, 40(1), 34–47.
Liu, Y., Cheng, M.-M., Hu, X., Bian, J.-W., Zhang, L., Bai, X., et al. (2019). Richer convolutional features for edge detection. IEEE Transactions on Pattern Recognition and Machine Intelligence, 41(8), 1939–1946.
Liu, Y., Jiang, P.-T., Petrosyan, V., Li, S.-J., Bian, J., Zhang, L., et al. (2018). DEL: Deep embedding learning for efficient image segmentation. In International joint conference on artificial intelligence (IJCAI).
Liu, Z., & Marlet, R. (2012). Virtual line descriptor and semi-local matching method for reliable feature correspondence. In British machine vision conference (BMVC) (pp. 16–1).
Lowe, D. G. (2004). Distinctive image features from scale-invariant keypoints. International Journal on Computer Vision, 60(2), 91–110.
Ma, J., Zhao, J., Jiang, J., Zhou, H., & Guo, X. (2019). Locality preserving matching. International Journal on Computer Vision, 127(5), 512–531.
Ma, J., Zhao, J., Tian, J., Yuille, A. L., & Tu, Z. (2014). Robust point matching via vector field consensus. IEEE Transactions on Image Processing, 23(4), 1706–1721.
Mikolajczyk, K., & Schmid, C. (2005). A performance evaluation of local descriptors. IEEE Transactions on Pattern Recognition and Machine Intelligence, 27(10), 1615–1630.
Mishchuk, A., Mishkin, D., Radenovic, F., & Matas, J. (2017). Working hard to know your neighbor’s margins: Local descriptor learning loss. In Neural information processing systems (NIPS) (pp. 4826–4837).
Mishkin, D., Radenovic, F., & Matas, J. (2018). Repeatability is not enough: Learning affine regions via discriminability. In European conference on computer vision (ECCV) (pp. 284–300). Springer.
Morel, J.-M., & Yu, G. (2009). Asift: A new framework for fully affine invariant image comparison. SIAM Journal on Imaging Sciences, 2(2), 438–469.
Muja, M., & Lowe, D. G. (2009). Fast approximate nearest neighbors with automatic algorithm configuration. VISAPP (1), 2(331–340), 2.
Mur-Artal, R., Montiel, J. M. M., & Tardos, J. D. (2015). ORB-SLAM: A versatile and accurate monocular slam system. IEEE Transactions on Robotics, 31(5), 1147–1163.
Philbin, J., Chum, O., Isard, M., Sivic, J., & Zisserman, A. (2007). Object retrieval with large vocabularies and fast spatial matching. In IEEE conference on computer vision and pattern recognition (CVPR) (pp. 1–8). IEEE.
Ranftl, R., & Koltun, V. (2018). Deep fundamental matrix estimation. In European conference on computer vision (ECCV) (pp. 284–299).
Rousseeuw, P. J., & Leroy, A. M. (1987). Robust regression and outlier detection (Vol. 589). New York: wiley.
Rublee, E., Rabaud, V., Konolige, K., & Bradski, G. (2011). ORB: An efficient alternative to sift or surf. In IEEE international conference on computer vision (ICCV) (pp. 2564–2571). IEEE.
Schonberger, J. L., & Frahm, J.-M. (2016). Structure-from-motion revisited. In IEEE conference on computer vision and pattern recognition (CVPR) (pp. 4104–4113).
Sturm, J., Engelhard, N., Endres, F., Burgard, W., & Cremers, D. (2012). A benchmark for the evaluation of RGB-d slam systems. In IEEE international conference on intelligent robots and systems (IROS) (pp. 573–580). IEEE.
Vedaldi, A., & Fulkerson, B. (2010). VLFeat: An open and portable library of computer vision algorithms. In ACM international conference on multimedia (ACM MM) (pp. 1469–1472). ACM.
Wilson, K., & Snavely, N. (2014). Robust global translations with 1DSFM. In European conference on computer vision (ECCV) (pp. 61–75). Springer.
Yi, K. M., Trulls, E., Ono, Y., Lepetit, V., Salzmann, M., & Fua, P. (2018). Learning to find good correspondences. In IEEE conference on computer vision and pattern recognition (CVPR) (pp. 2666–2674).
Yoon, J. S., Li, Z., & Park, H. S. (2018). 3D semantic trajectory reconstruction from 3D pixel continuum. In IEEE conference on computer vision and pattern recognition (CVPR) (pp. 5060–5069).
Zhang, H., Hasith, K., & Wang, H. (2019). GMC: Grid based motion clustering in dynamic environment. In Proceedings of SAI intelligent systems conference (pp. 1267-1280). Springer, Cham.
Zhang, Z. (1998). Determining the epipolar geometry and its uncertainty: A review. International Journal on Computer Vision, 27(2), 161–195.
Acknowledgements
This work was supported by Australian Centre of Excellence for Robotic Vision CE140100016, and the ARC Laureate Fellowship FL130100102 to Prof. Ian Reid. This work was supported by Major Project for New Generation of AI (No. 2018AAA0100403), NSFC (61922046), and Tianjin Natural Science Foundation (No. 18JCYBJC41300 and No. 18ZXZNGX00110) to Prof. Ming-Ming Cheng. This work was supported by the Singapore Ministry of Education (MOE) Academic Research Fund (AcRF) Tier 1 grant to Prof. Wen-Yan Lin. This work was supported by the Singapore MOE Academic Research Fund MOE2016-T2-2-154, and an internal grant from HKUST (R9429) to Prof. Sai-Kit Yeung. Besides, the authors thank Prof. Yasuyuki Matsushita for his contribution in the early stage of this paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Jiri Matas.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
1.1 Normalized SGD
We use the NSGD (Bian et al. 2019) to measure the geometric distance between two fundamental matrices (FMs), which is an extension of the SGD error (Zhang 1998). The method generates virtual correspondences using two models, and crossly computes the distance of correspondence to the epipolar line generated by the other model. The results are symmetrical, i.e., the error from F1 to F2 is equal to the error from F2 to F1. For generalization in different resolution images, we rescale the error to the range (0, 1) by dividing the length of image diagonal.
1.2 FM Ground Truth
The fundamental matrix between an image pair can be derived from the camera intrinsic and extrinsic parameters. The ground-truth camera parameters are provided in TUM and KITTI datasets, while they are unknown in T&T and CPC datasets. We derive ground-truth camera parameters for the latter by reconstructing image sequences using the COLMAP (Schonberger and Frahm 2016) library, as in Yi et al. (2018), Ranftl and Koltun (2018). Note that the SfM pipeline reasons globally about the consistency of 3D points and cameras, leading to accurate estimates with an average reprojection error below one pixel.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bian, JW., Lin, WY., Liu, Y. et al. GMS: Grid-Based Motion Statistics for Fast, Ultra-robust Feature Correspondence. Int J Comput Vis 128, 1580–1593 (2020). https://doi.org/10.1007/s11263-019-01280-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11263-019-01280-3