Abstract
This paper presents a general approach based on the shape similarity tree for non-sequential alignment across databases of multiple unstructured mesh sequences from non-rigid surface capture. The optimal shape similarity tree for non-rigid alignment is defined as the minimum spanning tree in shape similarity space. Non-sequential alignment based on the shape similarity tree minimises the total non-rigid deformation required to register all frames in a database into a consistent mesh structure with surfaces in correspondence. This allows alignment across multiple sequences of different motions, reduces drift in sequential alignment and is robust to rapid non-rigid motion. Evaluation is performed on three benchmark databases of 3D mesh sequences with a variety of complex human and cloth motion. Comparison with sequential alignment demonstrates reduced errors due to drift and improved robustness to large non-rigid deformation, together with global alignment across multiple sequences which is not possible with previous sequential approaches.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Non-rigid surface reconstruction from multiple view video has advanced to allow reconstruction of detailed surface deformation such as clothing. For scenes with complex non-rigid deformation multiple-view reconstruction is commonly performed independently at each frame resulting in an unstructured sequence of meshes with each mesh having different vertex positions and connectivity. Recent advances in active depth measurement have also introduced low-cost structured light and time-of-flight sensors allowing video-rate 2.5D acquisition of unstructured mesh sequences for the partial non-rigid surface visible from a single viewpoint. The lack of a temporally consistent mesh structure or surface correspondence limits captured sequences to replay of the dynamic scene and prevents subsequent manipulation or use in conventional graphics pipelines which assume deformable surfaces are represented with a consistent mesh structure with only the surface shape varying over time.
Conversion of reconstructed unstructured mesh sequences into a temporally coherent format is therefore an important problem which has received increasing interest in the literature. Research has focused on the problem of extracting a temporally consistent mesh representations over sequences by non-rigid surface tracking using either model-based (de Aguiar et al. 2008; Starck and Hilton 2003; Vlasic et al. 2008) or model-free (Ahmed et al. 2008; Bronstein et al. 2007; Cagniart et al. 2010b; Starck and Hilton 2007a; Tevs et al. 2011; Tung and Matsuyama 2010; Zeng et al. 2010) approaches. These single sequence alignment approaches commonly employ a sequential frame-to-frame registration assuming relatively small non-rigid deformation between consecutive frames. Impressive results have been demonstrated on highly non-rigid surfaces such as people with loose clothing performing complex movements. Sequential tracking approaches have two inherent limitations: drift due to accumulation of errors in alignment between successive frames; and alignment failure due to large changes in surface shape or reconstructed surface topology between successive frames. In addition sequential approaches do not allow alignment between different sequences.
In this paper we introduce a global non-sequential approach to non-rigid surface alignment which addresses three problems: reliable alignment of non-rigid surface sequences in the presence of large non-rigid deformations; reduced drift due to accumulation of errors in sequential alignment; and alignment across multiple sequences of the same non-rigid object performing different motions. The problem of alignment across multiple sequences commonly occurs for example in capturing a database of human movement composed of short-clips of different motions (Huang et al. 2009). Global alignment of a database of mesh sequences into a consistent mesh structure is an important step for the analysis of non-rigid surface dynamics, efficient storage and reuse of captured mesh sequences in computer graphics applications.
This paper extends recent research on global non-rigid mesh sequence alignment (Budd et al. 2011; Huang et al. 2011) by introducing a general formulation of the global alignment problem, presenting a comprehensive benchmark evaluation on multiple databases of captured 3D mesh sequences and comparative performance evaluation with state-of-the-art sequential non-rigid alignment (Cagniart et al. 2010b). In previous work Huang et al. (2011) only considered the problem of inter-sequence alignment assuming that individual sequences were aligned a priori using sequential alignment. In this paper we generalise the approach to simultaneous inter and intra sequence alignment across all frames in a database. Budd et al. (2011) introduced the shape similarity tree, in this paper we present a general approach to optimal tree construction based on the minimum spanning tree which is fully automatic avoiding any thresholds on similarity and present a comprehensive performance evaluation on multiple benchmark datasets.
1.1 Overview
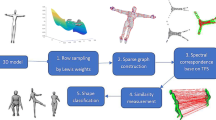
A global non-rigid surface alignment framework is presented which minimises the total deformation required to register all meshes from different input sequences into a temporally consistent structure. An overview of the global alignment framework is presented in Fig. 1. The input is a database of unstructured mesh sequences of different non-rigid motions reconstructed from multiple view video or other sensors. Shape similarity between pairs of meshes with unknown correspondence (Huang et al. 2010) is used as a measure of the cost of pairwise non-rigid alignment. The shape similarity tree is introduced to represent the non-sequential alignment which minimises the total non-rigid deformation. The optimal shape similarity tree is defined as the minimum spanning tree containing all meshes in the input databases with edge costs evaluated by shape similarity. Global alignment is achieved by pairwise non-rigid alignment based on the edges in the optimal shape similarity tree using any existing sequential non-rigid alignment technique (de Aguiar et al. 2008; Cagniart et al. 2010a, 2010b). This minimises the non-rigid deformation required to align pairs of meshes reducing errors due to drift in alignment. Non-sequential alignment also maximises the similarity between pairs of meshes to be aligned enabling robust alignment in the presence of larger inter-frame change in shape and reconstructed surface topology. Global alignment based on the shape similarity tree results in a temporally consistent mesh structure with correspondence across all frames.
Results demonstrate temporally coherent mesh sequences obtained for several public databases of mesh sequences for multiple people performing a variety of motions including complex break dance sequences and loose clothing, and for face sequences with an open-mesh. Quantitative evaluation for individual sequences against existing sequential alignment demonstrates improved accuracy in approximating the input sequence, reduced drift and robustness to large non-rigid deformations which may cause sequential approaches to fail. In addition, the proposed global approach allows alignment across multiple sequences enabling databases of temporally aligned mesh sequences to be represented as a 4D spatio-temporal non-rigid surface model.
2 Related Work
2.1 Sequential Non-rigid Alignment
A critical step for editing and reuse of 3D performance capture is the temporal alignment of captured mesh sequences to obtain a consistent mesh structure with surface correspondence over time. A number of approaches have been proposed for temporal alignment of mesh sequences based on sequential frame-to-frame surface tracking. These can be categorised into two methodologies: model-based approaches which assume a known non-rigid object class such as a person and align a prior model of the surface with successive frames (Carranza et al. 2003; de Aguiar et al. 2008; Starck and Hilton 2003; Vlasic et al. 2008); and surface-tracking or scene flow approaches which do not assume prior knowledge of the surface structure allowing alignment of freeform non-rigid surfaces (Cagniart et al. 2010a; Starck and Hilton 2005, 2007a; Tevs et al. 2011; Vedula et al. 2005; Wand et al. 2009).
2.1.1 Model-Based Sequential Alignment
Surface correspondence has been addressed using prior models of shape and appearance. Model registration and fitting at arbitrary time points provides an approximate surface correspondence via the intermediate domain of the model surface. Salzmann et al. (2007) construct a parameterised deformable model for the non-rigid motion of inextensible planar surfaces. Correspondence is derived in monocular image sequences using wide-baseline feature matching for registration and by fitting the parameterised model. In the medical domain, deformable models have been widely used to extract anatomical surfaces using landmark registration and model deformation (McInerney and Terzopoulos 1996). For human surface shape, parameterised models are widely used to derive the gross articulated motion of the human body (Moeslund et al. 2006, 2011). Deformable surface fitting has been performed given the pose of a skeleton model to extract the shape and appearance of a person at different time frames (Starck and Hilton 2003; Carranza et al. 2003). Model-based matching and fitting is however inherently limited to the shape and topology of the prior parameterised model, which constrains the space of feasible surface deformations. For example, a generic human body will not match a person with loose clothing or dynamic hair motion.
Carranza et al. (2003) presented one of the first model-based approaches utilising an articulated character model to estimate the skeletal pose by matching multiple view image silhouettes at each frame. This allowed reconstruction of complex human motions but did not recover detailed changes in surface shape. de Aguiar et al. (2008) used a high-resolution surface scan as a prior model together with a volumetric Laplacian mesh deformation scheme to align the high-resolution surface from frame-to-frame. This achieved convincing reproduction of surface deformation for loose clothing. A similar approach has recently been combined with physics-based cloth simulation to segment loose clothing deformation parameters allowing realistic synthesis of cloth motion based on novel character motion (Stoll et al. 2010). Vlasic et al. (2008) used an articulated deformable model to track surfaces across complex sequences together with manual interaction to correct tracking for frames where surface reconstruction is ambiguous. Subsequent work (Baran et al. 2009) introduced a method for transfer of captured surface deformation between sequences. Model-based approaches have the advantage of providing a consistent structured representation but may not allow accurate reconstruction of complex non-rigid surface deformation such as loose hair or clothing.
2.1.2 Free-Form Sequential Alignment
Simultaneous estimation of structure and motion for non-rigid surfaces has been addressed using flow-based algorithms to track surfaces in multiple view video sequences. Neumann and Aloimonos (2002) match a prior multi-resolution subdivision surface to spatio-temporal stereo and contour constraints. Carceroni and Kutulakos (2002) compute shape and non-rigid motion under known lighting conditions using relatively large scale 3D surface elements. Pons et al. (2007) present a variational approach for reconstruction and scene-flow providing a global solution for the motion estimation of a surface. For cloth motion, distinct features have been used in tracking to produce a consistent surface parameterisation requiring either highly texture surfaces (Pritchard and Heidrich 2003) or a colour-coded pattern (Scholz et al. 2005; White et al. 2007). Cloth motion has also been captured without patterns by establishing temporally coherent parameterisation for partial surface reconstructions and registration with a template mesh (Bradley et al. 2008). Furukawa and Ponce (2010) introduce a method for simultaneous reconstruction and tracking of dense 3D meshes from multiple view face sequences with textured makeup which was also demonstrated on patterned clothing. A registration to the first frame in the sequences was also employed to reduce drift.
Multiple-view scene reconstruction recovers a separate surface representation at each time instant and does not provide the structure and motion of the underlying scene. Vedula et al. (2005) introduced the concept of scene-flow as the extension of 2D optical flow to 3D non-rigid surfaces. Starck and Hilton (2005) employed a bijective mapping for surfaces of spherical topology to track the non-rigid deformation in a 2D domain which was applied to alignment of non-rigid sequences of people. The bijective mapping enforces a dense one-to-one correspondence for all surface points but for general surfaces requires the insertion of cuts to enforce the spherical topology for all frames. Specific approaches have also been introduced for extension of optical flow to tracking of 3D facial motion from reconstructed surface sequences (Zhang et al. 2004; Bradley et al. 2010). Tevs et al. (2011) propose an approach referred to as animation cartography where a consistent map for surface patches is constructed based on tracking of sparse landmarks. Dense mapping and correspondence of the surface is constructed assuming isometric deformation. This approach demonstrates robust alignment of partial surface sequences from 2.5D surface measurements. Cagniart et al. (2010a, 2010b) recently demonstrated impressive results for free-form surface tracking of complex sequences with changes in surface topology. Their approach employs iterative closest point matching of overlapping rigid-patches. A Laplacian mesh deformation framework (Sorkine 2006) is used to regularise the patch matching by enforcing soft constraints between adjacent patches.
Sequential alignment approaches have two inherent limitations: accumulation of errors in frame-to-frame alignment resulting in drift in correspondence over time; and gross-errors for large non-rigid deformations which can occur with rapid movements requiring manual correction to align the remainder of the sequence. In addition sequential approaches do not allow alignment across multiple sequences which may have large differences in shape and motion.
2.2 Non-sequential Non-rigid Surface Alignment
In this paper we introduce an approach for non-sequential alignment of databases of mesh sequences containing multiple motions. The approach is based on non-sequential alignment of frames using their shape and motion similarity. This ensures that sub-sequences of similar frames are aligned reducing errors in mesh sequence alignment due to drift or alignment failure due to large changes in shape between successive frames. Non-sequential alignment also identifies similar frames in different sequences allowing databases with multiple motions to be aligned.
Pairwise alignment of widely spaced image frames and 3D mesh models subject to large non-rigid deformations has previously been investigated. Feature based surface matching approaches have commonly been proposed for the problem of appearance matching in images and shape matching for surfaces. In wide-baseline image matching (Mikolajczyk and Schmid 2005) affine invariant feature descriptors are typically adopted as invariant to transformations between views. For monocular image sequences Liing and Jacobs (2005) introduce a local appearance distribution descriptor for deformation-invariant image matching. Belongie et al. (2002) proposed a local shape context descriptor for deformable 2D shape matching. Local feature descriptors have been developed for 3D shape matching in 3D shape recognition (Iyer et al. 2005). Gal et al. (2007) introduce a local shape distribution descriptor that is invariant to articulated pose. Gatzke et al. (2005) resample surface curvature onto a radial descriptor embedded on the surface. Elad and Kimmel (2003) construct bending invariant representations using an isometric embedding for a surface in a higher dimensional Euclidean space. Starck and Hilton (2007a) proposed a set of bending invariant local descriptors for both shape and appearance for dense matching between surfaces under large non-rigid deformations.
These approaches allow dense correspondence between pairs of non-rigid object surfaces at widely spaced timeframes but do not address the problem of alignment of entire sequences. Matching across large non-rigid deformations could also potentially be applied to pairwise alignment between sequences for different motions. However, these approaches are relatively computationally expensive and for sequential tracking would be subject to the accumulation of errors resulting in drift. Non-sequential approaches have recently been proposed in the context of reconstruction from video using structure-from-motion to reduce drift in reconstruction (Enqvist et al. 2011; Gherhadi et al. 2010). In this case reconstruction is performed over sub-sequences of the video and fused into a single scene reconstruction using a hierarchical tree structure. This non-sequential reconstruction improves efficiency and reduces accumulation of reconstruction errors across the sequence.
Beeler et al. (2011) presented an approach based on anchor frames to reduce drift for alignment of reconstructed non-rigid face sequences. The approach assumes anchor frames similar to a manually selected reference expression are distributed across the sequence. Pairwise alignment of anchor frames with the reference reduces alignment to subsequences reducing drift due to accumulation of errors in sequential alignment. This approach implicitly uses a non-sequential alignment based on a tree with branches from the reference pose to each of the anchor frame.
In this paper a non-sequential approach is presented based on the shape similarity tree representation (Budd et al. 2011). The shape similarity links frames with similar shape and motion across the sequence providing a general representation for non-sequential alignment over one or more sequences. Non-sequential alignment changes the order in which frames are aligned to maximise the similarity of adjacent frames allowing existing pairwise alignment algorithms to be applied whilst reducing drift and alignment failure.
3 Optimal Non-sequential Alignment
3.1 Problem Formulation
The problem of global non-rigid alignment of multiple mesh sequences can be stated as follows:
Given a set of non-rigid mesh sequences \(\{S_{i}\}_{i=1}^{N}\) of a deforming object such that each sequence S i is a sequence of unaligned meshes \(S_{i}=\{M_{i}(t_{u})\}_{u=1}^{N_{i}}\) where each mesh M i (t u )=(C i (t u ),X i (t u )) has a time varying vertex connectivity C i (t u ) and vertex positions X i (t u ). Then the problem is to obtain a single temporally coherent mesh representation for all sequences such that for each frame \(\hat {M}_{i}(t_{u}) = (\hat{C},\hat{X}_{i}(t_{u}))\) where \(\hat{C}\) is the global connectivity which is the same for all meshes \(\hat{M}_{i}(t_{u})\) over all aligned sequences \(\hat{S}_{i}\). Here \(\hat{ }\) denotes temporal consistency across all frames.
In addition we require that two conditions on the resampled mesh vertices \(\hat{X}_{i}(t_{u})\) are satisfied:
- Condition 1—Shape Preservation: :
-
Shape is preserved such that all vertices of the temporally aligned mesh lie on the unaligned mesh, \(\hat{X}_{i}(t_{u}) \in M_{i}(t_{u})\), and vice-versa, \(X_{i}(t_{u}) \in\hat {M}_{i}(t_{u})\);
- Condition 2—Temporal Correspondence: :
-
Temporal alignment is introduced such that if the rth vertex \(\hat{x}_{ir}(t_{u}) \in \hat {X}_{i}(t_{u})\) lies at position p(t u )∈M i (t u ) then \(\hat {x}_{jr}(t_{v}) = p(t_{v}) \in M_{j}(t_{v})\) where p(t v ) is the surface point position corresponding to p(t u ) for all times t v over all sequences j∈N.
In practice, conditions (1) and (2) should be satisfied within an error tolerance for resampling and tracking which is less than the surface reconstruction error.
Global alignment of a database of reconstructed mesh sequences is performed in three stages:
-
1.
Shape similarity evaluation: Evaluate the shape and motion similarity s(M i (t u ),M j (t v )) for all pairs of frames across all sequences.
-
2.
Shape similarity tree construction: Construct the minimum spanning tree given by the shortest path in shape similarity space for all frames.
-
3.
Global non-rigid alignment: All frames for all sequences are aligned and re-meshed to have a single connectivity \(\hat{C}\) based on the shortest paths defined by the shape similarity tree.
The branches of the shape similarity tree define the shortest path in similarity space between frames. This defines a non-sequential ordering of frames for alignment. Figure 1 presents an overview of the alignment process from raw unstructured mesh sequences to a single temporally coherent representation.
3.2 Shape Similarity
To construct the shape similarity tree we require a measure of similarity s(M i (t u ),M j (t v )) between pairs of meshes which can be evaluated without prior knowledge of the surface correspondence. A number of similarity measures for mesh sequences taking into account both shape and motion have been investigated (Tung and Matsuyama 2010; Huang et al. 2010). In this work we utilise the temporally filtered volumetric shape histogram as a measure of shape and non-rigid motion similarity which has been shown to give good performance on reconstructed mesh sequences of people (Huang et al. 2010).
The volumetric shape histogram subdivides ℜ3 space into radial and angular bins (Δr,Δθ,Δϕ) based on a spherical coordinate system located at the centroid of the mesh M (Huang et al. 2010), as illustrated in Fig. 2. The volumetric shape histogram H(M) represents the spatial occupancy of the bins for a given mesh M. We define a measure of shape similarity s(M i (t u ),M j (t r )) between two mesh M i (t u ) and M j (t v ) by optimising for the maximum overlap between their corresponding radial bins with respect to rotation about the centroid.

where ∥⋅∥ denotes the sum of squared differences over all bins in the histogram and H(M,θ,ϕ) is the spherical histogram H(M) rotated by angles (θ,ϕ) for invariance to orientation. For a database of mesh sequences the shape similarity matrix A between all frames is evaluated. Note small values of s() from (1) indicate a high similarity in shape between meshes. A measure of shape and non-rigid motion similarity is obtained by a weighted average of shape similarity over a temporal window. This can be efficiently evaluated by diagonal filtering of the shape similarity matrix A (Huang et al. 2010). An example similarity matrix is shown in Fig. 3(a), similarity values are colour mapped high-similarity (dark-blue) to low-similarity (red).
3.3 Shape Similarity Tree
For existing sequential pairwise approaches to non-rigid mesh sequence alignment errors increase as the difference in shape between meshes increases. In practice pairwise alignment error ϵ increases non-linearly with the difference in shape Δ (ϵ∝Δγ where γ>1) and for large differences in shape pairwise alignment may fail to give a valid alignment. The exact relationship will depend on both the method of pairwise alignment and the data as the similarity is only an approximation of the unknown non-rigid deformation between shapes.
We therefore propose a tree structure representing a database of mesh sequences based on their relative shape and motion similarity. This representation defines a non-sequential ordering for pairwise non-rigid alignment of frames. The optimal shape similarity tree which minimises the total cost of pairwise alignment is constructed.
Shape similarity is used to construct a tree representing the shortest non-rigid surface motion path required to align all meshes \(\{M_{i}(t_{u})\} _{u=1}^{N_{i}}\) from multiple captured mesh sequences. Initially a complete graph Ω is constructed with nodes for all meshes M i (t u ) in all sequences S i and edges e iujv =e(M i (t u ),M j (t v )) connecting all nodes. Edges e iujv are weighted according to the similarity measure s(M i (t u ),M j (t v )). The optimal shape similarity tree T sst which minimises the total non-rigid deformation required for alignment can then be evaluated as the minimum spanning tree (MST) of the complete graph Ω.
Equation (2) gives the optimal tree from the set of all trees T in the complete graph Ω which include all frames in the database as nodes. The minimum spanning tree T sst ∈Ω represents the minimum total path length in shape similarity space for alignment across all frames. The tree root node M root is defined as the mesh with minimum path length to all nodes in T sst . The minimum spanning tree can be efficiently evaluated using established algorithms with order O(nlog(n)) complexity where n is the number of nodes in the graph Ω (Prim 1957; Kruskal 1956). Evaluation of the shape similarity tree for the 1800 frame StreetDance database takes approximately 6.5 seconds on a single processor.
The optimal shape similarity tree is defined according to the minimum spanning tree rather than the shortest path tree (SPT) as MST minimises the total non-rigid deformation. Figure 4 shows a simple example of why the MST is preferable for non-rigid alignment. SPT will favour short paths with large inter-frame differences in shape where disproportionaly large errors in pairwise alignment may occur due to the non-linear relationship between error and dissimilarity. In contrast the MST identifies paths which favour small inter-frame differences in shape. Thus alignment based on the MST minimises the accumulation of errors in alignment. MST also orders similar frames closer to the root with larger inter-frame changes towards the leaves of the tree, this limits the propagation of errors in alignment between meshes with relatively large differences in shape to the ends of the branches.
Figure 3 shows the similarity matrix and shape similarity tree for the StreetDance database of 1800 frames comprising six sequences of complex motion. Edges in the shape similarity tree corresponding to similar frames in the similarity matrix are shown in Fig. 3(b). Part of the resulting tree structure is illustrated in Fig. 3(c). The structure of the shape similarity tree will depend on the nature of the mesh sequences in the database. Figure 5 shows the optimal shape similarity tree for the flashkick sequence of 250 frames from the StreetDance database with frames coloured across the sequence. The branching structure of the tree shows that different segments from the start and end of the sequence are linked for non-sequential alignment, vertical branches indicate sub-sequences across which sequential alignment is performed. The reduced length and ordering of tree branches compared to the original sequences reduces drift due to propagation of alignment errors.
3.4 Non-rigid Alignment
The shape similarity tree T sst defines the non-sequential alignment path minimising the total non-rigid shape deformation to align every frame of the sequence. Starting from the root node M root we align meshes along the branches of the tree using a pairwise non-rigid alignment. It should be noted that non-sequential alignment using the shape similarity tree can be combined with any sequential pairwise alignment approach.
In this paper non-rigid pairwise mesh alignment uses a coarse-to-fine approach combining geometric and photometric matching in a Laplacian mesh deformation framework (Sorkine 2006). This builds on recent work using Laplacian mesh deformation for sequential frame-to-frame alignment over mesh sequences (de Aguiar et al. 2008; Cagniart et al. 2010a). Here we use both photometric SIFT features (Lowe 2004) and geometric rigid patch matching (Cagniart et al. 2010a) to establish correspondence between pairs of meshes. The combination of geometric and photometric features increases reliability of matching by ensuring that there is a distribution of correspondences across the surface. Alignment is performed starting from a coarse sampling (30 patches) which allows large deformations and recursively doubles the number of patches in successive iterations to obtain an accurate match to the surface. Since estimated feature correspondences are likely to be subject to matching errors we use an energy based formulation to introduce feature matches as soft constraints on the Laplacian deformation framework as proposed in Sorkine (2006):
L is the surface Laplacian system formed by the connectivity of the triangulated mesh M and uses the discrete gradient operator G (Botsch and Sorkine 2008) with L=G T DG, D is a diagonal matrix of triangle areas. δ(X 0) are the mesh differential coordinates for the source mesh with vertex positions X 0. X is a vector of mesh vertex positions used to solve for LX=δ. X c are soft constraints on vertex locations given by the feature correspondence with a diagonal weight matrix W c . The Laplacian L can either be fixed L root for a single reference mesh M root which limits drift for shapes close to the original but biases the solution towards the root mesh shape, or updated L(X 0) on a per frame basis according to the change in shape X 0. Experimental evaluation for alignment across databases of complex sequences with large deformations from the reference mesh shape indicate that it is preferable to use an updated Laplacian.
Equation (3) solves for the optimal deformation which minimises the change in shape whilst approximating the feature correspondence constraints. Solving this system directly leads to the well known problem with linear interpolation of large rotations. Instead as in previous work (Sumner and Popovic 2004; de Aguiar et al. 2008) we adopt an iterative approach to updating triangle rotations and deformation.
3.5 Multi-path Non-sequential Alignment
A potential problem with non-sequential alignment based on the minimum spanning tree (or any other tree based solution) is that only a single alignment path is defined for each node and consistency in alignment between adjacent nodes is not explicitly enforced. This may cause jumps in alignment where temporally adjacent frames in a sequence have different alignment paths. Pairwise non-rigid alignment will result in drift as the alignment is propagated across the tree resulting in accumulation of errors. Drift can potentially be alleviated by alignment to a reference mesh (Furukawa and Ponce 2010) or anchor frames (Beeler et al. 2011). However, there will be an accumulation of errors as the number of intermediate frames and path length across the tree increases. This may result in temporally adjacent frames having a different alignment producing a jump in the alignment between frames.
To ensure consistent alignment between adjacent frames we employ a multi-path alignment strategy. Consider the set of alignment paths given by the shape similarity tree T sst for each frame in an m frame window around the ith frame in a sequences \(\{P_{j}\}_{j=i-\frac{m}{2}}^{i+\frac{m}{2}}\). We can extend each of these alignment paths to estimate the alignment for the ith frame by adding the edges between the intermediate frames in the window. This gives a set of m alignment paths for the ith frame: \(\{ P_{j}^{i}\}_{j=i-\frac{m}{2}}^{i+\frac{m}{2}}\). However, due to the use of the minimum spanning tree to define the alignment paths many of them will overlap \(P^{i}_{j} \subset P^{i}_{k}\). Eliminating overlapping paths gives a set of K unique (non-overlapping) alignment paths: \(\{P_{k}^{i} \}_{k=1}^{K}\).
Each of the K unique paths gives an estimate of the non-rigid alignment for the ith frame. The problem is then to combine these estimates to obtain a temporally consistent alignment. A measure of the confidence c k in each alignment estimate is given by the path length \(c_{k} = \sum_{e_{rs}\in P_{k}^{i}} f(s(M_{r},M_{s}))\), where f() is a monotonic function. Non-rigid alignment, (3), can be extended to incorporate multiple estimates of non-rigid correspondence as constraints for the ith frame alignment. The set of estimated alignments for each vertex are combined to define the constraints for each vertex X c by weighting their geodesic distance according to the alignment confidence to give a novel constraint point on the surface. This gives a smooth blend in alignment where tree branches meet.
4 Results and Evaluation
Evaluation is performed on three databases of unstructured 3D mesh sequences which are publicly available for benchmarking (Starck and Hilton 2007b). Each database is for a single person performing multiple different motions in various styles of clothing: StreetDance—6 sequences of a person with loose clothing performing rapid and complex street dance movements; GameCharacter—10 sequences of a female in tight clothing performing common game character motions; and Fashion—6 sequences of a female in a knee-length dress performing a variety of catwalk style motions. Table 1 details the number of frames for each sequences and the total number in each database.
Throughout this work shape similarity is computed with a spherical shape histogram of 1.5 m radius with bin sizes (Δr,Δθ,Δϕ)=(0.3 m,18∘,18∘) (Huang et al. 2010). Figure 6 presents the similarity matrix for each database of unstructured mesh sequences. The structure of the similarity matrix with off-diagonal blue areas indicates high similarity between frames in different sequences. This forms the basis for construction of the optimal shape similarity tree for global alignment of all frames in the database to minimise the total non-rigid deformation.
Table 1 presents the maximum length of branches in the shape similarity tree for individual StreetDance sequences and for global alignment of each database. The maximum branch length is the longest sequence of pairwise alignment. For individual sequences the longest alignment path is 25–50 % of the total sequence length leading to a significant reduction in the accumulation of errors due to drift in the sequential alignment process. For global alignment across databases of multiple sequences the longest alignment path is reduced to 10–30 % of the total number of frames. The shape similarity tree representation based on the minimum spanning tree optimises the path length according to the distance in shape similarity space giving a considerable reduction in path length over sequential alignment and enabling alignment across multiple sequences.
4.1 Results of Global Alignment
Global alignment is performed by first constructing the optimal shape similarity tree for each database as detailed in Sect. 3.3 and then performing pairwise non-rigid alignment over the branches of the tree, Sect. 3.4. Results of global alignment for the three databases are presented in Fig. 7. To illustrate the surface alignment a single texture map is applied to the root mesh of the shape similarity tree and transferred to all frames in this sequence based on the estimated correspondence. The texture map is consistently aligned across all frames for multiple motions in each database demonstrating qualitatively that the global alignment achieves reliable correspondence. Based on the estimated global alignment all frames are represented with a consistent mesh structure. Please see supplementary video.Footnote 1
Tables 2, 3, 4 present quantitative results for the global alignment accuracy in representing the original unstructured 3D mesh sequence. Three error measures are presented for individual sequences and for the global database alignment: root mean squared error between the original and aligned surface mesh; maximum error or Hausdorff distance between the original and aligned surface; and silhouette reprojection error across all captured views between the original and aligned mesh normalised by image size. Quantitative results demonstrate that the RMS error for the globally aligned meshes is <10 mm and the maximum error is <50 mm in all cases. This level of RMS error is comparable to the error in shape reconstruction from the multiple view images (Starck and Hilton 2007b). The maximum error typically occurs at extremities in the shape due to sharp folds in clothing or errors in the original reconstruction.
To demonstrate the performance on a sequence of partial surface reconstructions Fig. 8 presents a comparison of results for sequential and non-sequential alignment for a face performing large non-rigid deformations. Significant drift and pattern distortion occurs with sequential alignment around the eyes and mouth due to the accumulation of tracking errors. This problem is eliminated with the non-sequential alignment where the pattern remains accurately aligned with the face throughout the sequence.
A comparison of facial alignment using the anchor frame approach of Beeler et al. (2011) to our non-sequential approach is presented in Fig. 9 using publicly available datasets. Both approaches achieve accurate alignment to the face. Figure 9(c) shows a heat map of the absolute difference between vertex positions which are in the range 0–2 mm, this indicates that there are differences in areas of large deformation. Differences may be due to errors in either approach. In practice both approaches appear accurately locked to the surface without visible swimming (sliding of the mesh across the surface). Image mesh overlays are included in the accompanying video to allow visual assessment of alignment quality.
Comparison of non-sequential alignment using anchor frames of a single expression (Beeler et al. 2011) and minimum spanning tree (data courtesy Beeler et al. Disney Research)
4.2 Comparison to Sequential Alignment
Quantitative evaluation of non-rigid alignment accuracy is notoriously difficult due to the absence of ground-truth for real examples. Synthetic animation examples do not provide the complexity of either motion or dynamic surface appearance and shape detail which occurs in real sequences. Previous research has used hand-annotated correspondence as ground-truth for evaluation of non-rigid alignment accuracy (Starck and Hilton 2007a). However, this only provides ground-truth for very sparse surface points at which visible features can be tracked and is subject to errors in labelling. Therefore, as in previous research on non-rigid surface alignment, we evaluate the performance of the proposed global non-rigid alignment by comparison with a state-of-the-art sequential alignment approach (Cagniart et al. 2010b). Results for sequential alignment of the individual StreetDance database sequences are provided courtesy of (Cagniart et al. 2010b) using their implementation.
Figure 10 presents a visual comparison between frames from the original StreetDance sequence and the mesh obtained with the proposed global alignment and those obtained with sequential alignment of individual sequences. Aligned meshes are coloured with patches on the mesh illustrating that global alignment is consistent across all frames whereas the sequential approach is unaligned between sequences. In both cases global and sequential alignment result in meshes which give a good approximation of the original mesh shape. In the case of sequential alignment some alignment failures are visible, for example the right arm has collapsed in the sequential alignment for the frame 2nd from left. This commonly occurs in sequential alignment for long-sequences of complex motion where rapid motion and large non-rigid surface deformation result in alignment failure.
Quantitative comparison of the RMS, maximum and silhouette reprojection error for the StreetDancer sequence with the proposed non-sequential alignment versus a state-of-the-art sequential alignment (Cagniart et al. 2010b) are presented in Fig. 11. Comparison of the error curves illustrates that the RMS and maximum reconstruction errors for global alignment are consistently lower than errors for sequential alignment. In addition, the global alignment avoids or significantly reduces sharp peaks in RMS and maximum error around frames which occur with sequential alignment (frames 100, 400, 850–950, 1300–1400 and 1600–1700). The peaks indicate partial or complete failure of sequential surface alignment. Frames 1450–1600 were not aligned with the sequential approach. Silhouette re-projection error is similar (<1 %) for both approaches indicating that this is not a good measure for differentiating alignment accuracy. In both sequential and non-sequential alignment approaches used in this work silhouette reprojection error is not explicitly represented in the alignment cost function. As sequential alignment is reinitialised for each sequence the error for the first 5–10 frames is lower. It should be noted that sequential alignment is independent for each sequence and does not produce a globally consistent representation.
Comparison of errors with global alignment and sequential alignment of each sequence independently using Cagniart et al. (2010b) for the StreetDancer database of 6 sequences (sequences left-to-right separated by vertical blue lines: pop, lock, head, free, kickup, flashkick) (Color figure online)
Table 2 presents the quantitative error measures for sequential and non-sequential alignment averaged across each sequence and for the global non-sequential alignment of all sequences. In all cases the non-sequential alignment achieves lower RMS and maximum error than sequential alignment. This demonstrates that the reduction in alignment path length achieved with the shape similarity tree reduces the error due to drift in reconstruction.
Global non-sequential alignment achieves automatic alignment for all frames in the three databases used for evaluation. Peaks in the maximum error (Hausdorff distance) in Fig. 10 for sequential alignment indicate frames where rapid movement occurs. For large inter-frame deformations sequential alignment may fail to reconstruct the correct surface as illustrated in Fig. 10(c). Manual correction is required to re-initialise the sequential tracking in these cases and provide a fair comparison between non-sequential and sequential alignment for individual sequences.
4.3 Limitations of Non-sequential Alignment
A potential drawback of non-sequential alignment arises from the independent accumulation of alignment errors (drift) on different branches of the tree. This may result in alignment errors between consecutive frames which occur where branches meet. To quantify discontinuities in alignment where shape similarity tree branches meet we evaluate the RMS frame-to-frame vertex acceleration. Figure 12 presents the RMS acceleration characteristics for the StreetDance kickup sequence with fast complex motion. Peaks in RMS acceleration are visible for non-sequential alignment (red) which do not occur for sequential alignment (green). This is due to jumps where branches of the shape similarity tree meet (frames 97–98 and frames 144–145) resulting in jumps in surface alignment as shown in Fig. 13 (left-column). To ensure consistent alignment where branches meet we combine estimates using the multi-path approach presented in Sect. 3.5. This results in elimination of jumps in alignment as illustrated Fig. 13(right-column), and reduction of corresponding peaks in the RMS vertex acceleration characteristic Fig. 12(blue-line). Note the red and blue lines for non-sequential with/without multi-path combination are coincident except where branches meet.
5 Conclusion
A framework has been introduced for alignment of databases of unstructured 3D mesh sequences to obtain a structured representation with correspondence between frames. A non-sequential approach to non-rigid alignment is proposed based on the shape similarity tree representation. Shape similarity between all frames in the database is estimated without known correspondence based on a volumetric shape histograms which have previously been demonstrated to give good performance on 3D mesh sequences of people (Huang et al. 2010). The optimal shape similarity tree is defined as the minimum spanning tree in shape similarity space which minimises the total non-rigid deformation for alignment across all frames. Non-rigid alignment is performed by traversing the shape similarity tree with pair-wise alignment of meshes using any existing sequential non-rigid alignment technique (de Aguiar et al. 2008; Budd and Hilton 2009; Cagniart et al. 2010b; Tung and Matsuyama 2010). Alignment based on the shape similarity tree optimises the path for non-rigid alignment giving reduced drift and improved robustness over previous sequential approaches. The approach also enables alignment across multiple sequences which is not possible with previous sequential approaches. Drift due to accumulation of errors in sequential tracking is reduced by shortening the path lengths for pairwise alignment. Robustness to rapid movements resulting in large deformations is increased by identifying optimal paths for alignment of all frames based on linking frames with similar shape and motion across the database rather than purely temporal adjacency.
Evaluation is performed on three public benchmark databases of unstructured 3D mesh sequences of performers reconstructed from multiple view video (Starck and Hilton 2007b). This demonstrates accurate alignment for complex movement sequences and a variety of clothing. Comparison with a state-of-the-art sequential alignment approach (Cagniart et al. 2010b) demonstrates significant reductions in both RMS and maximum error, and elimination of gross errors in reconstruction. The non-sequential approach is robust to alignment failure which can occur with sequential approaches due to large non-rigid deformations. This approach is the first to demonstrate alignment across databases of multiple unstructured 3D mesh sequences of people and faces to obtain a consistent mesh structure and correspondence for all frames.
References
Ahmed, N., Theobalt, C., Roessl, C., Thrun, S., & Seidel, H.-P. (2008). Dense correspondence finding for parameterization-free animation reconstruction from video. In Conference on computer vision and pattern recognition.
Baran, I., Vlasic, D., Grinspun, E., & Popovic, J. (2009). Semantic deformation transfer. In Proc. ACM SIGGRAPH.
Beeler, T., Hahn, F., Bradley, D., Bickel, B., Beardsley, P., Gotsman, C., & Gross, M. (2011). High-quality passive facial performance capture using anchor frames. In Proc. ACM SIGGRAPH.
Belongie, S., Malik, J., & Puzicha, J. (2002). Shape matching and object recognition using shape contexts. IEEE Transactions on Pattern Analysis and Machine Intelligence, 24(24), 509–522.
Botsch, M., & Sorkine, O. (2008). On linear variational surface deformation methods. IEEE Transactions on Visualization and Computer Graphics, 14(1), 213–230.
Bradley, D., Heidrich, W., Popa, T., & Sheffer, A. (2010). High-resolution passive facial performance capture. In Proc. ACM SIGGRAPH.
Bradley, D., Popa, T., Sheffer, A., Heidrich, W., & Boubekeur, T. (2008). Markerless garment capture. ACM Transactions on Graphics, 27(3), 99.
Bronstein, A., Bronstein, M., & Kimmel, R. (2007). Calculus of non-rigid surfaces for geometry and texture manipulation. IEEE Transactions on Visualization and Computer Graphics, 13(5), 902–913.
Budd, C., & Hilton, A. (2009). Skeleton driven volumetric Laplacian deformation. In European conference on visual media production.
Budd, C., Huang, P., & Hilton, A. (2011). Hierarchical shape matching for temporally consistent 3D video. In IEEE conf. 3D imaging, processing, visualisation and transmission (3DIMPVT).
Cagniart, C., Boyer, E., & Ilic, S. (2010a). Free-form mesh tracking: a patch-based approach. In Conference on computer vision and pattern recognition.
Cagniart, C., Boyer, E., & Ilic, S. (2010b). Probabilistic deformable surface tracking from multiple videos. In European conference on computer vision.
Carceroni, R., & Kutulakos, K. (2002). Multi-view scene capture by surfel sampling: from video streams to non-rigid 3D motion, shape and reflectance. International Journal of Computer Vision, 49(2–3), 175–214.
Carranza, J., Theobalt, C., Magnor, M., & Seidel, H.-P. (2003). Free-viewpoint video of human actors. In Proceedings ACM SIGGRAPH (Vol. 22(3), pp. 569–577).
de Aguiar, E., Stoll, C., Theobalt, C., Ahmed, N., Seidel, H.-P., & Thrun, S. (2008). Performance capture from sparse multi-view video. In Proceedings of the ACM SIGGRAPH (Vol. 27(3)).
Elad, A., & Kimmel, R. (2003). On bending invariant signatures for surfaces. IEEE Transactions on Pattern Analysis and Machine Intelligence, 25(10), 1285–1295.
Enqvist, O., Kahl, F., & Olsson, C. (2011). Non-sequential structure from motion. In IEEE workshop on omnidirectional vision, camera networks and non-classical camera.
Furukawa, Y., & Ponce, J. (2010). Dense 3D motion capture for human faces. In Conference on computer vision and pattern recognition.
Gal, R., Shamir, A., & Cohen-Or, D. (2007). Pose oblivious shape signature. IEEE Transactions on Visualization and Computer Graphics, 13(2), 261–271.
Gatzke, T., Grimm, C., Garland, M., & Zelinka, S. (2005). Curvature maps for local shape comparison. In Shape modelling and applications.
Gherhadi, R., Toldo, R., Farenzena, M., & Fusiello, A. (2010). Samantha: towards automatic image-based model acquisition. In Proceedings of the 7th European conference on visual media production (CVMP 2010).
Huang, P., Budd, C., & Hilton, A. (2011). Global temporal registration of multiple non-rigid surface sequences. In Conference on computer vision and pattern recognition.
Huang, P., Hilton, A., & Starck, J. (2009). Human motion synthesis from 3D video. In IEEE int. conf. on computer vision and pattern recognition, CVPR.
Huang, P., Hilton, A., & Starck, J. (2010). Shape similarity for 3D video sequences of people. International Journal of Computer Vision, 89(2–3), 362–381.
Iyer, N., Jayanti, S., Lou, K., Kalyanaraman, Y., & Ramani, K. (2005). Three dimensional shape searching: state-of-the-art review and future trends. Computer Aided Design, 37(5).
Kruskal, J. B. (1956). On the shortest spanning subtree of a graph and the traveling salesman problem. Proceedings of the American Mathematical Society, 7(1), 48–50.
Liing, H., & Jacobs, D. (2005). Deformation invariant image matching. In IEEE int. conf. on computer vision (pp. 1466–1473).
Lowe, D. (2004). Distinctive image features for scale invariant keypoints. International Journal of Computer Vision, 60(2), 91–110.
McInerney, T., & Terzopoulos, D. (1996). Deformable models in medical image processing. Medical Image Analysis, 1(2), 91–108.
Mikolajczyk, K., & Schmid, C. (2005). A performance evaluation of local descriptors. IEEE Transactions on Pattern Analysis and Machine Intelligence, 27(10), 1615–1630.
Moeslund, T., Hilton, A., & Kruger, V. (2006). A survey of advances in vision-based human motion capture and analysis. Computer Vision and Image Understanding, 104(2–3), 90–127.
Moeslund, T., Hilton, A., Kruger, V., & Sigal, L. E. (2011). Visual analysis of humans: looking at people. Berlin: Springer.
Neumann, J., & Aloimonos, Y. (2002). Spatio-temporal stereo using multi-resolution subdivision surfaces. International Journal of Computer Vision, 47(1–3), 181–193.
Pons, J.-P., Keriven, R., & Faugeras, O. (2007). Multi-view stereo reconstruction and scene flow estimation with a global image-based matching score. International Journal of Computer Vision, 72(2), 179–193.
Prim, R. C. (1957). Shortest connection networks and some generalizations. Bell System Technology Journal, 36, 1389–1401.
Pritchard, D., & Heidrich, W. (2003). Cloth motion capture. Computer Graphics Forum, 22(3), 263–271.
Salzmann, M., Pilet, J., Ilic, S., & Fua, P. (2007). Surface deformation models for non-rigid 3D shape recovery. In IEEE trans. Pattern analysis and machine intelligence.
Scholz, V., Stich, T., Kechkeisen, M., Wacker, M., & Magnor, M. (2005). Garment motion capture using color-coded patterns. Computer Graphics Forum, 24(3), 439–448.
Sorkine, O. (2006). Differential representations for mesh processing. Computer Graphics Forum, 25(4).
Starck, J., & Hilton, A. (2003). Model-based multiple view reconstruction of people. In IEEE international conference on computer vision (pp. 915–922).
Starck, J., & Hilton, A. (2005). Spherical matching for temporal correspondence of non-rigid surfaces. In IEEE int. conf. computer vision (pp. 1387–1394).
Starck, J., & Hilton, A. (2007a). Correspondence labelling for wide-timeframe free-form surface matching. In IEEE int. conf. on computer vision.
Starck, J., & Hilton, A. (2007b). Surface capture for performance-based animation. IEEE Computer Graphics and Applications, 27(3), 21–31.
Stoll, C., Gall, J., de Aguiar, E., Thrun, S., & Theobalt, C. (2010). Video-based reconstruction of animatable human characters. In ACM SIGGRAPH ASIA.
Sumner, R., & Popovic, J. (2004). Deformation transfer for triangle meshes. In Proc. ACM SIGGRAPH.
Tevs, A., Berner, A., Wand, M., Ihrke, I., Bokeloh, M., Kerber, J., & Seidel, H.-P. (2011). Animation cartography—intrinsic reconstruction of shape and motion. ACM Transaction on Graphics.
Tung, T., & Matsuyama, T. (2010). Dynamic surface matching by geodesic mapping for animation transfer. In Conference on computer vision and pattern recognition.
Vedula, S., Baker, S., Rander, P., Collins, R., & Kanade, T. (2005). Three-dimensional scene flow. IEEE Transactions Pattern Analysis and Machine Intelligence, 27(3).
Vlasic, D., Baran, I., Matusik, W., & Popović, J. (2008). Articulated mesh animation from multi-view silhouettes. In Proc. ACM SIGGRAPH.
Wand, M., Adams, B., Ovsianikov, M., Berner, A., Bokeloh, M., Jenke, P., Guibas, L., Seidel, H.-P., & Schilling, A. (2009). Efficient reconstruction of non-rigid shape and motion from real-time 3D scanner data. ACM Transaction on Graphics, 28(2).
White, R., Crane, K., & Forsythe, D. (2007). Capturing and animating occluded cloth. In Proc. ACM SIGGRAPH (Vol. 26(3), p. 34).
Zeng, Y., Wang, C., Wang, Y., Gu, X., Samaras, D., & Paragios, N. (2010). Dense non-rigid surface registration using high-order graph matching. In Conference on computer vision and pattern recognition.
Zhang, L., Snavely, N., Curless, B., & Seitz, S. (2004). Spacetime faces: high resolution capture for modelling and animation. In Proc. ACM SIGGRAPH (pp. 546–556).
Acknowledgements
This research was support by the UK EPSRC Visual Media Platform Grant and EU IST FP7 projects i3Dpost and SCENE.
Open Access
This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Budd, C., Huang, P., Klaudiny, M. et al. Global Non-rigid Alignment of Surface Sequences. Int J Comput Vis 102, 256–270 (2013). https://doi.org/10.1007/s11263-012-0553-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11263-012-0553-4