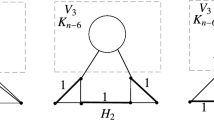
We consider a quite general problem from the geometric theory of functions, namely, the problem of finding the maximal value of the product of inner radii of n nonoverlapping domains that contain points of the unit circle and are symmetric with respect to this circle and the γ power of the inner radius of a domain containing the origin. The posed problem is solved for n ≥ 20 and \( 1<\gamma \le {n}^{\frac{2}{3}-q(n)} \).
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
M. A. Lavrent’v, “On the theory of conformal mappings,” Tr. Fiz.-Mat. Inst. Akad. Nauk SSSR, 5, 159–245 (1934).
G. M. Goluzin, Geometric Theory of Functions of Complex Variable [in Russian], Nauka, Moscow (1966).
G. V. Kuz’mina, “On the problem of maximum of the product of conformal radii of nonoverlapping domains,” Zap. Nauch. Sem. LOMI, 131–145 (1980).
P. M. Tamrazov, “Extremal conformal mappings and poles of quadratic differentials,” Izv. Akad. Nauk SSSR, Ser. Mat., 32, No. 5, 1033–1043 (1968).
V. N. Dubinin, “Method of symmetrization in the geometric theory of functions of complex variable,” Usp. Mat. Nauk, 49, No. 1(295), 3–76 (1994).
V. N. Dubinin, “Separating transformation of domains and the problems of extremal partition,” Zap. Nauch. Sem. LOMI, 168, 48–66 (1988).
A. K. Bakhtin, G. P. Bakhtina, and Yu. B. Zelinskii, Topological-Algebraic Structures and Geometric Methods in Complex Analysis [in Russian], Proc. of the Institute of Mathematics, Ukrainian National Academy of Sciences, Kiev (2008).
J. A. Jenkins, Univalent Functions and Conformal Mapping [Russian translation], Inostr. Lit., Moscow (1962).
G. P. Bakhtina, “On the conformal radii of symmetric nonoverlapping domains,” in: Contemporary Problems of Real and Complex Analysis [in Russian], Institute of Mathematics, Academy of Sciences of Ukr. SSR, Kiev, 149 (1984), pp. 21–27.
L. V. Kovalev, “On the inner radii of symmetric nonoverlapping domains,” Izv. Vyssh. Uchebn. Zaved., Ser. Mat., 6, 80–81 (2000).
L. V. Kovalev, “On three nonoverlapping domains,” Dal’nevost. Mat. Zh., 1, No. 1, 3–7 (2000).
Ya. V. Zabolotnyi and L. V. Vygovskaya, “On the product of inner radii of symmetric multiply connected domains,” Ukr. Mat. Visn., 14, No. 3, 440–451 (2017).
A. K. Bakhtin, I. V. Denega, and L. V. Vygovskaya, “Inequalities for the inner radii of symmetric disjoint domains,” Ukr. Mat. Zh., 70, No. 9, 1282–1288 (2018); English translation: Ukr. Math. J., 70, No. 9, 1477–1483 (2019).
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated from Ukrains’kyi Matematychnyi Zhurnal, Vol. 72, No. 11, pp. 1502–1509, November, 2020. Ukrainian DOI: 10.37863/umzh.v72i11.6064.
Rights and permissions
About this article
Cite this article
Zabolotnii, Y.V. The Problem of V. N. Dubinin for Symmetric Multiconnected Domains. Ukr Math J 72, 1733–1741 (2021). https://doi.org/10.1007/s11253-021-01884-4
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11253-021-01884-4