Abstract
We face complex global issues such as climate change that challenge our ability as humans to manage them. Models have been used as a pivotal science and engineering tool to investigate, represent, explain, and predict phenomena or solve problems that involve multi-faceted systems across many fields. To fully explain complex phenomena or solve problems using models requires both systems thinking (ST) and computational thinking (CT). This study proposes a theoretical framework that uses modeling as a way to integrate ST and CT. We developed a framework to guide the complex process of developing curriculum, learning tools, support strategies, and assessments for engaging learners in ST and CT in the context of modeling. The framework includes essential aspects of ST and CT based on selected literature, and illustrates how each modeling practice draws upon aspects of both ST and CT to support explaining phenomena and solving problems. We use computational models to show how these ST and CT aspects are manifested in modeling.
Similar content being viewed by others
Explore related subjects
Find the latest articles, discoveries, and news in related topics.Avoid common mistakes on your manuscript.
Introduction
The primary goals of science education for all learners are to explain natural phenomena, solve problems, and make informed decisions about actions and policies that may impact their lives, their local environments, and our global community. Models—representations that abstract and simplify a system by focusing on key features—have been used as a pivotal science and engineering tool to investigate, represent, explain, and predict phenomena across many fields (Harrison & Treagust, 2000; National Research Council, 2012; Schwarz et al., 2017). For example, En-ROADS, a computational model and simulator developed by Climate Interactive, an environmental think tank, has been used to educate members of the U.S. Congress, the U.S. State Department, the Chinese government, and the office of the UN Secretary-General on climate change on the impacts of proposed policies on global warming. The model was also a centerpiece of multiple presentations at the UN Climate Change Conference in Scotland in 2021 (Madubuegwn et al., 2021).
Modeling, which includes developing, testing, evaluating, revising, and using a model (National Research Council, 2012; Schwarz et al., 2017; Sengupta et al., 2013), necessitates many different thinking processes such as problem decomposition (Grover & Pea, 2018), causal reasoning (Levy & Wilensky, 2008), pattern recognition (Berland & Wilensky, 2015), algorithmic thinking (Lee & Malyn-Smith, 2020), and analysis and interpretation of data (Shute et al., 2017). These thinking processes often necessitate systems thinking and computational thinking, which are intrinsically linked to modeling (Richmond, 1994; Wing, 2017).
Richmond (1994) defines systems thinking (ST) as “the art and science of making reliable inferences about behavior by developing an increasingly deep understanding of underlying structure” (p. 139). To help manage the complexities of climate change, experts use a systems thinking approach to guide decision making and inform policy design (Holz et al., 2018; Sterman & Booth Sweeney, 2007). In the context of modeling, ST helps us to comprehend the causal connections between the components of a model––the elements of a problem or phenomenon that affect the system’s behavior (e.g., the relationship between the melting of polar ice caps and the increase in global temperatures)––and how changes in one component (e.g., the rate of melting of the polar ice caps) can cascade to other components and potentially affect the status of the entire system.
However, the multifaceted interactions within complex systems quickly outpace our ability to mentally simulate and predict system behavior, especially in systems that include time delays and feedback, common features of many complex phenomena (Cronin et al., 2009). For example, in the case of climate change, there is a delay between changing CO2 emissions and the cumulative effect on CO2 concentrations in the atmosphere (Sterman & Sweeney, 2002). Even highly educated people with strong mathematics backgrounds have trouble understanding and predicting the behavior of a system with these features (Cronin et al., 2009), and perform poorly when attempting to forecast the effect of any particular intervention (Sterman & Sweeney, 2002). Therefore, ST alone may not be sufficient for investigation of potential solutions to complex problems such as climate change.
To model successfully, we also need computational thinking (Wing, 2008). Computational thinking (CT) provides conceptual tools for finding answers to problems involving complex, multidimensional systems by applying logical and algorithmic thinking (Berland & Wilensky, 2015; Lee & Malyn-Smith, 2020). Wing (2006) views CT as thinking like a computer scientist, not like a computer, and as a competency appropriate and available to everyone, not only for computer scientists in science and engineering fields. In particular, CT helps us create algorithms by identifying patterns in phenomena to automate the transformation of data so that we can predict other phenomena in similar systems. Although CT does not require the use of a computer, a computer’s processing speed is helpful for testing solutions efficiently. For instance, scientists use computational models to test the effect of various policies on the amount of CO2 accumulating in the atmosphere in order to reduce the trapping of solar energy in our environment. Thus, to fully explain complex phenomena or solve problems using models requires both ST and CT (National Research Council, 2012).
A key challenge for science, technology, engineering, and mathematics (STEM) educators and researchers is to develop learning environments that provide opportunities for learners to experience how scientists approach explaining complex phenomena and solving ill-structured problems (Krajcik & Shin, 2022; National Research Council, 2000). Because science and engineering practices (e.g., modeling, computational thinking) should be integrated with scientific ideas including disciplinary core ideas and crosscutting concepts (e.g., systems and system modeling) in meaningful contexts to promote deep learning (National Research Council, 2012; NGSS Lead States 2013), we argue that incorporating modeling, ST, and CT into existing STEM subjects supports K-12 learners in making sense of phenomena and solving problems.
We propose a theoretical framework that foregrounds modeling and highlights how both ST and CT are involved in the process of modeling phenomena or problems. Because modeling is a key science practice for learners across K-12 education (National Research Council, 2012; NGSS Lead States 2013), it would be beneficial to expand the opportunities for applying ST and CT in the context of modeling. To successfully support learners in modeling with ST and CT in various STEM disciplines in K-12 education, educators and researchers need to further develop and explore learning environments that incorporate ST and CT in the modeling practices.
We postulate that this framework can (a) guide curriculum developers and teachers in integrating ST and CT in the context of modeling in multiple STEM courses, (b) assist software developers and curriculum designers in developing effective learning tools and pedagogical supports that involve learners in modeling, ST, and CT, and (c) help researchers and teachers in measuring learners’ understanding and application of modeling, ST, and CT. In this paper, we present our framework, which is based on a literature review of ST and CT as well as examples of models to illustrate how ST and CT are integrated in and support the modeling practices. We start by defining ST, CT, and the modeling practices that form the foundation of our framework, briefly introduce our framework, then identify ST and CT aspects. Finally, we describe the framework and associated aspects of ST and CT in each modeling practice by illustrating how the ST and CT aspects support the modeling process.
Theoretical background
What is systems thinking?
Systems thinking has been emphasized in K-12 science standards in the U.S. for nearly three decades (NGSS Lead States, 2013; National Research Council, 2007, 2012; American Association for the Advancement of Science, 1993). With the release of A Framework for K-12 Science Education (National Research Council, 2012), ST has been incorporated in the crosscutting concept of systems and system modeling. ST provides learners with a unique lens that, when combined with scientific ideas and practices, can enhance sense-making and problem-solving, and is particularly well suited for addressing the complexity found in many social and scientific phenomena—from human health and physiology to climate change. Although thinking in a systemic way about persistent problems has been around for centuries (Richardson, 1994), the term “systems thinking” (ST), as used in the literature across a wide variety of disciplines, has not been clearly defined.
From the world of business, Senge (1990) sees systems thinking as a paradigm shift toward consideration of the system as a whole, with a focus on interrelationships and change over time. Forrester (1961), Senge’s mentor and creator of the discipline known as system dynamics, speaks of “system awareness … a formal awareness of the interactions between the parts of a system” (p. 5). Meadows (2008) refers to a “system lens” and stresses that “seeing the relationship between structure and behavior we can begin to understand how a system works” (p. 1). Richmond (1994) and Sterman (1994) view ST and learning as being synergistically connected. Richmond views ST as both a paradigm and a learning method. He describes the ST paradigm as a lens through which one comes to view complex systems holistically, as well as a set of practical tools for developing and refining that lens. The “tools” that he describes closely match commonly defined modeling practices (National Research Council, 2012; Schwarz et al., 2009). More recently, systems thinking has been described as a set of skills that can be used as an aid to understanding complex systems and their behavior (Benson, 2007; Ben-Zvi Assaraf & Orion, 2005). In particular, Arnold and Wade (2015) define ST as “a set of synergistic analytic skills used to improve the capability of identifying and understanding systems” (p. 675).
For these authors ST represents a worldview, a way of thinking about the world that emerges as an individual grows in ability and willingness to see it holistically. Disciplined application of ST tools and skills supports and potentially alters one’s worldview, and one’s worldview conditions the choices one makes about the use of the tools. Building on the long tradition of ST applications in business together with more recent integration in K-12 education, ST can be defined operationally as the ability to understand a problem or phenomenon as a system of interacting elements that produces emergent behavior.
What is computational thinking?
Computational thinking is an important skill that is related to many disciplines (e.g., mathematics, biology, chemistry, design, economics, neuroscience, statistics), as well as numerous aspects of our daily life (e.g., optimizing everyday financial decisions or navigating daily commutes to minimize time spent in traffic). However, while computer science and CT have been key drivers of scientific development and innovation for several decades, only recently has CT been emphasized as a major academic learning goal in K-12 science education.
There is a wide range of perspectives on how to define CT—from a STEM-centered approach (Berland & Wilensky, 2015; National Research Council, 2012; Weintrop et al., 2016) to a more generic problem-solving approach (Barr & Stephenson, 2011; Grover & Pea, 2018; Lee & Malyn-Smith, 2020; Wing, 2006). A Framework for K-12 Science Education defines CT as utilizing computational tools (e.g., programming simulations and models) grounded in mathematics to collect, generate, and analyze large data sets, identify patterns and relationships, and model complex phenomena in ways that were previously impossible (National Research Council, 2012). Similar to the Framework, the STEM-centered approach describes CT as connected to mathematics for supporting data collection and analysis or testing hypotheses in a productive and efficient way, but also views CT as centering on sense-making processes (Psycharis & Kallia, 2017; Schwarz et al., 2017; Weintrop et al., 2016). In this view, although CT is intertwined with aspects of using specific rules (with quantitative data) to program computers to build models and simulations, it is more than an algorithmic approach to problem-solving (Brennan & Resnick, 2012; Shute et al., 2017). Instead, it is a more comprehensive, scientific way to foster sense-making that encourages learners to ask, test, and refine their understandings of how phenomena occur or how to solve problems.
Many researchers suggest that CT means “thinking like a computer scientist” when confronted with a problem (Grover & Pea, 2018; Nardelli, 2019; Shute et al., 2017; Wing, 2008). These scholars elaborate on the definition of CT, focusing on computational problem-solving processes, such as breaking a complex problem into smaller problems to trace and find solutions (Grover & Pea, 2018; Shute et al., 2017; Türker & Pala, 2020; Wing, 2006). Building on the ideas put forth by Wing (2006) and Grover and Pea (2018), as well as the view of the sense-making process from the STEM approach, we define CT operationally as a way of explaining phenomena or solving problems that utilizes an iterative and quantitative approach for exploring, unpacking, synthesizing, and predicting the behavior of phenomena using computational algorithmic methods.
What are modeling practices?
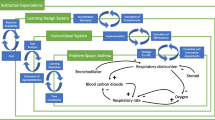
Modeling enables learners to investigate questions, make sense of phenomena, and explore solutions to problems by connecting and synthesizing their knowledge from a variety of sources into a coherent and scientific view of the world (National Research Council, 2011, 2012; Schwarz et al., 2017). Modeling includes several important practices, including building, evaluating, revising, and using models (National Research Council, 2012; Schwarz et al., 2017). Research shows that learners can deepen their understanding of scientific ideas through the development, use, evaluation, and revision of models (Schwarz & White, 2005; Wen et al., 2018; Wilkerson et al., 2018). Although modeling can be conducted without using computational programs (e.g., paper-pencil modeling), we are specifically interested in supporting student engagement in modeling, ST, and CT, so we are narrowing our focus to a computational approach. Therefore, we propose a Framework for Computational Systems Modeling that elucidates the synergy between modeling, ST, and CT. Building on the descriptions of the modeling process in the literature (Halloun, 2007; Martinez-Moyano & Richardson, 2013; Metcalf-Jackson et al., 2000; National Research Council, 2012; Schwarz et al., 2009), our framework includes five modeling practices: M1) characterize problem or phenomenon to model, M2) define the boundaries of the system, M3) design and construct model structure, M4) test, evaluate, and debug model behavior, and M5) use model to explain and predict behavior of phenomenon or design solution to a problem (Fig. 1).
In Fig. 1, the center set of boxes describes five modeling practices and the cyclic nature of the modeling process (represented by the arrows). The process is highly iterative, with involvement in one practice influencing both future and previous practices, inviting reflection and model revision throughout. Engagement in each of these practices necessitates the employment of aspects of ST (left side of framework diagram) and CT (right side of framework diagram). To develop the Framework for Computational Systems Modeling, we conducted a literature review study to identify and define essential aspects of ST and CT. Specifically, we explored important aspects of these two types of thinking necessary for the modeling practices. Through this exploration we considered the implications of these aspects for developing curriculum, learning tools, pedagogical and scaffolding strategies for teaching and learning, and valid assessments for promoting and monitoring learner progress. We, therefore, investigated two guiding questions: (1) What are the key aspects of each type of thinking? and (2) How do aspects of ST and CT intersect with and support modeling practices? Below we explain our review process.
Method
We employed the integrative review approach (Snyder, 2019) as we analyzed and synthesized literature, including experimental and non-experimental studies, as well as data from theoretical literature and opinion or position articles (e.g., books, book chapters, practitioner articles) on ST and CT. An integrative review method is appropriate for critically examining and analyzing secondary data about research topics for generating a new framework (Snyder, 2019; Whittemore & Knafl, 2005).
Literature search and selection strategies
Because our focus is on modeling as a process for making sense of phenomena, we took the view of Richmond (1994) as our starting point for ST and the view of Wing (2006) for CT, since both authors emphasize these thinking processes for learners to understand phenomena. We embarked on a literature review related to the two scholars’ research, and then extended our search using authors’ names who published studies related to the definition of ST or CT using Google Scholar. Our inclusion criteria of literature are (1) written between 1994 and 2021 with the keyword “system [and systems] thinking” and between 2006 and 2021 with the keyword “computational thinking”; and (2) directly related to the definition of ST or CT. We excluded authors who used previously defined ideas related to ST or CT and did not uniquely contribute new ideas. From these search results, we collected 80 manuscripts and narrowed our search to 55 manuscripts by selecting one representative manuscript in cases when an author had published several manuscripts (e.g., Richmond 1994 from Richmond 1993, 1994, 1997). In this way, our analysis aims to avoid misleading results that might be influenced by including the same authors’ ideas repeatedly. Our analysis included 27 of 45 manuscripts that defined ST and 28 of 35 manuscripts that defined CT.
Data analysis
We used the following filters sequentially, as we extracted a list of aspects of both ST and CT to create a usable framework: (a) the ST or CT aspect is described widely across the ST or CT literature in multiple scholars’ works, (b) the ST or CT aspect is not overly broad or generic; we excluded aspects that are ubiquitous across fields but not specific to ST or CT, and (c) the ST or CT aspect is operationalizable through observable behaviors (e.g., tangible artifacts or discussion).
We first created an initial list of aspects based on Richmond’s (1994) definition of ST and Wing’s (2006) definition of CT, respectively, to extract and sort information from each selected literature. For example, the aspects include causal reasoning, identifying interconnections, and predicting system behavior for ST (Fig. 1 left side), and problem decomposition, artifact creation, and debugging for CT (Fig. 1 right side). Second, each manuscript was reviewed by two of the authors independently, sorting texts based on which aspects were described. Third, the two authors confirmed their sorting of the texts by discussing each manuscript. Then, five of the authors reviewed the aggregated texts associated with each aspect presented from 27 ST and 28 CT manuscripts. As we reviewed the literature pertaining to definitions of ST and CT, we revised the aspects, expanding or dividing them as we gained new information and identified associated sub-aspects. All authors discussed the aspects and finalized them by resolving discrepancies and clarifying ambiguities. A shared spreadsheet was used to store and analyze all data.
Findings and discussion of literature review
Aspects and sub-aspects of systems thinking
From the reviews of ST literature in both business and education, and using our filters, we identified five aspects of systems thinking: (ST1) defining a system (boundaries and structure), (ST2) engaging in causal reasoning, (ST3) identifying interconnections and feedback, (ST4) framing problems or phenomena in terms of behavior over time, and (ST5) predicting system behavior based on system structure (Fig. 1 left side). Figure 2 shows the distribution of ST aspects that emerged from our review of 27 manuscripts.
Distribution of systems thinking aspects. (Note: ST1. Defining a system [boundaries and structure]; ST2. Engaging in causal reasoning; ST3. Identifying interconnections and feedback; ST4. Framing problems or phenomena in terms of behavior over time; ST5. Predicting system behavior based on system structure)
ST1, defining a system (boundaries and structure), requires an individual to clearly identify a system’s function and be as specific as possible about the phenomenon to be understood or the problem to be addressed. Table 1 presents a summary of the various ways 15 manuscripts have described defining a system.
Defining a system focuses attention on internal system structure (relevant elements and interactions among them to produce system behaviors) and limits the tendency to link extraneous outside factors to behavior. This focus allows learners to more clearly define the spatial and temporal limits of the system they wish to explain or understand (Hopper & Stave, 2008) Meadows (2008) discusses the importance of “system boundaries” and the need to clearly define a goal, problem, or purpose when attempting to think systemically. Considering scale is critical when deciding what content is necessary to explain the system behavior of interest (Arnold & Wade, 2017; Yoon et al., 2018).
To operationalize defining a system three sub-aspects are necessary: (ST1a) identifying relevant elements within the system’s defined boundaries (Arnold & Wade, 2015), (ST1b) evaluating the appropriateness of elements to see if their elimination significantly impacts the overall behavior of the system in relation to the question being explored (Ben-Zvi Assaraf & Orion, 2005; Weintrop et al., 2016), and (ST1c) determining the inputs and outputs of the system (Yoon et al., 2018).
ST2, engaging in causal reasoning, includes examination of the relationships and interactions of system elements. Causal reasoning is described as a key aspect of ST by most researchers, appearing in 25 manuscripts (Fig. 2). Table 1 presents a summary of the descriptions of causal reasoning. In addition, two other manuscripts imply the importance of causal reasoning as they state that causal reasoning serves as a foundation for recognizing interconnections and feedback loops in a system (ST3). For example, identifying interconnections among elements in a system (e.g., events, entities, or processes) requires understanding of one-to-one causal relationships (Forrester, 1994; Ossimitz, 2000).
For deep understanding of phenomena, learners should be able to describe both direct (impact of one element upon another) and indirect (the effects of multiple causal connections acting together in extended chains) relationships among various elements in a system of the phenomenon (Kim, 1999; Jacobson & Wilensky, 2006). Based on our review of causal reasoning, three sub-aspects are operationalizable: (ST2a) recognizing cause and effect relationships among elements (Arnold & Wade, 2015), (ST2b) quantitatively (or semi-quantitatively) defining proximal causal relationships between elements (Grotzer et al., 2017), and (ST2c) identifying (or predicting) the behavioral impacts of multiple causal relationships (Sterman, 2002; Levy & Wilensky, 2011).
ST3, identifying interconnections and feedback, involves analyzing causal chains that result in circular structural patterns (feedback structures) within a system. This aspect of ST was proposed by all 27 manuscripts (Fig. 2). Many studies in ST have focused on helping learners identify the relationships of interdependencies of system elements (Jacobson & Wilensky, 2006; Levy & Wilensky, 2011; Samon & Levy 2020; Yoon et al., 2018) (Table 1). Feedback structures are created when chains loop back upon themselves, creating closed loops of cause and effect (Jacobson et al., 2011; Pallant & Lee, 2017; Richmond, 1994). There are two basic types of feedback loops: balancing (or negative) feedback that tends to stabilize system behavior and reinforcing (or positive) feedback that causes behavior to diverge away from equilibrium (Booth-Sweeney & Sterman, 2000; Meadows, 2008).
This aspect provides learners an expansion of perspective, from one that focuses primarily on the analysis of individual elements and interactions to one that includes consideration of how the system and its constituent parts interact and relate to one another as a whole (Ben-Zvi Assaraf & Orion, 2005). Based on our literature review, it can be operationalized in two sub-aspects: (ST3a) identifying circular structures of causal relationships (Danish et al., 2017; Grotzer et al., 2017; Ossimitz, 2000) and (ST3b) recognizing balancing and reinforcing feedback structures and their relationship to the stability and growth within a system (Fisher, 2018; Meadows, 2008).
ST4, framing problems or phenomena in terms of behavior over time, requires that learners distinguish between phenomena that are best described as evolving over time and those that are not. Twenty-seven manuscripts reported that framing problems in terms of behavior over time is an important aspect of ST (Fig. 2), as shown in Table 1. Many advocates of ST refer to the recognition of the link between structure and behavior as “dynamic thinking” and acknowledge proficiency with it as difficult to obtain without the use of systems thinking tools (Booth-Sweeney & Sterman, 2000; Grotzer et al., 2017; Plate & Monroe, 2014).
This aspect is especially important when change over time is crucial for thoroughly understanding a system’s behavior. Some phenomena are best investigated without consideration of change over time, for instance, in open systems where change to a system input affects all of the internally connected system aspects. Other phenomena are better described using the cumulative patterns of change observed in a system’s state over time. Phenomena that evolve in this way are not significantly impacted by external factors but have an internal feedback structure that dictates how change will occur as time passes (Booth-Sweeney & Sterman, 2000, 2007). This aspect is operationalizable in two sub-aspects: (ST4a) determining the time frame necessary to describe a problem or phenomenon (Sterman, 1994, 2002) and (ST4b) recognizing time-related behavioral patterns that are common both within and across systems (Nguyen & Santagata, 2021; Pallant & Lee, 2017; Riess & Mischo, 2010; Tripto et al., 2018).
ST5, predicting system behavior based on system structure, necessitates an understanding of how both direct causal relationships and more comprehensive substructures (e.g., feedback loops, accumulating variables, and interactions among them) influence behaviors common to all systems (Forrester, 1994). This aspect was proposed in 18 of 27 manuscripts we reviewed (Table 1). Although a subset of manuscripts discussed this aspect specifically, those that do not imply that predicting system behavior based on system structure is important to systems thinking (e.g., describe learning activities such as predicting behaviors based on graphs or data sets) (Hmelo-Silver et al., 2017).
This aspect offers learners help in characterizing complex systems by identifying common structures that allows one to generalize about the connection between system structure and behavior and develop guidelines that can be applied to systems of different types (Laszlo, 1996). There are three operationalizable sub-aspects: (ST5a) identifying how individual cause and effect relationships impact the broader system behavior (Barth-Cohen, 2018), (ST5b) recognizing how the various substructures of a system (specific types and combinations of variables within systems) influence its behavior (Danish et al., 2017), and (ST5c) predicting how specific structural modifications will change the dynamics of a system (Richmond, 1994).
Through our analysis of the literature, we synthesized 13 sub-aspects associated with five ST aspects. Aspects that are vague or difficult to measure, such as using experiential evidence from the real world together with simulations to “challenge the boundaries of mental (and formal) models” (Booth-Sweeney & Sterman, 2000, p. 250) were not included, nor were aspects that are not commonly included in the literature. In addition, aspects related to CT and modeling practices, such as Richmond’s (1994) “quantitative thinking,” Hopper and Stave’s (2008) “using conceptual models and creating simulation models,” and Arnold and Wade’s (2017) “reducing complexity by modeling systems conceptually” were not listed in ST, but are included in CT or modeling.
Aspects and sub-aspects of computational thinking
From the review of the literature, we identified five key CT aspects in the context of modeling using the aforementioned filters: (CT1) decomposing problems such that they are computationally solvable, (CT2) creating artifacts using algorithmic thinking, (CT3) generating, organizing, and interpreting data, (CT4) testing and debugging, and (CT5) making iterative refinements (Fig. 1 right side). Figure 3 shows the distribution of CT aspects represented in the 28 manuscripts.
CT1, decomposing problems such that they are computationally solvable, consists of identifying elements and relationships observable in problems or phenomena and characterizing them in a way that is quantifiable and thus calculable. Problem decomposition deconstructs a problem into its constituent parts to make it computationally solvable and more manageable (Grover & Pea, 2018). All 28 manuscripts we reviewed specify this aspect (Fig. 3) in various ways as an essential characteristic of CT for understanding and representing problems to readily solve, as shown in Table 2. Based on the literature, this aspect is operationalizable in three sub-aspects: (CT1a) describing a clear goal or question that can be answered, as well as an approach to answering the question using computational tools (Irgens et al., 2020; Shute et al., 2017; Wang et al., 2021), (CT1b) identifying the essential elements of a phenomenon or problem (Anderson, 2016; Türker & Pala, 2020), and (CT1c) describing elements in such a way that they are calculable for use in a computational representation of the phenomenon or problem (Brennan & Resnick, 2012; Chen et al., 2017; Hutchins et al., 2020; Lee & Malyn-Smith, 2020).
CT2, creating artifacts using algorithmic thinking, refers to developing a computational representation so that the output can explain and predict real-world phenomena. This is the essential aspect of CT, as proposed in all manuscripts with extensive descriptions as shown in Table 2. This is a unique aspect of CT in that algorithmic thinking provides precise step-by-step procedures to generate problem solutions and involves defining a set of operations for manipulating variables to produce an output as a result of those manipulations (Ogegbo & Ramnarain, 2021; Sengupta et al., 2013; Shute et al., 2017). Weintrop and colleagues (2016) described CT in the form of a taxonomy focusing on creating computational artifacts (e.g., programming, algorithm development, and creating computational abstractions). This aspect is operationalizable in two sub-aspects: (CT2a) parameterizing relevant elements and defining relationships among elements so that a machine or human can interpret them (Anderson, 2016; Chen et al., 2017; Nardelli, 2019; Yadav et al., 2014) and (CT2b) encoding elements and relationships into an algorithmic form that can be executed (Aho, 2012; Hadad et al., 2020; Ogegbo & Ramnarain, 2021; Sengupta et al., 2013; Shute et al., 2017).
CT3, generating, organizing, and interpreting data, involves identifying meaningful patterns from a rich set of data to answer a question (ISTE & CSTA, 2011; National Research Council, 2010, 2012; Weintrop et al., 2016). This aspect has gained more attention as a unique characteristic of CT recently with the realization of the importance of data mining, data analytics, and machine learning (Lee & Malyn-Smith, 2020). All manuscripts described this aspect as pattern recognition using abstract thinking (Anderson, 2016; Shute et al., 2017), data practices (Türker & Pala, 2020), or data management (Lee & Malyn-Smith, 2020). Weintrop and colleagues (2016) considered CT in terms of data practices that involve mathematical reasoning skills such as collecting, creating, manipulating, analyzing, and visualizing data. During this process, it is critical to find distinctive patterns and correlations in data, make claims, and draw conclusions (Grover & Pea, 2018). This aspect is operationalizable in two sub-aspects based on our review: (CT3a) planning for, generating, and organizing data using visual representations (e.g., tables, graphs, or maps) (Basu et al., 2016; Hutchins et al., 2020) and (CT3b) analyzing and interpreting data to identify relationships and trends (Ogegbo & Ramnarain, 2021; Shute et al., 2017).
CT4, testing and debugging, refers to evaluating the appropriateness of a computational solution based on the goal as well as the available supporting evidence (Grover & Pea, 2018; ISTE & CSTA, 2011; Weintrop et al., 2016). All manuscripts described the importance of this aspect as an evaluation or verification of the solution (Anderson, 2016; Basu et al., 2016), or in terms of fixing behavior, troubleshooting, or systematic trial and error processes (Aho, 2012; Brennan & Resnick, 2012; Sullivan & Heffernan 2016) (Table 2). It involves comparing a solution with real-world data or expected outcomes to refine the solution and analyze whether the solution behaves as expected (Grover & Pea, 2013; Weintrop et al., 2016). Through analyzing the manuscripts, this aspect is operationalizable in three sub-aspects: (CT4a) detecting issues in an inappropriate solution (Basu et al., 2016; Sullivan & Heffernan, 2016), (CT4b) fixing issues based on the behavior of the artifact (Aho, 2012; Brennan & Resnick, 2012), and (CT4c) confirming the solution using a range of inputs (Kolikant, 2011; Sengupta et al., 2013).
CT5, making iterative refinements, is a process of repeatedly making gradual modifications to account for new evidence and new insights collected through observations (of the phenomenon and the output of a computational artifact), readings, and discussions (Grover & Pea, 2018; ISTE & CSTA, 2011; Shute et al., 2017; Weintrop et al., 2016). Seventeen authors refer to this aspect in terms of iterative and incremental refinement or development (Brennan & Resnick, 2012; Hutchins et al., 2020; Ogegbo & Ramnarain, 2021; Shute et al., 2017; Tang et al., 2020) (Fig. 3; Table 2). The authors we reviewed imply that iterative revision or refinement processes are essential for CT. Those who do not specify this aspect seem to include it in the process of CT2, developing computational artifacts, as they expect learners to revise their artifacts multiple times as they gain more knowledge about the phenomenon (Nardelli, 2019; Selby & Woollard, 2013). To refine a solution learners articulate the differences between their solution and the underlying phenomenon and reflect on the limitations of their solution. Through the review of CT literature, this aspect is operationalizable in three sub-aspects: (CT5a) making changes based on new conceptual understandings (Barr & Stephenson, 2011), (CT5b) making changes based on a comparison between computational outputs and validating data sources (Chen et al., 2017), and (CT5c) making changes due to an unexpected algorithmic behavior (Brennan & Resnick, 2012; Sengupta et al., 2013; Shute et al., 2017).
The analysis of our CT literature review synthesizes 13 sub-aspects associated with the five CT aspects. We did not include (1) generic features (e.g., generation, creativity, collaboration, critical thinking) although multiple authors listed them as CT, (2) perception or disposition features (e.g., confidence in dealing with complexity, persistence in working with difficult problems, tolerance for ambiguity, or the ability to deal with open-ended problems) (ISTE & CSTA, 2011), and (3) overly broad features (e.g., abstraction, problem-solving processes), which were often contextualized into more specific aspects of CT. For example, some authors unpack “abstraction” into the selection of essential steps by reducing repeated steps (Grover & Pea, 2018), which is covered by CT2, creating artifacts using algorithmic thinking, in our framework.
Integration of ST and CT in modeling
Integration of ST and CT in ST literature
Some researchers view ST as related to CT through quantitative thinking (Booth Sweeney & Sterman, 2000; Richmond 1994) and creating simulation models (Arnold & Wade, 2017; Barth-Cohen, 2018; Dickes et al., 2016; Forrester, 1971; Stave & Hopper, 2007). Forrester regarded systems thinking as “a method for analyzing complex systems that uses computer simulation models to reveal how known structures and policies often produce unexpected and troublesome behavior” (1971, p. 115). Because of the reference to computer simulation models, we interpret this description as combining ST and CT through modeling. Computational modeling thus provides new ways to explore, understand, and represent interconnections among system elements, as well as to observe the output of system behaviors (Wilkerson et al., 2018).
Integration of ST and CT in CT literature
Researchers in CT (Berland & Wilensky, 2015; Brennan & Resnick, 2012; Lee & Malyn-Smith 2020; Sengupta et al., 2013; Shute et al., 2017; Weintrop et al., 2016; Wing, 2011, 2017) claim that CT and ST are intertwined and support each other for successfully managing and solving complex problems across STEM disciplines. Wing (2017) contends that CT is “using abstraction and decomposition when designing a large complex system” (p. 8). CT supports representing the interrelationships among sub-parts in a system that are computational in nature and which form larger complex systems (Berland & Wilensky, 2015; Brennan & Resnick, 2012; Lee & Malyn-Smith 2020). For example, while ST supports learners to conceptualize a problem as a system of interacting elements, they use CT to make the relationships tractable through algorithms. This results in learners understanding larger and more complex systems (using ST) and finding solutions efficiently (using CT).
While CT overlaps with ST, Shute and colleagues (2017) distinguish CT from ST in that CT aims to design efficient solutions to problems through computation while ST focuses on constructing and analyzing various relationships among elements in a system for explaining and generalizing them to other similar systems. Although there are relationships between the two ways of thinking, we view CT and ST as co-equal in the context of modeling because of their unique characteristics. Our framework thus defines CT and ST as separate entities (Fig. 1).
Integration of ST and CT in computational modeling
Our review of ST and CT literature shows that computational modeling is a promising context for learners to engage in ST and CT (Arnold & Wade, 2017; Barr & Stephenson, 2011; Fisher, 2018; Hopper & Stave, 2008; Kolikant, 2011). Since ST and CT are intrinsically linked to computational modeling, they support learners’ modeling practices (Fisher, 2018). Computational models are non-static representations of phenomena that can be simulated by a computer or a human and differ from static model representations (e.g., paper-pencil models) because they produce output values.
Efforts to bridge CT and STEM in K-12 science have centered prominently on building and using computational models (Ogegbo & Ramnarain, 2021; Sengupta et al., 2013; Shute et al., 2017; Sullivan & Heffernan, 2016). Computational models provide useful teaching and learning tools for integrating CT into STEM to make scientific ideas accessible to learners and enhance student understanding of phenomena (Nguyen & Santagata, 2021). As learners begin to build models they can define the components and structural features so that a computer can interpret model behavior. CT aids learners in modeling for investigating, representing, and understanding a phenomenon or a system (Irgens et al., 2020; Sullivan & Heffernan, 2016).
Scholars have also developed computational modeling tools to promote ST (Levy & Wilensky, 2011; Richmond, 1994; Samon & Levy, 2019; Wilensky & Resnick 1999), and argue that the ability to effectively use computer simulations is an important aspect of ST (National Research Council, 2011). ST supports learners in modeling to define the boundaries of the system (Dickes et al., 2016) and reduce the complexity of a system conceptually (Arnold & Wade, 2017). Their research shows that learners develop proficiency for scientific ideas and ST while building computational models (e.g., Stella [Richmond, 1994], NetLogo [Levy & Wilensky, 2011; Samon & Levy, 2019; Yoon et al., 2017]). Below is a description of our framework, which encapsulates how modeling can integrate ST and CT, and how ST and CT can support learners’ modeling practices.
Framework for computational systems modeling
The framework illustrates how each modeling practice draws upon aspects of both ST and CT to support explaining phenomena and solving problems (Fig. 1). We use example models created using SageModeler to show how ST and CT aspects are manifested in modeling. SageModeler is a free, web-based, open-source computational modeling tool with several affordances (https://sagemodeler.concord.org). Learners have: (1) multiple ways of building models (system diagrams, static equilibrium modelsFootnote 1, and dynamic time-based models), (2) multiple forms (visual and textual) of representing variables and relationships that are customizable by the learner, (3) multiple ways of defining functional relationships between variables without having to write equations or computer code, and (4) multiple pathways for generating visualizations of model output. In order to better illustrate our approach to integrating ST and CT in the context of modeling, we describe how these features of SageModeler can be used to support ST and CT in each modeling practice.
M1. Characterize a problem or phenomenon to model
The ability to characterize a problem or phenomenon to model supports learners in gaining a firm conceptual understanding of the phenomenon and helps to facilitate the modeling process by narrowing the scope of the phenomenon and determining the best modeling approach to apply (Dickes et al., 2016; Hutchins et al., 2020). Models are often built as aids for understanding a problem or perplexing observation. When learners face a problem or encounter a phenomenon to be understood or explained, they need to clearly define the problem or ask a “central question” to be investigated (Meadows, 2008). This allows the learner to delineate model boundaries (see M2 below), choosing only those elements and connections that are deemed relevant to the question. At this stage, these elements reflect learners’ general observations of the phenomenon or problem and may initially lack the specificity needed to design a computational model. For example, when learners consider anthropogenic climate change, they are likely to first identify the elements as “carbon dioxide,” “ocean,” “ice caps,” “agriculture,” “human activity,” etc. This step helps foster learners’ initial sense-making.
To fully engage in this practice, learners need to use ST1, defining a system, ST4, framing problems or phenomena in terms of behavior over time when appropriate, and CT1, decomposing problems such that they are computationally solvable. ST1 and CT1 are important in this modeling practice because they help learners focus on the question that needs to be answered computationally (Brennan & Resnick, 2012; Lee & Malyn-Smith 2020). Science educators propose that “an explicit model of a system under study” (National Research Council, 2012, p. 90) can be a potential learning tool for deep understanding. In SageModeler, learners can create a text box for writing their questions, and select to use a number of different modeling strategies, which supports ST1, ST4, and CT1 (Fig. 4).
ST4, framing problems or phenomena in terms of behavior over time, can be helpful if the phenomenon being studied displays dynamic behavior. The understanding of how different aspects of the phenomenon evolve can aid in determining which elements of the system should be included in the model to be built (see M2 below). Such understanding also helps learners choose an approach for building a model (e.g., dynamic or static equilibrium). One key feature in SageModeler is that it allows for the development of dynamic models containing feedback structures that can more accurately portray the behaviors of real-world phenomena over time and directly support learners in ST4 (Fig. 4). However, this type of modeling may not be appropriate for all phenomena and should only be used when it is necessary to explain how the behavior of the system changes over time. When characterizing a problem or phenomenon to model, learners need to consider whether a static or dynamic structure will better suit their purpose. Although specifics of that structure will likely emerge as the model is being constructed, the type of model chosen and its purposes may influence the choice of system boundaries.
M2. Define the boundaries of the system and M3. Design and construct model structure
These two practices are often connected (hence a box surrounds them in the framework) and tend to occur in a synchronous fashion as learners build and revise models.
M2. Define the boundaries of the system
When learners define the boundaries of the system, they break down the system into specific elements that better suit the aims of their question and facilitate modeling. Within this practice it is essential to consider the size and scope of the question under study by reviewing the elements, selecting those essential to understanding the behavior of the system (Anderson, 2016; Türker & Pala, 2020), and ignoring irrelevant elements. ST1, defining a system, CT1, decomposing problems such that they are computationally solvable, and CT2, creating artifacts using algorithmic thinking, support learners as they define the boundaries of the system.
ST1, defining a system, guides learners to examine the system and consider what is included and what is excluded in the model, in other words, specifying the boundary of the system being modeled (Arnold & Wade, 2017). ST1 also encompasses considerations of how the model components are linked to each other to form model structures that will impact the emergent behavior of the system. CT1, decomposing problems such that they are computationally solvable, is vital to this modeling practice because it breaks down complex phenomena into logical sequences of cause and effect that can be described computationally (Aho, 2012; Basu et al., 2016; Berland & Wilensky, 2015; Sengupta et al., 2013; Shute et al., 2017; Türker & Pala, 2020). Learners also use CT2, creating artifacts using algorithmic thinking, at this stage to redefine and encode the elements as measurable variables (Cansu & Cansu, 2019; Kolikant, 2011). Learners must determine how the elements they have chosen are causally connected and transform their abstract conceptual understanding of the system into concrete language that can be encoded meaningfully and can be computed. For example, an element previously identified as “human activity” could be redefined as variables, such as “amount of fossil fuels burned in power plants,” “amount of greenhouse gases,” and “amount of forest fires” (Fig. 4).
M3. Design and construct model structure
After defining measurable variables, learners can begin to design and construct model structure. When designing and constructing model structure, learners are actively involved in defining relationships among variables within the model. In a model of climate change, for example, learners set a relationship between “temperature of the Earth” and the “# of ice caps melting” variables by defining functional relationships, as shown in Fig. 4. This modeling practice encourages learners to carefully examine cause and effect relationships within the system in a model (Levy & Wilensky, 2008, 2009, 2011; Wilensky & Resnick, 1999). ST2, engaging in causal reasoning, supports learners to describe both direct and indirect relationships among various components of a system model (Grotzer, 2003, 2017).
As learners continue to build and revise their models, the goal is to move their attention from simple relationships between two adjacent variables towards observing the cumulative behavior of longer causal chains (such as the relationship between the “amount of fossil fuels burned” and the “# of ice caps melting”), as well as broader structural patterns, such as feedback loops (Dickes et al., 2016; Fisher, 2018; Grotzer, 2003, 2017; Jacobson et al., 2011). Knowledge of the connections between model structure and behavior support learners in designing and building the model appropriately (Meadows, 2008; Perkins & Grotzer, 2005). Learners engaging in this modeling practice have an opportunity to use ST3, identifying interconnections and feedback. In turn, familiarity with ST4, framing problems or phenomena in terms of behavior over time, helps learners, when appropriate, to determine which variables represent accumulations in a system and how other variables interact with those accumulations over time. ST4 is also important when considering the length of time over which a model is to be simulated. A time frame that is too short may not reveal important behaviors in the model while one that is too long may hide important behavioral detail.
The aspect of CT2, creating artifacts using algorithmic thinking, is important in this modeling practice, particularly in building computational models, which encode variables and relationships such that a computer can utilize this encoding to run a simulation (Nardelli, 2019; Ogegbo & Ramnarain, 2021; Sengupta et al., 2013). SageModeler takes a semiquantitative approach to defining how one variable affects another, and how accumulations and flows change over time in dynamic models. Initial values of the variables are set using a slider that goes from “low” to “high” (Fig. 5) and learners use words with associated graphs to define the links between variables (Fig. 4). The links between variables also change visually to show how those relationships are defined. These features support learners in ST2, engaging in causal reasoning, ST3, identifying interconnections and feedback, and CT2, creating computational artifacts.
M4. Test, evaluate, and debug model behavior
As learners construct computational models, they are constantly revising those models based on new evidence, incorporating new variables to match their growing understanding of the system or removing irrelevant variables because they are outside the scope and scale of the question (Basu et al., 2016; Brennan & Resnick, 2012). During revisions learners consider relationships they have set among variables and whether or not they result in accurate or expected behaviors when the model is simulated (Hadad et al., 2020; Lee et al., 2020). This iterative testing and evaluation continues until the learner is satisfied that the created artifact sufficiently represents the phenomenon or system under consideration. This modeling practice combines ST5, predicting system behavior based on system structure, CT3, generating, organizing, and interpreting data, CT4, testing and debugging, and CT5, making iterative refinements.
A major advantage of computational models is the opportunity to run a simulation, allowing learners to generate output from the model and test if their model matches their conceptual understanding of the phenomenon. Simulation encourages learners to use ST5, predicting system behavior based on system structure, as they anticipate the model’s output based on the visual representation of the model’s structure. If learners’ computational models do not behave as expected by comparing their conceptual understanding with the model’s output using CT3, generating, organizing, and interpreting data (Aho, 2012; Selby & Woollard, 2013; Türker & Pala 2020) and CT4, testing and debugging (Barr & Stephenson, 2011; Sengupta et al., 2013; Sullivan & Heffernan, 2016; Yadav et al., 2014), they can use CT5, make iterative refinements, and re-engage in M2 and M3 by redefining the system under study and revising their models.
In addition to utilizing simulation outputs, learners also make use of data from real-world measurements or experiments to help evaluate and make iterative changes to their models. Such external validation helps learners recognize how their model structures do or do not reflect the system they are modeling and helps guide their subsequent model revisions. Generating model output supports learner involvement in CT3, generating, organizing, and interpreting data, and CT4, testing and debugging. Pattern recognition and identifying relationships in data are important in the creation of an abstract model because they support learners in evaluating the behaviors of a model (Lee & Malyn-Smith, 2020; Shute et al., 2017). The entire M4 practice is supported by CT5, making iterative refinements, to lead learners when revising their models systematically based on evidence.
Once variables are chosen and linked together by relationships that have been defined semi-quantitatively, SageModeler can simulate the model and generate model output that can be compared with expected behavior and external validating data sources (Fig. 5). Additionally, learners can create multivariate graphs using simulation output or external data to show the effect of any variable on any other variable in the model and to validate model output. For example, in Fig. 5, learners test their models by running simulations and changing the starting values of input variables (e.g., “# of cars burning gasoline”) to explore how downstream variables (e.g., “global temperature”) change, thus examining if the simulation outputs met their expectations. Learners also generate a graph between two key variables (“# of cars burning gasoline” and “global temperature”) to test the model. Research findings on learners who build, revise, and test computational models with SageModeler show promising impacts on student learning while they engage in ST and CT (Eidin et al., 2020).
M5. Use model to explain and predict behavior of phenomenon or design solution to a problem
Once a model reaches a level of functionality where it appropriately and consistently illustrates the behavior of the system under exploration, learners engage in the modeling practice of using the model to explain and predict behavior of phenomenon or design solution to a problem. This requires that learners utilize ST2, engaging in causal reasoning, and ST5, predicting system behavior based on system structure. Learners must read and interpret the model as a series of interconnected relationships among variables and make sense of the model output before they can use their model to facilitate a verbal or written explanation of the phenomenon or anticipate the outcome of an internal or external intervention on system behavior. Because the model serves as a tool to explain or predict a phenomenon or solve a problem, examining the usability of the model is critical (Schwarz & White, 2005). Therefore, learners should be able to articulate the differences between their model and the underlying real-world phenomenon, reflecting on both the limitations and usability of their model.
Further, CT3, the practice of generating, organizing, and interpreting data, supports learners as they compare model output to data collected from the real-world phenomenon and assess the similarities and differences between them. By engaging in the construction of a computational model that mimics reality and considering the limits of the model to produce accurate behavior, learners gain an understanding about the power of modeling to leverage learning and increase intuition about complex systems.
Table 3 summarizes how learners are engaged in 5 ST aspects with 13 associated sub-aspects and 5 CT aspects with 13 associated sub-aspects through modeling.
Implications and future directions
This framework serves as a foundation for developing curriculum, teacher and learner supports, assessments, and research instruments to promote, monitor, and explore how learners engage in ST and CT through model building, testing, evaluating, and revising. Specific aspects of ST and CT can guide the design of supports to help learners participate in knowledge construction through modeling, and can help researchers and practitioners develop indicators (evidence) that can clearly describe measurable behaviors that show whether learners use the desired ST and CT aspects. This approach provides a direction for designing activities to produce specific learner-generated knowledge products that can support modeling practices and their corresponding ST and CT aspects in K-12 STEM curricula.
Further studies in the context of well-developed curricula aligned with the Framework for Computational Systems Modeling are required to (1) explore additional ST and CT aspects learners use within the context of modeling, (2) confirm that these aspects can be observed through associated sub-aspects in modeling contexts, and (3) describe how and when learners use the ST and CT aspects through the five modeling practices defined in the framework.
Limitations
As is typical in an integrative review approach (Snyder, 2019), our literature review might be biased based on our conceptual understanding of modeling, ST, and CT because we limited it to scholars within our defined set of search criteria. Due to the broad conceptualizations of CT and ST and a wide range of fields where these are applicable, our literature collection may have missed relevant studies. Given the breadth of these fields, it is difficult to condense all of the literature into one coherent manuscript. As such we emphasized aspects of modeling, ST, and CT that synergized and supported each other.
Conclusions
Modeling, systems thinking, and computational thinking are important for an educated STEM workforce and the general public to explain and predict scientific phenomena and to solve pressing global and local problems (National Research Council, 2012). ST and CT in the context of modeling are critical for professionals in science and engineering to advance knowledge about the natural world and for civic engagement by the public to understand and evaluate proposed solutions to local and global problems. We suggest that schools provide learners with more opportunities to develop, test, and revise computational models and thus use aspects of both systems thinking and computational thinking.
Additional opportunities exist for learning scientists to carry out an integrated and comprehensive research and development program in a range of learning contexts for exploring the relationship between modeling, ST, CT, and student learning. Such a program of research should aim to integrate ST and CT through modeling to create pedagogically appropriate teaching and learning materials, and to develop and collect evidence to confirm learner engagement in modeling, ST, and CT. Our efforts in developing a framework contribute to this mission to educate learners as science-literate citizens who are proficient in building and using models that utilize a systems thinking perspective while taking advantage of the computational power of algorithms to explain and predict phenomena or seek answers and develop a range of potential solutions to problems that plague our society and world.
Availability of data and material
Not applicable. Data sharing is not applicable to this article as no datasets were generated or analysed during the current study.
Code Availability
Not applicable.
Notes
A static equilibrium model consists of a set of variables linked by relationships that define how one variable influences another. Any change to an input variable is immediately reflected in new values calculated for each variable in the system. There is no time component to this type of system model. Any change to the input instantaneously results in a new model state.
References
Aho, A. V. (2012). Computation and computational thinking. The Computer Journal, 55(7), 832–835. https://doi.org/10.1093/comjnl/bxs074
Anderson, N. D. (2016). A call for computational thinking in undergraduate psychology. Psychology Learning & Teaching, 15(3), 226–234
Arnold, R. D., & Wade, J. P. (2015). A definition of systems thinking: A systems approach. Procedia Computer Science, 44, 669–678
Arnold, R. D., & Wade, J. P. (2017). A complete set of systems thinking skills. Insight, 20(3), 9–17
Barth-Cohen, L. (2018). Threads of local continuity between centralized and decentralized causality: Transitional explanations for the behavior of a complex system. Instructional Science, 46(5), 681–705
Barr, V., & Stephenson, C. (2011). Bringing computational thinking to K-12: What is involved and what is the role of the computer science education community? Acm Inroads, 2(1), 48–54. https://doi.org/10.1145/1929887.1929905
Basu, S., Biswas, G., Sengupta, P., Dickes, A., Kinnebrew, J. S., & Clark, D. (2016). Identifying middle school students’ challenges in computational thinking-based science learning. Research and Practice in Technology-enhanced Learning, 11(1), 13. https://doi.org/10.1007/s11257-017-9187-0
Benson, T. A. (2007). Developing a systems thinking capacity in learners of all ages. Waters Center for Systems Thinking. WatersCenterST.org. Retrieved December 17, 2021, from https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.535.9175&rep=rep1&type=pdf
Ben-Zvi Assaraf, O., & Orion, N. (2005). Development of system thinking skills in the context of Earth system education. Journal of Research in Science Teaching, 42(5), 518–560
Berland, M., & Wilensky, U. (2015). Comparing virtual and physical robotics environments for supporting complex systems and computational thinking. Journal of Science Education and Technology, 24(5), 628–647
Booth-Sweeney, L. B., & Sterman, J. D. (2000). Bathtub dynamics: Initial results of a systems thinking inventory. System Dynamics Review: The Journal of the System Dynamics Society, 16(4), 249–286
Booth-Sweeney, L. B., & Sterman, J. D. (2007). Thinking about systems: Student and teacher conceptions of natural and social systems. System Dynamics Review: The Journal of the System Dynamics Society, 23(2–3), 285–311
Brennan, K., & Resnick, M. (2012, April). Using artifact-based interviews to study the development of computational thinking in interactive media design. In Annual American Educational Research Association Meeting, Vancouver, BC, Canada. Retrieved May 19, 2022, from https://citeseerx.ist.psu.edu/viewdoc/download;jsessionid=8D8C7AFCB470A17FA08153DA29D22AF8?doi=10.1.1.296.6602&rep=rep1&type=pdf
Cansu, S. K., & Cansu, F. K. (2019). An overview of computational thinking. International Journal of Computer Science Education in Schools, 3(1). https://doi.org/10.21585/ijcses.v3i1.53
Chen, G., Shen, J., Barth-Cohen, L., Jiang, S., Huang, X., & Eltoukhy, M. (2017). Assessing elementary students’ computational thinking in everyday reasoning and robotics programming. Computers & Education, 109, 162–175
Cronin, M. A., Gonzalez, C., & Sterman, J. D. (2009). Why don’t well-educated adults understand accumulation? A challenge to researchers, educators, and citizens. Organizational Behavior and Human Decision Processes, 108(1), 116–130
Danish, J., Saleh, A., Andrade, A., & Bryan, B. (2017). Observing complex systems thinking in the zone of proximal development. Instructional Science, 45(1), 5–24
Dickes, A. C., Sengupta, P., Farris, A. V., & Basu, S. (2016). Development of mechanistic reasoning and multilevel explanations of ecology in third grade using agent-based models. Science Education, 100(4), 734–776
Draper, F. (1993). A proposed sequence for developing systems thinking in a grades 4–12 curriculum. System Dynamics Review, 9(2), 207–214
Eidin, E., Bielik, T., Touitou, I., Bowers, J., McIntyre, C., Damelin, D. (2020, June 21–23). Characterizing advantages and challenges for students engaging in computational thinking and systems thinking through model construction. The Interdisciplinarity of the Learning Sciences, 14th International Conference of the Learning Sciences, Volume 1 (pp. 183–190). Nashville, Tennessee: International Society of the Learning Sciences. https://repository.isls.org//handle/1/6460 (conference canceled, online)
Fisher, D. (2018). Reflections on teaching system dynamics to secondary school students for over 20 years. Systems, 6(20), 12
Forrester, J. W. (1961). Industrial dynamics. Productivity Press
Forrester, J. W. (1971). Counterintuitive behavior of social systems. Theory and Decision, 2(2), 109–140
Forrester, J. W. (1994). System dynamics, systems thinking, and soft OR. System Dynamics Review, 10(2-3), 245–256
Grotzer, T. A., & Basca, B. B. (2003). How does grasping the underlying causal structures of ecosystems impact students’ understanding? Journal of Biological Education, 38(1), 16–29
Grotzer, T. A., Solis, S. L., Tutwiler, M. S., & Cuzzolino, M. P. (2017). A study of students’ reasoning about probabilistic causality: Implications for understanding complex systems and for instructional design. Instructional Science, 45(1), 25–52
Grover, S., & Pea, R. (2013). Computational thinking in K–12: A review of the state of the field. Educational Researcher, 42(1), 38–43. https://doi.org/10.3102/0013189X12463051
Grover, S., & Pea, R. (2018). Computational thinking: A competency whose time has come. In S. Sentence, E. Barendsen, & C. Schulte (Eds.), Computer science education: Perspectives on teaching and learning in school (pp. 19–38). Bloomsbury Academic
Hadad, R., Thomas, K., Kachovska, M., & Yin, Y. (2020). Practicing formative assessment for computational thinking in making environments. Journal of Science Education and Technology, 29(1), 162–173
Halloun, I. A. (2007). Modeling theory in science education (24 vol.). Springer Science & Business Media
Harrison, A. G., & Treagust, D. F. (2000). A typology of school science models. International Journal of Science Education, 22(9), 1011–1026
Hmelo-Silver, C. E., Jordan, R., Eberbach, C., & Sinha, S. (2017). Systems learning with a conceptual representation: A quasi-experimental study. Instructional Science, 45(1), 53–72. https://doi.org/10.1007/s11251-016-9392-y
Holz, C., Siegel, L. S., Johnston, E., Jones, A. P., & Sterman, J. (2018). Ratcheting ambition to limit warming to 1.5 C–trade-offs between emission reductions and carbon dioxide removal. Environmental Research Letters, 13(6), 064028. http://hdl.handle.net/1721.1/121076
Hopper, M., & Stave, K. A. (2008). Assessing the effectiveness of systems thinking interventions in the classroom. In The 26th International Conference of the System Dynamics Society (pp. 1–26). Athens, Greece
Hutchins, N. M., Biswas, G., Maróti, M., Lédeczi, Á., Grover, S., Wolf, R. … McElhaney, K. (2020). C2STEM: A system for synergistic learning of physics and computational thinking. Journal of Science Education and Technology, 29(1), 83–100. https://link.springer.com/article/10.1007/s10956-019-09804-9
ISTE (International Society for Technology in Education) & CSTA (Computer Science Teachers Association) (2011). Computational thinking teacher resources. Retrieved December 17, 2021, from https://cdn.iste.org/www-root/Computational_Thinking_Operational_Definition_ISTE.pdf
Irgens, G. A., Dabholkar, S., Bain, C., Woods, P., Hall, K., Swanson, H. … Wilensky, U. (2020). Modeling and measuring high school students’ computational thinking practices in science. Journal of Science Education and Technology, 29(1), 137–161. https://doi.org/10.1007/s10956-020-09811-1
Jacobson, M. J., & Wilensky, U. (2006). Complex systems in education: Scientific and educational importance and implications for the learning sciences. The Journal of the Learning Sciences, 15(1), 11–34
Jacobson, M. J., Kapur, M., So, H. J., & Lee, J. (2011). The ontologies of complexity and learning about complex systems. Instructional Science, 39(5), 763–783
Kim, D. H. (1999). Introduction to systems thinking (Vol. 16). Pegasus Communications
Kolikant, Y. B. D. (2011). Computer science education as a cultural encounter: a socio-cultural framework for articulating teaching difficulties. Instructional Science, 39(4), 543–559
Krajcik, J., & Shin, N. (2022). Project-based learning. In R. K. Sawyer (Ed.), Cambridge handbook of the learning sciences 3rd edition (pp. 72–92). Cambridge University Press
Laszlo, E. (1996). The systems view of the world: A holistic vision for our time. Hampton Press
Lee, I., Grover, S., Martin, F., Pillai, S., & Malyn-Smith, J. (2020). Computational thinking from a disciplinary perspective: Integrating computational thinking in K-12 science, technology, engineering, and mathematics education. Journal of Science Education and Technology, 29(1), 1–8. https://doi.org/10.1007/s10956-019-09803-w
Lee, I., & Malyn-Smith, J. (2020). Computational thinking integration patterns along the framework defining computational thinking from a disciplinary perspective. Journal of Science Education and Technology, 29(1), 9–18
Levy, S. T., & Wilensky, U. (2008). Inventing a “mid-level” to make ends meet: Reasoning between the levels of complexity. Cognition and Instruction, 26(1), 1–47
Levy, S. T., & Wilensky, U. (2009). Crossing levels and representations: The Connected Chemistry (CC1) curriculum. Journal of Science Education and Technology, 18(3), 224–242
Levy, S. T., & Wilensky, U. (2011). Mining students’ inquiry actions for understanding of complex systems. Computers & Education, 56(3), 556–573
Madubuegwn, C. E., Okechukwu, G. P., Dominic, O. E., Nwagbo, S., & Ibekaku, U. K. (2021). Climate change and challenges of global interventions: A critical analysis of Kyoto protocol and Paris agreement. Journal of Policy and Development Studies, 13(1), 01–10. https://www.researchgate.net/publication/354872613
Martinez-Moyano, I. J., & Richardson, G. P. (2013). Best practices in system dynamics modeling. System Dynamics Review, 29(2), 102–123
Meadows, D. (2008). Thinking in systems: A primer. Chelsea Green Publishing
Metcalf, J. S., Krajcik, J., Soloway, E. (2000). Model-It: A design retrospective. In Jacobson, M. J., Kozma, R. B. (Eds.), Innovations in science and mathematics education (pp. 77–115). Mahwah, NJ: Lawrence Erlbaum
Nardelli, E. (2019). Do we really need computational thinking? Communications of the ACM, 62(2), 32–35
National Research Council. (2000). How people learn: Brain, mind, experience, and school: Expanded edition. The National Academies Press
National Research Council. (2007). Taking science to school: Learning and teaching science in grades K-8. National Academies Press
National Research Council. (2010). Report of a workshop on the scope and nature of computational thinking. National Academies Press
National Research Council. (2011). Key points expressed by presenters and discussants. Report of a workshop on the pedagogical aspects of computational thinking (pp. 6–35). The National Academies Press. https://doi.org/10.17226/13170
National Research Council. (2012). A framework for K-12 science education: Practices, crosscutting concepts, and core ideas. National Academies Press
NGSS Lead States. (2013). Next generation science standards: For states, by states. The National Academies Press
Nguyen, H., & Santagata, R. (2021). Impact of computer modeling on learning and teaching systems thinking. Journal of Research in Science Teaching, 58(5), 661–688
Ogegbo, A. A., & Ramnarain, U. (2021). A systematic review of computational thinking in science classrooms. Studies in Science Education, 1–28. https://doi.org/10.1080/03057267.2021.1963580
Ossimitz, G. (2000). Teaching system dynamics and systems thinking in Austria and Germany. In The 18th International Conference of the System Dynamics Society. Bergen, Norway
Pallant, A., & Lee, H. S. (2017). Teaching sustainability through system dynamics: Exploring stocks and flows embedded in dynamic computer models of an agricultural land management system. Journal of Geoscience Education, 65(2), 146–157
Perkins, D. N., & Grotzer, T. A. (2005). Dimensions of causal understanding: The role of complex causal models in students’ understanding of science. Studies in Science Education, 14(1), 117–166. https://doi.org/10.1080/03057260508560216
Plate, R., & Monroe, M. (2014). A structure for assessing systems thinking. The Creative Learning Exchange, 23(1), 1–3
Psycharis, S., & Kallia, M. (2017). The effects of computer programming on high school students’ reasoning skills and mathematical self-efficacy and problem solving. Instructional Science, 45(5), 583–602
American Association for the Advancement of Science (1993). Project 2061: Benchmarks for Science Literacy. New York: Oxford University Press.
Richmond, B. (1993). Systems thinking: Critical thinking skills for the 1990s and beyond. System Dynamics Review, 9(2), 113–133. https://doi.org/10.1002/sdr.4260090203
Richmond, B. (1994). System dynamics/systems thinking: Let’s just get on with it. System Dynamics Review, 10(2–3), 135–157
Richmond, B. (1997). The thinking in systems thinking: how can we make it easier to master? The Systems Thinker, 8(2), 1–5
Riess, W., & Mischo, C. (2010). Promoting systems thinking through biology lessons. International Journal of Science Education, 32(6), 705–725
Samon, S., & Levy, S. T. (2020). Interactions between reasoning about complex systems and conceptual understanding in learning chemistry. Journal of Research in Science Teaching, 57(1), 58–86. https://doi.org/10.1002/tea.21585
Schwarz, C. V., Passmore, C., & Reiser, B. J. (2017). Helping students make sense of the world using next generation science and engineering practices. NSTA Press
Schwarz, C. V., & White, B. Y. (2005). Metamodeling knowledge: Developing students’ understanding of scientific modeling. Cognition and Instruction, 23(2), 165–205
Schwarz, C. V., Reiser, B. J., Davis, E. A., Kenyon, L., Achér, A., Fortus, D. … Krajcik, J. (2009). Developing a learning progression for scientific modeling: Making scientific modeling accessible and meaningful for learners. Journal of Research in Science Teaching, 46(6), 632–654
Selby, C. C., & Woollard, J. (2013). 5–8 March). Computational thinking: the developing definition. Special Interest Group on Computer Science Education, Atlanta GA. Retrieved December 17, 2021, from https://core.ac.uk/download/pdf/17189251.pdf
Senge, P. M. (1990). The fifth discipline: The art and practice of the learning organization. Currency Doubleday
Sengupta, P., Kinnebrew, J. S., Basu, S., Biswas, G., & Clark, D. (2013). Integrating computational thinking with K-12 science education using agent-based computation: A theoretical framework. Education and Information Technologies, 18(2), 351–380
Shute, V. J., Sun, C., & Asbell-Clarke, J. (2017). Demystifying computational thinking. Educational Research Review, 22(1), 142–158
Snyder, H. (2019). Literature review as a research methodology: An overview and guidelines. Journal of Business Research, 104, 333–339. https://doi.org/10.1016/j.jbusres.2019.07.039
Stave, K., & Hopper, M. (2007). What constitutes systems thinking? A proposed taxonomy. In 25th International Conference of the System Dynamics Society. Boston, Massachusetts. Retrieved March 25, 2022, from https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.174.4065&rep=rep1&type=pdf
Sterman, J. D. (1994). Learning in and about complex systems. System Dynamics Review, 10(23), 291–330
Sterman, J. D. (2002). May 29–30). System dynamics: Systems thinking and modeling for a complex world. Massachusetts Institute of Technology Engineering Systems Division. MIT Sloan School of Management. http://hdl.handle.net/1721.1/102741
Sterman, J. D., & Sweeney, L. B. (2002). Cloudy skies: assessing public understanding of global warming. System Dynamics Review: The Journal of the System Dynamics Society, 18(2), 207–240. https://dspace.mit.edu/bitstream/handle/1721.1/102741/esd-wp-2003-01.13.pdf?sequence=1
Sullivan, F. R., & Heffernan, J. (2016). Robotic construction kits as computational manipulatives for learning in the STEM disciplines. Journal of Research on Technology in Education, 48(2), 105–128
Tang, X., Yin, Y., Lin, Q., Hadad, R., & Zhai, X. (2020). Assessing computational thinking: A systematic review of empirical studies. Computers & Education, 148, 103798. https://doi.org/10.1016/j.compedu.2019.103798
Tripto, J., Ben-Zvi Assaraf, O., & Amit, M. (2018). Recurring patterns in the development of high school biology students’ system thinking over time. Instructional Science, 46(5), 639–680
Türker, P. M., & Pala, F. K. (2020). The effect of algorithm education on students’ computer programming self-efficacy perceptions and computational thinking skills. International Journal of Computer Science Education in Schools, 3(3), 19–32. https://doi.org/10.21585/ijcses.v3i3.69
Wang, C., Shen, J., & Chao, J. (2021). Integrating computational thinking in STEM education: A literature review. International Journal of Science and Mathematics Education, 1–24
Weintrop, D., Beheshti, E., Horn, M., Orton, K., Jona, K., Trouille, L., & Wilensky, U. (2016). Defining computational thinking for mathematics and science classrooms. Journal of Science Education and Technology, 25(1), 127–147
Wen, C., Chang, C., Chang, M., Chiang, S. F., Liu, C., Hwang, F., & Tsai, C. (2018). The learning analytics of model-based learning facilitated by a problem-solving simulation game. Instructional Science, 46(6), 847–867
Whittemore, R., & Knafl, K. (2005). The integrative review: Updated methodology. Journal of Advanced Nursing, 52(5), 546–553
Wilensky, U., & Resnick, M. (1999). Thinking in levels: A dynamic systems approach to making sense of the world. Journal of Science Education and Technology, 8(1), 3–19. https://doi.org/10.1023/A:1009421303064
Wilkerson, M. H., Shareff, R., Laina, V., & Gravel, B. (2018). Epistemic gameplay and discovery in computational model-based inquiry activities. Instructional Science, 46(1), 35–60
Wing, J. M. (2006). Computational thinking. Communications of the ACM, 49(3), 33–35
Wing, J. M. (2008). Computational thinking and thinking about computing. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 366(1881), 3717–3725
Wing, J. M. (2011). Computational thinking–What and why? News from the School of Computer Science, 6, 20–23
Wing, J. M. (2017). Computational thinking’s influence on research and education for all. Italian Journal of Educational Technology, 25(2), 7–14. https://doi.org/10.17471/2499-4324/922
Yadav, A., Mayfield, C., Zhou, N., Hambrusch, S., & Korb, J. T. (2014). Computational thinking in elementary and secondary teacher education. ACM Transactions on Computing Education (TOCE), 14(1), 1–16
Yoon, S. A., Anderson, E., Koehler-Yom, J., Evans, C., Park, M., Sheldon, J. … Klopfer, E. (2017). Teaching about complex systems is no simple matter: Building effective professional development for computer-supported complex systems instruction. Instructional Science, 45(1), 99–121
Yoon, S. A., Goh, S., & Park, M. (2018). Teaching and learning about complex systems in K–12 science education: A review of empirical studies 1995–2015. Review of Educational Research, 88(2), 285–325. https://doi.org/10.3102/0034654317746090
Acknowledgements
This material is based upon work supported by the National Science Foundation under Grant Nos. DRL-1842035 and DRL-1842037. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.
Funding
National Science Foundation under Grant Nos. DRL-1842035 and DRL-1842037.
Author information
Authors and Affiliations
Contributions
All authors contributed to the conceptualization of the framework. The first draft of the manuscript was written by Namsoo Shin, Jonathan Bowers, Steve Roderick, and Cynthia McIntyre and all authors commented on previous versions of the manuscript. All authors read and approved the final manuscript. Namsoo Shin conducted literature reviews and led the direction of the manuscript. Jonathan Bowers co-wrote the manuscript throughout the entire writing process of this manuscript. Steve Roderick conducted initial literature reviews and wrote the first draft of the systems thinking section, and selected students’ models based on the framework as examples. Cynthia McIntyre co-wrote and reviewed the description of the framework. Lynn Stephens searched, conducted, and co-wrote extensive literature reviews of systems thinking. Emanuel Eidin provided necessary manuscripts and reviewed the analysis of the literature. Joseph Krajcik oversaw the direction of the manuscript, and iteratively reviewed and revised the manuscript. Daniel Damelin led the entire development of the framework.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no competing interests.
Ethics approval and consent to participate
We obtained ethics approval and consent to participate.
Consent for publication
All authors agreed with the content, all gave explicit consent to submit, and all obtained consent from the responsible authorities at the institute/organization where the work was carried out before the work was submitted.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Shin, N., Bowers, J., Roderick, S. et al. A framework for supporting systems thinking and computational thinking through constructing models. Instr Sci 50, 933–960 (2022). https://doi.org/10.1007/s11251-022-09590-9
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11251-022-09590-9