Abstract
Instructional design deals with the optimization of learning processes. To achieve this, three aspects need to be considered: (1) the learning task itself, (2) the design of the learning material, and (3) the activation of the learner’s cognitive processes during learning. Based on Cognitive Load Theory, learners also need to deal with the task itself, the design of the material, and the decision on how much to invest into learning. To link these concepts, and to help instructional designers and teachers, cognitive load during learning needs to be differentially measured. This article reviews studies using a questionnaire to measure intrinsic, extraneous and germane cognitive load in order to provide evidence for the instruments’ prognostic validity. Six exemplary studies from different domains with different variations of the learning material were chosen to show that the theoretically expected effects on different types of load are actually reflected in the learners’ answers in the questionnaire. Major hypotheses regarding the different load types were (1) variations in difficulty are reflected in the scale on intrinsic cognitive load, (2) variations in design are reflected in the scale on extraneous cognitive load, and (3) variations in enhancing deeper learning through activation of cognitive processes are reflected in the scale on germane cognitive load. We found prognostic validity to be good. The review concludes by discussing the practical and theoretical implications, as well as pointing out the limitations and needs for further research.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction and theoretical background
Instructional Design (ID) deals with the goal of optimizing learning processes. However, what is optimal mainly depends on the goals of learning. Based on the given goals, instructional design focuses on the question “What needs to be presented and how should it be presented to the learner to reach these goals”. There are approaches that focus (1) on the learning task itself, (2) on the design of the learning material, and (3) on the activation of the learner’s cognitive processes to invest effort into learning.
Approaches that focus on the learning task itself. Deciding on the learning content and the task itself is one of the most important parts instructors need to think about. Based on these decisions, instructors identify the prior knowledge needed to understand the content and the complexity of the task to be completed. Besides adjusting the task complexity, one could also enhance learners’ prior knowledge by providing pre-training. The pre-training principle focuses on equipping “the learner with knowledge that will make it easier to process the lesson” (Mayer 2009, p. 190), which means familiarizing the learner with vocabulary and characteristics of key components of the learning content to follow. Another technique is reducing complexity, especially element interactivity, by presenting the material through an isolated elements procedure (Pollock et al. 2002; Ayres 2006), meaning that in a first step, complexity is reduced by de-constructing the task, and therefore learning is conducted element-by-element to allow learners to construct partial schemas, which can be combined in a second step. The goal of both described techniques is an increase of prior knowledge before the actual task needs to be performed.
Approaches that focus on the design of the learning material. Widely and systematically investigated are differences in the design of learning material and their effects on learning. There exists a large variety of principles and effects stating that one representation of learning material outperforms the other when it comes to measures of learning outcome or task performance. For an overview, see Mayer (2005b, 2009). All of these principles state dos and don’ts that should be considered when designing learning material. For example, adding a relevant picture to a text improves learning more than just presenting the text alone (multimedia principle; Fletcher and Tobias 2005), integrating the text into the picture would result in an even better learning outcome or performance than presenting both representations separately (split-attention effect; Kalyuga et al. 1998). Alternatively, the given text could be presented in an auditory format to avoid overloading working memory (modality principle; Moreno and Mayer 1999). In the majority of cases, the goal of these techniques is to avoid unnecessary search or navigation processes between different representations or overload when, for example, using just one modality.
Approaches that focus on the activation of the learner’s cognitive processes to invest effort into learning. A range of approaches follow the idea of cognitive activation in order to “direct learners' attention to cognitive processes that are relevant for learning or schema construction” (Sweller et al. 1998, p. 262). These approaches often use cognitive or metacognitive prompts to hustle the learner in the right direction or to give the learner cues on how to best process the given learning content (prompting effect; Bannert 2009). The goal of these principles is to foster the construction of schemata and mental models.
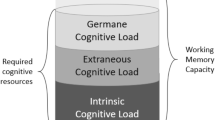
Besides the question of whether learners perform better through one or more of these approaches, (e.g., achieve higher learning outcomes), instructional designers should be interested in the question regarding the effectiveness of the learning process. Therefore, effects of the presented three approaches should be investigated more closely. One should ask if subjective complexity really was lower (approach 1), if the material was designed to help learning (e.g., the included picture enhanced the building of a correct mental model; approach 2), and whether activation of the learner’s cognitive processes was successful (approach 3). To answer these questions, a differentiated investigation of invested cognitive resources during learning is needed. Cognitive Load Theory (CLT; Chandler and Sweller 1991, Sweller 2010a) presents a model describing different aspects of load that are relevant during learning. CLT assumes that working memory is limited in capacity, whereas long-term memory is limitless. The goal of learning in CLT is to construct domain-specific knowledge structures (i.e., cognitive schemas; van Merriënboer and Ayres 2005). But schema construction occurs in working memory with its limited capacity. Based on CLT, this capacity needs to be divided between different sources of load imposed on working memory during learning or dealing with different tasks. Traditionally, three independent sources of load, namely intrinsic, extraneous and germane cognitive load (e.g., Sweller et al. 1998) are differentiated. A refined view on CLT (Sweller et al. 2011) only separates intrinsic and extraneous cognitive load, and will be discussed later. The traditional view, from a practical perspective, helps in the investigation of the above-mentioned questions of instructional designers more clearly: (1) Investigating intrinsic cognitive load helps in understanding the subjective complexity placed on the learners, (2) investigating extraneous cognitive load helps in understanding the impact of differences in design, and (3) investigating germane cognitive load helps to understand the effort learners invested in learning. Therefore, in the following, the different concepts from the traditional view are described more in-depth (but can easily be adapted to the new view on CLT), used in the following studies, and used as a basis in the questionnaire to access cognitive load during learning.
Intrinsic cognitive load (ICL). The number of interacting elements (element interactivity) is the primary determinant of the amount of perceived intrinsic cognitive load (Sweller 1994; Sweller and Chandler 1994). For example, adding two random numbers no higher than 10 is less complex than adding three random numbers higher than 100. Therefore, adding the lower numbers results in less element interactivity, and theoretically, in less ICL imposed on a learner. Also, prior knowledge is an important factor for the perceived intrinsic load. Although experts are able to treat associated elements as one based on existing schemas, and are thus able to effectively augment their working memory capacity, novices cannot (Artino 2008). The combination of both prior knowledge (with respect to expertise of a learner) and nature (complexity) of the material therefore determine the perceived ICL of a learner (Sweller et al. 1998). To sum up, from an instructional design perspective, ICL can only be influenced by providing less or simpler learning content, or by providing some pre-training to activate prior knowledge and existing schemata. Therefore, investigating ICL more closely during learning is linked to the question of instructional designers, which content should be presented, and which prior knowledge of learners is assumed to effectively and successfully handle the given the task (approach 1).
Extraneous cognitive load (ECL). ECL results from the design of learning material. Therefore, to minimize ECL, anything that distracts the learner and hampers the learning process should be avoided in the design of learning material. High ECL results from all activities a learner needs to perform, even if they are not task relevant. This can be searching for relevant and masking/ignoring the irrelevant information, or the need to process an unnecessarily high number of elements simultaneously in working memory because of instructional design factors. High ECL therefore negatively affects the acquisition of knowledge. In instructional design research, this type of load has been especially addressed during the last few decades. A variety of multimedia design principles, effects, or strategies (for different overviews, see Sweller et al. 1998; Mayer 2009, 2005b; Plass et al. 2010) have been invented and investigated to identify the design needs of good learning material and to reduce the unproductive load placed on a learner’s working memory. Two of these principles are used in the presented studies, and are therefore described more closely: (1) The worked-examples effect (for an overview, see Atkinson et al. 2000; Renkl 2005) states that learning from an example is more effective than learning through problems: Providing learners with the steps of how to come to a correct solution, and the solution of a problem itself helps them to construct schemata of how to solve a problem, and avoids means-ends analyses. Also, activities connected to general search strategies—needed when provided with problems instead of worked examples—are unproductive for learning, and therefore produce unnecessary (which means extraneous) cognitive load (Renkl and Atkinson 2010). (2) The split-attention principle (Ayres and Sweller 2005, also known as contiguity principle: Moreno and Mayer 1999) states that it is important to physically and temporally integrate different sources of information to avoid unnecessary search processes during learning. When providing learners with multiple representations, mapping between various sources of information is necessary to construct an integrated mental model of these resources. Searching for corresponding elements in all parts of the learning material causes unproductive ECL and could be avoided by presenting information in an integrated format, so learners do not need to perform search processes because of instructional design factors. This means that the different sources of information should be spatially integrated (e.g., corresponding parts of the text are near the corresponding elements in the picture, or different pictures are arranged to represent their natural formation). Figure 1, which was used in Study 4 of this paper, is a good example of this. Concluding, from an instructional design perspective, investigating effects of design is very important for providing learners with effective learning material that enables learners to allocate their attention to task-relevant issues. Investigating ECL, therefore, is linked with the question of how instructional designers can design less demanding learning material (approach 2).
Germane cognitive load (GCL). As already mentioned, GCL is the load imposed on working memory that can have a positive impact on learning. Therefore, unlike the other two loads, GCL is a productive load that helps with schema acquisition and automation (Moreno and Park 2010). GCL arises within the learner during constructing, processing, and automating mental models or schemas. A possible strategy for learners to invest more into, for example, building a mental model, is to use learning strategies, such as, cognitive, metacognitive, or resource-oriented strategies. Directly connected to learning and building mental models are cognitive strategies, such as rehearsal strategies, organization of the learning material, and elaboration strategies, which can help one to gain deeper knowledge of the learning content. As a designer or creator of learning material, GCL can be fostered, for example, by including cognitive or metacognitive prompts, or by including desirable difficulties. Both instructional means have the potential to increase learners invested germane resources. (1) Prompts (Bannert 2009) can activate learning strategies and foster self-explanations (e.g. as done in Study 5 of this paper by encouraging the learner to imagine a picture of the content to be learned). This should enrich the mental model that originated from the written text. (2) Including desirable difficulties into the learning material, such as disfluency—which leads to a less fluent learning experience—to increase subjective difficulty (Alter and Oppenheimer 2009) may also foster learning. Whether this increase in learning can be seen as an effect of increased germane load is still under debate. However, we argue from the definition of germane load that learners invest increased effort into cognitive processes. In contrast to the direct effects of prompts, disfluency can be seen as a more subtle trigger, which nevertheless can have the same effects: Learners evaluate the learning material as more difficult and thus adjust their invested effort and the depth of their processing (Kühl and Eitel 2016). It should also be mentioned that the potential positive trigger of disfluency might come along with the negative costs of increased extraneous load. Both effects, the increase in germane as well as in extraneous load have been demonstrated in Seufert et al. (2017), who analyzed increasing levels of illegible fonts in their experiment. They found that only in the worst legible condition ECL was affected. With standard variations of only one disfluent condition in contrast to a fluent condition as is also used by Eitel et al. (2014) no differences in ECL could be found. Therefore, with variations which are less legible than normal text but not too disturbing, ECL seems unaffected which – together with the assumed increase in GCL – could then lead to deeper processing during reading and thus to improved learning outcomes. Besides fostering GCL through instruction, motivation seems to be an important factor (Debue and van de Leemput 2014): GCL was found to be positively related with motivation. Higher intrinsic motivation resulted in a higher reported ability to devote cognitive resources to learning. To sum up for GCL, instructional design is interested in effective activation of the learner’s cognitive processes (approach 3) to help with schema construction, automation, and building of enriched mental models to foster learning.
As already mentioned, the refined view on Cognitive Load Theory (Sweller et al. 2011) only separates intrinsic and extraneous cognitive load which derives from the features of the learning material. To handle these affordances, learners have to allocate their working memory resources in accordance: when they deal with the intrinsic affordances they invest germane resources, when they deal with extraneous affordances they invest extraneous resources. The allocated resources in working memory to deal with the extraneous cognitive load, do not need further assessment because they reflect nothing other than ECL in its former view (Kalyuga 2011). Allocation of germane resources for dealing with the imposed intrinsic cognitive load, needs to be examined more closely: The perceived intrinsic load reflects what learners perceive as the objective affordances (i.e. the complexity defined by the numbers of inter-related elements) in relation to their own capabilities to deal with the learning task (i.e. their prior knowledge). However, when it comes to germane resources, it could be that learners allocate much more germane resources than needed to deal with the imposed intrinsic load by the learning material itself. The additionally allocated working memory resources can then be used to foster understanding, for example, building mental models and schemata or automation by using for example different learning strategies like elaboration strategies, metacognitive strategies or the use of given prompts. This would reflect the original concept of germane cognitive load.
Overall, coming back to instructional design, instructors and designers of learning material need to know how learners process the learning material, how mentally loading these materials turn out to be, and whether activation of learners’ cognitive processes is successful. Therefore, in the last few decades, measuring cognitive load during the learning process has become important. For a long time, cognitive load during the learning typically was measured by asking learners about their invested mental effort. This item was invented by Paas (1992), and is widely used in CLT research. Unfortunately, it is not possible to differentiate different aspects of load with one item. Therefore, a few researchers have made an attempt to find other measures of cognitive load. For an overview, see Brünken et al. (2010), or Brünken et al. (2003): There are some objective measures through physiological parameters (e.g., pupil dilation, brain activity), behavior (e.g., time-on-task), and performance (e.g., learning outcome, dual-task performance), as well as subjective ones, which, strictly speaking, are self-reports (e.g., invested mental effort, stress level). But all these approaches only allow one to assess the overall amount of load a learner experiences during learning.
Newer research has focused on the development to measure the different aspects of cognitive load separately. For an overview, see Klepsch et al. (2017). Whereas many approaches have not been investigated more closely, or have been developed to fit one instructional design research study, two approaches stand out: (1) Leppink et al. (2013) developed a questionnaire, which was enhanced in Leppink et al. (2014). Leppink et al. (2013) developed 10 items, three to measure ICL, three to measure ECL, and four to measure GCL. They found the three factors in their questionnaire to be robust, but mentioned that there is no evidence that these three factors represent the three types of cognitive load (Leppink et al. 2014). (2) Klepsch et al. (2017) also developed a questionnaire to measure cognitive load in a differentiated way. They also have been able to provide a questionnaire showing three factors: they used two items to measure ICL, three items to measure ECL, and three items to measure GCL. Based on their research design, they claim to actually measure differences in the types of loads, but mention that the questionnaire still must be validated in different and more ecologically valid learning contexts.
Besides both approaches needing more investigation, Leppink et al. (2014) stated that they are more in line with the proposed reconceptualization of CLT, whereas Klepsch et al. (2017) stuck to the traditional view of CLT. This, in our view, makes the questionnaire of Klepsch et al. (2017) more helpful when one, like us in this paper, is interested in instructional design effects and their impact on the learning task itself (approach 1), the design of the material (approach 2), and the activation of the learner’s cognitive processes (approach 3). To help in theory building of CLT, both questionnaires should be considered in further research.
In this paper, we were especially interested in the effects of instructional design and their explanation through CLT, and therefore the three-factor structure of CLT because it is more practically useful when dealing with instructional design. Therefore, we needed a measurement method of CLT that, in a first step, differentiates between different types of load, and in a second step, could be used in various learning situations and with a wide variety of learning materials. As adoption of the questions with the questionnaire of Leppink et al. (2013) is more complex, and therefore might lack comparability over different topics we used the questionnaire of Klepsch et al. (2017). In their paper they found evidence for the factor structure with the three types of load as well as satisfying reliability scores for the questionnaire. However, they validated the questionnaire by using rather short and artificial learning tasks. Thus, with the current paper we want to add the missing element on validating the questionnaire by using real life learning settings. Therefore, we review a set of different studies in natural learning settings. The six studies use different approaches to instructional design that are linked to concepts in CLT: (1) Differences in element interactivity (Study 1) or variations of difficulty based on knowledge (Study 2) are used to manipulate intrinsic cognitive load by varying the learning task itself. (2) By manipulating the design through the worked example principle (Study 3) and the split attention principle (Study 4) different levels of extraneous cognitive load were triggered allowing us to investigate the influence of different designs on ECL. (3) Variations in prompted imagination of written learning material (Study 5), as well as differences in legibility of learning material (Study 6), are used to directly or indirectly activate the learner’s cognitive processes, and therefore induce germane cognitive load, to create or foster enriched mental models.
Our goal is to substantiate the sensitivity of the questionnaire by Klepsch et al. (2017) for instructional design-based variations in cognitive load. We want to find out if the questionnaire is able to differentiate exactly the type of load that has been intentionally varied based on theoretical assumptions and previous empirical studies. This would be a strong argument for its prognostic construct validity. In addition, we will also add some information on the reliability of the questionnaire by Klepsch et al. (2017) based on our six studies.
Hypotheses
H1a
Concerning ICL, we expect no difference in Studies 3, 4, 5, and 6 between the experimental conditions of each study because learning content has not been varied in element interactivity, complexity, or quantity.
H1b
Concerning ICL, based on CLT and the assumptions about element interactivity and prior knowledge, we expect that ICL varies significantly between the three conditions in Studies 1 and 2 because in these studies, ICL was varied on purpose: We expect the participants in the boredom conditions to report the lowest ICL, and the participants in the overload condition to report the highest ICL.
H2a
Concerning ECL, we expect no significant differences in Studies 1, 2, 5, and 6, because the design of the learning material has not been varied.
H2b
Concerning ECL, the design of the learning material was varied on purpose in Studies 3 and 4, therefore we expect significant differences between the two conditions of each study.
H3a
Concerning GCL, we do not expect differences between the experimental conditions in Studies 1, 2, 3, and 4, because we did not include any direct or indirect activation of the learner’s cognitive processes.
H3b
Concerning GCL, we expect significant differences between the experimental groups for Studies 5 and 6 because either activation of the learner’s cognitive processes was directly implemented (prompts) or indirectly triggered (legibility of learning material).
H4
Concerning learning outcomes, we expect a significant difference in task performance in the experimental groups for all studies. In Study 1 and 2, task performance in the boredom group should be highest where ICL is lowest, whereas task performance in the overload condition will be lowest where ICL is highest. In Study 3 and 4, task performance should be highest in the groups where multimedia principles are applied correctly to help learning, where ECL should be lowest. In Study 5 and 6, task performance should be highest when schema construction was activated, or deeper processing was induced, and therefore GCL should be highest.
Method
In the following, 6 studies are described: two of them varying ICL, two of them ECL, and two of them GCL. All the studies follow the same methodological approach of varying one type of load on purpose, and measuring the effects of this variation on all three types of load, as well as on learning outcomes. Thus, there are many similarities which will be presented in the following for all studies together. In the subsequent paragraph, the differing key features of each study (e.g., the operationalization in the load variation) will be presented. For an overview of all six studies, see Table 1.
Participants
Each study had between 31 and 62 participants, with at least 15 participants in each experimental condition. Table 1 provides an overview of the distribution between the sexes and average age for each study, and its experimental conditions.
Design
All studies followed the same experimental design principle: They are all between-subject studies with either two (Study 3, 4, 5, and 6) or three (Study 1 and 2) experimental conditions. Independent variables are the variations of one type of load each, which has been operationalized in different experimental conditions for each study. In Study 1 and 2, where ICL has been varied, the conditions vary in task difficulty. In Study 3 and 4, where ECL has been varied, the conditions varied in the design features of the learning material. In Study 5 and 6, where GCL has been varied, the conditions differ in features that should activate the learner’s cognitive processes. All these variations should result in measurable differences of the dependent variables (i.e., in either intrinsic, extraneous, or germane cognitive load), as well as in learning outcome (Study 3 to 6) or task performance (Study 1 and 2).
As control variables, age and sex have been assessed in each study. For Studies 3 to 6, prior knowledge also has been assessed. There was no prior knowledge assessed in the studies varying ICL because the tasks we used were adopted from flow research and were programmed to adopt to participants prior knowledge and their skills. While playing Tetris (Study 1) the program stayed either way below participants’ skill, adopted to their skill or was way too difficult and exceeded their skill. Thus, prior knowledge in this case would reflect prior experience, coming along with the skill to fluently react on the given task. Nevertheless, we did not measure it directly because it was implemented in the program’s logical structure of referring to the learners’ skills. For answering questions in “Who Wants to be a Millionaire” (Study 2) we referred to learners’ general knowledge as prior knowledge, which we didn’t measure directly either. Instead, we ensured that learners had sufficient educational background with the “Abitur”, a diploma from German secondary school qualifying for university admission or matriculation. In Studies 5 and 6, in which the induction of GCL is varied, we also assessed learners’ current motivational state (FAM; Rheinberg et al. 2001).
Procedure
The procedure was also the same for all the studies. In the beginning, learners were informed about the procedure of the study they participated in and signed an informed consent form. All participants were aware that they could withdraw their data at any point in the study without having any disadvantage. Then, each participant was randomly assigned to one of the experimental groups. As a next step in each study, each participant filled out a questionnaire asking for demographic data.
Then learners' prior knowledge and motivation were assessed, whenever needed, as described above. Afterwards, participants had to deal with the task or the learning material as described separately for each study in section “3.4 Material”.
After learning or performing the task, the cognitive load questionnaire (Klepsch et al. 2017) had to be answered, followed by a knowledge test for the corresponding study in Studies 3 to 6. Performance in Study 1 and 2 was calculated directly through task performance by the used programs (see “Material”), and in these cases, only the cognitive load questionnaire had to be answered after performing the given task.
Material
In the following six paragraphs, the used learning materials, the characteristics of the experimental variations, and the specific features of the learning task are described for each study. Also, additionally included questionnaires are described. In a 7th paragraph, the questionnaire for measuring the three types of load is described in more depth.
Study 1 (varying ICL): problem solving – Tetris game.
The Tetris game (Keller and Bless 2008) used was originally designed for research on flow experiences (Keller and Bless 2008). We used it to vary intrinsic cognitive load. The three conditions, (1) boredom, (2) flow, and (3) overload, varied in element interactivity in relation to the learner’s skills by changing complexity of the task as an independent variable. In the boredom condition, blocks came down slowly and the participants had plenty of time to position them in the right place. In the flow condition, the program adapted itself to the performance of the participant. If one produced fewer mistakes, the level increased and therefore the game became more difficult, if one made mistakes, the game got easier. The overload condition was programmed to start on a high level and did not reduce the level based on performance. Participants were instructed to create as many full lines as possible and they played the game for three minutes. Despite learning to play Tetris or practicing Tetris is not related to knowledge acquisition it nevertheless is a task where information has to be processed in working memory to reach a certain goal and to refine their strategies in solving this task. As the information (blocks) interact with each other it can be seen as an operationalization of element-interactivity which is a key feature of intrinsic load. Time was restricted, as otherwise participants would have the possibility to try many different strategies, and we did not like to induce germane load. Based on the given instruction participants dealt with a problem-solving task. Through the log files of the program, the number of blocks a participant got during the game, and the number of finished lines was documented during the three minutes of game play. Therefore, task performance could be estimated as followed: ((finished lines × 10) / (received blocks × 4)) × 100.
Study 2 (varying ICL): general knowledge – quiz.
The Knowledge Quiz (Keller et al. 2011) was a computerized quiz based on questions from the German version of the board game “Who Wants to be a Millionaire?” (Jumbo Spiele® 2000), which is based on a TV show equally named. Each question has four possible answers, and only one is correct. Participants played the game for three minutes, and they had to answer each question within a limited time period. Similar to Study 1 participants were randomly assigned to one of three conditions: (1) boredom, (2) flow, and (3) overload. This conditions varied ICL as independent variable by varying the difficulty of the presented questions. In the boredom condition, questions were easy and stayed at this level. In the flow condition, difficulty of the level was adapted to the skills of each participant. If one could handle a certain number of tasks in one level, the level went up and questions became more difficult. If one failed to answer a certain number of questions right, the level went down. As a result, the game always adjusted to fit to the skills of the participant. In the overload condition, the questions were so difficult that participants most times only had the option to guess. Task performance was converted into percentage of correct answers based on the individually reached number of questions, which varied based on the pace in which questions were answered.
Study 3 (varying ECL): mathematics – extremum problems and Taylor polynomial tasks.
Each learner had to deal with two types of mathematical learning material: (1) extremum problems and (2) Taylor polynomial tasks. Prior knowledge was assessed after participants received an example task for each type of material: in two questions, they had to answer on a 7-point Likert-type scale whether they were familiar with such tasks, and in a second step, they had to write down how they would solve the task. Afterwards, both learning materials started with a short introduction on the topic, followed by two example tasks. To realize differences in ECL as an independent variable, (1) problem solving or (2) worked examples were included. In the problem-solving group, the right solution was presented, but how the solution could be calculated was missing. In the worked example group, the process of calculating the right answer for the example tasks was written down. Presentation of the two materials was randomized. Participants had 5 min time for each domain to learn the content, and another 15 min to do the post test. Performance was measured by a post test for each domain containing two analogue tasks (similar to the example tasks in the learning material), and one complex transfer task. For each task, 6 points could be reached, and therefore as a maximum 36 points could be reached in the post test. Task Performance was calculated by summing up points given for correct answers and converted into percentage.
Study 4 (varying ECL): biology – kidney.
Prior knowledge about the human kidney was assessed through 10 open questions, covering content of the following learning material. The material about the structure and functions of the kidney itself consisted of four pictures and seven corresponding texts. As a dependent variable, ECL was varied through either (1) split source material or (2) integrated material. In the split attention group, the text was on the left side of the paper and the four pictures on the right side. References, in the form of numbers, connected the pictures with the text. In the integrated format, the interplay between the four pictures was made clear and each text was connected within the corresponding part in the pictures. Through this approach, search processes between text and pictures could be minimized. Each participant had 30 min to learn the content. To assess learning performance, a post test had to be filled in consisting of 13 tasks. Altogether, 35 points could be reached. Individual performance was converted into a percentage.
Study 5 (varying GCL): technology – clutch.
Prior knowledge was assessed through eight questions, including multiple choice questions, open questions, and a task asking to draw a clutch. The learning material about clutches in cars itself consisted of three parts, with overall 682 words. Instruction on imagination of the learning content varied between groups because GCL was the independent variable: Both groups received the instruction to learn the text and were allowed to make notes during learning, but only one group was instructed to imagine a picture of the described clutch and its functions. The time needed by each learner to work through the learning material was measured. To assess learning performance, a post test was conducted consisting of 14 questions, with at most 39 points. Performance was recalculated into percent. Before the learning phase in this study, current motivational state with the subscales anxiety of failure, probability of success, interest, and challenge (FAM; Rheinberg et al. 2001) was additionally assessed.
Study 6 (varying GCL): geography – Earth’s time zones.
Seufert et al. (2017) already reported a study on text legibility and allowed us to use their data. Prior knowledge about the Earth’s times zones was assessed through six tasks on time differences, which were either open or multiple-choice tasks. The learning material was a text about the Earth’s time zones (adapted from Schnotz and Bannert 1999). It included 1,100 words and a table with time differences for eight cities. To vary GCL as an independent variable, the texts legibility was either (1) fluent (Arial, black 12 pt) or (2) disfluent (Monotype Corsiva, black, 12 pt). Time for learning was not restricted, and therefore measured (about 13 min: M = 763 s, SD = 227.51). Learning performance was measured through a post-test with 17 questions, where, at most, 34 points could be reached. Again, performance was converted to percent to foster comprehension of the six studies. For this study, learners’ current motivational state (FAM) was also measured.
Cognitive load questionnaire (CLQ).
To measure cognitive load differentially, the cognitive load questionnaire (CLQ) by Klepsch et al. (2017) was used. This questionnaire has eight items to measure the different aspects of cognitive load. The eight items disperse on three scales. A scale with two items asking for perceived ICL, a scale with three items asking for perceived ECL, and finally a scale of three items asking for perceived GCL. The GCL scale includes an item on “elements that helped one to understand the content,” which directly addresses, for example, something like prompts. Klepsch et al (2017) argued that this item could be excluded if there are no such elements in the learning material, and thus would decrease internal consistency. Based on theoretical assumptions, we would assume that in studies 1–4 and 6, reliability should be higher when leaving out the third GCL item. For Study 5, we assume that reliability should be best if all items are included. To demonstrate this, in each study, all items of the questionnaire had to be answered. All items must be rated on 7-point Likert-type scales ranging from “completely wrong” to “absolutely right”. For our studies, the items are presented in German, the scale’s original language (see Appendix 1 for the English and German version).
Data analysis
Data were analyzed in the same way for all six studies: For all three scales of the differentiated questionnaire on Cognitive Load, reliability was estimated by using McDonald’s ω. To provide evidence for the already described issue, with the third item of the GCL scale, the scale on GCL was analyzed with the third item (GCL3) and without (GCL2). A confirmatory factor analysis was conducted following Klepsch et al. (2017). We analyzed the data for two models: Model 1 assumes that one unitary factor accounts for all load items. Model 2 represents the theoretical assumptions of three inter-related types of cognitive load and suggests the three-factor model with separable but related factors. Adequate model fit is indicated by a low chi-square (χ2) value, a high Tucker-Lewis index (TLI ≥ 0.95), a high comparative fit index (CFI ≥ 0.95), and a low root-mean-square error of approximation (RMSEA ≤ 0.05). Additionally, the Akaike information criterion (AIC) was used as a model comparison index: The model yielding the lowest AIC is preferred in terms of close model fit and parsimony of the model relative to competing models.
The variables on prior knowledge, age, and, if accessed, other control variables (as described in part 3.1 Design, Materials and Procedure) have been tested for group differences to check for differences in randomization. Also, correlations between these variables and the dependent variables have been calculated. Whenever a significant difference between groups or a significant correlation could be found, the affected variable was included in the following analyses of variance as a covariate. All correlations tables can be found in Appendix 2.
To identify group differences for all studies one-way AN(C)OVAS were conducted to enable comparability of the six studies. In studies with three conditions (Study 1 and 2), contrasts were also reported to show differences between the experimental groups. Whenever multiple contrast analyses have been conducted, we adjusted the alpha level.
Results
McDonalds ω was conducted to assess the reliability of the three scales of the differentiated cognitive load questionnaire. For ICL, two items, and for ECL, three items were included. The analysis for GCL was conducted with two items. Only for Study 5, as recommended by Klepsch et al. (2017), we also conducted an analysis for GCL with three items as the prompts in the material correspond to the third GCL-question. McDonalds ω for all scales in all studies is reported in Table 2.
The confirmatory factor analysis was conducted over all studies. All participants of all studies were included in one overall analysis. Model fits can be found in Table 3. Based on the sample size a multilevel or multigroup analysis, as it has been conducted in Klepsch et al. (2017) was not possible, as there are not enough participants in the different studies or conditions. Model 1 assumes one unitary factor and its model fit is rather bad. Model 2 represents the theoretical assumptions of three inter-related types of cognitive load (three factor model with separable but related factors). Model fit is not perfect as the chi-square (χ2) value is still quite large, the Tucker–Lewis index is lower than 0.95 the root-mean-square error of approximation is higher than 0.05.
In the following six sections, differences in the experimental groups of each study are reported using a one-way ANOVA or ANCOVA, if covariates (age or prior knowledge) are included. For Study 1 and 2 contrasts are also reported because these studies include three experimental groups.
Study 1 (varying ICL): problem solving – Tetris game
To repeat: In this study three experimental groups were compared by varying ICL while playing Tetris: (1) The boredom condition, where the Tetris game was adjusted to be simple (− > low ICL), (2) the flow condition, where the game adapted to learners’ performance (− > medium ICL), and (3) the overload condition, where the game was quite difficult (− > high ICL).
For ICL, as expected, we found a significant main effect (F(2,59) = 10.01, p < 0.001, η2 = 0.25): Contrasts showed that ICL was lowest for participants in the boredom condition. They reported significantly lower ICL than participants in the flow (T(59) = 3.51, p < 0.01, d = 1.25) or overload (T(59) = 4.15, p < 0.001, d = 1,19) condition. We found no difference between the flow and overload condition (T(59) = 0.59, p = 0.56, d = 0.18).
For ECL, we found a significant main effect (F(2,59) = 12.19, p < 0.001, η2 = 0.29) that was not expected. Contrasts showed that ECL was lowest for participants in the boredom condition. They reported significantly lower ECL than did participants in the flow (T(59) = 3.85, p < 0.01, d = 1.13) or overload (T(59) = 4,59, p < 0.001, d = 1.74) conditions. We found no difference between the flow and overload condition (T(59) = 0.69, p = 0.49, d = 0.19).
For GCL, as expected, we found no significant main effect (F(2,59) = 2.86, p = 0.07, η2 = 0.09), nor could we find any significant contrasts (boredom-flow: T(59) = 1.93, p = 0.06, d = 0.75; boredom-overload: T(59) = 1,93, p = 0.06, d = 0.50; flow-overload: T(59) = 0.18, p = 0.99, d = 0.23).
For task performance, we found a significant main effect (F(2,59) = 86.04, p < 0.001, η2 = 0.75): Contrasts showed that the participants in the boredom condition scored significantly higher than participants in the flow condition (T(57) = 6.16, p < 0.001, d = 0.43) and participants in the overload condition (T(57) = 13.11, p < 0.001, d = 3.94). Also, participants in the flow condition scored higher than participants in the overload condition (T(57) = 6.95, p < 0.001, d = 3.05).
All means and standard deviations can be found in Table 4, and effects can be found in Fig. 2.
Study 2 (varying ICL): knowledge quiz
In this study, ICL was also varied. Three experimental groups were answering quiz questions with varying difficulty: (1) in the boredom condition, quiz questions where simple (− > low ICL), (2) in the flow condition, questions adopted to learners’ knowledge (− > medium ICL), and (3) in the overload condition, questions were too difficult to know the answer (− > high ICL).
For ICL, as expected, we found a significant main effect (F(2,59) = 8.76, p < 0.001, η2 = 0.23): Contrasts showed that ICL was lowest for participants in the boredom condition. They reported significantly lower ICL than participants in the flow (T(59) = 3.40, p < 0.01, d = 1.24) or overload (T(59) = 3.84, p < 0.001, d = 1.32) conditions. We found no difference between the flow and overload conditions (T(59) = 0.54, p = 0.59, d = 0.14).
For ECL, we found no main effect (F(2,59) = 2.79, p = 0.07, η2 = 0.09): Contrasts showed no differences between participants in the boredom and flow conditions (T(59) = 0.94, p = 0.35, d = 0.34) or in the boredom and overload conditions (T(59) = 1,38, p = 0.17, d = 0.43). But there was a significant difference between the flow and overload conditions (T(59) = 2.35, p < 0.02, d = 0.66).
For GCL, as expected, we found no significant main effect (F(2,59) = 0.21, p = 0.81, η2 = 0.01), nor could we find any significant contrasts (boredom-flow: T(59) = 0.07, p = 0.94, d = 0.02; boredom-overload: T(59) = 0,59, p = 0.56, d = 0.21; flow-overload: T(59) = 0.53, p = 0.60, d = 0.14).
For task performance, we found a significant main effect (F(2,54) = 585.56, p < 0.001, η2 = 0.96): Contrasts showed that the participants in the boredom condition scored significantly higher than participants in the flow condition (T(54) = 20.74, p < 0.001, d = 6.56) and participants in the overload condition (T(54) = 34.11, p < 0.001, d = 15.33). Also, participants in the flow condition scored higher than participants in the overload condition (T(54) = 15.22, p < 0.001, d = 4.33).
All means and standard deviations can be found in Table 5, and effects can be found in Fig. 3.
Study 3 (varying ECL): mathematic – extremum problems and Taylor polynomial tasks
Keep in mind, in this study, two experimental groups are compared varying ECL: (1) The problem-solving condition, where only solutions are presented for example tasks (− > high ECL), and (2) the worked examples condition, where approach and solution have been presented for sample tasks (− > low ECL).
For ICL, as expected, we found no significant main effect (F(1,38) = 0.09, p = 0.77, η2 = 0.23): ICL was reported to be equal in the experimental groups.
For ECL, as expected, we found a main effect (F(1,38) = 8.91, p < 0.01 η2 = 0.19): In the worked examples group, ECL was reported to be lower than in the group without worked examples.
For GCL, as expected, we found no significant main effect for GCL (F(1,38) = 1.18, p = 0.28, η2 = 0.03): Both groups reported similar GCL ratings.
For task performance, age was included as covariate into the analysis because we found a significant correlation between these two variables (r = − 0.38, p < 0.05). For task performance, we found a significant main effect (F(1,37) = 9.44, p < 0.01, η2 = 0.20): In the worked examples group, task performance was significantly higher than in the group without worked examples.
All means and standard deviations can be found in Table 6, and effects can be found in Fig. 4.
Study 4 (varying ECL): biology – kidney
During this study, two experimental groups are compared varying ECL: (1) The split-source condition had separated representations of text and pictures (− > high ECL), and (2) the integrated format condition worked with an integrated version of text and pictures (− > low ECL).
For ICL, as expected, we found no significant main effect (F(1,49) = 3.33, p = 0.07, η2 = 0.06): ICL was reported to be equal in the two experimental groups.
For ECL, age was included as covariate into the analysis because we found a significant correlation between these two variables (r = − 0.42, p < 0.01). For ECL, as expected, we found a main effect (F(1,48) = 9.60, p < 0.01 η2 = 0.17): In the integrated format group, ECL was reported to be significantly lower than in the split source group.
For GCL, prior knowledge was included as covariate in the analysis because we found a significant correlation between these two variables (r = 0.29, p < 0.05). For GCL, as expected, we found no significant main effect for GCL (F < 1 n.s.): Both groups reported similar GCL ratings.
For task performance, prior knowledge was included as covariate into the analysis because we found a significant correlation between these two variables (r = 0.43, p < 0.01). For task performance, we found a significant main effect (F(1,48) = 5.83, p < 0.05, η2 = 0.11): In the integrated group, task performance was significantly higher than in the split-source group.
All means and standard deviations can be found in Table 7, and effects can be found in Fig. 5.
Study 5 (varying GCL): technology – clutch.
Remember that in this study, two experimental groups are compared varying GCL while learning about clutches: (1) The group without a special instruction on how to handle the learning content (− > low GCL), and (2) the group with the instruction to imagine the learning content as a picture (− > high GCL).
In this study, the subscale on anxiety of failure of the questionnaire on actual motivation (FAM) was included in each analysis as a covariate because we found a significant difference between groups (T(27) = 3.21, p < 0.01, d = 1.31).
For ICL, additionally, prior knowledge and time on task were included in the analysis as covariates because we found significant correlations between these variables and ICL (prior knowledge: r = − 0.65, p < 0.01; time on task: r = 0.42, p < 0.05). For ICL, as expected, we found no significant main effect (F < 1, n.s.): ICL was reported to be equal in both experimental groups.
For ECL, additionally, the subscales interest and challenge of the questionnaire on actual motivation (FAM) were included in the analysis as covariates because we found significant correlations between these variables and ECL (interest: r = − 0.40, p < 0.05; challenge: r = 0.45, p < 0.05). For ECL, as expected, we found no significant main effect (F < 1, n.s.): Both experimental groups rated ECL similarly.
For GCL, additionally, time on task and the subscale interest of the questionnaire on actual motivation (FAM) were included in the analysis as covariates because we found a significant correlation between these variables and GCL (time on task: r = 0.26, p < 0.05; interest: r = 0.27, p > 0.05). For GCL, as expected, we found a significant main effect (F(1,51) = 3.14, p1 = 0.03, η2 = 0.07): The group that was instructed to imagine the learning content reported higher GCL than the group that was not instructed to imagine the learning content.
For task performance, additionally, prior knowledge and the subscales interest and challenge of the questionnaire on actual motivation (FAM) were included in the analysis as covariates because we found a significant correlation between these variables and task performance (prior knowledge: r = 0.40, p < 0.01; interest: r = 0.40, p > 0.01; challenge: r = 0.42, p < 0.01). For task performance, we found no main effect (F < 1, n.s.): Both groups reached similar performance levels.
All means and standard deviations can be found in Table 8, and effects can be found in Fig. 6.
Study 6 (varying GCL): geography – earth’s time zones
In this study, we compared two experimental groups varying GCL: (1) The fluent condition, with highly legible material (− > low GCL), and (2) the disfluent condition, with less legible material, which increases the subjective difficulty of the material (− > high GCL).
In this study, prior knowledge was included in each analysis as a covariate because, we found a significant correlation with each dependent variable (ICL: r = − 0.51, p < 0.01; ECL: r = − 34, p < . 05; GCL: r = 35, p < 0.05; task performance: r = 0.49, p < 0.01).
For ICL, as expected, we found no significant main effect (F(1,33) = 1.80, p = 0.18, η2 = 0.05): ICL was reported to be equal in the two experimental groups.
For ECL, probability of success was additionally included in the analysis as a covariate because we found a significant correlation between the two variables (r = − 0.43, p < . 01). For ECL, as expected, we found no significant main effect (F < 1, n.s.): Both experimental groups rated ECL similarly.
For GCL, as expected, we found a significant main effect (F(1,33) = 3.36, p1 = 0.04, η2 = 0.09): Learners who received the disfluent learning material reported higher levels of GCL compared to learners who received the fluent learning material.
For task performance, we found no main effect (F(1,33) = 1.65, p = 0.21, η2 = 0.05): Both groups reached similar performance levels.
All means and standard deviations can be found in Table 9, and effects can be found in Fig. 7.
Discussion
In a first step, we discuss the results of our six studies based on hypotheses (see “Validity”). Then we address the question regarding which of the items of the GCL scale are necessary in terms of internal consistency and whether a confirmatory factory analysis reveals similar results as found by Klepsch et al. (2017) (see “Reliability and Confirmatory Factor Analysis”). Also, strengths and weaknesses of the six-study approach in general are discussed (see “Strengths and Weaknesses”), and further directions are addressed (see “Further directions”). In a second step, we discuss the usefulness of a differentiated measurement of cognitive load, especially the theoretical and practical implications and the need for further research (see “Conclusion”).
Reliability and confirmatory factor analysis
The first criterion of a good measurement is its reliability. For ICL we found the scale to be robust in reliability with ω’s higher than 0.80 (all studies), which is in line with the results found by Klepsch et al. (2017). Reliability of the ECL and GCL scale was lower but still acceptable for experimental field studies with ω’s higher than 0.70. The GCL scale was calculated with two items (leaving out the item “The learning task consisted of elements supporting my comprehension of the task”) only for Study 5 we in addition calculated it with 3 items This was based on theoretical assumptions: We expected that the item should best be excluded in Studies 1–4 and 6 because they do not comprise any elements that explicitly foster learners’ germane load investment. Only Study 5 contained an element that theoretically is assumed to be supportive, as imagination of the content was prompted. This, in our eyes, would have been an explicit element referring to the third GCL item. Unfortunately, ω dropped to 0.64 when doing so, which is not acceptable anymore. To find out why learners do not rate this item as expected, and not consistently with the other two germane load items, more studies should be conducted to investigate the function of this item. Perhaps the problem with reliability of this item can be found in the nature of prompts and other germane load enhancing techniques: When learners use them for the first time, they might not see them as helpful and activating in a positive sense. Using a prompt for the first time might result in higher effort in trying to solve the given task, but might—at the same time—be demanding, and does not feel supportive. This might be because of the so-called mathemathantic effect (Clarck 1990): “Instructional treatments unintentionally produced a condition where students were less able to use learning skills or have less access to knowledge in some domain than before entering the experiment” (Clarck 1990, p. 1). The mathemathantic effect usually is applied to training situations, where a given training in a first step reduces performance. Given the prompts in our Study 5 (Technology – clutch), the prompts could interfere with typically used learning strategies, and therefore reduce the use of learning skills that are normally used. Apart from that, they seem to be helpful, because task performance has not been affected negatively, but they are not rated as supportive subjectively.
The conducted confirmatory factor analysis showed a better model fit for Model 2 assuming three inter-related types of cognitive load compared to Model 1 with one overall load-factor. Model fit was nevertheless lower than presented in Klepsch et al. (2017) and not always ideal. This may be because the six studies comprise real learning settings and are thus less artificial but also less clear-cut as the tasks in the original paper. The number of participants did not allow us to conduct a multi-group or multi-level confirmatory factor analysis. The aggregation over all six studies is a second reason for why we could not get a perfect model fit: Combining all studies results in difficulties of comparability, as the six studies vary for example in time on task (e.g. 3 min in Study 2 vs. 40 min in Study 3) and the given learning task (e.g. problem solving in Study 1 vs. remembering facts and relations in Study 4). Nevertheless, the results show that a replication is possible in less artificial learning environments, even if reliability and model fit are not as perfect as under artificial and very controlled circumstances.
Validity
The second criterion of a good measurement instrument is validity. Validity is the degree to which a test measures what it states to be measuring, but what does that mean in terms of experienced cognitive load? As cognitive load is something highly influenced by learners’ prerequisites, it is impossible to secure experienced cognitive load to a specific point on a given scale, based on theoretical assumptions. We can state that one version of a learning material should, in contrast to the other version of the same material, result in higher or lower cognitive load for each type of load, but we are unable to operationalize this effect in absolute numbers. Therefore, for our purpose, validity means there exists a relative differentiation between two versions of a learning material (i.e., learners rate their experienced load on the three scales of the CLQ differently for the two versions). Comparing two completely different materials with different contents, length, complexity, etc. to each other, for example, the materials from Study 3 (mathematics) and Study 5 (clutch) of this paper, in our eyes, is not possible and not meaningful. Therefore, sensitivity to differences in learning materials is much more important than securing it to a point on a scale. The additivity theory of cognitive load states that there might not be enough resources left in working memory when too much ICL and ECL is already imposed on the learners’ working memory. Thus, one could conclude that the given scale in the CLQ also might be subjectively different for each participant due to interindividual variances in working memory capacity. Also, their ability to chunk information allows them to reduce complex material, leaving more resources left for ECL or GCL. In summary, we discuss the findings of our six studies regarding the measuring tools’ sensitivity towards the measuring tools’ ability to differentiate between different types of loads.
For ICL, we found the scale to be sensitive to differences in complexity of the given task (Study 1 and 2). Even if we did not find differences between the flow and overload conditions in both studies, the results showed that participants were able to differentiate between low and high intrinsic load tasks. As the flow condition means that task difficulty is adopted to the persons skill, the flow conditions stay complex but on a level that can be handled, which is reflected in task performance. The overload conditions are even more complex so that the participant can’t handle the task, resulting in significantly lower task performances in both studies. In contrast, whenever the number of elements to be learned and their inter-relatedness stayed the same for the experimental groups (Studies 3–6) we found no differences in perceived ICL.
For ECL, we found the scale to be sensitive for design changes (Studies 3 and 4). Unexpectedly, we also found differences in learners’ ECL rating when element interactivity has been varied (Study 1). Sweller (2010b) argued that variations in element interactivity might have an impact on all types of load and thus it might not be possible to measure ICL and ECL differentially. The results of the Tetris study seem to provide evidence for this assumption. Unfortunately, faster gameplay seems to also impact ECL. But which aspect of the increased element interactivity causes ICL and which one ECL in our study? We operationalized the increased element interactivity by reducing the time to react, so what does faster gameplay mean with respect to cognitive processing? The blocks come down faster, the preview of he next block is shown shorter, and the keys need to be tapped quicker in order to rotate and move the blocks. Therefore, interaction with the game becomes more complex and perhaps also leads to a higher stress level. The handling of the game, the tapping and moving operations on the keyboard can be seen as extraneous, while the mental operations of filling lines while taking all the elements that interact into account can be seen as intrinsic. However, as both, the mental operation as well as the manual operation has to be aligned, the learners cannot easily distinguish the two sources of load, resulting in increased scores on both scales. To prove this argument, one would have to run a Tetris experiment where learners simply have to mentally rotate the blocks. This would allow disentangling intrinsic from extraneous affordances, even if the design of such a study would be quite a challenge. An additional source of extraneous load might also arise from managing the additional stress level and thus maybe from the suppression of negative emotions or at least an uncomfortable level of arousal. However, such aspects would not be addressed in the questionnaire we used to measure ECL and hence this argument would also need further analyses to be substantiated. Overall, based on studies by Leppink et al. (2013, 2014), the study of Klepsch et al. (2017) and also the knowledge quiz study in this paper we would nevertheless argue that it is possible to distinguish ICL and ECL by psychometric measures. However, when ICL and ECL are intertwined, a differentiated task analysis and maybe also more sophisticated instruments would be necessary to understand the underlying processes and too disentangle intrinsic or extraneous load sources.
Also, the GCL scale was sensitive to differences attempting to induce different levels of GCL (Studies 5 and 6) and could not find any differences when a variation of GCL was not intended (Studies 1–4). However, the validity of the scale is not overall convincing, as we did not find differences in task performance. This would have been crucial from a theoretical point of view, as an increase in GCL should come along with an increase in task performance. For the same reason Leppink et al. (2013) did not accept their measurement of GCL to be valid and useful. The interplay between perceived load and performance might be more complex and should be analyzed more in-depth: As expected, for Studies 1–4 we found theoretically assumed differences in task performance. Load was lower when reaching higher levels of task performance: In Studies 1–4, lower reported ICL and/or ECL came along with higher task performance. In Studies 5 and 6, we found no significant differences in task performance. From a theoretical point of view, resulting from the definitions of GCL, we would have expected that task performance should be significantly higher when GCL increases. From a practical point of view this is not always true: Learners might invest germane cognitive load into learning and try really hard, but nevertheless fail when they need to retrieve facts and relations from memory and deal with given tasks. Using prompts or the more subtle hint of disfluent text to induce GCL might, as already mentioned, have interfered with their usual learning strategies. So even if they feel to have invested as much GCL as possible, there is no guaranty that they can retrieve their knowledge from memory when needed. Future research could address this complex interplay between the processes that can be triggered by instruction, the perceived germane, extraneous and intrinsic load and the resulting learning performance.
To further substantiate the prognostic validity of the CLQ, it would be interesting to combine it with other differentiated measurement methods of cognitive load during learning. The questionnaire by Leppink et al. (2013) especially could be used to demonstrate concurrent validity. Unfortunately, most of the studies presented in this paper have been conducted before the questionnaire of Leppink et al. (2013) was published. Using the item invented by Paas (1992) would not have been fruitful to use as criterion for concrete validity, because it does not differentiate between ICL, ECL, and GCL. As an example: in Study 6 we would not have been able to show if text legibility is reflected in ECL or GCL.
Strengths and weaknesses of the six studies
All studies in this paper have been designed to explicitly and only vary one aspect of load. In real life learning material this usually is not given. For example, Rogers et al. (2014) used the questionnaire published by Klepsch et al. (2017) in their study on learning piano. They developed a novel media-based piano learning system and compared it to an existing media system and standard sheet notation. Varying the system resulted in significant differences for ICL, ECL, and GCL because motivation and self-regulation during learning had a high impact on cognitive load.
Once again: The six studies are classic experimental studies. Three of them included many more female than male participants, but fortunately, distribution over experimental groups was equal within each study. Two studies included less than 20, but had at least 15 participants in each experimental group. We are aware that the number of participants in each experimental group is not ideal and results in power restrictions. Further research, for example doing a study in a large lecture with many students under real-life conditions, could help overcome this problem and could also provide insights as to whether the questionnaire can be used to evaluate learning material. The low number of participants is especially relevant in the presented confirmatory factor analysis, where the number of participants restricted us to run an overall confirmatory factor analysis and neither nesting nor grouping was possible. As showing the underlying factor structure of the questionnaire was not our primary intention with this paper, a second check to confirm the findings of Klepsch et al. (2017) with a larger sample would be of interest for the whole instructional design community. Covering a variety of learning domains can be seen as positive as well as negative. On the one hand, comparability of the studies is hardly given because the amount of load between the studies cannot be ranked. On the other hand, the different domains demonstrate that the CLQ can be easily used with different learning materials, environments, and domains. One only must be careful that learners are explicitly instructed which aspect they should rate. Especially in rich learning environments, one person might only be interested in the effectiveness of one presented video, whereas another might be interested in the whole environment. But as stated by Klepsch et al. (2017), the items can easily be adopted to direct the learners to the intended object of investigation.
Especially the studies varying ICL might be questionable as they are not classical learning tasks. First within both studies we did not assess prior knowledge and second the tasks involve no classical learning processes with the goal of schema construction. Nevertheless, both programs used are paradigms in flow research (Keller and Bless 2008; Keller et al. 2011): For both programs Keller et al. (2011; Keller and Bless 2008) could show that participants in the boredom-conditions have skills exceeding the task demands while in the flow-condition they experience a fit between their skills and the task demands and in the overload condition the task demands are perceived as too high compared to one’s skills. With reference to load this would mean that the intrinsic load should be rated low for the boredom condition, as it is evaluated with reference to the task affordances in relation to prior knowledge or prior experience (i.e. the skills). Respectively the flow condition should be rated intermediate in ICL and the overload condition as high. These increasing judgments could actually be substantiated in a study of Westphal and Seufert (2016). In the Tetris study, the flow condition was designed with adapting demands to learner’s skills. The other two conditions are programmed so skills and demands do not fit together. In the boredom conditions skill exceeds demands, whereas in the overload conditions demands exceed skills. This could be linked to prior knowledge: Even if we did not assess prior knowledge, based on the different playing modes we can assume that prior knowledge, or better prior skills, were higher than needed in the boredom condition, just perfect in the flow condition and too low in the overload condition of the Tetris games. For the quiz-program our argument is similar. First, in this study only participants with at least a diploma from German secondary school qualifying for university admission or matriculation were allowed to participate. Therefore, we can assume similar general knowledge. Based on this, sufficient general knowledge is available, so skills exceed demands in the boredom condition. The flow condition is adapting to the participants general knowledge. The overload condition includes, as is classic for this game, very specific knowledge questions, which should exceed general knowledge of rather fresh high school graduates. They only got right about one third of the questions which is just marginally above guess probability. To sum up, for both studies, even if we did not access something like prior knowledge, we would like to note that the programs are developed to control this objectively by themselves.
Further directions for the use of a differentiated measurement of cognitive load
The presented six studies are more meaningful than the rather artificial learning scenarios used by Klepsch et al. (2017) to develop their questionnaire. But the present studies have still been done in the lab. As a next step, it would be necessary to use the questionnaire in a real-life setting. Therefore, we tend to implement it into a classroom setting within a university setting: for example, students of natural sciences are in need of participation in lab practice, where they need to conduct experiments. Often the experiment is shown by a tutor and has to be repeated by the students. Training the tutors using cognitive apprenticeship (Collins et al. 1987) might help reduce ECL and foster GCL because students learn what, and especially why, the tutor is doing something while conducting the experiment.
As described by Seufert (2018), it is not only learning the content that causes load on learners’ working memory. Also, self-regulatory demands, such as planning, monitoring, and evaluation, can be seen as a source of imposed cognitive load on the learners’ working memory. In her paper, Seufert (2018) analyses which self-regulatory activities could cause which type of load. For further analyses of these relations between self-regulation and load the differentiated scale could be helpful. With respect to the present series of studies self-regulatory demands could have also played a role. Asking learners to “try to imagine the learning content as a picture” as done in Study 5, can result in deeper processing of the learning content. In addition, learners might constantly be monitoring whether, or not they reached this goal. This metacognitive monitoring process could be seen as the investment of germane resources, which nevertheless can also be extraneous as they might interfere with the cognitive processes. Thus, learners might report an increased GCL, which might not necessarily lead to higher learning performance. At the very least, cognitive and metacognitive processes compete for the same limited resources.
To sum up, in our six studies, the CLQ to measure different types of imposed cognitive load during learning contributes to the theory of cognitive load and instructional design theories, effects, and principles. Based on our hypotheses and found results, we state that the questionnaire can be rather useful when it is important to differentiate the imposed load on a learner.
Conclusion – what is it good for?
In the last few paragraphs, we argued that the CLQ of Klepsch et al. (2017) is reliable and sensitive to variations in different types of load. But how can a differentiated measurement of cognitive load contribute to the focus of instructional design: optimizing learning. Developing instructional material means (1) deciding on the task, (2) a design, and (3) a method of activating learners’ cognitive processes. All three approaches can be fostered by considering theoretical assumptions and studies on instructional design. Usually an increase in learning performance is the goal of instructional design, but this also should be accompanied with the wish to understand the investment of cognitive resources during learning. Therefore, measuring cognitive load during instructional design studies is important to sharpen, confirm, or disprove theoretical assumptions and instructional design effects and principles. Especially measuring cognitive load in studies on instructional design in a differentiated way helps to understand the mechanics of different multimedia principles, as well as aptitude treatment interactions, such as expertise reversal effects. Besides contributing to the understanding of models of learning and instruction and providing evidence for assumptions in studies on multimedia principles, using a differentiated questionnaire to measure aspects of cognitive load can also help to gain insight into effects of learner prerequisites and their impact on individual task performance.
On the one hand, differentially measuring cognitive load helps to understand mechanisms important for learning, as have been proposed by CLT, multimedia principles, or instructional design principles. On the other hand, based on these insights into learning, instructions and materials for learning can be optimized by testing them beforehand.
Understanding theories and effects of learning and instruction
Based on theoretical assumptions of CLT and the Cognitive Theory of Multimedia Learning (CTML; Mayer 2005a), as well as the integrated model of text and picture comprehension (IMTPC; Schnotz 2005), many instructional design principles have been developed and investigated. These principles or effects usually make assumptions on the load that is imposed on the learner, whether they are considered (or not). A systematic testing of these theories and the effects related to them, while also measuring cognitive load in a differentiated way, seems to be fruitful for a deeper understanding of theories and effects of instructional design. At the moment, this is possible with the questionnaires of Leppink et al. (2013, 2014), or Klepsch et al. (2017). For giving practical implications to instructional designers, the traditional view of CLT seems even more helpful than the refined view, which makes using the CLQ by Klepsch et al. (2017) the better option. But further research should, as already mentioned, consider a comparison, or even a combination of both questionnaires. Sweller (2010b), for example stated, that element interactivity is associated with ICL, ECL and GCL. Getting more information on this assumption might not be possible when just asking for the experienced overall cognitive load. In one of our studies, while playing Tetris (Study 1 – see also “Validity”), participants reported significantly different amounts of ECL between conditions, even when the design of the game did not change. It just got faster, and therefore interaction became trickier, and information appeared and disappeared more quickly. Gaining expertise in the game might result in less ECL as one gets used to the fast-paced interaction (like pressing different keys rather fast) with the game. Such an enhanced expertise might also come along with the opportunity of chunking elements. Therefore, expertise might also result in less ICL in higher levels of the game, which brings us to the importance of individual learning processes.
Understand individual learning processes
Individual learning processes and aptitude treatment interactions are important parts of the already mentioned advantages of measuring cognitive load differentially, to confirm or reject theoretical assumptions. For example, measuring cognitive load differentially can be fruitful when comparing experts and novices. Asking only for invested mental effort could result in high load for both groups. Whereas, for example, signaling could ease search processes for novices, and therefore lower ECL, and thus enable them to invest germane resources. For experts’ signals could interfere with their prior knowledge and strategies, and therefore result in high ECL. As this example shows, learners’ prerequisites are important for understanding effects of instructional design principles. Especially when it comes to adaption of learning material to learners’ prerequisites and prior knowledge, it is important to test the given materials with the target group of learners (e.g., experts/novices, or learners with high/low working memory capacity), and to get feedback on their invested cognitive resources. This might be especially important when fading out assistance in learning. Only through a differentiated measure it is possible to find the correct point to start fading out assistance. Otherwise, one might always have to guess whether, for example, less performance after fading out assistance happens because the new strategy is not yet fluently available, was not understood, or could be applied, but the next step was just too difficult to manage because the last step was not practiced enough.
Getting feedback to optimize instructions and materials for learning
Based on the knowledge about different principles, instructors are able to design effective learning material. But only an evaluation of their content and material can provide insight here and offer concrete feedback. A differentiated measurement of cognitive load in an evaluation of learning material can bring us closer to our goal of designing an effective learning experience by finding problems and stumbling blocks. In a rich learning environment (e.g., an online learning environment), measuring load could also be fruitful in combination with measurement methods of user experience. Rogers et al. (2014), as already mentioned, investigated cognitive load in a computerized learning environment for playing the piano. They developed a system with a projected roll notation of notes in order to learn how to play piano. While applying some well-known instructional design principles in smaller and specialized parts of their program (split-attention effect, testing effect, segmenting principle, signaling etc.), there was no evidence offered on how participants would react to the whole system. By combining a user experience questionnaire with the CLQ, they gained insight into cognitive resources devoted to learning during the system usage, as well as insights into the user experience of their whole learning environment.
In summary, we argue that a differentiated measurement of cognitive load in instructional design research is necessary. Based on the question of instructional designers presented at the beginning, the differentiated measurement of cognitive load, on the one hand, helps researchers to understand theories and design principles in more depth, especially when it comes to the role of learners’ prerequisites, such as prior knowledge, working memory capacity, or spatial abilities. On the other hand, it helps instructors and designers to evaluate parts of their learning material and content (e.g., one instructional video), or – in combination with other methods – in evaluating rich learning material as a whole (e.g., a complex online learning environment).
References
Alter, A. L., & Oppenheimer, D. M. (2009). Uniting the tribes of fluency to form a metacognitive nation. Personality and Social Psychology Review,13(3), 219–235.
Artino, A. R., Jr. (2008). Cognitive load theory and the role of learner experience: An abbreviated review for educational practitioners. AACE Journal,16(4), 425–439.
Atkinson, R. K., Derry, S. J., Renkl, A., & Wortham, D. (2000). Learning from examples: Instructional principles from the worked examples research. Review of Educational Research,70(2), 181–214.
Ayres, P. (2006). Impact of reducing intrinsic cognitive load on learning in a mathematical domain. Applied Cognitive Psychology,20(3), 287–298.
Ayres, P., & Sweller, J. (2005). The split-attention principle in multimedia learning. In R. E. Mayer (Ed.), The Cambridge handbook of multimedia learning (pp. 135–146). Cambridge, New York: Cambridge University Press.
Bannert, M. (2009). Promoting self-regulated learning through prompts. Zeitschrift für Pädagogische Psychologie,23(2), 139–145.
Brünken, R., Plass, J. L., & Leutner, D. (2003). Direct measurement of cognitive load in multimedia learning. Educational Psychologist,38(1), 53–61.
Brünken, R., Seufert, T., & Paas, F. G. W. C. (2010). Measuring cognitive load. In J. L. Plass, R. Moreno, & R. Brünken (Eds.), Cognitive load theory (pp. 181–202). Cambridge, New York: Cambridge University Press.
Chandler, P., & Sweller, J. (1991). Cognitive load theory and the format of instruction. Cognition & Instruction,8(4), 293–332.
Clarck, R.E. (1990). When teaching kills learning. research on mathemathantics. In H. Mandl, E. de Corte, N. Bennett, & H.F. Friedrich (Eds.), Analysis of complex skills and complex knowledge domains: Learning and instruction: European research in an international context: Volume II: Selection of papers from the Second European Conference for Research on Learning and Instruction held in Tübingen, West Germany, in September 1987 (pp. 1–22). Oxford: Pergamon Press.
Collins, A., Brown, J.S. & Newman, S.E. (1987). Cognitive apprenticeship. teaching the craft of reading, writing, and mathematics. Technical Report.
Debue, N., & van de Leemput, C. (2014). What does germane load mean? An empirical contribution to the cognitive load theory. Frontiers in Psychology,5, 1099.
Eitel, A., Kühl, T., Scheiter, K., & Gerjets, P. (2014). Disfluency meets cognitive load in multimedia learning: Does harder-to-read mean better-to-understand? Applied Cognitive Psychology,28(4), 488–501.
Fletcher, J. D., & Tobias, S. (2005). The multimedia principle. In R. E. Mayer (Ed.), The Cambridge handbook of multimedia learning (pp. 117–134). Cambridge, New York: Cambridge University Press.
Jumbo Spiele®,. (2000). Wer wird Millionär? [Who wants to be a millionaire?]. Herscheid (DE): Jumbo Spiele GmbH.
Kalyuga, S. (2011). Cognitive load theory: How many types of load does it really need? Educational Psychology Review,23(1), 1–19.
Kalyuga, S., Chandler, P., & Sweller, J. (1998). Levels of expertise and instructional design. Human Factors: The Journal of the Human Factors and Ergonomics Society,40(1), 1–17.
Keller, J., & Bless, H. (2008). Flow and regulatory compatibility: An experimental approach to the flow model of intrinsic motivation. Personality & Social Psychology Bulletin,34(2), 196–209.
Keller, J., Bless, H., Blomann, F., & Kleinböhl, D. (2011). Physiological aspects of flow experiences: Skills-demand-compatibility effects on heart rate variability and salivary cortisol. Journal of Experimental Social Psychology,47(4), 849–852.
Klepsch, M., Schmitz, F., & Seufert, T. (2017). Development and validation of two instruments measuring intrinsic, extraneous, and germane cognitive load. Frontiers in Psychology,8, 1997.
Kühl, T., & Eitel, A. (2016). Effects of disfluency on cognitive and metacognitive processes and outcomes. Metacognition and Learning,11(1), 1–13.
Leppink, J., Paas, F. G. W. C., van der Vleuten, C. P. M., van Gog, T., & van Merriënboer, J. J. G. (2013). Development of an instrument for measuring different types of cognitive load. Behavior research methods,45(4), 1058–1072.
Leppink, J., Paas, F. G. W. C., van Gog, T., van der Vleuten, C. P. M., & van Merriënboer, J. J. G. (2014). Effects of pairs of problems and examples on task performance and different types of cognitive load. Learning and Instruction,30, 32–42.
Mayer, R. E. (2005a). Cognitive theory of multimedia learning. In R. E. Mayer (Ed.), The Cambridge handbook of multimedia learning (pp. 31–48). Cambridge, New York: Cambridge University Press.
Mayer, R. E. (Ed.). (2005b). The Cambridge handbook of multimedia learning. Cambridge, New York: Cambridge University Press.
Mayer, R. E. (2009). Multimedia learning (2nd ed.). Cambridge: Cambridge University Press.
Moreno, R., & Mayer, R. E. (1999). Cognitive principles of multimedia learning: The role of modality and contiguity. Journal of Educational Psychology,91(2), 358–368.
Moreno, R., & Park, B. (2010). Cognitive load theory: Historical development and relation to other theories. In J. L. Plass, R. Moreno, & R. Brünken (Eds.), Cognitive load theory (pp. 9–28). Cambridge, New York: Cambridge University Press.
Paas, F. G. W. C. (1992). Training strategies for attaining transfer of problem-solving skill in statistics: A cognitive-load approach. Journal of Educational Psychology,84(4), 429–434.
Plass, J. L., Moreno, R., & Brünken, R. (Eds.). (2010). Cognitive load theory. Cambridge, New York: Cambridge University Press.
Pollock, E., Chandler, P., & Sweller, J. (2002). Assimilating complex information. Learning and Instruction,12(1), 61–86.
Renkl, A. (2005). The worked-out examples principle in multimedia learning. In R. E. Mayer (Ed.), The Cambridge handbook of multimedia learning (pp. 229–246). Cambridge, New York: Cambridge University Press.
Renkl, A., & Atkinson, R. K. (2010). Learning from worked-out examples and problem solving. In J. L. Plass, R. Moreno, & R. Brünken (Eds.), Cognitive load theory (pp. 91–108). Cambridge, New York: Cambridge University Press.
Rheinberg, F., Vollmeyer, R., & Burns, B. D. (2001). FAM: Ein Fragebogen zur Erfassung aktuller Motivation in Lern- und Leistungssituationen. Diagnostica,47(2), 57–66.
Rogers, K., Röhlig, A., Weing, M., Gugenheimer, J., Könings, B. & Klepsch, M., et al. (2014). P.I.A.N.O. In R. Dachselt, N. Graham, K. Hornbæk, & M. Nacenta (Eds.), ITS ‘14 Proceedings of the Ninth ACM International Conference on Interactive Tabletops and Surfaces (pp. 149–158).
Schnotz, W. (2005). An integrated model of text and picture comprehension. In R. E. Mayer (Ed.), The Cambridge handbook of multimedia learning (pp. 49–70). Cambridge, New York: Cambridge University Press.
Schnotz, W., & Bannert, M. (1999). Einflüsse der Visualisierungsform auf die Konstruktion mentaler Modelle beim Text- und Bildverstehen. Experimental Psychology,46(3), 217–236.
Seufert, T. (2018). The interplay between self-regulation in learning and cognitive load. Educational Research Review,24, 116–129.
Seufert, T., Wagner, F., & Westphal, J. (2017). The effects of different levels of disfluency on learning outcomes and cognitive load. Instructional Science,45(2), 221–238.
Sweller, J. (1994). Cognitive load theory, learning difficulty, and instructional design. Learning and Instruction,4(4), 295–312.
Sweller, J. (2010a). Cognitive load theory: Recent theoretical advances. In J. L. Plass, R. Moreno, & R. Brünken (Eds.), Cognitive load theory (pp. 29–47). Cambridge, New York: Cambridge University Press.
Sweller, J. (2010b). Element interactivity and intrinsic, extraneous, and germane cognitive load. Educational Psychology Review,22(2), 123–138.
Sweller, J., & Chandler, P. (1994). Why some material is difficult to learn. Cognition & Instruction,12(3), 185.
Sweller, J., van Merriënboer, J. J. G., & Paas, F. G. W. C. (1998). Cognitive architecture and instructional design. Educational Psychology Review,10(3), 251–296.
Sweller, J., Ayres, P., & Kalyuga, S. (2011). Cognitive load theory. New York: Springer.
van Merriënboer, J. J. G., & Ayres, P. (2005). Research on cognitive load theory and its design implications for E-learning. Educational Technology Research and Development,53(3), 5–13.
Acknowledgements
We like to thank our former students involved in one of the six studies. They contributed to this research as part of their curriculum, in form of a bachelor or master thesis, or in exertion of their position as student research assistants.
Funding
This work was supported by the Federal Ministry of Education and Research Germany within the program “Aufstieg durch Bildung: Offene Hochschulen” as part of the project “Effizient Interaktiv Studieren II (EffIS-II)” (grant number 16OH22032). Open Access funding provided by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
MK and TS contributed to the conception and design of the studies. MK developed the used material and questionnaires, and led data collection for studies 1–4. TS developed the used material and questionnaires, and led data collection for studies 5 and 6. MK analyzed and interpreted the data. MK drafted the work, which was revised critically by TS. All authors provided approval of the final submitted version of the manuscript and agreed to be accountable for all aspects of the work by ensuring that questions related to the accuracy or integrity of any part of the work was appropriately investigated and resolved.
Corresponding author
Ethics declarations
Ethical approval
All six studies were exempt from an ethic committee approval due to the recommendations of the German Research Association: No subject was in risk of physical or emotional pressure, we fully informed all subjects in all studies about the goals and processes of the study they participated in, and none of the subjects were patients, minors, or persons with disabilities. In all studies, participation was voluntary, and all subjects signed a written informed consent and were aware that they had the chance to withdraw their data at any point of the study.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Klepsch, M., Seufert, T. Understanding instructional design effects by differentiated measurement of intrinsic, extraneous, and germane cognitive load. Instr Sci 48, 45–77 (2020). https://doi.org/10.1007/s11251-020-09502-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11251-020-09502-9