A Coarse Grained Molecular Dynamics Model for the Simulation of Lubricating Greases

Abstract

The rheological properties of lubricating greases are determined by the viscosity of the base oil, the interaction between base oil and thickener, and the interaction between thickener particles. The contribution of the oil–thickener interactions to the viscosity is well known, but the contribution of the thickener–thickener interactions has not yet been studied by employing theoretical or computational frameworks. In this paper, we use coarse-grained molecular dynamics to simulate a fibrous microstructure, and we show that the experimentally observed viscoelastic/plastic behaviour can be well reproduced. A parametric study shows that the apparent viscosity increases with increasing fibre length, fibre stiffness and thickener concentration. This is as expected, showing that this modelling approach is useful to study effects on grease rheology that are not accessible experimentally, such as impact of fibre entanglement or agglomeration.

1 Introduction

Lubricating greases have been used for more than 3000 years. Mutton and beef fat were originally used as axle greases. The development of modern greases started with the discovery of oil in the USA, and multipurpose greases were developed in the 1930–1940 s. Today, more than 50% of the market consists of lithium hydroxystearate-thickened grease, invented in 1942 by Earle [1], and its most demanding application is rolling bearings. Since then, great progress has been made by grease manufacturers to increase the performance by developing improved manufacturing processes, additive chemistry and (synthetic) base oils. Lithium grease is an organogel where the thickener molecules form fibres to create a microstructure. The length/thickness/structure of the fibres is not only given by the chemistry and content of all ingredients, but also by the specific manufacturing process. This type of microstructure is characteristic of many more grease types. There is a trend to move away from lithium because of the increasing shortage of it in the market [2]. Other metals will be used, but this will not fundamentally change the lubrication mechanisms/rheology.

The performance of a lubricating grease is a function of its rheology, which determines the grease mobility in a bearing. The grease rheological properties are determined by the microstructure and the fibres themselves, which may both change due to shear [3]. The microstructure gives lubricating greases their semi-solid, shear-thinning character. Grease behaves as a solid (or material with high viscosity) when it is not sheared. This implies that grease will not leak out of rolling bearings easily, which is its major advantage over oil. Moreover, this means that grease is not mobile in the so-called unswept area of the bearing where no shear force is acting, i.e. on the bearing shoulders, on the seals and, if applicable, in bearing housings. Here, semi-stationary grease reservoirs are formed. As a shear-thinning material, however, grease flows when subjected to a minimum shear rate, and its apparent viscosity decreases with increasing shear rate. At high shear rates, the viscosity approaches the base oil viscosity, making it highly mobile in a bearing in the “swept area”, i.e. in-between the rolling elements. Here, much of the grease is located after filling the bearing with fresh grease, which will then start flowing when the bearing starts rotating. Here, grease is “pushed” sideways, leaving only a thin layer in the running tracks, but thick enough to lubricate the bearing. Once these layers are exhausted, they are replenished by the so-called bleed of oil from the semi-stationary grease reservoirs, giving the bearing a long life [4]. The formation and quality of these reservoirs are determined by the grease rheology. An extensive description of various grease types and the lubricating process of grease in rolling bearings can be found in [5].

The grease lubricating process in rolling bearings can be divided into a “churning phase” and a “bleed phase”  [6]. The first phase is short but the imposed shear energy on the grease is substantial [7]. The second phase persists for an extended duration. During the bleed phase, only creep flow can take place [8, 9], possibly disturbed by macroscopic flow “events” [10].

Grease bleed can be modelled by assuming grease to be a porous medium with a certain porosity and permeability [11, 12]. The permeability is determined not only by the chemistry of base oil and thickener (affinity or wetting properties) but also by the microstructure itself.

Relatively simple models have been developed for the viscosity of suspensions formed by particles of different shapes in a liquid phase, such as the fibres in lithium lubricating grease. Suspended particles contribute to the resistance to shear. This resistance can be calculated based on hydrodynamic equations, as was first done by Einstein, who derived an expression for the viscosity of suspensions in equilibirum conditions [13, 14]:

$$\begin{aligned} \eta _r = 1+ \phi \left[ \eta \right] \end{aligned}$$

(1)

where $\phi$ is the particle concentration (volume fraction), $\eta _r$ is the relative viscosity ($\eta$/$\eta _{l}$ ratio), and $\left[ \eta \right]$ is the intrinsic viscosity, which depends on the particle shape and is defined as

$$\begin{aligned} \left[ \eta \right] = \lim _{\phi \rightarrow 0 } \frac{\eta - \eta _l}{\eta _l \phi } \end{aligned}$$

(2)

where $\eta$ is the viscosity of the solution and $\eta _l$ is the viscosity of the liquid (base oil viscosity in the case of grease). For the specific case of rigid spheres, $\left[ \eta \right] =2.5$ [15]. In the case of rigid-hard spheres in a fluid, viscous forces “perturb” the microstructure, while Brownian motion restores it [16]. At extremely low shear rates, Brownian diffusion prevails over viscous effects, resulting in significantly high viscosities when the concentration is sufficiently elevated.

Greases may have spherical thickener particles such as calcium sulphonate complex thickened greases [17]. When particles are non-spherical, there is an extra resistance to shear and therefore an increase in viscosity. For randomly oriented long, slender rodlike bodies, such as for lithium greases, the intrinsic viscosity reads [18]

$$\begin{aligned} {[}\eta ] = \frac{4 a_r^2}{15 \ln a_r} \end{aligned}$$

(3)

where $a_r$ is the length–diameter ratio of the particles (rods). Equation 3 describes the contribution of the shear stress imposed by the base oil on the fibres to the total stress for grease under shear. The impact of the interaction between fibres is still missing.

At high enough concentration (above the percolation threshold), fibres in greases and other suspensions form a percolating network with a certain “stiffness” where the motion of a particular fibre may be obstructed by other fibres in contact with it [19]. The interaction between fibres has an important influence on the rheological properties of greases, which are not captured by the single-fibre models presented above.

In the present work, we introduce a modelling framework, based on coarse-grained molecular dynamics, for the simulation of grease. With this new methodology, we are able to take into account the effects of the interaction between fibres on the global and local rheological behaviour of grease.

With the modelling framework that we propose, the study of shear thinning and shear ageing of grease becomes possible. Shear thinning in grease forms the first phase of its “degradation” mechanism. It is the result of a semi-permanent alignment of fibres by shear, an effect that destroys the percolated network [20] and that cannot be described using Eqs. 1–3. This is illustrated for a lubricating grease by Madiedo et al. [21], who showed that the viscosity may drop from e7 Pas to 10 Pas by applying a shear rate of only 10 s$^{-1}$. For high shear rates viscous effects dominate. This gives a Cross-type model [22], which well represents the behaviour of greases at high shear rates, where the viscosity approaches the base oil viscosity, which is typically in the order of only 0.05 Pas.

2 Methodology

Appendix E contains a list of symbols.

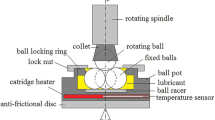
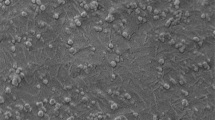
In the present work, we aim to qualitatively simulate the mechanical and rheological behaviour of lithium-based greases. Greases are composed mainly of a fluid base oil and a thickener that gives them their characteristic semi-solid consistency. In the case of lithium greases, the thickener is composed by fibres that are formed during synthetisation via a saponification process. A typical atomic force microscope image showing the microstructure of a lithium grease is presented in Fig. 1. Here, we see a microstructure formed by thickener fibres with typical concentration of 10–20%. The fibres consist of molecules that are weakly bonded by means of ionic forces, Van der Waals forces and hydrogen bonds [23]. The fibres are strong enough to give the grease its consistency.

Fig. 1

Typical AFM image of a fresh lithium grease. From [24], with permission

2.1 Modelling Approach

As mentioned above, the rheological and mechanical behaviours of lithium greases are determined by the properties of the base oil, the interactions between thickener fibres, and the interaction between such fibres and the base oil. In order to model the behaviour of greases at the meso-scale, we use coarse-grained molecular dynamics as implemented in the software LAMMPS [25]. All physical quantities are expressed in terms of “reduced”, “dimensionless” or “Lennard–Jones” units [26], where the unit for distance is ${\sigma ^{*}}$, for mass ${m^{*}}$, for time ${\tau ^{*}}$, for energy ${\epsilon ^{*}}$, and the Boltzman constant $k_B=1$. They conform to the relation $\epsilon ^* = m^*{\sigma ^*}^2 / {\tau ^*} ^2$ and all other units can be consistently deduced from these. A rough discussion on how these units would be mapped to real units is included in section 5.4 of our Discussion section.

Cubic simulation domains with a side length $L_{box}$ of 3.25 times the length of the fibres are used in all cases to avoid finite size effects. Periodicity is applied in all directions. We use a time step of $\Delta t = 0.005 \tau ^*$, except for shear strain sweeps in oscillatory shear simulations, where we use a time step of $\Delta t = 0.0005 \tau ^*$ to access larger shear rates. Equations of motion are integrated with the velocity-Verlet algorithm [27].

We consider a suspension of interacting homogeneous semi-flexible fibres evolving in an implicit solvent (base oil). Having an implicit solvent entails that we cannot capture hydrodynamic effects. Each coarse-grained fibre is discretised as a chain of bonded uncharged beads of the same constant unit mass ($m_b = 1\,m^*$) and unit diameter ($d_{b}=1 ~\sigma ^*$). The number of beads ${N_{b}}$ composing each fibre is a parameter of the model and is set to values around $N_b = 20$ to conform to the length-to-width ratio measured in [28].

The interactions between bonded beads are described using a harmonic potential centred around the equilibrium position $r_{0}^{b} = 0.95 ~\sigma ^*$. Additionally, the angle between consecutive bonds is governed by an angular cosine potential with equilibrium angle $\theta _0 = \pi$. The equilibrium values are chosen in such a way that there is a certain degree of overlap between bonded beads, and to give stiffness to the chains, avoiding their individual collapse. They are defined by the following two equations:

$$\begin{aligned} U^{B}_{H}\left( r\right)= & {} K_r\left( r - r_{0}^b\right) ^{2} \nonumber \\ U^{B}_{\theta }\left( \theta \right)= & {} K_\theta \left[ 1 - \cos \left( \theta - \theta _0\right) \right] \end{aligned}$$

(4)

where ${K_{r}}$ and ${K_{\theta }}$ are constants and take the respective values of $100 ~\epsilon ^*/{\sigma ^*}^2$ and $10 ~\epsilon ^*$.

Non-bonded beads are set to interact via the N-M potential [29], a short-range Lennard–Jones-like potential originally developed for ionic liquids:

$$\begin{aligned} U^{NB}_{NM}\left( r\right) = \frac{\epsilon _{nm}}{\left( n-m\right) } \left[ m \left( \frac{r_{0}^{nb}}{r} \right) ^n - n \left( \frac{r_{0}^{nb}}{r} \right) ^m \right] \end{aligned}$$

(5)

where $n = 18$ and $m = 16$. We set the equilibrium distance to $r_{0}^{nb} = 1.06 ~\sigma ^*$, and the attraction strength to ${\epsilon _{nm}} = 1 ~\epsilon ^*$. We discuss the choice of this potential and the value of $\epsilon _{nm}$ in Appendix B.

The stochastic collisions involving base oil molecules and thickener fibres (${\textbf {F}}_{oil}$) are implicitly considered, their dynamics being governed by Langevin dynamics [30, 31]. The beads are subjected to a random force (${\textbf {F}}_{r}$), based on the temperature of the system, and a frictional drag (${\textbf {F}}_{d}$), as described by the following equations:

$$\begin{aligned} {\textbf {F}}_{oil \rightarrow i}= & {} {\textbf {F}}_{d} + {\textbf {F}}_{r} \nonumber \\ {\textbf {F}}_{d}= & {} - \frac{m_{b}}{damp} \, {\textbf {v}}_i \nonumber \\ {\textbf {F}}_{r}\propto & {} \sqrt{\frac{k_B T m_{b}}{dt \, damp}} \end{aligned}$$

(6)

where ${\textbf {v}}_i$ is the velocity of bead i; T, $k_B$ and damp are the temperature, the Boltzman constant and the damping factor, respectively. The magnitude of ${\textbf {F}}_{r}$ is derived from the fluctuation/dissipation theorem [32]. We note the drag coefficient $\gamma _{drag} = m_{b} / damp$ such that the drag force can be rewritten as ${\textbf {F}}_{d} = - \gamma _{drag} {\textbf {v}}_i$, and its value is set to $\gamma _{drag} = 100 \, \epsilon ^* \tau ^* /{\sigma ^*}^2$. Further details about this choice are discussed in Appendix C.

A schematic showing the interactions considered in our simulation framework is presented in Fig. 2.

Fig. 2

Schematic representation of the coarse-grained fibres and their interactions

2.2 System Preparation

Before making any rheological measurements, we prepare the systems in the following manner, see Fig. 3: the fibres are initially uniformly placed in a three-dimensional lattice matching the desired volume fraction ${\rho }$, computed as the ratio between the volume of the fibres and the volume of the simulation box ($\rho = V_{fibres} / L_{box}^3$), such that 1/3 of them are aligned along the x-axis, 1/3 along the y-axis, and 1/3 along the z-axis. Two successive equilibration steps are subsequently performed. During the first one, the system is left to evolve until the pressure, the temperature and the total energy reach constant values, and until the fibres become completely randomly oriented. During the second one, we wait until the system is decorrelated with respect to the initial state. More details of the process are presented in Appendix A.

Fig. 3

Schematic representation of the methodology used to prepare grease samples and apply shear deformations

2.3 Nonequilibrium Simulations

Once the systems are equilibrated, we proceed to the characterisation of their rheological properties by independently applying steady shear or oscillatory shear deformations, as shown in Fig. 3. We aim at measuring the shear thinning and the viscoelastic behaviour of the different systems/grease samples.

2.3.1 Steady Shear

For the steady shear simulations, the system is subjected to a shear deformation at a constant shear rate $\dot{\gamma }$ by tilting the simulation box under Lees-Edwards boundary conditions [33]. During shearing, the temperature is regulated using a Langevin thermostat. We record the stress and the velocity profile and use them as indicators of a steady state: the simulations are only stopped when the former reaches a plateau and the latter becomes linear. The stress tensor is computed [34] from Eq. 7:

$$\begin{aligned} \tau _{IJ} = \frac{1}{V} \sum _{k=1}^N m_k v_{kI} v_{kJ} + \frac{1}{V} \sum _{k=1}^{N'} r_{kI} f_{kJ} \end{aligned}$$

(7)

where the first term is the kinetic tensor, and the second one is the virial. I and J are x, y or z. $\overrightarrow{r}_k$ and $\overrightarrow{f}_k$ are the position and force vector of atom k. $N'$ includes atoms from neighbouring subdomains (so-called ghost atoms). We compute the shear-rate-dependent viscosity ${\eta }$ as follows:

$$\begin{aligned} \eta = \frac{\tau \left( t \rightarrow \infty \right) }{\dot{\gamma }} \end{aligned}$$

(8)

where the final steady-state value of the stress is noted as ${\tau } \left( t \rightarrow \infty \right) { = \tau _{xy}}$. Flow curves are ultimately fitted by the Herschel-Bulkley model, which describes the viscoelastic behaviour during continuous shear, as follows [35]:

$$\begin{aligned} \tau =\tau _y + K \dot{\gamma }^n, \end{aligned}$$

(9)

where $\tau$ is the shear stress, K is the consistency index, n is the flow index, and ${\tau _{y}}$ is the yield stress. This can be rewritten in terms of viscosity, with $\eta = \tau / \dot{\gamma }$:

$$\begin{aligned} \eta = {\left\{ \begin{array}{ll} \eta _o &{} \text {if } \dot{\gamma } < {\dot{\gamma }}_{0} \\ \frac{\tau _y}{ \dot{\gamma }} + K \dot{\gamma }^{n-1} &{}\text {if } \dot{\gamma }\ge {\dot{\gamma }}_{0} \end{array}\right. } \end{aligned}$$

(10)

where $\dot{\gamma }_0$ is the transition shear rate according to the Herschel-Bulkley model.

Independent simulations are run using different shear rates, with the aim of exploring the regime around the shear-thinning region, which typically begins at shear rates close to the inverse relaxation time ${\tau _{relaxation}}^{-1}$. We compute the latter as presented in Appendix A; it is an indication of the time required for the fibres to significantly change their orientations and positions.

We also compute the segmental orientation [36, 37] of the fibres S resulting from the imposed flow, which comes from the computation of the second raw moment of $\cos \theta$, where $\theta$ is the angle between the end-to-end vector of a fibre and the direction of the shear deformation. We use the following equations:

$$\begin{aligned} \langle \cos ^2 \theta (t) \rangle= & {} \frac{1}{N_{fibres}} \sum _{j=1}^{N_{fibres}} \, \left( \frac{ \overrightarrow{u_j}(t) \cdot \overrightarrow{x} }{\left\Vert \overrightarrow{u_{j}(t)} \right\Vert } \right) ^2 \nonumber \\ S(t)&= \frac{3 \langle \cos ^2 \theta (t) \rangle - 1}{2} \end{aligned}$$

(11)

where $N_{fibres}$ is the total number of fibres, $\overrightarrow{x}$ is the direction of the shear deformation, and $\overrightarrow{u_j}(t)$ is the end-to-end vector of fibre j at time t. This coefficient shows how much the flow is aligned with a given axis. When $S = 1$, all fibres are perfectly aligned with the reference axis, as opposed to $S = 0$, where they are completely randomly oriented. Finally, when $S = -0.5$, fibres are perpendicular to the reference axis.

The final value of the segmental orientation at a given shear rate is referred to as the steady-state segmental orientation $S_\infty = S(t \rightarrow \infty )$. We compute it as the average value of the last 10 recorded points.

2.3.2 Oscillatory Shear

For this deformation method, the system is subjected to an oscillatory shear deformation, by tilting the box in opposite directions. The temperature is also controlled using Langevin dynamics. The oscillatory deformation as a function of time ($\gamma (t)$) is characterised by a shear strain amplitude ${\gamma _{0}}$ and a frequency f, as follows:

$$\begin{aligned} \gamma (t) = \gamma _0 \sin \left( 2 \pi f t\right) \end{aligned}$$

(12)

The corresponding resulting stress $\tau (t)$ response is given by

$$\begin{aligned} \tau (t) = \tau _0 \sin \left( 2 \pi f t + \delta \right) \end{aligned}$$

(13)

where ${\tau _{0}}$ corresponds to the shear stress amplitude, and $\delta$ is the phase lag between shear stress and shear strain.

Fig. 4

Instantaneous segmental orientation as a function of the shear strain obtained at various shear strain rates. All steady shear simulations start from the same equilibrated grease sample. We also present snapshots of the systems at different shear strains. Note: the actual box distortion is more pronounced than depicted in the images because LAMMPS periodically resets its shape for practical reasons, affecting its overall aspect ratio. The pictures above thus show the mechanical displacement modulo $2 \, L_{box}$

In practice, we measure $\tau _0$ and $\delta$ by computing the Fast Fourier Transform (FFT) of the stress response. The storage modulus $G'$ and loss modulus $G''$ are then calculated with the following equations:

$$\begin{aligned} G'= & {} \frac{\tau _0}{\gamma _0} \cos \delta \nonumber \\ G''= & {} \frac{\tau _0}{\gamma _0} \sin \delta \end{aligned}$$

(14)

We perform parametric studies varying the frequency and the shear strain amplitude. When varying the frequency, the shear strain amplitude $\gamma _0$ is set to a constant value ($10 \%$) within the linear viscoelastic region (LVER). When varying the shear strain amplitude, we choose a frequency value ($0.03 ~{\tau ^*}^{-1}$) that allows the system to reach the crossover between the storage and loss moduli $G'$ and $G''$; we ensure that ${G'} > {G''}$ at low amplitudes.

Before making any measurement, we ensure that the system has reached a steady state. In the LVER region (frequency sweeps), only 7 periods are needed to both equilibrate and record the data, while outside of the LVER region, 150 periods are needed (shear strain sweeps).

3 Results for Continuous Shear

3.1 Pre-shear and Fibre Alignment

It is well known that a good-quality experimental rheological measurement requires pre-shear. Pre-shear is needed to ensure that the grease sample is in a stable, uniform state before measuring its flow properties and to improve the accuracy and reliability of the results. A standard experimental procedure for the measurement of grease properties is described in [38, 39]. It is believed that this is needed to provide sufficient alignment of the fibres.

In order to reproduce the pre-shear done in experimental measurements, we apply shear for a given time to our systems, before any measurement is performed. The duration of this pre-shear stage is dependent on the shear rate applied, and it lasts until the segmental orientation of the fibres reaches a stable value.

Fig. 5

Steady-state segmental orientation $S_\infty$ as a function of the shear rate, obtained from steady shear simulations. We study the influence of a the length of the fibres, b their volume concentration, c and their stiffness. $N_b$ is the number of beads composing a single chain. Lines are guides to the eyes. In inset figures, the steady-state segmental orientation is represented as a function of the shear rate rescaled by the relaxation time

Fig. 6

Flow curves obtained from steady shear simulations showing the shear-thinning behaviour of the sample. The data (empty circles) are fitted with the Herschel-Bulkley model (solid lines) using its regularisation such that one can define the zero-shear viscosity. We study the influence of a the length of the fibres, b their volume concentration, c and their stiffness

In Fig. 4, we show the result of pre-shear simulations where the orientation of the fibres is plotted as a function of the shear strain for various shear rates. The figure shows that the steady-state segmental orientation highly depends on the shear rate. At lower shear rates, the fibres have enough time to diffuse and maintain a disordered state ($S \rightarrow 0$), while at higher shear rates, the fibres are forced to reorganise themselves in a direction parallel to the applied shear ($S \rightarrow 1$).

Figures 5a–c show the impact of length, concentration and stiffness of the fibres on their alignment during continuous shear, measured after a steady state is reached. The three figures show the steady-state segmental orientation $S_\infty$ as a function of the shear rate $\dot{\gamma }$, and, in the insert, as a function of a dimensionless shear rate, where the shear rate is scaled by the relaxation time ($\tau _{relaxation}$), see Appendix A.

It can also be seen that longer and stiffer fibres are oriented closer to the shearing direction than shorter and more flexible ones. Similarly, with higher fibre concentrations, fibres tend to rotate to an orientation closer to the shearing direction, even at lower shear rates.

Fig. 7

Relative viscosity from steady shear deformations as a function of length-to-diameter ratio of the fibres following Eq. 3. Error bars are computed from the standard deviation of the viscosity data points (Fig. 6a) in the zero-shear limit, ie in the region where the shear rate is lower than the HB critical shear rate $\dot{\gamma _0}$

3.2 Flow Curves

Flow curves show the evolution of the viscosity of a fluid, calculated using Eq. 8, as a function of the shear rate. In Fig.  6a–c, we show flow curves for different fibre lengths, concentrations, and stiffness, respectively. The dots represent simulations results, while the lines are fit by the Herschel-Bulkley model, see Eq. 9.

For all the cases considered, the simulated greases show a well-defined Herschel-Bulkley behaviour, characterised by a yield stress and a rate-dependent plastic flow. There is evidence of a rate-independent elastic modulus, causing the grease to behave elastically at low shear rates, but to exhibit plastic flow at higher shear rates.

Our simulations also show a clear increase of the viscosity with the length of the fibres, their concentration and their stiffness.

3.3 Intrinsic Viscosity

In order to be able to compare our simulation results with state of the art models –see Eq. 3, which can be used for the calculation of the theoretical intrinsic viscosity of randomly oriented, long, slender, rodlike bodies– we normalise our values for the simulated viscosity ($\eta$) with an effective base oil viscosity, $\eta _{oil}$, and obtain a relative viscosity, $\eta _r$. This effective base oil viscosity $\eta _{oil}$ is defined in such a way that the theoretical intrinsic viscosity artificially coincides with the relative viscosity for a length-to-diameter ratio of 30, the longest fibres that we analyse.

Figure 7 shows a comparison of the relative viscosity calculated with our simulations (labelled “simulations”) with the intrinsic viscosity calculated using Eq. 3 (labelled “theory”), as a function of the length of the fibres ($a_r$). This figure shows that the current simulations follow the same trend as theoretically predicted for rod-type particles in a liquid phase.

The disparity between the ’theory’ and ’simulations’ curves may arise from the significant ambiguity surrounding the definition of the viscosity of the base oil $\eta _{oil}$, as it is only implicitly defined in our simulations. When we alter parameters, here the length of the fibres, there is a possibility that the effective base oil viscosity also changes due to shifts in scales. Additionally, as shown on Fig. 6a, for short fibres the flow curves deviate from the ideal Herschel-Bulkley behaviour observed in experiments at low shear rates. Therefore, the ’simulations’ curve may deviate from the theoretical predictions as much as our simulations become unable to extract a physical zero-shear viscosity.

3.4 Fibre Stretching

We consider two manners for analysing the effect of the shear deformations on the individual fibres: first, we calculate the length of all the bonds composing the fibres (the distance between consecutive particles/beads), and, second, we calculate the energy associated with the bonds. These two measurements are done at a reference stage, when the system is in equilibrium, and during the application of a shear stress in the system (after a steady state is reached).

Figure 8 shows a histogram of the bond lengths for a system in equilibrium (top) and for a system subjected to a shear rate of $\dot{\gamma } = 0.04~{\tau ^*}^{-1}$. It can be seen that applying a shear deformation on the sample shifts the bond length distributions to the right, elongating the fibres, evidence of the presence of tensile stresses.

Fig. 8

Normalised distributions of bond lengths for various chain lengths ($N_b$ being the number of beads) at the equilibrium (top) and when the grease sample is subjected to a shear deformation (bottom) at a constant shear rate $\dot{\gamma } = 0.04~{\tau ^*}^{-1}$. The vertical lines represent the average bond length

To compute the energy per bond, we take the previously measured bond lengths in the system, and we compute the average value. Finally, we use Eq. 15 to compute the energy associated with the average bond length.

$$\begin{aligned} \overline{U_{b}} = \frac{1}{2} K_r \left( \overline{L} - r_0^b \right) ^2 \end{aligned}$$

(15)

where $r_0^b = 0.95 ~ \sigma ^*$ is the equilibrium bond length imposed by the harmonic potential defined in Eq. 4, $K_r$ the stretching stiffness and $\overline{L}$ the average bond length.

Results of the calculations of the energy for different fibre lengths in equilibrium, and when subjected to a steady shear rate deformation of $\dot{\gamma } = 0.04 ~{\tau ^*}^{-1}$, are presented in Fig. 9. It can be seen that the energy per bond is independent of the fibre length for systems in equilibrium. Conversely, when a shear deformation is applied, the energy per bond increases with the length of the fibres. In practice, this means that longer fibres are subject to higher stresses than the shortest ones, making them more susceptible to break.

Fig. 9

Average energy per bond as a function of fibre length at equilibrium and when the grease sample is subjected to a steady shear deformation at a shear rate $\dot{\gamma } = 0.04 ~{\tau ^*}^{-1}$

4 Results for Oscillating Shear

Two sets of simulations were performed while applying an oscillatory shear deformation, while measuring the corresponding storage and loss moduli ($G'$ and $G''$), see Fig. 3 for the overall methodology: First, a so-called frequency sweep is performed, where different values of oscillating frequency (f) are sampled and, second, a “shear strain sweep”, where different values of shear strain are applied to the systems. Note that each frequency and shear strain value corresponds to an independent simulation, and that the measurements are only performed once a steady state is reached.

4.1 Frequency Sweep

Figure 10 shows the results for the frequency sweep, where frequencies going from e-5  to $\approx {e0\,.}$ are considered. In all cases, we see a monotonic increase of both the storage and the loss moduli at lower frequencies. At higher frequencies, the increase rate diminishes, an effect that is more evident for the loss modulus. We also see increases of both moduli for longer and stiffer fibres and for denser systems.

Fig. 10

Elastic (solid lines, filled circle) and viscous (dashed lines, empty circles) moduli plotted as a function of the oscillatory frequency f (with an oscillatory shear strain amplitude of $\gamma _0 = 0.1$). We study the influence of the length of a the length of the fibres, b their volume concentration, c and their stiffness. Lines are guides to the eyes

4.2 Shear Strain Sweep

Results of the shear strain sweep are presented in Fig. 11. Note that, even though we impose the shear strain in the simulations, the figures show the evolution of the moduli as a function of the stress. For all the cases considered, we see an increase on both moduli for longer and stiffer fibres and for denser systems. We also note that the same trend is followed by the crossover point of the two moduli; they tend to shift towards higher stress values. The plateaus at low shear stress confirm that with the applied shear strain amplitude $\gamma _0 = 0.1$ , the systems are indeed in the LVER, justifying the value used to perform the frequency sweeps in Fig. 10.

Fig. 11

Elastic (solid lines, filled circle) and viscous (dashed lines, empty circles) moduli plotted as a function of the stress amplitude $\tau _0$ (at constant frequency $f = 0.03 ~{\tau ^*}^{-1}$). We study the influence of a the length of the fibres, b their volume concentration, c and their stiffness

5 Discussion

5.1 Continuous Shear

In Sect. 3.1, the alignment of fibres was simulated. From the simulations, it was seen that stiffer and longer fibres, and higher concentrations of fibres lead to steady-state segmental orientations closer to the applied shear direction at a certain applied shear rate. Stiffer fibres, which are less likely to deform under stress, will align closer to the shearing direction due to their greater resistance to deformation (they do not collapse, but remain straight), allowing them to maintain their orientation in the direction of the applied shear stress. We note a deviation on the evolution of the steady-state segmental orientation for the fibres with the higher stiffness, when $K_{\theta } = 20 \epsilon ^*$. Further investigation shows that at equilibrium and at low shear rates, such high stiffness leads to the agglomeration of the fibres, as shown in Fig. 12. We ascribe the more pronounced orientation of the fibres at lower shear rates to such agglomerations. For longer fibres, the longer length is likely to increase the torque exerted by shear, promoting alignment. For higher concentrations, once a steady state is reached, the lower mobility of the fibres caused by the increased interactions will force them to maintain the orientation of the applied shear stress.

Fig. 12

Slices of the simulated grease at the end of the equilibration step for various bending stiffness: a $K_\theta = 1 ~\epsilon ^*$, b $K_\theta = 10 ~\epsilon ^*$, c $K_\theta = 20 ~\epsilon ^*$

Closely related to the alignment of the fibres is the viscosity. In Sects. 3.3 and 3.2, it was shown that the viscosity increases with the stiffness, length and concentration of the fibres. Note that this behaviour follows the trend found for the alignment of the fibres, measured through the steady-state segmental orientation. With respect to the length of the fibres and their concentration, we point out that longer fibres in higher concentrations have less mobility than shorter fibres in more diluted systems, due to their increased interactions with other fibres. This makes it more difficult for them to move, which increases the viscosity of the grease. With specific regard to the fibres concentration, the same results are also found in rheological experiments with model lithium greases, where the apparent viscosity is seen to increase with soap concentration due to the higher density of physical interactions among fibres [40, 41].

The change of the energy and length of the bonds, introduced in Sect. 3.4, represents a first approximation to the study of individual fibre breaking in greases. In 1951, Moore and Cravath [42] formulated a grease thickener degradation model where they call fibre breakage an event that takes place only when a number of factors combine that cause a stress level that exceeds the strength of the fibre. This stress is caused not only by the hydrodynamic stress of oil onto the fibres but also by the interaction of these fibres. Within the current approach, one could devise models that track the evolution of such quantities and breaks the fibres when predefined bounds are surpassed. In real greases, breakage of a bond will occur when the imposed stress leads to a critical fibre elongation, which can be regarded as a critical energy. The interaction stress between fibres increases with fibre length, causing that the energy imposed to a fibre (at a certain shear rate) therefore also increases with fibre length. This leads to a larger probability of breakage for longer fibres. This model approach, in combination with shear ageing experiments, makes it possible to develop predictive models for grease shear ageing in the future. Note: this degradation mechanism, which is irreversible, differs from the shear thinning demonstrated in the current work. Shear thinning here simply comes from the "destruction" of the percolating network of fibres, and it is thus reversible.

5.2 Oscillating Shear

The storage and loss moduli for a grease under oscillatory shear with angular frequency $\omega$, following the Maxwell model read [43]:

$$\begin{aligned} G'= & {} \frac{t_c^2 \omega ^2}{1+t_c^2 \omega ^2}G \end{aligned}$$

(16)

$$\begin{aligned} G''= & {} \frac{t_c \omega }{1+t_c^2 \omega ^2}G \end{aligned}$$

(17)

with characteristic time

$$\begin{aligned} t_c=\frac{\eta }{G} \end{aligned}$$

(18)

where $\eta$ is the viscosity of the damper and G is the stiffness of the spring.

The molecular dynamics simulation results are shown in Fig. 10. Computing time restrictions makes it possible to simulate for low frequencies only, but the results show clear similarities with the Maxwell model. With the molecular dynamics model, $G'$ and $G''$ are seen to increase with fibre length, concentration and stiffness. Experimentally, higher values of the linear viscoelastic functions have also been found in commercial [40] and model [44] lithium greases with higher fibres concentration.

Rheology measurements done on polystyrene [45] showed similar results. They call the low-frequency regime in which the moduli increase with increasing frequency the “flow (melt) region” where the molecules reptate through entanglements and relax. They call the regime in which the moduli are almost constant the "rubbery plateau" where no reptation takes place and where there is motion between entanglements. This is also something that we see here. Measurements with grease at such low frequencies are impossible due to wall slip, caused by the formation of a thin oil layer close to the wall, showing the advantage of this type of models.

5.3 Limitations

In the previous sections, we have shown some of the capabilities of our coarse-grained MD model for the simulation of the behaviour of grease. Nevertheless, this simulation methodology remains an approximation and has certain limitations.

Some of the limitations come from the use of an implicit solvent. This means that we are not explicitly simulating the oil of the grease (we do not have particles representing the oil), but we use Langevin dynamics as an approximation. The implicit treatment of oil provides a computationally efficient way to model the solvent environment, but it does not capture the detailed structure and dynamics of the solvent, which can affect the accuracy of the simulation. Additionally, implicit solvent models can only capture the solvent effects that are averaged over the solvent molecules and may not capture local solvent effects or solvent–solute interactions.

For the specific case of grease, one clear limitation is that, although this model can capture the flow curves and the evolution of the viscosity with varying shear rate, it cannot capture the zero-shear viscosity, which is based on Brownian diffusion arguments that are shape-dependent.

5.4 Qualitative Mapping to Real Units

Because of the limitations discussed, it is not always trivial to do a quantitative comparison between this model’s predictions and experimental data. Nevertheless, it is useful to provide a strategy to map the dimensional and LJ-based quantities of the model to real units when possible. The mapping of some LJ units is straightforward: the length scale $\sigma ^*$ can be mapped to the thickness of the fibres as observed in AFM images ($\sim {0.1\,\mathrm{\upmu \text {m}}}$), and a bead mass $m^*$ of the order of $\sim$e-19 $\hbox {Kg}$ leads to a density of the fibres in the reasonable range of ${1}\, \hbox {g}\,\hbox {m}^{-3}$. The energy scale $\epsilon ^*$ could in principle be derived from the interaction energy between two fibres, but that is not easy to access experimentally. In alternative, it can be calibrated on the zero-shear viscosity of the system, since the strength of the interactions will correlate to the contribution of the fibres’ interaction to the viscosity. Time scales are notoriously accelerated in MD simulations compared to experiments, but one could think in terms of Deborah numbers, where the shear rate is reduced by a characteristic time scale of the system. Looking at experimental flow curves [21] and matching the critical shear rate, one could do a rough mapping of $\tau =1s$ for our LJ units. Finally, the Langevin drag coefficient directly correlates with the viscosity contribution of the solvent and could then be calibrated to the experimental values of base oil viscosity.

5.5 Outlook

With the presented modelling framework, we open the door to the study of the impact of agglomerations of thickener material on the grease rheological properties, and to the calculation of the stresses on fibres due to fibre–fibre interactions. This is a first step towards the understanding of novel concepts, such as “microstructural flexibility” [46], a favourable property for a lubricating grease. This flexibility prevents breakage of fibres during shear and leads to a short churning phase with little grease degradation.

6 Conclusions

In the present article, we introduced a modelling framework based on coarse-grained molecular dynamics for the simulation of the mechanical properties of model greases. In the framework, the fibres of the grease are treated as chains of interconnected beads held together by harmonic bonds and an angular potential. The fibres interact with one another via a Lennard–Jones-like potential, and the base oil is implicitly modelled using Langevin Dynamics.

Two main types of simulations were performed to characterise the behaviour of model grease systems: the first set was done using continuous shear, and the second set using oscillating shear. Thanks to the flexibility of the modelling approach, parametrics studies were done for various values of the length and stiffness of the fibres and fibre concentrations. The following conclusions can be drawn from the simulations:

• Fibres that are longer and more rigid tend to align more closely with the direction of shear compared to those that are shorter and more pliable. This phenomenon is also observed in systems with a higher density of fibres, where the fibres are prone to orienting themselves closer to the shearing direction, even under less intense shear forces.

• The simulations mimic the trend of rodlike particles in liquid. They display a clear Herschel-Bulkley behaviour with yield stress and plastic flow that depends on the rate. The grease shows elasticity at low shear rates and plasticity at higher ones.

• We obtain increases of the viscosity with the length of the fibres, their concentration, and their stiffness. These results are consistent with existing analytical models developed for randomly oriented, long, slender rodlike bodies.

• The modelling framework is able to capture details about the stresses in individual fibres. We see that shear deformation elongates fibres and increases tensile stresses. While energy per bond is constant in equilibrium, it rises with fibre length under shear, making longer fibres more prone to breaking due to higher stresses.

• For all the systems considered, both the storage and loss moduli increase monotonically at lower frequencies, with the rate of increase slowing at higher frequencies. This effect is more pronounced for the loss modulus. Both moduli also increase for longer, stiffer fibres and denser systems.

The comprehensive and adaptable modelling framework introduced in this study enables the exploration of grease behaviour at time and length scales, and under conditions not accessible to experiments. While the findings are presently qualitative, we anticipate that this type of framework will serve as a valuable tool for increasing the understanding of grease behaviour and as inspiration for the development of novel greases.

Appendices

Appendix A

1.1 System Relaxation and End-to-End Correlation

The end-to-end correlation at a present time t of a given system is the correlation of the current state of the system with respect to a past state taken at a reference time $t_0$. A state is defined by the orientations and positions of the fibres, which are represented by their end-to-end vectors. We use the following definition to compute $C_{ee}(t)$, the end-to-end correlation at time t:

$$\begin{aligned} C_{ee}(t) = \frac{1}{N} \sum _{j=1}^{N} \frac{\overrightarrow{u_j(t_0)} \cdot \overrightarrow{u_j(t)}}{\left\Vert \overrightarrow{u_j(t_0)} \right\Vert ^2} \end{aligned}$$

(A.1)

with N being the total number of fibres, $t_0$ the reference time, and $\overrightarrow{u_j(t)}$ the end-to-end vector of fibre j at time t.

When the system is in a configuration close to the reference state, the end-to-end correlation is close to one. As the two states become decorrelated, the end-to-end correlation tends to zero and becomes random afterwards.

We monitor the end-to-end correlation during the decorrelation step (cf. Fig. 3), to assert that the configurations used in the shear deformation simulations are properly equilibrated and no longer depend on the initial configuration. We assume that the system is equilibrated when the end-to-end correlation is close to 0.

We also measure the relaxation or decorrelation time, which is the characteristic time of the exponential decay of the end-to-end correlation, as described by the following equation:

Fig. 13

End-to-end correlation as a function of time for several concentrations, obtained during the second equilibration step (decorrelation). This shows that at the final step, the sample can be considered equilibrated and that a system with a higher concentration tends to relax slightly slower

$$\begin{aligned} C_{ee}^{model}(t) = A \exp ^{-t / \tau _{relaxation}} \end{aligned}$$

(A.2)

with $\tau _{relaxation}$ being the relaxation time and A an additional fitting parameter.

The relaxation time is therefore an indication of the time required for the fibres to significantly change their orientations and positions. The evolution of the end-to-end correlation function for systems of different concentrations is shown in Fig. 13. Additional calculations showed that the decorrelation time increases with increasing fibre length or bending stiffness.

Appendix B

1.1 Interaction Potential

We have investigated two potentials for the description of the interactions between particles: the N-M potential, presented in the body of this article, and the Weeks-Chandler-Andersen (WCA) potential [47]. The latter corresponds to the repulsive part of the Lennard–Jones potential and is presented in the following equation.

$$\begin{aligned} U_{WCA}(r) = 4 \epsilon \left[ \left( \frac{\sigma }{r} \right) ^{12} - \left( \frac{\sigma }{r} \right) ^6 \right] H\left( 2^{1/6} \sigma - r \right) {+ \epsilon } \end{aligned}$$

(B.1)

with r being the distance between two particles, and H is the Heaviside step function, $\epsilon = 1 \, \epsilon ^*$ is an energy parameter and $\sigma = 1 \, \sigma ^*$ is a distance parameter.

Overall, WCA closely resembles potentials with volume exclusion interactions or hard-core repulsion, which prevent the fibres from crossing, but without the short-range attraction that the N-M potential has.

Here, we aim at illustrating the relevance of a short-range attraction in the interaction between the thickener fibres. We also show the influence of the attraction strength by varying $\epsilon _{NM}$ in the N-M interaction. We limit our tests to values of $\epsilon _{NM} = 0.5 \, \epsilon ^*$ and $\epsilon _{NM} = 1 \, \epsilon ^*$, because larger values lead to agglomeration, which we want to avoid.

Fig. 14

Rheology of simulated grease. We compare the use of the WCA and the N-M potential for different attraction strengths. This figure shows similar behaviour for the flow curves and the steady-state segmental orientations, but not for the dynamic moduli measures. a Flow curves obtained from steady shear simulations. The data (empty circles) are fitted with the Herschel-Bulkley model (solid lines). b Elastic (solid lines, filled circle) and viscous (dashed lines, empty circles) moduli plotted as a function of the oscillatory frequency f (with an oscillatory shear strain amplitude of $\gamma _0 = 0.1$). Lines are guides to the eye. c Steady-state segmental orientation as a function of the shear rate, obtained from steady shear simulations. In the inset figure, the shear rate is rescaled by the relaxation time. Lines are guides to the eyes

On Figs. 14a and c, we find that adding short-range interactions overall does not change the flow curves and the steady-state segmental orientation. The only significant change can be seen on Fig. 14b: at high shear rates, the dynamics of the system changes. With $\epsilon = 1 \, \epsilon ^*$ and a N-M potential, it seems that $G^{\prime \prime }$ starts to reach plateau; on the other hand, $G^{\prime \prime }$ starts decreasing with the WCA potential.

Experimental measurements show that, at higher frequencies than the ones accessible with our simulations, $G^{\prime \prime }$ stabilises (or slightly increases) [48]. The N-M potential is thus more promising to reproduce experimental results, and is the potential used throughout this work.

Appendix C

1.1 Drag Coefficient

The drag coefficient controls dissipation in the model. Increasing this parameter has two main effects on the storage and loss moduli, see Fig. 15a. The first effect is that both moduli tend to increase; the second one is that both moduli tend to stabilise at lower frequencies. These two effects modify crossover point of $G'$ and $G''$.

With respect to the viscosity, see Fig. 15b, the manner how it evolves with frequency remains unchanged: in every case, we observe a power-law decay at high shear rates and a plateau at low shear rates. What changes are the magnitude, larger drag coefficients increase viscosity, and the shear rate at which the viscosity stops being constant, it increases when the drag is reduced.

We choose the value of the drag coefficient is such a way that our simulations are able to capture the crossover point $G'$ and $G''$. For this, we need to find a balance between the total duration of the simulations and the limitations of current computing hardware, and the magnitude of the shear rates that can be applied without causing instabilities in the numerical integration of the equations of motion.

As a result, we use the value of $\gamma _{drag} = 100 \, \epsilon ^* \tau ^* / {\sigma ^*}^2$ so that the crossover point between $G^{\prime }$ and $G^{\prime \prime }$ falls into the range of stable shear rates.

Fig. 15

Rheology of simulated grease changing the drag coefficient in Langevin dynamics. a Elastic (solid lines, filled circle) and viscous (dashed lines, empty circles) moduli plotted as a function of the oscillatory frequency f (with an oscillatory shear strain amplitude of $\gamma _0 = 0.1$). Lines are guides to the eye. b Flow curves obtained from steady shear simulations. The data (empty circles) are fitted with the Herschel-Bulkley model (solid lines)

Appendix D

1.1 Simulation Parameters

See Table 1.

Table 1 Input parameters used for the simulations (see the list of symbols in Appendix E), including those shown in the appendices. HB denotes the (output) parameters of the Herschel-Bulkley model extracted by fitting the flow curves. $\epsilon _{NM} = WCA$ means that the WCA potential is used, instead of the NM (see Appendix B)

Appendix E

1.1 Symbols

List of recurrent Symbols

$\sigma ^{*}$:

Length scale of the system

$m^{*}$:

Mass scale of the system

$\tau ^{*}$:

Time scale of the system

$\epsilon ^{*}$:

Energy scale of the system

$N_{b}$:

Number of beads constituting each fibre

$K_{r}$:

Spring constant of bonds between two consecutive beads (stretching stiffness of the fibres)

$K_{\theta }$:

Spring-like constant of angular bonds between two consecutive bonds (bending stiffness of the fibres)

$\epsilon _{nm}$:

Energy parameter for the NM-potential (binding energy, or attraction strength)

$\rho$:

Thickener volume concentration

$\dot{\gamma }$:

Shear rate

$\eta$:

Apparent viscosity

$\tau$:

Shear stress

$K$:

Consistency index (Herschel-Bulkley model)

$n$:

Flow index (Herschel-Bulkley model)

$\tau _{y}$:

Yield stress (Herschel-Bulkley model)

$\dot{\gamma _{0}}$:

Transition shear rate (Herschel-Bulkley model)

$\tau _{relaxation}$:

Relaxation time of the fibres

$S$:

Segmental Orientation

$\gamma _0$:

Oscillatory shear strain amplitude

$f$:

Oscillatory shear strain frequency

$\tau _0$:

Shear stress amplitude of the stress response in oscillatory shear simulations

$G'$:

Storage modulus

$G''$:

Loss modulus