Abstract
Repeated single cavitation bubble experiments were performed primarily on 316L stainless steel, and some on nickel–aluminum–bronze (NAB) and pure aluminum. The bubble dynamics were recorded with two high-speed cameras and correlated with surface images, also acquired in situ. These experiments were performed for a range of stand-off distances γ (the ratio of the distance of the solid surface from the bubble to the bubble’s maximum radius) from 0.3 to 2.15. For all stand-off distances, single pits were the only surface change detected at the beginning of damage formation. Later phases of the collapse are not axisymmetric but show regions of “stronger” collapse, and the pits occur on the material underneath those regions. For γ < 0.4, the damage is attributed to the second collapse. For γ > 0.4, the first bubble collapse is most likely responsible for pitting. Shock-wave emission was detected from the collapse regions that were linked to the damage. On 316L, the pitting rate was found to be linearly dependent on the bubble radius, indicating a non-zero lower limit for the bubble radius below which pits do not occur. In terms of stand-off distance, the pitting rate (defined here as average pits per bubble) was non-monotonic, with maxima for bubbles initiated closest to the sample (γ = 0.3) and at γ = 1.4.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Cavitation bubbles near a solid boundary collapse towards the solid. Even technical alloys can be damaged by these collapses. Cavitation is typically found in nozzles, pumps, turbomachinery, or ship propellers [1,2,3]. There, it can cause erosion [4, 5], noise [6], and reduced efficiency [7]. Besides the problems caused by cavitation, it can also be useful, for example, in surface cleaning [8], material synthesis [9], or medical applications [10, 11]. Whether it is to control cavitation or to use it, it is of great interest to understand how cavitation affects a nearby solid surface.
In technical applications, cavitation bubbles usually occur in large numbers simultaneously, making fundamental studies of the phenomenon difficult. However, a focused laser pulse can be used to induce single bubbles, allowing controlled experiments to be performed more easily [12]. Detailed studies of the collapse dynamics of free bubbles, e.g., [13], as well as bubbles close to solid surfaces were performed this way [14,15,16,17,18,19]. Several studies also investigated the effects of the such collapses on a deformable surface [20,21,22,23]. In particular, the bubble collapse dynamics and thereby the surface damage depend on the dimensionless stand-off distance γ—the ratio of the distance of the bubble center from the surface to the maximum bubble radius [20]. During collapse, shock waves are emitted from the bubble [24] and a liquid jet can hit the surface with up to 1000 m/s [25, 26] (though usually much slower), depending on the stand-off distance.
Early work on surface damage by laser-induced single bubbles was published by Tomita and Shima (1986). They discussed the possible role of the shock wave in damage development [27]. In their pioneering 1998 work, Philipp and Lauterborn (hereafter abbreviated with P&L 1998) performed a comprehensive study of bubble dynamics, but more importantly, possible damage mechanisms and resulting damage patterns [20]. In particular, the liquid jet as well as the shock waves occurring at different stages of collapse were correlated with surface damage [20]. However, the influence of the various phenomena during the collapse on the resulting damage is still not clear. A recent study by Dular et al. using aluminum foil laminated on glass—substrates found the mechanism (e.g., shock waves, jet) to depend on the stand-off distance [21]. Although P&L 1998 investigated technical alloys to some extent, the focus of their work, like that of most that followed, was on the study of relatively soft materials such as aluminum [21,22,23]. However, such “model” materials are unsuitable for most engineering applications where cavitation occurs. The extent to which the studies on aluminum can be transferred to technical alloys is not clear.
Cavitation resistance testing of technical alloys is typically performed according to ASTM G32 using ultrasonic cavitation [28, 29]. In these tests, e.g., [30] and more application-oriented tests [31], multi-bubble phenomena occur [32, 33], making it impossible to directly correlate individual bubbles with the damage caused. However, there are some indications that the damage mechanisms in ultrasonic cavitation do correspond to those triggered by many successive individual bubbles [34].
Little work has been done on single bubble damage to technical alloys. A recent study by Reuter et al. showed that at very small stand-off distances (γ = 0.05 to 0.2), even technical alloys can be severely damaged by self-focusing of the shock waves [35]. Gonzales-Parra et al. performed experiments with many consecutive single cavitation bubbles on brass, the focus being the prevention of damage by laser-machined periodic surface structures [36].
In our previous work, we investigated the damage process on 316L stainless steel, nickel–aluminum–bronze (NAB) and aluminum [37,38,39], the latter to make a better connection to the literature. Most of the experiments were performed with 2 mm to 3 mm bubble diameter and stand-off distances around 1.4 [37]. It was found that pits occurred stochastically on the technical alloys in the same locations relative to the bubble as on aluminum but were smaller and less frequent. However, it was also found that on technical alloys the visible damage process can start from the very first bubble, as it does for aluminum [38]. The surface changes after each bubble were correlated with the corresponding bubble dynamics to better understand the pit formation. In particular, we saw that in the second collapse of a bubble, there can be parts of the then toroidal bubble that have elevated dynamics, i.e., a locally “stronger” collapse. The occurrence of these stronger collapse areas (SCA) was spatially correlated with the surface pitting in that pits only occurred in close proximity to the SCAs [37]. A recent study by Kida et al. [40] measured the pressure near the sample surface for γ = 1.5 with an optical pressure sensor and recorded the bubble dynamics from two perspectives. Consistent with our work, they found asymmetric regions across the toroidal second collapse in the bubble dynamics and the highest pressures away from the center. An important conclusion from our experiments is that material damage from single bubbles can be caused by the summation of many individual pits. How fast the initial damage progresses can then be indicated by the pitting rate [38].
Since most of our previous work was for γ = 1.4 but the bubble dynamics are very different for different stand-off distances [20], the question arises how generic the findings summarized above are. Therefore, we investigated the correlation of bubble dynamics with pit occurrence for the entire range of stand-off distances that our experiment can usefully produce, γ = 0.3 to 2.15. In the course of the investigation, a few other aspects were seen to be relevant and are, thus, covered here, namely, local and global collapse asymmetry, a visualization of shockwaves, and an initial investigation into the scaling of the initial damage evolution with the absolute bubble diameter. As before, the experiments were performed mainly on 316L, but differences and similarities compared to NAB and aluminum were also investigated.
2 Materials and Methods
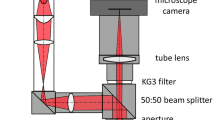
The experiment has been described in detail in our previous work [37]. Here, a brief summary is given, and new features are described. Figure 1 shows a simplified view of the illumination and image detection. The cavitation bubbles were generated by a focused 10-ns laser pulse (1064 nm) above the center of the polished cylindrical samples. The repetition rate of the laser pulses, and thus, the bubbles, was varied between 15 and 0.5 Hz. For both the pit–bubble correlation experiments and the pitting-rate experiments, a low repetition rate was preferred because longer intervals between bubbles mean less residual gas from the previous collapse that complicates imaging the surface. For experiments with many cavitation bubbles (more than 1000), the maximum repetition rate was chosen to reduce the duration of the experiment.
The bubble dynamics are recorded simultaneously with two high-speed cameras. In addition, the surface of the sample was recorded before and after each bubble. The high-speed cameras (Phantom Veo 710L, Phantom v1216, and/or Photron SA-Z) were operated at repetition rates adapted to the relevant part of the bubble dynamics (between 60 and 160 kHz). A camera with low frame rate but higher resolution allowed examining the surface in situ via reflected-light microscopy. Two beam splitters are utilized in the optical train of the light microscope. A 50:50 splitter directs the illuminating LED light towards the sample, while a second 90:10 splitter projects the image onto two cameras. The majority of the light (90%) is directed towards the high-speed camera. The exposure time of the high-speed camera for the side view was set to 5 µs. For most of the experiments, the camera for the top view was operated at about 10 µs. For some experiments (e.g., Fig. 10a), it was 5 µs. The high-resolution camera was exposed for 3000 µs. The circular field of view varied between 3 and 1 mm in diameter, depending on the radius and stand-off distance of the bubble. For most experiments, the LED illumination was continuous, but to visualize shock waves, the LED was pulsed with 200 ns pulse duration.
The cylindrical specimens, 12 mm in diameter and 7 mm in height, were first ground, and in the final preparation step, the sample was lightly etched to visualize grains [37, 39]. Most of the experiments were performed on the stainless steel 316L, but differences and similarities compared to a nickel–aluminum–bronze (NAB) and pure aluminum were also investigated. In typical ultrasonic cavitation erosion testing, aluminum shows very little cavitation resistance, 316L much more, and the NAB is most resistant. More detailed material specifications and material properties can be found in [34, 38, 39].
3 Results and Discussion
For clarity, some definitions are provided first: during the life of the bubble, several collapses and rebounds take place [20, 41]. This work examines both the initial collapse of the bubble, as well as the second collapse that occurs after the bubble rebound. A collapse is defined here as the shrinking of the spatial extent of the gas phase in the fluid towards a local minimum. However, in the literature, this local minimum itself is often called the “collapse.” In keeping with this, if it is not explicitly stated which of the individual spatio-temporal minima is meant (first, second), “collapse” may also refer to the overall process. During this process, the sample surface becomes subject of load due to different phenomena like liquid jets or shockwaves. A pit is defined here as a permanent depression (plastic deformation) in the surface caused by a single event in the bubble collapse that is short compared to the overall time of the bubble collapses and rebounds. As will be seen, the radius of pits is always more than one order of magnitude smaller than the maximum bubble radius. More generally, (cavitation) damage is defined as any permanent change in the surface. Such a change does not necessarily mean erosion, which is the removal of material, but may simply be due to plastic deformation. Two kinds of mechanisms appear in our discussion: on the one hand, the way the fluid dynamics lead to a presumed load on the material (jet, shock waves), on the other, how that load leads to damage in the material.
3.1 Pitting Damage Patterns
Figure 2 shows the regions in which successive bubble collapses caused damage in form of pits at stand-off distances from 0.25 to 1.90. The in situ images were selected so that the damaged region and individual pits are clearly visible. For γ = 0.25 (Fig. 2a), the pits form a ring with two regions along the laser beam propagation axis where the damage is significantly increased. The damage in these regions is composed of multiple pits. For γ = 0.9, two regions away from the laser axis contain the majority of the pits. For a stand-off distance of 1.0, pits occur in a much smaller region that is elliptical with the long axis perpendicular to the laser direction. For γ = 1.2, a circular damage pattern can be seen with more damage along the laser axis, although the damage is more pronounced towards the laser incidence. A similar damage pattern is observed for γ = 1.36, except that the circle is significantly larger. At γ = 1.55, the pits occur in a ring similar to γ = 1.36, but an additional circle of pits formed around the center of this ring. At a stand-off distance of 1.78, only one circle of pits is seen directly below the center of the bubble. Finally, Fig. 2a shows damage at the upper end of the stand-off distances that cause pits. Here, at γ = 1.9, pitting occurred only in a relatively limited area, again directly below the bubble center.
In situ images of pits at various stand-off distances for a bubble radius of about 1.2 mm. The stand-off distance, number of bubbles, and the exact radius are given in each image. The laser is incident from the bottom left corner (red arrow). a Overview images showing the entire damaged area. The images are shown at different magnifications. Each scale bar corresponds to 500 µm. b Sub-regions of the images in a at higher magnification. Here, each image has the same magnification, represented by the 250 µm bar (Color figure online)
The number of bubbles that must collapse on the surface to produce significant damage patterns varied widely, i.e., from 100 (γ = 0.25) to 200,000 (γ = 0.9). The damage patterns in Fig. 2 are consistent with recordings of equivalent experiments on aluminum by P&L 1998 [20] and Isselin et al. [22]. This is also true for the asymmetries typical of laser-induced single bubbles [42,43,44]. These asymmetries in the likelihood of a pit occurring in a particular spot are probably caused by the asymmetry of the plasma. However, the ring-shaped patterns (e.g., at γ = 1.36) show that this asymmetry seen in damage patterns is not universal and pits can occur everywhere along the ring.
Figure 2b shows sub-regions of the damage shown in Fig. 2a with all images on the same spatial scale. This type of presentation facilitates a comparison of the lateral dimensions of pits. For all γ > 0.3, the pits are quite similar in size. This is true for both pits at a fixed distance as well as for pits across different stand-off distances. This may imply that the surface loading by the fluid dynamics is not so different across these cases, which in turn points towards the mechanism in the flow being similar. For γ = 0.25, however, the pits look distinctly different. The special nature of very small stand-off distances with γ < 0.3 has recently been highlighted by Reuter et al. [35] who identified a self-focusing mechanism of the shockwaves that leads to strong deformation of the material. This might be the cause of the more pronounced damage region on the laser axis in Fig. 2b. This region is also composed of multiple pits that occurred in a small area. Note that the images shown in Fig. 2 for γ = 0.25 are at a lower number of bubbles than the other images.
Up to bubble counts of several 10,000 (depending on γ), pitting is the only damage observed on 316L. As shown in a previous study, before material is lost in cavitation erosion, plastic deformation leads to material elevation and a rise of the grain boundaries [39]. Therefore, if these phenomena have not yet occurred, there cannot be material loss, as shown in Fig. 2 where none of the sample shows significant change of the material structure at the grain boundaries. How the accumulation of pits finally leads to erosion depends on the material [39], and the pitting rate was also found to be material-dependent [38]. For 316L and aluminum after many pits plastic flow occurs. Grain boundaries stop this flow and this is where the first material removal (erosion) was observed [39]. For NAB, plastic flow on a large scale was hindered by the disperse intermetallic particles. Nevertheless, the first material removal occurred at grain boundaries [39]. In the current work, pits were found for every material and stand-off distance investigated up to an upper boundary discussed in the section “Pitting rate”. Thus, any damage due to multiple bubbles at a given stand-off distance for which pits occur has the potential to eventually lead to material loss due to the plastic flow as summarized above [39].
3.2 Correlation of Damage and Bubble Dynamics
The surface changes are now correlated with the corresponding bubble collapse. The method for that was presented in detail in our previous work [37] and is summarized in Fig. 3. For this evaluation images from the beginning of a bubble series when only a few pits have formed, were used (unlike the examples in Fig. 2 where pits overlap, making counting impossible). First, a pit was searched for in the high-resolution images before and after the bubble collapse. If a pit was found, its location was identified in the high-speed data, and these were examined in more detail. Figure 3a, b shows the surface before and after the collapse. The pit is marked with a red circle. Figure 3c, d shows selected images from the second collapse of the bubble. The position of the pit is marked with a red x in these high-speed images. Here, the pit is located where an SCA was found in the collapse. Our previous work examined how the phenomena in the second collapse of bubbles with γ = 1.35 ± 0.05 are related to the pitting [37]. The same procedure is now applied to stand-off distances from 0.3 to 1.9. The findings are first discussed for γ > 1, where only the second collapse occurs close to the sample surface, and γ < 1, where both the first and second collapse occur in direct vicinity of the sample surface.
3.3 γ > 1
Figure 4 shows the side view of selected bubble dynamics from γ = 1.1 to 1.8 of bubbles at r = 1.4 mm. The dynamics of the bubble collapse processes were described in detail in other work [20] and are used here just as a reference for the reader. As can be seen in Fig. 4a–e, at none of these stand-off distances does the first collapse occurs close to the sample surface. Therefore, the second collapse is considered relevant for pitting.
Figure 5 shows the dynamics around the second collapse of the same bubbles as shown in Fig. 4, now in top view. All bubbles shown here caused at least one pit. The position of the pits is marked with a red x. A collapse ring with different radii for different γ can be seen for all stand-off distances. The collapses at γ = 1.25 to 1.8 (Fig. 5c–e) also have a “spot” of gas phase in the center of the ring. A more complete view of the dynamics from the top view can be found in Fig. 14 in the “Appendix”.
Two selected images from the top view of the dynamics around the second collapse of the bubbles shown in Fig. 4. Pits are marked with a red x and SCA-like structures that did not cause pits are marked with white arrows (Color figure online)
In each of the examples shown in Fig. 5, a pit could be assigned to an SCA in the second collapse. In fact, from γ = 1.1 to 1.8 this was the case for thousands of image series we visually examined. Pits usually occur in the center of the SCA. As in the example in Fig. 5b, when two pits occurred, two SCAs are seen. It is not true that each SCA necessarily leads to a pit, but each pit can be attributed to an SCA. SCAs that did not cause pitting can for example be seen in Fig. 5c, d on the torus opposite of the pitted region (white arrows). In Fig. 5e inward motion blur indicates an SCA that is not on the torus ring but closer to the center. The overall damage patterns in Fig. 2a indeed show that for γ = 1.55–1.9 damage occurs more centrally.
SCAs can occur in any part of the second collapse. However, the as described in the previous section, the accumulated damage is not axisymmetric. It appears that the asymmetry that is inherent in the experiment caused an asymmetric lateral distribution of the probability of SCA occurrence on the area of the second collapse. We observed that an SCA occurred more often in certain areas, consistent with the asymmetry in the accumulated damage.
3.4 γ < 1
For stand-off distances from 0.25 to 1 both the first and the second collapses occur in the immediate vicinity of the surface. Since from above, a pit becomes visible only after the disappearance of the gas phase and thus, after the final collapse of the bubble, pits could not be easily as attributed to the second collapse as for γ > 1. Thus, we need to examine the bubble dynamics in more detail here.
Figure 6 shows the first and second collapses of bubbles with γ < 1. Each of these bubbles caused at least one pit whose location is marked with a red x. The first collapse is always toroidal with a high degree of symmetry, whereas the second collapse is strongly asymmetric, with SCAs so pronounced that only a faintly toroidal shape can be seen. For γ = 0.25, the first-collapse toroid is elliptical and has two SCAs, and the second collapse occurs entirely in two distinct SCAs away from the laser axis. In all cases, the pits are found where SCAs appeared. For γ = 0.66 to 0.95 (Fig. 6a–d), the pits are located in the center of the SCAs in the second collapse—just as for the larger distances discussed in the previous section. For γ = 0.4, this is approximately so, but for γ = 0.25 (Fig. 6e, f), one of the two pits is adjacent to the SCA. From all these observations, and considering that for γ > 0.5, Reuter and Kaiser showed that during the first collapse, there is always a water layer of at least 5 µm thickness between bubble and solid [45], we conclude that for our millimeter-sized bubbles, the second collapse is responsible for pitting for γ > 0.4. For γ = 0.4 and 0.25, the first collapse may already cause damage. As discussed in the section pitting-induced damage patterns, this is consistent with the recent work of Reuter et al. in which for γ = 0.3 and less a very damaging shock wave self-focusing mechanism occurred during the first collapse [35].
In other works, the liquid jet associated with the first collapse was seen as at least partly responsible for the pitting, especially at small stand-off distances [20, 21]. However, these findings came from soft materials. On 316L, even at small stand-off distances and high bubble counts (Fig. 2d 200,000 bubbles), no surface changes were observed that could be attributed to the central jet, consistent with Reuter et al. [30]. Such damage should be seen in the area that is below the center of the first ring collapse in Fig. 6. The most likely explanation is that the load on the surface caused by the jet is not sufficient for pitting in technical alloys. Instead, here, SCAs in the second or first collapse are responsible for pitting.
Results for the other technical alloy tested here, NAB, can be found in the “Appendix” in Figs. 15 and 16. The findings are similar, which confirms that the fluid dynamics of the bubble is decisive for damage in the form of pits on the surface where SCAs occur in the second collapse. In the sections “Pitting rate” and “Influence of the material,” we will compare 316L and NAB in in terms of the pitting rate and the accumulated damage of many pits.
3.5 SCA and Shock Wave
It is known that during the several rebounds of the bubble, shock waves are emitted at the minimum presence of gas in liquid, i.e., at each collapse [20, 24, 27, 44]. Based on the results presented in the previous section, shock waves in the second collapse are of particular interest. Our experiment with its limited frame rate is not as suitable for visualizing shock waves as the more purpose-built experiments with ultra-high frame rates, e.g., [20, 35]. Nevertheless, by reducing the illumination duration of each frame to 200 ns, we did indeed capture shock waves.
Figure 7 shows the second collapse from the side (Fig. 7a) and from the top (Fig. 7b), as well as the sample surface just before and after this collapse. In the side view of the collapse, in addition to the collapse ring itself, two other features can be observed. One is that the bubble torus is detached from the surface [Fig. 7a white arrow. Figure 17 in the “Appendix” includes a second example in which this detachment is clearer (but the shockwave is less clear). The Supplementary Material includes the two corresponding video sequences]. The vertical distance between the gas-phase shadow and its reflection on the sample surface indicates that the distance between gas phase and sample surface is several tens of micrometers. In none of the about 300 bubbles recorded with the shorter, 200-ns illumination did the damage occur in the region exhibiting this vertical detachment. The detachment was also found by Reuter et al. for a similar γ [35]. The second feature is a shock wave with its center at the torus of the second collapse on the side of the laser incidence. There is some spatial uncertainty, but combined the side and top view indicate that this shock wave was apparently emitted by the very SCA that is associated with the pit found after the bubble. Since the energy per unit area of a spherically propagating shock wave decreases with the square of the distance from the origin, only locations on the sample surface close to the origin are affected. The emission of shock waves from such an asymmetric region of the torus was already found by P&L 1998 [20] but now can be associated with the formation of a single, specific pit.
Second collapse of a bubble with γ = 1.4. a Side view, b top view close to and after the collapse, and c detail (corresponding to the white rectangle in sub-figure b) of the surface before and after the bubble. The resulting pit is marked with a red circle; the pit location is marked with a red x in the high-speed images in b. Note that the sample shown here had previously been subjected to bubbles of various stand-off distances, which is where we cannot see a simple and regular pit pattern as in, e.g., Fig. 2 (Color figure online)
3.6 Controlled Asymmetry
The damage of the sample surface is related to asymmetries in the collapse that in turn stem from asymmetry in the experiment, i.e., in the laser-induced plasma. Since we could not eliminate these asymmetries, we instead introduced further, controlled ones. To that end, bubbles were created near the edge of the sample. The presence of the edge has a strong influence on the bubble dynamics that are globally described by the Kelvin impulse [17]. Figure 8 shows the dynamics of such a bubble from the side. Even before the first collapse (126 µs), the bubble shrinks faster on the side closer to the edge, and it moves away from the edge of the sample. From 308 to 364 µs, we see that the collapse does not occur simultaneously. Rather, the region closest to the edge collapses first, and that farthest away last. Figure 9 shows this process again from above. Both the top view and the side view show that the second collapse of the bubble at 364 µs occurs in a limited area and is shifted towards the sample center. In this area, an SCA can be observed. This is also the area where this bubble caused damage, as marked in Fig. 9 at 364 µs. In repeated bubbles as in Figs. 8 and 9, no pit or SCA occurred in any other location. Thus, it is reasonable to conclude that SCAs are related to the fact that the bubble does not collapse simultaneously everywhere. Although the externally introduced asymmetry clearly had an effect on where a pit forms, even this strong asymmetry did not cause pits to occur more frequently than in comparable experiments in the center of the sample—in both cases, the pitting rate (discussed in more detail below) was about 0.085 pits/bubble for the given material, stand-off distance, and bubble radius.
Top view of the bubble dynamics of the collapse from Fig. 8. The pit is marked with a red x The edge of the sample is on the left (Color figure online)
Figure 10 shows three bubbles with different stand-off distances shortly before and at the second collapse. These bubbles were induced above the sample center. All bubbles caused a pit that could be linked to an SCA. Figure 10a shows only a part of the toroidal collapse from the case with γ = 1.4. It can be seen that the ring section does not narrow uniformly (− 13 µs, − 6 µs, 0 µs). Instead, shrinkage is slowest in the region where the SCA occurs and the pit is formed. In Fig. 10b, c, two bubble collapses are shown where this phenomenon can be seen even earlier before the second collapse (Fig. 10b: t = − 28 µs, Fig. 10c: t = − 33 µs). The non-simultaneous shrinking process of these bubbles and the coincidence with SCAs indicates that even in bubbles where a strong asymmetry is not intentionally introduced (as in Fig. 9), SCAs and thus pits, are connected to the temporal non-uniformity of the collapse of the bubble. These findings are consistent with the “energy focusing” seen by Reuter et al. [35] (there, “Appendix H”). In particular, their subsonic energy focusing in the second collapse is consistent with our findings concerning the likely effect of the second collapse being non-simultaneous [35].
3.7 Pitting Rate
The pitting rate is a metric of how fast early cavitation damage is developing [38, 46]. In our experiments, in the high-resolution image after each bubble the new pits that stem from that bubble can be identified and counted. Some bubbles do not leave any pits while others create several [38]. This method can be applied until pits start to overlap, which was generally after 50 to 100 bubbles. The pitting rate is then defined as the average number of pits per bubble over this image series [38]. Here, we will discuss the pitting rate on 316L for various stand-off distances and bubble sizes.
Figure 11a shows the pitting rate at a fixed stand-off distance of γ = 1.40 ± 0.05. The maximum range in bubble size usefully attainable with the experiment was from 0.75 to 1.5 mm radius. The error bar in radius represents the standard deviation of the maximum radius of each experiment. This variation may stem from the uncertainty in the experimental parameters. Also, since the occurrence of pits is partially stochastic, for a finite number of bubbles the pitting rate determined from two bubble series can differ for the exact same experimental parameters.
Figure 11a shows that the pitting rate decreases with decreasing radius. The data suggest a linear trend, and the corresponding linear fit has a slope of 0.55 pits/(bubble mm). The fit reaches zero pitting rate at a finite radius of r = 0.4 mm, suggesting that below that lower limit, the maximum load exerted by the bubble collapse is no longer sufficient for plastic deformation of the sample. Accordingly, this limit should be material-dependent. In previous work [37, 38], we performed quantitative surface elevation measurements with a confocal scanning microscope. This showed the pits on the NAB to be smaller than on 316L (about 10 vs. 25 μm, respectively), and we still easily see the former in the in situ images, and they in fact appear smaller. This indicates that we are not systematically underestimating the pitting rate for the smaller of the bubbles in the investigated range. However, we currently have no experimental evidence for what happens with bubbles smaller than 0.75 mm radius. The further regression of the pitting rate towards zero may not be linear.
Isselin et al. found that the shockwave pressure emitted by the first collapse increases linearly with the maximum bubble radius [22]. Unfortunately, they did not investigate the second collapse, which we have seen to be more relevant for the sample damage. Nevertheless, the consistency of that scaling with Fig. 11a lends some support to the idea that the pits are directly caused by shock wave emission close to the surface.
The influence of γ on the pitting rate is shown in Fig. 11b. The radius of the bubbles was r = 1.3 ± 0.2 mm for 316L. The variation in radius is included in the error, which from Fig. 11a is estimated to be about 10%. At γ = 2.15, 500 bubbles did not generate a pit, i.e., the pitting rate is less than 0.004 pits/bubble, which we considered essentially zero for current purposes. Towards small stand-off-distances, the pitting rate increases and peaks at about γ = 1.4, decreasing again with decreasing stand-off distance to less than 0.1 pits/bubble at γ = 1. For 0.4 < γ < 1, the pitting rate remains below 0.7 pits/bubble. The steep increase for γ = 0.3 to over 0.6 pits/bubble again points to a different mechanism at work for these small stand-off distances [35]. An obvious outlier in the otherwise relatively smooth relation of pitting rate vs. standoff distance is γ = 1.75, with 0.425 pits/bubble. This might be explained by the sudden change in area onto which the bubble collapses at γ = 1.75. As the stand-off distance is increased from 1.55 to 1.75, the area on the sample that the bubble collapses onto significantly changes, its shape being a large ring for the former but a solid circle for the latter (Fig. 2f, g). For γ > 1.75, we suggest that with increasing γ less and less energy is reaching the sample surface and an SCA creating a load sufficient for plastic deformation becomes less likely. In addition to the data from 316L, Fig. 11b shows the pitting rate on NAB. The general trend corresponds to that on 316L, with the absolute pitting rate being lower for most γ. For γ = 0.5 and 0.76, the pitting rate is slightly higher than on 316L. Most likely this is because the bubble radius was about 10% larger in these two measurements. The upper boundary for pit occurrence was not significantly different on NAB.
P&L 1998 report two series of measurements on aluminum in the range 0.3 < γ < 2.15, examining the depth of the pits [20, Fig. 20]. The data of this measurement series is also plotted in Fig. 11b. Despite the different material, that metric yields a graph that is similar to our pitting-rate data on 316L and NAB. This similarity may imply that both the depth of the pits and the probability of a pitting event are proportional to the load on the surface. In contrast to the pitting rate that is the average over multiple bubbles on the same sample, the pit depth data, each stemming from a single bubble, scatters more. The upper boundary of detectable pit depth in P&L 1998 on aluminum was similar to the boundary for our pitting rate on 316L and NAB. Recently, also in laser single-bubble experiments, Abedini et al. estimated the damage to the oxidic surface layer on an aluminum sample from time integration of the measured transient electric current [47]. Consistent with the trends here, they found that the greatest damage occurred at γ = 0.3 and 1.4.
3.8 Influence of the Material
Figure 12 shows the damage progression on 316L and NAB at approximately γ = 1.1 up to 170,000 and 80,000 bubbles, respectively. The pits form mainly in two regions on the laser axis. In both samples, a ring corresponding to the region of the second collapse can be seen at this γ (see Figs. 4, 5). The larger radius in the NAB damage pattern is due to the slightly larger maximum radius of the bubbles. On 316L, material damage can be seen beyond the pits at the grain boundaries (black arrows). This type of damage was also found in experiments in our previous work for γ = 1.4. It is a step in the transition from single pits to eventual material loss [39]. Comparable damage does not occur in the bronze due to the different microstructure [39]. In our experiments here, we found that for all investigated stand-off distances, the effect of pitting on the material was similar to the damage process described in [39]. Therefore, even if for a given combination of stand-off distance and bubble size, the pitting rate is low, the evolution of damage into erosion happens in a similar manner, just more slowly.
From Fig. 12, but also from comparison of the damage patterns shown in Fig. 2 to damage on aluminum in the literature (e.g., [20, 22]), the similarity of damage pattern across ductile materials investigated here is evident.
Some experiments were also carried out on aluminum, which we previously had only done at γ = 1.4 [37, 38]. The correlation of SCAs and pits on aluminum can be seen in Fig. 13b. For this particular bubble, two SCAs and two pits occurred. As on steel (Figs. 2a, 6b, c), the pits occur in two opposite regions away from the laser axis. The images for 50 and 200 bubbles in Fig. 13a show a phenomenon also observed in previous work on aluminum: at constant stand-off distance, the pit size varies more than on the technical alloys [37, 38]. Large scatter in pit metrics caused by single bubbles on aluminum was also found by P&L 1998 [20] and Sagar et al. [23]. This is probably caused by the variation in the load exerted by the individual collapse events. Compared to the technical alloys, on aluminum far, weaker parts of the collapse are sufficient to cause plastic deformation, and thus, there is a greater variation in the load that causes pitting.
Aluminum surface after 6, 7, and 50 and 200 bubbles imaged in situ (a) and surface elevation from ex situ confocal microscopy after 200 bubbles (c) at γ = 0.74 and r = 1.4 mm. In addition, the second collapse of the seventh bubble is shown (b). The red circles mark the pits caused by the seventh bubble. The red x marks the pit location in the images of the second collapse. The projection of the bubble center on the surface is marked with a black x. All images refer to the same spatial scale as c. The laser incidence is from the right (Color figure online)
In Fig. 13, the center of the bubble projected onto the surface of the sample is marked with a black x in some of the images. This is the point where the liquid jet of the bubble hits the surface [20]. Both the surface quantitative elevation map from confocal microscopy and the qualitative in situ microscope image show that plastic deformation of the sample surface did not occur in this area. Apparently, even on a material as soft as pure aluminum, 200 bubble collapses with a stand-off distance well below 1 were not sufficient to lead to deformation by the jet.
4 Conclusions
In this study, we investigated the formation of early cavitation damage on two technical alloys and on pure aluminum for a wide range of stand-off distances and bubble diameters. The experiments focused on 316L, a ductile technical alloy. Some experiments were also performed with a nickel–aluminum–bronze (NAB)—a more cavitation-resistant, multi-phase material—and with pure aluminum, a soft metal. The damage caused by cavitation bubbles was correlated with the bubble dynamics, including an example of shockwaves emitted during the second collapse. Pits occur on 316L for stand-off distances less than γ = 2.15. Over a series of single bubbles, they accumulate in patterns that depend on the stand-off distance and are influenced by asymmetries in the experiment. This is consistent with the literature [20, 22, 23].
We showed that for stand-off distances larger than 0.4 in general “stronger” parts (SCAs) in the second collapse spatially correlate with pits, while for smaller stand-off distances stronger parts of the first collapse correlate with pits. In experiments focusing on the second collapse with γ = 1.4, these SCAs were also found to be the regions where shock waves are emitted. SCAs appear to be those parts of the bubble that locally collapses last. This became most obvious in experiments where the bubble collapse was forced to be asymmetric but is most likely more generally true. The central jet associated with the first collapse was found irrelevant for damaging of any of the materials investigated here.
For 316L, the pitting rate was investigated for different radii at fixed stand-off distance and for different stand-off distances at fixed radius. The results show that the average number of pits caused by a collapsing bubble is strongly dependent on both parameters. The pitting rate increases linearly with the bubble size in the studied interval from 0.75 to 1.5 mm radius. While our experiment cannot reproducibly create smaller bubbles, linear extrapolation implies a limiting radius of 0.4 mm below which at γ = 1.4 316L is not damaged by pitting. The dependence of pitting rate on stand-off distance is more complex. Pits occurred at all stand-off distances up to γ = 2.15, and there is a global maximum in the pitting rate at the smallest stand-off distances investigated here, γ = 0.25, and a local one at γ = 1.4. This shape of this curve of pitting rate vs. stand-off distance was the same for 316L and NAB, closely resembles that for other damage metrics vs. γ on aluminum [20], and is consistent with the damage on the oxide layer of aluminum recently deduced from transient electric current measurements [47].
In experiments with large numbers of bubbles, effect of the summation of pits was found to be similar for 316L and NAB, and the damage progressed in the same way for stand-off distances other than the previously investigated γ = 1.4. Although different materials experience different pitting rates [38], the pits vary more in size in softer materials, and the process leading to material loss due to pitting can be different [37, 39], all indications are that the fluid dynamic mechanisms responsible for pit creation are the same. Therefore, if single cavitation bubbles cause pitting, a sufficient number of bubbles will eventually cause material loss as described in [39] for the tested materials.
A somewhat consistent picture of single-bubble damage on flat metal surfaces emerges:
-
The first optically detectable change of the solid surface due to collapsing single cavitation bubbles is pits that are much smaller than the bubble diameter [20, 22, 37, 38].
-
Already the very first bubble can cause pitting, even on technical alloys [37, 38].
-
But not every bubble causes pits, even on soft aluminum [37, 38].
-
The spatial patterns in which pits occur are the same for technical alloys as for soft materials and are mainly dependent on the stand-off distance [20, 38].
-
The central liquid jet that is associated with the first collapse does not play a significant role in causing damage [20, 35].
-
For stand-off distances greater than 0.4, pits are primarily associated with “stronger” parts of the second collapse. These are regions where the bubble locally collapses last, consistent with “subsonic energy focusing” [35].
-
Shock waves are emitted from these regions into the fluid. It seems reasonable that shock waves also are emitted into the solid and are at least partly responsible for the pits [20, 35].
-
For stand-off distances less than 0.4, pits are more closely related to the stronger parts of the first—not the second collapse [35, 47].
-
The pitting rate—an indicator of early damage progression—decreases with decreasing bubble radius.
-
Linear extrapolation indicates that a non-zero minimum bubble diameter is required to cause any pits.
-
The pitting rate varies non-monotonically with γ, peaking at γ = 1.4 and for γ < 0.4. This trend is consistent across materials and with other damage metrics [20].
-
Over many single bubbles the accumulation of pits triggers material-specific damage mechanisms that finally lead to erosion [39].
Data Availability
The data supporting the findings reported in this paper are camera images, both snapshots and image sequences. Some of the image sequences („movies“) are already contained in the Supplementary Data of this article. They are available from the authors upon request—please contact jonas.kuehlmann@uni-due.de.
References
Luo, X., Ji, B., Tsujimoto, Y.: A review of cavitation in hydraulic machinery. J. Hydrodyn. 28, 335–358 (2016). https://doi.org/10.1016/S1001-6058(16)60638-8
Hutli, E., Nedeljkovic, M.S., Radovic, N.A., Bonyár, A.: The relation between the high speed submerged cavitating jet behaviour and the cavitation erosion process. Int. J. Multiph. Flow 83, 27–38 (2016). https://doi.org/10.1016/j.ijmultiphaseflow.2016.03.005
Kuiper, G.: Cavitation research and ship propeller design. Flow Turbul. Combust. 58, 33–50 (1997). https://doi.org/10.1023/A:1000754928962
Dular, M., Stoffel, B., Širok, B.: Development of a cavitation erosion model. Wear 261, 642–655 (2006). https://doi.org/10.1016/j.wear.2006.01.020
Kim, K.-H., Chahine, G., Franc, J.-P., Karimi, A.: Advanced Experimental and Numerical Techniques for Cavitation Erosion Prediction. Springer, Dordrecht (2014)
Ramamurthy, A.S., Bhaskaran, P.: Velocity exponent for erosion and noise due to cavitation. J. Fluids Eng. 101, 69–75 (1979). https://doi.org/10.1115/1.3448737
Kumar, P., Saini, R.P.: Study of cavitation in hydro turbines—a review. Renew. Sustain. Energy Rev. 14, 374–383 (2010). https://doi.org/10.1016/j.rser.2009.07.024
Ohl, C.-D., Arora, M., Dijkink, R., Janve, V., Lohse, D.: Surface cleaning from laser-induced cavitation bubbles. Appl. Phys. Lett. 89, 74102 (2006). https://doi.org/10.1063/1.2337506
Barcikowski, S., Plech, A., Suslick, K.S., Vogel, A.: Materials synthesis in a bubble. MRS Bull. 44, 382–391 (2019). https://doi.org/10.1557/mrs.2019.107
Brennen, C.E.: Cavitation in medicine. Interface Focus 5, 20150022 (2015). https://doi.org/10.1098/rsfs.2015.0022
Xiang, G., Chen, J., Ho, D., Sankin, G., Zhao, X., Liu, Y., Wang, K., Dolbow, J., Yao, J., Zhong, P.: Shock waves generated by toroidal bubble collapse are imperative for kidney stone dusting during Holmium:YAG laser lithotripsy. Ultrason. Sonochem. 101, 106649 (2023). https://doi.org/10.1016/j.ultsonch.2023.106649
Lauterborn, W.: High-speed photography of laser-induced breakdown in liquids. Appl. Phys. Lett. 21, 27–29 (1972). https://doi.org/10.1063/1.1654204
Obreschkow, D., Tinguely, M., Dorsaz, N., Kobel, P., de Bosset, A., Farhat, M.: The quest for the most spherical bubble: experimental setup and data overview. Exp. Fluids (2013). https://doi.org/10.1007/s00348-013-1503-9
Gonzalez-Avila, S.R., Klaseboer, E., Khoo, B.C.O., Ohl, C.-D.: Cavitation bubble dynamics in a liquid gap of variable height. J. Fluid Mech. 682, 241–260 (2011). https://doi.org/10.1017/jfm.2011.212
Reuter, F., Gonzalez-Avila, S.R., Mettin, R., Ohl, C.-D.: Flow fields and vortex dynamics of bubbles collapsing near a solid boundary. Phys. Rev. Fluids (2017). https://doi.org/10.1103/PhysRevFluids.2.064202
Brujan, E.A., Keen, G.S., Vogel, A., Blake, J.R.: The final stage of the collapse of a cavitation bubble close to a rigid boundary. Phys. Fluids 14, 85–92 (2002). https://doi.org/10.1063/1.1421102
Blake, J.R., Leppinen, D.M., Wang, Q.: Cavitation and bubble dynamics: the Kelvin impulse and its applications. Interface Focus 5, 20150017 (2015). https://doi.org/10.1098/rsfs.2015.0017
Vogel, A., Lauterborn, W., Timm, R.: Optical and acoustic investigations of the dynamics of laser-produced cavitation bubbles near a solid boundary. J. Fluid Mech. 206, 299–338 (1989). https://doi.org/10.1017/S0022112089002314
Lauterborn, W., Ohl, C.-D.: Cavitation bubble dynamics. Ultrason. Sonochem. 4, 65–75 (1997). https://doi.org/10.1016/S1350-4177(97)00009-6
Philipp, A., Lauterborn, W.: Cavitation erosion by single laser-produced bubbles. J. Fluid Mech. 361, 75–116 (1998). https://doi.org/10.1017/S0022112098008738
Dular, M., Požar, T., Zevnik, J., Petkovšek, R.: High speed observation of damage created by a collapse of a single cavitation bubble. Wear 418–419, 13–23 (2019). https://doi.org/10.1016/j.wear.2018.11.004
Isselin, J.-C., Alloncle, A.-P., Autric, M.: On laser induced single bubble near a solid boundary: contribution to the understanding of erosion phenomena. J. Appl. Phys. 84, 5766–5771 (1998). https://doi.org/10.1063/1.368841
Sagar, H.J., Hanke, S., Underberg, M., Feng, C., El Moctar, O., Kaiser, S.A.: Experimental and numerical investigation of damage on an aluminum surface by single-bubble cavitation. Mater. Perform. Charact. 7, 20180038 (2018). https://doi.org/10.1520/MPC20180038
Supponen, O., Obreschkow, D., Kobel, P., Tinguely, M., Dorsaz, N., Farhat, M.: Shock waves from nonspherical cavitation bubbles. Phys. Rev. Fluids (2017). https://doi.org/10.1103/physRevFluids.2.093601
Koch, M., Rosselló, J.M., Lechner, C., Lauterborn, W., Eisener, J., Mettin, R.: Theory-assisted optical ray tracing to extract cavitation-bubble shapes from experiment. Exp. Fluids (2021). https://doi.org/10.1007/s00348-020-03075-6
Reuter, F., Ohl, C.-D.: Supersonic needle-jet generation with single cavitation bubbles. Appl. Phys. Lett. 118, 134103 (2021). https://doi.org/10.1063/5.0045705
Tomita, Y., Shima, A.: Mechanisms of impulsive pressure generation and damage pit formation by bubble collapse. J. Fluid Mech. 169, 535 (1986). https://doi.org/10.1017/S0022112086000745
G02 Committee: Test Method for Cavitation Erosion Using Vibratory Apparatus. ASTM International, West Conshohocken (2021)
Priyadarshi, A., Krzemień, W., Salloum-Abou-Jaoude, G., Broughton, J., Pericleous, K., Eskin, D., Tzanakis, I.: Effect of water temperature and induced acoustic pressure on cavitation erosion behaviour of aluminium alloys. Tribol. Int. 189, 108994 (2023). https://doi.org/10.1016/j.triboint.2023.108994
Kozmus, G., Zevnik, J., Hočevar, M., Dular, M., Petkovšek, M.: Characterization of cavitation under ultrasonic horn tip—proposition of an acoustic cavitation parameter. Ultrason. Sonochem. 89, 106159 (2022). https://doi.org/10.1016/j.ultsonch.2022.106159
Abbasi, A.A., Viviani, M., Bertetta, D., Delucchi, M., Ricotti, R., Tani, G.: Experimental analysis of cavitation erosion on blade root of controllable pitch propeller. In: Rizzuto, E., Ruggiero, V. (eds.) Technology and Science for the Ships of the Future. IOS Press, Amsterdam (2022)
Khavari, M., Priyadarshi, A., Morton, J., Porfyrakis, K., Pericleous, K., Eskin, D., Tzanakis, I.: Cavitation-induced shock wave behaviour in different liquids. Ultrason. Sonochem. 94, 106328 (2023). https://doi.org/10.1016/j.ultsonch.2023.106328
Yusuf, L., Symes, M.D., Prentice, P.: Characterising the cavitation activity generated by an ultrasonic horn at varying tip-vibration amplitudes. Ultrason. Sonochem. 70, 105273 (2021). https://doi.org/10.1016/j.ultsonch.2020.105273
Hanke, S., Kaiser, S.A.: Comparison of damage mechanisms: acoustic cavitation versus series of single laser-induced bubbles. Wear 476, 203641 (2021). https://doi.org/10.1016/j.wear.2021.203641
Reuter, F., Deiter, C., Ohl, C.-D.: Cavitation erosion by shockwave self-focusing of a single bubble. Ultrason. Sonochem. 90, 106131 (2022). https://doi.org/10.1016/j.ultsonch.2022.106131
Gonzalez-Parra, J.C., Robles, V., Devia-Cruz, L.F., Rodriguez-Beltran, R.I., Cuando-Espitia, N., Camacho-Lopez, S., Aguilar, G.: Mitigation of cavitation erosion using laser-induced periodic surface structures. Surf. Interfaces 29, 101692 (2022). https://doi.org/10.1016/j.surfin.2021.101692
Kühlmann, J., Lopez de Arcaute y Lozano, C., Hanke, S., Kaiser, S.A.: Correlation of laser-induced single bubbles with cavitation damage via in situ imaging. Wear 522, 204723 (2023). https://doi.org/10.1016/j.wear.2023.204723
Kühlmann, J., Lopez de Arcaute y Lozano, C., Hanke, S., Kaiser, S.A.: In situ investigation of the onset of cavitation damage from single bubbles on technical alloys. Tribol. Lett. 70, 122 (2022). https://doi.org/10.1007/s11249-022-01665-5
Lopez de Arcaute y Lozano, C., Kühlmann, J., Kaiser, S.A., Hanke, S.: Observing early cavitation damage evolution from repeated laser-induced single bubbles on aluminium, austenitic steel and nickel–aluminium bronze. Wear 523, 204862 (2023). https://doi.org/10.1016/j.wear.2023.204862
Kida, H., Matsumoto, K., Ogasawara, T., Takahira, H.: Correlation between simultaneous images of bubble collapse in two directions and the impulsive pressure distribution near a wall. Jpn. J. Multiph. Flow 37, 38–45 (2023). https://doi.org/10.3811/jjmf.2023.003
Akhatov, I., Lindau, O., Topolnikov, A., Mettin, R., Vakhitova, N., Lauterborn, W.: Collapse and rebound of a laser-induced cavitation bubble. Phys. Fluids 13, 2805–2819 (2001). https://doi.org/10.1063/1.1401810
Noack, J., Vogel, A.: Laser-induced plasma formation in water at nanosecond to femtosecond time scales: calculation of thresholds, absorption coefficients, and energy density. IEEE J. Quantum Electron. 35, 1156–1167 (1999). https://doi.org/10.1109/3.777215
Sinibaldi, G., Occhicone, A., Alves Pereira, F., Caprini, D., Marino, L., Michelotti, F., Casciola, C.M.: Laser induced cavitation: plasma generation and breakdown shockwave. Phys. Fluids 31, 103302 (2019). https://doi.org/10.1063/1.5119794
Vogel, A., Busch, S., Parlitz, U.: Shock wave emission and cavitation bubble generation by picosecond and nanosecond optical breakdown in water. J. Acoust. Soc. Am. 100, 148–165 (1996). https://doi.org/10.1121/1.415878
Reuter, F., Kaiser, S.A.: High-speed film-thickness measurements between a collapsing cavitation bubble and a solid surface with total internal reflection shadowmetry. Phys. Fluids 31, 97108 (2019). https://doi.org/10.1063/1.5095148
Franc, J.-P.: Incubation time and cavitation erosion rate of work-hardening materials. J. Fluids Eng. 131, 021303 (2009). https://doi.org/10.1115/1.3063646
Abedini, M., Hanke, S., Reuter, F.: In situ measurement of cavitation damage from single bubble collapse using high-speed chronoamperometry. Ultrason. Sonochem. 92, 106272 (2023). https://doi.org/10.1016/j.ultsonch.2022.106272
Acknowledgements
The authors thank Christina Lopez de Arcaute y Lozano for material preparation and confocal imaging. The authors would also like to thank their collaborators Stefanie Hanke and Christina Lopez de Arcaute y Lozano for many valuable discussions.
Funding
Open Access funding enabled and organized by Projekt DEAL. This research was funded by the German Research Foundation (DFG) under Grant Number 451715773.
Author information
Authors and Affiliations
Contributions
Both authors contributed to the study conception and design. Jonas Kühlmann built the experimental apparatus, performed the experiments, and evaluated the data. Sebastian A. Kaiser reviewed the experiment and the data processing. The first draft of the manuscript was written by JonasKühlmann and both authors commented on various versions of the manuscript. Both authors read and approved the final manuscript
Corresponding author
Ethics declarations
Conflict of interest
The authors have no relevant financial or non-financial interests to disclose.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Supplementary file1 (AVI 4099 KB)
Supplementary file2 (AVI 4660 KB)
Appendix
Appendix
1.1 Bubble Dynamics in Top View
Figure 14 shows additional images of the bubble collapses in Figs. 4 and 5 in top view. The visual appearance is consistent with other works [20]. The depth of field is very shallow, and therefore, only the surface and the bubble dynamics very close to it are in focus. The bright-dark rings in the upper-right corner of Fig. 14 (γ = 1.35) and the lower-right corner of upper-right corner Fig. 14 (γ = 1.6) are caused by ripples in the water/air interface. They are far away from the bubble and do not affect it.
1.2 Bubble Dynamics, SCAs, and Pit Locations on NAB
Figure 15 shows images of bubble collapses at different stand-off distances. Each of the bubbles shown here caused at least one pit. The dynamics are consistent with other work [19, 20, 27]. A discussion of the dynamics can be found in [20].
Figure 16 shows the second collapse of the bubbles shown in Fig. 17. Pit locations are marked with a red x. Again, the pit location could be linked to SCAs at all stand-off distances.
Second collapse of two bubbles with short illumination. a The same bubble as in Fig. 7. b A bubble that did not cause a pit. The edge of the gas phase is marked in blue for the bubble and red for the reflection (Color figure online)
1.3 Bubble Detachment
Figure 17 shows two bubbles at the second collapse. The first bubble is the same shown in Fig. 7 and the second is a bubble from the same bubble sequence that did not cause a pit. The edges of the gas phase are marked in color to aid distinguishing the bubble shape from its reflection on the surface. While the bubble in Fig. 17a is only partially detached from the solid surface, detachment appears almost over the complete torus of the bubble in Fig. 17b.
1.4 Repetition-Rate Dependence of the Pitting Rate
Figure 18a shows the pit count at four different bubble repetition rates. After 50 bubbles, there are 25 or 26 pits at all repetition rates. Figure 18b shows the pitting rate calculated from Fig. 18a. The errors bars represent the uncertainty of the linear fit. All four measurements are quite close. At the highest repetition rate of 5 Hz, the rate slightly decreases. However, the average bubble radius was also slightly lower for this measurement. This may be due to the fact that more dissolved gas bubbles refract part of the laser beam which can result in smaller bubbles. We conclude that within the range relevant for our experiment, the repetition rate has no significant effect on the pitting rate.
a Pit count for 50 bubbles at different frequencies, b repetition rates dependence of the pitting rate, and c, d liquid in the region where the bubble is induced just before the plasma breakdown at a bubble repetition rate of 1 Hz and 3 Hz, respectively. Arrows mark two of many gas bubbles in the liquid
These measurements allow further conclusions regarding the influence of the experimental conditions on pit formation. Figure 18c, d show example images of the sample in water a few microseconds before the plasma breakdown at a repetition rate of 1 Hz and at 3 Hz. In the latter case, more dissolved gas bubbles are seen in the bulk liquid and also directly on the surface (white arrows) than in the former case. However, the pitting rate is the same. Thus, more dissolved gas bubbles, which is the main effect of higher frequencies, do not seem to have a significant effect on pitting.
Two aspects can be inferred from the dissolved gas bubbles in the fluid and the lack of change in pitting rate over the repetition-rate variation. First, these bubbles did not move in the high-speed sequences, indicating that there is no significant flow left in the fluid from the previous bubble. Second, pitting in connection with bubbles on the surface excited by a shock wave—as described in our previous work [37]—is not a dominant mechanism in our experiment.
1.5 Aluminum Example
Figure 19 shows the damage to an aluminum sample and the first and second collapse of a bubble at γ = 0.5. The first bubble caused a pit (red circle). After 50 bubbles, more pits can be observed in this region (A), but there are also surface changes that do not look like the previously described pits (B). This change looks more like a large-scale displacement of material that builds up over the whole area at once. The images of the first collapse (Fig. 19 110 µs, 120 µs) and the second collapse (Fig. 19 250 µs, 260 µs) show that the first collapse is not responsible for the pit. In the second collapse, however, there is a SCA that can be associated with the pit. In addition, it can be seen that the damaged region (B) lies on the first collapse (red semicircle). In contrast to the technical materials, there is a surface change here that is not in the form of pits and is caused by a wide area of the collapse.
Finally, Fig. 19 also shows a confocal microscope image of the damage after 100 individual bubbles. The material displacement can be seen very well. The center of the bubble collapse is marked with a black X. This is where the liquid jet hits the sample surface. It can be seen that despite the small stand-off distance, no surface change occurred in this area. This shows the limitations of aluminum as a model material in the sense that damage occurs here that cannot be transferred to technical alloys. Damage occurs that can be associated with the initial collapse and cannot be attributed to SCAs and pits. Corresponding damage due to many bubbles at these stand-off distances was not observed on either the 316L or the NAB.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kühlmann, J., Kaiser, S.A. Single-Bubble Cavitation-Induced Pitting on Technical Alloys. Tribol Lett 72, 55 (2024). https://doi.org/10.1007/s11249-024-01851-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11249-024-01851-7