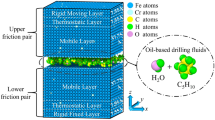
Abstract
Oil-based drilling fluids are usually assumed to provide lower friction compared to their water-based alternatives. However, clear evidence for this has only been presented for steel–rock and steel–steel contacts, which are representative of the interface between the drillstring and the borehole or casing. Another crucial interface that needs to be lubricated during drilling is that between the cutter (usually diamond) and the rock. Here, we present pin-on-disc tribometer experiments that show higher boundary friction for n-hexadecane-lubricated diamond–granite contacts than air- and water-lubricated contacts. Using nonequilibrium molecular dynamics simulations of a single-crystal diamond tip sliding on α-quartz, we show the same trend as in the experiments of increasing friction in the order: water < air < n-hexadecane. Analysis of the simulation results suggests that the friction differences between these systems are due to two factors: (i) the indentation depth of the diamond tip into the α-quartz substrate and (ii) the amount of interfacial bonding. The n-hexadecane system had the highest indentation depth, followed by air, and finally water. This suggests that n-hexadecane molecules reduce the hardness of α-quartz surfaces compared to water. The amount of interfacial bonding between the tip and the substrate is greatest for the n-hexadecane system, followed by air and water. This is because water molecules passivate terminate potential reactive sites for interfacial bonds on α-quartz by forming surface hydroxyl groups. The rate of interfacial bond formation increases exponentially with normal stress for all the systems. For each system, the mean friction force increases linearly with the mean number of interfacial bonds formed. Our results suggest that the expected tribological benefits of oil-based drilling fluids are not necessarily realised for cutter–rock interfaces. Further experimental studies should be conducted with fully formulated drilling fluids to assess their tribological performance on a range of rock types.
Graphical Abstract

Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Drilling fluids, or drilling muds, are crucial to the safety and efficiency of drilling operations, performing around 20 different functions [1]. These include facilitating the removal of cuttings from the borehole, cleaning and cooling the cutter while in operation, maintaining the stability of the wellbore, preventing the inflow of fluids from the wellbore, and helping to form an impermeable filter cake [1]. Drilling fluids should also be non-damaging to the producing formation and non-hazardous to the environment [1]. The fluids used to drill geothermal wells, which are typically hotter and often deeper than those for oil and gas, have additional requirements of high thermal stability and specific rheological properties [2]. The three main types of drilling fluid are water-based, oil-based, and gas-based [1]. Water-based drilling fluids are generally lower in cost and more environmentally friendly compared to their oil-based alternatives. Consequently, approximately 80% of wells are drilled using water-based fluids [3]. The base oils used in oil-based drilling fluids generally have lower molecular weight and viscosity than those in engine oils and are closer to diesel fuels. As with engine oils, mineral-based fluids are being progressively replaced by synthetics, such as poly(α-olefins), which have improved performance in a range of areas, including a lower environmental impact [4]. Biodiesel-based fluids have also been studied to supplement or even replace oil-based fluids [5]. Modern drilling fluids are complex, multi-component formulations, with the base fluid containing several types of additives including salts, surfactants, polymers, and nanoparticles [3, 6]. These are added to tailor various important properties such as viscosity, density, thermal conductivity, permeability, and friction [3].
The key tribological function of the drilling fluid is to minimise friction at the metal drillstring–rock borehole (or metal casing) interface, as well as the diamond cutter–rock interface. One of the main benefits of oil-based drilling fluids are that they give lower friction, leading to decreased torque and drag on the drillstring [7], and thus increased drilling efficiency. In a recent review, it was stated that for oil-based drilling fluids, the friction coefficient (ratio of the shear stress to the normal stress), µ < 0.1, while for water-based drilling fluids µ ≈ 0.2 [8]. This implies that using oil-based fluids rather than water-based ones leads to much higher drilling efficiency and thus lower energy consumption. In general, oils are better lubricants than water-based fluids, which is mainly due to the fact that the viscosity of water does not rise considerably with pressure [9]. This property is essential to the elastohydrodynamic lubrication (EHL) [10] mechanism by which oils form lubricating fluid films in high-pressure, non-conformal contacts of hard materials, such as those in gears and bearings [9]. In tribometer experiments with steel-rock contacts, which are representative of the drillstring–borehole interface, significantly lower friction is usually reported for oil-based fluids than water-based ones [11, 12]. This suggests a conventional EHL mechanism for this interface. Lower friction has also been observed for oil-based drilling fluids than water-based ones in rock–rock contacts [13]. However, for diamond–rock contacts, which are representative of the polycrystalline diamond compact (PDC) [14] cutter–rock interface, similar or higher friction has been noted for oil-based compared to water-based drilling fluids [15,16,17]. For diamond–impregnated bits on quartzite rocks, the addition of organic compounds to water to improve cutting performance unexpectedly increased the friction coefficient at the bit–rock interface [18]. Moreover, for certain minerals, such as magnesium oxide, much higher friction coefficients have been noted for microscratching experiments using diamond tips in n-hexadecane oil (µ = 0.41–0.65) than in water (µ = 0.12–0.19) [19]. This observation was attributed to the promotion of near-surface dislocation mobility by magnesium oxide in n-hexadecane compared to water [20]. On the other hand, for many other interfaces, such as zirconia–zirconia [21], silicon nitride–silicon nitride [22], and silicon–silicon [23], using n-hexadecane as a lubricant results in significantly lower friction than water. Similar comparisons for a range of ceramic–ceramic, ceramic–steel, and steel-steel contacts also showed that mineral oil was a better lubricant than water. [24]
Rehbinder [25] showed that adding surfactants to water-based drilling fluids could markedly increase the drilling speed of hard rocks. Rehbinder suggested that this observation was due to an adsorption-induced reduction in the rock surface energy [26]. Subsequently, Mills and Westwood [27] proposed an alternative explanation that surfactants increase the rock hardness, thus reducing the ploughing contribution to friction. Controversy persists in this area due to the plethora of competing physicochemical processes that affect drilling performance. As in many areas of tribology, it is still a considerable challenge to study the sliding buried interface with in situ experimental techniques. [28]
One method that has provided a number of important insights into the behaviour inside tribological contacts is nonequilibrium molecular dynamics (NEMD) simulations [29]. Through a combination of NEMD simulations and macroscale tribometer experiments, we have recently shown that interfacial bonding can directly impact the friction [30] and wear [31] of diamond–rock contacts. In this current study, we use the same combination of experiments and simulations to compare the kinetic friction of diamond pins on granite substrates lubricated by air, water, and n-hexadecane. Our aim is to uncover the fundamental tribological differences between additive-free oil-based and water-based drilling fluids. As in recent NEMD studies of steel–steel lubricated by an oil-based drilling fluid (cyclopentane/water mixtures) [32, 33] and diamond–rock interfaces lubricated by water [30, 31], we employ the reactive force field (ReaxFF) method [34] to study the effects of interfacial bonding on friction.
2 Methodology
2.1 Experimental Procedure
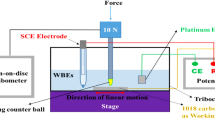
For the friction measurements, we used a RTEC MFT-5000 (San Jose, California, U.S.A.) pin-on-disc rotary tribometer. A previous study [35] showed that the friction coefficients obtained in these experiments can be directly related to rate of penetration in industry-standard tests, such as the ultradeep single-cutter drilling simulator [36] or vertical turret lathe [14]. The type of sliding contact studied in these tribometer experiments is experienced by worn or shaped cutting elements. The cutting action (indentation depth) is low in these elements, so interfacial friction dominates the overall energy losses at the bit-rock interface [30]. The experimental velocities and loads were selected to ensure a sliding-dominated friction response, where the friction forces were mainly due to interfacial interactions, rather than ploughing. After the friction measurements, the diamond pins were examined using optical microscopy following the tests, which confirmed that negligible wear occurred.
We selected Sierra white granite cores as the rock sample. The cores were ground to the same smooth surface finish (Rq ≈ 12.0 μm) prior to conducting the tribometer experiments [37]. We used smooth (Rq = 3.7 μm), hemispherical polycrystalline diamond pins with a radius of 5 mm, which provide idealised point contacts. The root-mean-square surface roughness of the test specimens was measured using white light interferometry [38, 39]. Separate tests were conducted with the contact lubricated by air, water, and n-hexadecane. There was an average relative humidity, RH = 70% during the tribometer experiments. The friction tests were run at 60 revolutions per minute (rpm) with a radial distance of 20 mm. This gave a sliding velocity of 0.125 m s−1, which is somewhat lower than that used in operational PDC cutters (2–4 m s−1) [40]. The experiment is conducted at lower sliding velocity than operational PDCs to prevent uncontrollable frictional heating. Additional tests were performed at radial distances of 15 mm and 25 mm, leading to sliding velocities of 0.125 m s−1 and 0.150 m s−1, respectively. There was a negligible change in the friction over this velocity range. Prior to collecting the friction data, the rock samples were run in [41] for 5 min at 100 rpm with a low load of 10 N applied while the radial position was varied sinusoidally from 10 to 30 mm to establish a consistent smooth surface that was free from contaminants. Neither the diamond pins nor granite substrates underwent any detectable wear during the running-in phase, but it improved the repeatability of the subsequent friction measurements. During the friction tests, the load was progressively increased from 10 to 100 N at 10 N intervals and held at each load for 3 min while the friction data were gathered. The maximum Hertz pressure [42, 43], Pmax, ranged between 0.8 to 1.8 GPa for the loads considered. The presence of micrometre-level roughness on the rock and diamond surfaces will have resulted in peak asperity pressures that were somewhat higher than predicted by the Hertz equation. However, the nondimensional parameters calculated for these systems (α = 0.01–0.03) indicate that Hertz theory should provide a reasonable estimate of the contact pressures (within 5%). [44]
2.2 Simulation Procedure
Rocks are heterogeneous mixtures of various minerals, which lead to location-dependent surface chemistry [45]. Even though ReaxFF-based NEMD simulations are several orders of magnitude less computationally expensive than first-principles techniques [46], they are still limited to the study of nanoscale-sized systems [29]. Therefore, α-quartz, the most prominent mineral in granite [47] is used as a simplified model. The atomically smooth α-quartz{0001} surface is chosen because previous density functional theory (DFT) studies have shown it to be the most thermodynamically stable face [48]. The dimensions of the substrate were x = 13.7 nm, y = 5.8 nm, and z = 3.7 nm.
Experiments by Pashley and Kitchener [49] showed that quartz is hygroscopic. Therefore, the surface of quartz becomes covered by a monolayer of water when it is exposed to air. In the NEMD simulations of the air system, 100 water molecules were added on top of the quartz substrate. This choice is consistent with previous experiments, which showed that the thickness of water films on dehydroxylated quartz is equivalent to approximately one monolayer at the ambient humidity used in the tribometer experiments (RH = 70%) [50]. For the water-lubricated system, 500 water molecules are added to ensure full immersion of the contact interface, which is consistent with the corresponding experiments. For the n-hexadecane system, because the tribometer experiments are not conducted in an inert atmosphere, the same number of water molecules (100) is maintained from the air systems. Previous estimates have suggested that the concentration of water in n-hexadecane is similar to that in air [51, 52]. In total, 25 n-hexadecane molecules were added to ensure that the total number of heavy atoms (C and O) was the same in both the n-hexadecane and water systems. Given that the n-hexadecane molecules are expected to lie flat on the α-quartz surface [53], this is sufficient to form a complete monolayer (coverage ≈ 0.3 nm−2), as is expected from previous ellipsometry experiments [54]. Fig. 1 shows each of the systems after energy minimisation and equilibration, before compression and sliding.
NEMD simulation setups for diamond–quartz contacts in air a, water b, and n-hexadecane c systems shown after energy minimisation and equilibration, before compression and sliding. Silicon atoms are shown in red, oxygen in blue, carbon in grey, and hydrogen in green. Rendered using OVITO [57] (Color figure online)
The pin was modelled as a hemispherical single-crystal diamond tip with a radius of 2.5 nm. [55] The tip radius is several orders of magnitude smaller than the experiments (5 mm), resulting in a significantly reduced contact area, Ac. Therefore, the load is reduced to approximately match the mean Hertzian pressure for point contacts. A previous study showed that the shear stress (τ = FF/Ac) at diamond–quartz interfaces is independent of both the tip radius and the tip geometry. [56]
Figure 1 shows that in the air system (a), water forms a monolayer on the α-quartz surface. For the water system (b), multilayers form, which completely immerse the contact interface. In the n-hexadecane system, water also forms a monolayer on the quartz surface because the polar molecules have a stronger affinity to the surface than the non-polar alkane molecules [58]. The n-hexadecane molecules adsorb mostly on the non-polar diamond tip to maximise the van der Waals interactions. [59]
2.3 Simulation Details
We carried out NEMD simulations using the open-source large atomic/molecular massively parallel simulator (LAMMPS) software package [60]. We employed the velocity-Verlet integration algorithm [61] with a time step of 0.25 fs. Periodic boundary conditions were applied in the x- and y-directions, while a reflective boundary was added at the top of the simulation cell in the z-direction to prevent desorbed species from escaping. The lowermost layer of atoms in the substrate (2 Å) remained frozen in the z-direction throughout the simulations. The temperature was maintained at 300 K using a Langevin thermostat with a coupling time of 25 fs. [62] The thermostat was only applied to the central layers of atoms in the z-direction of the tip and substrate (4 Å), as shown in Fig. 1. The lowermost layer of atoms in the tip and the topmost atoms in the substrate are not fixed or thermostatted.
The energy of the systems was minimised, followed by a short equilibration simulation at 300 K for 0.1 ns. During the equilibration, a constant normal force (Fn = 1 nN) in the z-direction was added to the topmost layer of atoms in the tip (2 Å) to bring it into contact with the substrate. The normal force was then increased to the target value (Fn = 5–40 nN) and, at the same time, a sliding velocity (vs = 10 m s−1) was added in the x-direction to the topmost layer of atoms in the tip. This range of applied normal forces resulted in maximum Hertz pressures from Pmax = 1.85–2.85 GPa. Our previous investigation of diamond–quartz contacts [30] showed that there was a negligible change in the friction force between 1 and 10 m s−1. The sliding NEMD simulations were performed for 1.5 ns, which was sufficient for the friction force and number of interfacial bonds to reach a steady state. The indentation depth is measured by the change in the position of bottommost atom in the tip in the z-direction when it first comes into contact with the substrate during equilibration and at the end of the compression and sliding simulation.
2.4 ReaxFF Parameters
ReaxFF is a bond order-based force field, originally developed by van Duin et al. [34] to investigate the reactivity of hydrocarbons. The version of ReaxFF implemented in LAMMPS uses the functional form that was outlined by Chenoweth et al. [63] and fully described by Aktulga et al. [64]. The point charges on the atoms are calculated using the charge equilibration (Qeq) method [64,65,66], and they change dynamically during the NEMD simulations.
We selected the Si/O/H/C ReaxFF parameters that were developed by Newsome et al. [67] to study the oxidation of silicon carbide by oxygen and water. This force field combined ReaxFF parameters developed previously to investigate the oxidation of hydrocarbons [63] and silicon [68, 69]. Data from previous first-principles calculations for Si/C, Si/O, Si/Si, and Si/H were also included for silicon [70], silicon oxide [68], and poly(dimethylsiloxide) [71]. Newsome et al. [67] performed new DFT calculations to obtain the equation of state and heat of formation of silicon carbide and previous DFT data by Wang et al. [72] for the binding energy of oxygen at various locations on the silicon carbide surface were also included. Using this combined training set, Newsome et al. [67] calculated Si–C bond lengths and Si–C–O and C–Si–O bond angle parameters. The resulting force field is not only applicable to silicon carbide materials, but also to silicon oxides, diamond, and graphite [73]. The Newsome et al. [67] force field has been recently employed by Bhati et al. [74] to identify the adhesion properties of Si/polymer interfaces, Hilbert et al. [75] to investigate how Si doping enhances thermal stability of diamond-like carbon, Vashisth et al. [76] who combined atomistic and continuum methods to study how temperature influences interfacial fracture in SiC/SiO2 composites, as well as several other groups. We have also recently applied the Newsome et al. [67] ReaxFF parameters to study the friction [30] and wear [31] of diamond–quartz interfaces.
The chemical bonding information was output every 1.0 ps, using a bond order cutoff of 0.3 to identify covalent bonds [63]. The choice of bond order cutoff only affects the post-processing analysis and does not influence the ReaxFF energy or force calculations [64].
3 Results and Discussion
3.1 Tribometer Experiments
First, we measured the change in the friction force, FF, with the normal force, FN, in macroscale tribometer experiments (Fig. 2) with diamond–granite contacts lubricated by air (purple), water (green), and n-hexadecane (red). For all three systems, FF increases linearly with FN with a negligible intercept. This is consistent with Amontons’ friction equation, which states that the friction coefficient, μ = FF/FN. The near-zero intercept implies that there is minimal adhesion between the diamond pin and the granite substrate. Since the real contact area increases linearly with FN between randomly rough surfaces [43], this linear dependence of FF on FN expected in most macroscale contacts. The linear fits in Fig. 2 give μ = 0.15, μ = 0.15, and μ = 0.36 for the air-, water-, and n-hexadecane-lubricated contacts, respectively. Thus, n-hexadecane significantly increases interfacial friction compared to water and air. Similar friction behaviour was also observed at sliding velocities, vs, ranging from 0.125 m s−1 to 0.150 m s−1, as shown in the Supporting Information (Figure S1 and Figure S2). Unlike other rocks, such as limestone [30], minimal granite residue was found to have adhered to the diamond tip following the tribometer experiments.
Change in the friction force, FF, with normal force, FN, from macroscale tribometer experiments with air (purple), water- (green), and hexadecane-lubricated (red) diamond-granite contacts. Normal forces, FN, are between 10 and 100 N and tangential velocity, v = 0.125 m s-1. Dashed lines are linear fits to Amontons’ friction equation. Shaded regions represent 95% confidence intervals (Color figure online)
Previous experiments of diamond-rock contacts have shown similar friction coefficients for formulated oil-based drilling fluids and water-based drilling fluids [15, 16]. However, at an equivalent normal stress, Smith et al. [16] noted that the friction coefficient for a single PDC cutter on shale rock was consistently higher in oil than in water. This agreed with a previous study by Hibbs and Sogoian [17], who consistently noted higher friction in PDC-rock contacts lubricated by diesel oil than water. The largest difference they observed was at high velocity (5 m s−1) for sandstone (mostly quartz), where µ = 0.05 when water was used as a lubricant, but µ = 0.30 when diesel oil was used. These observations challenge the common perception that oil lubricates the interface between the drill bit and rock more effectively than water [16]. Despite this, a recent review on the topic have suggested that oil-based drilling fluids give superior tribological performance [8]. While this may be the case when lubricating steel–steel and steel–rock contacts [11, 12], which are representative of the drillstring–rock/casing interface, the results presented by Smith et al. [16], Hibbs and Sogoian [17], and those shown in Fig. 2 suggests that oil-based drilling fluids give inferior performance than water-based drilling fluids at the cutter–rock interface.
One aspect that has not been considered in the current study is the effects of the various additives present in oil-based and water-based drilling fluids [1]. Many of these additives are surface active, and thus, they may affect the relative tribological performance, even if they are not added to explicitly added to reduce friction. The potential effects of surfactants on rock friction have been discussed by Rehbinder [25] and Mills and Westwood [27]. Therefore, it is recommended that future work compares the friction coefficient of fully formulated (including surfactants) oil-based and water-based drilling fluids on a wide range of rock types to definitively establish which type of fluid gives the best tribological performance.
3.2 NEMD Simulations
To further investigate the unexpected results from the tribometer experiments, we performed NEMD simulations to compare the atomistic behaviour at the sliding diamond–quartz interfaces lubricated by oil and water.
Figure 3 shows the change in the friction force, FF, with sliding time in the NEMD simulations. The friction force initially increases (< 0.25 ns) before plateauing towards a steady-state value. There is some oscillatory behaviour, which is indicative of stick–slip. Previous NEMD simulations of silica–silica interfaces [77] and AFM experiments of diamond–silica contacts [78] also showed stick–slip behaviour. The NEMD simulations revealed that stick–slip was caused by collective rupture of interfacial bonds causing an instantaneous interface slip [77]. The n-hexadecane and air simulations display clearer stick–slip behaviour than the water system. Stick–slip also becomes more prominent at higher loads (> 30 nN). The friction forces presented from this point refer to steady-state averages over the last 0.5 ns of sliding.
Figure 4 shows that FF increases approximately linearly as a function of FN in all the NEMD simulations, which agrees with the experimental data (Fig. 2) and is consistent with Amontons’ Eq. [43, 79] For the idealised point contact used in our simulations, Hertz theory [42] predicts that FF ∝ FN2/3. [43] However, the linear relationship between FF and FN suggests that the interfacial shear strength behaves as a direct function of normal stress, which could be due to interfacial bonding across the contact [30]. Fig. 4 shows that the friction coefficient is highest for the n-hexadecane-lubricated system (μ = 0.33), followed by air (μ = 0.22), and finally water (μ = 0.08). This is the same order of the systems that was observed experimentally in Fig. 2. For the n-hexadecane-lubricated system, the friction coefficient values are similar in the experiments and NEMD simulations. In the experiments, the air and water friction coefficients are similar, whereas there is a clear difference in the NEMD simulations. This could be due to the simplified air model used in the NEMD simulations, whereby the quartz surfaces are coated by a monolayer of water based on previous experiments. [50] In the experiments, it is possible that thicker water layers are formed, leading to contact conditions and thus friction more similar to the water case. The friction coefficient values for water and n-hexadecane are also consistent with previous high-velocity (vs = 5 m s−1) experiments of PDC–sandstone (also mostly quartz) contacts by Hibbs and Sogoian in water (μ = 0.05) and diesel oil (μ = 0.30), respectively [17]. For the n-hexadecane-lubricated system, the finite intercept (~ 1 nN) indicates that there is some adhesion between the tip and substrate [43]. Previous experiments have shown that friction coefficients of granite–granite [80], quartzite–quartzite [80], silicon–silicon [81], and diamond–diamond [82] contacts are heavily dependent on the amount of water present. In general, with increasing levels of humidity, the friction coefficient decreases. First-principles NEMD simulations have shown that the addition of water molecules at the silica–silica [83] and silica–diamond [84] interfaces significantly reduces friction by preventing interfacial bond formation. For n-hexadecane-lubricated mica–diamond contacts in AFM experiments, Cafolla et al. [85] found that the formation of water nanodroplets can lead to significantly increased friction compared to pure n-hexadecane. Due to the relatively large size of the water nanodroplets (20–50 nm), this effect is not considered in the current NEMD simulations. The fact that higher friction is observed for water-containing n-hexadecane than pure water also suggests that this effect does not significantly affect our macroscale friction measurements.
Change in friction force, FF, with normal force, FN, from the NEMD simulations for the air (purple), water- (green), and hexadecane-lubricated (red) contacts. Steady-state forces averaged over the final 500 ps of sliding. Dashed lines are fits to Amontons’ friction equation. Shaded regions represent 95% confidence intervals (Color figure online)
In both the tribometer experiments and NEMD simulations, the indentation depth was minimised to ensure that friction was dominated by interfacial interactions, rather than ploughing of the substrate by the tip. Our previous NEMD simulations of diamond–quartz contacts [30] showed that at similar loads, indentation depths were always below 3 Å. This is also the case for the current simulations, as shown in the Supplementary Information (Figure S3). The low indentation depths are due to the relatively low loads applied (5–40 nN) and the high hardness of quartz (~ 15 GPa) [86]. Bowden and Tabor [87] presented a model to quantify the ploughing contribution to the friction coefficient based on simple geometrical considerations. Previously, we showed that the ploughing contribution to the friction coefficient of water-lubricated diamond–quartz contacts predicted with the Bowden-Tabor equation based on the measured indentation depth was much lower than the friction coefficient measured in the NEMD simulations [30]. Thus, there was a minimal ploughing contribution to the friction coefficient in these NEMD simulations [30]. Previous experiments by MacMillan et al. [19] showed that the friction of diamond–magnesium oxide contacts was higher in n-hexadecane than water, which they attributed to ‘softening’ of the surface. Since the hardness is correlated with the indentation depth [88], a reduced hardness implies a greater indentation depth for n-hexadecane than water. This is indeed observed in our NEMD simulations, as shown in the Supporting Information. (Figure S4). The water-lubricated system (0.5 Å) has a much lower indentation depth than the other two systems; however, the n-hexadecane system (2.0 Å) only has a slightly larger indentation depth than the air system (1.5 Å). Thus, the differences in hardness and indentation depth can go some way to explaining the friction observed for the three systems in the NEMD simulations; however, other factors must also contribute.
Based on observations from our previous NEMD simulations [30], another factor controlling the differences in friction between the systems could be the number of interfacial bonds, as shown in Fig. 5. Most of the interfacial bonds are direct C–O bonds between the tip and the substrate, while there are no direct C–Si bonds [30]. Since some of the interfacial bonds are broken during sliding, we also show the number of interfacial bonds formed and ruptured separately in the Supporting Information (Figure S5). The multibond friction model proposed by Filippov et al. [89] suggests that interfacial bonds continuously form and rupture during sliding, such that, as a particular interfacial bond ruptures, the force experienced by the other bonds increases, resulting in synchronised bond formation and rupture. This dynamic behaviour of continual formation and breakage of interfacial bonds results in oscillations in the friction force, which can be observed as stick–slip behaviour (Fig. 3). There are larger oscillations in the friction force with sliding time than for the total number of interfacial bonds (Fig. 5). This suggests that the formation and breakage of interfacial bonds occur simultaneously and are probably spatially localised at the leading and trailing edge of the tip, respectively [30].
Change in the total number of interfacial bonds between the tip and the surface during sliding for the air (purple), water- (green), and n-hexadecane-lubricated (red) contacts for different loads, FN = 5 nN to 40 nN. Black dashed lines are fits to the first 250 ps of interfacial bond formation data assuming first-order reactions used to calculate initial rates (Color figure online)
The steady-state number of interfacial bonds all three systems increases with increasing load, which contributes to higher friction forces than at lower loads. For all the simulated loads, the total number of interfacial bonds is greatest for the n-hexadecane system, followed by the air system, and finally the water system. This contributes to higher friction and increased stick–slip (Fig. 3) for n-hexadecane compared to air and particularly water. Li et al. [77] also showed using NEMD and ReaxFF that an increasing number of interfacial bonds in dry silica–silica contacts resulted in higher friction. The cause of the lower number of interfacial bonds and friction for the water system is likely more effective passivation of the diamond–quartz interface. Previous NEMD simulations with ReaxFF by Yeon et al. [90] showed that water passivates the sliding interface between hydroxylated amorphous silica and oxidised silicon interface. Potential bonding sites became terminated with hydroxyl groups and could no longer form interfacial bonds [90]. Further ReaxFF simulations by Wang et al. [91] found that an increase in hydroxyl group density reduced the friction between silica surfaces. De Barros Bouchet et al. [82] also reported from first-principles calculations that hydroxyl and hydride passivation of diamond from dissociative adsorption of water molecules kept the sliding surfaces further apart, which prevented interfacial bonding.
Figure 6 shows how the number of passivated surface sites on the tip and substrate changes as a function of sliding time. These sites are potential interfacial bonding sites, Si and O atoms in the substrate, which are passivated to become Si–OH/Si–H and O–H, and C atoms in the tip, which are passivated to become C–OH/C–H, by dissociation of the water molecules. For all systems and loads considered, the number of passivated sites reaches a steady state after approximately 500 ps. The steady-state number of passivated sites remains consistent across the loads studied. The number of passivated sites is highest for the water-lubricated system, followed by the n-hexadecane and finally the air system. Thus, the water system shows the highest number of passivated sites (Fig. 6), the least interfacial bonds (Fig. 5), and the lowest friction (Fig. 3). The n-hexadecane system shows more passivated sites than the air system, but fewer interfacial bonds, and lower friction, even though both of these systems contain the same number of water molecules (100). This apparent contradiction is because n-hexadecane molecules dissociate and passivate mostly C sites in the diamond tip, which does not seem to be as effective in reducing interfacial bonding compared to the passivation of Si and O atoms in the substrate through water dissociation. On the other hand, the presence of n-hexadecane molecules close to the surface hinders the ability of water to dissociate and passivate the α-quartz substrate. Water and n-hexadecane have previously been shown to compete for binding sites on silicate surfaces. [85]
Figure 7 shows how the rate of interfacial bonding changes with normal stress. The rate of interfacial bonding in all systems increases exponentially with normal stress, suggesting that this is a stress-augmented thermally activated (SATA) process [92]. The activation energy in SATA processes is reduced with the application of stress, leading the following modified Arrhenius equation:
where A is a prefactor, Ea is the activation energy, N is Avogadro’s number, \(\sigma\) is the applied normal stress, \(\Delta V^{\ddag }\) is the activation volume, R is the universal gas constant, and T is the temperature [92]. As in our previous study, we use the normal stress in Eq. 1, rather than the shear stress. [30]
Change in the rate of interfacial bonding with normal stress for air (purple), water- (green), and n-hexadecane-lubricated (red) contacts. Inset shows a linear increase in ln(rate) with normal stress. Dashed lines are fits to Equation 1 (Color figure online)
For single-asperity point contacts, Hertz theory predicts that the contact area, Ac, will increase with load as Ac ∝ FN2/3. However, NEMD simulations have shown that the real contact area, Areal ∝ FN. [43] Higher contact areas result in an increased number of tip and substrate atoms being sufficiently close to form interfacial bonds. The rates of interfacial bonding are calculated over the first 250 ps of sliding (dashed lines in Fig. 5), where the indentation depth (and thus contact area) is very similar for all the systems and conditions studied [30]. Thus, it is not necessary to normalise the rates shown in Fig. 7 by the contact area. There is minimal wear and adhesion of diamond the tip (Fig. 2), so we apply Hertzian contact mechanics to estimate the normal stress inside the contact in Fig. 7. In this case, the normal stress range is similar for the three systems. We also calculated the normal stress by dividing the normal force by the contact area calculated from the number of atoms in contact [93]. In this method, the contact area is calculated by multiplying the lattice constant for diamond with our ReaxFF parameterisation (0.362 nm) [94] by the number of atoms in contact, which are defined as those that form interfacial bonds. [93] More details can be found in our previous study [31]. This method results in significantly higher normal stresses than those calculated using Hertz theory, which is due to the smaller contact area [95]. The corresponding plot for Fig. 7 using the atoms in contact method rather than Hertz theory is shown in the Supporting Information (Figure S6). In this case, the normal stress is higher for the water systems than air and particularly n-hexadecane systems, due to the reduced interfacial bonding (Fig. 5).
From Fig. 7, the rate of interfacial bonds in the n-hexadecane-lubricated system is the highest, followed by the air systems, and finally, the water-lubricated system. From the fits to Eq. 1, Fig. 7 yields activation volumes of 2.1 ± 0.2 Å3, 2.4 ± 0.1 Å3, and 1.8 ± 0.1 Å3, for the air, n-hexadecane, and water systems, respectively. These values are consistent with single-atom dimensions [96] and are similar to the values previously reported for and water-lubricated diamond–quartz contacts (1.3 ± 0.1 Å3) [30]. This implies that the stress-dependence of interfacial bond formation is highest for the n-hexadecane-lubricated system. When the atoms in contact method is used to determine the contact area and normal stress (Figure S6), we obtain the activation volumes of 0.52 ± 0.04 Å3, 0.55 ± 0.02 Å3, and 0.47 ± 0.04 Å3, for the air, n-hexadecane, and water system, respectively [95].
Figure 8 shows the steady-state number of interfacial bonds that form in the three systems across the load range studied. The number of interfacial bonds increases with load for all the systems studied. The number of interfacial bonds is greatest for the n-hexadecane system, followed by air, and finally water. For the air system, most of the interfacial bonds are direct C–O bonds between the tip and the substrate. For the n-hexadecane and water systems, a significant proportion of the bonds are C–H–O hydrogen bonds from H atoms released from dissociated water or n-hexadecane molecules. These C–H–O bonds will be much weaker than the direct C–O bonds. Some C–O–Si bonds also form with oxygen atoms released from dissociated water molecules, which will have equal strength to the direct C–O bonds. [30]
Figure 9 shows the mean friction force as a function of the mean number of interfacial bonds during steady-state sliding. For all three systems, the friction force increases linearly with the total number of interfacial bonds formed. This observation is consistent with the multibond friction model due to Filippov et al. [89] as well as previous NEMD simulations by Mo et al. [43]. The gradients of each line indicate the relative strength of each interfacial bond and the amount of mechanical energy required to break each bond. The slope in the air system is much steeper than the other two systems, which is because it has the lowest proportion of weaker C–H–O bonds (Fig. 8). Even when scaling the number of bonds by their relative strength, the friction force data from the three surfaces do not collapse onto the same curve, which reinforces that other factors (i.e. ploughing contribution from differences in indentation depth) also play a significant role.
4 Conclusion
We have performed macroscale tribometer experiments that have revealed that for diamond–granite interfaces, n-hexadecane-lubricated contacts display unexpectedly high friction compared to air- and water-lubricated contacts. This implies that additive-free, oil-based drilling fluids give poorer boundary lubrication performance at the cutter–rock contact than water-based ones. Using ReaxFF NEMD simulations of a single-crystal diamond tip sliding on α-quartz, we show the same trend in increasing friction from water-, to air-, and n-hexadecane-lubricated systems. The simulations suggest that the difference in friction between these systems is due to two factors: (i) the indentation depth and (ii) the amount of interfacial bonding. The indentation depth was much lower for the water-lubricated system, followed by air, and finally n-hexadecane. This suggests that n-hexadecane reduces the hardness of the α-quartz surface. The n-hexadecane system also had the highest number of interfacial bonds, followed by air, and finally water. For all the systems, the rate of interfacial bond formation increases exponentially with the normal stress, which shows that this is a SATA process. The calculated activation volume is similar for all the systems, implying a similar stress dependence of interfacial bonding. The simulations reveal that water molecules passivate potential sites of interfacial bond formation with either hydroxyl or hydride groups on the sliding surfaces. Even though the air and hexadecane systems have an equal number of water molecules present, there are more passivated sites in the n-hexadecane system. However, increased interfacial bond formation is observed for the n-hexadecane system, which leads to increased friction. Finally, we show that for each system, the friction force increases linearly with the number of interfacial bonds during steady-state sliding. We anticipate that these findings will be useful for the design of new drilling fluid formulations that reduce bit–rock interfacial bonding and subsequently friction.
Data Availability
Data are available on request to the corresponding author.
References
Caenn, R., Chillingar, G.V.: Drilling fluids: state of the art. J. Pet. Sci. Eng. 14, 221–230 (1996)
Mohamed, A., Salehi, S., Ahmed, R.: Significance and complications of drilling fluid rheology in geothermal drilling: a review. Geothermics 93, 102066 (2021)
Aftab, A., Ismail, A.R., Ibupoto, Z.H., Akeiber, H., Malghani, M.G.K.: Nanoparticles based drilling muds a solution to drill elevated temperature wells: a review. Renew. Sustain. Energy Rev. 76, 1301–1313 (2017)
Friedheim, J.E.: Second-generation synthetic drilling fluids. J. Petrol. Technol. 49, 724–728 (1997)
Aboulrous, A.A., Haddad, A.S., Rafati, R., Boyou, N.V., Alsabagh, A.M.: Review of synthesis, characteristics and technical challenges of biodiesel based drilling fluids. J. Clean. Prod. 336, 130344 (2022)
Quintero, L.: An overview of surfactant applications in drilling fluids for the petroleum industry. J. Dispers. Sci. Technol. 23, 393–404 (2002)
Brandon, N.P., Wood, R.J.K.: The influence of interfacial potential on friction and wear in an aqueous drilling mud. Wear 170, 33–38 (1993)
Zhao, X., Li, D., Zhu, H., Ma, J., An, Y.: Advanced developments in environmentally friendly lubricants for water-based drilling fluid: a review. RSC Adv. 12, 22853–22868 (2022)
Lee, S., Spencer, N.D.: Materials science: sweet, hairy, soft, and slippery. Science 2008(319), 575–576 (1979)
Spikes, H.: Basics of EHL for practical application. Lubr. Sci. 27, 45–67 (2015)
David Ytrehus, J.; Taghipour, A.; Golchin, A.; Saasen, A.; Prakash, B. The Effect of Different Drilling Fluids on Mechanical Friction. Journal of Energy Resources Technology, Transactions of the ASME 2017, 139
Zheng, Y., Amiri, A., Polycarpou, A.A.: Enhancements in the tribological performance of environmentally friendly water-based drilling fluids using additives. Appl. Surf. Sci. 527, 146822 (2020)
Yan, X., You, L., Kang, Y., Li, X., Xu, C., She, J.: Impact of drilling fluids on friction coefficient of brittle gas shale. Int. J. Rock Mech. Min. Sci. 106, 144–152 (2018)
Appl, F.C., Wilson, C.C., Lakshman, I., Appl, F.C., Wilson, C.C., Lakshman, I.: Measurement of forces, temperatures and wear of PDC cutters in rock cutting. Wear 169, 9–24 (1993)
Kuru, E., Wojtanowicz, A.K.: An experimental study of sliding friction between PDC drill cutters and rocks. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 32, 277–283 (1995)
Smith, J.R., Lund, J.B., Galloway, R.K.: Friction on PDC cutters at high normal stress. J. Energy Resour. Technol. 124, 146–153 (2002)
Hibbs, L. E.; Sogoian, G. C. Wear Mechanisms for Polycrystalline-Diamond Compacts as Utilized for Drilling in Geothermal Environments. Sandia National Laboratories Technical Report 1983, SRD-82–092.
Selim, A.A., Schultz, C.W., Strebig, K.C.: The effect of additives on impregnated diamond bit performance. Soc. Petrol. Eng. J. 9, 425–433 (1969)
Macmillan, N.H., Huntington, R.D., Westwood, A.R.C.: Chemomechanical control of sliding friction behaviour in non-metals. J. Mater. Sci. 9, 697–706 (1974)
Westwood, A.R.C., Goldheim, D.L.: Mechanism for environmental control of drilling in MgO and CaF2 monocrystals. J. Am. Ceram. Soc. 53, 142–147 (1970)
Fischer, T.E., Anderson, M.P., Jahanmir, S., Salher, R.: Friction and wear of tough and brittle zirconia in nitrogen, air, water, hexadecane and hexadecane containing stearic acid. Wear 124, 133–148 (1988)
Jahanmir, S., Fischer, T.E.: Friction and wear of silicon nitride lubricated by humid air, water, hexadecane and hexadecane + 0.5 percent stearic acid. Tribol. Trans. 31, 32–41 (1988)
Reddyhoff, T., Ku, I.S.Y., Holmes, A.S., Spikes, H.A.: Friction modifier behaviour in lubricated MEMS devices. Tribol. Lett. 41, 239–246 (2011)
Zum Gahr, K.H.: Sliding wear of ceramic-ceramic, ceramic-steel and steel-steel pairs in lubricated and unlubricated contact. Wear 133, 1–22 (1989)
Rehbinder, P.A., Shchukin, E.D.: Surface phenomena in solids during deformation and fracture processes. Prog. Surf. Sci. 3, 97–187 (1972)
Westwood, A.R.C., Ahearn, J.S., Mills, J.J.: Developments in the theory and application of chemomechanical effects. Colloids Surf. 2, 1–35 (1981)
Mills, J.J., Westwood, A.R.C.: Influence of chemomechanically active fluids on diamond wear during hard rock drilling. J. Mater. Sci. 13, 2712–2716 (1978)
Marks, L.D., Warren, O.L., Minor, A.M., Merkle, A.R.: Tribology in full view. MRS Bull. 33, 1168–1173 (2008)
Ewen, J.P., Heyes, D.M., Dini, D.: Advances in nonequilibrium molecular dynamics simulations of lubricants and additives. Friction 6, 349–386 (2018)
Bhamra, J.S., Ewen, J.P., Latorre, C.A., Bomidi, J.A.R., Bird, M.W., Dasgupta, N., van Duin, A.C.T., Dini, D.: Interfacial bonding controls friction in diamond-rock contacts. J. Phys. Chem. C 125, 18395–18408 (2021)
Bhamra, J.S., Ewen, J.P., Ayestarán Latorre, C., Bomidi, J.A.R., Bird, M.W., Dini, D.: Atomic-scale insights into the tribochemical wear of diamond on quartz surfaces. Appl. Surf. Sci. 639, 158152 (2023)
Zhu, X., Luo, Y., Liu, Y., Wang, X., Zhang, H., Jiang, Y.: Interfacial friction evolution in an oil-based drilling fluid environment: an atomic understanding from ReaxFF simulations. Tribol. Lett. 71, 76 (2023)
Luo, Y., Zhu, X., Liu, Y., Wang, X., Zhang, H., Li, B., Peng, Y.: Effect of oil-based drilling fluid on the evolution of friction interface: a reactive molecular dynamics study at different temperatures. Tribol. Int. 188, 108820 (2023)
Van Duin, A.C.T.T., Dasgupta, S., Lorant, F., Goddard, W.A., Goddard, W.A., III.: ReaxFF: a reactive force field for hydrocarbons. J. Phys. Chem. A 105, 9396–9409 (2001)
Dougherty, P.S.M., Pudjoprawoto, R., Higgs, C.F., III.: Bit cutter-on-rock tribometry: analyzing friction and rate-of-penetration for deep well drilling substrates. Tribol. Int. 77, 178–185 (2014)
Lyons, K.D., Honeygan, S., Mroz, T.: NETL extreme drilling laboratory studies high pressure high temperature drilling phenomena. J. Energy Resour. Technol. 130, 0431021 (2008)
Reeves, M.J.: Rock surface roughness and frictional strength. Int J Rock Mech. Min. Sci. Geomech. 22, 429–442 (1985)
Ersoy, A., Waller, M.D.: Wear characteristics of PDC pin and hybrid core bits in rock drilling. Wear 188, 150–165 (1995)
Yahiaoui, M., Paris, J.Y., Delbé, K., Denape, J., Gerbaud, L., Colin, C., Ther, O., Dourfaye, A.: Quality and wear behavior of graded polycrystalline diamond compact cutters. Int. J. Refract. Metals Hard Mater. 56, 87–95 (2016)
Wheeler, D.W.: Applications of Diamond to improve tribological performance in the oil and gas industry. Lubricants 6, 84 (2018)
Blau, P.J.: On the nature of running-in. Tribol. Int. 38, 1007–1012 (2005)
Hertz, H.: Ueber die berührung fester elastischer körper. J. Reine Angew. Math. 1882, 156–171 (1882)
Mo, Y., Turner, K.T., Szlufarska, I.: Friction laws at the nanoscale. Nature 457, 1116–1119 (2009)
Greenwood, J.A., Johnson, K.L., Matsubara, E.: A surface roughness parameter in Hertz contact. Wear 100, 47–57 (1984)
Lai, P., Moulton, K., Krevor, S.: Pore-scale heterogeneity in the mineral distribution and reactive surface area of porous rocks. Chem. Geol. 411, 260–273 (2015)
Senftle, T.P., Hong, S., Islam, M.M., Kylasa, S.B., Zheng, Y., Shin, Y.K., Junkermeier, C., Engel-Herbert, R., Janik, M.J., Aktulga, H.M., Verstraelen, T., Grama, A., Van Duin, A.C.T.: The ReaxFF reactive force-field: development, applications and future directions. npj Comput. Mater. (2016). https://doi.org/10.1038/npjcompumats.2015.11
Van der Molen, I.: The shift of the α-β transition temperature of quartz associated with the thermal expansion of granite at high pressure. Tectonophysics 73, 323–342 (1981)
De Leeuw, N.H., Higgins, F.M., Parker, S.C.: Modeling the surface structure and stability of α-quartz. J. Phys. Chem. B 103, 1270–1277 (1999)
Pashley, R.M., Kitchener, J.A.: Surface forces in adsorbed multilayers of water on quartz. J. Colloid Interface Sci. 71, 491–500 (1979)
Gee, M.L., Healy, T.W., White, L.R.: Hydrophobicity Effects in the condensation of water films on quartz. J. Colloid Interface Sci. 140, 450–465 (1990)
Kinser, C.R., Schmitz, M.J., Hersam, M.C.: Conductive atomic force microscope nanopatterning of hydrogen-passivated silicon in inert organic solvents. Nano Lett. 5, 91–95 (2005)
Schatzberg, P.: Solubilities of water in several normal alkanes from C7 to C16. J. Phys. Chem. 67, 776–779 (1963)
Miranda, P.B., Shen, Y.R.: Liquid interfaces: a study by sum-frequency vibrational spectroscopy. J. Phys. Chem. B 103, 3292–3307 (1999)
Gee, M.L., Healy, T.W., White, L.R.: Ellipsometric studies of alkane adsorption on quartz. J. Colloid Interface Sci. 131, 18–23 (1989)
Yue, D.C., Ma, T.B., Hu, Y.Z., Yeon, J., van Duin, A.C.T., Wang, H., Luo, J.: Tribochemical mechanism of amorphous silica asperities in aqueous environment: a reactive molecular dynamics study. Langmuir 31, 1429–1436 (2015)
Brazil, O., Pharr, G.M.: Direct observation of partial slip in micrometre-scale single asperity contacts. Tribol. Int. 155, 106776 (2020)
Stukowski, A.: Visualization and analysis of atomistic simulation data with OVITO-the open visualization tool. Model. Simu. Mat. Sci. Eng. 18, 015012 (2010)
Budi, A., Stipp, S.L.S., Andersson, M.P.: Calculation of entropy of adsorption for small molecules on mineral surfaces. J. Phys. Chem. C 122, 8236–8243 (2018)
Martin, D.S., Domke, A.H., Weightman, P.: An Atomic force microscopy study of the adsorption of n-hexadecane onto a polished natural IIb diamond surface. Appl. Surf. Sci. 144–145, 598–602 (1999)
Thompson, A.P., Aktulga, H.M., Berger, R., Bolintineanu, D.S., Brown, W.M., Crozier, P.S., in’t Veld, P.J., Kohlmeyer, A., Moore, S.G., Nguyen, T.D., Shan, R., Stevens, M.J., Tranchida, J., Trott, C., Plimpton, S.J.: LAMMPS—a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comput. Phys. Commun. 271, 108171 (2022)
Verlet, L.: Computer, “experiments” on classical fluids. I. thermodynamical properties of lennard-jones molecules. Phys. Rev. 159, 98 (1967)
Schneider, T., Stoll, E.: Molecular-dynamics study of a three-dimensional one-component model for distortive phase-transitions. Phys. Rev. B 17, 1302–1322 (1978)
Chenoweth, K., van Duin, A.C.T., Goddard, W.A., III.: ReaxFF Reactive force field for molecular dynamics simulations of hydrocarbon oxidation. J. Phys. Chem. A 112, 1040–1053 (2008)
Aktulga, H.M., Fogarty, J.C., Pandit, S.A., Grama, A.Y.: Parallel reactive molecular dynamics: numerical methods and algorithmic techniques. Parallel Comput. 38, 245–259 (2012)
Rappe, A.K., Goddard, W.A., III.: Charge equilibration for molecular dynamics simulations. J. Phys. Chem. 95, 3358–3363 (1991)
Nakano, A.: Parallel multilevel preconditioned conjugate-gradient approach to variable-charge molecular dynamics. Comput. Phys. Commun. 104, 59–69 (1997)
Newsome, D.A., Sengupta, D., Foroutan, H., Russo, M.F., Van Duin, A.C.T.: Oxidation of silicon carbide by O 2 and H 2O: A ReaxFF reactive molecular dynamics study, part I. J. Phys. Chem. C 116, 16111–16121 (2012)
Van Duin, A.C.T., Strachan, A., Stewman, S., Zhang, Q., Xu, X., Goddard, W.A.: ReaxFFSiO reactive force field for silicon and silicon oxide systems. J. Phys. Chem. A 107, 3803–3811 (2003)
Fogarty, J.C., Aktulga, H.M., Grama, A.Y., van Duin, A.C.T., Pandit, S.A.: A reactive molecular dynamics simulation of the silica-water interface. J. Chem. Phys. 132, 174704 (2010)
Buehler, M.J., van Duin, A.C.T., Goddard, W.A., III.: Multiparadigm modeling of dynamical crack propagation in silicon using a reactive force field. Phys. Rev. Lett. 96, 095505 (2006)
Chenoweth, K., Cheung, S., van Duin, A.C.T., Goddard, W.A., III., Kober, E.M.: Simulations on the thermal decomposition of a poly(dimethylsiloxane) polymer using the ReaxFF reactive force field. J. Am. Chem. Soc. 127, 7192–7202 (2005)
Wang, J., Zhang, L., Zeng, Q., Gérard, V.L., Guette, A.: First-principles investigation on initial stage of 2H-SiC(001) surface oxidation. Chin. Sci. Bull. 54, 1487–1494 (2009)
van Duin, A.C.T., Dasgupta, S., Lorant, F., Goddard, W.A., III.: ReaxFF: a reactive force field for hydrocarbons. J. Phys. Chem. A 105, 9396–9409 (2001)
Bhati, M., Senftle, T.P.: Identifying adhesion properties at Si/polymer interfaces with ReaxFF. J. Phys. Chem. C 123, 27036–27047 (2019)
Hilbert, J., Mangolini, F., McClimon, J.B., Lukes, J.R., Carpick, R.W.: Si doping enhances the thermal stability of diamond-like carbon through reductions in carbon-carbon bond length disorder. Carbon N Y 131, 72–78 (2018)
Vashisth, A., Mirsayar, M.M.: A combined atomistic-continuum study on the temperature effects on interfacial fracture in SiC/SiO2 composites. Theoret. Appl. Fract. Mech. 105, 102399 (2020)
Li, A., Liu, Y., Szlufarska, I.: Effects of interfacial bonding on friction and wear at silica/silica interfaces. Tribol. Lett. 56, 481–490 (2014)
Li, Q., Tullis, T.E., Goldsby, D., Carpick, R.W.: Frictional ageing from interfacial bonding and the origins of rate and state friction. Nature 480, 233–236 (2011)
Persson, B.N.J., Sivebæk, I.M., Samoilov, V.N., de Zhao, K., Volokitin, A.I., Zhang, Z.: On the origin of amonton’s friction law. J. Phys.: Condens. Matter 20, 395006–395017 (2008)
Dieterich, J.H., Conrad, G.: Effect of Humidity on time- and velocity-dependent friction in rocks. J. Geophys. Res. 89, 4196–4202 (1984)
Patton, S.T., Cowan, W.D., Eapen, K.C., Zabinski, J.S.: Effect of Surface chemistry on the tribological performance of a MEMS electrostatic lateral output motor. Tribol. Lett. 9, 199–209 (2001)
De Barros Bouchet, M.-I., Zilibotti, G., Matta, C., Righi, M.C., Vandenbulcke, L., Vacher, B., Martin, J.-M.: Friction of diamond in the presence of water vapor and hydrogen gas. coupling gas-phase lubrication and first-principles studies. J. Phys. Chem. C 116, 6966–6972 (2012)
Ootani, Y., Xu, J., Hatano, T., Kubo, M.: Contrasting roles of water at sliding interfaces between silicon- based materials: first-principles molecular dynamics sliding simulations. J. Phys. Chem. C 122, 10459–10467 (2018)
Cutini, M., Forghieri, G., Ferrario, M., Righi, M.C.: Adhesion, friction and tribochemical reactions at the diamond-silica interface. Carbon N Y 203, 601–610 (2023)
Cafolla, C., Voïtchovsky, K.: Impact of water on the lubricating properties of hexadecane at the nanoscale. Nanoscale 12, 14504–14513 (2020)
Broz, M.E., Cook, R.F., Whitney, D.L.: Microhardness, toughness, and modulus of mohs scale minerals. Am. Miner. 91, 135–142 (2006)
Bowden, F., Tabor, D.: Friction, lubrication and wear: a survey of work during the last decade. Br. J. Appl. Phys. 17, 1521–1544 (1966)
Broitman, E.: Indentation hardness measurements at macro-, micro-, and nanoscale: a critical overview. Tribol. Lett. 65, 23 (2017)
Filippov, A.E., Klafter, J., Urbakh, M.: Friction through dynamical formation and rupture of molecular bonds. Phys. Rev. Lett. 92, 135503 (2004)
Yeon, J., van Duin, A.C.T., Kim, S.H.: Effects of Water on tribochemical wear of silicon oxide interface: molecular dynamics (MD) study with reactive force field (ReaxFF). Langmuir 32, 1018–1026 (2016)
Wang, M., Duan, F., Mu, X.: Effect of surface silanol groups on friction and wear between amorphous silica surfaces. Langmuir 35, 5463–5470 (2019)
Spikes, H.: Stress-augmented thermal activation: tribology feels the force. Friction 6, 1–31 (2018)
Jacobs, T.D.B., Martini, A.: Measuring and understanding contact area at the nanoscale: a review. Appl. Mech. Rev. 69, 060802 (2017)
Jensen, B.D., Wise, K.E., Odegard, G.M.: Simulation of the elastic and ultimate tensile properties of diamond, graphene, carbon nanotubes, and amorphous carbon using a revised ReaxFF parametrization. J. Phys. Chem. A 119, 9710–9721 (2015)
Wang, Y., Qin, J., Xu, J., Sun, J., Chen, L., Qian, L., Kubo, M.: Definition of atomic-scale contact: what dominates the atomic-scale friction behaviors? Langmuir 38, 11699–11706 (2022)
Jacobs, T.D.B., Carpick, R.W.: Nanoscale wear as a stress-assisted chemical reaction. Nat. Nanotechnol. 8, 108–112 (2013)
Acknowledgements
J.S.B. thanks Baker Hughes for Ph.D. funding. J.P.E. thanks the Royal Academy of Engineering (RAEng) for a Research Fellowship. D.D. acknowledges the support via his Shell/RAEng Research Chair in Complex Engineering Interfaces. We acknowledge the use of the Research Computing Service at Imperial College London (https://doi.org/10.14469/hpc/2232) and the UK Materials and Molecular Modelling Hub, which is partially funded by Engineering and Physical Sciences Research Council (EPSRC) grant EP/T022213/1, EP/W032260/1, and EP/P020194/1.
Funding
Engineering and Physical Sciences Research Council, EP/T022213/1, EP/W032260/1, and EP/P020194/1, Baker Hughes, PhD Funding, Royal Academy of Engineering, Research Fellowship and Research Chair, Research Fellowship and Research Chair
Author information
Authors and Affiliations
Contributions
JSB performed the simulations and produced the figures and EHE performed the experiments. JARB, DD, and JPE supervised the project. JSB wrote the first draft of the manuscript and all authors reviewed the manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bhamra, J.S., Everhard, E.M., Bomidi, J.A.R. et al. Comparing the Tribological Performance of Water-Based and Oil-Based Drilling Fluids in Diamond–Rock Contacts. Tribol Lett 72, 19 (2024). https://doi.org/10.1007/s11249-023-01818-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11249-023-01818-0