Analytical Theory of Ice-Skating Friction with Flat Contact

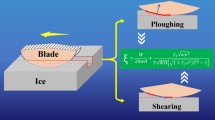
Abstract

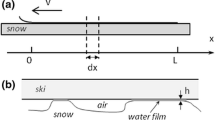
Although a thin meltwater layer that acts as lubricant attributes to the low friction on ice, there still lacks analytical theories that can forecast the friction force on ice. Based on the evolution of the thin meltwater layer, this study builds an analytical theory to the friction force on ice with flat contacts, which matches experimental measurement nicely. This study reveals that a dynamic balance between the ice melting caused by frictional heat and the water squeezing caused by slider regulates the thickness of the self-lubricating interstitial meltwater layer, which guarantees the low friction on ice. This analytical model provides a self-consistent explanation to the ice friction, which may help to regulate the friction on ice purposely.

Graphical Abstract

Appendices

Appendix 1

This Appendix contains (A1) a list of material constants used in this study, (A2) analysis of heat transfer along the slider, (A3) derivation of friction from the boundary lubrication region, (A4) numerical checking of the meltwater layer thickness evolution near the leading contact edge and (A5) a collection of experimental measurement of CoF related to skating.

1.1 A1: A List of Material Constants

Parameter	Unit	Value
Heat diffusion coefficient of ice, $D$	${\mathrm{m}}^{2}/\mathrm{s}$	$1.15\times {10}^{-6}$
Melt point of ice, ${T}_{m}$	$\mathrm{^\circ{\rm C} }$	0
Heat conductivity coefficient of ice, $k$	$\mathrm{W}/\mathrm{m}/\mathrm{K}$	2.2
Specific heat of ice, $c$	$\mathrm{J}/\mathrm{kg}/\mathrm{K}$	2090
Density of ice, ${\rho }_{i}$	$\mathrm{kg}/{\mathrm{m}}^{3}$	916.82
Density of water, $\rho$	$\mathrm{kg}/{\mathrm{m}}^{3}$	999.84
Latent heat of water, ${l}_{f}$	$\mathrm{kJ}/\mathrm{kg}$	330
Viscosity of water, $\mu$	$\mathrm{Pa}\cdot \mathrm{s}$	$1.76\times {10}^{-3}$

1.2 A2: Analysis of Heat Transfer Along the Slider

General speaking, the frictional heat generated between the skate and ice transfers to the ice substrate and the slider, which varies with time and space during the whole sliding process. Considering the various shapes of skate blades and the frequently change of the contact condition between the skate and ice, modeling the precise heat transfer in this skate-ice system is not a trial task. So, in this section, we aim to present a rough estimation of the heat loss along the skate blade during skating. We restrict our discussion to the quasi-steady state that a stable temperature field is built in the skate-ice system, which happens when the skate has slide sufficient long distance with a constant velocity on ice. Under this condition, one part of the heat flux flows along the skate to the blade mount and the other part losses into air through skate body with forced convective, as shown schematically in Fig. 

Fig. 6

Schematic of heat transfer along the skate blade

6. Given the good ability of heat transfer of steel, we assume that the blade has a constant temperature around the body, which is the same as the blade-ice interfacial temperature; that is the ice melt point. As the persistent contact with air, the mounted shoes on the blade are assumed to have the same temperature as air or the environmental temperature.

The flux of heat flow along the blade mount is determined by

$${J}_{bm}=-{k}_{bm}\frac{dT}{dz}$$

(A1)

where ${k}_{bm}$ is the heat conductivity coefficient of the blade mount, $dT/dz$ is the temperature gradient at the blade mount, which can be approximated as

$$\frac{dT}{dz}=\frac{{T}_{0}-{T}_{b}}{{h}_{bm}}$$

(A2)

where ${T}_{b}$ and ${T}_{0}$ are the temperature of the blade and air, ${h}_{bm}$ is the connection length between the blade and the shoes, as shown in Fig. 6. So, the power of heat flow along the blade mount is

$${P}_{bm}={J}_{bm}{A}_{bm}=-{A}_{bm}{k}_{bm}\frac{{T}_{0}-{T}_{b}}{b}$$

(A3)

where ${A}_{bm}$ is the cross section area of the blade mount.

For the forced convective heat transfer, the flux ${J}_{a}$ that losses into air through the skate body is determined by the Newton's law of cooling [38, 50], which is given by

$${J}_{a}=\alpha \left({T}_{b}-{T}_{0}\right)$$

(A4)

where $\alpha$ is the heat exchange coefficient. The average heat exchange coefficient $\alpha$ of the blade is related to the Nusselt number $Nu$ as

$$Nu=\frac{\alpha {L}_{b}}{{k}_{a}}$$

(A5)

where ${L}_{b}$ is the length of the total blade, which is contrast to contact length between the blade and ice of $L$, as shown in Fig. 6. ${k}_{a}$ is the heat conductivity coefficient of air. On the other hand, the Nusselt number $Nu$ can be related to the Prandtl number $Pr$ and Reynolds number $Re$ as follows

$$Nu=0.664R{e}^\frac{1}{2}{Pr}^\frac{1}{3}$$

(A6)

if the airflow on the blade surface belongs to laminar flow, which happens when the Reynolds number is below $5\times {10}^{5}$. The Reynolds number, which measures the onset of turbulent flow on the surface of solid, is defined as $Re=v{L}_{b}/{\mu }_{a}$, with $v$ the velocity of the slider and ${\mu }_{a}$ the viscosity of air. The Prandtl number is defined as $Pr={c}_{p}{\mu }_{a}/{k}_{a}$, with ${c}_{p}$ the specific heat of air at constant pressure. If the Reynolds number is larger than $5\times {10}^{5}$, Eq. (A6) is replaced by

$$Nu=\left(0.037{Re}^\frac{4}{5}-871\right){Pr}^\frac{1}{3}.$$

(A7)

Combining Eqs. (A5)–(A7), the average heat exchange coefficient $\alpha$ can be determined accordingly. Then, based on Eq. (A4), the power of heat flow to air ${P}_{a}$ as a result of the forced convective is

$${P}_{a}=2{J}_{a}A=2\alpha A\left({T}_{b}-{T}_{0}\right)$$

(A8)

where $A$ is the area of the blade. The coefficient of 2 accounts that both sides of the blade contributed to the heat loss through forced convective.

Based on Eqs. (A3) and (A8), the power of the total flux diffused away along the blade can be determined as:

$$P={P}_{bm}+{P}_{a}=\left(\frac{{A}_{bm}{k}_{bm}}{{h}_{bm}}+2\alpha A\right)\left({T}_{m}-{T}_{0}\right)$$

(A9)

where the blade temperature ${T}_{b}$ has been replaced by the melt point of ice ${T}_{m}$. Considering the power of the total frictional heat generation, which is

$${P}_{t}=\xi Wv$$

(A10)

where $\xi$ is the dynamic CoF as determined in the main text, the ratio of the flux diffused away along the blade to the total created frictional heat $\eta$ can be given as

$$\eta =\frac{P}{{P}_{t}}=\left(\frac{{A}_{bm}{k}_{bm}}{b}+2\alpha A\right)\frac{\left({T}_{m}-{T}_{0}\right)}{\xi Wv}.$$

(A11)

A nature consequence from Eq. (A11) is that if the environmental temperature is equal to the melt point of ice, there is no heat loss along the blade. On the contra, there is even a heat flux flows from air to the blade if the environmental temperature is higher than the ice melt point, which always happens in the indoor skating.

A rough estimation of the ratio of the flux diffused away along the blade to the total created frictional heat $\eta$ is shown in Fig. 

Fig. 7

The ratio $\eta$ of heat flux diffused away along the blade to the total created frictional heat as a function of sliding velocity while under ice substrate temperature of a −5 $\mathrm{^\circ{\rm C} }$ and b −10 $\mathrm{^\circ{\rm C} }$. The lines with different colors represent environmental temperature ranging from $3$ to $-10\mathrm{^\circ{\rm C} }$. The shadowed regions corresponding to $\left|\eta \right|<0.05$

7, with the parameters used in this estimation given in Table

Table 1 Parameters used in the estimation of heat transfer along the skate blade

1. Keep in mind that the environment temperature will influence various properties of air, such as density, heat conductivity coefficient, viscosity, specific heat, whereas the velocity of the slider will influence the Reynolds number, the dynamic CoF. Figure 7a and b shows the value of $\eta$ as a function of the environmental temperature and the sliding velocity while under relatively high ($-5\mathrm{^\circ{\rm C} }$) and low ($-10\mathrm{^\circ{\rm C} }$) ice substrate temperature, respectively. Both figures show that, under relatively high environmental temperature, such as in the range of $-3\mathrm{^\circ{\rm C} }\sim 3\mathrm{^\circ{\rm C} }$, the value of $\eta$ lies in the range of −0.05 ~ 0.05 when the sliding velocity is above about $10\mathrm{ m}/\mathrm{s}$, which corresponding to the situation of indoor competitive skating. This small value of $\eta$ implies the effect of the heat losses as a result of flow along skate is ignorable, which is the circumference of this study.

However, when the situation changes such as when the environmental temperature is much lower than the melt point of ice, which may happen during outdoor skating, or the sliding speed is lower than $5\mathrm{ m}/\mathrm{s}$, the absolute value of $\eta$ becomes larger than 0.3 and even exceeding 0.5. This large value of $\eta$ indicates the contribution of heat transfer along the skate cannot be ignored and sometime, it even turns to be the dominant factor that consumes the frictional heat. So, under these conditions, the heat transfer along slider cannot be ignored. We leave this situation for further investigation.

A3: Derivation of Friction from the Boundary Lubrication Region

As shown in Fig. 

Fig. 8

Schematic of heat transfer in the blade-ice system in the cross section along the sliding direction

8 of the schematic of heat transfer, during boundary lubrication condition, the frictional heat comes from the friction motion of the quasi-liquid layer on ice, which transfers into the ice substrate and the slider. In general, it is a three-dimensional heat transfer problem. However, considering that the length of the slider is much longer than the wideness, this heat transfer problem can be simplified into a two-dimensional heat transfer problem with each cross section along the sliding direction to be determined individually. In the cross section as shown in Fig. 8, the typical diffusion length ${h}_{d}$ of frictional heat along the vertical direction is given by:

$${h}_{d}=\sqrt{D{t}_{b}}=\sqrt{\frac{D{L}_{bl}}{v}}$$

(A12)

where $D$ is the heat diffusion coefficient of ice and ${t}_{b}={L}_{bl}/v$ is the total contact time during the slider with the boundary lubrication length of ${L}_{bl}$ passes a fixed point with a sliding velocity of $v$. Given the heat diffusion coefficient of ice (A1), the typical boundary lubrication length ${L}_{bl}$, which is always shorter than $1\mu m$ (see Fig. 

Fig. 9

a Boundary lubrication length and b CoF contributed by the boundary lubrication region as a function of sliding velocity while under various ratios between reduced quasi-liquid layer thickness and its reduced viscosity from 1 to 0.001 shown by lines with different colors. The solid lines correspond to ice substrate temperature of $-5 ^\circ{\rm C}$ while that of dashed lines correspond to $-10 ^\circ{\rm C}$. The skate blade wideness $w$ of $1\mathrm{ mm}$ and its supported weight $W$ of $800\mathrm{N}$ is used in (b)

9a), and the typical skating velocity of $v=15m/s$, the diffusion length ${h}_{d}$ along vertical direction is shorter than 0.28 $\mu m$. Considering the wideness of modern blade, which is close to $1mm$, the diffusion length along the vertical direction accounts to no more than 0.001 of the wideness of the slider. So, we can safely treat the heat transfer process as a one-dimensional problem. The basic solution for putting unit heat at the boundary on a half infinite isothermal body is given by [38]

$$T\left(s,t\right)=\frac{1}{\sqrt{\pi Dt}}\mathrm{exp}\left(-\frac{{s}^{2}}{4Dt}\right)$$

(A13)

where $T$ is the temperature field, which is a function of the distance to the boundary $s$ and the effect time $t$ since the heat acts. So, the boundary temperature $T\left(t\right)$ as a result of the boundary heat flux $J\left(t\right)$ is given by

$$T\left(t\right)={T}_{s}+{\int }_{0}^{t}\frac{J\left(t\right)dt}{{\rho }_{i}c\sqrt{\pi Dt}}$$

(A14)

where ${T}_{s}$ is the initial temperature of ice, ${\rho }_{i}$ is the density of ice and $c$ is the specific heat of ice.

Under boundary lubrication condition, the frictional heat flux ${J}_{t}$ is

$${J}_{t}=\frac{{\mu }_{bl}{v}^{2}}{{h}_{bl}}$$

(A15)

where ${\mu }_{bl}$ is the viscosity and ${h}_{bl}$ is the thickness of the quasi-liquid layer. At present, there is no consensus of the values of the physical parameters related to the quasi-liquid layer, such as the viscosity ${\mu }_{bl}$ and its dependence with the quasi-liquid layer thickness ${h}_{bl}$, this thickness and its dependence with ice substrate temperature. For example, for sub-nanometer hydrophilic confinement of water layer [51], the experimental measurements show 2 [52], 4 [53, 54] or 6 [55] orders of magnitude increase in the viscosity with respect to bulk water. Reference [15] gives a summary of the thickness of the quasi-liquid layer as a function of ice temperature, which ranges from $0.1$ to $10\mathrm{ nm}$ that corresponds to different research groups via different experimental techniques [17, 19,20,21, 56]. So, a variation of normalized viscosity ranging from 10² to 10⁶ and a variation thickness of the quasi-liquid layer ranging from $0.1$ to $10\mathrm{ nm}$ may be used to estimate the frictional heat generation. Assuming the frictional heat flux generation is constant before ice melts and all the frictional energy is used to increase its temperature, whereas there is no melt happens, the interface temperature can be determined from Eqs. (A14) and (A15) as

$$T\left(t\right)={T}_{s}+\frac{{\mu }_{bl}{v}^{2}}{{h}_{bl}}{\int }_{0}^{t}\frac{dt}{{\rho }_{i}c\sqrt{\pi Dt}}={T}_{s}+\frac{2{\mu }_{bl}{v}^{2}\sqrt{t}}{{h}_{bl}{\rho }_{i}c\sqrt{\pi D}}$$

(A16)

where we have ignored the heat transfer along the skate blade, as discussed in section A2. As the interface temperature will not exceed the melt point of ice, the contact time at the instant that the ice substrate begins to melt can be determined from Eq. (A16), which gives the boundary lubrication length ${L}_{bl}$ as

$${L}_{bl}=\frac{\pi {\left({T}_{m}-{T}_{s}\right)}^{2}k{\rho }_{i}c{h}_{bl}^{2}}{4{\mu }_{bl}^{2}{v}^{3}}$$

(A17)

where $k$ is the heat conductivity coefficient of ice. With this boundary lubrication length ${L}_{bl}$, the friction force ${F}_{bl}$ contributed by the boundary lubrication region can be given as

$${F}_{bl}=w{L}_{bl}\frac{{\mu }_{bl}v}{{h}_{bl}}=\frac{\pi w{\left({T}_{m}-{T}_{s}\right)}^{2}k{\rho }_{i}c{h}_{bl}}{4{\mu }_{bl}{v}^{2}}.$$

(A18)

So, the contribution of this boundary lubrication region to the dynamical CoF turns

$${\xi }_{bl}=\frac{{F}_{b}}{W}=\frac{\pi w{\left({T}_{m}-{T}_{s}\right)}^{2}k{\rho }_{i}c{h}_{bl}}{4{\mu }_{bl}{v}^{2}W}.$$

(A19)

In Fig. 9, the length of the boundary lubrication region ${L}_{bl}$ and its contribution to CoF ${\xi }_{bl}$ is determined according to Eqs. (A17) and (A19), respectively. As both Eqs. (A17) and (A19) show the dependence of ${h}_{bl}/{\mu }_{bl}$, a variety values of reduced ${h}_{bl}/{\mu }_{bl}$ are shown in Fig. 9 by lines with different colors, where the reference quasi-liquid layer thickness is $1\mathrm{ nm}$ and its reference viscosity is that of bulk water. For the reduced value of ${h}_{bl}/{\mu }_{bl}$ to be 1, which indicates that the quasi-liquid layer thickness is $1\mathrm{nm}$ and its viscosity equals to that of bulk water, Fig. 9a shows the boundary lubrication length ${L}_{bl}$ lies in the region of micrometer scale if the sliding velocity is above $5\mathrm{m}/\mathrm{s}$ for both ice substrate temperature of $-5 ^\circ{\rm C}$ and $-10 ^\circ{\rm C}$. As the viscosity of the quasi-liquid layer is much larger than that of bulk water, the boundary lubrication length will be much shorter than micrometer. Given that the typical skate blade has a contact length $L$ in the centimeter scale, the boundary lubrication length ${L}_{bl}$ can be deemed as a minor quantity and its effect can be ignored. Furthermore, the value of CoF contributed by this boundary lubrication region, as shown in Fig. 9b, is no more than 10^–6 even for the reduced value of ${h}_{bl}/{\mu }_{bl}$ to be 1. Considering the typical value of CoF, which spans from 0.002 to 0.012 (Fig. 4 in the main text and Table

Table 2 A collection of reported CoF related to skating

2), the contribution of this boundary lubrication region to the total friction force is ignorable. Taken together, the contribution of the boundary lubrication region to the total friction on ice during skating is negligible, as claimed in the main text.

A4: Numerical Checking of the Meltwater Layer Thickness Evolution Near the Leading Contact Edge

The meltwater layer thickness evolution follows Eq. (2) in the main text. When doing numerical calculation, there is a singularity point at $x=0$; that is the value of the right side of Eq. (2) is infinite if $x=0$. This singularity problem can be avoided by shift the initial value of $x$ to a small quantity. After setting the initial value of $x$ to be $0.1\mathrm{ \mu m}$, $1\mathrm{ \mu m}$ and $10\mathrm{ \mu m}$, which are small quantities compared to the contact length of the blade on ice, the meltwater layer thickness evolution is determined from Eq. (2) in the main text, which is shown in Fig. 

Fig. 10

Meltwater layer thickness evolution along the slider length with various initial value of $x$ ranging from $0.1$ to $10\mathrm{ \mu m}$ shown in lines with different colors and symbols. The insert shows the expanded region near the leading edge. A zero rotating angle and a sliding velocity of $15\mathrm{m}/\mathrm{s}$ are used

10. It shows that the initial value of $x$ will influence the meltwater layer thickness at the region that is in micrometer scale (about $40\mathrm{ \mu m}$ if the initial value of $x$ is $10\mathrm{ \mu m}$) near the leading contact edge. Beyond this region, the meltwater layer has the same thickness for all the initial values of $x$ that is used. As the contact length of the skate lies in centimeter scale, which is three orders longer than the region near the leading contact edge, the effects of the singularity point at $x=0$ to the meltwater layer thickness evolution is negligible.

A5: A Collection of Experimental Measured CoF Related to Skating

Table 2 gives a collection of CoF related to skating while under various experimental conditions, together with the related physical parameters.