Why Curling Stones Curl: Modelling and Numerical Experiments

Abstract

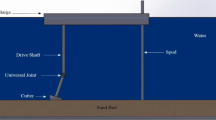
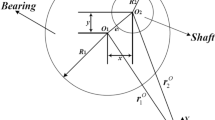
In curling, a sport played on ice, players release stones on the ice sheet at initial speeds of translation and rotation aiming to a target location with curled trajectory. To elucidate why the stones curl, we focus on the fact that asperities on the leading and trailing parts of the bottom of stone pass through the same spot on the ice surface twice within a short period of time. We also consider the fact that the ice is at a very high temperature close to its melting point and the recovery from the damaged state after the microscopic fracture and plastic deformation by the friction takes place quickly. Theoretical models for the magnitude and direction of the friction force between the stone and ice are developed and the motion of the stone was numerically analysed. Contribution of several factors that may be involved in friction on ice surfaces was investigated in detail. Analysis results were compared with experimental ones in literature and some were found to be in good agreement.

Appendices

Appendix

Motion of a non-rotating stone

When the stone is not rotating, the equation of motion for the stone is

$$m\frac{dv}{dt}=-\mu mg,$$

(38)

$$v=\frac{dy}{dt},$$

(39)

where m, y and v are the mass, position and velocity of the stone, respectively. μ is the dimensionless coefficient of kinetic friction and written as follows:

$$\mu ={\mu }_{0}{v}^{\xi }.$$

(40)

The pre-factor μ₀ of the kinetic friction coefficient is a function of temperature, pressure, etc., and the dimension is m^−ξs^ξ. Experimental studies have shown that the velocity exponent ξ is roughly − 1 ≤ ξ ≤ − 0.5. Integrating Eq. (38), we obtain

$$v={\left\{-{\mu }_{0}gt(1-\xi )+{{v}_{0}}^{1-\xi }\right\}}^{\frac{1}{1-\xi }},$$

(41)

where v₀ is the initial velocity. Let t_stop be the time at which the stone stops its motion. We have from v = 0,

$${t}_{stop}=\frac{1}{{\mu }_{0}g(1-\xi )}{{v}_{0}}^{1-\xi }.$$

(42)

The travel distance is calculated by integrating Eq. (41) and given by

$$y=\frac{1}{-{\mu }_{0}g(2-\xi )}{\left\{-(1-\xi ){\mu }_{0}gt+{{v}_{0}}^{1-\xi }\right\}}^{\frac{2-\xi }{1-\xi }}+\frac{1}{{\mu }_{0}g(2-\xi )}{{v}_{0}}^{2-\xi }.$$

(43)

The distance y_stop after the stone stops the movement is

$${y}_{stop}=\frac{1}{{\mu }_{0}g(2-\xi )}{{v}_{0}}^{2-\xi },$$

(44)

where, v₀ is the initial velocity. When ξ = − 0.5, y_stop is

$${y}_{stop}=\frac{2}{5{\mu }_{0}g}{{v}_{0}}^\frac{5}{2}$$

(45)