1 Introduction

The indentation [1,2,3,4,5,6,7,8,9,10,11,12,13] and scratching [14,15,16,17,18,19,20,21,22,23,24] of surfaces has been intensely studied using molecular dynamics simulation. While the majority of these studies use rigid tools—in the sense that the indenter is undeformable and also non-rotating—also the effect of rotational motion has been investigated in several case studies [25,26,27,28,29,30,31,32,33,34,35,36,37]. Such a rotating tool may model processes such as surface polishing, milling or grinding, in which the orientation of the tool with respect to the surface may change during the process.

For the case of rolling motion—i.e., with the rotation axis parallel to the surface and perpendicular to the scratch direction—it is been found [38] that particle rotation induces sizable effects only if the angular velocity is large compared to the rolling velocity, defined by \(\omega _{\text{sf}}= v/R\), where v ist the particle translational speed and R is its radius. For metallic substrates [25,26,27,28,29,30], dislocation production in the sample is reduced, corresponding to a reduction of material hardness; for large rotational velocities, substrate amorphization sets in. Studies in ceramics, such as SiC and also Si, [31,32,33,34,35,36] also found that rotational motion of the tool may change the deformation mechanism in machining.

These studies are as a rule done with purely repulsive tools. However, in reality the interaction between the tool and the substrate surface may include some adhesion. In previous studies, it was found that the presence of an attractive interaction may strongly influence the machining and damage formation process in the substrate [39,40,41,42]. More generally, adhesion plays an important role in tribological wear processes and the evolution of surface roughness in contacts [43, 44]. Thus the observed hardness may decrease, while the tool friction increases.

In the present study, we investigate to what extent adhesive forces between tool and substrate influence the machining by a rotating tool. For specificity, we focus on a Fe surface, since—besides the specific interest in this important material—a considerable number of studies investigated this material [10, 18, 22, 23, 38, 42, 45,46,47]; it may serve as a prototypical system of a metallic substrate. The tool will be modeled as a spherical diamond nanoparticle, since both its translational and rotational motion can then be easily specified during the indentation and scratching processes. The indentation and scratching of Fe by such a rotating particle will be studied by varying both rotational angular velocity and adhesion strength.

2 Method

Fig. 1
figure 1

Schematics of the simulation setup (Color figure online)

Full size image

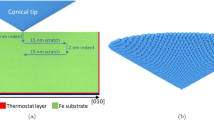
We use a single-crystalline block of Fe with a (100) surface as substrate. It has lateral extension of 74.8 nm \(\times\) 85.0 nm and a depth of 41 nm, and consists of \(22.4 \times 10^6\) atoms, see Fig. 1. After relaxation of the Fe crystal, two atomic layers at the bottom and the lateral sides are fixed to prevent the sample from any translational or rotational movement during indentation and scratch. The next four layers are kept at a temperature of 1 mK by a Langevin thermostat. This low temperature was chosen to minimize thermally activated processes and ease the detection of defects.

The particle is modeled as an atomistic sphere (radius \(R=10\) nm) cut out from a diamond crystal. It is kept in a rigid array such that the diamond atom positions cannot change relative to each other.

Fe atoms interact via the Mendelev potential [48] with each other. The interaction between Fe and C atom is based on a pair-wise Lennard-Jones (LJ) potential,

$$\begin{aligned} \Phi _{\text{LJ}}(r) = 4 \epsilon \left[ \left( \frac{\sigma }{r} \right) ^{12} - \left( \frac{\sigma }{r} \right) ^{6} \right] , \end{aligned}$$
(1)

with a well depth \(\epsilon =94.63\) meV, and a length parameter \(\sigma = 2.05\) Å [49]. Since in the present study, the adhesion strength between Fe and C is to be changed arbitrarily, we modify the Lennard-Jones potential Eq. (1) as follows [42]:

$$\begin{aligned} \Phi (r) = \left\{ \begin{array}{ll} \Phi _{\text{LJ}}(r) - \Phi _{\text{LJ}}(r_0) -D, &{} r \le r_0 ,\\ -D ( 2x^3 - 3 x^2 +1 ), &{} r_0 < r \le r_c, \\ 0, &{} r > r_c, \end{array} \right. \end{aligned},$$
(2)

where \(x= (r-r_0) / (r_c-r_0)\), \(r_0=2.30\) Å is the equilibrium Fe-C bond length, and \(r_c=5.4\) Å is the cut-off radius of the potential. This potential has always the same form for distances \(r<r_0\), while the depth of the potential, \(-D\), can be set arbitrarily. We will denote D as the adhesion strength of the potential and use values of \(D=0\), \(0.5\epsilon\), \(1\epsilon\), and \(2\epsilon\) in the present study. For further details on the potential, the reader is referred to Ref. [42].

Also the substrate interaction is unchanged; this means that all plastic processes in the substrate occur as faithfully as the potential [48] allows. This is in contrast to other studies [50] where the attractive part of the interaction between substrate atoms is altered with the aim of changing the material ductility and hence the plastic processes. As the repulsive tip-substrate interaction—i.e., at distances smaller than the equilibrium distance, \(r_0\)—is unchanged, all differences resulting from simulations with varying \(\epsilon\) arise from the attractive part of the tip-substrate potential.

Note that the potential, Eq. (2), decays more slowly than the LJ potential, Eq. (1); hence the attractive forces between Fe and C are smaller but extend further out than for the LJ potential. This indeed changes the interaction of the particle with the substrate, see the Supplementary Material (SM) [51]. However, the advantage of our approach, Eq. (1), in this model study is that the repulsive part of the particle-substrate interaction is unchanged when the attractive part is varied.

The particle starts from a position above the substrate and moves perpendicularly into the substrate up to the final depth of \(d=4\) nm; there it is held for 100 ps to allow the substrate to relax. The contact radius for full indentation is given by

$$\begin{aligned} a_c= \sqrt{ R^2-(R-d)^2} \end{aligned}$$
(3)

which amounts to 8 nm. For scratching, the particle moves in [010] direction for a total scratching length of 15 nm; then it is retracted. The particle velocity amounts to \(v=20\) m/s in all stages; the indentation phase lasts 200 ps and the scratch phase 750 ps.

The particle rotates along an axis parallel to the surface, in [001] direction. This axis is chosen such that it is orthogonal to the scratch direction and describes a rolling motion such that the particle moves downward in its front part (moving in scratch direction) and upwards in its rear part, cf. Fig. 1. For an assessment of the angular rotation speed \(\omega\), consider the case of rolling without slip, \(\omega _{\text{sf}}= v/R\); this amounts to a slip-free angular rotation velocity of \(\omega = 0.115^\circ\)/ps. Besides this angular velocity, we will also consider the larger value of \(\omega = 0.6^\circ\)/ps to study the effect of intense rotation, and compare to the non-rotating case, \(\omega = 0\) studied previously [42]. We note that for \(\omega = 0.6^\circ\)/ps, the particle rotates a total angle of \(120^\circ\) during the indentation, \(60^\circ\) during hold and \(450^\circ\) during the scratch process.

We use the open-source LAMMPS code [52] with a constant time step of 1 fs to perform the simulations. The dislocation extraction algorithm (DXA) [53] is used to identify the dislocations, to determine their Burgers vectors, and to measure the total length of the dislocation lines, \(L_{\text{disl}}\). The free software tools ParaView [54] and OVITO [55] are employed to visualize the atomistic configurations.

3 Results

In the following, we focus on the results for \(\omega =0.6^\circ\)/ps; if not otherwise mentioned, results for this angular rotation velocity are meant. Simulation results for \(\omega =0.115^\circ\)/ps are shown in the SM [51]. In the tables and for the discussion, however, we use all results and compare also to previous findings for a non-rotating particle [42].

3.1 Indentation

Fig. 2
figure 2

Evolution of the normal force with indentation depth. The arrows indicate the direction of the loading and unloading parts of the curve. The load drop at \(d=4\) nm occurs during the hold stage (Color figure online)

Full size image
Fig. 3
figure 3

Snapshots of the defects formed at the end of the indentation stage a after full indentation and b after particle retraction. Yellow: deformed surface and other unidentified defects. Dislocations are colored according to their Burgers vector \({\varvec{b}}\): blue \(\frac{1}{2} \langle 111 \rangle\), red \(\langle 100 \rangle\) (Color figure online)

Full size image
Fig. 4
figure 4

Substrate atom transport caused by the rotating particle. Color denotes the distance substrate atoms move backwards, i.e., in \([0\bar{1}0]\) direction, see Fig. 1 (Color figure online)

Full size image
Table 1 Characteristics of the indentation hardness and the plastic zone after full indentation of a particle rotating with various angular velocities \(\omega\)
Full size table

Figure 2 shows the evolution of the load (normal force, \(F_n\)) necessary to indent the surface. For a purely repulsive particle, the load-depth curve shows the well known features of (i) a more or less regular increase up to the maximum indentation depth \(d=4\) nm, (ii) a decrease of the load during the holding phase, and (iii) a decrease while the the particle is retracted from the substrate. The fluctuations during phase (i) are caused by dislocation emission; whenever a dislocation is generated in the vicinity of the indenting particle, the substrate material yields and the load is temporarily reduced. For a similar reason, the load decreases during the holding stage (ii); here, re-organization of the dislocation network formed leads to a reduction of stresses in the material and consequently to a decrease of the load necessary to hold the particle at depth d. Finally, in the retraction stage (iii), the load continuously sinks and vanishes when the particle has lost contact with surface atoms inside the indent pit created.

With increasing adhesion strength D, a number of new features show up. Most pronouncedly, the indentation load in stage (i) decreases systematically with increasing adhesion strength. This decrease is quite pronounced, amounting to almost a factor of 2 when D increases from 0 to \(2\epsilon\). Also during the holding stage (ii), the load drop increases in magnitude with D, such that for the maximum \(D=2\epsilon\), the load necessary to hold the particle in the indent particle is almost zero. Finally, particle adhesion leads to a negative normal force in the retraction phase for all values of \(D>0\) as adhesion pulls the particle towards the substrate.

Note that these adhesion-induced features are considerably stronger for a rotating particle than for a non-rotating particle. For the latter, the load reduction in phase (i) was small except for the largest \(D=2\epsilon\), and loads after the holding phase were always positive, see Fig. 2 in Ref. [42].

Figure 3 shows the dislocation networks generated after full indentation [end of phase (i)], Fig. 3a, and after particle retraction [end of phase (iii)], Fig. 3b. The dislocation network shows a forward-backward asymmetry in that it is considerably more extended towards the direction into which atoms beneath the rotating particle are moved. In particular the emission of dislocation loops occurs predominantly, or even exclusively, into this direction. In addition, the dislocation network adherent to the indent pit is less extended for large adhesion strengths. This feature is even more pronounced after particle retraction.

Table 1 quantifies these features by assembling the total length of dislocations, \(L_{\text{disl}}\), in the network adherent to the indentation pit. The reduction in \(L_{\text{disl}}\) when D increases from 0 to \(2\epsilon\) amounts to 29 %, and 21 % for angular velocity \(\omega =0.115^\circ\)/ps. Note that the decrease of \(L_{\text{disl}}\) with D is not monotonic but is subject to fluctuations caused by the fact that dislocation emission, migration, and reactions are stochastic processes. For the non-rotating particle, no systematic trend of \(L_{\text{disl}}\) with D shows up. We characterize the size of the plastic zone developing under the indented particle by the plastic-zone radius \(R_{\text{pl}}\), defined as the maximum distance of a dislocation line in the dislocation network adherent to the indent particle from the center of the contact zone [56]. Here, a reduction of \(R_{\text{pl}}\) is visible for the rotating particle and also for the non-rotating particle. Only the rolling particle, \(\omega =0.115^\circ\)/ps, shows no reduction after full indentation; however, after particle retraction, also in this case a considerable reduction in \(R_{\text{pl}}\) of 39 % shows up. Instead of \(R_{\text{pl}}\), often the reduced size \(f=R_{\text{pl}}/R\) is used for discussions [57]; in our case, where the indenter radius R is kept fixed, this does not change the analysis.

We calculate the contact pressure during indentation as the ratio of the normal force, \(F_n\), and the contact area A. The contact area is easiest determined as

$$\begin{aligned} A^{\text{geo}}= \pi a_c^2, \end{aligned},$$
(4)

where \(a_c\) is the instantaneous contact radius, cf. Eq. (3). The contact pressure saturates after an indentation depth of 2 nm, such that the average of \(H^{\text{geo}}= F_n/A^{\text{geo}}\) is defined as the geometrical hardness. Note that the contact area may also be be determined atomistically by counting the substrate atoms contacting the particle and determining the atomistic contact area A from these, since it is only these which can transfer forces between the particle and the substrate [6]. This evaluation gives rise to the atomistically determined hardness, \(H=F_n/A\). Its value is slightly smaller than \(H^{\text{geo}}\), since A is somewhat larger than \(A^{\text{geo}}\).

We assemble the hardness values in Table 1. In agreement with our discussion of the normal forces above, we observe a strong decrease of hardness with increasing attraction. Particle rotation strongly enhances this effect.

Substrate atoms are transported under the rotating particle from the front towards the rear. This phenomenon is illustrated in Fig. 4 by coloring atoms with the distance they move backwards, i.e., in \([0\bar{1}0]\) direction, see Fig. 1. Even for a non-adhesive particle, \(D=0\), atom transport towards the rear is visible, resulting in an asymmetric pile-up. This transport is induced by the high shear stresses that are generated by the particle rotation in the immediate vicinity of the particle; even though substrate atoms do not adhere to the particle, the high hydrostatic pressure built up beneath the particle and the atomically rough particle surface allow the entrainment of substrate material with the particle rotation. This pile-up intensifies strongly with increasing adhesive strength. For \(D=1\epsilon\) and \(2\epsilon\), the pile-up at the rear of the indent pit continuously proceeds to form a cover on the particle; the arc of this cover spans the \(120^\circ\) the particle rotates during the indent phase. Note that the distance over which substrate atoms are transported under the particle are on average around 10 nm, but may even reach 14 nm. As the velocity of the rotating particle at the contact to the substrate amounts to \(v_{\text{roll}} = \omega R = 105\) m/s, the maximum possible path that an atom is transported during the indent time \(t_{\text{ind}} = 200\) ps amounts to \(v_{\text{roll}} t_{\text{ind}} = 21\) nm. Actual path lengths are shorter since we measure only the transport length along the \([0\bar{1}0]\) direction. In summary, Fig. 4 shows that a rotating particle leads to atom transport at its bottom side and adhesion strongly enhances this phenomenon.

The stress distribution inside the substrate follows largely the spatial distribution of dislocations generated. We provide in the SM [51] examples of the stress at the end of the indentation stage. The differences induced by varying adhesion strength D and rotation velocity \(\omega\) are minor and follow largely the discussion above of the changes in the plastic-zone size.

We conclude that particle-substrate adhesion induces major changes in the load necessary to indent the particle and also to keep it at maximum indentation depth. As a consequence, material hardness and the dislocation network formed decrease. The effect of adhesion is considerably more pronounced for a rotating particle than for a non-rotating particle because particle rotation strongly intensifies substrate atom transport beneath the particle.

3.2 Scratching

Fig. 5
figure 5

Evolution of the a normal and b tangential force with scratching length (Color figure online)

Full size image
Fig. 6
figure 6

Evolution of the friction coefficient with scratching length. Data have been averaged over a length of 4 Å (Color figure online)

Full size image
Table 2 Characteristics of the forces, friction coefficients, and torques acting—averaged over the last 7 nm of scratching—and the plastic zone produced after scratching and retraction of a particle rotating with various angular velocities \(\omega\)
Full size table

After full indentation of the particle to a depth \(d=4\) nm, the particle moves laterally sideways for a scratching length of 15 nm. Figure 5a displays the normal force that has to act on the particle in order to keep it at depth 4 nm, and Fig. 5b the lateral force needed to keep the particle at constant scratch velocity of 20 m/s.

We discuss first the normal forces. For a non-adhesive particle, \(D=0\), the force remains constant on the level it had after indentation, while for adhesive particles, the force rises initially, but assumes a plateau value after a scratching length of around 8 nm. The initial increase of \(F_n\) with scratching length characterizes an onset regime, in which the particle starts forming a scratch groove and the particle-substrate contact assumes equilibrium values. Note that for a non-rotating particle, the normal force decreases in this onset regime [23, 24], since the rear half of the particle loses contact with the substrate during scratching, even for an adhesive particle [42]; thus less load is needed to keep the particle at constant depth. For a rotating particle, this situation is different; as during rotation, constantly new material is transported from the front part of the particle towards the rear part, it requires a larger load to keep the particle at the prescribed depth. We note that for small angular rotation velocities, the onset regime first features the drop in normal force – as for a non-rotating particle—before the force later rises to values above those needed for indentation, see the SM [51].

These results are quantified in Table 2, where the average values of the forces—averaged over the last 7 nm of scratching where the forces have assumed equilibrium values—are assembled. They show that in all cases, the normal force decreases with increasing adhesion strength; this result is analogous to our findings for the indentation stage. In addition, \(F_n\) rises when \(\omega\) increases from 0 to \(\omega _{\text{sf}}=0.115^\circ\)/ps. Note that this rotation velocity is special since it specifies the case of slip-free rolling. For larger \(\omega\), \(\omega =0.6^\circ\)/ps, \(F_n\) decreases again since now rotation also allows for slip of the particle over the substrate surface since \(\omega > \omega _{\text{sf}}\). Slipping during scratch reduces the load needed to keep the particle at constant depth.

For the tangential force, \(F_t\), Fig. 5b also features the onset regime, in which \(F_t\) increases with scratching length before reaching saturation values at around 8 nm. This increase is a common feature in scratching, both for non-adhesive [23] and adhesive [42] particles. It is caused by the fact that before starting the scratch, due to symmetry, the tangential force must be 0; then during scratch it rises to its saturation value. Note that—in contrast to a non-rotating particle [38]—the tangential force after indentation does not vanish: The rotating particle exerts a negative tangential force—i.e., in the direction of rotation at the bottom of the particle—on the substrate. This force is already present for a repulsive particle, but increases in magnitude with adhesion strength.

The equilibrium values of the tangential force are assembled in Table 2. An overall increase of \(F_t\) with adhesion strength is observed, which was already found for a non-rotating particle [42], and which is due to the fact that adhesion bonds substrate atoms to the particle, thereby augmenting its tangential area and enlarging the resistance of the substrate against particle motion. As a second characteristics, \(F_t\) strongly sinks with increasing rotation velocity. Such a decrease has already been observed for a non-adhesive rotating particle and is caused by the fact that rolling motion assists the forward motion of the particle by transporting material backwards from the front of the groove towards the rear [38]. These two trends clash for the large rotation velocity, \(\omega =0.6^\circ\)/ps, when D rises from 0 to \(0.5\epsilon\). Here, the increase in D leads to a reduction of \(F_t\), since it is the adhesion that allows for efficient transport of substrate material from the front of the particle to its rear.

The ratio of tangential to normal force defines the friction coefficient, \(\mu =F_t/F_n\). Its evolution with scratching length is given in Fig. 6, and its saturation values are assembled in Table 2. The friction coefficient shows considerable fluctuations in the onset regime for the case of strongest adhesion, \(D=2\epsilon\); these are mainly caused by the fact that \(F_n\) changes sign at around 2 nm scratch length, see Fig. 5a. The saturation values, Table 2, can be discussed by comparing to a simple geometrical prediction [58],

$$\begin{aligned} \mu ^{\text{geo}} = \frac{A_{\text{trans}}^{\text{geo}}}{A_{\text{norm}}^{\text{geo}}}. \end{aligned}$$
(5)

Here, the normal contact area, \(A_{\text{trans}}^{\text{geo}}=\pi a_c^2/2\), is assumed to be of a semi-circular form with radius \(a_c\), Eq. (3), while the tangential contact area is given by the circular segment of the particle submersed in the substrate. Eq. (5) assumes that the hardness values in normal and tangential direction are identical. For our geometry, it is \(A_{\text{norm}}^{\text{geo}}= 100.5\) nm\(^2\), \(A_{\text{trans}}^{\text{geo}}= 44.7\) nm\(^2\) and hence \(\mu ^{\text{geo}} = 0.45\).

Previous work [42] showed that this value describes well the friction coefficient of a non-rotating repulsive particle immediately at the end of the onset regime. In the saturation regime, \(\mu\) increases to a value of 0.57, see Table 2, due to the pile-up forming in front of the particle. With increasing adhesion strength, the friction coefficient of the non-rotating particle increases due to the increase of the tangential force and the concomitant decrease of the normal force discussed above.

The trend of an increasing friction coefficient with increasing D holds true for all rotation velocities investigated, but is not as pronounced as for the non-rotating particle. This is caused by the counteracting trends of \(F_t\) increasing with D but decreasing with \(\omega\): for larger values of \(\omega\), \(F_t\) does not strongly rise or even decreases with D since adhesion assists the transport of substrate atoms from the particle front to its back as described above. Note also that \(\mu\) assumes values smaller than for the non-rotating particle and often even smaller than the geometrical estimate, Eq. (5), even though pile-up formation would lead to a friction coefficient larger than \(\mu ^{\text{geo}}\). This is mainly caused by the small tangential forces for rotating particles as described above.

This decrease of the friction coefficient for a rotating particle constitutes the main finding of this study. One might have naively assumed that adhesive particles have a higher friction coefficient than non-adhesive particles, since adhesion increases the tangential force. However, the transport of substrate material from the front towards the back of the particle is intensified by adhesion, and this process reduces the tangential force and hence the friction coefficient.

We conclude that the scratch dynamics of a rotating particle is considerably different from that of a non-rotating particle. As rotational motion helps transporting substrate material from the front of the particle to its rear side, the tangential force is diminished with rotation. This effect is strongly intensified for adhesive particles. In addition, adhesive particles require less load to keep them at constant depth in the substrate. In total, the friction coefficient shows only little increase, or even a decrease, with adhesion for rotating particles. This is in contrast to non-rotating particles which feature a strongly increasing friction coefficient with adhesion strength.

3.3 Work

Table 3 Total work W and its contributions \(W_f\), Eq. (6), and \(W_\tau\), Eq. (7), during the indent and scratch phases
Full size table
Fig. 7
figure 7

Evolution of the torque during the a indentation and b scratch phase (Color figure online)

Full size image

We calculate the total work \(W = W_f + W_\tau\) done by the particle as composed of two contributions: the work done by the forces,

$$\begin{aligned} W_f= \int F v \, {\text{d}}t , \end{aligned}$$
(6)

and the work done by the torque \(\tau\),

$$\begin{aligned} W_\tau = \int \omega \tau \, {\text{d}}t . \end{aligned}$$
(7)

For \(W_f\), only the force parallel to the particle velocity is needed, i.e., the normal force for indentation and the tangential force during scratch. For \(W_\tau\), the torque \(\tau\) exerted on the particle in the direction of \(\omega\) is determined.

We display the evolution of the torque with indentation depth in Fig. 7a and with scratching length in Fig. 7b. During the indentation phase, the torque grows continuously with indentation depth, similar to the normal force in Fig. 2. Adhesion increases the torque, as it is plausible since adhesion increases the interaction of the particle with the substrate; note that this is in contrast to the normal force, which is decreased by adhesion.

Also during scratch, adhesion increases the torque. For vanishing adhesion, \(D=0\), the torque is less than the value at full indentation; this is due to the fact that the particle is not fully immersed in the substrate during the scratch phase. The values of torque, averaged over the last 7 nm of scratching, are included in Table 2.

For the small angular velocity, \(\omega _{\text{sf}}=0.115^\circ\)/ps, the torque decreases during the onset phase of scratching, see the SM [51]; its value after the onset phase is reduced by almost one order of magnitude compared to the larger angular velocity, \(\omega = 0.6^\circ\)/ps, cf. Table 2. The smallness of the torque is caused by the fact that at this angular velocity, the particle rolls without sliding, thus reducing the interaction with the substrate.

The contributions to the work done by the rotating particle are assembled in Table 3. During indentation, \(W_f\) decreases with adhesion strength D, analogously to the normal force \(F_n\), see Fig. 2, while the work done by the torque, \(W_\tau\), increases. The total work done, W, decreases with adhesion strength for \(\omega \le \omega _{\text{sf}}\), since \(W_\tau\) is negligible, but increases with D for the high angular frequency \(\omega =0.6^\circ\)/ps, since here \(W_\tau\) is dominant. In all cases studied, the work during indentation is larger for a rotating particle than for a non-rotating particle.

This situation is changed during the scratch phase. Here the total work done for the rolling particle, \(\omega = \omega _{\text{sf}}\), is smaller than for a non-rotating and for a fast rotating particle, see Table 3. This is caused by the fact that (i) the work \(W_f\) decreases for a rotating particle with \(\omega\), since the tangential force decreases, see Table 2; (ii) the work \(W_\tau\) increases with rotation, but this increase is only mild for \(\omega = \omega _{\text{sf}}\), as here the torque is small. The dependence of \(W_f\) on the adhesion strength D closely follows that of the tangential force; and similarly for \(W_\tau\), which follows the torque.

We conclude that scratching with a rotating particle costs least work if the particle rolls without slip over the surface. In this case, the decrease in the tangential force and in the work done by this force is larger than the additional work needed to keep the particle rolling (\(W_\tau\)).

3.4 Plasticity, Groove, Pile-Up, and Adhesion to Particle

Fig. 8
figure 8

Snapshots of the defects formed after scratching and retraction of the particle. Color code as in Fig. 3 (Color figure online)

Full size image
Fig. 9
figure 9

Snapshots showing the scratch groove and pile-up after scratching and retraction of the particle. Color denotes height above the original surface (Color figure online)

Full size image
Fig. 10
figure 10

View of the particle after scratching and retraction. The spherical particle is in gray. Color denotes height of Fe atoms above the original surface and illustrates the adhesion of substrate atoms to the particle (Color figure online)

Full size image

Figure 8 displays the dislocation network built up during the scratching process, after retraction of the particle. The forward-backward asymmetry observed after indentation, Fig. 3, has been destroyed during the scratching process, as the particle moved towards the right-hand side and added dislocations in that direction. However, the pronounced reduction of the size of the plastic zone and the amount of damage produced with increasing adhesion strength are clearly seen. The values of the total dislocation length, \(L_{\text{disl}}\), assembled in Table 2 quantify this reduction. It is even larger for scratching—reaching reductions of 35–40 % when increasing D from 0 to \(2\epsilon\)—while for indentation it was 29 % at maximum. Note that also for the non-rotating particle, increasing D leads to a considerable reduction in \(L_{\text{disl}}\) [42]. The reduction in the size and length of the dislocation network is in agreement with the smaller normal forces needed to hold the particle at its depth.

The scratch groove is displayed in Fig. 9 after scratching and retraction of the particle. Let us first discuss the case of a repulsive particle, \(D=0\). The structure of the pile-up for a repulsive particle exhibits a left-right symmetry caused by the {111} slip directions operating for material transport to the surface [23] which populate the pile-up at an angle of \(45^\circ\) to the front of the groove. Due to the particle rotation, material is also transported towards the back of the groove; this feature is absent for a non-rotating particle [23].

Adhesion leads to a rough groove bottom, as has already previously been observed for non-rotating adhesive particles in the case of indentation [42]. Additionally, particle rotation leads to oscillatory patterns in the groove bottom, which can be seen most clearly for \(D=0.5\epsilon\). Such patterns have been observed for (repulsive) rotating particles previously only for considerably higher rotation velocities [38]. Note that for the smaller rotation velocity, \(\omega =0.115^\circ\)/ps, the groove bottom shows a significantly reduced roughness, see Fig. S6 in the SM [51], indicating that only at rotation velocities considerably exceeding the roll-without-slip condition, significant roughness is produced. For a rolling particle, \(\omega =\omega _{\text{sf}}\), where there is no backward material transport and also the scratching work is minimum, see Sect. 3.3, the groove bottom remains smooth. The systematic pile-up structure observed for the repulsive particle is destroyed for adhesive particles, even for small adhesion strength. In particular the frontal pile-up generated by {111} slip is destroyed as substrate atoms adhere to the particle and are removed from the surface. Interestingly, the pile-up at the backside of the groove continues to show the left-right symmetry, as substrate atoms are shoveled back under the rotating particle and are brought to the surface by backwards {111} slip. We note that even for the small adhesive strength of \(D=0.5\epsilon\), substrate atoms are occasionally bound to the particle and roll over its surface, but they are eventually re-inserted into the substrate.

Figure 10, finally, shows the material adherent to the particle after retraction. For the cases of \(D=0\) and \(D=0.5\epsilon\), no substrate atoms are found adherent to the particle after retraction. For \(D=1\epsilon\), around 50 % of the particle surface area are covered by substrate atoms while for \(D=2\epsilon\), the particle surface is completely covered by substrate atoms at all places that contacted the substrate. Besides substrate atoms directly bonded to the particle, also some atoms are found in a second-layer shell and even farther out around the particle, cf. also Fig. 4 for the substrate cover of the particle after indentation. Thus, \(D=1\epsilon\) constitutes an intermediate case, where the particle becomes only partially covered, while for \(D=2\epsilon\), the particle is fully covered with the exception of two spots at the rotation axis which never got into contact with the substrate since the particle was only immersed by 4 nm into the substrate. Note that for the rotation velocity used here, \(\omega =0.6^\circ\)/ps, the particle rotates a total angle of \(450^\circ\) during the scratch process.

We conclude that adhesion of the substrate material to the particle leads to a strong reduction of the dislocation network formed and the size of the plastic zone; this is in agreement with the smaller normal forces needed during scratching In addition, it roughens the groove bottom strongly and changes the pile-up structure.

4 Summary

We used molecular dynamics simulation to study the indentation and scratch of an Fe surface by a rotating adhesive particle. During the indentation phase, adhesion systematically decreases the load needed for indentation. This effect is considerably more pronounced than for a non-rotating particle, as rotation helps material removal out of the indentation pit. In particular, we could demonstrate a considerable substrate atom transport beneath the rotating particle from its front to its back side, As a consequence, also the effective material hardness is decreased. The strength of this effect increases with particle rotation velocity. Simultaneously, the dislocation network built up during penetration is reduced for stronger particle adhesion. This agrees with the reduced hardness and reduced normal force needed to indent.

Also in the scratch phase, the normal force during scratch decreases. In addition, the tangential force increases. The effect on the tangential force is not as pronounced as with a non-rotating particle, as the substrate material in contact with the particle is constantly exchanged with rotation. In the friction coefficient, both effects combine, such that the friction coefficient increases with adhesion strength. However, the effect is smaller for a rotating particle than for a non-rotating particle as rotation assists the transport of substrate material from the front to the back of the particle and thereby diminishes the tangential force. This is possible even for a purely repulsive particle, but is considerably more effective for an adhesive particle. Similar to the indentation phase, the dislocation network formed by scratching is reduced for stronger particle adhesion.

For non-rotating particles, during the onset regime of scratching, the normal load sinks; for a rotating particle, however, it increases. This is again caused by the particle transporting material from the front of the groove towards the back.

The groove and pile-up formed by scratching particles are affected by both rotation velocity and adhesion strength. Considerable atomic roughness at the groove bottom is caused by substrate atom adhesion to the particle while the particle gets partially covered with substrate atoms.

The total work needed for scratching shows an interesting dependence on rotation velocity in that it is minimum for particles rotating with the no-slip rolling velocity, \(\omega _{\text{sf}}\). In this case, the decrease in the tangential force overcompensates the additional work needed to keep the particle rolling. In this sense, a rolling particle induces the most efficient scratching process. For indentation, we do not find such a compensation process: rotating particles always require more work for indentation than the non-rotating particle. However, here the situation of ‘drilling’—with the rotation axis perpendicular to the surface—should be studied to assess whether drilling with the no-slip rolling velocity also reduces the total work. To our knowledge, such a study has not yet been performed.

The results presented here can provide a model scenario of the processes occurring when a surface is scratched by a moving particle that can undergo both translation and rotation. In reality, where translational and rotational motion are not prescribed but may evolve freely under the influence of external forces and torques—for instance, by the dynamics of an embedding fluid—the processes may be more involved.

The effect of rotating particles on the substrate will strongly depend on the particle shape. While the effect of indenter shape on the processes of indentation, scratching, and cutting has been discussed in MD simulations of non-rotating particles [24, 59, 60], such a discussion is still lacking for rotating particles.