An EHL Extension of the Unsteady FBNS Algorithm

Abstract

Many engineering applications rely on lubricated gaps where the hydrodynamic pressure distribution is influenced by cavitation phenomena and elastic deformations. To obtain details about the conditions within the lubricated gap, solvers are required that can model cavitation and elastic deformation effects efficiently when a large amount of discretization cells is employed. The presented unsteady EHL-FBNS solver can compute the solution of such large problems that require the consideration of both mass-conserving cavitation and elastic deformation. The execution time of the presented algorithm scales almost with $N\log (N)$ where N is the number of computational grid points. A detailed description of the algorithm and the discretized equations is presented. The MATLAB$^{\copyright }$ code is provided in the supplements along with a maintained version on GitHub to encourage its usage and further development. The output of the solver is compared to and validated with analytical, simulated, and experimental results from the literature to provide a detailed comparison of different discretization schemes of the Couette term in presence of gap height discontinuities. As a final result, the most favorable scheme is identified for the unsteady study of surface textures in ball-on-disc tribometers under EHL conditions.

1 Introduction

In the case of lubrication flows in narrow gaps, the Reynolds equation [1] is a handy tool to determine the hydrodynamic pressure distribution in a simpler way than by using the full Navier-Stokes Equations (NSE) [2, Ch. 7]. Since cavitation commonly occurs in lubrication flows, various models have been developed to describe this phenomenon [3]. Especially when it occurs within surface textures, mass-conserving properties of the cavitation model are required to properly describe the flow’s transition from the cavitation region to the full-film region, because this full-film reformulation interface has a great effect on the extension of the cavitated area and the subsequent downstream rise in pressure within the full-film region [4]. The required mass-conserving properties can be taken into account with the Jakobsson-Floberg-Olsson (JFO) [5, 6] cavitation model [3]. Starting from the cavitation algorithm of Elrod [7], Giacopini et al. [8] developed a one-dimensional finite element method (FEM) solver that couples the Reynolds equation with the mass-conserving JFO cavitation model through a complementarity formulation. This work was extended by Bertocchi et al. [9] to consider two-dimensional problems with compressible, piezoviscous, and shear-thinning fluid behavior. The arising complementarity problem was reformulated to be expressed by an unconstrained equation system by Woloszynski et al. [10], resulting in the Fischer-Burmeister-Newton-Schur (FBNS) algorithm. As demonstrated by Woloszynski et al., the FBNS algorithm is of remarkable computational efficiency also for high spatial resolutions.

In many cases, the hydrodynamic pressure can deform the lubricated surfaces notably leading to the regime of Elasto-Hydrodynamic Lubrication (EHL) [11]. Various solvers have been developed to tackle EHL problems, some of the most prominent ones are the finite difference method (FDM) Multigrid solver of Venner and Lubrecht [12] and the FEM solver of Habchi [13]. Some algorithms are also capable of simulating surface contact along with the Reynolds equation [14,15,16,17,18]. Since the full-film reformulation interface is often not of relevance in EHL problems, many EHL solvers do not employ mass-conserving cavitation models. However, in some cases - such as starved lubrication—mass-conserving cavitation is crucial and has been considered in several works [19, 20]. Among them, the coupling of pressure, mass-conserving cavitation, elastic deformation, a roughness asperity contact model and the FBNS algorithm was achieved by Ferretti [21, 22]. In contrast to Ferretti’s work, the FBNS algorithm is coupled with the elastic deformation of an elastic half-space within this paper, thus presenting the new EHL-FBNS algorithm. Due to the half-space assumption, the elastic deformation is a linear convolution of a kernel function with the hydrodynamic pressure field. This allows exploiting the fast Fourier transformation (FFT) to speed up the computation of the elastic deformation [23]. Furthermore, a proportional integral derivative (PID) controller is employed to meet the load balance equation through adjustment of the rigid body displacement as already introduced by Wang et al. [24]. Eventually, the EHL-FBNS algorithm is capable of efficiently computing the solution of large problems that require the consideration of both mass-conserving cavitation and elastic deformation at the same time.

In the beginning of this paper, the basic equations and the general procedure of the EHL-FBNS algorithm are summarized. The algorithm is implemented in MATLAB$^{\copyright }$ with the finite volume method (FVM) and a generic order spatial discretization scheme for the Couette term of the Reynolds equation. The discretized equations are supplied in Appendix. Then, the performance of the steady EHL-FBNS implementation is compared to the original FBNS algorithm of Woloszynski et al. [10]. Afterward, one- and two-dimensional literature reference cases [9, 25] of a convergent slider with rectangular pocket are used to compare the EHL-FBNS output to analytical and simulated reference results, assess the influence of the discretization order of the Couette term in the presence of gap height discontinuities through grid convergence studies and give an example case where both mass-conserving cavitation and elastic properties of the solver are required. Moreover, unsteady EHL-FBNS simulations are performed for the set-up of a single texture that passes through the EHL contact of a ball-on-disc tribometer. The results are compared to experimental and simulated data of Mourier et al. [26]. This allows to demonstrate the stability of the EHL-FBNS algorithm under EHL operating conditions with discontinuous surface textures and to provide recommendations about the most suitable discretization scheme. Eventually, the EHL-FBNS algorithm is validated for surface texture investigations with ball-on-disc tribometers under unsteady EHL operating conditions.

The MATLAB$^{\copyright }$ code, set-up, and visualization scripts are provided in the supplements. The MATLAB$^{\copyright }$ scripts are thoroughly commented to encourage their usage and further development. A maintained and publicly available version of the code can also be found on GitHub: https://github.com/ErikHansenGit/EHL.

2 Numerical Methods

2.1 Governing Equations

Fig. 1

Schematic sketch of the lubricated gap

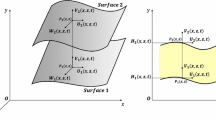
The lubrication flow in a narrow gap (schematically depicted in Fig. 1) is governed by the Reynolds equation considering mass-conserving cavitation with the JFO model [5, 6] at any set of spatial coordinates $x_1$ and $x_2$ and time t [9]:

$$\begin{aligned} \frac{\partial }{\partial x_1}\left( \frac{\rho _l h^3}{12 \mu _l} \frac{\partial p}{\partial x_1} \right) +\frac{\partial }{\partial x_2}\left( \frac{\rho _l h^3}{12 \mu _l} \frac{\partial p}{\partial x_2} \right) -\frac{\partial }{\partial x_1}\left( \rho _l h u_{\text{m}} \left( 1-\theta \right) \right) - \frac{\partial }{\partial t}\left( \rho _l h \left( 1-\theta \right) \right) =0. \end{aligned}$$

(1)

In this equation, h denotes the gap height, $\rho _l$ is the density of the liquid phase and $\mu _l$ describes the dynamic viscosity of the liquid phase. All of them can vary in space and time. The mean velocity $u_m=\frac{U_{\text {up}}+U_{\text {low}}}{2}$ is composed of $U_{\text {up}}$ as the velocity of the upper surface and $U_{\text {low}}$ as the velocity of the lower surface in $x_1$-direction. The relative pressure $p=p_{\text {hd}}-p_{\text {cav}}$ and the cavity fraction $\theta = 1 - \frac{\rho }{\rho _l}$ are the solution variables, where $\rho$ is the mixture density of the flow. The hydrodynamic pressure $p_{\text {hd}}$ is prevented from falling below the cavitation pressure $p_{\text {cav}}$ by adding the following complementary constraints [9]:

$$\begin{aligned} p\cdot \theta = 0, \quad p \ge 0, \quad \theta \ge 0. \end{aligned}$$

(2)

Depending on whether the liquid phase is modeled as iso- or piezoviscous through the Barus or Roelands model, its dynamic viscosity reads [12, Ch. 1.3.3], [27]:

$$\begin{aligned} \mu _{l} = {\left\{ \begin{array}{ll} \mu _0,\\ {\mu _0\exp \left( \alpha _B\left( p_{\text {hd}}-p_{\text {cav}}\right) \right) }\\ \mu _0\exp \left( \left( \ln \left( \mu _0 \right) + 9.67 \right) \cdot \left( -1 + \left( 1 + \frac{\left( p_{\text {hd}} - p_{\text {cav}} \right) }{p_{0,R}} \right) ^{z_R} \right) \right) , \end{array}\right. } \end{aligned}$$

(3)

where $z_R=\frac{\alpha _R p_{0,R}}{\ln \left( \mu _0 + 9.67 \right) }$ [26] is the pressure viscosity index, $\alpha _B$ and $\alpha _R$ denote the pressure viscosity coefficient and $p_{0,R}$ is a constant in the Roelands equation. The dynamic viscosity of the liquid phase at ambient pressure is $\mu _0$. Moreover, depending on whether the liquid phase is assumed to be of constant density or to be compressible according to the Dowson-Higginson model, the liquid phase density is given by [12, Ch. 1.3.4], [9, 27]:

$$\begin{aligned} \rho _l = {\left\{ \begin{array}{ll} \rho _0,\\ \rho _0 \frac{C_1 + C_2 \left( p_{\text {hd}} - p_{\text {cav}} \right) }{C_1 + \left( p_{\text {hd}} - p_{\text {cav}} \right) }, \end{array}\right. } \end{aligned}$$

(4)

where $\rho _0$ is the density of the liquid phase at ambient pressure and $C_1$ and $C_2$ are constants.

The gap height h can be constructed as a superposition of the rigid body displacement of the two surfaces $h_{\text{d}}$, the variation of the gap height due to the rigid geometry of the surfaces $h_{\text{g}}$ and the elastic deformation of the gap height $h_{\text{el}}$ due to the hydrodynamic pressure [2, Ch. 19.2]:

$$\begin{aligned} h = h_{\text {d}} + h_{\text {g}} + h_{\text {el}}. \end{aligned}$$

(5)

Depending on whether the upper and lower surfaces are assumed to be rigid or elastic half-spaces, the elastic deformation of the gap height can be expressed as [12, Ch. 1.3.5]:

$$\begin{aligned} h_{\text{el}}\left( x_1,x_2 \right) = {\left\{ \begin{array}{ll} 0, \\ \frac{2}{\pi E'}\int _{-\infty }^{+\infty }\int _{-\infty }^{+\infty } \frac{p_{\text {hd}}\left( x_1',x_2' \right) }{\sqrt{\left( x_1-x_1' \right) ^2 + \left( x_2-x_2' \right) ^2}} \mathrm {d}x_1' \mathrm {d}x_2', \end{array}\right. } \end{aligned}$$

(6)

where the reduced elastic modulus is stated as [12, Ch. 1.3.5]:

$$\begin{aligned} E' = \frac{2}{\frac{1-\nu _{\text {low}}^2}{E_{\text {low}}}+\frac{1-\nu _{\text {up}}^2}{E_{\text {up}}}}. \end{aligned}$$

(7)

In this equation, E denotes the corresponding Young’s modulus and $\nu$ the Poisson ratio of the upper and lower surface. If a constant rigid body displacement $h_{\text{d}}$ is prescribed, the provided set of equations is sufficient to describe the EHL problem. If, however, a constant imposed normal load force $F_{N,\text {imp}}$ is prescribed, it needs to be satisfied by the normal force $F_N$ resulting from the hydrodynamic pressure profile [28]:

$$\begin{aligned} F_{N,\text {imp}} = F_N = \int _{-\infty }^{+\infty }\int _{-\infty }^{+\infty } p_{\text {hd}} - p_{\text {amb}}\mathrm {d}x_1 \mathrm {d}x_2, \end{aligned}$$

(8)

where $p_{\text {amb}}$ is the ambient pressure. The rigid body displacement $h_{\text{d}}$ needs to be set such that the load balance Equation (8) is fulfilled.

2.2 EHL-FBNS Algorithm

The set of equations described above can be solved numerically with the EHL-FBNS algorithm presented in the following. This new algorithm is based on the FBNS algorithm developed by Woloszynski et al. [10] and extends it by taking elastic surface deformation and the load balance equation into account. First of all, the dimensionless Reynolds equation considering mass-conserving cavitation is defined as:

$$\begin{aligned} G = \underbrace{\frac{\partial }{\partial x_1^*}\left( \xi _{\text{Po}}^*\frac{\partial p^*}{\partial x_1^*} \right) + \left( \frac{x_{1,ref}}{x_{2,ref}} \right) ^2\frac{\partial }{\partial x_2^*}\left( \xi _{\text{Po}}^*\frac{\partial p^*}{\partial x_2^*} \right) }_{\mathrm {Poiseuille \, term}} \underbrace{- \frac{\partial }{\partial x_1^*}\left( \xi _{\text{Co}}^* \left( 1 - \theta \right) \right) }_{\mathrm {Couette \, term}} \underbrace{- \frac{\partial }{\partial t^*}\left( \xi _{\text{Ti}}^* \left( 1 - \theta \right) \right) }_{\mathrm {Unsteady \, term}}. \end{aligned}$$

(9)

It can be derived by inserting the following non-dimensional quantities (indicated by $^*$) and reference quantities (denoted by the index $_{ref}$) into and reformulating Equation (1):

$$\begin{aligned} \begin{aligned}&x_1 = x_1^*x_{1,ref}, \quad x_2 = x_2^*x_{2,ref}, \quad t = t^*t_{ref}, \quad \rho _l = \rho ^* \rho _{ref}, \\&\quad \mu _l = \mu ^* \mu _{ref}, \quad h = h^*h_{ref}, \quad u_{\text{m}} = u_{\text{m}}^*u_{\text{m},ref}, \quad p = p^*p_{ref}. \end{aligned} \end{aligned}$$

(10)

Similar to Venner and Lubrecht [12, Ch. 6.3], the coefficients of the Poiseuille, Couette, and unsteady term within the dimensionless Reynolds equation can be consolidated as:

$$\begin{aligned} \xi _{\text{Po}}^* = \frac{\rho ^*h^{*3}}{\mu ^*}, \quad \xi _{\text{Co}}^* = 12\frac{ x_{1,ref} u_{\text{m},ref} \mu _{ref}}{h_{ref}^2 p_{ref}}\rho ^* h^* u_{\text{m}}^*, \quad \xi _{Ti}^* = 12 \frac{x_{1,ref}^2 \mu _{ref}}{t_{ref} h_{ref}^2 p_{ref}}\rho ^* h^*. \end{aligned}$$

(11)

The complimentary constraints (2) are replaced by the Fischer-Burmeister equation in non-dimensional form [10]:

$$\begin{aligned} F = p^* + \theta - \sqrt{p^{*2} + \theta ^2}. \end{aligned}$$

(12)

The EHL-FBNS algorithm uses the Newton-Raphson method to determine the values of $p^*$ and $\theta$ such that G and F get sufficiently close to 0, thus solving the dimensionless Reynolds Equation (9) and the dimensionless Fischer-Burmeister Equation (12). By evaluating the discretized form of G and F at each discrete position, an equation system is created. The discretized equations are obtained though the FVM, where the second-order midpoint rule is applied to evaluate surface and volume integrals. The required values and derivatives of the Poiseuille term are discretized with a second-order central scheme, of the Couette term by either the first-order upwind interpolation (UI) or the third-order quadratic upwind interpolation (QUICK) and the unsteady term with the first-order Euler implicit scheme [29, Chs. 3.3, 4, 6.3.2]. The discretized expressions of Equations (9) and (12) are provided in Appendix A.1. The set of discrete dimensionless Reynolds equations $\vec {G}$ can be expressed in matrix-vector notation through the pressure coefficients contributed by the Poiseuille term $A_{\text{Po}}$, the discretized dimensionless relative pressures $\vec {p^*}$, the cavity fraction coefficients contributed by the Couette and unsteady term B, the discretized cavity fractions $\vec {\theta }$, and the remaining constants from the Couette and unsteady term $\vec {c}$ [10]:

$$\begin{aligned} \vec {G} = A_{\text{Po}}\vec {p^*} + B \vec {\theta } + \vec {c}. \end{aligned}$$

(13)

The set of discrete dimensionless Fischer-Burmeister Equations (12) are denoted by $\vec {F}(\vec {p^*},\vec {\theta })$. The non-dimensional properties $\mu ^*$ and $\rho ^*$ at each discrete point are computed according to the respective Eqs. (3, 4 and 10).

The gap height h at each discrete point is computed according to Eqs. (5 and 6). It is prevented from becoming lower than 1 $\mathrm {nm}$ by using truncation at this instant. Afterward, the non-dimensional gap height $h^*$ is determined through Equation (10). If the surfaces are chosen to be elastic, Equation (6) is discretized by assuming a constant pressure over the rectangular discretization cell [30, Ch. 3.3], [31, Ch. 3.1], the discretized equation is also provided in Appendix A.2. Since the resulting equation is a linear convolution of a kernel function with the hydrodynamic pressure field, it is computed in Fourier space by means of FFT to speed up the computation. Attention is paid to double the size of the kernel in each direction and to zero pad the hydrodynamic pressure field such that a linear instead of a circular convolution is obtained. After the convolution, the deformation and pressure fields are resized to their original size [23, 32, 33].

After computing $\vec {G}$ and $\vec {F}$, the Newton-Raphson method is used to determine the updates of non-dimensional relative pressure $\vec {\delta }_{p^*}$ and cavity fraction $\vec {\delta }_{\theta }$ [10]:

$$\begin{aligned} J \vec {\delta } =\begin{bmatrix} J_{F,p^*} &{} J_{F,\theta } \\ J_{G,p^*} &{} J_{G,\theta } \end{bmatrix} \begin{bmatrix} \vec {\delta }_{p^*} \\ \vec {\delta }_{\theta } \end{bmatrix} = - \begin{bmatrix} \vec {F} \\ \vec {G} \end{bmatrix} \end{aligned}$$

(14)

The most important extension of the EHL-FBNS algorithm compared to the original FBNS algorithm is the approximation of the pressure Jacobian $J_{G,p^*}$ of the dimensionless Reynolds equation when elastic deformation is taken into account. The idea is to consider the dependence $h^*(p^*)$ by inserting it into $\vec {c}$, thus creating the matrix $A_{\text{h}}$. Due to the kernel function, this would result in $A_{\text{h}}$ being a full matrix which is prone to lose its diagonal dominance and therefore being unfeasible to invert and likely to cause unstable behavior in the iteration process. This is rectified by approximating $A_{\text{h}}$ only by some of its diagonals as already done in the literature for other EHL algorithms: for example, Venner and Lubrecht [12, Chs. C.1, C.3.2] who combine it with distributive relaxation and multigrid methods or Wang et al. [15] who employ the semi-system method. In case of the EHL-FBNS algorithm, $A_{\text{h}}$ is reduced to the 5 diagonals that correspond to the South, West, Center, East, and North cells. Eventually, the Jacobians of $\vec {G}$ read $J_{G,p^*}= A_{\text{Po}} + A_{\text{h}}$ and $J_{G,\theta } = B$. The boundary conditions of $\vec {p^*}$ are considered in $A_{\text{Po}}$ and $\vec {c}$ and the boundary conditions of $\vec {\theta }$ in $\vec {F}$ and $J_{F,\theta }$. If Neumann boundary conditions are used for $\vec {\theta }$, the Jacobian $J_{F,\theta }$ would contain several diagonals. In this case, it is approximated only by its main diagonal. It is worthwhile to note that this approximation of the Jacobians eventually only affects the updates of non-dimensional relative pressure $\vec {\delta }_{p^*}$ and cavity fraction $\vec {\delta }_{\theta }$, but never the computation of $\vec {G}$ and $\vec {F}$. The discrete formulations of the Jacobians $J_{G,p^*}= A_{\text{Po}} + A_{\text{h}}$ and $J_{G,\theta }=B$ are provided in Appendix A.1 and A.3. The center entries of the Jacobians of the dimensionless Fischer-Burmeister equation $J_{F,p^*,C}$ and $J_{F,\theta ,C}$ for each discrete point are [10]:

$$\begin{aligned}&J_{F,p^*,C} = 1 - \frac{p_{C,\text {aux}}^*}{\sqrt{p_{C,\text {aux}}^{*2} + \theta ^2_{C,\text {aux}}}}, \end{aligned}$$

(15)

$$\begin{aligned}&J_{F,\theta ,C} = 1 - \frac{\theta _{C,\text {aux}}}{\sqrt{p_{C,\text {aux}}^{*2} + \theta ^2_{C,\text {aux}}}} \end{aligned}$$

(16)

Here, $p_{C,\text {aux}}^*$ and $\theta _{C,\text {aux}}^*$ are the auxiliary dimensionless pressure and cavity fraction which are adjusted such that $J_{F,p^*}$ and $J_{F,\theta }$ do not become singular [10]. To prevent them from having center entries close to zero within the range $(-\varepsilon , \varepsilon )$, they are adjusted as:

$$\begin{aligned}&p_{C,\text {aux}}^* = {\left\{ \begin{array}{ll} p_{C}^* &{} \text {if } p_{C}^* \ge \varepsilon \text { or } p_{C}^* \le -\varepsilon , \\ \varepsilon &{} \text {if } 0 \le p_{C}^*< \varepsilon , \\ -\varepsilon &{} \text {if } -\varepsilon< p_{C}^* <0, \\ \end{array}\right. } \end{aligned}$$

(17)

$$\begin{aligned}&\theta _{C,\text {aux}} = {\left\{ \begin{array}{ll} \theta _{C} &{} \text {if } \theta _{C} \ge \varepsilon \text { or } \theta _{C} \le -\varepsilon , \\ \varepsilon &{} \text {if } 0 \le \theta _{C}< \varepsilon , \\ -\varepsilon &{} \text {if } -\varepsilon< \theta _{C} <0, \\ \end{array}\right. } \end{aligned}$$

(18)

where machine epsilon is given by $\varepsilon \approx 2.2204 \cdot 10^{-16}$. As already done in the original FBNS algorithm, the corresponding columns of the Jacobian J and rows of the updates $\vec {\delta }$ are swapped if $J_{F,p^*,C}<J_{F,\theta ,C}$ to obtain a reordered system [10]:

$$\begin{aligned} \begin{bmatrix} A_F &{} B_F \\ A_G &{} B_G \end{bmatrix} \begin{bmatrix} \vec {\delta }_{a} \\ \vec {\delta }_{b} \end{bmatrix} = -\begin{bmatrix} \vec {F} \\ \vec {G} \end{bmatrix}. \end{aligned}$$

(19)

Due to the swapping, $A_F$ is better conditioned than $J_{F,p^*}$ which is exploited when Equation system (19) is solved [10]:

$$\begin{aligned}&\vec {\delta }_{b} = \left( B_G - A_G\left( A_F^{-1}B_F\right) \right) ^{-1}\left( -\vec {G} + A_G \left( A_F^{-1}\vec {F}\right) \right) , \end{aligned}$$

(20)

$$\begin{aligned}&\vec {\delta }_{a} = A_F^{-1}\left( -\vec {F} - B_F\vec {\delta }_{b}\right) . \end{aligned}$$

(21)

After obtaining $\vec {\delta }_{a}$ and $\vec {\delta }_{b}$, the earlier performed row swapping is reversed to get the updates of non-dimensional pressure $\vec {\delta }_{p^*}^n$ and cavity fraction $\vec {\delta }_{\theta }^n$ [10]. The new values $\vec {p}^{*,n}$ and $\vec {\theta }^{n}$ at iteration n are obtained by means of relaxation:

$$\begin{aligned}&\vec {p}^{*,n} = \vec {p}^{*,n-1} + \alpha _{p^*}\vec {\delta }_{p^*}^n , \end{aligned}$$

(22)

$$\begin{aligned}&\vec {\theta }^{n} = \vec {\theta }^{n-1} + \alpha _{\theta }\vec {\delta }_{\theta }^n, \end{aligned}$$

(23)

where $\alpha _{p^*}$, $\vec {p}^{*,n-1}$, $\alpha _{\theta }$ and $\vec {\theta }^{n-1}$ are the relaxation factors and previous solutions of non-dimensional relative pressure and cavity fraction. Depending on the simulated case, relaxation coefficients between 0.05 and 1 resulted in good tradeoffs between convergence speed and stability. Preventing $\vec {p}^{*,n}$ from having values below 0 and $\vec {\theta }^{n}$ from having values below 0 or above 1 through truncation furthermore enhances favorable convergence properties.

If a constant load force is prescribed, the dimensionless rigid body displacement $h_\text {d}^*=h_\text {d}/h_{ref}$ is adjusted through a PID controller to meet the load balance Equation (8) as already done by Wang et al. [24]. This is done by first determining the resulting normal load force $F_N^n$ through the discretized load balance equation:

$$\begin{aligned} F_N^n = \sum ^{N_{x_2}} \sum ^{N_{x_1}}\left( p_{\text {hd},C}^n - p_{\text {amb}}\right) \Delta x_1 \Delta x_2, \end{aligned}$$

(24)

where $N_{x_1}$, $\Delta x_1$, $N_{x_2}$, and $\Delta x_2$ are the amount and spacing of the discretization cells in $x_1$- and $x_2$-direction and $p_{\text {hd},C}^n$ is the hydrodynamic pressure at the center of each discrete cell. The residual of the load balance equation is defined as:

$$\begin{aligned} r_{F_N}^n = \frac{F_N^n - F_{N,\text {imp}}}{F_{N,ref}}, \end{aligned}$$

(25)

where $F_{N,ref}$ is a reference normal force that is usually just set equal to the imposed normal force $F_{N,\text {imp}}$. Note that $r_{F_N}^n$ can be either positive or negative, depending on whether $F_N^n$ is larger or smaller than $F_{N,\text {imp}}$. This is required for the PID controller to work properly. Finally, $r_{F_N}^n$ is fed into the PID controller to determine $h_\text {d}^{*,n+1}$ of the next iteration step [24]:

$$\begin{aligned} h_{\text {d}}^{*,n+1} = K_P r_{F_N}^n + K_I \sum ^{n-1}_i r_{F_N}^{i} + K_D \left( r_{F_N}^n - r_{F_N}^{n-1} \right) . \end{aligned}$$

(26)

Fig. 2

Flowchart of the most relevant steps of the EHL-FBNS algorithm

Note that $K_I$ is only multiplied with the sum up until $r_{F_N}^{n-1}$, since $r_{F_N}^{n}$ is already considered by $K_P$. For all of the later considered simulations with imposed normal load force, $K_P=0.001$, $K_I=0.02$, and $K_D=0.001$ worked well. At last, the following residuals are computed:

$$\begin{aligned} \begin{aligned} r_{\text {max},\delta p^*}^n =&\max \left( \text {abs} \left( \vec {\delta }_{p^*}^n\right) \right) ,\\ r_{\text {max},\delta \theta }^n =&\max \left( \text {abs} \left( \vec {\delta }_{\theta }^n\right) \right) ,\\ r_{\text {max},\delta G}^n =&\text {max}\left( \text {abs} \left( \vec {G}^n - \vec {G}^{n-1}\right) \right) ,\\ r_{\text {max},G}^n =&\max \left( \text {abs} \left( \vec {G}^n\right) \right) ,\\ r_{\text {max},\delta F}^n =&\text {max}\left( \text {abs} \left( \vec {F}^n - \vec {F}^{n-1}\right) \right) ,\\ r_{\text {max},F}^n =&\max \left( \text {abs} \left( \vec {F}^n\right) \right) , \end{aligned} \end{aligned}$$

(27)

$$\begin{aligned} r_{\text{EHL-FBNS}}^n = \max \left( r_{\text {max},\delta p^*}^n, r_{\text {max},\delta \theta }^n, r_{\text {max},\delta G}^n, r_{\text {max},G}^n, r_{\text {max},\delta F}^n, r_{\text {max},F}^n \right) . \end{aligned}$$

(28)

Note that the residuals $r_{\text {max},\delta G}^n$ and $r_{\text {max},\delta F}^n$ are directly affected by the relaxation factors and $\vec {G}^n$ and $\vec {F}^n$ are computed through the solutions $\vec {p}^{*,n-1}$ and $\vec {\theta }^{n-1}$. The EHL-FBNS algorithm is repeated as long as $r_{\text{EHL-FBNS}}^n$ and in case of an imposed normal load force $\text {abs}(r_{F_N}^n)$ are above the tolerance $tol=10^{-6}$. The most important steps of the algorithm structure are also visualized in Fig. 2. The initial guess is always a zero cavity fraction field and a pressure field at ambient pressure. If an unsteady simulation is performed, the solution at $t=0$ is obtained through the steady problem caused by the geometry at $t=0$. Furthermore, the PID controller also takes the residuals of the load balance equation of the previous time steps into account if $t>0$.

3 Results and Discussion

In order to assess the performance of the presented EHL-FBNS algorithm, it is firstly employed in a numerical literature test case of a textured parallel slider. Then, the results of the EHL-FBNS algorithm are compared to the analytical solution of a rigid one-dimensional convergent slider with rectangular pocket to show the effect of the discretization order of the Couette term on the accuracy of the simulation result when gap height discontinuities are present. Subsequently, the slider is extended to a two-dimensional geometry and an elastic model is employed to give an example case where both mass-conserving cavitation and elasticity show relevant effects. Afterward, another experimental–numerical literature case is simulated with the EHL-FBNS algorithm to validate the code for textured ball-on-disc investigations, evaluate the code’s stability in unsteady EHL conditions, and compare different spatial discretization schemes. For all considered cases, the second-order midpoint rule is used for the evaluation of integrals arising from the FVM and the Poiseuille term is always discretized with a second-order central scheme. Consequently, the resulting order of the dimensionless Reynolds equation discretized with the FVM in the steady case is first order with the UI and second order with the QUICK scheme. In the unsteady case, only first order is achievable for both UI and QUICK since the first-order Euler implicit scheme is employed. All of the EHL-FBNS simulations are performed with MATLAB$^{\copyright }$ R2020a.

3.1 Parallel Slider with a Varying Amount of Trapezoidal Pockets

The parallel slider with a varying amount of trapezoidal pockets used by Woloszynski et al. [10] serves as first test case. This set-up is chosen because it can cause a generic amount of distinctive cavitation regions. This is to demonstrate the good performance and stability properties of the EHL-FBNS algorithm since the simulation of such cases showed to be difficult or inefficient with other codes from the literature. Furthermore, the solid properties are chosen such that noticeable effects due to elastic deformations on the pressure profile occur. Thereby, it is shown that the consideration of elasticity does not alter the performance scaling. While being of little physical interest, this numerical set-up allows a comparison of the performance scaling to the original FBNS algorithm of Woloszynski et al.

The variation of the gap height due to the rigid geometry of the surfaces $h_{\text{g}}$ is constructed by assembling several unit geometries. Each unit geometry is composed of $20 \cdot 20$ cells with $h_{\text {g}}=h_{\text {min}}+h_{\text{p}}$. This square is surrounded by a one cell thick layer with $h_{\text {g}}=h_{\text {min}}+h_{\text{p}}/2$, which is in turn surrounded by a layer of four cells with $h_{\text {g}}=h_{\text {min}}$, resulting in a square of $30 \cdot 30$ cells. Depending on the desired size of the computational domain, a certain amount $K_{x_1} \cdot K_{x_2}$ of these unit cells is attached to each other and finally surrounded by a layer of cells for the Dirichlet boundary conditions of hydrodynamic pressure at $p_{\text {amb}}$ and zero cavity fraction. At last, the coordinates of each cell center are set such they are in the range of $[0 \; L_{x_1}] \otimes [0 \; L_{x_2}]$. The resulting array of cells in the exemplary case of $K_{x_1}=K_{x_2}=2$ is visualized in Fig. 3. The rigid body displacement $h_{\text {d}}$ is set to 0 since it is already considered in $h_{\text {g}}$.

Fig. 3

Exemplary cell array resulting in the case of $K_{x_1}=K_{x_2}=2$

Table 1 Summary of the parameters and values used in the EHL-FBNS simulations of the parallel slider with a various amount of trapezoidal pockets

The values of the parameters used in the EHL-FBNS simulations are summarized in Table 1. Piezoviscosity and compressibility of the liquid phase are not considered. The amount of unit geometries in $x_1$-direction $K_{x_1}$ is varied while $K_{x_2}=K_{x_1}$ is always enforced such that the resulting mesh is always quadratic. By increasing the amount of unit geometries, the total amount of discretization cells N is increased. Each resulting geometry is simulated with UI and QUICK for the rigid and elastic case. In the elastic case, the solid bodies’ Young’s modulus E and Poisson ratio $\nu$ are set such that the elastic deformation shows notable effects even though the overall pressures are low. At the same time, this set-up produces many distinctive cavitation regions. The rigid simulations use relaxation factors of $\alpha =1$. Since the elastic simulations are generally more unstable, the relaxation factors have to be reduced to 0.5.

To quantify the algorithm’s performance independently of the hardware’s computational power, the non-dimensional code execution time is defined as:

$$\begin{aligned} t_{\text {ex}}^* = \frac{t_{\text {ex}}\left( N\right) }{t_{\text {ex}}\left( N=1024\right) }, \end{aligned}$$

(29)

where $t_{\text {ex}}$ is the code execution time for a certain total amount of discretization cells N. The non-dimensional code execution time $t_{\text {ex}}^*$ of the EHL-FBNS algorithm in the rigid UI case is compared with the one of the original FBNS algorithm of Woloszynski et al. [10] in Fig. 4. Their code was also implemented in MATLAB$^{\copyright }$, considered rigid geometries and was discretized with the FVM, where the Poiseuille term was discretized with second-order central differences and a first-order upwind scheme was employed for the cavity fraction. While Woloszynski et al. [10] use different tolerances for different residuals ($10^{-3}$ for $r_{\text {max},G}^n$ and $10^{-6}$ for $r_{\text {max},\delta G}^n$), the EHL-FBNS algorithm employs an even stricter convergence criterion ($10^{-6}$ for $r_{\text{EHL-FBNS}}^n$ given by Equation (28)). Furthermore, three reference curves for the scaling of the non-dimensional code execution time are displayed: linear $t_{\text {ex},\text {lin}}^* = M_1 N$, logarithmic $t_{\text {ex},\text {log}}^* = M_2 N \log (N)$ and quadratic $t_{\text {ex},\text {quad}}^* = M_3 N^2$. The coefficients $M_1=9.7656\cdot 10^{-4}$, $M_2=1.4089\cdot 10^{-4}$ and $M_3=9.5367\cdot 10^{-7}$ are chosen such that $t_{\text {ex}}^*(N=1024)=1$ in all cases. It can be seen that the original FBNS algorithm has a performance scaling close to the linear reference while the EHL-FBNS algorithm performs a little bit slower than the $N\log (N)$ reference for large N but is always much faster than the quadratic reference. The difference between the FBNS and EHL-FBNS performances might be due to the fact that the EHL-FBNS algorithm constructs the matrices $A_{\text {Po}}$ and B and vector $\vec {c}$ at each iteration step, while the FBNS algorithm might exploit that they are constant in a rigid and isoviscous simulation with an incompressible liquid phase. However, the exact details of the implementation of the original FBNS algorithm are unknown and the difference in time scaling cannot be pinned down rigorously.

Fig. 4

Performance of EHL-FBNS and FBNS algorithm along with reference scalings. The performance of the FBNS algorithm was taken from Woloszynski et al. [10]

Next, it is investigated how combinations of UI or QUICK discretization and rigid or elastic geometry affect the performance. The code execution times $t_{\text {ex}}$ are provided in Table 2. The corresponding non-dimensional code execution times $t_{\text {ex}}^*$ are displayed in Fig. 5. Because all curves have almost the same inclinations in the double logarithmic diagram, it can be deduced that the performance scaling of the EHL-FBNS algorithm stays similar in all cases. To prove that the operating conditions were chosen such that discretization scheme and elastic model have a noticeable impact on the results while the performance scaling remains unchanged, exemplary results are considered in the following for the geometry with $K_{x_1}=8$. The pressure profiles of the UI simulations are visualized in Fig. 6 for the rigid (a) and elastic (b) case. The contour of the regions where the hydrodynamic pressure $p_{\text {hd}}$ reaches the cavitation pressure $p_{\text {cav}}$ is visualized by orange lines. The elastic deformation drastically reduces the resulting pressure profile in comparison to the rigid simulation. The results of the same cases but with the QUICK scheme are shown in Fig. 7 for the rigid (a) and elastic (b) case for comparison. Differences between the UI and the QUICK scheme are noticeable.

Fig. 5

Performance of combinations of rigid, elastic, UI, and QUICK EHL-FBNS simulations

Fig. 6

Hydrodynamic pressure profiles $p_{\text {hd}}$ for a UI simulation with $K_{x_1}=8$: a rigid and b elastic case

Fig. 7

Hydrodynamic pressure profiles $p_{\text{hd}}$ for a QUICK simulation with $K_{x_1}=8$: a rigid and b elastic case

Table 2 Summary of the code execution times of the FBNS algorithm given by Woloszynski et al. [10] and the ones of the EHL-FBNS algorithm with UI or QUICK discretization and rigid or elastic geometry to simulate the parallel slider with a various amount of trapezoidal pockets

3.2 Convergent Slider with Rectangular Pocket

The next test case is a convergent slider with a single rectangular pocket that introduces discontinuities in the gap height. For this set-up, a mass-conserving cavitation model is essential to predict the full-film reformulation properly. The aim of the simulations is to show the effect of the spacial discretization order on the pressure distribution when gap height discontinuities are present. For this steady case, the UI scheme eventually results in first and the QUICK scheme in second-order accuracy. The investigation is firstly done for a rigid one-dimensional geometry because it has the analytical solution of Fowell et al. [25] for comparison. Next, the two-dimensional set-up of Bertocchi et al. [9] is used on the one hand to demonstrate that the algorithm of Bertocchi et al. and the EHL-FBNS algorithm give consistent results in the rigid case and on the other hand to show that the additional consideration of elastic deformations even at traditional hydrodynamic operating conditions is of great relevance. A sketch of the one-dimensional configuration is depicted in Fig. 8a while its extension to the two-dimensional geometry is described in Fig. 8b.

Fig. 8

Schematic sketch of the convergent slider with rectangular pocket: a one-dimensional configuration, b two-dimensional geometry with one-dimensional configuration along center line. Adapted from Bertocchi et al. [9]

The analytical solution of a rigid one-dimensional converging slider with rectangular pocket and incompressible isoviscous liquid phase was derived by Fowell et al. [25] and was also used for code verification by Giacopini et al. [8]. The parameters used in the current study are summarized in Table 3. The one-dimensional geometry was replicated by a pseudo one-dimensional grid with three discretization points in $x_2$-direction and Neumann boundary conditions for pressure and cavity fraction at the south and north boundary.

Table 3 Summary of the parameters and values used in the EHL-FBNS simulations of the one-dimensional convergent slider with rectangular pocket

To investigate the grid convergence properties of the spacial schemes for this kind of set-up, the resulting pressure profiles of the UI and QUICK schemes are shown in Figs. 9 and 10 for different grid resolutions alongside the analytical solution. While both schemes converge toward the same analytical solution, the first-order UI scheme converges faster at much lower resolutions than the second-order QUICK scheme. It is therefore concluded that for rigid geometries, lower order discretization schemes are preferable when gap height discontinuities are present.

Fig. 9

Hydrodynamic pressure profile $p_{\text{hd}}$ for UI simulations with different resolutions $N_{x_2} \cdot N_{x_1}$ in comparison to the analytical solution derived by Fowell et al. [25]

Fig. 10

Hydrodynamic pressure profile $p_{\text{hd}}$ for QUICK simulations with different resolutions $N_{x_2} \cdot N_{x_1}$ in comparison to the analytical solution derived by Fowell et al. [25]

Next, the two-dimensional set-up of a converging slider with rectangular pocket is considered. It is the same set-up that was used by Bertocchi et al. [9] to show the agreement of their code with the formulation of Ausas et al. [4] and Giacopini et al. [8]. This set-up is simulated to demonstrate the good agreement of the EHL-FBNS algorithm with the aforementioned algorithms in the rigid case and to point out that the resulting pressure distribution is greatly affected when common elastic bodies instead of rigid ones are used.

The parameters employed in the EHL-FBNS simulations are summarized in Table 4. In the rigid case, Bertocchi et al. [9] used a domain width of $L_{x_2}=10$ $\mathrm {mm}$ and pocket width of $w=7$ $\mathrm {mm}$ to compare their results with the formulation of Ausas et al. [4] and employed a domain width of $L_{x_2}=300$ $\mathrm {mm}$ and pocket width of $w=210$ $\mathrm {mm}$ to approximate a one-dimensional case along the center line of the computational domain which was compared to the one-dimensional results of Giacopini et al. [8]. Differently to the non-equidistant mesh used by Bertocchi et al. consisting of 3528 elements, the EHL-FBNS simulations are performed with a mesh of 8320 cells and an equidistant spacing in each of the respective directions. Dirichlet boundary conditions of $p_{\text {amb}}$ and zero cavity fraction are employed. Piezoviscosity is modeled with the Barus model and compressibility of the liquid phase with the Dowson-Higginson model. Differently to Bertocchi et al. shear thinning is neglected. As the following comparison of the EHL-FBNS results with the ones of Bertocchi et al. show, shear thinning has a negligible effect for this problem. The EHL-FBNS simulations are performed with the UI and QUICK scheme and for rigid and elastic surfaces.

Table 4 Summary of the parameters and values used in the EHL-FBNS simulations of the two-dimensional convergent slider with rectangular pocket

Figure 11 shows the pressure distribution of the rigid UI EHL-FBNS simulations along the center line for both geometry widths next to the results of Bertocchi et al. [9]. The curve of Bertocchi et al. was read in with the software Engauge Digitizer and can therefore be subject to minor deviation from the original data. Still, the results of the EHL-FBNS algorithm and Bertocchi et al. are similar. Furthermore, Bertocchi et al. found their results being in close agreement to Ausas et al. [4] and Giacopini et al. [8]. This indicates that the EHL-FBNS algorithm is consistent with all the mentioned works.

Fig. 11

Distribution of hydrodynamic pressure $p_{\text{hd}}$ along the center line of the inclined slider with pocket against the results obtained by Bertocchi et al. [9]. Simulations were performed for the small ($L_{x_2}=10$ $\mathrm {mm}$, $w=7$ $\mathrm {mm}$) and large ($L_{x_2}=30 \cdot 10$ $\mathrm {mm}$, $w=30 \cdot 7$ $\mathrm {mm}$) geometry

In the following, only the small geometry ($L_{x_2}=10$ $\mathrm {mm}$, $w=7$ $\mathrm {mm}$) is considered to show that even at traditional hydrodynamic operating conditions with low pressures between 1 and 10 $\mathrm {MPa}$, the employment of common elastic parameters can induce small variations in the gap height which in turn severely alter the resulting hydrodynamic pressure and cavity fraction profiles. The resulting pressure profiles of the rigid and elastic simulations are shown in Fig. 12 for the UI scheme. The boundary of the cavitation region is indicated by an orange line and the center line is marked in green. The resulting pressure profiles are severely weakened due to the introduced elastic deformation and the cavitation region has a larger downstream extension.

Fig. 12

Distribution of hydrodynamic pressure $p_{\text {hd}}$ in the inclined slider with pocket for UI discretization and rigid a and elastic b model

The gap height h, hydrodynamic pressure $p_{\text {hd}}$ and cavity fraction $\theta$ along the center line are compared in Fig. 13 for the rigid, elastic, UI, and Quick simulations. It becomes visible that the differences between rigid and elastically deformed gap height are small compared to the corresponding differences in the hydrodynamic pressure. The maximum hydrodynamic pressure is not only reduced to about $20 \%$, but also the general shape and peak change drastically. In the elastic case, the cavitation region extends over the whole length of the pocket, thus reducing the area of positive pressure gradient in front of the downstream end of the pocket and eventually causing only a small pressure increase compared to the rigid case. Comparing the UI and QUICK schemes shows a tendency of the higher order scheme to cause oscillations at the downstream end of the cavitation region and minor discrepancies in the pressures profiles at the end of the pocket.

From these results, it is concluded that even at low pressures between 1 and 10 $\mathrm {MPa}$, small elastic deformations can significantly alter the hydrodynamic pressure and cavity fraction profiles. Consequently, results of traditional hydrodynamic simulations with mass-conserving cavitation but no elastic deformation model must be handled with care when making statements about the possible increase of the load carrying capacity due to surface textures. Furthermore, the performed simulations show that the EHL-FBNS algorithm is a useful tool to build up on the considered reference investigations since it can take the additionally required elastic deformation effects into account. Moreover, the implementation of the solver allows to switch conveniently between first- and second-order discretization schemes of the Couette term. This allows to quickly identify the preferable scheme through grid convergence studies.

Fig. 13

Distribution of gap height h a, hydrodynamic pressure $p_{\text {hd}}$ b and cavity fraction $\theta$ c along the center line of the inclined slider with pocket for rigid, elastic, UI, and QUICK simulations

3.3 Ball-on-Disc Tribometer with a Single Texture

The second set-up is the ball-on-disc tribometer with a single texture used in the simulations and experiments of Mourier et al. [26]. These were performed to investigate the unsteady effect of isolated dimples passing through an EHL contact at pure rolling and rolling-sliding conditions. Mourier et al. state that they used shallower dimples in the simulations than in the experiments because the deep dimples compromised convergence. In the following, both geometries are simulated with the EHL-FBNS algorithm to show that the presented algorithm can provide converged results in either case. Firstly, grid convergence studies are performed to identify the preferable discretization scheme. Then, the gap height measurements of Mourier et al. are used to validate the EHL-FBNS algorithm for ball-on-disc tribometers. Lastly, differences in the simulated results of Mourier et al. and the EHL-FBNS algorithm are discussed and additional deductions about the discretization schemes are drawn.

The rolling-sliding condition of the EHL contact is characterized through the slide-to-roll ratio SSR as provided by Mourier et al. [26]:

$$\begin{aligned} SSR = \frac{U_{\text {low}}-U_{\text {up}}}{U_{\text {low}}+U_{\text {up}}}. \end{aligned}$$

(30)

The time dependent variation of the gap height due to the rigid geometry of the surfaces is expressed as [26]:

$$\begin{aligned} h_g(x_1,x_2,t) = \frac{x_1^2}{2R_{x_1}} + \frac{x_2^2}{2R_{x_1}} + d \cos \left( \frac{\pi }{2}\cdot \frac{D}{1.2r} \right) \exp \left( -2\left( \frac{D}{1.2r}\right) ^2\right) , \end{aligned}$$

(31)

where d is the dimple depth, r is the dimple radius and D is the distance of any position to the moving dimple center [26]:

$$\begin{aligned} D = \sqrt{(x_1 - x_{1,d})^2 + (x_2 - x_{2,d})^2}. \end{aligned}$$

(32)

The dimple center has the coordinates $x_{1,d}$ and $x_{2,d}$ with [26]:

$$\begin{aligned} x_{1,d} = x_{1,0} + t u_{tex},\quad x_{2,d} = x_{2,0}. \end{aligned}$$

(33)

The initial position of the dimple center is described by $x_{1,0}$ and $x_{2,0}$ at time $t=0$ $\mathrm {s}$. The dimple moves with velocity $u_{tex}=U_{\text {low}}$. The parameters used in the EHL-FBNS simulations are summarized in Table 5. All simulations are performed with the same mean velocity $u_{\text {m}}$, but different SSR and therefore different $U_{\text {up}}$, $U_{\text {low}}$ and number of time steps $N_t$. In the case of $\text{SSR}=0$, $N_t=257$ time steps and a dimple radius of $r=15.5$ $\mathrm {\mu m}$ are used. To replicate the experiment, a dimple depth of $d=7$ $\mathrm {\mu m}$ is employed, while $d=0.175$ $\mathrm {\mu m}$ is used to be consistent with the numerical set-up of Mourier et al. [26]. For $\text{SSR}=-0.5$, the dimple radius $r=21.5$ $\mathrm {\mu m}$ is considered. Since the dimple moves more slowly in this case, $N_t=513$ time steps are required while the time step length $\Delta t$ stays constant. A dimple depth of $d=1.3$ $\mathrm {\mu m}$ is used for the experiment replication, while $d=0.16$ $\mathrm {\mu m}$ is used to be consistent with the numerical set-up of Mourier et al.

The solution of the first time step at $t=0$ $\mathrm {s}$ is computed with the steady Reynolds equation and the dimple at its starting position to obtain an initial solution for the unsteady Reynolds equation. The cavitation pressure $p_{\text {cav}}$ is set to the ambient pressure of $p_{\text {amb}} =0$ $\mathrm {Pa}$ and Dirichlet boundary conditions are used for the hydrodynamic pressure. The boundary conditions of $\theta$ correspond to zero cavity fraction at the West boundary and zero gradient Neumann condition at all other boundaries. The imposed normal force is $F_{N,\text{imp}}=15$ $\mathrm {N}$ and the initial guess of the rigid displacement is set to $h_{d,\text {ini}}=-1$ $\mathrm {\mu m}$. Elastic deformation, Roelands, and Dowson-Higginson models are employed to stay consistent with the simulations of Mourier et al. [26] who used the FDM multigrid solver of Venner and Lubrecht [12]. As stated by Mourier et al., the accuracy of this solver is of second order in space and time. Due to the Euler implicit discretization of the unsteady term in the EHL-FBNS solver, the achieved accuracy is generally limited to first order for both the UI and the QUICK scheme.

Table 5 Summary of the parameters and values used in the EHL-FBNS simulations of the ball-on-disc tribometer with single texture

In order to perform a grid convergence study, simulations with the UI and QUICK scheme at $\text{SSR}=0$, respectively, for the deep and shallow dimple geometries, are employed to assess both schemes with and without gap height discontinuities. For this grid convergence study, the less strict definition $r_{\text{EHL-FBNS}}^n =\mathrm {mean}\left( \text {abs} \left( \vec {\delta }_{p^*}^n\right) \right)$ is used instead of Equation (28). This is necessary in order to perform the QUICK simulations at low resolutions, otherwise a stall in the convergence of the residual $r_{max,G}^n$ can occur at some time steps for the used value of the underrelaxation coefficient. Nonetheless, for the highest grid resolution, the stricter residual of Equation (28) does not lead to a stall and the maximum deviation in the resulting gap heights along the center line when the dimple is at position $x_{1,d}=0$ is less than $0.1\%$ when compared for both residual definitions. Note also that for any other simulation in this publication, the stricter definition given by Equation (28) (and thus following the suggestion by Woloszynski et al. [10]) is employed. The effect of the residual definition on the amount of required iterations for the highest resolution is discussed at the end of this section.

For the deep dimple at position $x_{1,d}=0$, the resulting gap height profiles along the center line obtained for different resolutions are displayed in Fig. 14 for the UI and in Fig. 15 for the QUICK scheme. The comparison of both figures shows that the QUICK scheme has a worse convergence behavior around the dimple than the UI scheme and even converges toward a different solution at the downstream end of the dimple. It is therefore concluded that in this case, the UI scheme with the first-order discretization of the Couette term is preferable over the QUICK scheme.

Fig. 14

Profiles of gap height h along center line for the deep dimple at position $x_{1,d}=0$, UI discretization scheme and different resolutions of $N_{x_1}\cdot N_{x_2}\cdot N_{t}$

Fig. 15

Profiles of gap height h along center line for the deep dimple at position $x_{1,d}=0$, QUICK discretization scheme and different resolutions of $N_{x_1}\cdot N_{x_2}\cdot N_{t}$

For the shallow dimple at position $x_{1,d}=0$, the resulting gap height profiles along the center line obtained for different resolutions are displayed in Fig. 16 for the UI and in Fig. 17 for the QUICK scheme. For this geometry with no discontinuity, both schemes converge toward the same solution, but the second-order discretization of the Couette term with the QUICK scheme delivers the better convergence properties and is therefore preferable.

Fig. 16

Profiles of gap height h along center line for the shallow dimple at position $x_{1,d}=0$, UI discretization scheme and different resolutions of $N_{x_1}\cdot N_{x_2}\cdot N_{t}$

Fig. 17

Profiles of gap height h along center line for the shallow dimple at position $x_{1,d}=0$, QUICK discretization scheme and different resolutions of $N_{x_1}\cdot N_{x_2}\cdot N_{t}$

The following simulations are performed at the highest resolution level and with the residual definition of Equation (28) to further support the previously identified arguments about the preferable discretization scheme of the Couette term. The results of the EHL-FBNS simulations are provided as videos in the supplements. Exemplary results of gap height h, hydrodynamic pressure $p_{\text {hd}}$ and cavity fraction $\theta$ at $t=0$ $\mathrm {s}$, $\text{SSR}=0$ and $d=7$ $\mathrm {\mu m}$ are shown for UI and QUICK simulations in Fig. 18. The contour line of $p_{\text {hd}}=p_{\text {cav}}$ is marked in orange while the center line is displayed in green. Apart from more pronounced spikes in the hydrodynamic pressure at the downstream end of the EHL-contact zone with the more accurate QUICK scheme, both simulations produce almost the same results at first glance.

Fig. 18

Distribution of gap height h a,b, hydrodynamic pressure $p_{\text {hd}}$ c,d and cavity fraction $\theta$ e,f in the ball-on-disc tribometer with single texture at $t=0$ $\mathrm {s}$ for UI (left) and QUICK (right) discretization

In the following, the EHL-FBNS results are compared to the experimental and simulated counterparts of Mourier et al. [26]. The data of Mourier et al. was read in with the software Engauge Digitizer (https://markummitchell.github.io/engauge-digitizer/) and can therefore be subject to minor deviation from the original data. The data of Mourier et al. consists of gap height measurements in the experimental case and of gap height and pressure distributions in the simulated case at five distinctive dimple center positions.

Figure 19a shows the UI and QUICK results of the EHL-FBNS algorithm along with the experimental results of Mourier et al. in case of the deep dimple with $\text{SSR}=0$. Due to the large depth of the dimple in comparison to the remaining gap height within the EHL contact, the gap height distribution shows a strong discontinuity at the rim of the deep dimple. At the first and last dimple position, the dimple is just entering or leaving the visualized domain. Most of the domain is still unaffected by the dimple and basically corresponds to the steady solution without a dimple. Small differences in the gap height h between UI and QUICK can be observed while the more accurate QUICK scheme closely fits the experimental results in the center of the domain. The systematic difference in the gap height between UI and QUICK is mostly due to a different value of the rigid body displacement $h_{\text{d}}$ which is set such that the load balance equation is eventually met. For the dimple positions 2–4, the QUICK scheme produces large deviations in the gap height compared to the experimental results at the discontinuity at the downstream rim of the dimple. There, the UI scheme manages to fit the experimentally measured gap height better. These results are consistent with the finding of LeVeque [34, Ch. 11] that for discontinuous problems, first-order methods give smoother results while second-order methods cause oscillations. Both schemes deviate from the experimental results at the downstream rim of the dimple when it is leaving the EHL contact at position 5. At all five positions, the hydrodynamic pressure distributions of UI and QUICK are mostly in close agreement, but the UI scheme produces higher pressure spikes at the downstream rim of the dimple which in turn cause larger elastic deformations. This explains why the UI scheme shows better agreement in the gap height since this more diffusive scheme eventually tends to smooth the discontinuity at the rim of the dimple by adjusting the hydrodynamic pressure accordingly. Consequently, the lower order UI scheme is recommendable close to discontinuities in the gap height while the QUICK scheme is more advantageous at smoother parts of the geometry.

The UI and QUICK results along with experimental values of Mourier et al. in case of the deep dimple with $\text{SSR}=-0.5$ are depicted in Fig. 19b. In this case, the downstream area of the dimple also gets deformed because the dimple moves at a lower speed than the mean velocity $u_\text{m}$. This means that some of the fluid that is initially within the dimple leaves the texture behind which causes a deformation since more volume is occupied outside of the dimple. This behavior is principally also replicated by the EHL-FBNS results but in a more pronounced way than in the experiments. The higher order QUICK scheme matches the experimental results closer than the UI scheme in the vicinity of this effect as depicted at dimple position 3. The UI scheme causes higher hydrodynamic pressures downstream of the dimple which this time cause a larger overestimation of the occurring deformation than done by the QUICK scheme. However, the stronger this effects becomes, the larger the deviation between experiment and simulation becomes as shown at dimple position 4. Still, experimental and EHL-FBNS results generally show a good agreement in the gap height distribution. The EHL-FBNS algorithm is thereby validated for simulations of discontinuous textures in ball-on-disc tribometers under EHL operating conditions.

Fig. 19

At $\text{SSR}=0$ (a) and $\text{SSR}=-0.5$ (b): distribution of gap height h (top) and hydrodynamic pressure $p_{\text{hd}}$ (bottom) along the center line of the ball-on-disc tribometer with single texture for UI and QUICK discretization against the experimental results of Mourier et al. [26]

Next, the EHL-FBNS results are compared to the simulated results of Mourier et al. [26]. Figure 20a shows the UI and QUICK results of the EHL-FBNS algorithm along with the simulated results of Mourier et al. in case of the shallow dimple with $\text{SSR}=0$. Unlike the deep dimple, the rim of the shallow dimple is only weakly discontinuous. At the first dimple position, the simulated results of Mourier et al. agree well with the gap height and hydrodynamic pressure produced by the QUICK scheme. This is expected because both eventually correspond to second-order spatial discretizations of an almost steady case since the shallow dimple does not affect the displayed domain yet. Similar to the deep dimple case, the first-order UI scheme results in practically the same hydrodynamic pressure distribution as the QUICK scheme but a slightly different systematic offset in the gap height distribution. When the shallow dimple introduces unsteady effects at positions 2–5, the gap height distributions of QUICK stay closer to the results of Mourier et al. than in the case of UI discretization. Nonetheless, all three methods deliver different gap heights close to the dimple. While the hydrodynamic pressure distributions of UI and QUICK show similar oscillations around the dimple, it stays almost undisturbed in the simulations of Mourier et al.. Since differently to the deep dimple, the results of UI and QUICK are still reasonably close to each other at the rim of the shallow dimple, errors or oscillations caused by the discretization scheme of the Couette term are not believed to be of dominant role. Instead, the differences in the results of EHL-FBNS algorithm and Mourier et al. during the introduction of unsteady phenomena are likely caused by the first-order Euler implicit discretization of the EHL-FBNS algorithm while Mourier et al. use a second-order discretization in time.

These findings are complemented by the results in case of the shallow dimple at $\text{SSR}=-0.5$ as depicted in Fig. 20b along with the outcome of the simulations of Mourier et al. Gap height and hydrodynamic pressure of QUICK and Mourier et al. are in close agreement while the lower order UI results slightly differ at some points. The reason for the closer agreement of the EHL-FBNS results with Mourier et al. is expected to be due the dimple moving at a lower speed, thus introducing slower unsteady effects. Since the discrete time steps are of the same length as in the case of $\text{SSR}=0$, the time resolution is relatively higher for $\text{SSR}=-0.5$, thus enabling all schemes to deliver almost the same results.

Fig. 20

At $\text{SSR}=0$ (a) and $\text{SSR}=-0.5$ (b): distribution of gap height h (top) and hydrodynamic pressure $p_{\text{hd}}$ (bottom) along the center line of the ball-on-disc tribometer with single texture for UI and QUICK discretization against the simulated results of Mourier et al. [26]

In order to better understand the performance of the EHL-FBNS algorithm in unsteady EHL conditions, the required amount of iterations $N_n$ at each position of the dimple center $x_{1,d}$ is displayed in Fig. 21. The most iterations are needed to compute the steady solution at the initial position of the dimple and once the dimple reaches the EHL-contact zone. Since it produces more irregular results, the deep dimple generally requires more iterations than the shallow one. UI and QUICK simulations need a similar amount of iterations for each respective pair of simulation. Each of the eight simulations required between 2 and 6 $\mathrm {h}$ code execution time on a desktop computer.

Fig. 21

Amount of iterations $N_n$ required by the EHL-FBNS algorithm for the simulation of the ball-on-disc tribometer with single texture for each position of the dimple center $x_{1,d}$

The amount of required iterations can be significantly reduced if the residual definition of Equation (28) is changed to $r_{\text{EHL-FBNS}}^n =\mathrm {mean}\left( \text {abs} \left( \vec {\delta }_{p^*}^n\right) \right)$. While the difference between the resulting gap height profiles is negligible as demonstrated in the beginning of this section, the less strict residual definition reduces the required amount of iterations noticeably, as displayed in Fig. 22. Furthermore, this reduces the code execution time per simulation to a range between 0.5 and 2.5 $\mathrm {h}$.

Fig. 22

Amount of iterations $N_n$ required by the EHL-FBNS algorithm for the simulation of the ball-on-disc tribometer with single texture for each position of the dimple center $x_{1,d}$ when the residual definition of Equation (28) is changed to $r_{\text{EHL-FBNS}}^n =\mathrm {mean}\left( \text {abs} \left( \vec {\delta }_{p^*}^n\right) \right)$

Summarizing, the EHL-FBNS algorithm manages to deliver converged results even in unsteady EHL operating conditions with deep dimples with strong discontinuities at their rim. Moreover, the first-order UI scheme gives closer agreement to the experimental results of Mourier et al. [26] in the vicinity of deep dimples than the higher order QUICK scheme. Therefore, lower order spatial discretization schemes are recommended close to strong gap height discontinuities while higher order schemes are recommended at smoother parts of the geometry due to their higher accuracy in these areas. Moreover, the extreme pressure spikes at the rim of the deep dimples raise the question whether the elastic half-space assumption is still valid in this area. Nonetheless, the good agreement of the gap height distribution with the experimental data of Mourier et al. validates the EHL-FBNS algorithm for simulations of textures in ball-on-disc tribometers under unsteady EHL operating conditions.

4 Conclusion

The EHL-FBNS algorithm is presented in this paper. It allows the simulation of the unsteady hydrodynamic pressure build up under consideration of mass-conserving cavitation with the JFO model within lubrication gaps. Furthermore, its versatile implementation enables the simulation of various combinations of isoviscous or piezoviscous flows, incompressible or compressible liquid phases, rigid or elastic surfaces, first- or second-order spatial discretizations of the Couette term, imposed rigid body displacements or normal forces and Dirichlet or Neumann boundary conditions. The algorithm is explained in detail within this paper and the implemented MATLAB$^{\copyright }$ code with the corresponding set-up and visualization scripts is provided in the supplements. That way, the results can be reproduced by downloading the code and repeating the simulations. Moreover, the usage and further development of the thoroughly commented code is encouraged through its public accessibility and maintenance on GitHub: https://github.com/ErikHansenGit/EHL.

Within this paper, the EHL-FBNS algorithm results were compared to analytical, simulated and experimental literature data of Woloszynski et al. [10], Fowell et al. [25], Bertocchi et al. [9] and Mourier et al. [26]. The key findings are:

• The performance of the EHL-FBNS code almost scales with $N\log (N)$ in simulations with N discretization cells and a constant rigid body displacement $h_{\text{d}}$.

• The EHL-FBNS code can deliver converged results even when extreme gap height discontinuities are present.

• Higher order spatial discretizations of the Couette term can cause large errors in the gap height distributions when gap height discontinuities are present in the EHL contact. Therefore, lower order spatial discretization schemes are recommended close to strong gap height discontinuities while higher order schemes are recommended at smoother parts of the geometry due to their higher accuracy in these regions.

• In order to evaluate whether surface textures in a geometry introduce discontinuities in the gap height that in turn worsen the result quality of higher order discretizations of the Couette term, performing a grid convergence study with different discretization orders is recommended.

• The EHL-FBNS algorithm is validated for the investigation of deep dimples with discontinuous rims in ball-on-disc tribometers under EHL operating conditions.

• Even at traditional purely hydrodynamic operating conditions with low pressures between 1 and 10 $\mathrm {MPa}$, the employment of elastic models is recommended because the resulting pressure profiles are strongly influenced by slight elastic deformations.

• The EHL-FBNS algorithm is a convenient tool to perform grid convergence studies with different discretization orders of the Couette term while taking both elastic deformation and mass-conserving cavitation effects into account.

Since it was shown that both higher and lower order discretization schemes are beneficial in different parts of a geometry, a hybrid approach is suggested for future implementation (for example by means of flux limiters [29, Ch. 4.4.6]) to achieve maximum accuracy for profiles that show both smooth and discontinuous features.

Appendix Discretized Equations

1.1 Discretized Dimensionless Reynolds Equation Considering Mass-Conserving Cavitation and Discretized Dimensionless Fischer-Burmeister Equation

Applying the FVM with a two-dimensional grid as schematically depicted in Fig. 23 to Equation (9) eventually results in the discrete dimensionless Reynolds equation considering mass-conserving cavitation at each cell center $G_C$:

$$\begin{aligned}&G_C = \int \limits _{\partial A^*} \left( \xi _{\text{Po}}^* \begin{pmatrix} \frac{\partial }{\partial x_1^* } \\ \left( \frac{x_{1,ref}}{x_{2,ref}}\right) ^2 \frac{\partial }{\partial x_2^*} \end{pmatrix} p^* \right) \cdot \begin{pmatrix} n_1 \\ n_2 \end{pmatrix} \mathrm {dL^*}\nonumber \\&\quad - \int \limits _{\partial A^*} \xi _{\text{Co}}^* (1-\theta ) n_1 \mathrm {dL^*} \nonumber \\&\quad - \iint \limits _{A^*} \frac{\partial }{\partial t^*}\left( \xi _{Ti}^*(1-\theta )\right) \mathrm {d}x_1^* \mathrm {d}x_2^*\nonumber \\&\quad = A_{\text{Po},S}p_S^* + A_{\text{Po},W}p_W^* + A_{\text{Po},C}p_C^* + A_{\text{Po},E}p_E^* + A_{\text{Po},N}p_N^* \nonumber \\&\quad + B_{\text{WW}} \theta _{\text{WW}} + B_{W} \theta _{W} + B_{C} \theta _{C} + B_{E} \theta _{E} + c_C \end{aligned}$$

(34)

where the two-dimensional cell is of area $A^*$, has the boundary $\partial A^*$ and its outward pointing normal vector $\vec {n}$ is of length 1. Since a rectangular mesh aligned with a Cartesian coordinate system is used, the components $n_1$ and $n_2$ can take the values of ±1 or 0. The line increment of the cell boundary is denoted by $L^*$. The scalar product is implied by $\cdot$. The integrals are discretized with the second-order midpoint rule. Values or derivatives at the boundaries of the Poiseuille term are discretized with a second-order central interpolation or differential scheme. Its coefficients $A_{\text{Po}}$ read:

$$\begin{aligned}&A_{\text{Po},S} = -\frac{1}{\Delta x_2^*} \left( \frac{x_{1,ref}}{x_{2,ref}} \right) ^2(-\Delta x_1^* \xi _{\text{Po},s}^*), \end{aligned}$$

(35)

$$\begin{aligned}&A_{\text{Po},W} = -\frac{1}{\Delta x_1^*}(-\Delta x_2^* \xi _{\text{Po},w}^*),\end{aligned}$$

(36)

$$\begin{aligned}&A_{\text{Po},C} = \frac{1}{\Delta x_2^*} \left( \frac{x_{1,ref}}{x_{2,ref}} \right) ^2(-\Delta x_1^* \xi _{\text{Po},s}^*) + \frac{1}{\Delta x_1^*}(-\Delta x_2^*\xi _{\text{Po},w}^*) \nonumber \\&\quad -\frac{1}{\Delta x_1^*} (\Delta x_2^* \xi _{\text{Po},e}^*) -\frac{1}{\Delta x_2^*} \left( \frac{x_{1,ref}}{x_{2,ref}} \right) ^2(\Delta x_1^* \xi _{\text{Po},n}^*),\end{aligned}$$

(37)

$$\begin{aligned}&A_{\text{Po},E} = \frac{1}{\Delta x_1^*}(\Delta x_2 \xi _{\text{Po},e}^*),\end{aligned}$$

(38)

$$\begin{aligned}&A_{\text{Po},N} = \frac{1}{\Delta x_2^*}\left( \frac{x_{1,ref}}{x_{2,ref}} \right) ^2(\Delta x_1 \xi _{\text{Po},n}^*). \end{aligned}$$

(39)

The dimensionless cell spacings are defined as $\Delta x_1^* = \Delta x_1/x_{1,ref}$ and $\Delta x_2^* = \Delta x_2/x_{2,ref}$. At the cell boundaries, $\xi _{\text{Po}}^*$ is determined as:

$$\begin{aligned}&\xi _{\text{Po},s}^* = \frac{\xi _{\text{Po},C}^* + \xi _{\text{Po},S}^*}{2},\end{aligned}$$

(40)

$$\begin{aligned}&\xi _{\text{Po},w}^* = \frac{\xi _{\text{Po},C}^* + \xi _{\text{Po},W}^*}{2},\end{aligned}$$

(41)

$$\begin{aligned}&\xi _{\text{Po},e}^* = \frac{\xi _{\text{Po},E}^* + \xi _{\text{Po},C}^*}{2},\end{aligned}$$

(42)

$$\begin{aligned}&\xi _{\text{Po},n}^* = \frac{\xi _{\text{Po},N}^* + \xi _{\text{Po},C}^*}{2}. \end{aligned}$$

(43)

The components of $B = B_{\text{Co}} + B_{\text{Ti}}$ and $\vec {c} = \vec {c}_{\text{Co}} + \vec {c}_{\text{Ti}}$ contain contributions of the Couette and unsteady term, which are detailed now. Values at the boundaries of the Couette term are discretized with a generic order upwind interpolation scheme. Depending on how a, b, and c are set, first-order upwind interpolation (UI: $a=0$, $b=1$, $c=0$), third-order quadratic upwind interpolation (QUICK: $a=-1/8$, $b=6/8$, $c=3/8$), second-order linear upwind interpolation (LUI: $a=-1/2$, $b=3/2$, $c=0$) or second-order cubic upwind interpolation (CUI: $a=-1/6$, $b=5/6$, $c=2/6$) can be chosen [29, Ch. 4.4]. The coefficients of $B_{\text{Co}}$ read:

$$\begin{aligned}&B_{\text{Co},\text{WW}} = a (-\Delta x_2^* \xi _{\text{Co},w}^*),\end{aligned}$$

(44)

$$\begin{aligned}&B_{\text{Co},W} = b (-\Delta x_2^* \xi _{\text{Co},w}^* ) + a (\Delta x_2^* \xi _{\text{Co},e}^*),\end{aligned}$$

(45)

$$\begin{aligned}&B_{\text{Co},C} = c (-\Delta x_2^* \xi _{\text{Co},w}^*) + b (\Delta x_2^* \xi _{\text{Co},e}^*),\end{aligned}$$

(46)

$$\begin{aligned}&B_{\text{Co},E} = c (\Delta x_2^* \xi _{\text{Co},e}^*). \end{aligned}$$

(47)

Special attention has to be paid close to the boundaries if no WestWest neighbor cell exists. In this case, the first-order upwind interpolation scheme is used for the approximation of $\theta _{w}= \theta _W$. Then, the coefficients of $B_{\text{Co}}$ read:

$$\begin{aligned}&B_{\text{Co},\text{WW}} = 0,\end{aligned}$$

(48)

$$\begin{aligned}&B_{\text{Co},W} = (-\Delta x_2^* \xi _{\text{Co},w}^* ) + a (\Delta x_2^* \xi _{\text{Co},e}^*),\end{aligned}$$

(49)

$$\begin{aligned}&B_{\text{Co},C} = b (\Delta x_2^* \xi _{\text{Co},e}^*),\end{aligned}$$

(50)

$$\begin{aligned}&B_{\text{Co},E} = c (\Delta x_2^* \xi _{\text{Co},e}^*). \end{aligned}$$

(51)

At the cell boundaries, $\xi _{\text{Co}}^*$ is determined as:

$$\begin{aligned}&\xi _{\text{Co},w}^* = a \xi _{\text{Co},\text{WW}}^* + b \xi _{\text{Co},W}^* + c \xi _{\text{Co},C}^*,\end{aligned}$$

(52)

$$\begin{aligned}&\xi _{\text{Co},e}^* = a \xi _{\text{Co},W}^* + b \xi _{\text{Co},C}^* + c \xi _{\text{Co},E}^*, \end{aligned}$$

(53)

except when there is no WestWest neighbor cell, such that $\xi _{\text{Co},e}^*$ stays the way it is but $\xi _{\text{Co},w}^*$ becomes:

$$\begin{aligned} \xi _{\text{Co},w}^* = \xi _{\text{Co},W}^*. \end{aligned}$$

(54)

The unsteady term is discretized with the first-order Euler implicit scheme. The coefficient of $B_{\text{Ti}}$ reads:

$$\begin{aligned} B_{\text{Ti},C}= \Delta x_1^* \Delta x_2^*\frac{\xi _{\text{Ti},C}^*}{\Delta t^*}, \end{aligned}$$

(55)

where $\Delta t^* =\Delta t/t_{ref}$ is the dimensionless time step. The components of $\vec {c}_{\text{Co}}$ and $\vec {c}_{\text{Ti}}$ read:

$$\begin{aligned}&c_{\text{Co},C} = -\Delta x_2^* (-\xi _{\text{Co},w}^*) + \Delta x_2^* (-\xi _{\text{Co},e}^*), \end{aligned}$$

(56)

$$\begin{aligned}&c_{\text{Ti},C} = -\Delta x_1^* \Delta x_2^*\frac{\xi _{\text{Ti},C}^{*,} - \xi _{\text{Ti},C}^{*,\text{prev}}\left( 1-\theta _C^{\text{prev}} \right) }{\Delta t^*}, \end{aligned}$$

(57)

where $\xi _{\text{Ti},C}^{*,\text{prev}}$ and $\theta _C^{\text{prev}}$ correspond to the values of the previous time step. The discrete non-dimensional Fischer-Burmeister Equation (12) at each cell center reads:

$$\begin{aligned} F_C = p_C^* + \theta _C - \sqrt{p_C^{*2} + \theta _C^2}. \end{aligned}$$

(58)

Fig. 23

Schematic sketch of a two-dimensional FVM grid of size $L_{x_1}^* \cdot L_{x_2}^*$ with an exemplary stencil within the computational domain

1.2 Discretized Elastic Deformation

In its non-dimensional form, the gap height equation (5) reads:

$$\begin{aligned} h^* = \frac{h_{\text{d}}}{h^*} + \frac{h_{\text{g}}}{h^*} + \frac{h_{\text {el}}}{h^*} = h_{\text{d}}^* + h_{\text{g}}^* +h_{\text {el}}^*, \end{aligned}$$

(59)

where the discretized dimensionless elastic deformation of the gap height can be expressed as a linear convolution of a non-dimensional kernel function $K^*=K p_{ref}/h_{ref}$ with the non-dimensional hydrodynamic pressure field $p_{\text{hd}}^*$:

$$\begin{aligned} h_{\text{el},C}^*=h_{\text {el}}^*(x_{1,C}^*,x_{2,C}^*) = \sum ^{N_{x_2^{*\prime }}}\sum ^{N_{x_1^{*\prime }}} K^*(x_{1,C}^* - x_1^{*\prime }, x_{2,C}^* - x_2^{*\prime }) p_{\text{hd}}^*(x_1^{*\prime }, x_2^{*\prime }). \end{aligned}$$

(60)

This convolution can be interpreted as the alignment of the non-dimensional hydrodynamic pressure field $p_{\text{hd}}^*$ below the mirrored non-dimensional kernel function $K^*$ as shown in Fig. 24. This is explained in detail in the following. The non-dimensional kernel function is mirrored in $x_1^*$- and $x_2^*$-direction. Afterward, the center entry $K^*(0,0)$ is aligned with $p_{\text{hd},C}^*=p_{\text{hd}}^*(x_{1,C}^*,x_{2,C}^*)$. That way, aligned pairs of $K^*$ and $p_{\text{hd}}^*$ are created. The product of each respective pair is computed, for example $K^*(0,0) \cdot p_{\text{hd},C}^*$ or $K^*(-\Delta x_1^*,0) \cdot p_{\text{hd},E}^*$. The sum over all of the products is equal to $h_{\text{el},C}^*$. If instead of $h_{\text {el},C}^*=h_{\text {el}}^*(x_{1,C}^*,x_{2,C}^*)$ the dimensionless elastic deformation at the West cell $h_{\text {el},W}^*=h_{\text {el}}^*(x_{1,W}^*,x_{2,W}^*)$ is desired, the center entry $K^*(0,0)$ of the mirrored non-dimensional kernel function has to be aligned with $p_{\text{hd},W}^*=p_{\text{hd}}^*(x_{1,W}^*,x_{2,W}^*)$.

Fig. 24

Schematic sketch of the alignment of the mirrored dimensionless kernel function $K^*$ with the dimensionless pressure field $p_{\text{hd}}^*$ to obtain the dimensionless elastic deformation $h_{\text{el},C}^*$ via convolution

Assuming the hydrodynamic pressure being constant over the rectangular discretization cell of area $A=\Delta x_1 \Delta x_2$, the kernel K can be expressed as [30, Ch. 3.3], [31, Ch. 3.1]:

$$\begin{aligned}&K(\tilde{x}_1,\tilde{x}_2) = \frac{2}{\pi E'} \left( (\tilde{x}_1 + q_1)\ln \left( \frac{ (\tilde{x}_2 + q_2)+\sqrt{(\tilde{x}_2 + q_2)^2+(\tilde{x}_1 + q_1)^2} }{ (\tilde{x}_2 - q_2)+\sqrt{(\tilde{x}_2 - q_2)^2+(\tilde{x}_1 + q_1)^2} }\right) \right. \nonumber \\&\quad + (\tilde{x}_2 + q_2)\ln \left( \frac{ (\tilde{x}_1 + q_1)+\sqrt{(\tilde{x}_2 + q_2)^2+(\tilde{x}_1 + q_1)^2} }{ (\tilde{x}_1 - q_1)+\sqrt{(\tilde{x}_2 + q_2)^2+(\tilde{x}_1 - q_1)^2} }\right) \nonumber \\&\quad + (\tilde{x}_1 - q_1)\ln \left( \frac{ (\tilde{x}_2 - q_2)+\sqrt{(\tilde{x}_2 - q_2)^2+(\tilde{x}_1 - q_1)^2} }{ (\tilde{x}_2 + q_2)+\sqrt{(\tilde{x}_2 + q_2)^2+(\tilde{x}_1 - q_1)^2} }\right) \nonumber \\&\quad \left. + (\tilde{x}_2 - q_2)\ln \left( \frac{ (\tilde{x}_1 - q_1)+\sqrt{(\tilde{x}_2 - q_2)^2+(\tilde{x}_1 - q_1)^2} }{ (\tilde{x}_1 + q_1)+\sqrt{(\tilde{x}_2 - q_2)^2+(\tilde{x}_1 + q_1)^2} }\right) \right) , \end{aligned}$$

(61)

where the certain terms are consolidated as:

$$\begin{aligned}&\tilde{x}_1 = x_{1,C} - x_1^{\prime }, \end{aligned}$$

(62)

$$\begin{aligned}&\tilde{x}_2 = x_{2,C} - x_2^{\prime }, \end{aligned}$$

(63)

$$\begin{aligned}&q_1 = \frac{\Delta x_1}{2}, \end{aligned}$$

(64)

$$\begin{aligned}&q_2 = \frac{\Delta x_2}{2}. \end{aligned}$$

(65)

1.3 Discretized Pressure Jacobian of the Dimensionless Reynolds Equation

In the rigid case, the following procedure is obsolete and the pressure Jacobian of the dimensionless Reynolds Equation is simply $J_{G,p^*}= A_{\text{Po}}$. In order to consider the relationship between $h^*$ and $p^*$ in $J_{G,p^*}$ in the elastic case, the coefficients of the Couette and unsteady term are reformulated:

$$\begin{aligned} \xi _{\text{Co}}^* = \xi _{\text{Co},h}^* h^*, \quad \xi _{\text{Ti}}^* = \xi _{\text{Ti},h}^* h^*, \end{aligned}$$

(66)

with

$$\begin{aligned}&\xi _{\text{Co},h}^* = 12\frac{x_{1,ref}u_{\text{m},ref}\mu _{ref}}{h_{\text{m},ref}^2 p_{ref}} \rho ^* u^*, \end{aligned}$$

(67)

$$\begin{aligned}&\xi _{\text{Ti},h}^* = 12\frac{x_{1,ref}^2 \mu _{ref}}{t_{ref} h_{ref}^2 p_{ref}} \rho ^*. \end{aligned}$$

(68)

Using the previously mentioned generic order upwind interpolation scheme for the Couette term, this results in:

$$\begin{aligned}&\xi _{\text{Co},w}^* = a\xi _{\text{Co},h,\text{WW}}^* h_{\text{WW}}^* + b\xi _{\text{Co},h,W}^* h_W^* + c\xi _{\text{Co},h,C}^* h_C^*, \end{aligned}$$

(69)

$$\begin{aligned}&\xi _{\text{Co},e}^* = a\xi _{\text{Co},h,W}^* h_{W}^* + b\xi _{\text{Co},h,C}^* h_C^* + c\xi _{\text{Co},h,E}^* h_E^*. \end{aligned}$$

(70)

Except if no WestWest neighbor cell exists and $\xi _{\text{Co},w}^*$ has to be replaced by:

$$\begin{aligned} \xi _{\text{Co},w}^* = \xi _{\text{Co},h,W}^* h_W^*. \end{aligned}$$

(71)

Afterward, these expressions and Equations (59) and (60) are inserted into $c_C$ of Equation (34) (thus equations (56) and (57)) and only the coefficients of $p_S^*$, $p_W^*$, $p_C^*$, $p_E^*$ and $p_N^*$ are considered to obtain $J_{G,p^*}= A_{\text{Po}} + A_h =A_{\text{Po}} + A_{\text{Co}} + A_{\text{Ti}}$. Eventually, a generic scheme can be found to find the coefficients of an arbitrary diagonal D of matrix $A_{\text{Co}}$:

$$\begin{aligned} \begin{aligned}&A_{\text{Co},D}(i_d,j_d)= \Delta x_2^*(\\&\quad a\xi _{\text{Co},h,\text{WW}}^* K^*(\Delta x_{1,\text{WW}}^*,\Delta x_{2,\text{WW}}^*)+ b\xi _{\text{Co},h,W}^* K^*(\Delta x_{1,W}^*,\Delta x_{2,W}^*)\\&\quad + c\xi _{\text{Co},h,C}^* K^*(\Delta x_{1,C}^*,\Delta x_{2,C}^*) \\&\quad -(a\xi _{\text{Co},h,W}^* K^*(\Delta x_{1,W}^*,\Delta x_{2,W}^*)+b\xi _{\text{Co},h,C}^* K^*(\Delta x_{1,C}^*,\Delta x_{2,C}^*)\\&\quad +c\xi _{\text{Co},h,E}^* K^*(\Delta x_{1,E}^*,\Delta x_{2,E}^*)) ). \end{aligned} \end{aligned}$$

(72)

Note that $i_d$ and $j_d$ are not the indices of matrix $A_{\text{Co}}$, but counters that correspond to its diagonals $A_{\text{Co},D}$. For cells close to the boundary that do not have a WestWest neighbor cell, the following expression is used instead:

$$\begin{aligned} \begin{aligned}&A_{\text{Co},D}(i_d,j_d)= \Delta x_2^*( \xi _{\text{Co},h,W}^* K^*(\Delta x_{1,W}^*,\Delta x_{2,W}^*) \\&\quad -(a\xi _{\text{Co},h,W}^* K^*(\Delta x_{1,W}^*,\Delta x_{2,W}^*)+b\xi _{\text{Co},h,C}^* K^*(\Delta x_{1,C}^*,\Delta x_{2,C}^*)\\&\quad +c\xi _{\text{Co},h,E}^* K^*(\Delta x_{1,E}^*,\Delta x_{2,E}^*)) ). \end{aligned} \end{aligned}$$

(73)

Some of the above equations are consolidated as:

$$\begin{aligned} \begin{aligned} \Delta x_{1,\text{WW}}^*&= (-i_d-2)\Delta x_1^*, \quad \Delta x_{2,\text{WW}}^* = -j_d\Delta x_2^* \\ \Delta x_{1,W}^*&= (-i_d-1)\Delta x_1^*, \quad \Delta x_{2,W}^* = -j_d\Delta x_2^* \\ \Delta x_{1,C}^*&= -i_d\Delta x_1^*, \quad \Delta x_{2,C}^* = -j_d\Delta x_2^* \\ \Delta x_{1,E}^*&= (-i_d+1)\Delta x_1^*, \quad \Delta x_{2,E}^* = -j_d\Delta x_2^* \end{aligned} \end{aligned}$$

(74)

In order to construct the South, West, Center, East, and North diagonals of $A_{\text{Co}}$, the counters $i_d$ and $j_d$ have to be set as shown in Table 6.

Table 6 Description on how to set $i_d$ and $j_d$ to obtain the desired diagonal entry of $A_{\text{Co}}$

The unsteady term is discretized with the first-order Euler implicit scheme. The coefficients of $A_{\text{Ti}}$ read:

$$\begin{aligned} \begin{aligned} A_{\text{Ti},S}&= -\Delta x_1^* \Delta x_2^*\frac{\xi _{\text{Ti},h,C}^*}{\Delta t^*} K^*(0,\Delta x_{2}^*) \\ A_{\text{Ti},W}&= -\Delta x_1^* \Delta x_2^*\frac{\xi _{\text{Ti},h,C}^*}{\Delta t^*} K^*(\Delta x_{1}^*,0) \\ A_{\text{Ti},C}&= -\Delta x_1^* \Delta x_2^*\frac{\xi _{\text{Ti},h,C}^*}{\Delta t^*} K^*(0,0) \\ A_{Ti,E}&= -\Delta x_1^* \Delta x_2^*\frac{\xi _{\text{Ti},h,C}^*}{\Delta t^*} K^*(-\Delta x_{1}^*,0) \\ A_{\text{Ti},N}&= -\Delta x_1^* \Delta x_2^*\frac{\xi _{\text{Ti},h,C}^*}{\Delta t^*} K^*(0,-\Delta x_{2}^*) \end{aligned} \end{aligned}$$

(75)