1 Introduction

Sheet metal forming of aluminum alloys is a well established production process in several industrial applications, from automotive and aerospace sectors to the production of daily life objects such as beverage cans, light reflectors or fuel tanks. The production of complex shapes from flat metal sheets is significantly influenced by friction. For example, in the process of deep drawing, an excessive friction between the aluminum and the forming tool can create fractures on the sheet [1, 2]. On the contrary, if friction is smaller than a certain threshold, the piece could be rejected due to wrinkling [3,4,5]. Thus, in sheet metal forming, tribology is a crucial factor for the improvement of the industrial process [6].

However, there is no fully predictive theory of friction. Friction is a system property that requires extensive experimental campaigns to understand the interaction between the sheet, the tool surface and the lubricant, depending on the normal load, the sliding velocity and the temperature. In dry contact, the emergent frictional behavior is determined by various effects at different length scales, spanning from atomic and molecular forces to plastic deformations and collisions between surface asperities, including debris formation and transport due to wear [7, 8]. As a first approximation, the resulting friction force at macroscopic level is the well-known Amontons-Coulomb (AC) law [9], stating that the force is proportional to the applied normal load and independent of the sliding velocity. This simple behavior has been connected by Bowden and Tabor to the linearity of the real contact area with the normal load [10].

Thus, friction is deeply linked to the topography of contact surfaces and their roughness. Real surfaces are not only rough, so that the contact area is a small fraction of the apparent one, but they often display a typical self-affine structure [11,12,13]. Since the seminal work of Greenwood and Williamson [14], many models relating the real contact area to roughness parameters have been proposed [15]. Analytical models [16, 17] and numerical techniques including the finite-element method [18, 19] and the boundary-element method [20,21,22,23,24,25] help estimate the real contact area as function of load. In particular, it is now well established that, for two perfectly elastic surfaces, given the gap between them h(x, y), the real contact area is inversely proportional to the root-mean-squared slope, i.e. the quantity \(R_{dq} \equiv \sqrt{\langle |\nabla h|^2\rangle }\):

$$\begin{aligned} A_{\text {real}} = \kappa \frac{F}{R_{dq} E^{\prime }} \end{aligned}$$
(1)

where \(\kappa\) is a proportionality constant, F is the normal force, \(E^{\prime }\) is the effective Young’s Modulus, which can be expressed in terms of the Young’s moduli and Poisson ratios of the two surfaces as \(1/E^{\prime }= (1-\nu ^2_{1})/E_{1}+ (1-\nu ^2_{2})/E_{2}\). Note that \(R_{dq}\) depends on spatial resolution and a good experimental measure is challenging since this quantity is prone to measurement noise. A proper evaluation is however crucial to estimate friction [26] since the total tangential force may be assumed to be proportional to the real contact area [10].

Additional difficulties in many practical applications such as metal forming are due to changes to surface texture caused by inelastic deformation during sliding and the mixed mode lubrication regime, i.e. both liquid and solid surface asperities share the load during the contact. Lubrication allows to minimize the frictional resistance [27], but it poses open challenges due to the coupling between elasto-plastic and hydrodynamic effects. Many methods have been introduced to investigate these systems [28], among them the Reynolds equations [29, 30] coupled with those for solid deformations in the thin lubricant film regime [31, 32]. Efficient solution techniques have been proposed [33, 34] to obtain useful insights for these systems, but issues can arise for convergence [35] and the required computational power [36]. Molecular dynamics simulations have been used for studying microscopic interactions between fluids and rough boundaries [37,38,39], but they cannot be extended to macroscopic systems.

Another option is an approach based on the load sharing concept, firstly introduced in [40]. The key point is to calculate the fractions of real contact area occupied by dry and lubricated contact, e.g. by means of half-space theory [41] or theories based on Greenwood-Williamson incorporating plasticity [42, 43]; then, friction can be calculated averaging the friction contribution of each by means of effective laws [44]. Despite significant progresses in understanding the interplay between system parameters, work still remains to be done to provide practical indications for specific engineering and industrial applications, since effective friction coefficients and viscosity parameters of each lubricant must be obtained independently with further studies and measurements [45].

In this paper, we present a simple mechanistic model for frictional contact between an aluminum sheet and a steel tool, using the aluminum sheet’s measured surface topography and its mechanical properties. Since the modulus and strength of the steel tool are larger than the aluminum, and its surface roughness is smaller, the steel contact surface is approximated as a plane rigid surface. We compare the model with experimental measurements of friction of an aluminum 6016 alloy sliding against steel pads, reproducing benchmark conditions of a strip drawing friction test. Experimental results are completed by topography scans of the aluminum surfaces, obtained in the final cold rolling pass during sheet production, using Electro-Discharge Texturing surface-treated rolls (EDT). These height profiles are used as input for calculations with a Boundary Element Method (BEM) to deduce the real contact area as a function of the applied pressure. The mixed lubrication regime reduces the real contact area which is in dry state [40] and is taken into account by means of a simple steepest-descent geometrical model, aiming to find a realistic liquid distribution on the surface. Following a Bowden-Tabor approach [10], the friction force is taken to be proportional to the real contact area in dry contact state.

Therefore, the aim of this study is to evaluate the effect of the lubricant distribution on these specific textured surfaces, implementing a robust procedure that uses experimental surfaces as input and, by means of mechanical models and numerical simulations, can formulate predictions about the observed frictional behavior. The paper is structured as follows: in Sect. 2, we present the experimental apparatus and the procedures to perform the friction tests. In Sect. 3, we present the surface topographies obtained with the scans and discuss their statistical properties. In Sect. 4, we describe our theoretical approach, briefly present the BEM algorithm, and the comparison of the friction coefficient in dry and lubricated conditions. Section 5 presents the conclusions.

2 Experimental Setup

The analyzed material is an EN AW-6016 T4 aluminum alloy with an EDT surface finish. Its arithmetic average asperity heights, Sa, is \(0.9 \pm 0.1\,\mu \text {m}\) with points sampled at an elementary length \(l=0.67 \,\mu \text {m}\). Two different amounts of a standard oil based lubricant used in automotive sheet metal forming are applied by electrostatic deposition onto this sheet material: \(0.45\, \text {g}/\text {m}^2\) and \(0.9\,\text {g}/\text {m}^2\), kinematic viscosity \(\nu = 250\,\text {mm}^2\)/s at \(20{^{\circ }}\text {C}\).

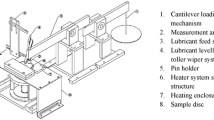
A tensile testing machine equipped with a strip drawing test rig is used to investigate the friction behavior. Hereby, aluminum strip samples are pulled through two steel pads applying a constant normal pressure to both sides of the sample during each test, as shown in Fig. 1. The 70 mm wide and 600 mm long aluminum sheet strips are pulled over a distance of 200 mm along their length, at a speed of 5 mm/s. The steel pads are made of D2 tool steel (hardness Rc 62-65). The contact area of each pad is 40 mm by 44 mm, both with rounded edges and an average roughness Sa = \(0.10 \pm 0.02\,\mu \text {m}\) with sampling length \(l=0.67 \,\mu \text {m}\). Note that the roughness of steel pads is an order of magnitude smaller than the roughness of the aluminum alloy. All tests of this study are performed at room temperature. A new sample is used for each test, i.e. samples are not tested twice. Different levels of normal pressure are applied with one or two repeats. After completion of each test series at a specific normal pressure, the normal pressure level is further increased by 1 MPa, until galling appears, i.e. the lubrication film breaks and aluminum particles adhere to the steel pads.

The friction coefficient is identified by dividing the measured pulling force by two times the measured normal force, as sliding occurs on both sides of the aluminum sheet. For each test, an average friction coefficient is determined in the pulling distance range between 64 mm and 190 mm. Therefore, only the dynamic friction regime is considered and the initial force peak at the start of each test representing static friction is ignored in this study. The surface roughness of the steel pads and of the aluminum samples were measured before and after the tests using a confocal microscope.

In Fig. 2a, we show a measurement of the friction coefficient, i.e. the instantaneous ratio of the friction force divided by the normal force as a function of test time. By averaging these results, the curves of the friction coefficient as a function of the applied pressure for two typical lubricant density have been obtained, Fig. 2b. These curves display a decreasing trend with the applied pressure, consistently with experimental results on similar systems [46].

Fig. 1
figure 1

Schematic of the strip drawing test, with the aluminum sheet pulled between the steel pads

Full size image
Fig. 2
figure 2

Measurements of the evolution with time of the friction coefficient during the sliding test with lubricant density \(0.45\,\text {g}/\text {m}^2\) (a). By averaging between 15 and 40 s, corresponding to sliding distance 64 mm to 190 mm, for various repetitions, the value of the dynamic friction coefficient can be estimated as a function of pressure and lubricant density (b)

Full size image

3 Surface Statistics

The topography of a non-lubricated aluminum surface before any test is shown in Fig. 3a. The typical profile produced by the EDT process is characterized by many plateaus with asperities on top of asperities, as in the plateau region shown in Fig. 3b. The sampling distance in both directions is \(l=0.67\) μm, with about 3400 sampled points for each side. Surfaces are oriented so that the x-axis is the sliding direction of the experiments.

Fig. 3
figure 3

Topography of a surface area of a not yet lubricated aluminum sample with the heights measured with respect to the average (a). The example of a plateau, corresponding to the boxed area in (a), illustrates the self-affine structure of the textures (b); only asperity heights on the plateau region are shown and the rest is left blank to highlight the roughness on a smaller scale above the plateau. A three-dimensional view of the same region (c)

Full size image

Given the two-dimensional height profile h(x, y), to describe the surface roughness we calculate the power spectral density (PSD) [26]. Due to the convolution theorem, this corresponds to the square modulus of the Fourier transform, i.e. \(P(q) \equiv |{\mathcal {F}}(h)|^2\), where q is the frequency. Surfaces are not isotropic between orthogonal axis, as can be observed directly from the topography. Thus, we calculate the Fourier transform along only one axis while fixing the coordinate of the orthogonal one, then we average P over all these fixed values, in symbols: \(P_x(q) \equiv \langle |{\mathcal {F}}(h(x,y={\overline{y}})|^2 \rangle _{{\overline{y}}}\), where \(\langle ...\rangle _{{\overline{y}}}\) denotes the average over all the values of the y-axis. A similar definition holds for \(P_y(q)\).

In Fig. 4, we show the PSDs in both directions, reporting as benchmark the PSD of the initial surfaces compared with those obtained after the experiment for various pressures and lubricant densities. In all cases, the curves follow a power-law behavior with Hurst exponent \(0.7< \text {H} < 0.8\). The power spectrum slightly deviates from an exact power-law behavior which would have been typical of a perfect self-affine surface. In any case, the scanned surfaces give access to sufficient data to compute meaningful statistical properties.

Moreover, the PSDs before and after a sliding experiment highlight the modification occurred due to the shearing of asperities, depending on the applied pressure and the lubricant amount. We have also verified that pushing with the same pressure but without sliding the aluminum sheet against its steel counterpart does not produce significant modifications in the PSD, i.e. plastic deformations are exclusively caused by the sliding. As expected, larger modifications are found for larger pressure and smaller lubricant density.

Fig. 4
figure 4

Comparison between PSDs of aluminum sheet surfaces before and after the experiment for various applied pressures and lubricant density, along the \(x-\) (a) and \(y-\)axis (b). Non-negligible modifications occur in both cases, particularly for larger pressure and smaller lubricant density. In both plots, the dashed line indicates the slope of a power-law with Hurst exponent \(\text {H}=0.8\)

Full size image

To estimate the steady state friction coefficient, we start by using the stable final surface topography, i.e. measured after the sliding tests. These surface profiles give a means to compute, by using the boundary element method, the real contact area and, consequently, the total friction force. However, before calculating the real contact area, surfaces must be treated with a smoothing procedure to remove the noise of the experimental data. The real contact area, which is known to depend on the root-mean-squared slope, Sect. 1, is prone to experimental noise. Without applying a smoothing procedure, we have found that the real contact area is underestimated due to artificial spikes that increase the estimated gap between the surfaces. This effect is particularly enhanced for purely elastic models, whereas a model incorporating plasticity introduces naturally some smoothing. However, due to the modifications induced by the sliding test, plastic deformations already occurred and the contact solutions of surface topographies obtained after the sliding tests are dominated by elasticity.

Therefore, a low-pass filter is applied to the surface scans after the experiment by means of a Hann window [26, 47] in the frequency domain in both directions. With a Hann window too large, the smoothing is ineffective, while, if it is too small, too many surface features are removed. The real contact area generally depends on the selected window size. We have found that it reaches a maximum plateau for a window between 300-\(700l^{-1}\). Therefore we have chosen a window of 512\(l^{-1}\) as a sufficient filter size to reduce the noise.

4 Theoretical Calculations

4.1 Boundary Element Method Solution

To calculate the real contact area of experimental surfaces, we use TAMAAS, an open-source library implementing several boundary element method (BEM) algorithms [48]. We assume as a first step that our surfaces are not lubricated. Using TAMAAS, it is possible to solve the normal dry contact problem between a deformable rough surface and a rigid flat plate. The rough surface represents our aluminum alloy, while the rigid flat surface represents the steel pad. TAMAAS enables accounting both for purely elastic deformations by using the Polonsky-Keer algorithm [49, 50] and for plasticity [25], by assuming a simple pressure saturation model [23, 51], i.e. contacting asperities cannot sustain pressures larger than a threshold pressure that we assume to be the flow stress of our aluminum alloy. These algorithms are accelerated by means of the Fast Fourier Transform (FFT) method [52], providing an efficient solution for the displacement and the stress field. From these, the contact clusters can be identified and the real contact area can be computed. In Fig. 5, we show an example of contact solution obtained with the saturated pressure model applied to the experimental surface shown in Fig. 3.

Note that surface profiles after sliding are loaded in the elastic domain, since they have already undergone a plastic smoothening due to the sliding and their contact solution is dominated by elasticity. For these surfaces, modifications induced by using a solver with plasticity are smaller than statistical fluctuations. Instead, when performing the computation from the rougher surface profiles before sliding, which have not yet been subjected to any prior loading, plasticity is significant, thus requiring the pressure saturation model.

For this model, we have used a saturation pressure \(p_{\text {sat}}=240\,\text {MPa}\), which has been estimated from tensile tests on the aluminum sample. Given the material’s elastic parameters and the applied pressures, modifications due to the elasticity of the steel counterparts are negligible with respect to the statistical fluctuations of different surfaces. Another source of error could be the finite thickness of the sheets of 1 mm, whereas the BEM calculations assume an infinite half space. Since we apply a uniform pressure, and the roughness scale is three orders of magnitude smaller than the thickness, effects of the boundary conditions on the contact surface should be negligible. We have verified with Finite Element simulations that, by varying the thickness for an equivalent roughness scale, the error for a thickness of 1 mm is limited to 2%, so that they are negligible with respect to the statistical fluctuations.

Fig. 5
figure 5

Contact solution obtained with the BEM solver for a saturated pressure model for the experimental surface shown in Fig. 3. The contact clusters are coloured in black

Full size image

4.2 Dry Friction

We now compare the dry contact theoretical prediction to the friction experiments that have been described in Sect. 2. As a first step, we have calculated the dynamic friction coefficient by assuming a perfect Bowden-Tabor law in dry condition and that all the microscopic contact junctions have a shear strength corresponding to that of the bulk aluminum alloy. Thus, we can estimate the friction coefficient as:

$$\begin{aligned} \mu = \frac{A_{\text {real}}}{A_{\text {apparent}}} \frac{\tau _y}{P}, \end{aligned}$$
(2)

where \(A_{\text {real}}\) is the real contact area, \(A_{\text {apparent}}\) the apparent contact area, P the applied normal pressure and \(\tau _y\) the shear strength of the aluminum alloy, which we evaluated as \(\tau _y=70\) MPa, based on a direct measurement on a sample of the aluminum alloy used for experiments. Elastic parameters are summarized in Table 1. The real contact area is calculated for a given surface profile and applied pressure with the software TAMAAS adopting a purely elastic BEM solver, see Sect. 4.1. We have used as input the smoothed surface topographies after the experiments to include the plastic modifications induced by the frictional sliding. Since the occurred surface topography modifications are influenced by the lubricant density, we can compare the dry contact modeling results for two cases of tested lubricant densities. Given that the experimental samples have two sides subjected to friction, the friction coefficients for both the reported experimental data and the theoretical calculations have been estimated with the average for both sides and each test repetition.

Results of the friction coefficients are shown in Fig. 6. Experimental data display a decreasing trend as a function of the pressure, while numerical results are increasing. This shows that lubrication is a crucial factor, indeed estimates are close to experimental data only in the regime of small pressure and smaller lubricant density, for which we expect lubrication to play little role. Simulation data have been obtained by averaging 4 experimental surface profiles, and the large error bars are due to large fluctuations of the real contact area between different samples. This can be explained by the effect of the shearing on the roughness, which is dominated by relevant but random modifications due to the frictional sliding.

Fig. 6
figure 6

Comparison between experimental results and the friction coefficients estimated by means of Eq. 2 for two cases of lubricant density

Full size image
Table 1 Material properties of the aluminum alloy used in numerical simulations
Full size table

4.3 Lubrication

As observed in Sect. 3, surface topographies are characterized by a self-affine structure, so that for our partially lubricated surfaces, the lubricant can be distributed in pockets located on top of larger asperities that are in contact during the sliding. In order to include this effect on the emergent friction coefficient, a simple method is to modify formula 2 with a purely geometric approach, assuming that zones in contact filled by liquid do not contribute to friction, nor have effect on the elastic problem. Therefore we assume that the real contact area must be reduced by the contact area occupied by the lubricant, namely \(A_{\text {lub}}\):

$$\begin{aligned} \mu = \frac{A_{\text {real}} - A_{\text {lub}}}{A_{\text {apparent}}} \frac{\tau _y}{P}, \end{aligned}$$
(3)

A full solution of the contact problem with the fluid, and accounting for its viscosity is beyond the scope of this work and will be the subject of future work, whereas this simple first order approximation aims to verify if it is possible to obtain at least qualitatively the experimental behavior observed in Fig. 2. The key point for this approach is to calculate the lubricant distribution on the surface, in particular the presence of regions occupied by the fluid inside the contact clusters calculated by means of the BEM solver.

A simple calculation reveals that, given the experimental lubricant densities, the surfaces are not fully covered by oil and are partially lubricated. This can be understood by filling the surfaces from the bottom up to a fixed flat quota of the topography, so that the total lubricant density matches the experimental one. In this case, the tips of the asperities would be in dry contact, whereas, as previously observed, the lubricant can be also located in pockets on top of asperities.

Thus, we have developed a random deposition algorithm to find the regions filled by fluids for a given topography. Experimental scans with the surface heights h(x, y) are themselves a discrete square grid of points (x, y) with spacing along orthogonal axis \(l=0.67\, \mu \text {m}\), corresponding to the sampling distance.

We create a droplet of lubricant in a random initial position on the surface. The droplet volume is \(d l^2\), where d is a free parameter representing the height increase due to the droplet. Then, the droplet is shifted by a single discrete step in the direction of the steepest descent, calculated by means of the minimum gradient between the initial point i and its four nearest neighbor j along orthogonal axis, in symbols \(\varDelta h \equiv \min _{j}(h_j-h_i)\). This procedure is iterated until the droplet reaches a local minimum. This is filled by a quantity corresponding to \(\min (d,\varDelta h)\), so that the local minimum cannot be filled more than its edges.

If the droplet reaches a stationary point, i.e. \(\varDelta h=0\), all the adjacent points at the same height are calculated. This region represents a set of stationary points, which is a common feature once the bottom parts of the surface are filled. In this case, we calculate the gradient with all the neighboring points of this region. If the minimum gradient is positive, then the whole region is a local minimum and is filled by a quantity \(\min (d,\varDelta h)\). Otherwise, the droplet follows the steepest descent further below the stationary region. Once that the droplet is deposited on its final location and the surface height has been updated, a new droplet is created. The algorithm scheme is reported in the Appendix.

This algorithm is repeated until the total amount of deposited liquid divided for the area of the surface is equal to the nominal experimental density. Final results are not affected by the choice of d if \(d<l\) or, in other words, if the number of droplets used to fill the surface is much larger than the total number of grid points, so to avoid empty regions due to the random deposition. In our calculation, we have used \(d=0.1\,\mu \text {m}\). An example of lubricated surface obtained with this algorithm is reported in Fig. 7, showing that, due to the peculiar topography, most of the liquid fills pockets between plateaus. However, lubricant can be also found on top of these, as shown in the linear height profile in the same figure.

For these simulations, we use as input surface topographies before the experiment, since we want to address the effect of different lubricant densities on the same starting surface, whilst topographies after the experiment have been already modified depending on the oil density. For this reason, we use the BEM solver with a saturated pressure model to take into account the plasticity.

When the contact problem is solved, we obtain the contact clusters that contain regions covered with oil, as shown in Fig. 8, which is a zoom on part of the surface of Fig. 3 to highlight the contact regions filled by lubricant. By subtracting the lubricated area, see Eq. 3, we calculate the corrected friction coefficient. Results are shown in Fig. 9. Despite the approximations made, we obtain the correct decreasing trend of the friction with pressure, indicating that the suggested correction is crucial to capture the dominant effect due to lubrication. We note that, beyond the initial assumptions about the lubricant distribution, there are no arbitrary parameters in this model formulation: the only source of uncertainty is the noise of the experimental surfaces and the choice of the Hann window value, but the BEM solver and the lubrication algorithm use only experimental data and material properties. We emphasize that the random deposition algorithm is an essential component. We have tried a bottom-fill approach for the lubricant, as an alternative to random deposition. For the low lubricant densities considered here, the bottom-fill approach did not lead to any reduction of the friction coefficient. Moreover, it is possible to calculate the spillover volume, i.e. the amount of fluid that would be squeezed out of the pockets when the surfaces are pushed in contact by assuming that the elastic surface is not modified by liquid pressure. This amount is a few percent of the total volume, so that it can be neglected in our calculations.

Despite the approximations leading to notable differences with the experimental results, and in particular an overestimation of the friction coefficient, this simple mechanistic model is an interesting starting point for further investigations. The gap between simulations and the experimental data could be explained by many factors. In particular, the roughness of the steel pads facing the aluminum sheet was neglected although it must contribute to ploughing friction. The pressure generated by the fluid trapped in pockets between the contact surfaces should be accounted for in the BEM solver, as it directly affects the estimation of the real contact area. In particular, the load bearing capacity of the fluid introduces a further reduction of the friction coefficient with respect to the current estimates. Since most of the real contact area is in dry contact, this can provide the small correction towards the experimental results.

Moreover, the viscosity of the oil should be taken into account, since neglecting friction contributions of the fluid corresponds to assuming a zero or negligible viscosity. Thus, a friction contribution due to the fluid should be included, e.g. by means of an effective formula taking into account viscosity and pressure [28]. This would increase the estimation of the friction coefficient. However, due to the viscosity, the presence of liquid outside the stationary points of the topography should also be considered, increasing the lubricated fraction of the real contact area. This effect can also explain the observation that, for both numerical and experimental results, the curves of the friction coefficient for a larger oil density are shifted towards smaller values, but numerical data underestimate the differences between the two densities. Finally, there are effects due to the dynamical evolution during the sliding, in particular the plastic deformations that modify the surface topography and the re-distribution of the fluid due to the effect of spillover of trapped fluid from the initial pockets.

Fig. 7
figure 7

Lubricant distribution on a portion of the surface of Fig. 3 with colors representing the lubricant thickness (b), the dry surface topography on the same area in reported for comparison (a). The longitudinal profile along the dashed line indicated on the topography is reported, with the liquid level highlighted in blue (c) (Color figure online)

Full size image
Fig. 8
figure 8

Zoom on contact clusters obtained from the surface of Fig. 3 coloured in orange, obtained with an applied pressure of 7 MPa. In black the contact regions occupied by fluid obtained by means of the random deposition algorithm (Color figure online)

Full size image
Fig. 9
figure 9

Comparison between experimental data and numerical results obtained with the BEM solver according to Eq. 3 and the random deposition algorithm

Full size image

5 Conclusions

We have reported experimental data regarding the frictional sliding of aluminum sheets between steel pads. This process is fundamental for metal forming in industrial applications and friction must be controlled for a robust production process and to avoid defects in the final product. Aluminum surfaces, which have been textured with the EDT process, display approximately a self-affine topography, characterized by smaller asperities on top of larger plateaus, but their PSDs are modified by the frictional sliding between the steel pads. Experimental friction coefficients display a decreasing trend with the pressure.

These results have been compared with theoretical predictions by assuming a simple Bowden–Tabor law, and the real contact area has been calculated from experimental surfaces by means of a BEM solver. Lubrication is the fundamental factor to take into account, since calculations assuming dry friction cannot reproduce the experimental trend. Thus, a simple random deposition model has been developed to calculate the lubricant distribution on experimental surfaces for a given experimental oil density, and the Bowden-Tabor law has been modified by subtracting from the real contact area the area occupied by the fluid. This correction significantly improves the results, reproducing the qualitative decreasing trend with the pressure and approaching the experimental values. The residual gap can be explained by the approximations introduced to simplify the model, in particular the effect of the fluid in the contact problem and the viscosity of the lubricant have been neglected. These effects will be addressed in future work. The results achieved with the simple approach presented here are a promising starting point towards a better understanding of the factors determining friction in processes like sheet metal forming.