1 Background

There is currently great concern to increase the efficiency of machine components so as to save energy and thereby reduce greenhouse gas emissions. From the point of view of tribology, a clear pathway to this is to reduce the friction between lubricated machine elements. In road vehicles, the main focus of attention has been on lowering crankcase engine friction, where most friction losses occur in the piston pack and engine bearings. These components are based on sliding, conformal contacts which operate primarily in the hydrodynamic lubrication regime where contact pressures are relatively low, typically less than 50 MPa. The principal route to reducing friction in this regime is simply to reduce the dynamic viscosity of the lubricant, and therefore, progressively lower and lower viscosities are being employed in engine oil formulation. Since lower viscosity implies thinner hydrodynamic films and thus an increase in asperity contact, a concomitant requirement is, of course, to maintain low boundary friction.

In contrast to crankcase engines, mechanical transmissions are most commonly designed around machine elements such as gears and rolling bearings that both roll and slide together. In these, the non-conforming contacts required for elements to roll result in very high localised contact pressures, generally greater than 500 MPa, and the main lubrication regime then becomes elastohydrodynamic (EHD) lubrication. In this regime, the combination of very high pressure with high strain rate means that the lubricant film experiences extensive shear thinning so that the effective viscosity and thus the friction is only weakly dependent on the low shear rate viscosity. Instead it is strongly dependent on the shape and flexibility of the organic molecules on which the lubricant is based since these determine how easily the molecules slide past one another in high pressure, low free-volume conditions.

Friction losses from mechanical transmissions and thus from EHD-lubricated contacts are already important in determining the efficiency of many types of machine but are likely to become even more significant as electrically powered vehicles (EVs) replace internal combustion engine-powered ones and transmission losses become a greater proportion of the whole. Thus, it is very important to measure and understand EHD friction and how to design lubricants able to deliver very low such friction.

There have been numerous studies of EHD lubrication with respect to both lubricant film thickness [1] and friction [2] and the history and origins of our understanding EHD friction have been reviewed by the current authors [3]. In EHD contacts, the very high local pressures compress the lubricant film and greatly reduce available free volume between its molecules resulting in an extremely large rise in low shear rate viscosity. If some sliding is present, this film is subjected to a high strain rate and thus, because of its high viscosity, to a very high shear stress. As the sliding speed and thus the strain rate is increased, the shear stress becomes so large that the lubricant film starts to shear thin. This occurs when the shear stress reaches a critical value of typically 5 to 10 MPa. It is important to note that this shear thinning is not primarily due to molecular alignment as it is with polymers; base oils with small molecules of MWt less than 200, experience shear thinning. The precise model to describe the ensuing shear-thinning response has been the subject of some controversy [3] but using molecular dynamics simulation it has recently been shown that, except for a small intermediate strain rate region in which molecules align, it can be described by an activated flow model known as the Eyring shear-thinning model [4]. In this, the rate at which molecules slide past one another increases exponentially with stress so that the shear stress and thus the EHD friction increases with the logarithm of the sliding speed. This model has been extensively used to calculate EHD friction in machine components. It has also been suggested that lubricant films may eventually reach a limiting shear stress where the stress no longer increases with strain rate but instead levels out at a constant value [5]. Such behaviour is known to occur with some fluids based on highly inflexible molecules that are designed specifically to give very high-EHD friction (traction fluids) but it is not yet clear whether it is a property of all lubricants at very high pressure and thus shear stress.

In gear contacts, mean pressures are typically between 1 and 2 GPa and most research on EHD friction, with one main exception [6], has been made at these pressures. However, there are some machine components, in particular rolling bearings, but also some constant velocity joints [7] and continuously variable transmission components [8] that may operate at significantly higher contact pressures, as indicated in Table 1.

Table 1 Contact pressures in some transmission components
Full size table

The current paper describes EHD friction measurements on a range of base oil types up to very high pressures using a newly developed ball-on-disc friction machine. Parallel film thickness measurements are also made so that the measured friction curves can be converted to curves of mean shear stress versus strain rate. At very high pressures, significant shear heating can occur in lubricated contacts even at quite low-sliding speeds and in the current work this is calculated and corrected so as to obtain isothermal shear stress versus strain rate curves. The aims of the study are as follows:

  1. (i)

    To explore the EHD friction of a range of widely used base fluid types up to very high pressure

  2. (ii)

    To see whether differences in EHD friction between the various API base oil types observed at lower pressures persist up to extremely high pressures.

  3. (iii)

    To determine whether base fluids reach a limiting shear stress at very high pressure

2 Test Methods

2.1 EHD Friction Measurement

Much previous work on EHD friction has been carried out on the minitraction machine, MTM (PCS Instruments, Acton UK). In this a ball is loaded against the upper flat surface of disc immersed in lubricant. Ball and disc are driven by separate motors to enable any desired combination of entrainment speed and sliding speed to be obtained. Friction is measured by a load cell attached to the ball shaft housing. The MTM has a maximum applied load of 75 N and this limits the maximum attainable mean contact pressure to 0.85 GPa for steel/steel ball and disc or 1.86 GPa for WC/WC. Because of the ellipsoidal Hertzian pressure distribution, maximum contact pressures are 1.5 times these values.

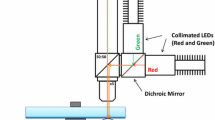
To surpass the 75 N load limit, PCS Instruments have recently developed the ETM. This has an applied load range of 100 to 1650 N and thus, with 19 mm diameter balls, a maximum attainable mean pressure of 2.36 GPa for steel/steel and 5.16 GPa for WC/WC. Figure 1 shows the configuration of the contact. As in the MTM, the ball shaft is tilted so that its axis intercepts the centre of rotation of the upper surface of the disc to minimise spin in the contact. For most of this study, the ETM was employed, but some tests at low loads were carried out using an MTM2.

Fig. 1
figure 1

Diagram of ETM ball-on-disc set-up

Full size image

In this study, balls and discs of three materials were used, AISI 52100 steel, tungsten carbide (WC), and zirconia (ZrO2), with properties listed in Tables 2 and 3. Two very important properties in the context of EHD friction are the thermal conductivity and the elastic modulus. The thermal conductivity, in combination with density and specific heat, control the flash temperature and thus the temperature of the oil film in the contact as discussed below. The elastic modulus is required to determine the contact pressure and contact radius from the applied load using the Hertz equations [9];

$$ p_{{{\text{mean}}}} = \left( {\frac{1}{\pi }} \right)\left( {\frac{{16WE^{*2} }}{{9R^{2} }}} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}}} $$
(1)
$$ a = \left( {\frac{3WR}{{4E^{*} }}} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}}} $$
(2)
Table 2 Elastic modulus, E, Poisson’s ratio, ν, and hardness
Full size table
Table 3 Thermal properties, thermal conductivity K, specific heat c, and density ρ
Full size table

where W is the applied load, R the radius of the ball and E* the reduced elastic modulus defined as

$$ {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {E^{*} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${E^{*} }$}} = {\raise0.7ex\hbox{${\left( {1 - \nu_{1}^{2} } \right)}$} \!\mathord{\left/ {\vphantom {{\left( {1 - \nu_{1}^{2} } \right)} {E_{1} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${E_{1} }$}} + {\raise0.7ex\hbox{${\left( {1 - \nu_{2}^{2} } \right)}$} \!\mathord{\left/ {\vphantom {{\left( {1 - \nu_{2}^{2} } \right)} {E_{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${E_{2} }$}} $$
(3)

where E1 and E2 and ν1 and ν2 are the elastic moduli and Poisson’s ratios of the two contacting bodies, respectively.

In Table 2, the elastic moduli of the WC specimens were measured using nanoindentation and it is of interest to note that they differ between the balls and discs. This is believed to result from different concentrations of cobalt dopant in the two types of specimen. The elastic modulus of AISI 52100 steel was taken from the literature. In Table 3, the thermal conductivities of the steel and WC specimens and the ZrO2 balls were measured using frequency domain thermal reflection (FDTR) [10]. This measures the thermal conductivity and specific heat of a solid within about 5 to 10 μm of its surface. It should be noted that the thermal conductivity of the AISI 52100 steel specimens is considerably lower than the value normally cited in the literature for this material; this is discussed in [11]. The elastic modulus of ZrO2 were not measured and are taken from the literature so most of this study focussed on tests using steel and WC.

Table 4 lists the root mean square roughness, Rq, of the ball and disc specimens, measured with a stylus profilometer.

Table 4 Root mean square roughness, Rq, of test specimens (nm)
Full size table

The ball and disc specimens were stored in toluene for at least 24 h and then rinsed in toluene and Analar acetone and air-dried before use. Measurements were made at the applied loads listed in Table 5 and also at 1000 N. The tests at 12.5 N and 42 N were made using the MTM2 and the remainder with the ETM. At each load, measurements were carried out at eleven temperatures from 10 to 110 °C in increments of 10 °C, to enable isothermal correction as described below. In each measurement sequence, friction was measured while increasing slide-roll ratio in a series of stages from 0.1% to 20% (50% in a few tests), where slide-roll ratio is defined as

$$ {\text{SRR}} = \frac{{\text{Sliding speed}}}{{\text{Entrainment speed}}} = \frac{{\left| {u_{1} - u_{2} } \right|}}{{\left( {u_{1} + u_{2} } \right)/2}} $$
(4)

u1 and u2 are the surface speeds of ball and disc with respect to the contact and the entrainment speed is (u1 + u2)/2. For each individual measurement, friction was measured with the ball travelling faster than the disc and vice versa so as to enable cancellation of any offset in the load cell. All tests were carried out at a fixed entrainment speed of 3.0 m/s that ensured full-EHD film conditions at all temperatures and loads.

Table 5 Main contact loads and pressures used
Full size table

2.2 EHD Film Thickness

The EHD film-forming properties of the base oils were measured at test temperatures from 10 to 120 °C using optical interferometry (EHD2, PCS Instruments, Acton, UK). In this, an AISI 52100 steel ball was loaded at 20 N against a coated glass disc and film thickness measured over a range of entrainment speeds in nominally pure rolling. It is well known that slide-roll ratio has negligible effect on EHD film thickness below SRR = 50% [12, 13], so values measured in pure rolling are applicable to the rolling–sliding contacts used in this study. However, the relatively low applied load and low reduced elastic modulus of steel/glass (57.7 GPa) mean that the mean contact pressure (0.53 GPa) is considerably lower than those present in the friction tests. To account for this, the Chittenden and Dowson equation [14] that indicates that central EHD film thickness depends of load and elastic modulus by:

$$ h_{{\text{c}}} W^{ - 0.73} E^{* - 0.124} $$
(5)

was used to estimate EHD film thicknesses at the load and with the material combinations employed in friction measurements from those obtained from optical interferometry.

2.3 Thermal Correction

When studying EHD friction it is important to recognise that except at very low sliding speeds, considerable heat is dissipated in the EHD contact and this increases the temperature of the oil film above its supply temperature. This generally has negligible effect on EHD film thickness, which depends on the lubricant properties in the contact inlet, but for most lubricants it does result in a reduction in EHD friction at high SRRs. The temperature rise in the contact can be estimated and used to back-correct the EHD friction to a value that corresponds to the supply temperature as follows [15].

The mean oil film temperature in an EHD contact comprises the inlet supply temperature and two temperature rise terms, the mean flash temperature rise, \({\Delta }\overline{T}_{{{\text{flash}}}}\), which is the transient increase in temperature of the bounding surfaces, and the maximum oil film temperature rise, \({\Delta }\overline{T}_{{{\text{oil}}}}\) above the temperature of the bounding surfaces, i.e.

$$ \overline{T} = T_{{{\text{supply}}}} + \Delta \overline{T}_{{{\text{flash}}}} + \Delta \overline{T}_{{{\text{oil}}}} $$
(6)

When the two bounding solids are of the same material these terms can be expressed in terms of the contact conditions and thermal properties of the solids and the lubricant by [16];

$$ \overline{T} = T_{{{\text{supply}}}} + \frac{1}{{\left( {2\pi K\rho c} \right)^{0.5} }}t^{0.5} q^{{^{\prime\prime}}} + \frac{{h_{{\text{c}}} }}{{8K_{{{\text{oil}}}} }}q^{{^{\prime\prime}}} $$
(7)

where K, ρ and c are the thermal conductivity, density and specific heat of the bounding solids, t is the time that the surfaces are in the contact and Koil is the thermal conductivity of the lubricant film. \(q^{{^{\prime\prime}}}\) is the rate of heat generation per unit area = given by;

$$ q^{{^{\prime\prime}}} = \frac{{\mu Wu_{{\text{s}}} }}{A} = \overline{\tau }\dot{\gamma }h_{{\text{c}}} $$
(8)

where μ is the friction coefficient, W the applied load, us the sliding speed, \(\overline{\tau }\) the mean shear stress (friction/contact area), \(\dot{\gamma }\) the strain rate (us/hc), A the contact area (πa2) and hc the central film thickness.

In terms of shear stress and strain rate Eq. 7 becomes;

$$ \overline{T} = T_{{{\text{supply}}}} + \left( {\frac{1}{{\left( {2\pi K\rho c} \right)^{0.5} }}\left( \frac{2a}{U} \right)^{0.5} + \frac{{h_{{\text{c}}} }}{{8K_{{{\text{oil}}}} }}} \right)\overline{\tau }\dot{\gamma }h_{c} $$
(9)

where a is the contact radius (given by Eq. 2) and U is the entrainment speed.

All of the terms in this equation are known, so that actual mean film temperature for each friction measurement can be calculated. Since, for each applied load, friction was measured at many different temperatures, a set of friction values at known \(\dot{\gamma }\) and \(\overline{T}\) are obtained. Friction values are converted to mean shear stresses using \(\overline{\tau } = \mu \overline{p}\). A 2D polynomial equation of \(\overline{\tau } = f\left( {\dot{\gamma },\overline{T}} \right)\) is then fitted to this data and this is used to correct each measured value at temperature \(\overline{T}\) to one at the oil supply temperature so as yield isothermal shear stress versus strain rate curves [15].

The main uncertainties in Eq. 9 lie in the second term that describes the mean temperature rise of the lubricant film above its bounding surfaces. The value 8 in the denominator assumes that heat is dissipated evenly through the film and describes the temperature of the oil film’s median line, which should represent the maximum temperature. Other assumptions give values of typically between 4 and 12, though it should be noted that a recent study of temperature rises inside EHL contacts measured using infrared spectroscopy suggests that 8 or 9 gives the best fit to experiment [17]. Another uncertainty in this second term concerns the value of thermal conductivity of the lubricant film at the high contact pressure. This is based on measurements on hydrocarbon-based fluids at pressure up to only 1 GPa [18] and these have been extrapolated to higher pressure. The combination of these two uncertainties may, the authors believe, lead to the second term in Eq. 9 being in error by up to ± 30%. Fortunately, except at low temperature (< 30 °C) and low pressure (< 2 GPa) this second term is much smaller than the more reliable first term; for example at the median condition of 3 GPa and 60 °C the second term is only one-tenth of the first, flash temperature term. Since isothermal correction was applied only up to a maximum temperature rise of 10 °C, errors in determining this temperature rise should always be less than 1 °C.

3 Test Fluids

Six base oils were employed in this study as listed in Table 6. These represent one fluid from each of API Groups I, II, III, III+ , IV and V [19]. It should be noted that Group III + is not part of the formal API/ATIEL definition but is a widely used term to differentiate higher VI base oils within the Group III category. Shell XHVI is a GTL base oil. The Group I to IV fluids all had a similar kinematic viscosity of ca 4 cSt at 100 °C. This is a typical base oil viscosity used to formulate modern engine as well as some transmission [20] oils. The Group V ester was bis-(2-ethylhexylsebacate) and had somewhat lower viscosity. It must be emphasised that the EHD friction behaviour observed in this study is specific to these six base oils and that other Group II base oils, for example, may not behave precisely the same as the one studied here since they will have different molecular composition. However, the observed behaviour is believed to be representative.

Table 6 Base oils studied
Full size table

4 Results

4.1 Influence of Solid Materials

Figure 2 compares plots of EHD friction versus SRR for a steel ball against ETM discs of three different materials, all lubricated by Group II oil at 1000 N load and 40 °C. All three curves have classical EHD friction curve shape with a rapid rise in friction at low SRR followed by a levelling out due to shear thinning and then a fall in friction at high SRR due to shear heating. It is evident that disc material has a large impact on behaviour. This is because of differences in its elastic modulus and thermal conductivity. The elastic modulus of disc in combination with that of the ball determines the reduced elastic modulus (Eq. 3) and thus the contact pressure (Eq. 1). This means that the steel/steel and steel/ZrO2 contacts have lower pressure and thus, as will be indicated later in this paper, lower friction coefficients at low SRR. The steel and ZrO2 also have lower thermal conductivities than WC so that their flash temperature rise is greater, leading to considerably lower EHD friction at high SRR, especially for the nearly insulating ZrO2.

Fig. 2
figure 2

EHD friction curves of Group II base oil at 1000 N load and 40 °C using steel balls against three different disc materials

Full size image

Figure 3 compares friction behaviour where both ball and disc are of the same material. The very low thermal conductivity of the ZrO2 results in a very large temperature rise in the contact, estimated to be 80 °C at 20% SRR despite the low-friction coefficient. In consequence, friction falls rapidly with increasing SRR and the test was terminated at SRR = 35% due to the onset of scuffing. With WC/WC friction reaches a higher value than with WC/steel because heat is removed more effectively from the contact due to WC’s relatively high-thermal conductivity.

Fig. 3
figure 3

EHD friction curves of Group II base oil at 1000 N load and 40 °C using three different ball and disc materials

Full size image

The impact of thermal conductivity on friction can be separated from that of elastic modulus by carrying out tests on different materials at different applied loads so as to give the same mean contact pressure. This is shown in Fig. 4 for tests using steel, WC and ZrO2 ball and disc combinations at loads that give a mean contact pressure of 1.5 GPa. The steel/steel and ZrO2/ZrO2 combinations were tested in the ETM while the WC/WC was tested at much lower load in the MTM2. It is evident that the differences in EHD friction at low SRR due to contact pressure are now largely eliminated but those at high SRR due to contact temperature rise persist.

Fig. 4
figure 4

EHD friction curves of Group IV base oil tested at 40 °C in three different ball and disc material contacts; steel/steel, WC/WC and ZrO2/ZrO2, all at the same mean contact pressure of 1.5 GPa

Full size image

As indicated in Eq. 8, it is straightforward to convert friction coefficient to mean shear stress (\(\overline{\tau } = \mu W/\pi a^{2}\)) and SRR to strain rate (\(\dot{\gamma } = {\text{SRR}} \cdot U/h_{{\text{c}}}\)), where U is the entrainment speed, since both are linear transformations. Figure 5 shows resulting plots of mean shear stress versus strain rate for steel/steel and WC/WC calculated from the data in Fig. 4.

Fig. 5
figure 5

Mean shear stress versus strain rate curves determined from Fig. 3 for Group IV base oil in two material combinations at 1.5 GPa and 40 °C

Full size image

4.2 Validation of Isothermal Correction

Figures 4 and 5 show that the ability to measure EHD friction over a large load range makes it possible to compare friction curves of quite different material combintions and this can be used to validate the isothermal correction method outlined in the previous section.

Figure 6 shows the mean shear stress values from Fig. 5 plotted against log(strain rate), This highlights the behaviour at low SRRs and shows almost linear mean shear stress versus log(strain rate) in this region. Also shown in Fig. 6 are isothermal mean shear stress values based on the thermal calculation and isothermal correction methods outlined earlier in this paper, using the thermal properties of steel and WC listed in Table 3. Two things are evident. One is that removing the effect of shear heating by adjusting all mean shear stresses back to 40 °C extends the linearity of the mean shear stress versus log (strain rate) plots and shows that deviation from this line is solely due to shear heating. The second is that the steel/steel and WC/WC isothermal plots coincide, which validates the isothermal correction procedure. It should be noted that the isothermal correction is only applied to measurements where the calculated oil film temperature rise was less than 10 °C.

Fig. 6
figure 6

Mean shear stress versus log(strain rate) for Group IV oil at mean pressure 1.5 GPa and test temperature 40 °C. Also shown are curves isothermally corrected to a mean oil film temperature of 40 °C

Full size image

4.3 EHD Friction Up to Very High Pressures

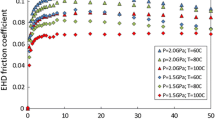
Figure 7 shows EHD friction curves for all six base oils at five different mean contact pressures ranging from 1 to 5 GPa. All tests shown are at a test temperature of 80 °C. At 1 GPa there are quite large differences in the friction curves, with friction in the order

$$ {\text{Group I }} = {\text{ Group II }} > {\text{ Group III }} > {\text{ Group III+}} \, > {\text{ Group IV }} > {\text{ Group V}}. $$
Fig. 7
figure 7

EHD friction curves for six base oils at five mean contact pressures. All tests at 80 °C

Full size image

This is as expected from previous work, where the EHD friction of various Group I and II oils have been found to overlap or be very similar, with significantly lower friction being seen only in higher Groups [15, 21]. Some previous studies have found ester to give lower EHD friction than PAO as seen in this study [22] but some have found the opposite [23]. This is almost certainly because the EHD friction of esters is quite strongly dependent on their molecular structure and thus varies depending on the specific ester studied [15, 24]. The differences in EHD friction between Groups I to IV originate from their molecular composition. Groups I and II containing substantial proportions of naphthenic molecules with inflexible, saturated ring structures. Group III and III+ are almost entirely based on paraffinic molecules that are linear with some branching, while Group IV is generally synthesised from a medium chain α-olefin such as dec-1-ene, so its molecules have very highly linear alkyl structures that slip easily past one another at high stress.

As the pressure is increased, four main patterns of behaviour are clear. One is that the initial part of the curves become much steeper, i.e. friction rises more rapidly with SRR at low SRRs at high pressure. The second is that the differences in EHD friction between the six API Group oils reduces as pressure is increased until, at very high pressure, the curves for all oils are quite similar although they still maintain the same order as seen at 1 GPa. The third is that the maximum EHD friction coefficient at intermediate SRRs increases, especially the higher API Group oils, to stabilise eventually at 0.07 to 0.08 for all oils at 5 GPa. Finally, as the contact pressure and thus the shear stress are increased, the drop in friction at very high SRRs becomes more marked. The last of these is simply because more heat is dissipated in contact at high friction and thus high shear stress.

In Fig. 7, it can be seen that under most conditions the friction curves are very smooth. The exception is at a mean pressure of 2 GPa where the curves are slightly irregular. This is because this condition employed a load of 101 N in the ETM, which is on the borderline of the lower limit of the test rig’s load range.

Figure 8 shows the influence of test temperature on EHD friction curves for two of the base oils at low and high contact pressures. It can be seen that EHD friction is quite strongly dependent on temperature, decreasing with increasing temperature, at both contact pressures. This is different from the behaviour seen with traction fluids whose EHD friction coefficients are relatively independent of both temperature and pressure [15].

Fig. 8
figure 8

Influence of test temperature on EHD friction curves for Group II and Group IV base oils at two mean pressures

Full size image

5 Discussion

This paper has revealed both practically important and theoretically interesting features of the impact of extremely high contact pressures on EHD friction. In practical terms it must be emphasised that although, as indicated in the Background at the beginning of this paper, some machine elements may operate at pressures up to 4 GPa, such conditions are quite rare and are likely to represent maximum rather than mean pressure. The fatigue life of bearing steels decreases very rapidly with pressure (L10 ∝ 1/p9) and this limits designed-for contact pressures, though these may, of course, be exceeded inadvertently. Thus, so far as component performance is concerned, only the EHD friction measurements made up to \(\overline{p}\) = 3 GPa in this study are likely to be of practical relevance. Even so, as indicated in Fig. 7 there are some notable changes in friction response from 1 up to 3 GPa. Apart from an overall increase in friction coefficient at medium to high SRRs, the most important change is the large increase in friction at very low SRRs due to much steeper EHD friction curves. Rolling element bearings do not operate in pure rolling but typically for deep groove ball bearings, at about 1% to 2% SRR over much of their ball/raceway contact. Other rolling bearings can have higher SRRs. Figure 9 shows the influence of mean pressure on friction coefficient at 1% SRR, with friction of the high API Group oils rising fourfold over the pressure range pmean = 1 to pmean = 3. The practical effect of this on bearing friction is evident.

Fig. 9
figure 9

Influence of mean contact pressure on friction coefficient of the six base oils at 1% SRR and two test temperatures

Full size image

One of the aims of this study was to see whether lubricants reach a limiting shear stress, similar to that seen for traction fluids, at very high pressures. To test this, isothermal correction was carried out to remove the shear heating effect and obtain EHD friction curves in which the mean oil film temperature is held constant at the oil supply temperature. This is shown by the black lines in Fig. 10 at the five mean contact pressures for the Group II and Group IV oils at 80 °C. It is evident that this eliminates the levelling out and fall in mean shear stress at high strain rates to show that, at constant temperature, shear stress increase linearly with log(strain rate) even at a mean contact pressure of 5 GPa (pmax = 7.5 GPa). Similar isothermal shear stress versus strain rate behaviour was seen for all the tested base oils at all test temperatures. It is thus clear that none of the base oils reaches a limiting shear stress (as opposed to a thermally-produced one), even at extreme pressure. In Fig. 10, the shift in friction response seen at very low SRRs for the 5 GPa tests may result from accommodation of some shear due to elastic shear deformation of the surface even for the very stiff WC specimens.

Fig. 10
figure 10

Mean shear stress versus log(strain rate) curves for Group II and Group IV base oils at five mean contact pressures and 80 °C test temperature. Both measured data (coloured points) and isothermally corrected data (black lines)

Full size image

All the plots in Fig. 10, except possibly that of Group IV oil at 1 GPa and 80 °C, show a linear response of mean shear stress to log(strain rate) at high shear rates. This is as predicted from the Eyring stress activation model of liquid flow [3]. In this model, shear stress depends on the inverse sinh of the strain rate according to;

$$ \tau = \tau_{{\text{e}}} \sinh^{ - 1} \left( {\frac{{\eta \dot{\gamma }}}{{\tau_{{\text{e}}} }}} \right) $$
(10)

where τe is a limiting stress above which shear thinning occurs, known as the Eyring stress, and η is the low shear rate viscosity of the fluid at the prevailing pressure [3]. At shear stresses above about 1.5 τe, this reduces to the linear/log shear stress/strain rate relationship;

$$ \tau = \tau_{{\text{e}}} \log_{{\text{e}}} \left( {\frac{{2\eta \dot{\gamma }}}{{\tau_{{\text{e}}} }}} \right) $$
(11)

The plot of mean shear stress versus log(strain rate) at 1 GPa and 80 °C for Group IV oil in Fig. 10 only approaches linearity at the very highest strain rate, suggesting that at these conditions the film may be in the intermediate region in which molecules align and in which behaviour follows a Carreau response [4], or indeed, in the initial Eyring region in which the sinh−1 behaviour of Eq. 10 prevails, before the fully logarithmic response of Eq. 11 ensues.

Equation 11 indicates that at high strain rates, τe can be determined from the gradient of shear stress plotted against log(strain rate) and Fig. 11 shows Eyring stresses calculated from Eq. 11. Values are only shown up to 4 GPa since at the highest mean pressure of 5 GPa there were insufficient calculated isothermal points to fit a reliable straight line. This is because isothermal correction was only carried out on measurements where oil film temperature rise was less than 10 °C and at 5 GPa there were very few of these. For both oils, Eyring stress increases linearly with pressure. According to Eyring’s model this suggests that the “activation volume”, which loosely represents the cross sectional area of a molecular flow unit times the distance this unit moves during its passage past a neighbouring unit, decreases with pressure. Figure 12 shows how the values of the low shear rate viscosity of the two base oils calculated from Eq. 11 vary with mean contact pressure. Viscosity rises less than exponetially with pressure and there is no upturn of the curves at very high pressure as seen for some fluids in high pressure viscometry [25]. The reason for this is not clear but may be related to the fact that at high shear rates there is likely to be some dilatency, resulting in lower viscosity than would be present at the very low shear rates present in high pressure viscometry.

Fig. 11
figure 11

Variation of Eyring stress, calculated from isothermal shear stress versus log(strain rate) curves, with mean contact pressure for two base oils at 80 °C

Full size image
Fig. 12
figure 12

Variation of low shear rete, estimated using the Eyring-activated flow model, with mean contact pressure for two base oils at 80 °C

Full size image

6 Conlusions

EHD friction curves have been measured up to very high pressure (pmean = 5 GPa, pmax = 7.5 GPa) using a newly developed, rolling-sliding, ball on disc machine, the ETM. Six base fluids have been studied, spanning the API base oil categories Group I to Group V.

At high pressures, thermal effects become substantial even at quite modest slide-roll ratios, and these must be considered when analysing friction measurements in terms of underlying rheological properties of the oils at high pressure and shear rate. By comparing measurements from steel/steel and WC/WC ball and disc combinations with very different thermal conductivities, the use of thermal correction to derive isothermal friction curves has been validated.

At relatively low pressures (mean pressure = 1 GPa) there are substantial differences between the EHD friction properties of the various API Group base oils, but as pressure is raised these diminish as the EHD friction coefficients of all the Groups approach a similar maximum value at a given temperature. EHD friction continues to be quite strongly temperature dependent even at very high pressure.

As pressure is increased, EHD friction curves become progressively steeper, so that friction coefficients at very low slide-roll ratios (1 to 2% SRR) become several times greater than at low pressure. This has important practical implications for the efficiency of rolling element bearings at high pressures since these components normally operate in this SRR range.

There is no evidence of any of the base oils reaching a limiting shear stress over the whole pressure and temperature range studied. Instead shear stress continues to increase with log(strain rate) in accordance with the Eyring-activated flow model up to very high pressures. This model can thus be used to predict friction in high-pressure EHD contacts.