1 Introduction

Roughness is usually responsible for destroying adhesion, and in particular after some debate, there is some consensus that it is the longest wavelength of roughness which is responsible for this so that extremely accurate measurement of roughness should not be needed [1,2,3,4,5]: in other words, the roughness root-mean-square (rms) is the first simple parameter of choice in “killing” adhesion. Fifty years ago, indeed to first measure adhesion, very smooth soft rubber spheres and optically smooth glass was used ([6] JKR in the following, generalizing the Hertz contact theory to short range adhesion). Immediately later, the same type of experiment was repeated by Fuller and Tabor [7] on roughened Perspex plates, showing that micrometer roughness was sufficient to reduce adhesion to a very small fraction. Already in Fuller and Tabor’s experiments, it was seen that at very small roughness amplitude, there appeared to be an enhancement of pull-off with respect to the smooth case rather than decay, although of a not too large factor (\(\sim 20\) to 30%). Similar enhancement was found in other experiments by Briggs and Briscoe [8], or Fuller and Roberts [9] which was considered an embarrassment for asperity models (on nominally flat surfaces) like Fuller and Tabor’s which predicted only a decay. For a long time, theoretical understanding did not improve, while there was significant confusion about the effect of fractal features in the geometrical description of surfaces [10]. The Fuller and Tabor model [7] indeed depends not only on roughness height rms, but also (although in a weaker form) on an asperity “radius,” which could not be easily defined for real surfaces [11].

1.1 The Persson and Tosatti (PT) Theory

A significant improvement came only about 25 years later, when Persson and Tosatti [12] proposed a very simple model to describe the role of roughness (including fractal features). The simple criterion of Persson and Tosatti ( [12], PT in the following) in fact states that the apparent work of adhesion \(\Delta \gamma _\mathrm{app}\) (or “surface energy”) changes from the intrinsic value \(\Delta \gamma \), according to two contributionsFootnote 1

$$\begin{aligned} \frac{\Delta \gamma _\mathrm{app}\left( \zeta \right) }{\Delta \gamma }=\frac{ A_\mathrm{true}\left( \zeta \right) }{A_{0}}-\frac{U_\mathrm{el}\left( \zeta \right) }{ \Delta \gamma A_{0}}, \end{aligned}$$
(1)

where \(U_\mathrm{el}\left( \zeta \right) \) is the elastic strain energy we need to completely flatten the random roughness, \(\zeta =\lambda _\mathrm{L}/\lambda _\mathrm{s}\) is the so-called “magnification,” where \(\left\{ \lambda _\mathrm{L},\lambda _\mathrm{s}\right\} \) are, respectively, the longest and the smallest wavelength in the roughness spectrum, \(A_{0}\) is the nominal contact area and \(A_\mathrm{true}\) is the true contact area considering roughness. However, notice that a significant increase of adhesion could be related to this factor only if we consider roughness having root mean square slopes (\( h_\mathrm{rms}^{\prime }\)) near unity or larger, and this perhaps motivated Dalvi et al. [13] in their adhesion experiments to measure roughness up to the limit of almost atomic scale, with a mix of measuring equipment including quite sophisticated ones. We shall investigate this issue in detail, because Dalvi et al. [13] used in their discussion of adhesion criteria always the highest resolution, while in all our comparison we shall explore the effect of changing resolution on the extrapolation of the apparent work of adhesion and on the correlation of the theory with data. This especially in view of the fact that some quantities converge with the “magnification,” and some others do not, while \(\zeta \) could be either a true intrinsic feature of the surface, but more simply could be the choice made a priori on the measuring apparatuses used to measure roughness in the range of wavelengths \(\lambda _\mathrm{s}<\lambda < \lambda _\mathrm{L}\).

Indeed, the elastic energy term \(U_\mathrm{el}\left( \zeta \right) \) and \( A_\mathrm{true}\left( \zeta \right) /A_{0}\) depend differently on “magnification.” For a rough surface with 2D radial averaged Power Spectral Density (PSD) \( C^{\text{iso}}\left( q\right) \) [10] the stored elastic energy at full contact isFootnote 2

$$\begin{aligned} \frac{U_\mathrm{el}\left( \zeta \right) }{A_{0}}=\frac{E^{*}}{8\pi }\int _{q_\mathrm{L}}^{q_\mathrm{s}}q^{2}C^{\text{iso}}\left( q\right) \mathrm{d}q, \end{aligned}$$
(2)

where \(q=2\pi /\lambda \) is the wavenumber associated to the wavelength \( \lambda \) (hence \(q_\mathrm{s}=2\pi /\lambda _\mathrm{s}\) and \(q_\mathrm{L}=2\pi /\lambda _\mathrm{L}\)), \( E^{*}=E/\left( 1-\nu ^{2}\right) \) is the plane strain elastic modulus, being E the Young’s modulus and \(\nu \) the Poisson’s ratio. Real surfaces typically have fractal dimension D \(<2.5\) hence \(U_\mathrm{el}\left( \zeta \right) /A_{0}\) converges rapidly with \(\zeta =q_\mathrm{s}/q_\mathrm{L}\rightarrow +\infty \) [14, 15].Footnote 3

Perhaps a more important point is that PT theory does not distinguish between loading and unloading phases because it assumes thermal equilibrium, corresponding to infinitely slow approach and retraction, and in this limit there is no contact hysteresis, nevertheless it seems that experiments show a different behavior even in the limit of extremely slow loading velocity as those used by Dalvi et al. [13]. Hence, Dalvi et al. [13] concentrated on loading curves, assessing PT theory and some variants, but did not attempt to discuss the unloading curves, which showed quite different behavior. Obviously, one possible mechanism for hysteresis (i.e., energy dissipation) with soft materials could be viscoelasticity, still not well understood, particularly in the presence of roughness [18,19,20]. This is strongly dependent on the loading rate, and in some experiments, very slow loading rates are used attempting to reduce its effect [13]).

1.2 The Guduru’s Theory and Experiments

Another mechanism for adhesion enhancement with respect to the smooth case (during unloading), particularly appropriate to the case of a macroscopic body in the presence of roughness (rather than the nominally flat case [21,22,23], see also [24,25,26]), was theoretically predicted and experimentally proved by Guduru [27] and Guduru and Bull [28], and anticipated for 2D roughness (which behaves similarly to axisymmetric one) by numerical simulations by Carbone et al. [29]. Guduru considered a very simplified geometry, that of a soft sphere with a single, axisymmetric, waviness of amplitude h and wavelength \(\lambda \), squeezed against a smooth flat hard surface. Guduru showed that if the contact is complete (there is no crack within the contact patch) there is a large difference between the loading and unloading curves, with the loading curve giving a reduction and the unloading curve giving an enhancement of adhesion with respect to the JKR theory [6, 27, 28]. This geometry showed experimentally pull-off force enhanced by a factor up to 20 with respect to the JKR case, due to the energy that was dissipated through jump instabilities during the unloading stage. Later, Kesari and Lew [30] showed that if the wavelength \(\lambda \) is small enough the approach and retraction curves would coincide with two “envelope” solutions, which Ciavarella [31] demonstrated depended only on the Johnson parameter for a single sinusoidal contact [23]

$$\begin{aligned} \alpha =\sqrt{\frac{2\Delta \gamma \lambda }{\pi ^{2}E^{*}h^{2}}} \end{aligned}$$
(3)

which is proportional to the square root of the ratio of the work of adhesion and the elastic strain energy to squeeze the sinusoid flat, in other words, \(\sqrt{\Delta \gamma /U_\mathrm{el}}\) in the PT notation.

Therefore, according to Guduru–Kesari and Lew–Ciavarella, the JKR curve for the sphere follows different loading and unloading branches, each perfectly of the JKR form, but with an apparent work of adhesion that differs during approach or retraction

$$\begin{aligned} \frac{\Delta \gamma _\mathrm{app}}{\Delta \gamma }=\left( 1\pm \frac{1}{\sqrt{\pi }\alpha }\right) ^{2}, \end{aligned}$$
(4)

where the positive sign holds for unloading, and the negative for loading (as long as \(\left( \sqrt{\pi }\alpha \right) ^{-1}<1\) beyond which adhesion is expected to be zero). Although Eq. (4) would predict unbounded enhancement for large roughness amplitude h, the enhancement can only appear up to a certain amplitude, above which internal cracks appear within the contact area (see Papangelo and Ciavarella [32] for a numerical solution).

Assuming the loading rate is extremely slow, hence viscoelasticity is negligible, one can imagine that the approach and retraction curves for rough surfaces could still be different due to the Guduru effect, i.e., local jump instabilities, although in a reduced form due to random roughness.

2 The Dalvi et al. [13] Experiments

Dalvi et al. [13] show recent experiments with soft materials against hard solids with roughness of the order of nanometers. Dalvi et al. [13] used several instruments and techniques to measure the roughness spectrum from the millimeter and down to the Ångström scale (stylus profilometers, optical instruments, atomic force microscopy, transmission electron microscopy). They report otherwise experiments qualitatively similar to the old Fuller and Tabor [7] ones. They used soft elastic polydimethylsiloxane (PDMS) hemispheres (2 to 3 mm diameter) having Young’s elastic modulus in the range from 0.7 to 10 MPa (see Table 1), in contact with four different polycrystalline diamond substrates whose 1D power spectral densities C1D [10] are shown in Fig. 1: Polished UltraNanoCrystalline Diamond (PUNCD), UltraNanoCrystalline Diamond (UNCD), NanoCrystalline Diamond (NCD), MicroCrystalline Diamond (MCD). The manufacturing technique permits rms roughness to be quite low, ranging from few to hundred nanometers (see Table 2). In each experiment, they reached a maximum load of 1 mN and attempted to remove all possible viscoelastic effects by conducting the approach and retraction experiments at the very low speed of 60 nm/s. Indeed, control experiments of the PDMS hemispheres against smooth silicon wafer coated with a low-work of adhesion octadecyltrichlorosilane (OTS) monolayer suggest that energy dissipation due to viscoelasticity in a full loading unloading cycle is at least one order of magnitude smaller than that measured due to roughness, although up to 50% difference in \(\Delta \gamma _\mathrm{app}\) at approach and retraction could be found even in this test case for the lowest elastic modulus (\(E=0.7\) MPa).

When using rough crystalline diamond substrates, they obtain values of apparent work of adhesion that differ significantly between approach and retraction, and specifically of a factor up to \(\sim \)6 (see Table 1), therefore the experiments are quite unique for our purposes, since we expect the hysteresis to be mainly due to roughness.

Fig. 1
figure 1

One-dimensional PSD obtained from 1D measurements C1D [10] for the 4 different substrates PUNCD, UNCD, NCD, and MCD (Color figure online)

Full size image
Table 1 Mean values for work of adhesion \(\Delta \gamma _\mathrm{app}\) upon approach and retraction reported by Dalvi et al. [13]
Full size table
Table 2 Main roughness parameters measured for the different roughened plates (at full magnification)
Full size table

Starting from the surface PSD the root mean square height \(h_\mathrm{rms}\) and slopes \(h_\mathrm{rms}^{\prime }\) are defined as [10]

$$\begin{aligned}&h_\mathrm{rms}^{2}=\frac{1}{2\pi }\int _{q_\mathrm{s}}^{q_\mathrm{L}}qC^{\text{iso}}\left( q\right) \mathrm{d}q;\nonumber \\&\left( h_\mathrm{rms}^{\prime }\right) ^{2}=\frac{1}{2\pi } \int _{q_\mathrm{s}}^{q_\mathrm{L}}q^{3}C^{\text{iso}}\left( q\right) \mathrm{d}q; \end{aligned}$$
(5)

Figure 2 shows that \(h_\mathrm{rms}\) converges quite quickly at about \( q_\mathrm{s}\approx 10^{7}\) \(\hbox {m}^{-1}\) (\(\zeta \approx 10^{4}\)), hence stylus profilometer measurements would be enough to characterize the surface in terms of height rms, maybe except for the smoothest substrate (PUNCD), which requires a bit higher resolution. On the contrary, as expected, \( h_\mathrm{rms}^{\prime }\) grows with \(q_\mathrm{s}\), does not reach any real plateau, and reaches different values for the various substrates. As the geometrical term \(A_\mathrm{true}\left( \zeta \right) /A_{0}\) depends on \(h_\mathrm{rms}^{\prime },\) any criterion like PT is sensitive to the finest scale of the PSD. On the contrary, the term \(U_\mathrm{el}\left( \zeta \right) /\left( \Delta \gamma A_{0}\right) \) for low fractal dimension converges with \(\zeta \) rapidly similarly to \(h_\mathrm{rms}\), as shown in Fig. 2c for the substrates of Dalvi et al. [13] (to make a single plot, we set the adhesion length \(l_{a}=\Delta \gamma /E^{*}=10\) nm).

Fig. 2
figure 2

a Surface height root mean square \(h_\mathrm{rms}\), b slope root mean square \(h_\mathrm{rms}^{\prime }\) , and c the dimensionless elastic energy \( U_\mathrm{el}\left( \zeta \right) /\left( \Delta \gamma A_{0}\right) \) evaluated as a function of the cut-off wavenumber \(q_\mathrm{s}\) for the four roughened crystalline diamond substrates PUNCD, UNCD, NCD, MCD in Dalvi et al. [13] (Color figure online)

Full size image

In terms of theory, Dalvi et al. [13] introduced also a modified form of the PT theory in two respects: (i) they proposed to use a more precise estimate for the term \(A_\mathrm{true}\left( \zeta \right) /A_{0}\) and (ii) included the energy spent in increasing the surface area of the soft body, obtaining

$$\begin{aligned} \frac{\Delta \gamma _\mathrm{app}}{\Delta \gamma }=\frac{A_\mathrm{true}}{A_{0}}-\frac{ \gamma _{1}}{\Delta \gamma }\left( \frac{A_\mathrm{true}}{A_{0}}-1\right) -\frac{ U_\mathrm{el}\left( \zeta \right) }{\Delta \gamma A_{0}}, \end{aligned}$$
(6)

where \(\gamma _{1}\) is the work of adhesion of the elastomer alone, which itself may be a quantity which needs to be independently estimated and that Dalvi et al. [13] assumed equal to \(\gamma _{1}=25\) mJ/m\( ^{2}\) based on Literature results. Using Eq. (6) only for the loading data, Dalvi et al. [13] obtained as best fit \( \Delta \gamma =37\) mJ/m\(^{2}\) with a coefficient of determination \(R^{2}=0.67\) , while when using the original PT theory (1) they obtained \(\Delta \gamma =25\) mJ/m\(^{2}\), but a much poor \(R^{2}=0.29\). Notice that they obtained another slightly higher value from another estimate based on the energy loss by hysteresis (\(\Delta \gamma =46.2\) mJ/m\(^{2}\), \(R^{2}=0.8\) ). Hence, based on correlation with experiments, Dalvi et al. [13] concluded that their criterion better fits the experimental data with respect to the original form due to PT.

Dalvi et al. [13] discussed their criterion only fitting the apparent work of adhesion obtained during approach and with full “magnification” \(\zeta \) down to the nanometer scale. The very large difference with the retraction data remained unexplained. We shall extend this exercise here more at large, first finding the best-fitted intrinsic work of adhesion \(\Delta \gamma \) separately on approach and retraction curves to gain some insight, and then fitting all data. We will do this as a function of the truncation wavenumber \(q_\mathrm{s}\) and by adopting PT criteria (and their variants), and a new criterion inspired by the Guduru theory, which distinguished between loading and unloading stages, and which is specific for bodies having a macroscopic form (like a sphere).

3 PT Variants and a Modified Form of the Guduru Theory

The PT theory is originally devised as a criterion based on a energy balance for the full contact of nominally flat surfaces, although the original paper [12] already suggests it to be a crude approximation for a case of a body of macroscopic form, and attempts to adopt it for the Fuller and Tabor sphere adhesion. It cannot be expected to be rigorous even for a single sinusoid (see Johnson [23] for the details), where the connection is that even the single sinusoid does indeed depend only on the single parameter (3). For multiscale random roughness, we can define a generalization of the Johnson parameter (3), namely

$$\begin{aligned} \alpha \left( \zeta \right) =\sqrt{\frac{\Delta \gamma }{U_\mathrm{el}\left( \zeta \right) /A_{0}}} \end{aligned}$$
(7)

from which we can rewrite PT (1) as

$$\begin{aligned} \frac{\Delta \gamma _\mathrm{app}\left( \zeta \right) }{\Delta \gamma }=\frac{ A_\mathrm{true}\left( \zeta \right) }{A_{0}}-\frac{1}{\alpha ^{2}\left( \zeta \right) }. \end{aligned}$$
(8)

More importantly, this seems to suggest a possible generalization also for the Guduru–Kesari and Lew–Ciavarella theory (4) for multiscale rough surfaces

$$\begin{aligned} \frac{\Delta \gamma _\mathrm{app}}{\Delta \gamma }=\left( 1\pm \frac{1}{\sqrt{\pi } \alpha \left( \zeta \right) }\right) ^{2}, \end{aligned}$$
(9)

where the “+” sign gives enhancement and holds for the unloading curve, while the “-” sign holds for loading data and shows adhesion reduction (not too dissimilar form the PT theory, it should be remarked, except for the details of the functional dependence on \(\alpha \left( \zeta \right) ,\) and the presence of \(A_\mathrm{true}\left( \zeta \right) /A_{0}\)). Clearly, for the unloading curve (“+” sign) unbounded enhancement is predicted for small \(\alpha \left( \zeta \right) \), which cannot be the case for real surfaces as for the eventual appearance of internal cracks. Unfortunately, there is no sufficient evidence on what the maximum enhancement should be for random roughness, as numerical experiments are limited (see [33, 34]). We shall take a rather arbitrary modification of Eq. (9) at unloading giving a maximum enhancement of about 2.3 and quickly decaying for larger roughness similarly to the loading curve, introducing the following form between the phase of approach and retraction (MG, in the following)

$$\begin{aligned} \left\{ \begin{array}{l} \frac{\Delta \gamma _\mathrm{app}}{\Delta \gamma }=\left( 1-\frac{1}{\sqrt{\pi } \alpha \left( \zeta \right) }\right) ^{2},\qquad \text {approach phase} \\ \frac{\Delta \gamma _\mathrm{app}}{\Delta \gamma }=\left( 1+\frac{2}{\alpha \left( \zeta \right) }-\left( \frac{\sqrt{2}}{\alpha \left( \zeta \right) }\right) ^{2}\right) ^{2},\qquad \text {retraction phase} \end{array} \right. \end{aligned}$$
(10)

Obviously, the generality of this precise form can be questionable, and indeed there is not even guarantee that any form \(\Delta \gamma _\mathrm{app}/\Delta \gamma =f\left( \alpha \left( \zeta \right) \right) \) should work at all,Footnote 4 but the rationale was that it will be shown to give a satisfactory fit of the experimental data, and permits the separation between loading and unloading stages.

Summarizing, the criteria that will be used in the following analysis are as follows:

  • The original PT criterion [12]

    $$\begin{aligned} \frac{\Delta \gamma _\mathrm{app}}{\Delta \gamma }=\left( 1+\frac{1}{4\pi } \int _{q_\mathrm{L}}^{q_\mathrm{s}}q^{3}C^{\text{iso}}\left( q\right) \mathrm{d}q\right) -\frac{1}{ \alpha ^{2}\left( \zeta \right) }; \end{aligned}$$
    (11)

  • A modified PT criterion that neglects the effect of the increase of real contact area due to roughness (\(\hbox {NoA}_{\text {true}}\))

    $$\begin{aligned} \frac{\Delta \gamma _\mathrm{app}}{\Delta \gamma }=1-\frac{1}{\alpha ^{2}\left( \zeta \right) }; \end{aligned}$$
    (12)

  • The Dalvi variant of PT criterion [13]

    $$\begin{aligned} \frac{\Delta \gamma _\mathrm{app}}{\Delta \gamma }=\frac{A_\mathrm{true}}{A_{0}}-\gamma _{1}\left( \frac{A_\mathrm{true}}{A_{0}}-1\right) -\frac{1}{\alpha ^{2}\left( \zeta \right) }, \end{aligned}$$
    (13)

    where

    $$\begin{aligned} \frac{A_\mathrm{true}}{A_{0}}=1+\frac{\sqrt{\pi }}{2}h_\mathrm{rms}^{\prime }\exp \left( \frac{1}{h_\mathrm{rms}^{\prime 2}}\right) {\text {erfc}}\left( \frac{1}{ h_\mathrm{rms}^{\prime }}\right) \end{aligned}$$
    (14)

    and \(h_\mathrm{rms}^{\prime }\) is evaluated from ((5), second equation)Footnote 5;

  • The modified version of the Guduru model (10) proposed in the present paper.

All the above criteria can be easily written in terms of surface PSD by using Eqs. (2, 5, 7).

4 Results with the Dalvi Data

4.1 Fitting Loading Data Only

Let us first focus on the apparent work of adhesion obtained at approach (data in Table 1a). We looked for the best-fitted intrinsic work of adhesion \( \Delta \gamma \) as a function of the cut-off wavenumber \(q_\mathrm{s}\) using the four different models: MG (black solid line), PT (red long dashed line), Dalvi (blue short dashed line), and \(\hbox {NoA}_{\text {true}}\) (green dot-dashed line). The results are shown in Fig. 3 for the best-fitted intrinsic work of adhesion \(\Delta \gamma \) (panel a) and the corresponding coefficient of determination \(R^{2}\) (panel b) for all the four models. As expected the criteria belonging to the PT family (\(\hbox {NoA}_{\text {true}}\), PT, and Dalvi) provide identical results up to resolution \(q_\mathrm{s}\approx 10^{7}\) [m\(^{-1}\)] as indeed, at low magnification \(\zeta =q_\mathrm{s}/q_\mathrm{L},\) the corrective term \( A_\mathrm{true}\left( \zeta \right) /A_{0}\) is very small. By further increasing \( q_\mathrm{s}>10^{7}\) the model \(\hbox {NoA}_{\text {true}}\) converges to \(\Delta \gamma \simeq 42.5\) mJ/m\(^{2}\). On the contrary, the Dalvi and PT criteria provide lower \(\Delta \gamma \) that depend on \(q_\mathrm{s}\) even at large magnifications. In particular, the PT criterion overestimates the ratio \(A_\mathrm{true}\left( \zeta \right) /A_{0}\) with respect to the more exact derivation of Dalvi et al. [13] hence it provides a smaller intrinsic work of adhesion, in particular at the highest resolution (\(q_\mathrm{s}\simeq 1.3*10^{10}\) m\(^{-1}\) ) \(\Delta \gamma \simeq 25\) mJ/m\(^{2}\) \(\left( R^{2}=0.29\right) \) for PT and \( \Delta \gamma \simeq 37\) mJ/m\(^{2}\) \(\left( R^{2}=0.67\right) \) for Dalvi. Notice that the latter data coincide with those obtained by Dalvi et al. [13]. In other words, the Dalvi criterion corrects the geometric error in the original PT criterion, still does not obtain a very good correlation with the experimental data, despite the complexity of measuring the very fine tail of the PSD.

Moreover, the best result in terms of correlation with the experimental data (see the coefficient of determination \(R^{2}\) in Fig. 3b) is obtained with the Guduru generalized criterion (10, at approach), which has improved the correlation at all resolutions, and provides a significantly higher intrinsic work of adhesion (\(\Delta \gamma \simeq 50.5\) mJ/m\(^{2}\) with \( R^{2}=0.79\) at the highest resolution).

Fig. 3
figure 3

a Best-fitted intrinsic work of adhesion \(\Delta \gamma \) obtained using only the experimental data at approach (Table 1a) as a function of the cut-off wavenumber \(q_\mathrm{s}\) using the four different models: MG (10, at approach, black solid line), PT (red long dashed line), Dalvi (blue short dashed line), and \(\hbox {NoA}_{\text {true}}\) (green dot-dashed line). b Corresponding coefficient of determination \(R^{2}\) as a function of the cut-off wavenumber \(q_\mathrm{s}\) (Color figure online)

Full size image

4.2 Fitting Unloading Data Only

As we already remarked, Dalvi et al. [13] could not fit a unique JKR curve to the entire retraction curve and found that “there is no connection to the intrinsic value of work of adhesion determined from the approach data,” preferring to comment on the energy loss during an entire loading/unloading cycle. However, we are not too surprised that while the force moves from compression to tension there is region of almost constant contact radius, as this is exactly what happened with the Guduru geometry (see [28], Fig. 6), which is perhaps another indication that there are some analogies between the two problems, we think it may be misleading to fit only a subset of the data (like loading only), and we shall investigate exactly this point.

Fig. 4
figure 4

a Best-fitted intrinsic work of adhesion \(\Delta \gamma \) using only the experimental data at retraction (Table 1b) as a function of the cut-off wavenumber \(q_\mathrm{s}\) using four different models: MG (10, at retraction, black solid line), PT (red long dashed line), Dalvi (blue short dashed line), and \(\hbox {NoA}_{\text {true}}\) (green dot-dashed line). b Corresponding coefficient of determination \(R^{2}\) as a function of the cut-off wavenumber \(q_\mathrm{s}\) (Color figure online)

Full size image

Dalvi et al. [13] did obtain apparent work of adhesion at retraction either using (i) a single JKR equation for the pull-off data or using (ii) a local JKR fit using \(\sim \)6 points finding little difference (in Table 1b the data obtained with method (ii) are reported). Doing the same best-fitting exercise we have already reported for the loading data, we obtain Fig. 4 where it appears clear that the best fit \(\Delta \gamma \) for the three variants of the PT theory becomes much larger than the value on approach (a factor from 2 to 3, which is somehow very likely unjustified). This is clearly very frustrating, as this extrapolation was supposed to give an “intrinsic” property of the surfaces, and since Dalvi et al. [13] had reported all efforts were made to remove viscoelastic effects.

Given the unloading data now show either adhesion enhancement or reduction, we expect the corrective term \(A_\mathrm{true}\left( \zeta \right) /A_{0}\) to be more useful: indeed it does improve the correlation with the experimental data with respect to the \(\hbox {NoA}_{\text {true}}\) criterion although marginally and with the “intrinsic” value of the work of adhesion still apparently too large ( \(\Delta \gamma \simeq 95.0\) mJ/m\(^{2}\) \(\left( R^{2}=0.82\right) \) for Dalvi, and \(\Delta \gamma \simeq 122.5\) mJ/m\(^{2}\) \( \left( R^{2}=0.6\right) \) for \(\hbox {NoA}_{\text {true}}\)).

More consistent with the loading data appears instead the MG proposed criterion, which finds \(\Delta \gamma \simeq 60\) mJ/m\(^{2}\) quite insensitive to the magnification at least for \(q_\mathrm{s}>10^{7}\) m\(^{-1}\) and therefore would give the same result even if measuring the surfaces with good stylus profilometers. Notice that the highest correlation obtained by the MG criterion is similar to that of the PT and Dalvi criteria.

4.3 Fitting Both Approach and Retraction Data

Here the full set of experimental data of Dalvi et al. [13] is considered, i.e., both at approach and at retraction (Table 1a, b). It is expected that the best-fit \(\Delta \gamma \) will be somehow intermediate between the values obtained using the approach or retraction data alone.

Figure 5a shows the best fit \(\Delta \gamma \) as a function of \(q_\mathrm{s}\) for all the aforementioned criteria and Fig. 5b the corresponding coefficient of determination \(R^{2}\). It is immediately clear that the “PT-like”’ criteria poorly fit the full set of data as all of them obtain a R\(^{2}\approx 0.2\) with \(\Delta \gamma \) in a range 50–82 mJ/m\(^{2}\), sensitive to the choice of the truncation wavenumber. On the contrary, our proposed model (10) gives a more reasonable best-fit value \(\Delta \gamma =57.4\) mJ/m\(^{2}\) and correlates with the experimental data with a high \(R^{2}=0.90\), similar to the values obtained using just loading or unloading data.

Notice also that the MG criterion best-fit \(\Delta \gamma \) is almost converged already at the resolution \(q_\mathrm{s}\approx 2*10^{7}\) m\(^{-1}\) hence, for the Dalvi et al. [13] experiments, stylus profilometer measurements of the roughness profile would be already sufficient to characterize the adhesive performance of substrates.

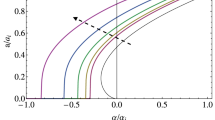
Figure 6 shows the dimensionless apparent work of adhesion \( \Delta \gamma _\mathrm{app}/\Delta \gamma \) versus \(1/\alpha \left( \zeta \right) \). Empty (filled) symbols refer to the retraction (approach) data, while the dashed (dot-dashed) curves refer to the MG model (10) at approach (retraction) where we used \(\Delta \gamma =57.4\) mJ/m\(^{2}\) obtained at full resolution (\(q_\mathrm{s}\simeq 1.3*10^{10}\) m\(^{-1}\)).

It is clear from the results summarized in Table 3 that the proposed MG criterion gives the most stable results in terms of extracted work of adhesion.

Table 3 Best-fit work of adhesion (and corresponding \(R^{2}\)) using data at loading, unloading, and both loading/unloading (at full magnification) for the three PT criteria, and the proposed Modified Guduru (MG) criterion
Full size table
Fig. 5
figure 5

a Best-fitted intrinsic work of adhesion \(\Delta \gamma \) using all the experimental data at approach and at retraction (Table 1ab) as a function of the cut-off wavenumber \(q_\mathrm{s}\) using four different models: MG (10, black solid line), PT (red long dashed line), Dalvi (blue short dashed line), and \(\hbox {NoA}_{\text {true}}\) (green dot-dashed line). b Corresponding coefficient of determination \(R^{2}\) as a function of the cut-off wavenumber \(q_\mathrm{s}\) (Color figure online)

Full size image
Fig. 6
figure 6

Dimensionless apparent work of adhesion \(\Delta \gamma _\mathrm{app}/\Delta \gamma \) versus \(1/\alpha \left( \zeta \right) \). Filled (empty) symbols for experimental data at approach (retraction). Dashed (dot-dashed) curves for approach (retraction) obtained with the MG model (Eq. (10), \( \Delta \gamma =57.4\) mJ/m\(^{2}\), \(q_\mathrm{s}\simeq 1.3*10^{10}\) m\(^{-1}\)). Data plotted for \(E=[0.7\) (diamond),  1.0 (square),  1.9 (triangle),  10 (circle)] MPa and for PUNCD (blue), UNCD (red), NCD (black), MCD (green) substrates (Color figure online)

Full size image

5 Discussion

Our proposal inspired by the Guduru theory shares with the Persson–Tosatti’s theory the use of the generalized Johnson parameter \(\alpha \left( \zeta \right) \). The differences are mainly two: (i) the adhesion enhancement in the PT theory is attributed to a geometric effect (the \(\frac{A_\mathrm{true}}{ A_{0}}\) term) which would act also for nominally flat surfaces, and which makes the results more sensitive to the tail of the PSD spectrum than what depends only on \(\alpha \left( \zeta \right) \); (ii) that there is no attempt to distinguish loading and unloading in the PT theory as the Guduru effect which was later discovered and corresponds to adhesion enhancement for bodies of macroscopic geometries having local deviations of the geometry which would cause the loading curve to oscillate about the nominal curve (JKR for a sphere).

The fact that we found a good correlation with our equation inspired by the Guduru model (10) with a limited set of experiments clearly is not sufficient to claim generality of this proposal. Actually, notice we did not find a good correlation with an equation more naturally extending Guduru’s model, such as \(\frac{\Delta \gamma _\mathrm{app}}{\Delta \gamma }=\left( 1+\frac{1}{ \sqrt{\pi }\alpha \left( \zeta \right) }-.....\right) ^{2},\) and this is perhaps because there is really a strong increase of effective work of adhesion in the Dalvi et al. [13] data which call for viscoelastic effects. While we have clearly made some progress in understanding the role of roughness in adhesion, there is really still insufficient quantitative understanding of the details.

With the present understanding of the role of roughness in adhesion, it becomes unclear what we can extract from best-fit exercises using too approximate theories, as we have clearly shown and discussed here. The measurement of roughness with very sophisticated experimental equipment and careful matching of the corresponding results from the different resolution set of measurement, is today possible, but by no means corresponds to a true capability to predict the role of roughness in adhesion experiments.

Actually, the present results reinforce the growing consensus that extremely accurate measurement of roughness should not be needed but it is the long wavelength content of roughness which matters most [1,2,3,4,5]. While Dalvi et al. [13] have used a more precise calculation of the roughness-induced increase of area \(A_{\mathrm{true}}/A_{0}\) which indeed seems to improve the correlation with experiments that they reported, it remains true that the role of \(A_{\mathrm{true}}/A_{0}\) seems insufficient to explain adhesion enhancement, and that the Guduru effect (which is still not entirely understood for random roughness), has some chance in explaining the adhesion enhancement.

6 Conclusions

In this work, we have discussed and analyzed the experimental data published by Dalvi et al. [13] on soft PDMS hemisphere pressed against differently roughened crystalline diamond substrates, in particular focusing on understanding the difference between the loading and unloading data. Dalvi experiments have been conducted at very low loading rate (60 nm/s) hoping that viscoelastic effects are reduced, although they are not entirely ruled out. We have used four different criteria to predict the apparent work of adhesion (i) at approach, (ii) at retraction, and (iii) considering all the data both at approach and retraction. The four criteria selected are (a) the PT criterion without correction of the real contact area, (b) the PT original criterion [12], (c) the improved PT criterion proposed by Dalvi et al. [13], and (d) a new model inspired by the Guduru theory (originally devised for a single wave of axisymmetric roughness on a sphere) and based on a generalization of the Johnson parameter. In contrast with the “PT-like” models {“a,” “b,” “c”}, the proposed model “d” distinguishes between the two phases of approach and retraction, and this gives a reasonably good correlation both at approach, at retraction, and when all data are considered, giving also more similar and realistic values of the “intrinsic” work of adhesion. The new criterion does not depend much on the tail of the measured roughness, which suggests that stylus profilometer measurements would have been enough. Nevertheless, the details of our fitting equation are based only on a good correlation with the experimental results, and the main result is qualitative: the idea that a generalization along the lines of the Guduru problem can provide a better understanding of this still poorly understood adhesion problem. The available experimental data are insufficient to rule out that the Persson–Tosatti model, with effectively quite different work of adhesion during loading and unloading, is still a valuable choice. Despite the very low retraction speed in unloading, there may be still quite strong effects due to the separation of polymer chains that get pulled out during retraction but not during approach or due to viscoelasticity.