Elastic Contacts of Randomly Rough Indenters with Thin Sheets, Membranes Under Tension, Half Spaces, and Beyond

Abstract

We consider the adhesion-less contact between a two-dimensional, randomly rough, rigid indenter, and various linearly elastic counterfaces, which can be said to differ in their spatial dimension D. They include thin sheets, which are either free or under equi-biaxial tension, and semi-infinite elastomers, which are either isotropic or graded. Our Green’s function molecular dynamics simulation identifies an approximately linear relation between the relative contact area $a_{\text {r}}$ and pressure p at small p only above a critical dimension. The pressure dependence of the mean gap $u_{\text {g}}$ obeys identical trends in each studied case: quasi-logarithmic at small p and exponentially decaying at large p. Using a correction factor with a smooth dependence on D, all obtained $u_{\text {g}}(p)$ relations can be reproduced accurately over several decades in pressure with Persson’s theory, even when it fails to properly predict the interfacial stress distribution function.

Graphical Abstract

1 Introduction

Mechanical contacts between nominally flat surfaces occur everywhere. Due to the microscopic roughness on most surfaces, real contact is only made in isolated, load-bearing patches in the interface, where local compressive stresses can exceed the nominal pressure significantly [1,2,3]. Depending on the applied load and the materials involved, plastic deformation can lead to a significant reduction of local stresses. However, to observe plastic deformation, the surfaces may have to be highly resolved [4]. At small or intermediate resolution, or, in the case of elastomers up to high resolution, an elastic description of the contact can be appropriate.

Describing elastic contacts has attracted much attention in the recent past not only for three-dimensional, semi-infinite bodies [3, 5,6,7] but also for (quasi) two-dimensional [8,9,10] elastic counterfaces, in parts because of their implications in biology [11, 12]. The studies were triggered to a significant degree by advances in the numerical modeling of surfaces [13,14,15,16], which made it possible to simulate systems sufficiently large to reflect the typical multi-scale nature of roughness [17,18,19,20]. Many of the simulations were conducted with the goal to test the validity of a contact-mechanics theory proposed by Persson 20 years ago [3, 21,22,23]. It accounts for the deformation of the elastic body outside of the contact region unlike traditional approaches to the contact mechanics conducted in the spirit of the Greenwood–Williamson model [24, 25]. The latter assumes the highest asperity to come into contact first, the second-highest to be second, and so on. Such so-called bearing-area models unavoidably lead to qualitatively incorrect conclusions [26], most notably they predict false displacement–load relations [7] and contact topographies [27], which are much too localized near the highest peak(s).

Persson’s theory has reproduced many experimental results as well as brute-force simulations to a rather great precision. This concerns in particular the dependence of the mean gap $u_{\text {g}}$ on pressure p [22, 28,29,30,31,32] including the distribution of the interfacial separation [33, 34] and the leakage rate that follows from it [34,35,36] as well as the auto-correlation function of the interfacial stress [27]. Nevertheless, Persson’s theory remains to be seen skeptically [37]. This is in parts due to a false implementation of the theory, which, as discussed before [38], is certainly not a flaw of the theory itself. In addition, it could be argued that Persson’s theory does not predict the pressure dependence of the relative contact area $a_{\text {r}}(p)$ very well. Twenty percent error in the predicted proportionality coefficient relating contact area with the applied pressure at small p are sometimes seen as problematic [5, 37]. Some authors even find logarithmic corrections to a linear $a_{\text {r}}(p)$ relation at small p [39, 40]. In this work, we will add algebraic correction for low-dimensional elastic body to this list. However, judging a contact-mechanics theory based on its ability to produce correct $a_{\text {r}}(p)$ dependencies can be seen critically, whenever the gap distribution function becomes quasi-singular near a gap of zero, since a significant fraction of the non-contact area may be within extremely small distances, e.g., within less than a Bohr radius and/or less than thermal fluctuations, when applied to real systems. Thus, the concept of contact area is somewhat ill defined outside the realm of continuum mechanics. In fact, the proper definition of contact area for atomistic systems remains a matter of occasionally heated debates [41,42,43,44].

The discussion in the precedent paragraph shows that meaningful tests of (contact-mechanics) theories are based on quantities that are insensitive to marginal changes of a criterion. The most simple quantities satisfying this requirement are the standard deviation of the interfacial stress $\varDelta \sigma _{{\text {p}}}$ (in partial contact) and the average interfacial separation, or, mean gap, both as a function of pressure. Neither of the two functions suffer from any sensitivity to how contact area is defined.

While most attention has been paid to the contact mechanics of semi-infinite solids, in which case the elastic energy to deform the surface with a single sinusoidal undulation scales linearly with the wave number q, it may also be interesting to study thin sheets. When the thickness of a freely suspended sheet is much less than the wave length, the elastic energy scales with $q^4$, as can be deduced by taking the $q\rightarrow 0$ limit of Eq. (A.11) in Ref. [45]. Once the thin elastic sheet, e.g., a membrane, is set under tension, the small-q scaling changes to a quadratic q-dependence without directional dependence for equi-biaxial tension [11, 46]. In all three cases, the areal energy density of a superposition of sinusoidal undulations can be written as

$$v_{\text {ela}}^{\text {full}} = \sum _{{\mathbf {q}}}\frac{k_n \,q^n}{2} \, \vert {\tilde{u}}({\mathbf {q}}) \vert ^2,$$

(1)

where ${\tilde{u}}(\mathbf{q})$ is the Fourier transform of the surface and

$$k_n = {\left\{ \begin{array}{ll} E^*/2 {} n = 1,\; {\text {semi-infinite}}\;{\text {solid}} \tau &{} n = 2,\; {\text {tensed}}\; {\text {membrane}}\\ E^*t^3/12 &{} n = 4,\; {\text { thin}}\; {\text {sheet}}. \end{array}\right. }$$

(2)

Here, $E^*$ is the contact modulus of a semi-infinite solid, $\tau$ the equi-biaxially applied tension, and t the thickness of a thin sheet. Systems described by $n = 2$ can be the human lung [11] but also human skin on (sub-)millimeter scales, as demonstrated in the model validation of this work.

For elastic solids being graded in the direction normal to the interface but isotropic and homogeneous in the normal direction, the prefactor to $\vert {\tilde{u}}({\mathbf {q}}) \vert ^2$ can depend on the wave number q in a more general way than assumed up to this point. As will be shown in a subsequent work, a non-integer exponent of $n = 1/2$—or any other value for $0< n < 1$ —could be (crudely) realized by an elastomer, e.g., a hydrogel, designed in such a way that its elastic stiffness increases as an appropriate function with increasing distance from its surface. The extreme case of $n = 0$ would correspond to an Einstein solid, or, depending on viewpoint to a Winkler foundation, in which atoms are coupled harmonically to their lattice site. As argued in more detail in Sect. 4.2, an Einstein foundation would be valid for an infinitely dimensional elastomer. This makes the extreme limits of the exponent n and the spatial dimension D considered in this work go from $D = 2$ for $n = 4$ via $D = 3$ for $n = 1$ to $D = \infty$ for $n = 0$. For $n = 2$ and $n = 0.5$ as well as for $n = 3$, which is added to the list of explored exponents, we abstain from providing effective spatial dimensions D but assume that D is monotonically decreasing in n.

While models with non-integer dimension or even $D>3$ are rarely studied in engineering, expansion of theories about spatial dimensions is common practice in statistical mechanics [47], among other reasons, because it allows properties for “allowed” (integer) dimensions to be predicted, or, at least to be better rationalized. In addition, mean-field theories are generally exact at (infinitely) large spatial dimension, which allows additional tests to be conducted for theories that make other approximations than mean field. This was our main motivation to include values for the exponent n in addition to those listed in Eq. (2), and their study turned out, as we find, quite illuminating.

Thus, in this study, we provide a unifying description of the contact mechanics from thin sheets to mean-field models and explore to what extent theoretical approaches are able to reflect the observed behavior. Towards this end, the model and the used Green’s function method are introduced first in Sect. 2. To provide the reader with a better intuitive understanding of some of the quite uncommon elastomers, their contacts with Hertzian indenters are summarized in Sect. 3. Persson’s theory for randomly rough indenters is extended to the generalized elastomers in Sect. 4, which also contains the closed-form solution for an indented Einstein solid. Results are presented in Sect. 5. In Sect. 6, we attempt to rationalize why Persson’s theory predicts the $u_{\text {g}}(p)$ relation so accurately, even when it fails to predict interfacial stress distribution functions. Finally, conclusions are drawn in Sect. 7.

2 Model and Numerical Method

The (default) model consists of an initially flat, linearly elastic counterface and a nominally flat indenter with a random, self-affine height profile. The elastic body is squeezed from above against the indenter, which is fixed in space. Periodic boundary conditions are applied within the xy plane. The two surfaces interact through a non-overlap constraint.

The elastic energy used in the Green’s function molecular dynamics (GFMD) simulation is given in Eq. (1). The used exponents are all integers between zero and four and in addition, $n = 0.5$. A motivation for the used values is given in the introduction, except for $n = 3$, which was added to the list, because it is the largest integer exponent with “decent” properties. (Thin sheets, or, $n = 4$, turned out to behave in a quite non-intuitive fashion and, moreover, were difficult to treat computationally.)

To realize the different expression in our existing C++ GFMD code, only a single (central) line needed to be modified, in which the prefactor of the restoring force in wave number space was initialized as $k_n\, q^n$ rather than as $E^*\,q/2$.

The periodically repeated surface has a default height spectrum satisfying

$$C(q) \propto \left\{ 1 + (q/q_{\text {r}})^2 \right\} ^{-1-H}\, {\Theta }(q_{{\text {s}}}-q),$$

(3)

where $q_{\text {r}}$ is the roll-off wave vector, $q_{\text {s}}$ the short-wavelength cut-off, and ${\Theta }$ the Heaviside step function. The absolute value of an individual Fourier coefficient ${\tilde{h}}(\mathbf{q})$ is set to $\sqrt{C(q)}$ and a linear random number is drawn from $(0,2\pi )$ to determine its phase.

We focus our attention on a single, default disorder realization of the randomly rough indenter. Since some of the calculations require a rather fine discretization, the ratio $q_\mathrm {s}/q_\mathrm {r}$ was set to a relatively large value of 1/100. The roll-off domain was also relatively narrow, i.e., the linear system size L was set to twice the roll-off wavelength $\lambda _{\text {r}} = 2\pi /q_\mathrm {r}$. While the smallest possible simulation reflecting the full spectrum using a discretization of the elastic system into $2^n \times 2^n$ surface elements ($n \in {\mathbb {N}}$) is $512\times 512$, simulations determining the contact area of thin sheets at small reduced pressure accurately necessitated a discretization into $16\mathrm {k}\times 16\mathrm {k}$ surface elements, 16k being shorthand notation for $2^{15}$. Thus, while some of the $512\times 512$ systems need less than a minute to relax on a single core when using the so-called FIRE variant of GFMD [48], others take a rather long time, in particular as the low-dimensional elastomers do not only need a fine discretization but also significantly more iterations to relax.

In order to explore the validity of the observations, surface topographies other than the default were also simulated. In addition, finite-width elastomers were simulated. Their response crosses over smoothly from bulk to thin-sheet elasticity as the wave length of a surface undulation increases. Changes to the pertinent default parameters are mentioned where results are presented.

Results for the normal displacements of elastomers in contact with a randomly rough indenter are expressed in units of the standard deviation of the height $h_{\text {std}}$ and pressures in units of the standard deviation of the stress in full contact $\varDelta \sigma$. For Hertzian indenters, the stress is normalized to the stress at the origin, in-plane lengths to the contact radius $a_{\text {c}}$, and lengths normal to the interface are expressed as multiples of $a_{\text {c}}^2/R_{\text {c}}$, where $R_{\text {c}}$ is the radius of curvature. These unit choices turn the numerical values used for $C(q_{\text {r}})$, $R_{\text {c}}$, or for the various generalized contact moduli $k_n$ irrelevant. Note also that the term stress and the symbol $\sigma$ are both meant to refer to compressive stress throughout this study. In addition, displacements increase with increasing (compressive) stress.

All simulations were run on single cores on a local workstation with 13 TB memory.

2.1 Model Validation

To demonstrate that $n\ne 1$ has real-world applications, we compare the displacement field u(x) of a periodically repeated acute ridge, which was determined numerically for all integer values $1 \le n \le 3$, to recent experiments [49], in which a human index finger was indented from below by sharp ridges, which were periodically repeated at a distance of $\lambda = 2.5$ mm, see Fig. 1. This period is well below the $O(10\,\mu {\text {m}})$ thickness of the stratum corneum.

Fig. 1

Experimentally measured displacement field [49] of a human index finger, u(x), (black lines) indented from below by a periodically repeated ridge (gray triangles) having a period of $\lambda = 2.5$ mm as well as numerical solutions for various exponents n (colored, dashed lines)

A displacement field produced with the correct dependence of stiffness on the wave vector should match the experimental characteristics for most of the shown domain, because the actual contact in the experiment was localized within a tiny fraction of the period. While the $n = 3$ displacement field is too pointed near the minima and too blunt near the maxima, the situation reverses for $n = 1$, where u(x) is also too pointed near the maxima well outside the actual contact. In contrast, the $n = 2$ data match the trends perfectly well. This result does certainly not imply that skin is a stressed membrane. Instead, it could hint to the possibility that the stiffness of skin decreases more continuously from its surface to the epidermis than generally assumed.

3 Hertzian Contacts of Generalized Elastomers

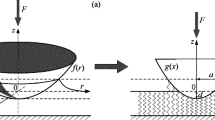
To better rationalize the results for randomly rough indenters, it may be in place to call to mind how the generalized elastic manifolds interact with a Hertzian (parabolic) indenter. Its height profile can be given by

$$h(r) = -\frac{1}{2}\;\frac{r^2}{R_{\text {c}}}.$$

(4)

While analytical solutions for the counterfaces have been identified in the literature [11], except potentially for $n = 0.5$, it is found beneficial to repeat some of the results here. It is seen particularly useful to (re-)derive the analytical solutions for the displacement fields for arbitrary n in terms of a Fourier representation, because the contact mechanics of randomly rough surfaces is arguably best interpreted in terms of spectral approaches, and results can be easily obtained for exponents n not considered so far.

The stress profiles for $0 \le n < 4$ obtained with GFMD are consistent with the relation

$$\sigma (r) = \sigma (0)\,\sqrt{1-(r/a_{\text {c}})^2}^\mu {\Theta }(a_{\text {c}}-r)$$

(5)

and

$$\mu = 2 - n.$$

(6)

Results are shown in Fig. 2. For $n=4$, stress is concentrated within the contact line, and both stress and displacement disappear for $r < a_{\text {c}}$. Moreover, the contact radius increases linearly with the cell dimension at fixed load, while for $n < 3$, or even for $n \le 3$, $a_{\text {c}}$ has a well-defined contact radius as a function of the normal load in the limit of large L.

Fig. 2

(Compressive) stress $\sigma (r)$ of generalized elastic manifolds as a function of the distance r from the symmetry axis when contact is made with a parabolic indenter. The stress is normalized to its value at $r = 0$, while r is expressed in units of the contact radius $a_{\text {c}}$

The displacement field $u({\mathbf {r}})$ is the other spatial field of interest in contact mechanics. Figure 3 shows it in the vicinity of the contact edge for the elastic bodies defined in Eq. (1). The values of n considered in this study happen to be critical values for Hertzian and related indenters (i.e., bodies of revolution leading to a single contact line at any given load), where the behavior of the displacement field changes qualitatively. These changes are summarized in Sect. 3.2. To arrive at those results, it is sufficient to consider point indenters, which is done next in Sect. 3.1. While these calculations do not necessarily enhance the understanding of the remaining sections, some of them are seen as useful for the interpretation of the contacts made with randomly rough surfaces, in particular as the asymptotic form of the point indenters closely mimics the true displacement fields up to the proximity of the contact radius, as can be appreciated in Fig. 3. For reasons of completeness, we state that GFMD simulations indicate that the gap between indenter and elastomer grows proportionally to $(r-a_{\text {c}})^{(1+n/2)}$ in the immediate vicinity but just outside the contact, which means that the $(1+n/2)$’th (fractal) derivative of u(x) is discontinuous at $r = a_{\text {c}}$.

Fig. 3

Displacement fields u(r) of generalized elastic manifolds, in units of $a_{\text {c}}^2/R_{\text {c}}$ as a function of the distance r from the axis of a parabolic indenter in units of the contact radius $a_{\text {c}}$. The indenter has a radius of curvature of $R_{\text {c}}$. Thin, black, broken lines indicate the asymptotic solutions of a point indenter presented in Sect. 3.1. They were shifted in vertical direction to match the (numerically) exact displacement field at large $r/a_{\text {c}}$

3.1 Derivation of Asymptotic Displacement Fields

The stress field associated with a point force acting on the origin of an infinitely large domain can be represented as

$$\sigma ({\mathbf {r}})= {} F\,\delta ({\mathbf {r}}) = {} \frac{F}{(2\pi )^2} \int \hbox {d}^{2}{q} \, e^{i{\mathbf {q}}\cdot {\mathbf {r}}}$$

(7)

so that its (symmetric) Fourier transform reads

$${\tilde{\sigma }}({\mathbf {q}}) = \frac{F}{\sqrt{2\pi }},$$

(8)

where F is the (compressive) force squeezing the sufaces together and $\sigma$ is the compressive stress. Using the stress–displacement relation

$${\tilde{\sigma }}({\mathbf {q}}) = k_n\, q^n\, {\tilde{u}}({\mathbf {q}}),$$

(9)

which follows from Eq. (1), the displacement field in real space, up to an additive constant, becomes

$$u({\mathbf {r}})= {} \frac{1}{(2\pi )^2} \, \frac{F}{k_n} \, \int \hbox {d}^{2}{q} e^{i{\mathbf {q}}\cdot {\mathbf {r}}} \frac{1}{q^n}$$

(10a)

$$= {} \frac{I_n\,F}{2\pi \,k_n\,r^{2-n}} \text { for } n{>}1/2 \text { {with} }$$

(10b)

$$I_n= {} \int _0^{\infty } \hbox {d}{{\tilde{q}}} {\tilde{q}}^{1-n}\, J_0 ({\tilde{q}}),$$

(10c)

where $J_0$ is a Bessel function of the first kind. The transition from Eqs. (10a) to (10b) can only be made for $1/2<n$, since the Bessel function approaches $\sqrt{2/(\pi \,x)}\,\cos (x-\pi /4)$ asymptotically for large x, which renders the integral on the r.h.s. of Eq. (10c) ill defined. For $n < 1/2$, a square or rectangular integration must be assumed for the wave vectors to make the $I_n$ convergent. For $n \ge 2$, the integrals $I_n$ diverge because the integrand grows too quickly as the integration variable approaches zero. However, for a given cell dimension of a periodically repeated indenter, the integral in Eq. (10a) can be converted back into a (quickly convergent) sum over wave vectors and/or $u(\mathbf{r })-u(0)$ is calculated, which alleviates the $q\rightarrow 0$ singularity of the integrand.

For $1/2< n < 2$, the integrals $I_n$ can be expressed, in principle, in terms of the gamma function and the regularized generalized hypergeometric function. However, this general solution does not proof particularly useful for our purposes. Only one of the considered exponents falls into this domain, namely $n = 1$, and for this exponent, it is easy to identify the asymptotic solution with elementary functions.

3.1.1 Asymptotic Displacement Field for $n = 0$

Since the displacement field is constant outside the contact for $n = 0$, the calculations outlined above in this section are not yet needed. The non-contact displacement field simply assumes the height of the indenter at the contact line, $u(a_{\text {c}}) = h(a_{\text {c}})$, which is mentioned here for reasons of completeness. The value of $h(a_{\text {c}})$ can also be seen as the (negative) indentation depth, i.e., $d_{n=0} \equiv u(r \rightarrow \infty ) = h(a_{\text {c}})$.

3.1.2 Asymptotic Displacement Field for $n = 1/2$

As already mentioned, $I_{1/2}$ is not well defined. However, it can be regularized by multiplying the integrand with factors such as $\exp (-\alpha qr)$ or $\exp \{-(\alpha qr)^2\}$, in which case it yields the (numerical) value of $I_{1/2} \approx 0.478(0)$ for $\alpha \rightarrow 0$. Thus, the displacement field reads

$$u(r) = d_{1/2} - \frac{0.478(0)\, F}{2\pi \,k_{1/2}\,r^{3/2}}.$$

(11)

The indentation depth $d_{1/2}$ cannot be determined from this analysis, since it is specific to the shape of the indenter.

3.1.3 Asymptotic Displacement Field for $n = 1$

Since $\int _0^\infty \hbox {d}{x} J_0(x) = 1$, it follows that

$$u(r) = d_1 - \frac{F}{2\pi k_1\,r},$$

(12)

where $d_1$ is the displacement in the limit $r \rightarrow \infty$. This is, of course, nothing but the well-known Boussinesq solution for regular semi-infinite solids, although in its usual formulation $k_1$ is substituted with $E^*/2$. For the case of a regular ($n = 1$) Hertzian indenter, the indentation depth is known to be $d_1 = a^2_{\text {c}}/R_{\text {c}}$

3.1.4 Asymptotic Displacement Field for $n = 2$

The integral $I_2$ is divergent, because its integrand scales as 1/x when its integration variable x is small. From this scaling, it follows that the indentation depth must be a logarithmic function of the linear dimension of the simulation cell L, because the natural lower bound for the integration variable q is $2\pi /L$. From the prefactor, it also becomes clear that a $1/r^{2-n}$ dependence for $n \rightarrow 2$ should result in a $\ln (r)$ dependence. To ascertain the prefactor to this relation, it is easier to calculate $u'(r)$ first, which is obtained by multiplying the integrand on the r.h.s. of Eq. (10a) with q, so that

$$u'_{n=2}(r) = \frac{I_{n=1}\,F}{2\pi \,k_2\, r}.$$

(13)

This yields, after inserting $I_1 = 1$ and after dropping the index $n = 2$ in the displacement field,

$$u(r) = \frac{F}{2\pi \,k_2}\,\ln (r/r_2),$$

(14)

where $r_2$ is a reference value defining at what distance from the origin the asymptotic displacement field has the height of the exact displacement field in the origin. A similar logarithmic dependence of the elastic Green’s function is obtained in $D = 2$ for $n=1$, or whenever $D-n=1$, as $D-n$ determines the scaling of the integral on the r.h.s. in Eq. (10a) with r, through prefactors would differ.

For $r_2 = \sqrt{e}\,a_{\text {c}}$, the just-derived displacement field coincides within line width with the data obtained in GFMD simulations in the immediate vicinity of the contact edge. For this value of $r_2$, the analytical displacement field has the same slope at $r = a_{\text {c}}$ as the indenter.

3.1.5 Asymptotic Displacement Fields for $n > 2$

For $n>2$, the long-wavelength contributions dominate the integral on the r.h.s. of Eq. (10a). For a periodically repeated indenter, this means that the first few Fourier coefficients determine the displacement, unless, of course, n is very close to 2. In addition, the displacement is best given relative to $r = 0$ rather than to $r = \infty$, because $d_{n>2}$ diverges, while $u(a_{\text {c}})-u(0)$ is finite.

The $n=3$ and the $n = 4$ displacement fields for periodically repeated point indenters resemble the $n=2$ and $n = 3$ solutions for the periodically repeated line-ridge indenters shown in Fig. 1, respectively, i.e., approximately linear right outside the contact for the smaller value of n and reasonably close to a single sinusoidal undulation for the larger value of n.

A reasonably accurate closed-form expression for the displacement field of a $n=3$ elastomer (indented by a periodically repeated point indenter) can be obtained by using discrete Fourier sums. The first summand would be taken explicitly while the remaining terms could be approximated by an integral with a well-chosen lower integration bound, e.g., a wave number half way inbetween $q_0$ and $\sqrt{2}\, q_0$. The solution of that integral then scales proportionally to r as expected from Eq. (10b), albeit with a different prefactor. Of course, this linear scaling only applies for $r \ll L$, but it may hold for $r \gg a_{\text {c}}$ if $a_{\text {c}}$ is sufficiently small compared to L. While this course of action leads to excellent results, the dashed $n = 3$ line accompanying the (orange) $n=3$ displacement field in Fig. 3 reflects the numerically exact displacement field obtained by GFMD for a point indenter.

In principle, the $n=4$ elastomer can be treated similarly as the $n = 3$ elastomer. However, this time the leading-order Fourier summand is almost sufficient to deliver a good approximation to the displacement field throughout non-contact.

3.2 Comparison of Different Asymptotic Solutions

The just-presented asymptotic solutions of the displacement fields allow a few conclusions to be drawn for localized indenters, which are repeated periodically on a square domain. They should hold not only for Hertzian but also for related indenters such as circular flat-punch or conical indenters, i.e., whenever the asymptotic fields are quickly approached for radii $r \gtrsim 2\, a_{\text {c}}$.

• (i) For $n<2$, the indentation depth $d_n$ is finite at constant normal force per indenter, even if L tends to infinity. For $n = 2$, $d_n$ diverges logarithmically and for $n > 2$ algebraically with increasing L.

• (ii) The far-field scaling relation $u(r) \propto r^{n-2}$ is rigorously valid as long as $r \ll L$ if $0.5 \le n < 2$. For smaller exponents, the $u(r\rightarrow \infty )$ asymptote is reached more quickly than with $r^{n-2}$, e.g., for $n = 0$, it is reached immediately at $r = a_{\text {c}}$, while for $n = 1/4$, numerical evidence (not shown explicitly) for a $u(r) \propto r^{-2.25}$ scaling was found. For $n = 2$, the displacement field is logarithmic in r.

• (iii) For $n>2$, the prefactor to the (derivative of the) displacement field depends not only on the load per indenter but also on the period even if $L \gg a_{\text {c}}$.

• (iv) The volume $\varDelta V$ displaced by an indenter diverges for $L \rightarrow \infty$, unless n is below a critical value $n_{\text {cI}}$ with $0.25< n_{\text {cI}} < 0.5$ at which $u(r) \propto r^{-2}$ holds.

3.3 Contact Radius and (Relative) Contact Area

The final analysis in this section on Hertzian indenters is the estimation of the contact radius $a_{\text {c}}$ and the ensuing relative contact area for periodically repeated indenters. Dimensional analysis is the simplest approach to obtain functional dependencies. Missing proportionality coefficients tend to be of order unity except close to critical points, where the dimensional analysis stops being applicable.

The displacement $u(r=0)$ of the indenting Hertzian tip relative to that at $r \rightarrow \infty$ scales as $a_{\text {c}}^2/R$ for $n < 2$ as becomes clear from Fig. 3. This in turn makes the potential energy of a single indenter in response to an external load $F_{\text {N}}$ scale as

$$U_{\text {pot}} \propto -F_N u_{\text {g}}^2/R_c.$$

(15)

A characteristic wave number can be associated with $1/a_{\text {c}}$ so that the elastic energy satisfies

$$U_{\text {ela}} \propto k_n a_{\text {c}}^{-n+2} a_{\text {c}}^4/R_{\text {c}}^2.$$

(16)

Minimizing the total energy, $U_{\text {ela}} + U_{\text {pot}}$, then yields

$$a_{\text {c}}^{4-n} \propto \frac{F_{\text {N}} R_{\text {c}}}{k_n},$$

(17)

which contains the well-known, regular ($n = 1$) case, for which the proportionality coefficient that is needed on the r.h.s. of Eq. (17) would be 3/2.

Equation (17) can be recast as

$$a_{\text {r}} = \kappa '_n \frac{p\, R_{\text {c}}}{k_n \, a^{2-n}_{\text {c}}}$$

(18)

for a periodically repeated indenter, whose contact radius is small compared to the linear dimension of the periodically repeated cell. Here, $\kappa '_n$ is a unitless proportionality parameter.

Equation (17) can also be written as

$$a_{\text {r}} = \kappa _n \, \frac{p }{\varDelta \sigma _{\text {c}}},$$

(19)

where $\varDelta \sigma ^2_{\text {c}}$ is defined as

$$\varDelta \sigma ^2_{\text {c}} = k_n^2 \left\langle \left\{ \frac{d^n}{dr^n} h(r) \right\} ^2 \right\rangle _{\text {c}}.$$

(20)

Here, $\langle \cdots \rangle _{\text {c}}$ indicates an average over the true contact with $h(r)=r^2/(2R_c)$ for a Hertzian indenter. Using the rule for (fractional) derivatives of polynomials, i.e., $d^n q^k / dq^n = {\Gamma }(k+1)\, q^{k-n} / {\Gamma }(k+1-n)$, $\varDelta \sigma _{\text {c}}$ can be calculated to be

$$\varDelta \sigma _{\text {c}} = \frac{k_n a_c^{2-n}}{R_{\text {c}} \, \sqrt{3-n} \, {{\Gamma }}(3-n)}$$

(21)

so that $\kappa '_n$ is shown to be $\kappa '_n = \kappa _n\, \sqrt{3-n}\, {\Gamma }(3-n)/ \pi$.

Equation (19) is a generalization of the $a_{\text {r}} \propto p^*$ relation, which was shown to be valid at small reduced pressures, $p^* \equiv p/\varDelta \sigma _{\text {c}}$ for periodically repeated indenters with harmonic height profiles, $\vert h(r) \vert = r^m/(m R_{\text {c}}^{m-1})$, squeezed against a three-dimensional elastic body [50]. The presented calculation can be repeated for arbitrary n and $0< m$, in which case the proportionality coefficient $\kappa _n$ acquires a second index. However, the proportionality between $a_{\text {r}}$ and $p^*$ remains valid for $n<2$.

The (Hertzian) proportionality coefficient $\kappa _n$ can be readily deduced for $n = 0$ and $n = 1$ from their analytical solution to be $\kappa _0 = 2/\sqrt{3}$ and $\kappa _1 = 3\pi /(8\sqrt{2})$. $\kappa _{1/2}$ was deduced numerically as follows: For a given normal force F and mesh size $\varDelta a$, the stress profile was computed and fitted with Eq. (5), which allows the determination of the contact radius with sub-mesh-size precision. For each normal force, the mesh size was decreased until the first fourth digit of $a_{\text {c}}$ only changed by plus-minus one. In the same way, F was divided by factors of 5 until its highest resolution value for $a_{\text {c}}$ leveled off. The numerical result yielded $\kappa '_{1/2} = 0.665(5)$, which translates into $\kappa _{1/2} = 0.994(7)$. Assuming the exact values to be simple rational exponents of expressions involving other simple rational numbers and the number $\pi$, we believe $\kappa '_{1/2} = (2/3)^2\,(8\pi /5)^{1/4}$ and thus $\kappa _{1/2} = (2/3)^3\,(8\pi /5)^{3/4}$ to be exact.

4 Theory for Randomly Rough Surfaces

4.1 Persson’s Theory

In this section, we adopt Persson’s theory for the contact mechanics between nominally flat, randomly rough indenters with (semi-)infinite elastomers to that with more general elastomers, i.e., those whose elastic energy is given by Eq. (1). In principle, the term $k_n\,q^n$ could be replaced with any arbitrary function k(q). Since the following treatment allows this generalization to be made in the final equations, we kept the original expression of the elastic energy.

Let the stress at a point $\mathbf{r }$ in the contact be given by $\sigma (\mathbf{r})$ when all roughness existing in the spectrum with wave vectors $\vert {\mathbf {q}}' \vert < q$ have been considered in an exact solution of the contact problem. When adding the Fourier coefficient associated with the wave vector ${\mathbf {q}}$ to a refined calculation, the stress at $\mathbf{r }$ will change by

$$\varDelta \sigma ({\mathbf {r}}) \approx i\, k_n \, q^{n} \, {\tilde{h}}({\mathbf {q}}) \, e^{i\,{\mathbf {q}}\cdot {\mathbf {r}}} + {\text {c.c.}}$$

(22)

if the closest non-contact point of $\mathbf{r }$ is further away than a distance $\gtrsim q^{-1}$.

The just-described change of the local stress would lead to an expected increase of the second moment of the stress distribution with $k_n^2 q^{2n} \left\langle \vert {\tilde{h}} \vert ^2 \right\rangle$ if the just-described changes happened everywhere in the contact. This, in turn, would lead to a scale-dependent smearing out of the (initial) pressure with a variance of

$$\varDelta \sigma ^2({q}) = \sum _{{\mathbf {q}}', q'\le q} k_n^2 \, {q'}^{2n} \, C({\mathbf {q}}')$$

(23)

if all roughness Fourier components with $q'\le q$ had been considered. The situation can be associated with that of a random walker and thus with a diffusive process. Once a walker has reached $\sigma = 0$, it is no longer considered to be in contact and drops out of the process. The adsorbing barrier of the random walk can be reflected by placing a mirror Gaussian at the negative nominal contact stress.

Compressive stress and pressure can be assigned the same sign, so that

$$\Pr (\sigma ) = {\bar{a}}_{\text {c}}\delta (\sigma ) + \frac{ \exp \left\{ -\frac{(\sigma -p)^2}{2\varDelta \sigma ^2}\right\} - \exp \left\{ -\frac{(\sigma -p)^2}{2\varDelta \sigma ^2}\right\} }{\sqrt{2\pi \varDelta \sigma ^2}},$$

(24)

where ${\bar{a}}_{\text {c}} = 1 - a_{\text {c}}$ is the relative non-contact area and

$$a_{\text {c}}\left( \frac{p}{\varDelta \sigma }\right) = \mathrm {erf}\left( \frac{p}{\sqrt{2}\varDelta \sigma } \right) .$$

(25)

As argued in the introduction, requiring a theory to reproduce the pressure dependence of contact area is not a particularly telling test. Instead, it may be more sensitive to investigate the second moment of the interfacial stress, as it is insensitive to a contact criterium, which, in case of reality and all-atom simulations suffers from ambiguity. Since the first moment of the interfacial stress in mechanical equilibrium is identical to the nominal contact pressure, the standard deviation of the interfacial stress in Persson’s theory satisfies

$$\frac{\sigma ^2_{{\text {p}}}}{\varDelta \sigma ^2}= {} \frac{1}{\varDelta \sigma ^2} \int _{-\infty }^\infty \hbox {d}{\sigma } (\sigma -p_0)^2 \, \Pr (\sigma ) = {} \mathrm {erf}\left( \frac{p_0}{\sqrt{2}\varDelta \sigma } \right) + \sqrt{\frac{2}{\pi }}\, \frac{p_0}{\varDelta \sigma } \exp \left( -\frac{p_0^2}{2\varDelta \sigma ^2} \right) - \frac{p_0^2}{\varDelta \sigma ^2} \, \mathrm {erfc}\left( \frac{p_0}{\sqrt{2}\varDelta \sigma } \right)$$

(26)

and includes the contribution of the zero, non-contact stress to the std stress.

To obtain the mean interfacial separation, we proceed as usual and equate the elastic energy in (partial) contact $v_{{\text {ela}}}$ with the work done by the external stress. The latter satisfies

$${\text {d}}v_{\text {ela}} = -p(u_{\text {g}}) {\text {d}}u_{\text {g}} = -p(u_{\text {g}}) \frac{{\text {d}}u_{\text {g}}}{{\text {d}}p} {\text {d}}p.$$

(27)

At infinite pressure, the mean gap is equal to zero and thus

$$u_{\text {g}} = \int ^\infty _p \hbox {d}{p'} \frac{1}{p'} v_{\text {ela}}^{\prime }(p^{\prime }).$$

(28)

In partial contact, elastic energy only has to be paid in the points of contact. Thus, the spectrum only enters with a certain weight.

$$v_{\text {ela}}(p) = \frac{k_n}{2} \sum _{{\mathbf {q}}} W(p,\mathbf{q}) q^n C(\mathbf{q}).$$

(29)

To lowest order, $W(p,\mathbf{q})$ can be assumed to be the relative contact area. However, the real elastic energy in partial contact was argued to be less, at least for (isotropic) semi-infinite solids. It was found that using weights

$$W = \left\{ \gamma _n + (1-\gamma _n)\, a_{\text {r}}^2 \right\} a_{\text {r}} ,$$

(30)

which are implicitly functions of p and ${\mathbf {q}}$, improve the agreement between theory with experiment or simulations [6]. At small partial contact, the weighting factor W is still linear in the relative contact area, however, with a (usually reduced) prefactor $\gamma _{\text {n}}$. As full contact is approached, W approaches unity. In Eq. (30), the dependence of W on $a_{\text {r}}$ was assumed to depend on the exponent n as denoted by the index n in $\gamma _{\text {n}}$. The origin of this correction factor, will be discussed further in Sect. 5.

The usual way to proceed from here would be to derive a double integral for the interfacial separation, which allows further analytical calculations to be conducted, albeit not without making approximations. For the present purpose, it was found beneficial to compute $v_{\mathrm {ela}}(p)$ and to evaluate its pressure derivative numerically. Technical details of how this was achieved are discussed in the following section.

4.1.1 Implementation of Persson’s Theory

Persson’s theory is carried out with an exact representation of the spectrum of the simulated system at large wavelengths $\lambda$ and with a quasi-continuum approximation at small $\lambda$. This was done by creating $n_\lambda = 500$ bins, such that the first bin represented the largest allowed wavelength and the last bin the shortest. The bins inbetween were chosen to have an equal width on a logarithmic scale. Each bin contains as entry the elastic energy that is required to make full contact with the modes associated with that bin as well as the stress variance accumulated over this and all lower-indexed bins.

For each bin, the relative contact area entering the weight function in Eq. (30) and thus also Eq. (29) is computed as follows: First, $a_\mathrm{r}$ is computed before and after (the modes contained in) a given bin is included into the sum and denoted by $a_\mathrm{r}^-$ and $a_\mathrm{r}^+$, respectively. If they do not differ by more than 10%, their mean value is assigned to $a_\mathrm{r}$, otherwhise the mean relative contact area is computed by

$${\bar{a}}_{\text {r}}= {} \frac{1}{\varDelta \sigma _+^2-\varDelta \sigma _-^2} \int _{\varDelta \sigma _-^2}^{\varDelta \sigma _+^2} \hbox {d}{\varDelta \sigma ^2} a_{\text {r}}(p/\varDelta \sigma ) .$$

(31)

The integral I on the right-hand-side yields

$$I= {} \left( p^2+\varDelta \sigma _-^2\right) \, \frac{ a_{{\text {r}}}^- }{2}\, + \frac{p\,\varDelta \sigma _-\,e^{-p^2/2\varDelta \sigma _-^2}}{\sqrt{2\pi }} - \left( p^2+\varDelta \sigma _+^2\right) \, \frac{ a_{{\text {r}}}^+ }{2}\, - \frac{p\,\varDelta \sigma _+\,e^{-p^2/2\varDelta \sigma _+^2}}{\sqrt{2\pi }} .$$

(32)

4.1.2 Comparison to Results for Periodically Repeated Indenters

Persson’s theory entails a similar relation as Eq. (19) at small $p^*$ for nominally flat contacts, except that the pressure is undimensionalized with the full-contact stress variance $\varDelta \sigma$ rather than with $\varDelta \sigma _{\text {c}}$, which is determined from the mean square n’th derivative of the height within the contact. If the theory were modified in a way that $\varDelta \sigma _{\text {c}}$ could be determined over the real contact, the proper real-space substitution of Eq. (23) would be Eq. (20). Proceeding this way, $\kappa _n$ is independent of n, since the linear expansion of Eq. (25) yields $a_{\text {c}} \approx \sqrt{2/\pi }\, p^*$ for all n so that a unique proportionality coefficient $\kappa _\mathrm{P} = \sqrt{2/\pi } \approx 0.798$ arises in Persson’s theory. Its value is in reasonable agreement with the results for Hertzian indenters and elastomers with exponents in the range $0< n < 1$. This agreement is worth noting, because spherically symmetric indenters violate the random-phase approximation, one of the most criticized assumption made in Persson’s theory, in the worst possible way.

4.2 Einstein Foundation

In the limit of infinitely large dimensions, $D\rightarrow \infty$, the elasticity of crystals becomes a mean-field model, in which each atom can be treated as if it were coupled harmonically to its lattice site. A hypercube of spatial dimension $D>3$ has several hypersurfaces, e.g., $D-1$, $D-2$, but also (zero-dimensional) vertices, (one-dimensional) edges, and (two-dimensional) surfaces. The atoms in such a two-dimensional surface (in contact with a randomly rough, two-dimensional surface) still have an infinite number of neighbors in the limit of $D \rightarrow \infty$. This is why their coupling also satisfies the Einstein model, even if the elastic coupling to lattice sites is potentially different for (hyper-)surface atoms than for bulk atoms. A realization of the Einstein solid would be a soft elastic body of thickness t resting on a perfectly rigid foundation, in which only undulations with wave vectors $q \ll 1/t$ would be allowed and a total displacement difference in the sheet well below t. In this case, the stiffness of a mode would be proportional to 1/t and independent of q as can be deduced from the $q\,t \rightarrow 0$ limit of Eq. (A.9) in Ref. [45]

The Winkler foundation is occasionally used as a contact-mechanics model [51]. It could be argued to be similar to the Einstein model, because it assumes a linear relation between displacements within the contact and a generalized stress field. However, it requires the latter to be transformed so that the resulting field can be interpreted as a true stress. Moreover, its use is only rigorous for indenters of rotational symmetry and singly connected contact patches. In the Einstein model, stresses do not have to be transformed and the model is exact for $D\rightarrow \infty$. This is why it was decided to use the terms Einstein solid and Einstein foundation in this study rather than Winkler foundation.

The Einstein model can be solved analytically for a variety of cases. This includes a Gaussian height distribution, which is acquired in the thermodynamic limit for indenters satisfying the random-phase approximation. More precisely, any observable considered in this work can be expressed in closed form as a function of the height of the non-contact zone $h_\mathrm {nc}$ relative to the mean height $h_0$ of the randomly rough indenter.

As can be clearly seen in Fig. 3, the probability distribution of the displacement field of an $n=0$ elastomer, ${\Pr }_{n=0}(u)$, is identical to that of the indenter given that the indenter height is above the non-contact height threshold $h_{\text {nc}}$, so that

$${\Pr }_{\text {n=0}}(u) = {\bar{a}}_\mathrm {r} \delta (h-h_\mathrm {nc}) + \Pr (h)\, {\Theta }(h_\mathrm {nc}-h),$$

(33)

where ${\bar{a}}_\mathrm {r} = 1 - a_\mathrm {r}$ is the relative non-contact area and

$$a_\mathrm {r} = \lim _{\varepsilon \rightarrow 0^+}\int ^{\infty }_{h_\mathrm {nc}+\varepsilon } \hbox {d}{h} \Pr (h).$$

(34)

Moments of the displacement relative to the non-contact height satisfy

$$\left\langle u^k \right\rangle = \int _{-\infty }^{h_{\text {nc}}} \hbox {d}{h} {\Pr }(h) \,(h_{\text {nc}}-h)^k ,$$

(35)

where the displacement is defined as positive if a point sits below the non-contact height.

Making the xy plane lie at the same height as the center of mass of the indenting surface and assuming a Gaussian height distribution yields the following first three, non-negative integer moments of the displacement field after some algebra

$$a_{\text {r}} \;= {} \frac{1}{2}\left\{ 1 + \mathrm {erf}\left( \frac{h_{\text {nc}}}{\sqrt{2}\,h_\mathrm {std}} \right) \right\}$$

(36a)

$$\langle u \rangle \;= {} h_{\text {std}} \frac{\exp \left\{ -h^2_{\text {nc}} / (2 h^2_{\text {std}})\right\} }{\sqrt{2\pi }} + h_\mathrm {nc} \, a_{\text {r}}$$

(36b)

$$\langle u^2 \rangle= {} h_{\text {std}} \, h_{\text {nc}} \frac{\exp \left\{ -h^2_{\text {nc}} / (2 h^2_{\text {std}})\right\} }{\sqrt{2\pi }} + (h^2_\mathrm {nc}+h^2_\mathrm {std}) \, a_{\text {r}} ,$$

(36c)

where $a_{\text {r}}$ may be interpreted as the zeroth moment of the displacement field for an Einstein foundation.

Equation (36) allows the dependence of the mean gap $u_{\text {g}}$ on the pressure to be determined. The mean gap can be seen as complementary to the displacement so that

$$\left\langle u_{\text {g}}(h_{\text {nc}}) \right\rangle = \left\langle u(-h_{\text {nc}}) \right\rangle$$

(37)

and the pressure reads

$$p = k_0 \, u(h_{\text {nc}}).$$

(38)

Finally, all properties of interest in this study can be calculated as analytical functions of $h_{\text {nc}}$ and then plotted against each other.

5 Results

To set the stage for further analysis, representative contact cross-sections at close to 10% relative contact area are shown in Fig. 4. Like any other bearing model ignoring elastic deformation outside the contact, the non-contact height is constant for the Einstein foundation ($n = 0$). As n increases, the long-wavelength structure of the substrate is ever more followed. At the same time, the contact patches spread out more and more. For example, in the shown cross section, the $n=0$ solid only makes contact at $r \approx -0.4\,L$ and at $r/L \approx 0.6$. For $n=1$, additional contacts arise at $r/L \approx 0.1$ and $r/L \approx 0.3$, while for $n \ge 2$, the contact appears to be almost uniformly spread out across the interface.

Fig. 4

Displacement field of different counterfaces at a relative contact area of $a_{\text {r}} = 0.1 \pm 0.005$ across one of two diagonals of the simulation cell. The thin sheet (orange, $n=3$) and the stressed membrane (green, $n=2$) have most points within or close to the line width of the randomly rough indenter (black). All other counterfaces, namely, the regular, semi-infinite solid (red, $n = 1$), the elastically graded elastomer (blue, $n=1/2$), and the Einstein solid (magenta, $n=0$) have separations, which are clearly visible at the given resolution

Due to the finite optical resolution, Fig. 4 can convey the impression that the large-n elastomers make more contact than those with small n. However, the figure does not immediately reveal that the large-n elastomers rarely reach the indenter’s valleys. Stress has the much greater sensitivity to reveal this trend.

To demonstrate to what extent the value of n affects the local contact geometry but also to introduce typical stress profiles of the various counterfaces, the stress profile of the asperity located near $r/L = -0.4$ is shown next in Fig. 5. While the $n=1/2$ elastomer makes almost perfect contact in that asperity, the $n=3$ elastomer makes close to its “usual” 10% contact. It does so by sampling predominantly the peaks of the rigid indenters.

Fig. 5

Local stress profiles at $a_{\text {r}} = 0.1 \pm 0.005$ for a $n = 0.5$ (dotted blue line with squares), $n = 1$ (solid red line with circles) as well as for b $n = 2$ (dotted green line with triangles down) and $n = 3$ (solid orange line with triangle up). Stresses for $n = 3$ are divided by a factor of two to make the data fit on the same graph as the one for $n = 2$. The discretization in a was 8k $\times$ 8k and in b 16k$\times$16k

Figure 5 also reveals that the way how the interfacial stress disappears with the distance d from a contact edge is similar to that for a Hertzian contact geometry. It obeys the $\sigma \propto d^{\mu /2}$ scaling with the same dependence of the exponent $\mu$ on n as stated in Eq. (6). To fully reveal the nature of the stress singularities at the contact edge of an $n=3$ elastomer, very fine discretizations are required. Using 32k$\times$32k elements of the full default surface is still insufficient. Confirming that $\mu (n=3) = -1$ also applies for randomly rough surfaces requires to zoom into individual asperities with even finer discretization.

Results for thin beams ($n = 4$) were not included in the comparison of contact topographies and stresses at 10% relative contact for different exponents. It is computationally impossible to reach that limit for $n = 4$, because of the singular nature of contact stresses at the contact line making $a_{\text {r}}$ somewhat difficult to define.

5.1 Contact Area and Stress Distributions

One of the two central, scalar quantities to be determined in an elastic contact-mechanics calculation is the contact area. Figure 6a shows the numerical results for the various elastic counterfaces as a function of reduced pressure $p^* \equiv p/\varDelta \sigma$ including the theoretical prediction by Persson‘s theory, while Fig. 6b shows the ratio of the numerical results and the theoretical prediction. Note that the present definition of the reduced pressure deviates by a factor of two from the usual convention $p^*_{{\text {usual}}}\equiv p/E^*{\bar{g}}$ for semi-infinite solids, where ${\bar{g}}$ is the root-mean-square height gradient.

Fig. 6

a Relative contact area $a_{\text {r}}$ as a function of reduced pressure $p^* \equiv p_0/\varDelta \sigma$ for different elastic counterfaces. b Ratio of computed and predicted relative contact area

While Persson’s theory predicts the deviations from full contact at large $p^*$ reasonably well for all studied systems, agreement for $a_{{\text {r}}}(p^*)$ at small $p^*$ is less satisfactory: for $0.5 \le n \le 2$, logarithmic corrections to a linear $a_{{\text {r}}}(p^*) = \kappa _n p^*$ dependence are required, while an entirely different power law is observed for $n = 3$. The need for the logarithmic corrections might disappear or at least be strongly suppressed in the thermodynamic limit, in particular for $n = 1$ [52]. However, the contact is spread out over many small patches for $n = 2$, Thus, finite-size corrections to Persson’s theory conducted similarly as those for the interfacial stiffness of semi-infinite elastomers [30] would not apply to the contact-area calculation of the $n=2$ elastomer. New improvements to the theory may have to be identified, as for example, the replacement of $\varDelta \sigma$ with $\varDelta \sigma _{\text {c}}$. Yet, as argued in the introduction, the reproduction of relative contact area is not seen as a critical assessment of a contact-mechanics theory for randomly rough surfaces, even if it is the most frequently performed traditional assessment of their validity.

A potentially more meaningful test for a contact-mechanics theory is to make it predict the interfacial stress distribution function $\Pr (\sigma )$. It is given by Eq. (24) in Persson’s theory, irrespective of the value of the exponent n. One of the difficulties in computing it in full simulations is that discretization effects lead to an overestimation of $\Pr (\sigma )$ at small, positive values of $\sigma$.

For non-adhesive contacts of semi-infinite ($n = 1$) solids with randomly rough surfaces, it is well established that $\Pr (\sigma )$ disappears as $\sigma$ approaches zero from above, for example, Wang and Müser found a $\Pr (\sigma ) \propto \sigma ^{0.7}$ at small $\sigma$ [10]. However, it is generally difficult to determine the precise (power) law with which this happens, also because very fine discretizations are required to unravel the asymptotic $\sigma \rightarrow 0$ behavior. For semi-infinite solids, this is because the stress in real space disappears proportionally with $\sqrt{d}$ with the distance d of a contact point from the contact edge. This implies that the number of points with small $\sigma$ is scarcely distributed.

The larger (smaller) n, the more continuous (discontinuous) is the disappearance of the stress with d in an individual contact. While a quantitative analysis would require precise contact patch and contact line statistics, this trend is consistent with the $\sigma \rightarrow 0$ behavior observed in Fig. 7, small exponents n enhance the probability of small stresses near the contact line relative to large exponents.

Fig. 7

Stress distribution function at 10% relative contact area, $\Pr (\sigma \vert a_{\text {r}} = 0.1)$, as a function of stress $\sigma$ in units of the standard deviation of the stress in full contact, $\varDelta \sigma$. Solid lines for the various elastic bodies are actual data. Not every data point is represented as symbols. The data for small $\sigma$ were produced with the help of a Richardson extrapolation

The functional form of $\Pr (\sigma )$ changes continuously with n. This becomes particularly noticeable for the asymptotic scaling in the $\sigma \rightarrow 0^+$ limit. For small, positive stresses, we find $\Pr (\sigma ) \propto \sigma ^\mu$, where $\mu (n=0.5) \approx 0.3$, $\mu (n = 1) \approx 0.6$, and $\mu (n = 2) = 1$ for the default system, where the uncertainty in the exponent is approximately 0.1. The exponent for the $n=3$ elastomer is difficult to determine for the default system. Using a discretization of 32k$\times$32k still turned out insufficient. For smaller systems, e.g., for an $H = 0.8$ indenter with a linear system size of merely $L = 20\,\lambda _{\text {s}}$, evidence for super-linear scaling at small $\sigma$ was identified. The small probabilities at small $\sigma$ for $n = 3$ is not surprising, because the lowest contact stresses appear in the center of the contact patches rather than on their edges, which makes small positive interfacial stresses be rare.

The $n = 3$ stress distribution function is also special at large stresses in that it is the only one lacking Gaussian tails. Instead, $\Pr (\sigma )$ disappears as a $\sigma ^{-2.5}$ power law at large stresses, an issue that we will come back to in Sect. 6. Non-Gaussian tails in $\Pr (\sigma )$ had also been observed previously for randomly rough, stepped indenters [53]. This similarity might originate from similar single-asperity stress profiles, as the flat-punch stress profile for a $n=1$ elastomer has the same functional dependence as the Hertzian stress profile of an $n=3$ elastomer.

The lowest-order, non-trivial, positive, integer moment of the interfacial stress distribution function (defined over the entire apparent area including non-contact) in partial contact is the second (central) moment, $\varDelta \sigma ^2_{\text {p}}$, as the first moment equals the nominal pressure. Therefore, it appears to be the most appropriate single number with which to quantify the shape of the stress distribution function as a function of pressure. Figure 8 compares the theoretical prediction, which again does not depend on n when stress is expressed in units of $\varDelta \sigma$, to the results of $\varDelta \sigma _{\text {p}}$ for different n obtained with GFMD. The trends of all shown data sets are rather similar except, again, for $n = 3$, which is discussed next.

Fig. 8

Standard deviation of the interfacial stress $\sigma _{\text {p}}$, averaged over the entire surface and expressed in units of $\varDelta \sigma$, as a function of the reduced pressure $p/\varDelta \sigma$. The data shown for $n = 3$ are only lower bounds obtained by discretizing the short-wavelength cut-off into 128 elements. Exact numbers are expected to diverge for $n=3$ in partial contact using an infinitesimally fine discretization

The $n = 3$ elastomer is the only studied case, in which the interfacial standard deviation of the stress increases with decreasing pressure. This trend, however, is easily rationalized: When the first non-contact patches arise, so do the stress singularities at the contact edges, which increase the stress variance. Since the stress variance in an isolated Hertzian contact diverges for $n=3$, it should also diverge as soon as the contact edges have a finite weight, i.e., whenever the relative contact area drops below unity. In fact, even close to full contact, a quasi-logarithmic increase of $\varDelta \sigma _{\text {p}}$ with the number of discretization points is observed.

In this entire section on stress distribution and contact areas, the $n = 4$ elastomers could not be considered, because of their peculiar contact mechanics, which makes the determination of the just-investigated properties impossible when contact is partial. However, it is clear that the discrepancies between theoretical prediction and exact results become much accentuated with increasing n for $n > 2$.

5.2 Mean Gap

The mean interfacial separation, or, short, the mean gap, $u_{\text {g}}$, is the other important, scalar quantity, allowing a contact-mechanics theory to be tested. It is the first (unitless) quantity studied in this work, whose dependence on the reduced pressure $p/\varDelta \sigma$ in Persson’s theory does depend on the exponent n. Figure 9 shows that the theory captures this dependence quite well for $0.5 \le n \le 4$ when the correction factors listed in Eq. ( 39) are used. The Einstein foundation is discussed separately, as it suffers from large size effects in $u_{\text {g}}(p^*)$ while allowing for an analytical solution in the thermodynamic limit.

Fig. 9

Mean gap $u_{\text {g}}$ in units of the height standard deviation $h_{\text {std}}$ as a function of the reduced pressure $p/\varDelta \sigma$; a with a logarithmic x-axis and linear y-axis and b with a linear x-axis and a logarithmic y-axis. The data relate to the default surface with a Hurst exponent of $H = 0.8$. Symbols show GFMD data. Solid lines correspond to Persson’s theory using the parameters listed in Eq. (39)

For the most part, relative errors for $0.5 \le n \le 4$ can be said to remain within close to 10% error for $u_{\text {g}}(p)$ at $p\le \varDelta \sigma$ and 20% for $p(u_{\text {g}})$ when $p \ge \varDelta \sigma$. This level of agreement was achieved with the following parameters

$$\gamma _n = {\left\{ \begin{array}{ll} 0.5 &{} {\text { for }} n = 0 \\ 0.45 &{} {\text { for }} n = 0.5 \\ 0.35 &{} {\text { for }} n = 1 \\ 0.2 &{} {\text { for }} n = 2 \\ 0.1 &{} {\text { for }} n = 3 \\ 0.02 &{} {\text { for }} n = 4. \end{array}\right. }$$

(39)

used for $\gamma _n$ throughout this study. These factors were identified to be useful after some trial and error, which is why further optimization might lead to a closer overall agreement between theory and simulation. However, we do not expect changes to be large, as the theory is not exact to begin with and fine tuning adjustable coefficients on one data set often leads to the deterioration of others in that case.

Given the dramatic difference between single-asperity contact mechanics for the different n and given that the theory requires as (dimensionless) input only the height spectrum, the exponent n, and one correction factor for each value of n, we would argue that the accuracy of the predictions is rather impressive. It can even be called surprising, because the prediction of the relative contact area, which enters the calculation of $a_{\text {r}}(p^*)$, is much less convincing than that of $u_{\text {g}}(p^*)$ in particular for $n = 4$, where relative contact areas could not even be determined with simulations. Yet, the agreement between theory and simulation might not be (entirely) fortuitous or it should have only been found for a single exponent n.

To demonstrate the effect that the correction factor $\gamma$ has on the pressure–displacement curve, we compare the results with and without correction factor exemplarily for the exponent $n = 2$ in Fig. 10. Close to zero contact area, the derivative $\partial u / \partial \ln p$ is reduced by a factor of $\gamma$ compared to the original theory in which $\gamma$ had not yet been introduced implying $\gamma \equiv 1$. Close to full contact, the mean gap in the corrected theory is reduced by a factor of $3-2\,\gamma _n$ compared to the original theory. These asymptotic scalings can be readily deduced from Eqs.,(28)–(30).

Fig. 10

Comparison of GFMD results (symbols) for the pressure–displacement relation of the $n=2$ elastomer to the original theory with a correction factor of $\gamma _2 = 0.2$ (solid lines) and without a correction factor ($\gamma _2 = 1$, dashed lines). The main graph a shows the displacement linearly and the pressure logarithmically, while the inset b shows the displacement logarithmically and the pressure linearly

5.2.1 Transferability Test for Correction Factors

A natural question to ask is whether the numerical factors $\gamma _n$, which were crudely optimized on the GFMD data for the default system, see Eq. (39), also apply to other systems. To answer this question, additional sets of simulations were run. These include a change of the Hurst exponent from $H = 0.8$ to $H = 0.3$ and the analysis of the $u_{\text {g}}$ for slabs of finite width, both presented in this section. Moreover, spectra were changed from roll-off to cut-off. Results were positive but are not reported for time reasons. Another issue appeared to be more urgent, namely the analysis of finite-size effects at extremely small stresses. This is an interesting topic in itself, which is discussed in a seperate section in the context of the Einstein foundation.

In all transferability tests, the resolution of the simulations was set to $\varDelta a = \lambda _{\text {s}}/2$ for reasons of computational efficiency, i.e., we abstained from performing systematically continuum corrections. However, $u_{\text {g}}$ is an extremely quickly converging quantity so that the continuum limit of $u_{\text {g}}$ and its estimate obtained at $\varDelta a = \lambda _{\text {s}}/2$ tend to differ by less than one percent.

For the $H = 0.3$ simulations, all parameters were kept unchanged, except, of course, for the Hurst exponent. Figure 11 shows that the quality of the prediction does not deteriorate.

Fig. 11

Mean gap $u_{\text {g}}$ in units of the height standard deviation $h_{\text {std}}$ as a function of the reduced pressure $p^* = p/\varDelta \sigma$. The randomly rough indenter is constructed as the default surface, however, with a Hurst exponent of $H = 0.3$. Symbols show GFMD data. Solid lines correspond to Persson’s theory using the parameters listed in Eq. (39)

In another set of simulations, the thickness t of the semi-infinite solid was reduced from infinity to different finite values. For these simulations, the Hurst exponent was set back to $H = 0.8$. The spectrum was changed from a roll-off to a cut-off spectrum

$$C(q) = C(q_{\text {r}}) (q/q_{\text {r}})^{-2-2H} \, {\Theta }(q-q_{\text {r}})\, {\Theta }(q_{\text {s}}-1),$$

(40)

for reasons that are mentioned in the section on finite-size effects. Moreover, the roll-off domain, or rather cut-off domain, was increased to $L/\lambda _{\text {s}} = 5.12$, while the ratio $\lambda _{\text {r}}/\lambda _{\text {s}}$ remained unchanged (=0.01). The cut-off domain was enlarged compared to the default simulations in order to increase the ratio of $u_{\text {g}}/h_{\text {std}}$, where simulations do not suffer from finite-size effects.

The boundary condition of the finite-width elastomer on the surface opposite to the interface is assumed to be constant stress. In this case, the contact modulus occurring in the expressions for stress and elastic energy for a semi-infinite solid must be multiplied with a prefactor so that

$$E^* \rightarrow \frac{\cosh \left( 2\,{\tilde{t}}\,\right) -2\,{{\tilde{t}}^2}-1}{\sinh (2\,{\tilde{t}}\,) + 2\,{\tilde{t}}} \, E^*,$$

(41)

where ${\tilde{t}} \equiv t\,q$ is the thickness of the three-dimensional $n=1$ elastomer in units of the inverse wave vector 1/q [45]. Thus, the elastomer behaves like a thin sheet for wave vectors $q \ll 1/t$ and bulk-like for $q \gg t$ with a continuous transition between these two limits.

Because of the effective continuous change from $n=1$ at short wave lengths to $n=4$ in at long wave lengths, the correction factor needs to be made a function of thickness so that the two limits are properly reflected. For the data presented in Fig. 12, the relation

$$\gamma ({\tilde{t}}) = \gamma _4 + \left( \gamma _1 - \gamma _4 \right) \, \tanh ({\tilde{t}}/6)$$

(42)

was used, however, it may well be that better switching functions can be designed.

Fig. 12

Mean gap $u_{\text {g}}$ in units of the root-mean square height $h_{\text {std}}$ as a function of the reduced pressure $p^* = p/\varDelta \sigma _{\text {si}}$ for three-dimensional elastomers of infinite width and a width in the range $0.01 \le t/\lambda _{\text {r}} < 0.1$. Here, $\varDelta \sigma _{\text {si}}$ is the stress standard deviation of the three-dimensional, semi-infinite elastic body in full contact. Symbols show GFMD data. Solid lines correspond to Persson’s theory using the parameters listed in Eq. (39)

While Persson’s theory does not reproduce the $u_{\text {g}}(p)$ relation for elastomers of varying thickness quite as convincingly as for the other models presented in this study up to this point, it is still at least semi-quantitative. Yet, at very large pressures, which are not shown explicitly at high resolution, it predicts the $u_{\text {g}}(p)$ dependence similarly well as before. To further improve agreement between theory and simulation, it might also be helpful to modify the $W(a_{\text {r}})$ dependence of Eq. (30).

5.2.2 Einstein Foundation and Finite-Size Effects

The results for the Einstein foundation are presented separately for mainly two reasons. First, the range of $u_{\text {g}}/h_{\text {std}}$, in which size effects are negligible, is somewhat reduced compared to the other elastic bodies, while the sensitivity to the specific random realization is much enhanced. Second, the $u_{\text {g}}(p)$ dependence of the Einstein foundation crosses the data for $n = 0$ and $n = 1/2$ in the shown range of reduced pressures, so that the readability of the pertinent figures deteriorates substantially. Moreover, an exact solution is available for the Einstein foundation in the thermodynamic limit, which makes additional analysis possible.

Before presenting results on the Einstein foundation, it is useful to discuss finite-size effects first. In the thermodynamic limit, that is, for $\varepsilon _{\text {t}} \equiv \lambda _{\text {r}}/L \rightarrow 0$, the height distribution is Gaussian. Consequently, the height difference between highest and lowest point $\varDelta h = h_{\text {max}}-h_{\text {min}}$ diverges. However, this limit is approached so slowly that it is far from being reached in real systems. Typical values for the used height spectrum $\varDelta h(\varepsilon _{\text {t}})$ in units of $h_{\text {std}}$ are $\varDelta h(1/2) \approx 6$ (as in the default model), $\varDelta h(1/8) \approx 8$, $\varDelta h(1/100) \approx 10$, and $\varDelta h(1/1000) \approx 11$. For a pressure, which is just slightly positive, a mean gap of roughly $\varDelta h/2$ can be reached. Figure 13 reveals these expectation to be accurate: deviations between the GFMD data and the exact solution start to matter when the mean gap approaches $\varDelta h/2$.

Fig. 13

Mean gap $u_{\text {g}}$ in units of the height standard deviation $h_{\text {std}}$ as a function of the reduced pressure $p/\varDelta \sigma$ for the Einstein foundation. The solid line represents Persson’s theory, the broken line the exact solution for the Einstein foundation derived in Sect. 4.2. Small squares and large circles represent GFMD results obtained for $L/\lambda _{\text {r}} = 2$ and $L/\lambda _{\text {r}} = 8$, respectively

An additional finding revealed in Fig. 13 is that Persson’s theory does not match the $u_{\text {g}}(p)$ relation of the Einstein foundation for $u_{\text {g}}/h_{\text {std}} \gtrsim 2.5$. Potential reasons are discussed separately in Sect. 6. An obvious concern is that $n>0$ foundation might behave similarly. To check this possibility, additional simulations were conducted for $n = 0.5$ and $n = 1$, in which the following ratios were used: $2 \le L/\lambda _{\text {r}} \le 32$, $\lambda _{\text {r}}/\lambda _{\text {s}} = 128$, and $\lambda _{\text {s}}/\varDelta a = 2$, where $\varDelta a$ is the mesh size. For small pressures, deviations between the new data and the one presented in Fig. 9 remained below symbol size. We conclude that the good agreement between GFMD simulations and theory revealed in Fig. 9 does not arise because of fortuitous error cancelation caused by finite-size effects.

6 Rationalizing the Accuracy of Persson’s Theory

Persson’s theory predicts $u_{\text {g}}(p)$ relations for different elastic counterfaces in an astoundingly accurate fashion, except for the Einstein foundation when $u_{\text {g}}/h_{\text {std}} \gtrsim 2.5$, where the predicted trend is inaccurate. The judgment “astoundingly” is used because results from the GFMD simulations appear to violate central assumptions made in the theory, in particular for large n.

• 1. The derivation of the $u_{\text {g}}(p)$ relation uses the scale-dependent relative contact area as intermediate step, however, in contrast to the final result, the precision of $a_{\text {r}}(p)$ is relatively poor and even qualitatively incorrect for $n > 2$.

• 2. The estimate for how an arbitrary point changes the stress upon adding small-scale roughness is justified for points far away from a contact edge but poor for points close to it. Any system in which contact exists predominantly in small contact patches violates that estimate, for example, for $n \ge 2$ but also for $n = 1$ with $H < 0.5$ [54].

• 3. The theory implicitly assumes that a point dropping out of contact is a point in which the stress has “diffused” continuously to zero upon the addition of small-scale roughness. However, the stress diverges near the contact edge for $n>2$ and discontinuously drops from infinity to zero when contact is lost due to the addition of small-scale roughness.

• 4. The calculation of the elastic energy assumes the displacement field to consist only of undulations with the same wave length as the indenter. However, for $n<1$, the slope of the displacement field is discontinuous at the contact edge. This implies the occurrence of short-wavelength modes whose elastic energy is not accounted for in the theory.

Some of this criticism has been uttered before [32, 37] and even been quantified [32] for regular semi-infinite bodies. However, points 1–3 are accentuated for $n>1$, while point 4 becomes more relevant for $n<1$.

Another reason why the accuracy of the predicted $u_{\text {g}}(p)$ relation is deemed astounding is that the theory is extremely simple, though this may as well be argued to be a reason for why it works so well. One page of text and graduate-level mathematics are sufficient to develop all equations needed in this work from first principles, i.e., from the stress–displacement relation of a single sinusoidal surface undulation, or, alternatively from the Boussinesq solution. The full Hertz solution, a central input ingredient to bearing-area models is much more complicated than that, and it is only the starting point of many more pages of mathematics used even in the simple, original GW model, with even more pages of mathematics in “improvements” of that model, which then do not even produce meaningful mean-gap–displacement relations. Keeping in mind that a randomly rough contact is the superposition of many individual contact patches each of which is much more complex than a Hertzian contact, it seems counterintuitive that a good, approximate solution of an extremely complex problem is simpler than the exact solution of a seemingly simple problem.

So, why does Persson’s theory work so well even when it should not? In the following, two main rationals will be stated, one of which can be used to potentially adjust the theory and to rationalize the correction factor $\gamma _n$, which appears as a drop of bitterness needed to turn the theory from qualitative to (semi-)quantitative. First, the author of this study showed that Persson’s theory is exact for $n=1$ up to at least second order (any surface) and third order (random-phase approximation) in a rigorous field-theoretical approach (cumulant expansion) to contact mechanics, in which the inverse range of repulsive interaction, $\zeta$, was treated as a perturbative parameter and thus as small compared to a height undulation [55]. The treatment presented in there can be easily generalized to arbitrary n by replacing the occurrence of any $qE'$ ($E'$ of Ref. [55] being $E^*$ in this study) to $2q^nk_n$. An interesting aspect of this work is that the formalism could be re-interpreted and re-used for the design of an effective repulsive-zone model. Assuming that the effect of all small-scale roughness has been absorbed into an effective potential, which would turn out as exponential repulsion for sufficiently large separation, including larger-wave-length undulations into the treatment would renormalize that potential and render the repulsion effectively longer ranged. In this procedure, assuming $\zeta$ to be small compared to the (additional) height fluctuation would actually be a meaningful starting point, while this was not well justified in the original work.

Another reason why the theory predicts even the $a_{\text {r}}(p)$ relation reasonably well, i.e., up to corrections logarithmic in p, is that it can be applied with a minor modification to single indenters with harmonic height profiles, for which the random-phase approximation is violated in the worst possible way. The generalization is that the stress variance $\varDelta \sigma$ is evaluated over the true contact rather than over the entire randomly rough surface. This modification is not only successful for said single indenters but also for randomly rough indenters not satisfying the random-phase approximation in contact with a regular semi-infinite, elastic counterface [52]. Thus, assuming $a_{\text {r}} = {\text {erf}}(p/\varDelta \sigma _{\text {c}})$ to hold, it needs to be understood how the true-contact-area stress variance $\varDelta \sigma _{\text {c}}^2$ deviates from the full-surface stress variance $\varDelta \sigma ^2$. Inspection of Fig. 4 reveals that the larger the exponent n, the more do the elastic counterfaces sample local peaks but no local valleys, while counterfaces with a small exponent n do sample local valleys in global (coarse-grained) peaks. This behavior automatically entails a reduction of $\varDelta \sigma _{\text {c}}$ and thereby a reduction of elastic energy compared to configuration forming conformal contact with the indenter, which increases with increasing n.

None of the just-made arguments explains the first item in the list of reasons stated at the beginning of this section for why Persson’s theory should not be accurate. To rationalize this point, the concept of contact area and stress distribution needs to be thought about. Are these properties defined doing a calculation such that the elastomer’s undulations $u({\mathbf {r}})$ are (a) fully resolved or (b) resolved only up to wave vectors which have been considered in the magnification-dependent representation of the randomly rough indenter? In the latter case, Persson’s theory would predict at least the correct order of magnitude for the second moment of the stress distribution function, since the tails of the probability distribution $\Pr (\sigma )$ appear to be quite accurate. In contrast, in the case of (a), any moment of the stress distribution function would be completely off. Thus, interpretation (b) seems to be the correct one, even if it still remains unclear why the $n=3$ gap–pressure relation is obtained so accurately by Persson’s theory (Fig. 14).

Fig. 14

Stress distribution for the $n = 3$ elastomer in contact with the default indenter for different discretizations ranging from $\lambda _{\text {r}}/\varDelta a = 2$ to $\lambda _{\text {r}}/\varDelta a = 64$ (various symbols). Comparison is made to Persson’s theory (solid line) and a $\Pr (\sigma ) \propto 1/\sigma ^{2.6}$ power law (dotted line)

The final result noted in this study pertains to the stress distribution function $\Pr (\sigma )$ points for $n = 3$ and its second moment in the continuum limit. For decreasing mesh sizes, $\Pr (\sigma )$ approaches an algebraic decay according to $\Pr (\sigma ) \propto 1/\sigma ^\beta$ with $\beta \approx 2.6$ (and estimated errors of 0.15) for $n = 3$ and $H = 0.8$. Since $\beta < 3$, the stress variance diverges. This is consistent with the results and the discussion of the second moment of the stress in Sect. 5.

7 Conclusions

In this work, Hertzian and randomly rough indenters in contact with linearly elastic counterfaces were studied using both numerical and analytical methods. The elastic bodies differed in the way how their elastic energy depended on the wave lengths $\lambda$ of surface undulations. In most cases, this dependence was a $\lambda ^{-n}$ power law, with n ranging from $n = 0$ (elastic bodies of infinite spatial dimension) to $n = 4$ (two-dimensional, freely suspended sheets) including $n = 1$, which is representative of regular semi-infinite solids. For both Hertzian and randomly rough indenters, out-of-contact displacement and in-contact stress fields depend smoothly on the exponent n, although critical values for n exist, at which the behavior changes qualitatively. For example, the (compressive) stress near a contact edge approaches zero for $n<2$ but diverges for $n > 2$, while it is positive and finite for $n = 2$. The latter exponent is representative for thin sheets under equi-biaxial tension.

A central result of this study is that Persson’s theory can be easily applied to the contact mechanics of the considered, generalized elastic bodies. The theory predicts the stress distribution function $\Pr (\sigma )$ and thus the relative contact area $a_{\text {r}}$ to depend only on the ratio of pressure p and the root-mean-square stress fluctuation in full contact $\varDelta \sigma$. Green’s function molecular dynamics (GFMD) simulations reveal dependencies of these quantities on n, which, however, are relatively minor for $n \le 2$. Deviations between GFMD and theory worth noting are logarithmic corrections to the predicted linear $a_{\text {r}}(p)$ relation at $p/\varDelta \sigma \ll 1$ and a $\Pr (\sigma ) \propto \sigma ^\beta$ power law dependence for small stress in the case of partial contact, in which the exponent $\beta$ appears as a smooth function of n rather than to assume the predicted constant value of $n = 1$. Despite these shortcomings, Persson’s theory reproduces the dependence of the mean interfacial separation on pressure at least semi-quantitatively, with the exception of the $n = 0$ Einstein (or Winkler or bearing-area) foundation at small pressures. For all other studied exponents in the range $0.5 \le n \le 3$, errors in either $u_{\text {g}}(p)$ at small p or $p(u_{\text {g}})$ at small $u_{\text {g}}$ remain below 20%. This is an astoundingly close and systematic agreement given that the theory is somewhat inaccurate for the $a_{\text {r}}(p)$ dependence, which enters the $u_{\text {g}}(p)$ calculation.

In order to achieve close agreement between theory and simulation, a correction factor needed to be introduced for the calculation of the elastic energy in partial contact. The correction factor, $\gamma _n$, was adjusted as a (smooth) function of n but not on the roughness profiles. For freely suspended elastic sheets of finite thickness t, it has to be made a function of the wave length so that $\gamma (q)$ reflects the semi-infinite and thin-sheet limits meaningfully, i.e., $\gamma (q\ll 1/t) = \gamma _1$ and $\gamma (q\gg 1/t) = \gamma _4$. Doing so allows elastic sheets of finite width to be modeled with a greater precision than before. Discrepancies between theoretical and computed $u_{\text {g}}(p)$ relations at small p no longer have to be hidden by avoiding their appropriate double- or semi-logarithmic representations.

The present work identifies a potential origin of the correction factor $\gamma _n$ used in Persson’s theory and why it decreases with n, the statistics entering the theory, i.e., the root-mean-square height gradient for $n=1$ and related quantities for other n, are not the same in partial contact and in full contact, and the way how true contact samples the roughness of the indenter depends on n. The larger n at fixed relative contact area, the more does the elastic body sample the global minima but only local heights. Consequently, the discrepancy between full averages of central quantities (i.e., root-mean-square height gradient for $n=1$ and related quantities for other n) and averages over partial contact deviate more for small n than for large n.

How can Persson’s theory be modified so that $\varDelta \sigma$ is determined over the true contact and not over the nominal contact? For small n, e.g., for $n \le 1$, it might make sense to argue that $\varDelta \sigma _{\text {c}}$ at a relative contact of $a_{\text {r}}$ should be averaged over the $100\cdot a_{\text {r}}$ highest (or lowest) percentile range of the indenter to determine $\varDelta \sigma _{\text {c}}$ according to Eq. (20). When doing so, the relative contact even at the smallest pressures would be predicted within $O(10\%)$ accuracy, as this version of Persson’s theory predicts the relative contact area of single Hertzian indenters within a few percent. As such, the range of validity of the theory can be further extended and also be applied to systems in which the random-phase approximation does not hold.

How could bearing-area models be modified so that they apply to systems with $n > 0$? The worthlessness of this exercise should become obvious even to a mathematically challenged tribologist, as the assumed topography of the elastic body is that of the $n=0$ curve shown in Fig. 4 no matter how large n. While there have been brave attempts to augment bearing-area models with rigorous boundary-value methods (BVM), they appear to be less accurate but computationally more demanding than a full BVM treatment as revealed, for example, in the contact-mechanics challenge [7]. And who would want to pay more for less?