1 Introduction

Predicting the leakage rate of seals requires the distribution of the interfacial separation between a surface and the seal to be known. This distribution function can only be obtained reliably with accurate contact mechanics models for the surface-seal system accounting for the microscopic roughness of solids. The quantitative description of such contacts can be said to have had three births. Greenwood and Williamson (GW) [1] formulated the problem in 1966 and suggested a solution to it in terms of non-interacting single-asperity contacts. Persson [2] redefined the problem in 2001 by shifting the description and the solution of the contact problem from the real space to Fourier space, which ultimately lead to quite different results than those obtained by GW. Meanwhile, Robbins, who is honored in this issue of Tribology Letters, lead the first efforts to rigorously model numerically the multi-scale nature of roughness [3, 4] and kept spearheading contact mechanics simulations. This gives us the chance to quickly sketch some of Mark’s pioneering contributions to contact mechanics.

Mark understood much better than most of us that modeling is a two-step process: “Reality” is first mapped onto mathematical equations, which then need to be solved, typically by invoking additional approximations to those while formulating the model. He was one of the few who was strong in both steps and who recognized that scrutinizing the validity of the respective approximations is best made separately. For example, in his second work in the field of contact mechanics [4] he analyzed (i) to what extent plastic deformation matters under what circumstances. He identified rules for (ii) the range of validity of continuum theories for small-scale contacts [5] and worked out (iii) criteria for when randomly rough surfaces are (locally) sticky [6]. In other work [7], he found that (iv) stress and contact auto-correlation functions decay proportionally to \(\Delta r^{-(1+H)}\), as predicted by Persson [8], and not with \(\Delta r^{-2\,(1+H)}\), as in bearing-area models like GW. Mark also (v) corroborated that Persson theory finds the correct load–displacement relation for randomly rough surfaces [9]. While it had already been established for moderate load when true contact is spread across the interface [10, 11], Mark contributed to noticing that it also applies—after some refinements—when contact is localized near a single asperity [12]. The just-summarized insights that Mark contributed to the contact mechanics of nominally flat surfaces is but a small fraction of his overall contribution to tribology.

The type of simulations that Mark conducted in his pioneering papers on nominally flat contacts has seen various subsequent works picking up the crumbs that he left over, such as the subject of this study: contact area percolation [13, 14] in randomly rough, mechanical interfaces and the subsequent Reynolds flow through it [11, 15,16,17,18,19].

The description of Reynolds flow in contacts between elastic, isotropic, randomly rough surfaces appears to be well established, at least as long as the surface topographies obey the random-phase approximation [11, 20,21,22,23] but also for plastically deformed surfaces violating it [19, 24]. At small pressures, the fluid conductance disappears extremely quickly with decreasing pressure until the dependence becomes roughly exponential at moderate loads—as has been known experimentally for a long time [25]—before it disappears quickly on approach to the percolation threshold [15, 19]. The exponential regime occurs for relative contact areas \(a_\text{c}\) between a few percent up to close to the relative contact area at the percolation threshold, \(a_\text{c}^*\), which is believed to be \(0.42\pm 0.02\) [11, 15, 19]. While other values have also been proposed for \(a_\text{c}^*\), it seems as if the estimate \(a_\text{c}^* \approx 0.4\) gets approached more closely as more care is taken to simulate meaningful system sizes [14]. Just below \(a_\text{c}^*\), the conductance disappears with a power law in \(a_\text{c} - a_\text{c}^*\) [15, 19], thereby reflecting the way how individual critical constriction close [19, 21, 26].

In contrast to many other percolation problems [27], in which a bond is either on or off, prefactors to leakage rates near \(a_\text{c}^*\) are very sensitive to the detailed geometry of a few last critical constrictions impeding the fluid flow resistance in a continuous fashion [15, 21, 28]. Results obtained experimentally or in large-scale simulations are reproduced quite accurately in terms of effective-medium approaches [11, 23, 29] going back to Bruggeman [30]. Good-quality predictions can also be made with the concept of critical constrictions [21, 28], unless relative contact areas are very small.

In recent works, Persson extended his contact mechanics theory as well as his subsequent Bruggeman and critical constriction approaches to anisotropic roughness [28, 29]. He pursues various approximations to calculate the conductance tensor for anisotropic media, in particular he assumes that (a) the percolation threshold does not depend on the direction in anisotropic surfaces and (b) quantitative measures for the height anisotropy and the conductance anisotropy are similar.

The assumption of an isotropic percolation threshold could be seen as potentially problematic for the following reason: the height profile for a Peklenik number \(\gamma >1\) results from assuming isotropic random roughness on a rectangular \(L/\sqrt{\gamma } \times \sqrt{\gamma } \, L\) domain, which is stretched by a factor of \(\sqrt{\gamma }\) parallel to the x-axis and compressed by the same factor parallel to the y-axis. In the original domain, both contact patches and fluid channels percolate more easily parallel to the shorter edge of the rectangle than to the longer one. After the stretching/compressing transformation, contact patches and fluid channels tend to be stripes for anisotropic domains and percolation should be eased in the direction of stripes. Thus, even if the flow channel topography could be obtained by the same stretching/compression operation that can be used to generate an anisotropic height profile, probabilities to have open or closed channels right at the percolation threshold would be directionally dependent. Superficial contemplation of flow channel geometries in small systems easily reinforces the impression that the critical contact area must be greater in the easy direction than in the compressed direction, see, e.g., Fig. 1. However, the two-dimensional anisotropic bond percolation model [31, 32] exhibits a crossover between one and two-dimensional critical behavior at large system sizes, which should also occur in our systems, even if this remains to be seen. Complications can also arise due to the possibility that the anisotropy of the contact area and thus of the gaps could be larger than that of the original heights, as is the case for elliptical Hertzian indenters [33]. Quantifying the just-described effects does not appear to be a trivial task, which is why we resort to large-scale simulations in this work.

The remainder of this paper is organized as follows: Sect. 2 presents the pursued models, methods, and some theoretical concepts including some addenda to the Bruggeman treatment for isotropic and anisotropic leakage. Section 3 contains the results and their discussion, while final conclusions are drawn in Sect. 4.

2 Model, Methods, Theory

Model, methods, and theory are mostly similar to those used in Refs. [11, 15, 26]. The main difference in the model is that we now also consider anisotropic surfaces and that the used contact mechanics code was optimized in the meantime. In this section, we focus on these up-dates as well as on aspects that might have remained unclear in previous works along with some additions or corrections to existing Bruggeman approaches to leakage.

2.1 Model

We consider an originally flat, linearly elastic body with contact modulus \(E^*\) in contact with a rigid randomly rough indenter on a periodically repeated domain. The height spectrum of the latter obeys the random-phase approximation, i.e., \({\tilde{h}}({\mathbf{q}}) = \sqrt{C(q_\text{P})}\exp (i\,2\pi \,u_{\mathbf{q}})\), where \({\tilde{h}}({\mathbf{q}})\) is the Fourier transform of the height profile, \(u_{\mathbf{q}}\) a linear independent random number drawn on (0, 1), \({\mathbf{q}}\) a wave vector and \(q_\text{P}\) its effective magnitude

$$\begin{aligned} q_\text{P} = \sqrt{\gamma \, q_x^2+q_y^2 / \gamma }. \end{aligned}$$
(1)

Here, \(\gamma \) denotes the so-called Peklenik number [34, 35], whose squared logarithm is a measure for anisotropy. If \(\gamma > 1\), “stretching” occurs parallel to the x-axis, while it is parallel to the y-axis if \(\gamma < 1\). Grooves show up parallel to the stretching direction remotely similar to a situation in which a surface was polished or scratched in that direction.

As default for the height spectrum, a continuous transition between the so-called roll-off regime at small wave vectors and the self-affine scaling at large wave vectors is used [36,37,38,39], specifically

$$\begin{aligned} C(q) \propto \frac{\varTheta (q_\text{s}-q)}{\sqrt{1+(q/q_\text{r})^2}^{\,1+H}}, \end{aligned}$$
(2)

where H is called the Hurst exponent, while \(\varTheta (...)\) is the Heaviside step function, which is unity for positive arguments and zero else. \(q_\text{s}\) and \(q_\text{r}\) are \(2\pi \) over short wavelength cutoff and roll-off wavelength, which are denoted by \(\lambda _\text{s}\) and \(\lambda _\text{r}\), respectively. As default for the height spectrum, \(\varepsilon _\text{t} \equiv \lambda _\text{r}/L = 1/\{4\,{\max (\sqrt{\gamma },1/\sqrt{\gamma })}\}\) and \(\varepsilon _\text{f} \equiv \lambda _\text{s}/\lambda _\text{r} = 1/16\) are used. The discretization is always made small enough to ensure the continuum limit to be closely approached. We chose such relatively small system sizes, as large anisotropy place large demands on the computational resources. More importantly, we ensured that conclusions do not change when the dimensionless numbers \(\varepsilon _\text{t,s}\) are decreased.

The linearly elastic body and the rigid substrate interact through a non-overlap constraint. They are squeezed against each other with a constant pressure p. Once the contact is formed, the interfacial separation is stored and used for further analysis of the Reynolds flow, i.e., we neglect the mechanical pressure exerted by the fluid flow on the contact mechanics. This is certainly a reasonable approximation for leakage problems, all the more the neglected coupling provides only a minor perturbation to the flow factor associated with an individual constriction, while leaving exponents unchanged that define the power laws with which flow approaches zero with increasing load [26].

The gap topography described by the field \(u({\mathbf{r}})\) defines the local fluid conductivity through the equation

$$\begin{aligned} \sigma ({\mathbf{r}}) = \frac{{u^3_\text{g}({\mathbf{r}})}}{12\eta }, \end{aligned}$$
(3)

where \(\eta \) denotes the viscosity of the fluid and \(u_\text{g}({\mathbf{r}})\) is the local interfacial separation, or brief, gap. The such obtained conductivity is then used in Reynolds thin-film equation

$$\begin{aligned} {\mathbf{j}}({\mathbf{r}}) = \sigma ({\mathbf{r}}) \nabla p_f({\mathbf{r}}), \end{aligned}$$
(4)

\( {\mathbf{j}}({\mathbf{r}})\) being the areal current density and \(\nabla p_f({\mathbf{r}})\) the in-plane fluid pressure gradient. Conductances are evaluated parallel to the two principal axes of the simulation cell. Periodic boundary conditions are assumed in the direction normal to the fluid pressure gradient to reduce finite size effects.

Please note that the term roll-off wavelength and the value of \(\lambda _\text{r}\) both refer by default to that of the original, isotropic surface. When adding the clause in the easy direction, we mean \(\lambda _\text{r}\) times \(\max (\sqrt{\gamma },1/\sqrt{\gamma })\). In addition, the stand-alone term pressure refers to the mechanical pressure squeezing the elastomer against the rigid substrate. The fluid pressure has the added clause fluid.

2.2 Methods

The elastic contact problem is solved with Green’s function molecular dynamics (GFMD) [40, 41], which is used in combination with the fast-inertial relaxation algorithm (FIRE) [42] as described elsewhere [43].

The cluster analysis is based on the Hoshen–Kopelman (HK) algorithm [44], which identifies connected contact or non-contact (fluid) clusters. If two nearest neighbors are either both contact or both non-contact they belong to the same cluster. A cluster is called percolating when it extends from one side of the domain to the other. Finally, the Reynolds equations is solved as described in Ref. [26] using the hypre package [45] and the conjugate-gradient minimizer supplied with it.

All simulations and analysis were conducted with house-written codes.

2.3 Theory

Different aspects of the contact mechanics theory by Persson relevant to this study have been described numerous times. Particularly relevant to this study are those works describing how to use the Bruggeman effective-medium approximation [11, 23, 29, 30] using the gap distribution function \(\Pr (u_\text{g})\).

2.3.1 Bruggeman Effective-Medium Approach

The self-consistent equation needed to be solved in order to estimate the conductance \(\sigma _0\) in the Bruggeman formalism reads [29]

$$\begin{aligned} \frac{1}{\sigma _0} = \int \mathrm{d}\sigma \, \Pr (\sigma ) \, \frac{D}{\sigma + \sigma _0\,(D-1)}, \end{aligned}$$
(5)

where \(\sigma \) is the conductivity at a given point, \(\Pr (\sigma )\) is its distribution function, and D the (effective) spatial dimension. In the original treatment, D is taken as the true spatial dimension, i.e., \(D = 2\) for an interfacial leakage problem.

The conductance approaches zero when the probability for zero conductivity exceeds \((D-1)/D\). This result inspired Dapp et al. [11] to use heuristically an effective spatial dimension

$$\begin{aligned} D = \frac{1}{1-a_\text{c}^*} \end{aligned}$$
(6)

in the Bruggeman effective-medium approach. In a similar spirit, Persson generalized Eq. (5) to

$$\begin{aligned} \frac{1}{\sigma _{x,y}} = \int \mathrm{d}\sigma \, \Pr (\sigma ) \, \frac{D-1 + {\tilde{\gamma }}^{\pm 1} }{\sigma + \sigma _{x,y} \,(D-1)\,{\tilde{\gamma }}^{\pm 1}} \end{aligned}$$
(7)

with

$$\begin{aligned} {\tilde{\gamma }} = \gamma \sqrt{\sigma _y/\sigma _x} \end{aligned}$$
(8)

for anisotropic media characterized by \(\gamma \ne 1\). One flaw of Eq. (7) is that it predicts different flows in x and y-direction when the entire contact is assigned the same microscopic conductivity when \(D \ne 2\) is used, i.e., if \(\Pr (\sigma ) = \delta (\sigma -\sigma _0)\). To fix this, we modified Eq. (7) to

$$\begin{aligned} \frac{1}{\sigma _{x,y}} = \int \mathrm{d}\sigma \, \Pr (\sigma ) \, \frac{1 + (D-1)\,{\tilde{\gamma }}^{\pm 1} }{\sigma + \sigma _{x,y} \,(D-1)\,{\tilde{\gamma }}^{\pm 1}}. \end{aligned}$$
(9)

As another consequence of our correction, the ratio \(\sigma _x/\sigma _y\) now approaches \(\gamma ^2\) for \(a_\text{c} \rightarrow a_\text{c}^*\) as is the case in the anisotropic Bruggeman solution using \(D = 2\), as well as in the critical constriction approach.

2.3.2 Addendum to the Bruggeman Approach on Isotropic Media

Persson theory allows the relative contact area and the average gap \({\bar{u}}_\text{g}\) to be estimated as a function of pressure [9,10,11, 46], even for generalized elastomers such as thin sheets or elastomers with gradient elasticity [47] much more easily than the gap distribution function. The question arises if simple order-of-magnitude estimates for the fluid conductance can be obtained using only \({\bar{u}}_\text{g}\) and the relative contact area. To achieve that, we rewrite Eq. (5) as

$$\begin{aligned} \frac{1}{\sigma _0} = \frac{D\,a_\text{r}}{ \sigma _0\,(D-1)} + \frac{D\,(1-a_\text{r})}{\sigma _\text{nc} + \sigma _0\,(D-1)}, \end{aligned}$$
(10)

where the characteristic non-contact conductivity \(\sigma _\text{nc}\) is defined through

$$\begin{aligned} \frac{1}{\sigma _\text{nc} + \sigma _0\,(D-1)} = \left\langle \frac{1}{\sigma + \sigma _0\,(D-1)}, \right\rangle _\text{nc} \end{aligned}$$
(11)

whose calculation necessitates knowledge of \(\sigma _0\). Here, \(\langle ... \rangle _\text{nc}\) indicates an average over non-contact.

Keeping \(\sigma _\text{nc}\) formally (although it still needs to be determined later), Eq. (10) can be solved for \(\sigma _0\) to yield

$$\begin{aligned} \sigma _0= & {} \sigma _\text{nc}\, \left( 1 - a_\text{c}/a_\text{c}^*\right) , \end{aligned}$$
(12)

which, after insertion into Equation (11), leads to the following self-consistent equation for \(\sigma _\text{nc}\):

$$\begin{aligned} \frac{1}{\sigma _\text{nc}} = \lim _{\sigma _\text{min}\rightarrow 0^+} \int _{\sigma _\text{min}}^\infty \!\mathrm{d}\sigma \, \Pr (\sigma )\, \frac{1+\Delta {\tilde{a}}}{\sigma + \sigma _\text{nc}\Delta {\tilde{a}}} \end{aligned}$$
(13)

with \(\Delta {\tilde{a}} \equiv (a_\text{c}^*-a_\text{c})/(1-a_\text{c}^*)\).

Since \(\sigma _\text{nc}\) cannot diverge but only be finite or approach zero as a tends to \(a_\text{c}^*\), \(\sigma _0\) is predicted to disappear linearly or even faster with decreasing distance from the percolation threshold.

The power law, with which \(\sigma \) disappears as \(a_\text{r}^*\) is approached, depends on the shape of the gap distribution function \(\Pr (u)\), from which the conductivity distribution function follows via \(\Pr (\sigma ) = (u^2/4\eta )\,\Pr (u)\). This is best discussed by approximating the gap distribution function at small u (which is decisive for whether or not the relevant integrals converge) with \(\Pr (u) \propto u^\mu \). For \(\mu >0\), \(\sigma _\text{nc}(a_\text{c}^*)\) is easily shown to remain positive no matter how closely the lower integration bound \(\sigma _\text{min}\) approaches zero, while a positive exponent \(\mu \) leads to an algebraic disappearance \(\sigma _\text{nc}(a_\text{c}^*)\) in \(\sigma _\text{min}\) for \(u \rightarrow 0^+\). For \(\mu = 0\), the disappearance is only logarithmic.

In the case of short-range adhesion, adhesive necks form with an infinite slope of the gap at the contact line, which effectively induces \(\mu > 0\). A linear dependence between \(\sigma _0\) and \(\Delta a' \equiv 1 - a_\text{c}/a_\text{c}^*\) follows, as observed in simulations using short-range adhesion [15, 26]. A faster than linear power law disappearance of \(\sigma _0\) in \(\Delta {a}'\) is predicted for repulsive contacts for which \(\mu < 0\). This is again consistent with previous simulations [15, 26] finding \(\sigma _0 \propto \Delta {a'}^\beta \) with \(\beta = 69/20\). Finally bearing-area models implicitly assume \(\mu = 0\) so that logarithmic corrections would apply to the \(\sigma _0 \propto \Delta a'\) proportionality. Although the critical behavior was not analyzed in detail, this is again consistent with the observation that the conductance disappears substantially more slowly with increasing contact area for overlap models than for true elastic contacts [11].

To account heuristically for any observed \(\sigma _0 \propto \Delta {a'}^\beta \) dependence, we propose to use

$$\begin{aligned} \sigma _\text{nc} = \frac{{\bar{u}}_\text{g}^3}{12\,\eta \,} \,f(a_\text{c}), \end{aligned}$$
(14)

where \(f(a_\text{c})\) is a correction function, or, depending on context or viewpoint also a “fudge-factor” function, into which correct criticality can be encoded by choosing it as

$$\begin{aligned} f(a_\text{c}) = f_0 \, \left( 1 - a_\text{c}/a_\text{c}^*\right) ^{\beta -1}, \end{aligned}$$
(15)

where \(f_0\) should be of order unity. A summary of the expected conductance reads,

$$\begin{aligned} \sigma \approx \frac{{\bar{u}}_\text{g}^3}{12\,\eta } \times {\left\{ \begin{array}{ll} \Delta {a'}^{69/20} &{} \text{regular contacts} \\ \Delta {a'} &{} \text{short-range adhesion} \\ \frac{\Delta {a'}}{1-\ln \Delta {a'}} &{} \text{bearing-area models,} \end{array}\right. } \end{aligned}$$
(16)

in which the prefactor \(f_0\) (and in the case of the bearing model an additive constant) was selected such that \(\sigma \) assumes a value of a \({{\bar{u}}_\text{g}^3}/{12\,\eta }\) at zero contact area, while the finite-contact area correction factor makes the conductance disappear with the correct power law as \(a_\text{c}^*\) is approach, as deduced from the scaling of \(\Pr (u_\text{g})\) in the limit of \(u_\text{g} \rightarrow 0^+\).

2.3.3 Critical Constriction Approach

The critical constriction approach to the leakage rate of seals was introduced in Refs. [20, 21] and extended to anisotropic roughness recently [28]. The theory is based on the idea that fluid flow at contact areas close to the percolation threshold is impeded by a random distribution of narrow constrictions through which the fluid has to be squeezed and that the dominant part of the fluid pressure falls off at these constrictions. In an interface, the number of such constrictions per unit length in x and y-direction scales as \(L_x / \sqrt{\gamma }\) and \(\sqrt{\gamma }\,L_y\), respectively. In a percolating channel, fluid flows through some narrow constrictions with random directions. Even in the case of anisotropy, the flow in a macroscopically large system has to go occasionally through a constriction in which the flow direction is perpendicular to the easy flow direction.

For \(\gamma = 1\) and \(L_x = L_y\), there are as many critical constriction in the x-direction as in the y-direction so that an equivalent circuit diagram of the fluid flow consists of a single critical constriction. This allows one to focus on just a single characteristic constriction and the question how it impedes fluid flow as a function of the geometry of this constriction. We refer to the original literature [20, 21] for how to estimate its geometry theoretically and thus its resistance to fluid flow.

3 Results

3.1 Preliminary Considerations

To set the stage for further discussion, flow channels for an isotropic but rectangular \((0.5\times 2)\) domain of a unit area are compared to those in a square, anisotropic domain, which is obtained from the former by scaling the x-direction with \(\sqrt{\gamma } = 2\) and the y-direction with \(1/\sqrt{\gamma }\). This comparison is made in Fig. 1, which shows the height profile in panel (a) and contrasts the points of finite conductivity at a relative contact area of \(a_\text{c} = 0.4\) for the isotropic and anisotropic surface in panels (b) and (c), respectively. The original, rectangular domain is characterized by \(H = 0.8\), \(L_x = 0.5\), \(L_y = 2\), \(\lambda _\text{r} = 0.25\), and \(\lambda _\text{s} = 0.025\). Both surfaces are at \(39.8\pm 0.1\)% relative contact area.

Fig. 1
figure 1

a Height profiles of an isotropic (\(\gamma = 1\), \(L_x = 0.5\), \(L_y = 2\)) and an anisotropic (\(\gamma = 4\), \(L_x = L_y = 1\)) unit area surface, which is periodically repeated in the y-direction. Fluid channels (blue) and contact areas (orange) of the shown b isotropic and c anisotropic surface at \(a_\text{c} \approx 0.4\). Fluid channels percolating from left to right are represented in dark blue, other non-contact in light blue. Note that the x and y-direction are not to scale for the isotropic surface, which makes it appear anisotropic to the eye. The height in panel (a) is stated in units of the maximum height (color figure online)

Full size image

The expectation that stretching cannot change the percolation threshold, because the flow channel topology remains the same before and after the stretching/compression operation [28] is not fully supported in the simulations. Although changes in the height profiles (not shown) are relatively minor, the fluid-channel topographies—and even topologies—shown in panels (b) and (c) of Fig. 1 differ between the original and the stretched surfaces. New percolating flow channels and percolating contact patches can open up after the stretching operation, while others disappear or merge. Both flow channels and contact patches of the elastic contact are even more stretched than the height profile. A related elongation of contact patches also occurs in isolated Hertzian contacts with elliptical indenters [33].

A superficial contemplation of just this one random realization depicted in Fig. 1 can easily convey the impression that an elastic contact characterized by the dimensionless numbers \(H = 0.8\), \(\gamma = 4\), and \(a_\text{c} = 0.4\) should percolate parallel to the stretching direction but not parallel to the orthogonal direction, even if the ratio of linear dimension and \(\lambda _\text{r}\) were larger than in the just-investigated example. However, a numerical analysis and finite size scaling (\(\varepsilon _\text{t} \rightarrow 0\)) is required to test the validity of this expectation.

3.2 Percolation Threshold

In this section, we investigate how different dimensionless numbers characterizing the surface topography affect the percolation threshold. Toward this end, ten independent random realizations were typically set up to determine the order of magnitude of the stochastic error bars. Figure 2a reveals that the percolation thresholds \(a_\text{r}^*\) along the two principal directions do not depend strongly on the ratio \(\varepsilon _\mathrm{f} \equiv \lambda _\mathrm{s}/\lambda _\mathrm{r}\), i.e., increasing it by a factor of 4 from 16 to 64 only has a relatively minor effect, which is clearly less than the stochastic error bar for \(\gamma \) close to unity.

Fig. 2
figure 2

Critical contact areas \(a_\text{c}^*\) in the stretching (blue) and contraction (red) directions as a function of the Peklenik number \(\gamma \). a Elastic contact with two different ratios of \(\varepsilon _\text{f} = \lambda _\text{s}/\lambda _\text{r}\) and b bearing-area contact with \(\varepsilon _\text{f} = 1/16\). All cases correspond to \(H = 0.8\) and \(L/\lambda _\text{r} = 4/\sqrt{\gamma }\) (color figure online)

Full size image

An interesting feature revealed in Fig. 2a is that the difference between the critical contact areas in the easy and the compression direction increases with increasing anisotropy, although the system size kept being increased proportionally to \({\max (1/\sqrt{\gamma },\sqrt{\gamma })}\). To test if this trend can be explained by the observation that the gap does not transform in the same self-affine fashion as the height, we also computed \(a^*_\text{r}\) along the two principal directions for a bearing model, in which stretching and compressing is an affine transformation. In bearing-area models, contact is implicitly assumed to occur above a given substrate height and non-contact, i.e., open fluid flow channels, below it. Fig. 2b reveals that the growth of asymmetry of the critical contact areas with increasing \(\gamma \) is similar for the bearing-area model as in the full elastic calculation. At moderate \(\gamma \), the main difference between the two is a shift of \(a_\text{c}^*(\gamma = 1) \approx 0.4\) in the elastic model to \(a_\text{c}^*(\gamma = 1) = 0.5\) in the bearing model.

Although the system size was increased proportionally to the square root of the (inverse) Peklenik number for the analysis presented in Fig. 2, the possibility remains that a further increase in system size suppresses the observed anisotropy in \(a_\text{c}^*\). This expectation is confirmed in Fig. 3, which shows that a unique percolation threshold of \(a_\text{c}^* {\approx 0.415 \pm 0.01}\) is approached for the investigated system with size corrections that are close-to-linear power laws in \(\varepsilon _\text{t}\).

Fig. 3
figure 3

Size dependence of \(a_\text{c}^*\) in the stretching (blue) and the contraction (red) directions for a system with a Hurst exponent \(H = 0.8\). Circles indicate constant \(\gamma = 2\) and varying \(L/\lambda _\text{r}\) ratios, while triangles assume a fixed ratio \(L/\lambda _\text{r} = 32\) but varying \(\gamma \). Black crosses show data for isotropic surfaces. Lines are fits according to \(a_\text{c}^*(\varepsilon _\text{c}) - a_\text{c}^* \propto \varepsilon ^{1/\nu }\) with the random bond percolation model exponent \(\nu = 4/3\) (color figure online)

Full size image

The size scaling revealed in Fig. 3 is consistent with results for regular random bond percolation models. Its correlation length \(\xi \) increases as \(\xi \propto 1/\vert a_\text{c} - a\vert ^\nu \) and an exponent of \(\nu = 4/3\) for an interfacial dimension of \(D = 2\) [48]. Thus, channels are expected to percolate along the easy direction at a finite size when \(\xi \approx \sqrt{\gamma }\, L\) so that the size-dependent corrections of the relative contact area, \(a^*_\text{c} - a^*\) satisfy

$$\begin{aligned} \sqrt{\gamma } L \propto \left| a^*_\text{c} - a^*_\text{c}(L) \right| ^{-\nu }, \end{aligned}$$
(17)

which yields a size correction to \(a^*_\text{c}\) of order \(L^{-1/\nu }\). Renormalization group theory arguments would then indicate that the exponents describing size directions for the easy flow direction and the contraction direction must be identical; however, the corrections must have opposite signs and may differ in magnitude.

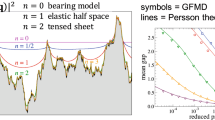
It is currently not clear to us why the exponent \(\nu \) are the same or at least close for the considered elastic contact problem and the regular bond percolation model, as there is no reason why percolation in elastic contacts should be in the same universality class as random bond percolation. In fact, the so-called Fisher exponent for the cluster-size distribution differs between them. It turns out \(\tau = 187/92 \approx 2\) for regular bond percolation [48] but \(\tau \approx 2 - H/2\) for the contact patch-size distribution in repulsive, elastic contacts [49] (Fig. 4). Finally we note that the way how \(a_\text{c}^*\) depends on \(\gamma \) does not appear to depend qualitatively on the Hurst exponent. This is revealed in Fig. 4. Moreover, estimates for the percolation threshold are identical for \(H = 0.3\) and \(H = 0.4\) within stochastic error bars in the limit of isotropy.

Fig. 4
figure 4

Critical contact areas \(a_\text{c}^*\) as a function of the Peklenik number \(\gamma \) for system sizes \(L = \lambda _\text{r}/\sqrt{\gamma }\) and \(\varepsilon _\text{f} = 1/16\) for \(H = 0.3\) (full triangles) and \(H = 0.8\) (open circles) (color figure online)

Full size image

3.3 Reynolds Flow

We start this section with the analysis of the Reynolds flow in isotropic contacts. It has already been demonstrated earlier [11, 15] that the Bruggeman effective-medium theory allows the “exact” Reynolds fluid conductance to be predicted quite accurately. In this paper, we test the validity of the closed-form analytical expressions proposed for the isotropic conductance, which are summarized in Eq. (16). In order to automatically yield good statistics, the system size was increased from its default size to \(L/\lambda _\text{r} = 16\), while the ratio \(\lambda _\text{r}/\lambda _\text{s} = 16\) was kept as before. Figure 5 reveals that the analytical approximations to the full Bruggeman theory are quite reasonable. Relative deviations from either the numerically accurate solution of the full Reynolds problem or the exact solution generally remain around 20% in the shown domains, except for the adhesive case, where the full and the approximate Bruggeman approach differed by a factor of two close to the percolation threshold.

Fig. 5
figure 5

Fluid flow conductance \(\sigma \) as a function of the relative contact area as obtained in full Reynolds calculation (circles). Comparison is made to full Bruggeman effective-medium treatments (full lines) as well as to the approximations (dashed lines) proposed in Eq. (16) for different contact models or treatments, i.e., a regular, elastic, non-adhesive contact, b short-range adhesive contact, and c bearing-area model. In the case of (a), comparison is also made to a full Bruggeman treatment assuming the critical contact area to be \(a_\text{c}^* = 0.5\), while the other lines in a, b are based on \(a_\text{c}^* = 0.4\) The conductance is normalized to the same reference conductance \(\sigma _\text{ref}\), which is the one obtained in the full Reynolds treatment at a relative contact area \(a_\text{c} = 0^+\)

Full size image

A comparison between exact Reynolds and full as well as approximate Bruggeman theory for adhesive interfaces is shown in Fig. 5b. Strength and range of adhesion were chosen such that they lead to a non-negligible enhancement of local contact area, i.e., at zero load we observed 1% “spontaneous” relative contact area and to induce a relative contact area of 10% (40%) only 1/8 (1/4) of the force was required as for its non-adhesive analog. In more detail, the local Tabor parameter, as defined in Ref. [50], was set to \(\mu _\text{T} = 2\), while the reduced surface energy, using the so-called Pastewka–Robbins parameter, see Eq. (16) in Ref. [50], was \(\gamma _\text{PR} = 0.135\). Thus, no (local) stickiness can be expected despite the relatively large contact area enhancement. Also the ratio of surface energy \(\gamma \) and the elastic energy per unit surface needed to bring the two surfaces into the contact, \(v_\text{ela}^\text{full}\), was well below unity, namely \(\gamma /v_\text{ela}^\text{full} = 0.203\) further supporting the absence of hysteresis. In fact, there is a roughly constant, mere 10% adhesion-induced reduction of the mean gap as a function of pressure in the studied range of forces but no signs of significant hysteresis. Thus, we would call the adhesion “intermediate”, i.e., strong enough to substantially increase the relative contact area but not so large as to induce a noticeable load–displacement hysteresis.

While the proposed dependence of conductance on mean gap and relative contact area summarized in Eq. (16) worked well for all case studies performed for this study, it should be clear that estimates can be rough close to the percolation threshold. This is because any short- but finite-range adhesion crosses over to \(\sigma \propto \Delta {a'}^{69/20}\) as the true percolation is approached, see also Fig. 5 in Ref. [15]. Likewise, if we had used very weak but zero-ranged adhesion, the trend might reverse, i.e., the conductance could be proportional to \(\Delta {a'}^{69/20}\) close but not too close to the percolation threshold but obey \(\sigma \propto \Delta {a'}\) in the immediate vicinity of the percolation threshold. Thus, to be on the safe side, we recommend doing a full Bruggeman analysis (if possible), while its closed-form approximation can only provide crude estimates for the conductance if the relative importance of adhesion is difficult to ascertain.

The last analysis of this work concerns the fluid conductance for anisotropic surfaces for a system described by a Peklenik number of \(\gamma = {2}\). Figure 6 reveals that the generalization of the Bruggeman treatment for anisotropic elastic contacts conveys correct trends but shows a slightly weaker agreement with the full Reynolds calculations than for the non-adhesive, isotropic contacts.

Fig. 6
figure 6

Fluid conductance \(\sigma \) in the stretching (easy) direction (blue) and the contraction direction (red) for a system described by a Peklenik number of \(\gamma = 2\) and \(L = 16\,\sqrt{\gamma }\,\lambda _\text{r}\). Results of a full Reynolds description are shown as symbols, while predictions based on Eq. (9) are shown in solid lines. The gray dotted line is obtained using the Bruggeman approach for isotropic surfaces (color figure online)

Full size image

A quantitative analysis of the conductances reveals a ratio of \(\chi \equiv \sigma _x/\sigma _y = 8\), which is twice the theoretically expected number \(\chi = \gamma ^2\) using the height Peklenik number (\(\gamma = 2\)) to quantify the conductance anisotropy. A certain discrepancy from the theoretical expectation remains when using instead the conductance Peklenik number of \(\gamma _\sigma \approx {2.5}\), which we deduced from the direction-dependent conductivity auto-correlation function (not shown). Thus using “true” conductivity Peklenik numbers leads to a predicted ratio of \(\chi \approx 6.25\), which reduces the error between exact Reynolds calculations (\(\chi \approx 8\)) and effective Bruggeman (\(\chi = 4\)) theory only by a little more than a factor of two.

To investigate the origin of the relatively large discrepancy between the exact Reynolds flow and the effective-medium results for elastic contacts, we also considered anisotropic bearing contacts, where conductivity and height anisotropy are similar by design. The results shown in Fig. 7 reveal a similarly close resemblance of the approximate solutions and the numerically exact results as for isotropic, non-adhesive, elastic contacts. This time, the ratio \(\sigma _x/\sigma _y\) turns out a little less than \(\gamma ^2\). However, the deviation is within the typical stochastic noise for the used system size.

Fig. 7
figure 7

Similar to Fig. 6 but for a bearing-area contact (color figure online)

Full size image

4 Summary and Conclusions

In this work, we found that the relative contact area at which fluid channels no longer percolate across a sufficiently large system is \(a_\text{c}^* ={0.415 \pm 0.01}\) and that this value also holds for surfaces with anisotropic random roughness. This confirms Persson’s conjecture that elastic anisotropic contacts have a percolation threshold, which does not depend on the direction. However, requirements on what is called “sufficiently large” are the more stringent the greater the anisotropy. In addition, quantitative measures for anisotropy, such as the Peklenik number, turn out larger for the fluid conductivity than for the height of the randomly rough indenter, at least within linearly elastic contact mechanics. For bearing models, both yield similar Peklenik numbers.

We also proposed a simplification as well as a minor correction to the Bruggeman effective-medium theory, which had been worked out by Persson for the description of leakage in mechanical (elastic) contacts. First, for isotropic contacts, we proposed quite simple, closed-form expressions for the fluid flow conductance in isotropic contacts, which necessitates only knowledge of the mean gap and the relative contact area as well as the type of contact (repulsive versus adhesive or in the odd case bearing-area contact) but it does not need as input the entire gap distribution function. Second, we corrected the way in which an effective dimension is used in the Bruggeman approach to anisotropic roughness in order to enforce the correct percolation threshold. Both addenda to previous treatments were supported to our satisfaction by full Reynolds simulations.

Finally, Persson’s adaptation of the effective-medium theory to describe direction-dependent conductances for anisotropic media works very well for bearing-area contacts, for which (a) the height- and conductance Peklenik numbers are identical and (b) the percolation threshold assumes the canonical value of \(a_\text{c}^* = 1/2\). However, the generalization to anisotropic, elastic contacts is not quite as satisfactory. It may well be that the way in which the correct percolation threshold is “enforced” for elastic contacts through the use of an effective interfacial dimensions, see Eq. (9), can be further improved. Nonetheless, we find the approximate solution astoundingly good in all cases given the simplicity of the effective-medium theory and the numerical complexity of a full Reynolds calculation.