Abstract
We investigate the underlying tribological mechanisms and running-in process of a semi-crystalline polymer using molecular-dynamics simulations. We subject a slab of simulated polyvinyl alcohol to a sliding contact asperity resembling a friction force microscope tip. We study the viscoelastic response of the polymer to the sliding and show both plastic and elastic contributions to the deformation, with their relative strength dependent on the temperature. As expected, the elastic deformation penetrates deeper into the surface than the plastic deformation. Directly under the tip, the polymer has a tendency to co-axially align and form a layered structure. Over time, the plastic deformation on and near the surface builds up, the friction decreases, and the polymers in the top layer align with each other in the sliding direction (conditioning).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Many of the objects surrounding us are made of polymers. The friction that we experience while walking on our shoes with rubber soles or the wear of the soles are macroscopic properties. This scale has been studied widely for obvious practical reasons and there are many non-trivial effects in friction and wear specific to polymers, such as non-linearities and non-trivial temperature dependence. The origin of many of those macroscopic effects can be found at smaller scale, especially the molecular scale. Studying the contact at this nanoscale can thus provide better understanding of the underlying tribological mechanisms leading to friction and wear on the macro-scale.
The past few decades have seen rapid nanoscale developments of experimental techniques such as friction force microscopy (FFM). This technique gives accurate measurement of surface properties and frictional behavior of a single asperity, and enables to some extent speculation about what is happening below the contact, see [1]. FFM experiments on polymers have already shown that molecular chain reorientation, due to displacement or rotation of a chain segment or a side group (relaxation), occurs during sliding [8, 10, 17]. This restructuring has an influence on the friction. Not surprisingly, in polymers the biggest changes in tribological properties in experiments occur at the same temperature where the polymer’s bulk mechanical properties also change drastically, the glass transition temperature \(T_{\text{g}}\).
Currently, theoretical understanding of the frictional behavior of polymers is still lacking. As a result, the development of novel low friction solid polymer materials can only be achieved through expensive testing. Nevertheless, tools for theoretically investigating this problem at the nanoscale exist: molecular-dynamics (MD) simulations. Massive MD simulations of this problem are however extremely challenging, due to the high level of complexity of both the material and friction phenomena. There is a large elastic response, but also plastic deformation and permanent damage. Polymers form semi-crystalline structures, with both crystalline and amorphous domains that may change during sliding. The simplest limit of this semi-crystalline structuring is the ideal, but unrealistic, single crystal, and this has been investigated numerically by Heo et al. [7]. It has also been shown that the structure of the polymers changes near the tip as a result of the high stresses during indentation and sliding [16].
The aim of the present study is to improve our understanding of polymer friction and wear, especially in relation to the structure in semi-crystalline polymers. We perform MD simulations that are designed to model an FFM experiment on polyvinyl alcohol (PVA), a commonly used prototype polymeric material. This approach allows us to investigate in detail what happens to the individual chains and monomers, something that is not possible in heavily coarse-grained finite element simulations or real experiments.
2 Simulation Setup
We simulate an FFM experiment by rubbing a model atomic force microscope (AFM) tip against a polymer surface. The molecular-dynamics software LAMMPS [14] is used to calculate particle motions via a coarse-grained model, see [11, 18]. In this study, we used the coarse-grained model for PVA (CG-PVA) developed by Meyer and Muller-Plathe [12].
Each simulation contains 200,000 coarse-grained monomers for the substrate and around 25,000 particles for the tip. The radius of the tip is \(4.68\,{\text{nm}}\). The atoms of the tip are arranged in a fcc configuration with a lattice spacing of \(2.08\,{\text{nm}}\). They are kept that way during the entire simulations. The tip is a rigid body. The lowest atoms (last row) are removed in order to create a flat contact surface. The melt relaxation, cooling, indentation and sliding take roughly 15000 CPU-hours for a simulation of 8 ns with a time-step of \({8\times 10^{-16}\,{\text{s}}}\).
2.1 Coarse-Grained Model
The coarse-grained model replaces a group of atoms by one coarse-grained particle while assuring that the overall structural characteristic of the polymer is preserved. In the coarse-grained model we use, this is done by assigning suitable bond, pair and angular potentials, Fig. 1.
The interactions between monomers consist of bonded and non-bonded contributions. Below, we express all quantities in terms of Lennard–Jones units, with \(\epsilon _{0}=7.6\times 10^{-21}\,{\text{J}},\tau _{0}=1.6\times 10^{-12}\,{\text{s}},\sigma _{0}=0.52\,{\text{nm}}\).
Our simulation box is 42 nm in the sliding direction. During our simulation, the tip passes over the same point around 5–10 times (Fig. 2).
The bonded interactions are between monomers in a chain, and the potential energy is a sum of stretching and bending contributions. The stretching of a bond is described by a harmonic potential \(V_{\text{bond}}=K(r-r_{0})^{2}\) where K characterizes the stiffness of a spring (\(K=1352\epsilon _{0}/\sigma _{0}\)), and \(r_{0}=0.5\sigma _{0}\) is the equilibrium bond length. To account for possible bond-breaking, this interaction is replaced by a Morse potential during the sliding simulations, \(V_{\text{bond}}=D[1-e^{-\alpha (r-r_{0})}]^{2}\), where \(D=95\epsilon _{0}\) determines the depth of the potential well (the bond energy), \(\alpha =3.77/\sigma _{0}\) is a stiffness parameter and \(r_{0}=0.5\sigma _{0}\) is the equilibrium bond distance. These values were chosen to preserve the equilibrium bond length and the second derivative in the minimum. The bending potential is approximated by an angular potential which is provided in table format. Because each monomer contains several carbon atoms, it accounts also for the torsion stiffness.
The non-bonded interaction is given by a Lennard–Jones 9–6 potential \(V_{\text{pair}}(r)=4\epsilon [(\frac{\sigma }{r})^{9}-(\frac{\sigma }{r})^{6})]\), where \(\epsilon =0.38\epsilon _{0}\) is the depth potential, \(\sigma =0.89\sigma _{0}\) is the distance at which the potential vanishes, and r is the distance between the monomers.
2.2 Melt Relaxation and Cooling
In order to obtain a realistic surface for our simulations, we start from a polymer melt and cool it down. Our simulation box is periodic in x and y, but confined by impenetrable hard walls in the z direction.
We generate physical initial conditions for the melt using the DPD-push-off method [15] which is designed to efficiently obtain equilibrated polymer melts. In this approach, we start from non-physical random overlapping initial conditions and a non-physical soft hybrid interaction potential. This potential consists of a 12–6 Lennard–Jones potential for the non-bonded interactions and a spring potential for the bonded interactions. After this system is equilibrated for 0.25 ns using the DPD-push-off protocol, the non-physical soft hybrid potential is replaced by the realistic coarse-grained PVA potential described above. The system is no longer in equilibrium for the PVA potential, so it is equilibrated again for another 0.25 ns. At this point, the melt is still unphysically hot, around 5000 K. The melt is coupled to a Nosé–Hoover thermostat at 520 K, slightly above the glass transition temperature, and time scale of 1 in LJ units. The system is then equilibrated for 4 ns at which point we have a physical and properly equilibrated melt at 520 K. We confirm this by checking that the radius of gyration is stable.
Next, the temperature is gradually decreased to 220 K with a cooling rate of 75 K/ns. We vary the cooling rate to obtain different structural properties.
2.3 Crystallinity
The crystallinity level is calculated at various stages during the simulation. The method to calculate the crystallinity is called Individual Chain Crystallinity, see [19]. We define this quantity as the ratio between the number of aligned bonds and the total number of bonds in our coarse-grained force field. For every bond we calculate the bond vector \({\mathbf{b}}_{i}\) and a directional vector made of the average of the ten neighboring bonds, \({\mathbf{d}}_{i}\). If the normalized scalar product of those two quantities is higher than 0.95 (18.2°), the bond is considered as aligned, i.e., a bond is deemed straight if
2.4 Sliding
Once we have obtained a simulation of a physical polymer surface, we perform indentation and sliding simulations using a simulated AFM tip. The tip is represented by a hemispherical rigid body consisting of a rigid fcc arrangement of the same PVA monomers, see Fig. 3. The interaction between tip particles and the monomers is given by the same non-bonded pair potential as the monomer–monomer interaction. A constant load is applied to the tip in the z direction. The center of mass of the tip is tethered to a support using a harmonic springs in the x and y directions with spring constant \(17.8\,\epsilon _{0}/\sigma _{0}^{2}\). During sliding, the support moves at a constant velocity in the x direction of 15 m/s. The force \(F_{\text{lat}}(t)\) needed to keep the support moving at constant velocity corresponds to the lateral force in an FFM experiment, and its average gives the friction.
To prevent the substrate from moving with the tip, the centers of mass of the chains in the lower quarter of the substrate are tethered to their original positions using springs with spring constant \(\epsilon _{0}/\sigma _{0}^{2}\). A Langevin thermostat with decay time \(1000\,\tau _{0}\) is also applied to these chains and set to the appropriate temperature for each simulation.
2.5 Collecting Statistics
In order to collect enough statistics to understand what is happening around the tip during sliding, we investigate averaged quantities in a frame that move with the tip so that the tip is always at the origin. The simulation box is divided into a grid that moves with the tip. For any given time and for each individual bin, the properties of the atoms present within the bin are recorded and averaged. We note that as the tip moves, the atoms enter and leave the co-moving bins. In the cases where we investigate the displacement over finite times, we assign the entire displacement to the atom’s initial bin.
The density is calculated by counting the average number of particles in the bin. To obtain a mapping of the orientation of the chain in the sliding direction, we compute the dot product between the bond vectors, \({\mathbf{b}}_{i}\), and the unit vector \({\mathbf{{\hat{x}}}}\).
3 Results and Discussion
We first discuss the equilibrium substrate. Examples of the substrates we obtain using the method described above are shown in Fig. 4, where one can see different structures depending on the chain length. The surface breaks the symmetry, and therefore the surface structure is not necessarily the same as the bulk. The shortest chains (\(m=10\)) form a layer of polymers perpendicular to the surface. For longer chains the substrate becomes more homogeneous with an increase of the amount of folded segments and entanglement of the chains.
The crystallinity level as a function of temperature during a cooling simulation with cooling rate of 75 K/ns. The glass transition temperature is estimated from the point of maximum slope, i.e., when the rate of change of the crystallinity is the highest. The final crystallinity level of the substrate was around 0.4. It represents the mass fraction of crystalline phase
Because of limitations in computation time, we restrict the study of the sliding to one chain length, \(m=50\). This chain length produces a surface that is representative of surfaces consisting of longer chains. The amount of end monomers at the surface is low, and the chains are long enough to fold back on themselves. We show the crystallinity as a function of the system temperature for a constant cooling rate of 75 K/ns in Fig. 5. In general, the glass transition temperature and melting temperature of a sample of this size are subject to finite-size effects. Nevertheless, we have estimated the glass transition temperature for our system from the temperature with maximum rate of change of the crystallinity and found it to be approximately 350.4 K, as can be seen from Fig. 5. We have estimated the melting temperature by melting a crystalline sample, and found it to be around 407 K.
3.1 Indentation
Still at 220 K, we place the tip over the slab of polymer and apply a specific load force to it. The tip is then pushed into the surface with some violence, and we wait for it to come to full rest, which takes 0.4 ns. After this, we switch the thermostat to the target temperature and equilibrate the system for 1.6 ns. We do not observe any significant further creep during this equilibration period that could be relevant for our sliding simulations.
3.2 Frictional Forces
a Lateral force as a function of time. b Friction as a function of the load. The noise in the lateral force was smoothed by using a moving average with small interval of 1.6 ps. At this velocity (15 m/s), the simulation box is completely traversed in approximately 2.8 ns. The vertical lines represent the time when the virtual atom which is attached to the spring goes back to his initial position. The friction is calculated from the lateral force by averaging over the last two passes of the simulation. Extrapolation to zero shows a non-zero friction at vanishing load, which indicates that there is a substantial contribution from adhesion
We show the lateral force as a function of time in Fig. 6a for different loads at \(T=220\) K. The frictional force decreases with time during the running-in period. The force fluctuates and has a repeating pattern due to repetitive crossing of the simulation cell. It takes around \({2.1\,{\text{ns}}}\) to cross this cell. The system has not fully reached the steady state as the friction is still going down slowly.
The average frictional force is calculated over the entire time interval and the results are shown in Fig. 6b. The friction shows a nearly linear dependence on the load. If we extrapolate the data to zero load, the frictional force will be around \({0.53\,{\text{nN}}}\), which is due to adhesion.
a Moving average of the frictional force vs time for different temperatures. At regular intervals, the total lateral forces between the tip and the substrate are measured. The data were then smoothed by a moving average with small interval of 1.6 ps in order to reduce the noise. b Average frictional force over the last two passes vs. temperature
In order to understand the effect of the viscoelasticity of the polymer, we investigate the dependence of the friction on temperature. We show the lateral force as a function of time in Fig. 7a for different temperatures at the same load of \({0.38\,{\text{nN}}}\). The lateral forces are initially very similar for the different temperatures. This is due to the fact that we have used very well controlled and similar initial states. Such initial similarities would not be achievable in experiments. As soon as the sliding begins, the systems at different temperatures start to diverge due to different mechanical properties of the polymer as well as thermal activation. The lateral force decreases with time for most temperatures, but increases slightly with time at the highest temperatures. This increase is related to more and more molecules adhering to the tip and thus needing to be dragged over the surface. Since this is occurs above the glass transition temperature, it is part of a purely viscous response. The mechanism by which the friction decreases with time below the glass transition temperature is more interesting and complicated, and we will discuss and investigate it in more detail below.
The average frictional force as a function of temperature is shown in Fig. 7b. The friction shows a non-linear dependence on the temperature with a minimum around 200 K. This is known to be the result of a competition between the local shear stress which decreases with the temperature and the contact area which increases with temperature [4].
3.3 Structure
A snapshot of the simulation cell after 15 passes of the tip at \(T=220\,{\text{K}}\), seen from above. The tip is the round red body and it is moving to the right. The particles being in the same chain are the same color. The polymer chains in the wear track have become aligned with the sliding direction
Figure 8 shows a snapshot of the substrate after multiple passes at temperature 220 K. From this figure, we see that there are significant changes in the structure on the surface. In order to understand what is happening during the running-in period, we investigate the structure in more detail.
The average density under the flat region of the tip as a function of the depth directly under the tip, normalized by the bulk density. The vertical line represents the lowest surface of the tip. It is the sum of the height of the tip lowest atom plus the value \(r_{0}\) of the Lennard–Jones potential
Figure 9 shows the average density in cross sections of the surface directly under the middle of the tip for three different temperatures. We note that the gentle density gradient in the first few nanometers of the surfaces is due to the fact that the surface is not atomically flat, but has some nm-scale roughness. There are a small number of alternating high- and low-density lines around the tip, as can be seen from the horizontal red lines in the figure. In Fig. 10, we quantify this further and show the density in the region under the flat part of the tip as a function of the depth under the tip. There is a fast decay in the fluctuation with respect to the height. The first maximum is around 3 times the bulk density and the first minimum is half of the bulk density. Temperature somewhat reduces the effect, as is to be expected, but is still quite pronounces, even above the glass transition. This formation of a layered structure is not unexpected; it is commonly found in strongly confined materials under high pressure.
Finally, the snapshot in Fig. 8 shows specifically that the chains in the center are aligned in the sliding direction in the wear track. Most of the adjacent chains to this wear track show partial alignment with respect to the sliding direction. The chains further away from the wear track show little to no sign of this. Such behavior has been observed experimentally for rubbers [3, 6, 13].
We investigate this more systematically by considering the orientation of the bonds in the chains. Figure 11 shows the average component of the bond in the sliding direction for different temperatures. In the first few nanometers from the surface, there is a strong preferential orientation of the chains in the sliding direction (combing effect). The thickness of this reorientation layer increases with the temperature (Fig. 12).
3.4 Dynamic
The viscoelastic flow of the material surrounding the tip is an important characteristic of the contact [9]. We therefore investigate the average displacement around the tip, including the elastic restoration and permanent plastic deformation; the former is removed from the system by the thermostat.
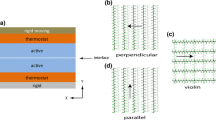
Figures 13a, c, e and 14a, c, e show the vector displacements calculated after a time interval \(\varDelta t\) of 0.08 ns and 0.4 ns, respectively. We first consider the temperatures below the glass transition, 50 K and 220 K. In front of the tip, the material near the surface moves downward and in the direction of the sliding. Directly below the tip, it moves upward and slightly in the direction opposite to the sliding. The atoms near the surface at the rear of the tip move slightly downwards and also in the direction opposite to the sliding. This change of direction before and after the tip indicates that elastic energy is stored in the deformation and returned. In addition, some energy is dissipated as heat and in plastic deformation. The latter can be seen from the displacements after the longer time interval in Fig. 14. At temperature 385 K, above the glass transition, there is predominantly a viscous response, and no elastic restoration. In this case, the substrate mainly moves towards the sliding direction.
Figures 13b, d, f and 14b, d, f show cross sections in the yz plane of the vector displacements calculated after time intervals \(\varDelta t\) of 0.08 ns and 0.4 ns. There are symmetrical displacements in the y and z directions. We also note that there are quite large fluctuations visible in Fig. 14. It is nevertheless possible to discern significant displacement near the tip.
Figure 15 shows the displacement in the x direction (sliding direction). There is a small zone surrounding the tip where the displacements are large, at least an order of magnitude higher, in the first few nanometers than in the bulk material. They also do not recover, indicating that this is plastic deformation, as can been seen from the top view displacement map after one pass of the tip, see Fig. 12. The thickness of the layer with plastic deformation increases with the temperature. This observation is in agreement with Briscoe hypothesis [5] of a thin top layer of polymer being submitted to higher shear stresses close to the surface. It is also consistent with alignment of the polymers on the surface in the sliding direction. The right side of the dashed line represents the front of the tip. As can be seen from Fig. 15, there are atoms counted at positions overlapping with the final position of the tip. This is due to the fact that we are investigating finite time intervals and we assign the entire displacement to the atoms initial bins.
In the displacements, we see no indication that the layers visible in Fig. 10 under the tip shear significantly with respect to one another. There is likely due to the fact that there are covalent bonds between the high-density planes where the polymer chains fold around from one to the next. The layer with high plastic displacement is roughly the same thickness as the area with more structure under the tip. Even though the precise rearrangements are different, this similarity in size is to be expected, because the monomers in this region are subjected to forces that are strong enough to cause significant structural rearrangements.
At \(T=55\) K and 220 K, the chains have a strong cohesion and are strongly attached to the substrate. Only the very surface of the substrate sees high deformation. At the rear of the tip, the substrate detaches from the tip. Part of the energy is restored where the substrate is moving backwards. One can notice the presence of transition zones going from negative to positive displacement. We suppose that this effect can be explained by the production of fast propagation of Schallamach waves during sliding, see [2].
At \(T=385\) K, the chains are not sufficiently attached to the substrate and are free to move with the tip. This free movement implies a reduction of the shear stress and an increase of the surface area (higher penetration).
Top views (z cross sections) displaying average displacement in the x direction (sliding direction) right below the tip. The average displacements are calculated after a time interval \(\varDelta t\) of \({2.8\,{\text{ns}}}\) corresponding to one pass of the tip. The plastic deformation can be identified from the fact that it is still present after a full pass of the tip through the simulation cell, returning to its original position
x and y cross sections displaying average displacement vector fields. The AFM tip move towards the x positive direction. The average displacements are calculated after a time interval \(\varDelta t\) of \({0.08\,{\text{ns}}}\). The dashed line and the green line represent, respectively, the initial and final position of the FFM tip
y cross section of the average displacement in the x direction (sliding direction) shown for three different temperatures and two different time intervals \(\varDelta t\). The dashed line and the green line represent, respectively, the initial and final position of the FFM tip. We assign the entire displacement to the initial bin of the atom
4 Conclusion
We have performed molecular-dynamics simulations of an AFM tip sliding on a polymer substrate of PVA chains. We have investigated structural changes occurring in the surface on the atomic scale, as well as the viscoelastic response. We have investigated the system at several temperatures below and around the glass transition and relate the response to the proximity of the glass transition.
We compute the friction as well as a number of structural and dynamic properties. For low temperatures, the friction decreases with temperature, as the shear strength decreases. For higher temperatures, but still below the glass transition, the friction increases again as the contact area increases due to larger plastic deformation. At low temperatures, we see that the polymer is mostly elastic, and we see this in a large recovery and backwards motion of the material in the substrate behind the tip. At higher temperatures, close the glass transition, there is a much larger viscous component. In all cases, the polymers near the surface reorient and align permanently with the sliding direction. While our simulations are for a specific polymer, the qualitative behavior is likely to be general and present in other polymers. Using MD simulations has allowed us to provide a detailed picture of the molecular behavior of sliding polymers. Nevertheless, much remains to be investigated, as there are many additional complications in many realistic polymers that can affect the structure and friction, such as stronger inter-chain interactions, cross-linking, or the presence of water and other contaminants.
References
Bennewitz, Roland: Friction force microscopy. Mater. Today 8(5), 42–48 (2005)
Best, B., Meijers, P., Savkoor, A.R.: The formation of schallamach waves. Wear 65(3), 385–396 (1981)
Bieliński, D.M.: Tribological consequences of rubber composition and structure—case studies. Arch. Civ. Mech. Eng. 7(4), 15–26 (2007)
Bowden, F.P., Bowden, F.P., Tabor, D.: The Friction and Lubrication of Solids, vol. 1. Oxford University Press, Oxford (2001)
Briscoe, B., Smith, A.C.: Time dependence effects in the shear of thin polymeric films. J. Phys. D: Appl. Phys. 15(4), 579–594 (1982)
Hegmon, R.R.: The contribution of deformation losses to rubber friction. Rubber Chem. Technol. 42(4), 1122–1135 (1969)
Heo, S.J., Jang, I., Barry, P.R., Phillpot, S.R., Perry, S.S., Sawyer, W.G., Sinnott, S.B.: Effect ofthe sliding orientation on the tribological properties of polyethylene in molecular dynamics simulations. J. Appl. Phys. 103(8), 083502 (2008)
Jansen, L., Schirmeisen, A., Hedrick, J.L., Lantz, M.A., Knoll, A., Cannara, R., Gotsmann, B.: Nanoscale frictional dissipation into shear-stressed polymer relaxations. Phys. Rev. Lett. 102(23), 236101 (2009)
Lafaye, S., Gauthier, C., Schirrer, R.: Analysis of the apparent friction of polymeric surfaces. J. Mater. Sci. 41(19), 6441–6452 (2006)
Ludema, K.C.: Friction, Wear, Lubrication: A Textbook in Tribology. CRC Press, Boca Raton (1996)
Luo, C., Sommer, J.-U.: Coding coarse grained polymer model for lammps and its application to polymer crystallization. Comput. Phys. Commun. 180(8), 1382–1391 (2009)
Meyer, H., Müller-Plathe, F.: Formation of chain-folded structures in supercooled polymer melts examined by md simulations. Macromolecules 35(4), 1241–1252 (2002)
Moore, D.F.: The Friction and Lubrication of Elastomers, vol. 9. Pergamon, Oxford (1972)
Plimpton, S.: Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 117(1), 1–19 (1995)
Sliozberg, Y.R., Andzelm, J.W.: Fast protocol for equilibration of entangled and branched polymer chains. Chem. Phys. Lett. 523, 139–143 (2012)
Solar, M., Meyer, H., Gauthier, C.: Analysis of local properties during a scratch test on a polymeric surface using molecular dynamics simulations. Eur. Phys. J. E 36(3), 29 (2013)
Sondhauß, J., Lantz, M., Gotsmann, B., Schirmeisen, A.: \(\beta\)-Relaxation of pmma: tip size and stress effects in friction force microscopy. Langmuir 31(19), 5398–5405 (2015)
Triandafilidi, V.: Molecular Dynamics Simulation of Polymer Crystallization Process. PhD thesis, University of British Columbia (2015)
Vettorel, T., Meyer, H., Baschnagel, J.: Etude de la cristallisation des polymères par simulation numérique. PhD thesis, Thèse de doctorat, Université Louis Pasteur–Strasbourg (2005)
Acknowledgements
We thank Dr. Angelika Brink and Dr. Sergio Armada for their insightful discussions. We also gratefully acknowledge Jenny Sheehan for her proofreading.
Funding
This work is supported by the Research Council Norway, Grant Number 259869.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Vacher, R., de Wijn, A.S. Nanoscale Simulations of Wear and Viscoelasticity of a Semi-Crystalline Polymer. Tribol Lett 69, 15 (2021). https://doi.org/10.1007/s11249-020-01369-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11249-020-01369-8