1 Introduction

Formation of a workhardened zone is one of the phenomena accompanying sliding wear in ductile metals and its alloys. This zone adjoining the worn surface exhibits macroscopic increase in hardness in comparison to the interior of the sample [1, 2]. This is due to the accumulation of strain induced by repeated passage of asperities of the counterface [3]. From microscopic point of view, the workhardened region is the part of the larger one called subsurface zone (SZ) located below the worn surface. The SZ contains different type of crystal lattice defects generated by sliding. Its formation of the SZ still is not clear. There is a puzzle why the depth of the SZ is extended up to hundred of micrometers while the sliding wear takes place at the surface in the region of asperities [4]. The process of plastic deformation in the region of asperities at the worn surface seems to be not sufficient to deform material at such a large depth.

The experimental studies of the SZ encounter difficulties, because it is expanded below the worn surface at the large depth. Measurements of the microhardness are performed at a cross section of the worn sample; however, the microhardness is not accurate method for detection of defects at atomic scale. The other methods: XDR, SEM or TEM are not sensitive to point defects which are generated in great amount during friction processes. The positron annihilation methods are suitable for these studies due to large penetration depth of implanted positrons and their sensitivity to different type of defects [5]. They can detect accurately the defect depth profile and the total range of the SZ.

The decrease in amount of open volume defects, like vacancies, their clusters or dislocations with the increase in the depth is the main feature of the SZ detected by positron annihilation techniques [4]. This result was obtained for instance in Bi exposed to dry sliding [6]. The exponential decrease in the defect concentration was clearly visible for other metals and alloys used for tribological applications, like Cu [4], Fe [7] and others Al, Mg and their alloys [8]. The total depth of the SZ increases with the increase in the applied load and also sliding speed [4]. It seems that the exponential decrease in defect concentration is a common feature of the SZ generated during dry sliding. However, our recent studies of pure Ti revealed another type of this dependency, i.e., the sigmoidal decrease in the defects concentration was detected [9]. There is observed the plateau close to the worn surface and then the gradual decrease at depth of about dozens of micrometers. Ti has poor tribological properties, and it exhibits large wear and high friction coefficient. This encourages us to perform positron studies of the SZ in other metals which are not used in tribological junctions. Their results can be useful for explanation of the SZ formation and show us its possible link with the wear.

Zr has only niche applications. Its excellent resistance to corrosion allows its using as an alloying element in materials that are exposed to aggressive environments, for instance alloys for surgical instruments. Because of low neutron-capture cross section of Zr nuclei, zircaloys are used for cladding of nuclear reactor fuels. We focused our interest on Zr because it exhibits a hexagonally close-packed crystal structure similar to Mg and Ti already studied. Its hardness is comparable to hardness of Ti but larger than Mg by the factor of about five. Thus, if hardness is an important factor for the generation of the SZ we expect results rather similar to Ti than to Mg.

Positron annihilation techniques were the main tool in our studies. We applied the conventional positron lifetime spectroscopy (PALS) which is sensitive to open volume defects and has been applied with success for detection of SZ in metals and alloys. Objects of our studies are samples of pure Zr exposed to dry sliding, compression or sandblasting.

2 Experimental Details

2.1 Positron Lifetime Measurements

It is well known that the time prior to annihilation which an implanted positron spends in condensed matter depends on the local electron density [5]. Briefly, the higher the electron density the lower the positron lifetime. The highest electron density is in the core region of an atom; however, the positively charged nuclei repel a positron into interstitial region occupied by valence and conduction electrons. Thus, only the latter contributes mainly to the positron lifetime. However, the crystalline lattice can be locally disturbed by defects, for instance open volume defects, like vacancies or their cluster and/or dislocations. Due to lower electron density and/or possible bound state in these regions a positron can be localize there. The increase in the trapped positron lifetime in this case is clearly visible. For instance, the lifetime of a positron trapped at monovacancy is longer than in bulk by a factor about one and a half. There are numerous papers devoted to the experimental measurements, and theoretical calculations of the positron lifetime for bulk and defects of different materials, because these values are fingerprints which can be used for defect identification. This is the outline of the PALS frequently used for materials studies [5, 10].

In our studies, we performed the conventional positron lifetime measurements. As the positron source the beta-plus decay of 22Na isotope was used. The isotope was enveloped into a 7 μm thick kapton foil. Its activity was about 30 μCi. One should note that the positrons emitted from the source have sufficient energy (E max = 544 keV) to penetrate a certain depth from the entrance surface of the sample. For Zr, the linear absorption coefficient for positrons is in this case equal to ca. 294 cm−1. In the top layer of thickness of 34 μm, about 64 % of positrons emitted from this source are stopped. For that reason, this technique is not sensitive to surface defects and near surface inhomogeneities. Mechanically mixed layer and oxide effects can be ignored in considerations.

The positron lifetime spectra (PLS) measurements were carried out using the conventional fast–fast spectrometer. The spectrometer was constructed of BaF2-based detectors and standard ORTEC electronic units; the time resolution of the system was 260 ps (FWHM). The positron source was located between two identical Zr samples in such a way that positrons are implanted through the worn surface, and this sandwich was positioned in front of the scintillator detectors of the positron lifetime spectrometer. The PLS contained more than 106 counts. All obtained spectra were deconvoluted using the LT code, subtracting the background and the source components [11].

The implantation profile of the positrons in the samples is not taken into account in the PLS analysis. It is assumed that over the positron penetration depth, about 34 μm the sample is homogeneous. The detail analysis devoted to the positron mean lifetime or the annihilation line shape parameter showed that implantation profile only slightly influences the obtained results. The main features of the obtained depth dependencies do not change significantly by the implantation profile [12]. At this stage, it is difficult to perform the deconvolution of the PLS including heterogeneity of the sample over the implantation profile, because the PLS do not exhibit rich features. However, it can be noticed that despite the fact that over the positron implantation profile in the studied sample a certain heterogeneous can be expected the PLS are deconvoluted with one or two components with Chi-square (χ 2) close to unity. (In Fig. 2 we depicted for comparison the positron implantation profile in Zr, the dashed line, together with the depth dependency of the mean positron lifetime. This shows that defect depth distribution is much larger than the positrons range.)

2.2 Sample Preparation

In our studies, we used Zr of purity of 99.2 % purchased from Godfellow. Samples had a shape of discs of 10 mm in diameter and 3 mm thick each, their surfaces were polished. Before treatments they were annealed in the flow of N2 gas at a temperature of 550 °C for 1 h and then slowly cooled to room temperature. After annealing, the samples were etched in the etching paste TS-K 2000 delivered by Pelox to reduce their thickness by 100 μm and clean their surface. The thickness of the sample was measured using a digital micrometer screw. After this procedure, only residual defects were present. In fact, the PLS measured for virgin samples contained only one lifetime component equal to 162 ± 1 ps. This corresponds well with the data reported in the literature as the bulk lifetime for Zr [10].

Usually, the PLS are described by the sum of exponential decay functions, each one characterized by the positron lifetime component τ 1 and its intensity I i , where i = 1, 2 ,…, N is the number of lifetime components. Each component can be linked with the positron state in the moment of annihilation, e.g., delocalized state in the prefect lattice or localized in the open volume defects. For many applications the positron mean lifetime is used, it is defined as the sum: \(\bar{\tau } = \tau_{1} I_{1} + \tau_{2} I_{2} + \cdots + \tau_{N} I_{N}\). This is a robust parameter which does not depend on the number of components resolved in PLS; however, it is still sensitive to all parameters corresponding to the annihilation states and properties of the sample at the atomic level.

2.3 Sample Treatments

2.3.1 Dry Sliding

After annealing and etching, a virgin sample of Zr was located in a tribotester and the base surface of the sample was sliding against the rotating disc with the load of 100 N. This disc of diameter of 50 mm was made of the martensitic steel (steel SW18 hardness about 670 HV0.1). The speed of the disc relative to the surface of the sample was about 5 cm/s. The treatment was performed in air during a certain time. No oxidation was observed. The average value of the friction coefficient determined during the tribotest was equal to 0.38 ± 0.02 and the specific wear rate, defined as worn volume per unit sliding distance per unit load was equal to (4.25 ± 0.08) × 10−13 m3/Nm.

2.3.2 Compression

Other annealed samples were deformed by compression at room temperature to reduce their thickness. For compression, the hydraulic press was used and after 15 s the pressure was released.

2.3.3 Sandblasting

The virgin samples of Zr were also exposed to sandblasting. In this process, the virgin samples were exposed to sandblasting with of Al2O3 particles of average radius 250 μm. The sandblasting was performed with pressure of 3 and 6 bar during 2 min.

3 The Review of Results

3.1 The Sample Exposed to Compression, the Calibration Test

It is well known that sliding is accompanied by plastic deformation in the region of asperities and that adjoined the worn surface [3]. The plastic deformation of ductile metals and alloys involves dislocation movements and leads to increase in the dislocation density. Point defects like vacancies and interstitial atoms can also be produced due to mutual interactions of moving dislocations. Their density also increases significantly above the equilibrium value [13]. The presence of open volume defects is well detected in the PLS components. At the beginning, we intend to link these components with the degree of deformation, i.e., the thickness reduction denoted as ε.

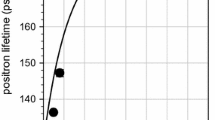
In Fig. 1 we depicted the obtained values of the positron lifetime components for selected thickness reduction values in the compression. It can be noticed that the PLS contain only single component for the thickness reduction less than 3 %, Fig. 1a, b (closed circles). These values of this component are slightly higher than the measured bulk value, i.e., 162 ps. However, for larger values of ε two lifetime components are resolved. The value of this component increases from 250 to 420 ps whereas its intensity decreases with the increase in ε, Fig. 1c (open squares). In the literature, there is reported the lifetime is about 252 ps for a positron trapped at the monovacancy in Zr. Larger values indicate the annihilation at vacancy clusters. In Appendix ab initio calculations of this relation are presented. Thus, this indicates that for larger deformation monovacancies and vacancy cluster up to about 13 vacancies are generated, Fig. 7. For ε ≈ 10 % again the single lifetime component is resolved, which values about 210 ps, Fig. 1b. This indicates the positron annihilation at jogs or vacancies on dislocation lines. It is interesting that the single lifetime component is present also for highest thickness reduction of about 72 %.

Fig. 1
figure 1

Values of the mean positron lifetime (a) and the first (b) and the second (c) (closed circles) positron lifetime components and the corresponding intensities (open squares) as a function of thickness reduction in compression of Zr sample. The dashed line in the best fit of Eq. (1) to the experimental points, see text. The calculated positron lifetime for monovacancy vacancy V 1 and vacancy cluster which consists of thirteen vacancies V 13 are shown by horizontal dashed lines

Full size image

We would like to draw attention to the mean lifetime calculated according to the relation given above. Its value increases and at the thickness reduction by about 7 % a maximum is observed, Fig. 1a. The maximum occurs when the second lifetime component reaches its highest value. Then, the mean lifetime saturates at the value about 210 ps. This is characteristic feature, occurring for instance for Ni [14], Cu [15] and also other metals exposed to the compression. The saturation can be explained by so large defect concentration, usually about 103, that after termalization all positrons are trapped at open volume defects where they annihilate. Like for other metals the obtained dependency for ε in the range 0–13 % can be described using a following function:

$$\bar{\tau } = \tau_{{\text{sat}}} + (\tau_{{\text{bulk}}} - \tau_{{\text{sat}}} )\,\exp \left( { - c\varepsilon } \right),$$
(1)

where ε is the thickness reduction in percent. The dashed line in Fig. 1a represents the best fit of this simple function, and the values of the adjustable parameters are as follows: τ sat = 217 ± 5 ps, c = 0.231 ± 0.056. The value of the bulk lifetime was kept constant and equal to τ bulk = 162 ps. This relation will be used in considerations below.

3.2 The Samples Exposed to Dry Sliding

The virgin sample was exposed to dry sliding with the normal load of 100 N during time of 12 min. We applied the sequenced etching method for detection of the SZ. The measurement of the PLS was performed after removing a layer of a thickness of about 10 μm from the worn surface by etching. Etching itself does not introduce new defects; thus, we assume that this process is neutral to the plastic deformed regions in the samples, no additional deformation of etched samples was observed. Sequenced etching and measurements of the PLS allows us to detect the defect profile in the SZ induced by dry sliding under conditions mentioned above. In Fig. 2 we depicted the results for this sample.

Fig. 2
figure 2

Values of the mean positron lifetime (a) and the first (b) and the second (c) (closed circles) positron lifetime component and the corresponding intensities (open squares) as a function of the depth from the worn surface of pure Zr sample. The sample was exposed to sliding against the rotating martensitic steel disc with load of 100 N during the time of 12 min. The calculated positron lifetime for monovacancy vacancy V 1 and vacancy cluster which consists of four vacancies V 4 are shown by horizontal dashed lines. The dashed curve (a) represents the depth dependence of the positron implantation profile in Zr, described by the function of: \(P(x) = \alpha_{ + } \exp \left( { - \alpha_{ + } x} \right)\), where α + is the linear absorption coefficient and x the depth from the enter surface

Full size image

These can be observed quite a different behavior than detected for other metals before. The mean positron lifetime increases below the worn surface and after reaching a maximum at the depth of about 50 μm it starts to decrease gradually, Fig. 2a. In other metals exposed to sliding, no maximum was observed. Regarding the number of components in the PLS, three regions can be distinguished in the SZ. The first one is the closest to the worn surface extending to the depth of 50 μm. In this region, only single lifetime component in the PLS is resolved, its value increases with the depth increases, Fig. 2b. The second region is extended from 50 to 320 μm with two lifetime components resolved in PLS, and the third one is extended beneath the depth of 320 μm where again single lifetime component is resolved.

The second region is the most interesting. The value of the first lifetime component decreases from 220 to about 140 ps, Fig. 2b (closed circles) and the value of the second one also decreases from 320 to 200 ps, Fig. 2c (closed circles). However, the intensity of the latter increases from about 10–50 % and then saturates at these value to the depth of 320 μm, Fig. 2c, (open squares). This indicates the presence of the clusters which consist of five vacancies, see Fig. 7 in Appendix. The size of the clusters decreases with the depth increase to the depth of 220 μm. However, between 160 and 300 μm we still notice two lifetime components, but the value of the first one is below the bulk value for Zr, Fig. 2b. This indicates the presence of regions without point defects with low concentration of dislocations. The value of the second lifetime below 252 ps indicates positron trapping at jogs on dislocation lines. No vacancy clusters are detected for the depth beneath 160 μm. Beneath 330 μm again only single lifetime component of value slightly above the bulk value indicates the presence of small amount of dislocations. The value of the single positron lifetime decreases slowly reaching the bulk value at the depth of about 400 μm, Fig. 2a.

The formation of the SZ depends on the time of sliding. In our former studies for other metals, the sliding test was performed during the time of 1 min. This was enough to create the well defined SZ. In Fig. 3 we depicted the measured mean positron lifetime depth profiles for three samples exposed to the sliding during 1 min but for three different loads. The main features of these dependencies in Fig. 2a are reproduced for the depth profile obtained for the load of 100 N. However, the maximum close to the worn surface is only slightly visible. The long tail is shorter and it is extended from 200 to 280 μm. For lower load of 50 N, the maximum is shifted toward the surface and the tail is even shorter. For the lowest load of 25 N, the maximum disappears; however, the small plateau at the depth of 20 μm can be recognized. The dependencies for 25 and 50 N do not differ significantly. Like for other metals the total depth of the SZ depends on the applied load, for 100 N it is 280 μm, for 50 N it is 160 μm and for 25 N c.a. 150 μm.

Fig. 3
figure 3

Values of the mean positron lifetime as a function of depth from the worn surface of pure Zr sample. The sample was exposed to sliding against the rotating martensitic steel disc with different loads of 25, 50 and 100 N during the time of 1 min

Full size image

3.3 The Sandblasted Samples

Studying the SZ in pure Mg we have noticed the similarity of the SZ induced by sliding and sandblasting. In the latter case, the surface was hit by particles of Al2O3 with high velocity. This process is used in the technology of metallic products. We postulated that during the sliding wear also the surface in the regions of asperities is hit by the asperities of counterface and hence the similarities of the SZ zones. The mean positron lifetime obtained from the measured PLS is depicted in Figs. 4 and 5.

Fig. 4
figure 4

Values of the mean positron lifetime (a) and the first (b) and the second (c) (closed circles) positron lifetime component and the corresponding intensities (open squares) as a function of depth from the worn surface of Zr sample. The sample was sandblasted with the pressure of 3 bar. The calculated positron lifetime for monovacancy vacancy V 1 and vacancy cluster which consists of four vacancies V 4 are shown by horizontal dashed lines

Full size image
Fig. 5
figure 5

Values of the mean positron lifetime (a) and the first (b) and the second (c) (closed circles) positron lifetime component and the corresponding intensities (open squares) as a function of depth from the worn surface of pure Zr sample. The sample was sandblasted with the pressure of 6 bar. The calculated positron lifetime for monovacancy vacancy V 1 and vacancy cluster which consists of four vacancies V 4 are shown by horizontal dashed lines

Full size image

The mean positron lifetime exhibits maximum which is clearly visible in Fig. 4a for the pressure of 3 bar at the depth of about 30 μm and at the depth of about 70 μm for the pressure of 6 bar in Fig. 5a. The long tail extended from the depth of 150–300 μm is also visible in Fig. 5a, however, for the lower pressure it is not present, Fig. 4a. Two lifetime components in the PLS are also detected. In Figs. 4b and 5b the values of the first lifetime component (closed circles) and its intensity (open squares) are depicted and in Figs. 4c and 5c the values for the second component. All dependencies look very similar to those in Fig. 2; however, the slightly lower values of the second lifetime component and its intensities can be noticed. It indicates the smaller vacancy clusters.

4 Discussion

The presence of the maximum in the mean positron lifetime dependencies for all the studied SZ and observed first time in our studies is the surprising results. We can propose two explanations: the maximum results from the structure changes induced by the sliding wear or a specific positron interaction with defects in Zr.

Salesky et al. [16] proposed the original model of SZ constitution for dry sliding. With the increase in the number of repeated passages of asperities of the counterface, the resulting dislocation density increases. This leads to the rearrangement of dislocations to the cell walls. The cell structure can undergo recovery due to local heating or mechanically induced instability. This can induce locally decrease in the dislocation density and strain. The recovery is limited to the region adjoined directly to the worn surface, but deeper heavily dislocated unrecovered region is still extended. According to these authors, the interface between these regions becomes a preferred location for the formation and propagation of delamination cracks. Thus, this model predicts a maximum of the dislocation density and strain at a certain depth below the worn surface. We doubt that this is the maximum seen in Fig. 2 because the depth of about dozens of micrometers is too large. Such thick debris is not observed. However, the recovery process is not observed at much lower depth about one micrometer too. For example, our earlier studies of Cu using a slow positron beam technique where positrons are located at the depth of one micrometer only from the worn surface have not indicated any recovery process also at such a depth [17]. The results have shown the constant density of defects in this region.

Another explanation is based on the results presented in Fig. 1, which reveals that only in the certain range of deformation the vacancy clusters are detected. For large and low deformation, only single lifetime in the measured PLS is resolved. It can be seen that when large deformation is reduced and the vacancy clusters occur the mean positron lifetime slightly increases, Fig. 1a. This maximum is reflected in Fig. 2a. Close to the worn surface the strain is larger than 13 %, thus the single lifetime is observed, in the deeper region strain diminishes and the vacancy clusters are present. The maximum indicates the depth at which the vacancy clusters occurs. With the depth increase, the size of the vacancy clusters decreases and this causes the decrease in the mean positron lifetime. It can be concluded that the strain in the SZ decreases with the depth increase but this is not reflected directly in the mean positron lifetime values, because of specific behavior of Zr under deformation. Usually the large deformation for metals induces the creation of large number of defects including vacancy cluster [18]. This is not the case for Zr.

The vacancy clusters can occur as the results of several processes. Generally, plastic deformation of crystalline metals involves creation and movement of dislocations and finally it leads to dramatic increase in the dislocation density. Due to their mutual interactions, point defects like vacancies and interstitial atoms can also be produced and their density increases significantly above the equilibrium value. At room temperature, vacancies are mobile and they can coalesce forming clusters.

The fact that vacancy clusters are observed only at relatively large depth from the worn surface is the interesting result. Usually they accompany regions close to cracks which induce debris formation according to different wear theories. Thus, they should be located much closer or on the worn surface as it was observed for Fe [7] and Cu [18]. In Zr this region contains great amount of dislocations. This can be connected to the presence of shear bands and twins which were found in the microstructure of the Zr of commercial purity cold-rolled to 71 % [19] and exposed to equal channel angular pressing [20].

The values of the second lifetime component for the sample exposed to compression vary in the wide range from 250 to 420 ps indicating the presence of vacancy clusters of different sizes from monovacancy to more than nine vacancies. For other samples, the range is narrower, i.e., 250–300 ps. The intensity of this component is roughly proportional to the concentration of these defects. It is interesting that its maximal value is higher for the sandblasted sample, Fig. 5c, i.e., about 70 %. The lowest value, about 35 % is noticed for the compressed sample. Briefly, the lowest amount of vacancy clusters occurs for this sample and much higher for the samples exposed to the dry sliding or sandblasting. This can support the similarity of vacancy cluster creation mechanism for friction and sandblasting. One should emphasize also the similarity between dependencies of the mean positron lifetime for these processes, Figs. 2a, 4a and 5a. Thus, they introduce deformation in a similar way, despite the lack of evident shear stress in the sandblasting process. Thus, these results confirm the previous one obtained for pure Mg [8]. We argue that microimpacts at the sliding surface are responsible for formation of the SZ, i.e., expansion of strain and defects in the interior. However, one should mention that speed of deformation and type of the crystalline lattice can affect on the type of generated defects [21].

From macroscopic point of view, we can argue that the SZ is the region with a certain gradient of strain. Assuming that static deformation and deformation during sliding are equivalent one can use the relation (1) and dependency from Fig. 2a and estimate the effective strain ε effect present at the different depths. For this we can use the following relation valid for uniaxial pressing [22]:

$$\varepsilon_{\text{effect}} = - \ln \left( {1 - \varepsilon /100} \right),$$
(2)

where ε is the thickness reduction express in percent. In Fig. 6 we depicted the obtained dependency. However, due to the saturation the validity of the obtained dependency is limited to the strain below 13 %, i.e., for the depth above 100 μm. In this range it can be noticed the exponential decay of the effective strain with the depth increase, the straight line in Fig. 6. Below 100 μm the calculation of the effective strain is impossible because the value of the mean positron lifetime is saturated at 210 ps. Nevertheless, one can suppose that closer the worn surface the stain increases too. Thus, the SZ exhibits the gradient of strain; the strain is the origin of defects. The PALS can be used for detection of the strain distribution for strain lower than about 10 %. Higher strain causes creation of large defect concentration and saturation of positron trapping at them and finally saturation in the positron characteristics, like as the mean lifetime.

Fig. 6
figure 6

Estimated values of the effective strain as the function of the depth from the worn surface for the Zr sample exposed to dry sliding against the rotating martensitic steel disc with load of 100 N during the time of 12 min. For calculation, the data from Figs. 1a and 2a were used. The straight line is best fit to the points described by the function: \(\varepsilon_{{\text{effect}}} = a\exp ( - b\,z)\), where z is depth in μm, a = 49.5 ± 4.1, b = 0.0154 ± 0.0008 μm−1

Full size image

The defect profiles obtained for Zr differ significantly from those obtained for Ti and Mg despite similarities in the crystalline structure. It seems that also hardness is a minor factor for generation of the SZ because significant differences of the results between Zr and Ti. Thus, it seems that other factors determine the SZ generation.

5 Conclusions

Sequenced etching and measurements of the PLS for pure Zr samples exposed to dry sliding revealed well defined defect depth profiles which are different from those detected in other metals and alloys. There are present dislocations, and vacancy clusters; however, their depth distribution is complex. Close to the worn surface only dislocations are present, at a certain depth the vacancy clusters occur, with the depth increase their size decreases. Further from the worn surface again dislocations are present. The total depth of the SZ depends on the applied normal load during sliding. The almost identical defect depth profile is observed also for the sandblasted Zr samples. Taking into account the positron lifetime measurements for Zr compressed samples the distribution of strain in the SZ was calculated. Exponential decay of effective strain with the depth increase was detected. There were found on similarities of the SZ to other metals with hexagonally close-packed crystal structure like Mg and Ti.