1 Introduction

The pressure dependence of viscosity was necessary to explain the presence of a film sufficiently thick to separate the roughness features of engineering surfaces in elastohydrodynamic lubrication (EHL) [1]. Therefore, piezoviscous response is at the foundation of the field. Faster-than-exponential, or super-Arrhenius pressure dependence of viscosity (in reference to the dependence of a material property which relies on an Arrhenius law), has been a feature of accurate measurements of viscosity at high pressure for 90 years [2]. This behavior has surprisingly been absent from the dialog of classical EHL since its beginning, and this absence is at least partly responsible for the spectacular failure of the field to provide an understanding of EHD friction using the thermophysical properties of the liquid. In this second installment [3] of a series differentiating classical from quantitative EHL, it will be shown that, although missing from the classical approach, super-Arrhenius piezoviscous response is the natural behavior of glass-forming liquids and that it is indispensable for understanding the behavior of liquids at high pressure and high shear stress.

2 The Behavior Observed in Viscometers

Faster-than-exponential pressure-viscosity behavior has been observed in nearly every type of viscometer. The guided falling cylinder viscometer used by Nobel Laureate, Bridgman [2] in 1926 was perhaps the first to achieve sufficiently high pressure (1.2 GPa) to see the transition, inflection in log(viscosity) versus pressure, from slower to faster than exponential in simple, low-viscosity liquids. However, by 1959, Lowitz et al. [4] using a rolling ball viscometer had obtained the inflection in diphenylethane at a pressure of only 75 MPa. In 1973, Hutton and Phillips [5] employed a Couette viscometer to demonstrate faster-than-exponential response to refute the incorrect slower-than-exponential behavior that had been derived from an EHL film-thickness analysis based on Newtonian viscosity. Jones et al. [6] in 1975 found faster-than-exponential response at low pressures for two lubricating oils with a capillary viscometer. Piermarini et al. [7] in 1978 and later Cook et al. [8] used diamond anvil cells as dropping ball and rolling ball viscometers, respectively, to observe the inflection in simple liquids such as methanol. In 2012 faster-than-exponential pressure response was reported for a mineral oil in an oscillating quartz viscometer at the Technical University of Clausthal [9].

Moreover, the primary dielectric relaxation time may be proportional to viscosity according to Harrison [10] and may be used to extend viscosity measurements on polar liquids to very high pressures and very large viscosities. Dielectric spectroscopy is relatively easy at high pressure compared to viscometry, requiring only an electrical connection to a sample filled capacitor in the pressure vessel. The technique has been shown to be useful for prediction of the pressure dependence of viscosity of lubricants over the years [11–13]. The pressure dependence of the dielectric relaxation time is always seen to be super-Arrhenius [14] since short relaxation times (low viscosities) are not accessible to the technique when applied within a pressure vessel. However, excellent agreement in the derivative analysis has been demonstrated for propylene carbonate [15] for viscosity compared with relaxation time. Viscosity and dielectric relaxation time for dibutyl phthalate can be described by the same super-Arrhenius function for pressure to 1.4 GPa [16]. In fact, the Paluch [17] equation for the pressure-viscosity effect at high pressure, below, is the analog of the Johari and Whaley equation for the pressure dependence of relaxation time.

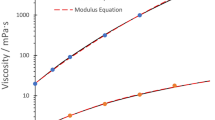
$$\mu = \mu_{0} \exp \left( {\frac{{C_{F} p}}{{p_{\infty } - p}}} \right)$$
(1)

The dielectric relaxation time for di-isobutyl phthalate (DiBP) from [18] is plotted in Fig. 1. New viscosity measurements from Georgia Tech are also plotted. The relaxation times have been multiplied by a constant, k = 0.4 GPa, to compare with the viscosity. The measurements extend across eleven orders-of-magnitude. The overlapping curves show that the pressure dependence of the shear viscosity is the same as the pressure dependence of the relaxation time and that it should be possible to calculate the viscosity up to 109 Pa s from a simple measure of relaxation time. This high viscosity is not accessible to viscometers. The equation fitted to the data in Fig. 1 is the hybrid model [19], Eq. (2), combining the McEwen equation for slower-than-exponential with the Paluch Eq. (1) for faster-than-exponential response.

$$\mu = \mu_{0} \left( {1 + \frac{{a_{0} }}{q}p} \right)^{q} \exp \left( {\frac{{C_{F} p}}{{p_{\infty } - p}}} \right)$$
(2)
Fig. 1
figure 1

Viscosity of di-isobutyl phthalate measured in a falling cylinder viscometer (this work) compared with the dielectric relaxation time (from [18]) multiplied by a constant. The measurements extend across eleven orders-of-magnitude

Full size image

The parameters are given in Table 1.

Table 1 Parameters of the hybrid model
Full size table

To summarize, faster-than-exponential pressure-viscosity behavior has been observed in

  1. 1.

    Falling cylinder viscometers

  2. 2.

    Rolling ball viscometers

  3. 3.

    Couette viscometers

  4. 4.

    Capillary viscometers

  5. 5.

    Falling ball diamond anvil viscometer

  6. 6.

    Rolling ball diamond anvil viscometer

  7. 7.

    Vibrating crystal viscometer

  8. 8.

    Dielectric spectroscopy normalized to viscometry

Therefore, the absence of this effect in the classical EHL description of the pressure dependence of viscosity cannot be justified.

In the following, examples are given of the necessity of super-Arrhenius piezoviscosity in explaining the response of liquids at high pressure and high shear stress.

3 EHD Friction Coefficient

An example can be made of the EHD friction of a polyolester (POE) and a polyalphaolefin (PAO) shown in Fig. 2. The measurements were performed in a skewed roller tribometer [20] which can resolve the friction at very low slide/roll ratio in a point contact. Here the rolling velocity was 2 m/s. For Hertz contact pressure of 1.4 GPa at 57 °C and slide-to-roll ratio of 10−3–10−1, this POE generates a substantially greater friction coefficient than does the PAO. The reason can clearly be seen in the pressure-viscosity response in Fig. 3. In spite of the POE having a lower initial pressure-viscosity coefficient, d ln (μ) / dp | p = 0 = 17.6 GPa−1 compared to 21.4 GPa−1 for POE, the viscosity at high pressure (>600 MPa) is much greater for the POE. The equation fitted to the data is the hybrid model (2), combining the slower-than-exponential with the faster-than-exponential response. The parameters are given in Table 1.

Fig. 2
figure 2

Friction measured in point contact for crossed rollers at 2 m/s rolling velocity

Full size image
Fig. 3
figure 3

Viscosities of the two oils fitted to the hybrid model

Full size image

Models which describe the inflection, such as Eq. (2) or free-volume [8], do not exist in classical EHL. Rather, the viscosity is described by a fictional story about a Barus equation [21] or by the most popular, Roelands equation [22].

$$\mu = \mu_{p} \left( {\frac{{\mu_{0} }}{{\mu_{p} }}} \right)^{{\left( {\frac{{p_{p} - p}}{{p_{p} }}} \right)^{Z} }}$$
(3)

Here the pole pressure and the pole viscosity have universal values of \(p_{p} = - 0.196{\text{ GPa}}\) and \(\eta_{p} = 6.31 \times 10^{ - 5} {\text{ Pa}}\,{\text{s}}\), respectively [22]. In Fig. 4, this equation has been fitted to the viscosities as instructed by Roelands. That is, only data at pressures less than the inflection pressure are fitted, up to 500 MPa for POE and up to 700 MPa for PAO. The parameters are given in Table 2. The results reported in Fig. 4 show that the viscosities at the high pressures of the friction generating regions of an EHD contact cannot be distinguished using the descriptions employed by classical EHL.

Fig. 4
figure 4

Viscosities of two oils fitted to the Roelands model. The POE is fitted to 500 MPa and the PAO is fitted to 700 MPa

Full size image
Table 2 Parameters of the Roelands model
Full size table

There is an interesting and common problem illustrated in Fig. 4. The Roelands model cannot accurately match the curvature of the PAO data at low pressures so that the value of μ 0 as regressed, 24 mPa s, is much greater than the measured value, 20 mPa s. To relieve this problem, a smaller pressure interval may be selected for the data fitting, say to 350 MPa. When this is done in Fig. 5, the viscosity of the PAO at pressure above 300 MPa is predicted to be greater than the POE, which is obviously incorrect. In defense of Roelands, it must be mentioned that he did not recommend his correlation for elastohydrodynamic pressures [22], only for hydrodynamic pressure.

Fig. 5
figure 5

Viscosities of two oils fitted to the Roelands model. The POE is fitted to 500 MPa and the PAO is fitted to a reduced pressure interval, to 350 MPa, to improve the fit at low pressure

Full size image

Clearly, the friction behavior of these two oils, a PAO and a POE, cannot be explained using the pressure-viscosity models most often employed in classical EHL, and the initial pressure-viscosity coefficients give no indication of the viscosity at high pressure where friction is generated. When the inflection cannot be modeled and two liquids with similar low pressure behavior have different inflection pressures, then the difference in viscosity in the Hertz zone cannot be accounted for. Different liquids may appear to have the same properties at low pressure while having quite different viscosity in the Hertz contact region. Inaccurate descriptions of the pressure dependence have influenced even the way that the shear dependence of viscosity has been represented as shown in the next section.

4 Logarithmic Dependence of EHD Friction on Sliding Speed

A particular aspect of the sliding speed dependence of EHD friction, the shape of the friction versus sliding velocity curve, once received much attention and was the motivation for the use of a thixotropy model to describe shear-thinning in classical EHL. For constant rolling speed, contact pressure and temperature, when the friction coefficient or average shear stress, \(\bar{\tau }\), is plotted against the sliding speed, average shear rate, \(\bar{\dot{\gamma }}\), or slide-to-roll ratio, a substantial portion of the friction gradient is logarithmic. That is, friction plotted versus the logarithm of sliding speed displays an interval of data which lie on a straight line in a region of low slide-to-roll ratio often held to be isothermal. Many laboratories observed this response, [23, 24] for examples. In Fig. 2, the friction coefficient for the POE varies with slide/roll ratio in logarithmic fashion.

The simplest explanation of this behavior has been to assume that the logarithmic response of the film over the range of pressures in the contact was exactly the shear response of the liquid under constant pressure and temperature [23, 24]. This would be the sinh-law for thixotropy which was given a theoretical foundation by Eyring [25].

$$\dot{\gamma } = \frac{{\tau_{0} }}{\mu }\sinh \left( {\frac{\tau }{{\tau_{0} }}} \right)$$
(4)

For this explanation, the value of the Eyring stress is found from the slope of the logarithmic part of the friction curve as \(\tau_{0} = {{{\text{d}}\ln \bar{\tau }} \mathord{\left/ {\vphantom {{{\text{d}}\ln \bar{\tau }} {{\text{d}}\dot{\gamma }}}} \right. \kern-0pt} {{\text{d}}\dot{\gamma }}}\). The logarithmic function plotted for the POE in Fig. 2 yields τ 0 = 8 MPa while the curve through the PAO data is a power-law. Such a hypothesis requires another assumption, that the viscosity not be strongly dependent upon pressure. If the viscosity, μ, is strongly dependent on pressure and Eq. (4) is correct, the pressure variation across the contact would alter the logarithmic friction response of the film. In classical EHL, which does not employ real viscosity as measured in viscometers, this assumption of weak pressure dependence could not, of course, be tested.

More than 20 years ago, it was found that the slope of the logarithmic friction gradient for two liquids could be quantitatively explained by the assumption of a limiting stress which was proportional to pressure [26] if real super-Arrhenius pressure dependent viscosity, as measured in viscometers, was employed. The constitutive equation is

$$\tau = \hbox{min} \left[ {\mu \dot{\gamma },\varLambda p} \right]$$
(5)

With this shear response and the Hertz pressure distribution for circular contact, 0 ≤ r ≤ 1,

$$p = p_{H} \sqrt {1 - r^{2} }$$
(6)

The shape of the friction curve results from the growth of the stress-limited circular region of the contact [26] and the logarithmic slope was found to be

$$\frac{{{\text{d}}\bar{\tau }}}{{{\text{d}}\ln \dot{\gamma }}} = \frac{2\varLambda }{\alpha }$$
(7)

where \(\alpha = \left. {{{{\text{d}}\ln \left( \mu \right)} \mathord{\left/ {\vphantom {{{\text{d}}\ln \left( \mu \right)} {{\text{d}}p}}} \right. \kern-0pt} {{\text{d}}p}}} \right|_{{p = p_{H} }}\). Thus, the use of Eq. (4) with \(\tau_{0} = {{{\text{d}}\bar{\tau }} \mathord{\left/ {\vphantom {{{\text{d}}\bar{\tau }} {\ln \left( {\dot{\gamma }} \right)}}} \right. \kern-0pt} {\ln \left( {\dot{\gamma }} \right)}}\) for a constitutive law was not justified. The liquids were a polyphenyl ether, 5P4E, and a mineral oil, LVI 260, which were shown to give logarithmic friction behavior [23]. The limit to shear stress can affect friction at low sliding velocity because of the large value of viscosity at the contact center which, of course, results from super-Arrhenius response.

In the example of the logarithmic function plotted for the POE in Fig. 2, the hybrid model (2) gives α = 19.6 GPa−1 for p H  = 1.42 GPa. Therefore, Eq. (7) yields Λ = 0.078, a reasonable estimate of the limiting stress coefficient.

4.1 The Present Issue

In a recent publication, Spikes and Zhang [27] have asserted that the relation between the logarithmic slope and pressure dependent viscosity given by Eq. (7) is not accurate. However, the technique employed was that of classical EHL, the adjustment of viscosity to suit the purpose at hand. The viscosity employed by Spikes and Zhang [27] is what they called the Barus equation

$$\mu = \mu_{0} \exp \left( {\alpha p} \right)$$
(8)

with μ 0 = 0.05 Pa s and α = 20 GPa−1. However, this is not the viscosity of 5P4E or LVI 260 or any other known lubricant for pressures up to the stated Hertz pressure of 1 GPa. Actually, Barus did not study liquids and his equation was not exponential but linear [21]. This exponential relation (Arrhenius relation), of course, cannot describe faster-than-exponential response of these liquids.

Indeed, the viscosity of 5P4E was measured at high pressure in a viscometer by Hutton and Phillips [5] and the viscosity of LVI 260 was measured at high pressure in a viscometer by one of the authors [28]. Neither data set supports the use of Eq. (8) of course. Measured viscosities for LVI 260 are plotted in Fig. 6 and compared with Eq. (8) which is plotted as the dot–dot–dash line.

Fig. 6
figure 6

Low-shear viscosity of LVI 260, measured and represented by two equations

Full size image

4.2 Friction Calculation with Real Viscosity

The accuracy of Eq. (7) can be tested using real viscosity in the form of the Paluch Eq. (1) for fragile liquids. This model is accurate for the pressure dependence of viscosity above the pressure inflection which can be seen in the viscosity of LVI 260 at pressure greater than 0.2 GPa in Fig. 6. Here, μ 0 = 0.181 Pa s, the fragility parameter is C F  = 21.7 and the divergence pressure is p ∞ = 1.61 GPa. This equation is shown to be appropriate for the viscosity in the Hertz zone in Fig. 6. The slope of the Paluch relation (1) at the Hertz pressure of 0.8 GPa, as shown by the heavy dashed line in Fig. 6, yields α = 53 GPa−1 for use in Eq. (7).

The average shear stress in contact is given by

$$\bar{\tau } = \frac{1}{A}\int_{A} {\tau {\text{d}}A} = \int_{0}^{1} {2r\hbox{min} \left[ {\mu \dot{\gamma },\varLambda p} \right]{\text{d}}r}$$
(9)

Numerical integration with viscosity given by Eq. (1) for Λ = 0.05 and 0.10 (to cover the range of values seen in mineral oils) yields the average stress shown as the points in Fig. 7. Lines given by Eq. (7) are plotted in Fig. 7 with slopes of 1.9 and 3.8 MPa for Λ = 0.05 and 0.10, respectively. Not only are the predictions of Eq. (7) excellent representations of the average stress across four decades of shear rate, they are comparable to the values of Eyring stress, 2 ≤ τ 0 ≤ 4 MPa, reported by Johnson and Tevaarwerk [23] for LVI 260. It was shown that ordinary shear-thinning simply shifts the friction curve to the right for point contacts [29].

Fig. 7
figure 7

Comparison of Eq. (7) relating the logarithmic slope to the pressure dependence of viscosity and limiting stress (lines) with values resulting from integration using the actual viscosity (points) for two values of Λ

Full size image

Now the same procedure may be used to test the sinh-law (4), written with shear rate as the independent variable.

$$\bar{\tau } = \int_{0}^{1} {2r\tau_{0} \sinh^{ - 1} \left( {\frac{{\mu \dot{\gamma }}}{{\tau_{0} }}} \right)dr}$$
(10)

In Fig. 8, for τ 0 =  4 MPa and viscosity specified by Eq. (1), the average shear stress is shown as data points calculated from Eq. (10), the integrated sinh-law, Eq. (4), which is plotted as well. The friction curves are clearly different. The hypothesis that the friction curve represents constitutive behavior in the form of the sinh-law is clearly false when the real viscosity of the mineral oil is used. Furthermore, the Eyring stresses reported by Eyring [30] for mineral oil were three orders-of-magnitude less than the values employed in classical EHL.

Fig. 8
figure 8

Test of the hypothesis that the logarithmic slope is related to the so-called Eyring stress through the sinh-law, Eq. (4). The curve is the sinh-law. The average stress from integration of the sinh-law over the contact is represented by the points (x). The hypothesis is clearly false

Full size image

The shear dependence of viscosity which has often been employed in classical EHL, the sinh-law, can only be justified by the shape of a friction curve if the pressure dependence of viscosity is not faster-than-exponential. The field would have developed along a different path if real pressure dependence had been assumed 40 years ago.

5 Linear Dependence of Shear Stress on Pressure

In the previous example, the appearance of logarithmic friction response was explained using super-Arrhenius piezoviscosity. In the next example, another type of non-intuitive response will be explained using natural pressure-viscosity behavior.

Höglund and Jacobson [31] employed the Luleå high-pressure chamber [32] to measure the shear stress supported by liquid lubricants sheared at low shear rate. At a specific test temperature, the pressure was raised in small increments after which the liquid was sheared at ostensibly constant shear rate. After a nearly exponential increase in stress with pressure, there was a range of pressure for which the stress variation was linear in pressure and the linear portion began at shear stress equal to about 2 MPa and reached to about 12 MPa. See Fig. 9 which is Fig. 6 of Höglund and Jacobson [31] for a mineral oil and which is also Fig. 9.6 of Jacobson [32]. The same response was seen at 40, 70 and 100 °C. Since this linear behavior is unexpected for a Newtonian liquid, the authors labeled the pressure at the onset of linear response as the “solidification pressure” and labeled the shear stress above that pressure as “limiting shear stress”. This definition differs from that used by the authors [Eq. (5)] where the limiting stress is defined by the appearance of rate-independent response.

Fig. 9
figure 9

Pressure dependence of the shear stress in an ostensibly constant shear rate experiment as reported in Fig. 6 of Höglund and Jacobson [31] reprinted by permission of ASME

Full size image

This linear pressure-shear stress response can be seen to naturally arise from the pressure and shear dependent viscosity typical of a mineral oil. One of the most thoroughly characterized mineral oils is Shell T9 which has been the subject of numerous EHD friction studies [33–36] since the thermophysical properties are known to high pressures. The viscosity of this mineral oil is shown in Fig. 10. Note that the measured T9 viscosity dependence with pressure follows a super-Arrhenius response which occurs at the three temperatures investigated (from 40 to 120 °C) beginning at pressures less than 1 GPa. The curves fitted to the data in Fig. 10 represent the improved Yasutomi model [37] below. An equation of state is not necessary to apply this correlation.

$$\mu = \mu_{g} \exp \left[ {\frac{{ - 2.303C_{1} \left( {T - T_{g} } \right)F}}{{C_{2} + \left( {T - T_{g} } \right)F}}} \right],\quad T_{g} = T_{g0} + A_{1} \ln \left( {1 + A_{2} p} \right),\quad F = \left( {1 + b_{1} p} \right)^{{b_{2} }}$$
(11)
Fig. 10
figure 10

Effect of pressure on the mineral oil, T9, measured (points) in a falling cylinder viscometer. The improved Yasutomi model was fitted (lines) to the measurements. For comparison, the Roelands correlation as reported in Liu et al. [38] for another Shell turbine oil, T33, is shown for the same temperatures

Full size image

The parameters are given in Table 3. The shear dependent viscosity [33] is given by

$$\eta = \mu \left[ {1 + \left( {\frac{\tau }{G}} \right)^{a} } \right]^{{\frac{{1 - \frac{1}{n}}}{a}}}$$
(12)

with a = 5 and n = 0.35. The shear does not localize for this mineral oil until the stress approaches 0.083 p [33].

Table 3 Parameters of the improved Yasutomi model
Full size table

The shear stress, \(\tau = \eta \dot{\gamma }\), is plotted for pressure steps of 25 MPa and the indicated temperatures in Fig. 11 where it is assumed that the shear rate is \(\dot{\gamma } = 10\) s−1. The same linear response beginning at τ ≈ 2 MPa as in Fig. 9 is present in Fig. 11. It is the faster-than-exponential piezoviscosity combined with shear-thinning which produces the sharp transition to linear behavior. It is not necessary that the shear rate be estimated accurately. Increasing the shear rate simply shifts the curves to the right in Fig. 11, whereas the slope of the linear part is determined by the local pressure-viscosity coefficient.

Fig. 11
figure 11

Shear stress in mineral oil for \(\dot{\gamma }\) = 10 s−1, calculated at pressure intervals of 25 MPa. Properties come from viscometer measurements

Full size image

A recent article from classical EHL [38] has addressed the thermal non-Newtonian EHL of another Shell turbine oil, T33, also a mineral oil. For the shear dependence, they employed the sinh-law (4) with τ 0 = 10 MPa. For the pressure and temperature dependence they used the full Roelands equation with parameters listed in Table 2.

$$\mu = \mu_{p} \left( {\frac{{\mu_{R} }}{{\mu_{p} }}} \right)^{{\left[ {\left( {\frac{{p_{p} - p}}{{p_{p} }}} \right)^{z} \left( {\frac{{T_{R} - T_{\infty } }}{{T - T_{\infty } }}} \right)^{s} } \right]}}$$
(13)

Roelands specified a universal value of the divergence temperature, T ∞ = −135 °C. The viscosity predicted by this model is plotted as the dashed curves in Fig. 10. Now the reader should recognize that this is not the pressure or temperature dependence of a mineral oil and that this was not the intended use of Roelands’ equation.

The shear stresses for the Roelands and Eyring assumptions are plotted for pressure steps of 25 MPa and the indicated temperatures in Fig. 12 where it is again assumed that the shear rate is \(\dot{\gamma } = 10\) s−1. The response reported in Fig. 12 is quite different from Figs. 9 and 11. There is no clear break point at stress of 2 MPa going from nearly exponential to linear. It is more difficult to identify any interval of linear behavior in Fig. 12.

Fig. 12
figure 12

Shear stress in mineral oil for \(\dot{\gamma }\) = 10 s−1, calculated at pressure intervals of 25 MPa. Roelands and Eyring Properties come from the rheology assumed in Ref. [38]

Full size image

The Luleå high-pressure chamber results cannot be explained by slower-than-exponential piezoviscosity and sinh-law shear dependence. It is clear that the simplest explanation of the linear shear response observed in the Luleå high-pressure chamber results from super-Arrhenius piezoviscosity and ordinary shear-thinning.

6 Conclusion

Ninety years of measurements of the dynamic properties of supercooled van der Waals liquids to high pressure have established that faster-than-exponential response to pressure is universal and must be accounted for in a quantitative approach to EHL. For ordinary lubricants, the low pressure response is most often slower-than-exponential, resulting in an inflection point in a log viscosity versus pressure plot. The absence of this real behavior from classical EHL has had serious consequences and is at the heart of the failure to understand the mechanism of friction.

For example, when the inflection is not acknowledged, and two liquids with similar low pressure behavior have different inflection pressures, then the difference in viscosity in the Hertz zone cannot be accounted for. Different liquids may appear to be the same at low pressure (similar pressure-viscosity coefficients) while having quite different viscosity in the Hertz contact region. Differences in friction between similar liquids can be explained by differences in inflection pressure. This behavior is critical for the understanding of friction in classical EHL, especially at low sliding speeds. By examples it was shown that the response of liquids to combined high pressure and high shear stress can only be understood when realistic pressure dependence of viscosity is employed.

Contact-based measurements have not provided accurate estimates of the pressure dependence of viscosity (see [3] for instance). Film thickness is sensitive only to the piezoviscous response near ambient pressure. If a perfect film thickness formula existed and a perfect definition of pressure-viscosity coefficient existed, then for a Newtonian liquid with the idealized compressibility, it would be possible to extract a pressure-viscosity coefficient from a perfect film thickness measurement carried out at perfectly stationary conditions. However, having just the coefficient gives no information regarding the functional form of the pressure-viscosity behavior.

Friction in the very low slide/roll regime is affected by roller elastic creep. At slightly greater slide/roll ratio, a true Newtonian regime may appear; however, it has not proven possible to deconvolve the pressure-viscosity function from friction measurement which is necessarily the average of the local shear stress over an area for which the pressure is variable and the surface not well defined. In the high sliding regime, the details of the piezoviscous response are obscured by thermal and non-Newtonian effects [35].

The departure from exponential pressure dependence is related to fragility, a property which quantifies the rapid increase in the sensitivity of the dynamic properties to changes in temperature and pressure as the glass point is approached from the liquid side. While the pressure fragility is related to the temperature fragility [14], there is no known formula for predicting one from the other.

It should be clear that, had classical EHL employed realistic pressure dependence of viscosity from its beginning, the field would have been in a better position today to solve engineering problems which involve the differences among lubricant chemical structures.