Rubber Friction on Ice: Experiments and Modeling

Abstract

Rubber friction on ice is studied both experimentally and theoretically. The friction tests involve three different rubber tread compounds and four ice surfaces exhibiting different roughness characteristics. Tests are carried out at four different ambient air temperatures ranging from $-5$ to $-13\,^{\circ }\hbox {C}$, under three different nominal pressures ranging from 0.15 to $0.45\,\hbox {MPa}$, and at the sliding speed 0.65 m/s. The viscoelastic properties of all the rubber compounds are characterized using dynamic mechanical analysis. The surface topography of all ice surfaces is measured optically. This provides access to standard roughness quantities and to the surface roughness power spectra. As for modeling, we consider two important contributions to rubber friction on ice: (1) a contribution from the viscoelasticity of the rubber activated by ice asperities scratching the rubber surface and (2) an adhesive contribution from shearing the area of real contact between rubber and ice. At first, a macroscopic empirical formula for the friction coefficient is fitted to our test results, yielding a satisfactory correlation. In order to get insight into microscopic features of rubber friction on ice, we also apply the Persson rubber friction and contact mechanics theory. We discuss the role of temperature-dependent plastic smoothing of the ice surfaces and of frictional heating-induced formation of a meltwater film between rubber and ice. The elaborate model exhibits very satisfactory predictive capabilities. The study shows the importance of combining advanced testing and state-of-the-art modeling regarding rubber friction on ice.

1 Introduction

Friction on ice has been studied for many years [3, 4, 6, 14, 15, 28]. We here focus on rubber friction on ice, a topic of great practical importance when it comes to grip of tires on icy road surfaces [9]. Notably, roughness characteristics of natural ice surfaces exhibit relatively large fluctuations, hence the scatter of results from outdoor testing. This is the motivation to perform well-controlled indoor tests on a linear friction tester, based on four different ice surface types I1–I4.

When a rubber block is sliding on an ice surface, friction will result largely from two processes, namely (1) from viscoelastic deformation of rubber activated by interactions with ice asperities [16, 23], referred to as viscoelastic contribution to friction, and (2) from shearing the area of real contact [4], referred to as adhesive contribution to friction. As for the latter contribution, it is important whether or not a thin meltwater film forms in the area of contact. The likeliness of meltwater formation increases with increasing sliding speed, with increasing nominal contact pressure, and with increasing ambient temperature. When a water film separates the sliding surfaces, the frictional shear stress is proportional to the small viscosity of water, such that the adhesive contribution to friction is in most cases negligible compared to the viscoelastic contribution. If no meltwater film is produced, the frictional shear stress results from the adhesive interaction between the ice surface and the rubber molecules at the sliding interface [27, 30], and the adhesive ice-rubber interaction will give an important contribution to the friction force.

Several experimental studies of rubber friction on ice have been performed. Grosch [10] as well as Southern and Walker [32] measured the friction coefficient $\mu$ at sliding speeds v below $\approx 1\,\hbox {cm/s}$ for many different temperatures. Introducing a temperature-velocity shift factor $a_{\mathrm{T}}$, they found that the $\mu (v)$ segments (referring to the investigated temperatures) can be shifted along the velocity axis, to form a smooth master curve $\mu (v)$ for the friction coefficient. The shift factor $a_{\mathrm{T}}$ obtained in this approach was found to be similar to the Williams–Landel–Ferry formula [35], which relates the temperature and frequency dependency of the rubber viscoelastic modulus. This is a somewhat surprising result, for the following reasons: Given the small sliding velocities investigated in Refs. [10, 32], frictional heating cannot be expected to result in a meltwater film in the asperity contact regions. Therefore, the frictional shear stress in the area of real contact is expected to give an important contribution to the friction, and it is surprising that the temperature dependency of friction coefficient is similar to the one of the viscoelastic modulus of the bulk rubber. A similar conclusion was drawn recently for dry surfaces, where it has been shown that the adhesive contribution to the friction from the real contact area exhibits a temperature dependency different from that of the viscoelastic modulus of the bulk rubber [20].

The real (microscopic) area of contact between a rubber block and an ice surface depends on the surface roughnesses of the two contact partners. Both exhibit roughness wavelengths covering several orders of magnitude. Since both rubber and ice are deformable solids, the real contact area is known to depend also on the viscoelastic modulus of the rubber and on the plastic yield stress of the ice [2]. Even if the macroscopic (average) contact pressure between rubber and ice is not large enough to deform ice plastically at the macroscopic scale referring to long-wavelength roughness components, plastic deformations (or even melting) may well occur at the microscopic scale referring to short-wavelength roughness components [23]. This will result in an effective smoothing of the ice surface at small-length scales, reducing the viscoelastic contribution of the rubber friction as compared to the case of a rigid substrate with the same surface roughness. That is, the yield stress (or penetration hardness), or surface melting, determines the large cutoff wavenumber $q_1$ to be used when calculating the viscoelastic contribution to the friction force. The penetration hardness of ice depends on the temperature and the indentation speed. This will result in a temperature (and velocity) dependency of the effective cutoff wavenumber $q_1$, contributing to the temperature dependency of rubber friction on ice.

In the present paper, we present and analyze an indoor friction test series involving three types of rubber compounds on four types of differently produced ice surfaces, with the aim to get insight into the dependency of friction coefficients on the ambient air temperature and on the nominal contact pressure. To this end, the friction tests are carried out at a constant sliding velocity which is representative for braking with an antiblockage system. As for the evaluation of the test series, we first fit an empirical friction formula after [13] and [12], in order to reproduce the measurements and to provide interpolations between tested scenarios, such as required for numerical simulations supporting the development of winter tires. The macroscopic and phenomenological nature of the fitting function is the motivation to extend our theoretical analysis toward the micromechanical Persson rubber friction and contact theory [7, 23, 24, 29]. The latter envisions two essential contributions to rubber friction on ice: (1) a contribution from the viscoelasticity of the rubber activated by ice asperities scratching the rubber surface, and (2) an adhesive contribution resulting from shearing the area of real contact under the real contact pressure. The elaborate theory provides interesting insight into the microscopic physical origin of rubber friction on ice. Going beyond the context of the performed indoor test series, the theory also allows for computing model predictions for untested scenarios, i.e., for different sliding velocities.

In more detail, this paper is structured as follows. In Sect. 2, we present experimental results for rubber friction on ice. We consider three different rubber tread compounds on four different ice surfaces, tested at four different ambient air temperatures (from −5 to −13 °C), under three different nominal pressures (from 0.15 to $0.45\,\hbox {MPa}$), and prescribed a sliding speed of 0.65 m/s. We also provide viscoelastic properties of the rubber compounds measured in dynamic mechanical analysis, and the surface topographies of the ice surfaces identified with an optical instrument. In Sect. 3, we present two modeling approaches to analyze the experimental friction results. First, we fit a macroscopic empirical formula to the measured friction coefficients. The formula depends on the hardness of the rubber compounds, the roughness of the ice surfaces, the ambient air temperature, and the nominal contact pressure [12, 13]. In order to gain a deeper insight into microscopic processes determining rubber friction on ice, we employ the Persson rubber friction and contact mechanics theory [7, 23, 24, 29]. This model accurately takes into account the viscoelastic contribution to the friction force, and also determines the area of real contact $A_1$ which is needed for quantifying the adhesive contribution to the friction. In our study, we include the (temperature-dependent) plastic smoothing of the ice surfaces, and the frictional heating-induced formation of a meltwater film between rubber and ice. In Sect. 4, we discuss the reproduction quality of the macroscopic formula and the predictive capabilities of the micromechanical model. This leads to the conclusions presented in Sect. 5.

2 Materials, Experimental Methods, and Test Results

We here present test results quantifying hardness and viscoelastic properties of the rubber specimens (Sect. 2.1). We also describe four different ice production methods and provide surface roughness measurements (Sect. 2.2). Finally, we report on results from indoor testing of rubber friction on ice (Sect. 2.3).

2.1 Hardness and Viscoelasticity of the Rubber Tread Compounds

Three different rubber tread compounds (denoted as R1, R2, and R3) are tested. Their material compositions were selected to be markedly different, in order to study a wide interval of rubber products representative for car tires. R1 is a highly silica-filled compound for all season tires, R2 a partially silica-filled compound for studless winter tires, and R3 a partially silica-filled compound for stud winter tires. Standard shore-A hardness and Poisson’s ratio of all three compounds were provided by the rubber producer, as well as Young’s modulus. The latter was calculated at 10 % strain by means of a strain test at 500 mm/min at 25 °C; see Table 1.

Table 1 Properties of the three tested rubber tread compounds

The viscoelastic properties of the rubber tread compounds are characterized using dynamic mechanical analysis at FZ-Jülich. Cyclic stretching with a strain amplitude $\varepsilon _0=0.04\,{\%}$ allows for characterizing the linear stress–strain response as a function of the stretching frequency f (with $\omega =2 \pi f$). The imposed strain history reads as

$$\begin{aligned} \varepsilon (t) = \varepsilon _0\,\sin (\omega \,t) \end{aligned}$$

(1)

where t is the time. The measured stress history exhibits an amplitude $\sigma _0$, and a phase lag $\delta$ relative to the applied strain:

$$\begin{aligned} \sigma (t) = \sigma _0\,\sin (\omega \,t + \delta ) \end{aligned}$$

(2)

In order to study $\sigma _0$ and $\delta$ as functions of temperature and stretching frequency $f= \omega /2 \pi$, we tested all three rubber compounds at many different temperatures ranging from $-70$ to $+120\,^{\circ }\hbox {C}$ using several frequencies between 0.25 and $28\,\hbox {Hz}$. Fig. 1a shows the real part of the elastic modulus $\hbox {Re}E =(\sigma _0/\varepsilon _0)\cos \delta$ and Fig. 1b $\tan \delta$ as functions of f. The presented curves refer to the reference temperature $T_0=20\,^{\circ }\hbox {C}$. They were obtained by shifting the measured frequency segments along the frequency axis in order to obtain as smooth master curves as possible. Their quality is underlined, since storage modulus $\hbox {Re}E(f)$ and loss modulus $\hbox {Im}E = (\sigma _0/\varepsilon _0)\sin \delta$ are related via the Kramers-Kronig relation [18], which must hold for any linear response function [21]. The glass transition temperatures $T_{{\mathrm{g}}}$ are defined in this context as the temperature where $\tan \delta (T)$ is maximal when testing at a test frequency $f = 0.01\,\hbox {Hz}$. For the three compounds R1, R2, and R3, they follow as $T_{{\mathrm{g}}} = -63.8$, $-59.9$, and $-73.0\,^{\circ }\hbox {C}$, respectively (see Table 1).

Fig. 1

Results of dynamic mechanical analysis of the three rubber tread compounds: a real part of the viscoelastic modulus, and b tangent of the phase lag between stress and strain, $\tan \delta$, both as functions of the frequency f. Reference temperature and linear strain amplitude amounted to $T_0=20\,^{\circ }\hbox {C}$ and to 0.04 %, respectively; obtained glass transition temperatures are listed in Table 1 (Color figure online)

In the friction tests, the local strains prevailing in the asperity contact regions may reach up to $\approx 100\,\%$. We have therefore performed strain sweeps up to $\approx 100\,\%$ strain amplitude, at the testing frequency $f=1\,\hbox {Hz}$, and at several temperatures ranging from $-20$ to $+50\,^{\circ } {{\mathrm{C}}}$. Stress amplitudes are quantified as the ratio of applied force and the cross-sectional area of the sample in the initial, prestrained state. Our measurements allow for evaluating the ratio between the viscoelastic moduli at a finite strain amplitude and at quasi-zero strain amplitude 0.04 % (see Fig. 2).

Fig. 2

Results of dynamic mechanical analysis of the three rubber tread compounds: ratio between the viscoelastic moduli at finite strain amplitudes and at quasi-zero strain amplitude amounting to 0.04 %; the shown results are the average over measurements performed at several temperatures and fixed frequency $f=1\,\hbox {Hz}$; the cross section of the pre-stretched sample (and not the one of the undeformed rubber strip) was used for calculating the stress (Color figure online)

2.2 Production and Roughness Characterization of Ice Surfaces

Four different ice surfaces (denoted as I1, I2, I3, and I4) are used in our study. In order to obtain markedly different surface roughness characteristics, we used the following four methods for the production of the ice surfaces at $-5\,^{\circ }\hbox {C}$:

• 1. Ice type I1 is produced by filling distilled water into an aluminum box and by letting it freeze. This is done in several layers, in order to reduce surface unevenness resulting from freezing-related swelling.

• 2. Ice type I2 is produced by pouring distilled water little by little over a tilted plastic surface and by letting the flowing water film freeze on the cooled surface. This way, we get a quite wavy ice surface which is visually free of air bubbles.

• 3. Ice type I3 is produced by pouring distilled water little by little over a horizontally arranged aluminum plate and by distributing it over the cooled surface using a standard squeegee.

• 4. Ice type I4 is obtained from turning an ice block of type I1 upside down.

One ice block of each type was used for all friction tests as well as for the roughness characterization. The roughness of the four ice surfaces is characterized using an optical roughness measurement system (RMS for short) produced by Dufournier Technologies [1]. It measures reflections of a laser beam with a resolution of 100 individual measurements per millimeter, in order to quantify the substrate height fluctuations h(x) from the average surface plane. Here x is a coordinate running along straight lines exhibiting a length $l = 150\,\hbox {mm}$. In other words, the instrument collects $N=15{,}000$ height data points per measured line. On each of the ice surfaces, conditioned to −5 °C, five different lines were scanned five times each, resulting in a statistically representative database (see Fig. 3 for 1 out of 25 available measurements per ice surface). From the measured substrate height fluctuations, we calculate three standard roughness parameters $R_{{\mathrm{a}}}$, $R_{{\mathrm{q}}}$ and $R_{{\mathrm{p}}}$, the root-mean-square slope $R_{\mathrm{dq}}$, and the surface roughness power spectra.

Fig. 3

Results from roughness characterization of the four ice surfaces: height fluctuations (with resolution 100 measurements per millimeter) along 150 mm long straight lines on the ice surfaces, as recorded by the roughness measurement system (RMS) produced by Dufournier Technologies [1]; the long-wavelength part of the surface roughness is not important for rubber friction on ice, because it is in the surface roughness roll-off region which has very small influence on the friction and the contact area (see Sect. 3) (Color figure online)

The average of the absolute value of the surface height fluctuations, $R_{{\mathrm{a}}}$, the root mean square of the fluctuations, $R_{{\mathrm{q}}}$, and the mean peak height, $R_{{\mathrm{p}}}$, represent three standard surface roughness quantities [33]. The former two are defined as

$$\begin{aligned} R_{{\mathrm{a}}} = {1\over N} \sum _{i=1}^{N} |h(x_i)| \qquad R_{{\mathrm{q}}} = \sqrt{{1\over N} \sum _{i=1}^{N} h^2(x_i)} \end{aligned}$$

(3)

As for $R_{\mathrm{p}}$, each measurement line is subdivided into five 30 mm intervals, and the maximum peaks inside these intervals are averaged [33]

$$\begin{aligned}&R_{{\mathrm{p}}} = \sum _{i=1}^5 \frac{z_i}{5} \quad \hbox {with} \quad z_i = \max _x h(x) \nonumber \\&\quad \hbox {and} \quad (i-1)\cdot 30\,\hbox {mm} \le x \le i\cdot 30\,\hbox {mm} \end{aligned}$$

(4)

Mean values (over 25 individual measurements) of surface roughness quantities $R_{{\mathrm{a}}}$, $R_{{\mathrm{q}}}$, and $R_{{\mathrm{p}}}$, show the same trends, i.e., ice types I3 and I4 exhibit the smallest surface roughness, ice type I1 ranges on an intermediate level, and ice type I2 is the roughest surface (see Table 2).

Table 2 Results from roughness characterization of the four ice surfaces: mean values (over 25 individual measurements) of surface roughness quantities $R_{\mathrm{a}}$, $R_{\mathrm{q}}$, $R_{\mathrm{p}}$, and $R_{\mathrm{dq}}$ (see (3)–(6))

The dimensionless root-mean-square slope $R_{{\mathrm{dq}}}$ is another useful quantity to assess the measured roughness profile. Quantification of $R_{{\mathrm{dq}}}$ is based on applying, in a first step, the following fifth-order Savitzky–Golay smoothing filter to the surface measurements

$$\begin{aligned} {\Delta }(x_i)&= -{1\over 60{\Delta } x} ( h_{i-3}-9h_{i-2}+45h_{i-1} \nonumber \\&\quad-45 h_{i+1}+9h_{i+2}-h_{i+3}) \end{aligned}$$

(5)

where $h_i = h(x_i)$ and ${\Delta } x = 10\,{{\mu \mathrm{m}}}$ denote the distance between two neighboring data points. The root-mean-square slope $R_{{\mathrm{dq}}}$ is quantified, in a second step, according to

$$\begin{aligned} R_{{\mathrm{dq}}} = \sqrt{{1\over N-6} \sum _{i=4}^{N-3}{\Delta }^2(x_i)} \end{aligned}$$

(6)

Ice surface type I1 exhibits the largest root-mean-square slope ($R_{{\mathrm{dq}}}=1.395$), followed by I4, and I2, and I3 exhibits the smallest root-mean-square slope ($R_{{\mathrm{dq}}}=0.549$) (see Table 2). We note that while the root-mean-square roughness $R_{{\mathrm{q}}}$ (and $R_{{\mathrm{a}}}$) depends mainly on the long-wavelength roughness components, the root-mean-square slope $R_{{\mathrm{dq}}}$ depends on all the roughness components, and in particular on the short-wavelength roughness components, and will therefore depend on the short cutoff wavelength (or large cutoff wavenumber) which in the study above is determined by the resolution ${\Delta } x = 10\,{{\mu \mathrm{m}}}$ of our topography instrument.

The surface roughness power spectrum C(q) allows for the most comprehensive quantification of surface roughness characteristics [26]. In the present case of surface roughness data measured along one-dimensional (1D) lines (i.e., not over two-dimensional areas), they are defined via the following Fourier transform

$$\begin{aligned} C_{1{\mathrm{D}}}(q) = \frac{1}{2\pi } \int_{- {\infty}}^{+ {\infty}} dx \ \langle h(x)\,h(0)\rangle \, \exp ({-iqx}) \end{aligned}$$

(7)

where $\langle \dots \rangle$ denotes ensemble averaging, and q stands for the wavenumber, which is inversely proportional to the wavelength $\lambda$, i.e., $q= 2\,\pi /\lambda$, of a surface roughness component. For surfaces with isotropic roughness properties, the 2D surface roughness power spectrum, which enters in the rubber friction theory, can be obtained from the 1D power spectrum via

$$\begin{aligned} C_{2{\mathrm{D}}}(q) ={1\over \pi } \int _{\mathrm{q}}^\infty dk {1 \over (k^2 -q^2)^{1/2}} \left[ -{dC_{1{\mathrm{D}}}\over dk}(k)\right] . \end{aligned}$$

(8)

Figure 4 shows the 2D power spectra, calculated from $C_{1{\mathrm{D}}}(q)$ using the equation above, for the four ice types and one rubber tread block. Notably, in the region of small wavelengths, i.e., in the region of wavenumbers $q>10^4\,\hbox {m}^{-1}$, the logarithm of the roughness power spectra decreases virtually linearly with increasing logarithm of the wavenumber (Fig. 4). In this wavenumber region, the slope in the double-logarithmic plot amounts to $\beta = -4$, and this corresponds to a Hurst exponent $H^* =-\beta /2-1=1$, i.e., to a self-affine fractal surface with fractal dimension $D_{{\mathrm{f}}} = 3-H^*=2$.

Fig. 4

The surface roughness 2D power spectra of the four ice surfaces and one rubber tread block surface. The ice surface 1D root-mean-square slope (including roughness in the studied wavenumber region) for surfaces 1–4 is 1.395, 0.780, 0.549, and 0.901, respectively (see Table 2). The dashed line has the slope $-4$ corresponding to the Hurst exponent $H=1$ (or fractal dimension $D_{{\mathrm{f}}} = 3-H=2$) (Color figure online)

2.3 Rubber Friction on Ice: Experiments on a Linear Friction Tester

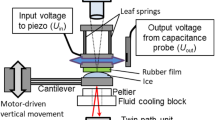
Friction tests of rubber tread blocks on ice are performed on the Linear Friction Tester of Vienna University of Technology. In each individual test, a rubber tread block is slid over 21 cm of an ice surface, at the prescribed sliding speed of 0.65 m/s. This velocity is representative for the slip velocities prevailing during tire braking with an antilock braking system [19, 31]. Tests are carried out under different ambient air temperatures ($=background \,temperatures \,T_0$) amounting to $-5$, $-8$, $-10$, and $-13\,^{\circ }{{\mathrm{C}}}$, and under different nominal contact pressures of 0.15, 0.30, and 0.45 MPa, respectively. During sliding, both the normal force and the tangential (friction) force are measured continuously using a piezoelectric sensor integrated in the test device. Notably, the desired sliding speed was actually not reached along the total 21 cm sliding distance, but after an accelerating distance of approximately 2.5 cm (the breaking distance has the same length). To ensure the comparability to other tests, which needed longer accelerating distances, we average the measured friction coefficients $\mu (x)$ over the central 11 cm interval to come up with one characteristic friction coefficient for each single test. For each test at a specific combination of test variables, i.e., for each rubber tread block type, for each ice surface type, for each background temperature, and for each nominal contact pressure, there was a minimum of four retests. The quality of the more than 720 identified friction coefficients is quantified by the mean standard deviation, which amounts to satisfactory 2–2.5 % of the mean values of friction coefficients.

An important aspect for the assessment of the test results is also the test procedure, especially because the delays between individual measurements might affect the surface roughness and indirectly the friction behavior. Therefore, we continue with describing the test procedure in more detail.

2.3.1 Test Procedure

The used linear friction tester can handle five rubber samples which are to be tested on the same test surface. Initially, the specimens are pneumatically clamped in specimen holders. For each individual friction test, the respective specimen is automatically handed over to the sledge of the friction tester and the test is performed. After that, the specimen is automatically returned and clamped back in the holder. This way, two successive friction tests are separated by a time interval of about 1 min. In total, 25 friction tests were performed automatically, i.e., five tests with each of the five rubber specimens (one reference sample and four test samples). This was organized in five subsequent testing rounds. Within each round, friction testing was started with the reference sample, followed by samples 1, 2, 3, and 4. After the fifth testing round, samples 1–4 were replaced by another set of samples. This manual intervention took some 5 min, before testing could be resumed. In this way, quasi-continuous testing was carried out for typically 8 h per day. Changes regarding the tested ice surface and/or the testing temperature were carried out, if necessary, at the end of each working day, as to ensure that temperature equilibrium was achieved in the morning before the test routine was started anew.

Summarizing, three characteristic time intervals separated two subsequent tests: either 1, 5 min, or 16 h. As we did not find significant differences in the friction coefficients obtained with the reference sample, we may conclude that possible ice aging during the delays between subsequent tests did not affect the quality of measurements.

2.3.2 Discussion of Friction Coefficients

In the sequel, we discuss selected friction tests in order to highlight typical relationships between friction coefficients, on the one hand, and compound, pressure and temperature, on the other hand. While the three different rubber tread compounds exhibit a markedly different friction performance, it is noteworthy that ice types I3 and I4 exhibit a similar friction behavior, while smaller friction coefficients are measured on ice surface types I1 and I2 (see Table 3). The observed sensitivities of friction coefficients with respect to different nominal pressures, different background temperatures, and different ice surface roughness are discussed next.

• For ice surface I1, the friction coefficients of compound R1 exhibit almost no pressure dependency, except for the lowest temperature (see Fig. 5a). Compound R2 exhibits a somewhat intermediate behavior, while the friction coefficient of compound R3 decreases significantly with increasing nominal contact pressures (Fig. 5c). This pressure sensitivity generally increases with decreasing background temperature, i.e., with increasing friction level.

• For ice surface I1, Fig. 6 shows that the friction coefficients measured under the same nominal contact pressures decrease virtually linearly with increasing temperature, and extrapolating to the ice melting temperature result in positive friction coefficients.

• When it comes to comparison of friction coefficients measured on different ice surfaces, one could expect—at a first glance— that the friction coefficients should increase with increasing ice surface roughness. Our measurements, however, indicate the seeming paradox that friction coefficients actually decrease with increasing ice surface roughness (see Table 3 under consideration of the roughness quantities listed in Table 2).

These experimental results indicate that it is quite challenging to model the observed behavior, as described next.

Table 3 Results from testing rubber friction on ice on a linear friction tester at sliding speed $v=0.65\,\hbox {m/s}$: measured friction coefficients of rubber tread compounds R1, R2, and R3 (Table 1) on ice surfaces I1, I2, I3, and I4, as functions of temperature and of nominal contact pressure $p_1=0.15$, $p_2=0.30$, and $p_3=0.45\,\hbox {MPa}$, respectively

Fig. 5

Results from testing rubber friction on ice on a linear friction tester at sliding speed $v=0.65\,\hbox {m/s}$: measured friction coefficient as a function of the nominal contact pressure for several background temperatures (from top to bottom): $T=-13$ ($\times$), $-10$ ($+$), $-8$ ($\circ$), and $-5\,^{\circ }{{\mathrm{C}}}$ ($*$); results refer to the three rubber compounds a R1, b R2, and c R3 on ice surface I1 (Color figure online)

Fig. 6

The measured friction coefficient as a function of temperature for several nominal contact pressures (from top to bottom): $p=0.15$, 0.30, and $0.45\,{\mathrm{MPa}}$. Results are shown for 3 rubber compounds: R1 (red), R2 (green), and R3 (blue) on ice surface I1. The sliding speed is $v=0.65\,\hbox {m/s}$ (Color figure online)

3 Modeling Rubber Friction on Ice

As for modeling, we envision two essential contributions to rubber friction on ice: (1) a contribution from the viscoelasticity of the rubber activated by ice asperities scratching the rubber surface, and (2) an adhesive contribution from shearing the area of real contact. At first, we use a macroscopic and empirical approach, i.e., we fit the variable coefficients of a phenomenological formula, such that the measurements of the friction coefficients are reproduced in an optimal fashion (see Sect. 3.1). Subsequently, we use a micromechanical approach, i.e., we apply the Persson rubber friction and contact mechanics theory in order to predict the measured friction coefficients, see Sect. 3.2.

3.1 Macroscopic, Empirical Description of Rubber Friction on Ice

As for practical applications related to tire development, the numerical simulation of rubber friction on ice is of interest, e.g., by means of the finite element method. This is a very challenging task, given the complexity of the underlying physical processes. One feasible solution to this problem is to use results of friction experiments as input for the numerical simulation. In this context, it is valuable to fit the variable coefficients of a phenomenological formula, with the aims to reproduce the experimental measurements and to provide a reasonable interpolation between tested scenarios, as described next.

This phenomenological approach is inspired by the empirical friction law after Huemer [13] and Hofstetter [12], which expresses the friction coefficient as a function of the nominal contact pressure p and of the sliding velocity v:

$$\begin{aligned} \mu = \frac{\alpha \cdot p^{n-1} + \beta }{a+b \cdot v^{-1/m} + c \cdot v^{-2/m}} \end{aligned}$$

(9)

where $\alpha$, $\beta$, a, b, c, m, and n represent fitting parameters. Notably, the rubber friction tests on ice reported herein were carried out at the same sliding velocity $v=0.65\,\hbox {m/s}$, such that the denominator in (9) is constant. Our extension of (9) regards explicit consideration of the background (or initial) temperature $T_0$, of the ice surface roughness $R_{{\mathrm{p}}}$, and of the rubber hardness H:

$$\begin{aligned} \mu =&\left[ a_1\,\left( \frac{p}{p_{ref}}\right) ^{a_5-1} + a_2 + \frac{a_3 \, (T_0-T_{\mathrm{m}})}{R_{{\mathrm{p}}}+ \big [(H-a_6)^{-a_8} -a_7\big ] \cdot a_4} \right] \nonumber \\&\cdot \Big [(H-a_6)^{-a_8} -a_7\Big ] \end{aligned}$$

(10)

where $T_{\mathrm{m}}$ denotes the melting temperature and $p_{ref}=1\,\mathrm {MPa}$. The coefficients in (10) are identified such that modeled friction coefficients agree—in a best possible fashion—with the measured friction coefficients. To this end, (10) is first specified for rubber hardness values H listed in Table 1, for ice roughness values $R_{{\mathrm{p}}}$ listed in Table 2, as well as for background temperatures and nominal contact pressures listed in Table 3, and then, coefficients are optimized numerically such that the correlation between modeled friction coefficients and measured friction coefficients listed in Table 3 attains a maximum. A standard least-squares method delivers

$$\begin{aligned} \begin{array}{lll} a_1 = 11.9 &{}\quad a_2 = -8.92 &{}\quad a_3 = 2.29\,\hbox {mm/K} \\ a_4 = 52.0\,\hbox {mm} &{}\quad a_5 = 0.780 &{}\quad a_6 = 45.0 \\ a_7 = 0.512 &{}\quad a_8 = 0.210&{}\\ \end{array} \end{aligned}$$

(11)

Equation (10) with the coefficients (11) reproduces the measured friction coefficients (Table 3) reliably, as quantified through a quadratic correlation coefficient amounting to satisfactory $r^2=98.5\,{\%}$ and a root-mean-square deviation of 3.29 % for the complete test series, and compare also Figs. 5 and 7.

Fig. 7

Friction coefficients obtained with fitted formula (10) specified for optimal coefficients (11): estimated friction coefficient as a function of the nominal contact pressure for several background temperatures (from top to bottom): $T=-13$ ($\times$), $-10$ ($+$), $-8$ ($\circ$), and $-5\,^{\circ }{{\mathrm{C}}}$ ($*$); results refer to the three rubber compounds a R1, b R2, and c R3 on ice surface I1 (Color figure online)

The performance of the fitted phenomenological friction model (10) is satisfactory, but the agreement with experiments remains a result of a fitting process. In addition, the identified optimal coefficients are of macroscopic and empirical nature, i.e., they do not provide insight into the microscopic processes (in the contact area between rubber and ice) which are responsible for the macroscopically observed friction behavior. This provides the motivation to apply the micromechanical Persson rubber friction and (multi-scale) contact mechanics theory, as discussed next.

3.2 Microscopic Description of Rubber Friction on Ice

We here consider two additive contributions to the rubber friction on ice: (1) an adhesive contribution, $\mu _{{\mathrm{adh}}}$, resulting from shearing the area of real contact between rubber and ice, and (2) a viscoelastic contribution, $\mu _{{\mathrm{vis}}}$, resulting from time-dependent deformations of the rubber surface, induced by ice asperities on many length scales:

$$\begin{aligned} \mu = \mu _{{\mathrm{adh}}} + \mu _{{\mathrm{vis}}} \end{aligned}$$

(12)

In the sequel, we quantify friction coefficients between rubber and ice at the extreme temperatures of $-5$ and $-13\,^{\circ }\mathrm {C}$, based on the Persson rubber friction and contact mechanics theory. Focusing on dominating physical processes, we aim at developing an approach which is as simple as possible and only as complex as necessary.

When rubber and ice come into contact, determination of the actual area of contact is challenging, because surfaces of solid objects generally exhibit roughness components on all length scales from the macroscopic size of the objects down to atomistic length scales. The apparent area of contact, A, depends on the utilized resolution of surface roughness. The corresponding resolution limit is either defined in terms of a minimum wavelength $\lambda _1$ or, alternatively, in terms of a maximum wavenumber $q_1= 2 \pi / \lambda_1$, whereby the latter is referred to as cutoff wavenumber. As $q_1$ increases, the contact area $A=A(q_1)$ decreases, while the apparent contact pressure p increases. The latter follows as $p = p_0\,A_0/A(q_1)$, where $p_0$ is the nominal contact pressure and $A_0$ the nominal contact area.

3.2.1 Plastic Deformation of Ice

Provided that contact pressure p reaches the order of magnitude of the penetration hardness of ice, $\sigma _{{\mathrm{Y}}}$, plastic deformations are likely to occur, and they will smoothen the ice surface at small length scales. Thus, the contact area will be nearly constant, even if smaller and smaller wavelength roughness components are included in the analysis. This underlines that the cutoff wavenumber $q_1$ depends on the penetration hardness of ice.

Penetration hardness of ice is still not fully understood, although many experimental studies exists. They have shown that penetration hardness depends, e.g., on the temperature, on the indentation speed, on the grain size, and on possible ice contamination such as by salt. Barnes et al. [2], for instance, have shown that the penetration hardness is temperature-activated in the temperature range from $-3$ to $-13\,^{\circ } {{\mathrm{C}}}$:

$$\begin{aligned} \sigma _{{\mathrm{Y}}} = \sigma _i\,\exp ({T_1/T}), \end{aligned}$$

(13)

where T is the absolute temperature. Pressure $\sigma _i$ and temperature $T_1$ were identified by Barnes et al. [2] in dynamic hardness experiments using loading times on the order of magnitude $\approx 10^{-4}\,{\mathrm{s}}$. In more detail, Barnes et al. impacted a hard ball on ice surfaces, at known velocities, and they measured the diameter of the plastic indent which formed on the ice surface. This delivered $\sigma _i \approx 0.11\,{\mathrm{Pa}}$ and $T_1 \approx 5332\,{\mathrm{K}}$. Specifying Eq.  (13) for these quantities delivers $\sigma _{\mathrm{Y}} = 89\,{\mathrm{MPa}}$ for $T=-13\,^{\circ } {{\mathrm{C}}}$ and $\sigma _{{\mathrm{Y}}} = 48 \ {\mathrm{MPa}}$ for $T=-5\,^{\circ } {{\mathrm{C}}}$. Notably, these values refer to very short loading time magnitude of $\approx 10^{-4}\,{\mathrm{s}}$. As for loading times on the significantly larger order of magnitude $\approx 1\,{\mathrm{s}}$, more traditional indentation experiments gave nearly the same temperature $T_1$, but a significantly smaller pressure $\sigma _i \approx 0.05\,{\mathrm{MPa}}$. Thus, Eq. (13) implies that indentation hardness decreases roughly by a factor of 2, if loading time is increased from $\approx 10^{-4}\,{\mathrm{s}}$ to $\approx 1\,{\mathrm{s}}$. This is the motivation to estimate the characteristic time of loading in the here-reported experiments. In this context, we envision that the ice asperities are in contact with the rubber block from the entrance side to the exit side, i.e., along the geometric dimension L of the rubber block, measured in sliding direction. The ice asperity contact time equals $t_0 = L/v$, where v is the sliding speed. In terms of orders of magnitude, the rubber tread blocks exhibit a characteristic size $L\approx 1\,\mathrm{cm}$ and the sliding speed amounts to $v\approx 1\,\hbox {m/s}$, delivering loading time as $t_0 \approx 0.01 \ {\mathrm{s}}$. For this estimate of “indentation” time, we interpolate between the aforementioned penetration hardness values, and this delivers $\sigma _{{\mathrm{Y}}} = 63\,{\mathrm{MPa}}$ for $T=-13\,^{\circ } {{\mathrm{C}}}$ and $\sigma _{{\mathrm{Y}}} = 34 \ {\mathrm{MPa}}$ for $T=-5\,^{\circ } {\mathrm{C}}$.

It turned out that for ice the penetration hardness values estimated from indentation experiments are too large as to allow for a reliable estimation of friction coefficients. As a remedy, we use yield strength $\sigma _{{\mathrm{Y}}} = 20\,{\mathrm{MPa}}$ at $T=-13\,^{\circ } {{\mathrm{C}}}$ and $\sigma _{{\mathrm{Y}}} = 5\,{\mathrm{MPa}}$ at $T=-5\,^{\circ } {{\mathrm{C}}}$. Frictional heating and the presence of shear stresses can explain why smoothing of the ice surface starts, during a friction test, at lower contact pressures (and, hence, larger length scales) than expected based on indentation experiments, as discussed next.

• In order to underline that frictional heating softens the ice surface and reduces the penetration hardness, it is sufficient to focus on the relevant physical process and to consider characteristic orders of magnitude. In this context, we note (1) that friction produces heat at the ice-rubber interface and (2) that this energy is penetrating into the ice body, such that the ice temperature increases in a region with a characteristic layer thickness l measured from the surface. It can be quantified as $l\approx (D\,t_0)^{1/2}$, where D denotes the thermal diffusivity of ice and where $t_0 \approx 0.01\,{\mathrm{s}}$ is the characteristic contact time between rubber and ice. With heat conductivity $\kappa = 2\,{\mathrm{W/(K\,m)}}$, heat capacity $c_{{\mathrm{p}}} = 2000\,\mathrm{J/(kg\,K)}$, and mass density $\rho = 10^3\,{\mathrm{kg/m^3}}$, the thermal diffusivity of ice follows as $D = \kappa /(\rho c_{{\mathrm{p}}}) \approx 10^{-6}\,{\mathrm{m^2/s}}$, and the characteristic temperature ingress distance follows as $l \approx 0.01\,{\mathrm{mm}}$. Notably, this is on the same order of magnitude as the cutoff wavelength $1/q_1$ (see below). While this underlines that frictional heating does affect the penetration hardness, we also note that even if the ice surface would heat up close to the melting temperature, indentation hardness would still be expected to be larger than $5\,{\mathrm{MPa}}$ (see [2]).

• The presence of shear stresses (in addition to the contact pressure) is a second mechanism which is likely to reduce the effective yield stress of ice subjected to a friction tests. Because the maximum sustainable shear stress of ice amounts to just a few megapascal in the studied temperature range [11], short-wavelength roughness is likely to be removed by shear deformations as indicated in Fig. 8. Notably, this picture is supported by recent measurements by Fülöp and Tuononen [8, 17].

We assume that the combination of the two discussed effects results in the effective penetration hardness values used in the present study.

Fig. 8

Schematic picture illustrating ice smoothing by shear-induced plastic flow. The regions above the dashed lines get removed by shear deformation and deposited as ice fragments in the valleys on the ice surface (Color figure online)

3.2.2 Identification of Cutoff Wavenumbers

Cutoff wavenumbers $q_1$ are determined for all the rubber compounds sliding on the ice surface I1 by calculating the apparent contact pressure $p(q) = p_0\,A_0/A(q)$ as a function of wavenumber q, and by identifying $q_1$ so that $p(q_1)=\sigma _{{\mathrm{Y}}}(T)$. In more detail, the area of contact A(q) is defined as the area of real contact when the surface roughness with wavenumber larger than q has been removed. Starting with the smallest available wavenumber, q is progressively increased in our calculations, such that the contact area A(q) decreases and the contact pressure p(q) increases. Once the contact pressure reaches the yield stress, the corresponding wavenumber represents the cutoff wavenumber. As detailed in [23], these calculations require as input (1) the sliding speed which was set equal to $v=0.65\,\hbox {m/s}$ as in the experiments, (2) the surface roughness power spectrum of ice surface I1 (see Fig. 4), and (3) the viscoelastic properties of rubber, while considering that the rubber bodies are perfectly flat. Since the viscoelastic properties of rubber differ from compound to compound, the calculations result in compound-specific cutoff wavenumbers (see Table 4 for numerical results). It is also noteworthy that the cutoff wavenumber is practically independent of the nominal contact pressure $p_0$, in the investigated regime from 0.15 to 0.45 MPa, which is far away from complete contact. Increasing the nominal contact pressure, namely, results in an increase in effective contact area, which is almost proportional to the increase in pressure, such that the actual contact pressure remains practically the same.

Table 4 Cutoff wavenumbers $q_1$ [1/m] used for simulation of friction of the three different rubber compounds R1–R3 over ice surface I1, as a function of testing temperature T and penetration hardness $\sigma _{{\mathrm{Y}}}$

In the remaining calculations of contact area and rubber friction, we use the measured surface roughness power spectrum C(q) in the wavenumber region $q<q_1$, and we assume $C(q)=0$ in the cutoff wavenumber region $q>q_1$, where we consider effective smoothing of the ice surface. Figure 9 shows the surface roughness power spectrum on ice surface I1. The vertical lines indicate the large cutoff wavenumber $q_1$ for the rubber compounds R1 (red lines), R2 (green lines), and R3 (blue lines) (see also Table 4). In each case, the line for the largest wavenumber is for $T=-13\,^{\circ } {{\mathrm{C}}}$ and the other line for $T=-5\,^{\circ } {{\mathrm{C}}}$. For the sake of completeness, we finally note that the present study envisions cutoff wavenumber $q_1$ to be independent of the nominal contact pressure.

Fig. 9

The 2D surface roughness power spectrum of ice surface I1. The vertical lines indicate the large cutoff wavenumber $q_1$ for the rubber compounds R1 (red lines), R2 (green lines), and R3 (blue lines). In each case, the line for the largest wavenumber is for $T=-13\,^{\circ } {{\mathrm{C}}}$ and the other line for $T=-5\,^{\circ } {{\mathrm{C}}}$. The cutoff wavenumbers $q_1$ are for the sliding velocity $v=0.65\,\hbox {m/s}$ (see also Table 4) (Color figure online)

3.2.3 Adhesive Contribution from the Real Contact Area Between Rubber and Ice

The adhesive contribution to the friction coefficient, $\mu _{adh}$, is directly proportional to the frictional shear stress $\tau _{{\mathrm{f}}}$ acting in the area of contact $A_1$:

$$\begin{aligned} \mu _{{\mathrm{adh}}} = \frac{\tau _{{\mathrm{f}}}\,A_1}{p_0\,A_0}. \end{aligned}$$

(14)

Provided that a meltwater film separates the ice and rubber surfaces, the frictional shear stress is a function of the viscosity of water $\eta$, the sliding speed v, and the thickness of the meltwater film, h, i.e.,

$$\begin{aligned} \tau _{{\mathrm{f}}} = \eta {v\over h}, \end{aligned}$$

(15)

In order to underline that the adhesive contribution to friction is negligible with respect to the viscoelastic contribution, it is sufficient to consider characteristic orders of magnitude. With a thickness of the meltwater film amounting to $h=10\,{\mathrm{nm}}$, a sliding speed of $v=1\,\hbox {m/s}$, and the viscosity of water, which amounts to $\eta \approx 1.8\times 10^{-3}\,{\mathrm{Pa}}\,{\mathrm{s}}$ at the ice melting temperature, the frictional shear stress amounts to $\tau _{{\mathrm{f}}} \approx 0.18\,{\mathrm{MPa}}$. Considering that the pressure in the area of real contact is close to the yield stress of ice allows for quantifying the adhesive contribution to the friction coefficient as $\mu _{adh} \approx \tau _{{\mathrm{f}}} /\sigma _{{\mathrm{Y}}} \approx 0.01$. This is clearly negligible compared to the viscoelastic contribution to the friction.

Even if the frictional heating is not large enough to generate a thin meltwater film, the temperature increase in the contact regions will reduce the frictional shear stress $\tau _{{\mathrm{f}}}$. In fact, frictional heating will result in a shear stress which drops continuously as the temperature approaches the ice melting temperature $T_{{\mathrm{m}}}$. It has been suggested elsewhere that at sliding speeds below the critical value where a uniform meltwater film is formed in the contact regions may occur a granular ice-water state, with small water and ice domains which fluctuate rapidly in time and space [25]. Alternatively, heat-softening (which may be related to surface premelting) of the ice may occur [25]. For the rubber–ice interface, there are no direct experimental studies of this effect, which would require using a very smooth ice surface in order to eliminate the viscoelastic contribution.

For inert materials, the frictional shear stress in the area of real contact is rather small even at sliding speeds where no meltwater film is formed. Thus, as an example, for velocity and temperature conditions similar to those in the experiments reported on above, for polyethylene sliding on ice [4] the friction coefficient is typically 0.1 or less, which is smaller by a factor of 3 or 4 than the friction we observe for rubber on ice. This indicates that even if no uniform meltwater film is formed, the friction at the sliding speed $\approx 1\,\hbox {m/s}$ and for temperatures above $-15\,^{\circ } {{\mathrm{C}}}$ is dominated by the viscoelastic contribution; hence, in the present study, we will neglect the contribution from the area of real contact.

Frictional heating and the formation of a melt water film is a complex topic involving flash temperature effects in the macroasperity contact area, and a gradual heating of the solids resulting as the cumulative effect of the flash temperature. We will briefly discuss this topic in Sect. 3.2.7. A detailed study on meltwater formation and fluid squeeze-out in the context of rubber friction on ice has been performed by Wiese et al. [34]. The nature of the frictional shear stress in the area of real contact, when the sliding speed is not high enough to generate a uniform meltwater film in the area of real contact, is discussed in Ref. [25].

3.2.4 Contribution from Viscoelasticity of Rubber

We have derived a set of equations describing the viscoelastic contribution to the friction force acting on a rubber block squeezed with the stress $p_0$ against a hard randomly rough surface [7, 23, 27, 29]. In the following, we summarize the basic equations:

$$\begin{aligned} \mu (t) \approx&{1\over 2} \int _{q_0}^{q_1} dq\,q^3 \,C(q) P(q,t) \nonumber \\&\times \int _0^{2\pi } \hbox {d}\phi \,{\mathrm{cos}}\ \phi \, {\mathrm{Im}}{E(qv(t)\,{\mathrm{cos}}\,\phi , T_{\mathrm{q}}(t))\over (1-\nu ^2)p_0}. \end{aligned}$$

(16)

The temperature at time t is the sum of the background temperature $T_{q0} (t)$ and the flash temperature:

$$\begin{aligned} T_{\mathrm{q}} (t) &\,=\,T_{q0} (t)+ \int _0^t dt'\,h(w(t,t'))\int _{q_0}^{q_1} dq' f(q',t') \nonumber \\&\times {1\over \pi } \int _0^\infty dk\,{4q^2\over k^2+4q^2}\,{4q'\over k^2+4q'^2} \exp [{-Dk^2(t-t')}], \end{aligned}$$

(17)

where

$$\begin{aligned} h(w)=1-{2\over \pi } w \left( 1-w^2\right) ^{1/2} -{2\over \pi } {\mathrm{arcsin}} w, \end{aligned}$$

(18)

for $w <1$ and $h(w)=0$ for $w>1$, and where $w(t,t')=[x(t)-x(t')]/2R$ depends on the history of the sliding motion. The function f(q, t) reads as

$$\begin{aligned} f(q,t) =&{v(t) \over \rho C_v} q^4 C(q) {P(q,t)\over P(q_{{\mathrm{m}}},t)} \nonumber \\&\times \int \hbox {d} \phi \,{\mathrm{cos}} \phi \,{\mathrm{Im}}{E(qv(t)\,{\mathrm{cos}}\,\phi ,T_{\mathrm{q}}(t))\over 1-\nu ^2}, \end{aligned}$$

(19)

where $v=\dot{x}(t)$ depends on time. The function P(q, t) (which also depends on time) is represented by:

$$\begin{aligned} P(q,t)={2\over \pi } \int _0^{\infty } dx\,{{\mathrm{sin}}x \over x} \mathrm{exp} \left[ -x^2G(q,t)\right] ={\mathrm{erf}}\left( { 1\over 2 \surd G}\right) , \end{aligned}$$

where

$$\begin{aligned} G(q,t)={1\over 8}\int _{q_0}^q dq\,q^3 C(q) \int _0^{2\pi } \hbox {d}\phi \, \left| {E(qv(t)\,{\mathrm{cos}}\,\phi , T_{\mathrm{q}}(t))\over (1-\nu ^2) p_0}\right| ^2. \end{aligned}$$

The background temperature $T_{q0} (t)$ is the cumulative effect of the flash temperature and varies slowly with time compared to the flash temperature. The equations determining $T_{q0} (t)$ are given in Ref. [7]. They not only depend on the thermal properties of the rubber, but also of the substrate (here ice) and on the rubber–ice heat transfer coefficient $\alpha$. For stationary sliding, where v(t) is constant, the equations above can be simplified.

During sliding, the rubber and ice temperatures at the sliding interface depend on the position x along the interface (with $x=0$ at the leading edge and $x=L$ at the trailing edge) and on the sliding distance $s=vt$. That is, the ice and rubber background temperatures at the sliding interface will increase with increasing sliding distance s, and also as x increases from 0 (leading edge) to L (trailing edge). While it will be interesting, in the future, to study heat transfer between rubber and ice in more detail, it is beyond the scope of the present paper. As a remedy, we here use a simplified approach, i.e., we calculate the friction coefficient after approximately half the sliding distance $s=(5\,{\mathrm{cm}}+15\,{\mathrm{cm}})/2= 10\,{\mathrm{cm}}$, and assuming the local temperature at the middle $x= L/2= 1.5\,{\mathrm{cm}}$ of the rubber block prevails everywhere in the sliding interface. Also in this context, we consider two bounding cases regarding the heat transfer coefficient $\alpha$, such that realistic scenarios will fall between these two limit cases:

(1):

We first neglect heat transfer from the rubber to the ice surface, i.e., we assume the heat transfer coefficient $\alpha = 0$, see Sect. 3.2.5.

(2):

Another more realistic assumption is that the rubber surface temperature in the asperity contacts is the same as the ice temperature (corresponding to $\alpha = \infty$). In the calculations below, we actually use $\alpha = 10^7\,{\mathrm{J}}/\mathrm{m}^2{\mathrm{K}}$ which gives a temperature which is nearly continuous in the ice-rubber contact regions (see Sect. 3.2.6).

In case (2), if the surfaces of the ice asperities are covered by thin meltwater films (see Sect. 3.2.3), the temperature in the ice-rubber contact regions may be equal to, or slightly larger than, the ice melting temperature $T_{{\mathrm{m}}}$ (i.e., $\approx 0\,^{\circ } {{\mathrm{C}}}$). In this situation, the calculation of the cutoff wavenumber $q_1$ will be more complicated than the procedure we used in Sect. 3.2.2. Part of the heat flow current J from the rubber to the ice surface will be used to melt the ice, and another part $J_1$ will diffuse into the ice surface. In this case, the cutoff wavenumber $q_1$ will depend on the smoothing of the ice surface by melting, and by lowering the penetration hardness and shear strength of the ice due to the ice temperature increase. An accurate study should also include the contribution to heating by the frictional energy dissipation in the area of contact, but as shown in Sect. 3.2.3, if a thin meltwater film prevails at the sliding interface, at the sliding speed $v=0.65\,\hbox {m/s}$ this contribution is negligible compared to the viscoelastic contribution. In general, taking into account ice melting is a rather complex (time-dependent) problem which we will very briefly address in Sect. 3.2.7.

3.2.5 Model Predictions for $\alpha =0$

Let us now present some numerical results. Using the assumptions above for the case (1) ($\alpha = 0$) in Fig. 10, we show the calculated viscoelastic contribution to the friction coefficient as a function of sliding speed for the rubber compounds R1 (a), R2 (b) and R3 (c) on ice surface I1. The solid lines are the results without and the dashed lines with frictional heating. The upper and lower curves are for the background temperatures $T=-13$ and $-5\,^{\circ } {{\mathrm{C}}}$, respectively. This figure already explains the very different dependency of the friction coefficient on the nominal contact pressure observed in the experimental data in Fig. 5: For compound R3 (Fig. 10c), the friction curve without frictional heating depends strongly on the sliding speed in the vicinity of $v=0.65\,\hbox {m/s}$. This implies that when the temperature increases as a result of frictional heating (which shifts the viscoelastic modulus to higher frequencies, and hence the $\mu (v)$ curve to higher velocities), the friction will rapidly drop. Since frictional heating increases when the nominal contact pressure increases, this explains the strong drop in the sliding friction coefficient for $v=0.65\,\hbox {m/s}$ as the nominal contact pressure increases. On the other hand, for compound R1 the friction curve is nearly horizontal (see solid line in Fig. 10a) so an increase in the temperature will only have a very small influence on the friction coefficient. This explains why the measured friction coefficient for compound R1 is very weakly dependent on the nominal contact pressure. This result is the most important conclusion of this paper.

Fig. 10

The viscoelastic contribution to the friction coefficient as a function of sliding speed for the rubber compounds a R1, b R2, and c R3 on ice surface I1. The solid lines are the result without frictional heating (so the rubber temperature equals the initial temperature) and the dashed lines with frictional heating (see text for details). The upper and lower curves are for the background temperatures $T=-13$ and $-5\,^{\circ } {{\mathrm{C}}}$, respectively. The nominal contact pressure $p_0=0.15\,{\mathrm{MPa}}$ and $\alpha = 0$ (Color figure online)

Figure 11 shows the friction coefficient as a function of sliding speed for the rubber compound R3 on ice surface I1. Results are shown for several nominal pressures and for the temperatures (a) $T=-5\,^{\circ } {{\mathrm{C}}}$ and (b) $-13\,^{\circ } {{\mathrm{C}}}$. The vertical dashed lines indicate the sliding speed $v=0.65\,\hbox {m/s}$. In Fig. 12, we compare the calculated friction coefficients for $v=0.65\,\hbox {m/s}$ with the measured data. Note that for $T=-5\,^{\circ } {{\mathrm{C}}}$ the theory predictions agree almost perfectly with the measured data, while for $T=-13\,^{\circ } {{\mathrm{C}}}$ the calculated is below the measured data, but the dependency of the friction on the nominal pressure is very similar.

Fig. 11

The friction coefficient as a function of sliding speed for rubber compound R3 on ice surface I1. Results are shown for several nominal pressures and temperatures a $T=-5\,^{\circ } {{\mathrm{C}}}$ and b $-13\,^{\circ } {{\mathrm{C}}}$. The upper (black) lines in (a) and (b) are the friction coefficient without frictional heating, i.e., the temperature in the rubber equals the initial temperature. In this case, there is negligible dependency of the friction coefficient on the nominal contact pressure in the studied pressure range (Color figure online)

Fig. 12

The measured (blue squares) and calculated (red squares, based on the data in Fig. 11) friction coefficient as a function of the nominal contact pressure for compound R3 on ice surface I1 and for the temperatures $T=-5$ and $-13\,^{\circ } {{\mathrm{C}}}$ (Color figure online)

3.2.6 Model Predictions for $\alpha =10^7\,{\mathrm{J}}/{\mathrm{m}}^2{\mathrm{K}}$

Figure 13 shows the same data as in Fig. 10 but now for $\alpha = 10^7\,{\mathrm{J}}/{\mathrm{m}}^2{\mathrm{K}}$. The results are similar to those in Fig. 10, but the friction coefficients including frictional heating (dashed lines) are higher than for $\alpha = 0$. This is expected because including heat transfer from the rubber to the ice gives a lower rubber temperature, which increases the viscoelastic contribution to the friction.

Fig. 13

The viscoelastic contribution to the friction coefficient as a function of sliding speed for the rubber compounds a R1, b R2, and c R3 on ice surface I1. The solid lines are the results without frictional heating (the rubber temperature equals the initial temperature) and the dashed lines with frictional heating (see text for details). The upper and lower curves are for the background temperatures $T=-13$ and $-5\,^{\circ } {{\mathrm{C}}}$, respectively. The nominal contact pressure $p_0=0.15\,{\mathrm{MPa}}$ and $\alpha = 10^7\,{\mathrm{J}}/{\mathrm{m}}^2{\mathrm{K}}$ (Color figure online)

Figure 14 shows the measured (filled squares) and calculated (open circles and stars) friction coefficient at the temperatures $T=-13$ and $-5\,^{\circ } {{\mathrm{C}}}$ for the rubber compounds R1, R2, and R3. The open circles are for $\alpha =0$ and the stars for $\alpha = 10^7\,{\mathrm{J}}/\mathrm{m}^2{\mathrm{K}}$. In all cases, the rating predicted by the theory agrees with the experimental data. The rather small numerical differences between theory and experiments can be attributed, at least in part, to the approximations involved in the study presented above, and which we briefly address in the next section.

Fig. 14

The measured (filled squares) and calculated (open circles and stars) friction coefficient at the temperatures $T=-13$ and $-5\,^{\circ } {{\mathrm{C}}}$ for the rubber compounds R1, R2, and R3. The open circles are for $\alpha =0$ and the stars for $\alpha = 10^7\,{\mathrm{J}}/{\mathrm{m}}^2{\mathrm{K}}$. For the sliding speed $v=0.65\,\hbox {m/s}$ and the nominal contact pressure $p_0=0.15\,{\mathrm{MPa}}$ (Color figure online)

3.2.7 Spatial Dependency of the Temperature and the Frictional Shear Stress

In the study above, we only calculated the temperature and friction coefficients at the center of the rubber–ice nominal contact region. However, the temperature T(x) and the (local) friction coefficient $\mu (x)$ (corresponding to a local frictional shear stress $\mu (x) p_0$) will depend on the position x on the rubber block along the sliding direction. Figure 15 shows (a) the temperature T(x) in the ice-rubber contact regions, and (b) the (local) friction coefficient $\mu (x)$, as a function of the position x with $x=0$ at the leading edge and $x=3\,{\mathrm{cm}}$ at the trailing edge. The results are for the initial rubber and ice temperature $-13\,^{\circ } {{\mathrm{C}}}$, the nominal contact pressure $p_0=0.3\,{\mathrm{MPa}}$, the sliding speed $v=0.65\,\hbox {m/s}$, and sliding distance $s=20\,{\mathrm{cm}}$. The red line is the result assuming no melting of the ice surface. Note that the temperature is maximal and the friction coefficient minimal at the trailing edge of the rubber block (results of measurements of similar temperature distributions under various conditions can be found in Refs. [12] and [22]).

Fig. 15

The temperature in the ice-rubber contact regions (a), and the (local) friction coefficient (b), as a function of the position x on the rubber block along the sliding direction with $x=0$ at the leading edge and $x=3\,{\mathrm{cm}}$ at the trailing edge. For the initial rubber and ice temperature $-13\,^{\circ } {{\mathrm{C}}}$, the nominal contact pressure $p_0=0.3\,{\mathrm{MPa}}$, the sliding speed $v=0.65\,\hbox {m/s}$, and sliding distance $s=20\,{\mathrm{cm}}$. The red line is assuming no melting of ice and the blue line with ice melting. For the read data, the friction coefficient at $x \approx 0.3 L_x$ is equal to the average friction coefficient (Color figure online)

The friction force acting on the rubber block is given by

$$\begin{aligned} F_x = {1\over L} \int _0^L dx\,\mu (x) F_{{\mathrm{N}}} \end{aligned}$$

(20)

where $F_{{\mathrm{N}}}$ is the normal force (we have assumed that the contact pressure $p_0$ is independent of x).

Note from Fig. 15 that the temperature for $x > 1.5\,{\mathrm{cm}}$ is larger than the ice melting temperature. Thus, the present calculation is not valid for $x > 1.5\,{\mathrm{cm}}$ because one needs to take into account that melting of the ice occurs in the contact region for $1.5\,{\mathrm{cm}} < x < 3\,{\mathrm{cm}}$. Assuming that the temperature in the ice-rubber contact regions in this distance interval is close to the ice melting temperature, one obtains instead for $x> 1.5\,{\mathrm{cm}}$ the blue lines in Fig. 15.

When the ice temperature at the start of sliding equals $-5\,^{\circ } {{\mathrm{C}}}$, we find under the same assumptions as above (neglecting melting of the ice), the friction coefficient and the temperature $0.1 \ {\mathrm{cm}}$ from the leading edge to be 0.36 and $-3.3\,^{\circ } {{\mathrm{C}}}$, respectively, and at the trailing edge 0.33 and $2.1\,^{\circ } {{\mathrm{C}}}$, respectively. Thus, also in this case, the ice will melt in some parts of the nominal contact area.

In the analysis of the experimental data as presented in Sects. 3.2.5 and 3.2.6, we have not included the spatial dependency of T(x) and $\mu (x)$ (which requires a much larger computational effort), but the basic physics is already contained in the discussion presented above, which is able to explain the main effects observed in our sliding friction experiments.

4 Discussion

In the sequel, we discuss several aspects of our combined experimental–theoretical research regarding rubber friction on ice. At first, we discuss whether or not the laser of the optical surface roughness measurement system could have melted the investigated ice surfaces, because this would have changed their roughness characteristics (see Sect. 4.1). Next, we discuss if surface roughness of ice might increase with decreasing temperature, and we clarify related implications for the shown analyses (see Sect. 4.2). We continue with comparing rubber friction on ice and on asphalt, i.e., we discuss the expected magnitude of local rubber strains and the related implications regarding rubber characterization (see Sect. 4.3). Also in the context of rubber characterization, we emphasize how the nonlinear viscoelastic behavior of rubber entered our theoretical analysis (see Sect. 4.4). After that, we assess model predictions regarding the untested dependency of friction coefficients on sliding velocities, based on result of a former indoor test series (see Sect. 4.5). Finally, we close this section with discussing the microscopic origin of the cutoff wavenumber (see Sect. 4.6).

4.1 Did the Roughness Measurement System Change the Topography of the Ice Surfaces?

It is interesting to check whether or not the laser of the used roughness measurement system could have significantly affected the obtained topography. The used laser exhibits a power of 1 mW, a spot diameter of $40\,\upmu \hbox {m}$, and the spot speed amounts to 12.5 mm/s [1]. Therefore, the maximum illumination time is 3.2 ms. During that time, the laser produces $3.2\,\mu \hbox {J}$ energy. Given that reflection coefficients of ice are larger than or equal to 40 % [5], less than or equal to $1.9\,\mu \hbox {J}$ arrive inside the ice body. Envisioning the unlikely extreme case that the total energy entering the ice body would be absorbed in the immediate vicinity of the ice surface, and noting that the specific heat of ice amounts to 2.05 kJ/(kg K) as well as that the melting energy of ice amounts to 334 kJ/kg, the energy entering ice with an initial temperature of $-5\,^{\circ }\hbox {C}$ allows for melting $5.6\times 10^{-12}\,\hbox {kg}$ of ice. Considering the mass density of ice as $920\,\hbox {kg/m}^3$, this mass is related to a volume of $6.08\times 10^{-15}\,\hbox {m}^3$. Dividing this volume by the spot area of the laser, i.e., by $1.26\times 10^{-9}\,\hbox {m}^2$, delivers a melting depth of $h_{\mathrm{m}}=4.83\,\upmu \hbox {m}.$ Since liquid water would flow into neighboring lower regions, this indicates that the laser might have affected surface asperities with a characteristic size of 5 microns or less.

In order to check whether or not the laser beam melted ice, we recall that roughness characterization was carried out five times along the same measurement lines. Melting would change—from one measurement to the subsequent one—the absolute height differences between neighboring measurement points. Corresponding mean values and standard deviations range from 4 to 8 microns, depending on the ice type (see Table 5). Interestingly, mean values and standard deviations change only marginally from one measurement to the subsequent one. This underlines that the laser of the used roughness measurement system did not significantly affect the obtained topography.

Furthermore, the power spectrum has only been used up to the cutoff wavenumbers as given in Fig. 9 and Table 4. In more detail, the maximum cutoff wavenumber is $0.19\times 10^6\,\hbox {m}^{-1}$. Since $q = 2\,\pi / \lambda$, this correlates with a wavelength of $33\,\upmu \hbox {m}$. Because all values in Table 5 are smaller than $33\,\upmu \hbox {m}$, they are not relevant for the theoretical analysis.

Table 5 Results from roughness characterization of the four ice surfaces: mean values and standard deviations of absolute height differences (in $\mu {\mathrm{m}}$) between neighboring measurement points, disregarding outliers larger than 50 $\mu {\mathrm{m}}$, for five consecutive measurements along the same measurement lines

4.2 Does Surface Roughness of Ice Depend on Temperature?

Notably, the roughness measurement system as used for the measurements described in Sect. 2.2, was, unfortunately, available for a few days only. Therefore, ice surfaces were characterized right after having completed the friction tests at $-5\,^{\circ }\hbox {C}$, i.e., right before the tests at $-8\,^{\circ }\hbox {C}$, but still at an ambient temperature of $-5\,^{\circ }\hbox {C}$. In other words, roughness characterization was carried out at one specific temperature, such that available topography characterization data cannot be used to asses whether or not surface roughness of ice is temperature dependent.

One might expect that surface roughness would increase by cooling ice from $-5\,^{\circ }\hbox {C}$ down to, e.g., $-13\,^{\circ }\hbox {C}$. Interestingly, this idea is consistent with the obtained modeling results. Model-predicted friction coefficients, namely, agree perfectly well with test data at $-5\,^{\circ }\hbox {C}$ (see Fig. 12), and this might well be related to consideration of highly realistic surface roughness (see Fig. 3). At $-13\,^{\circ }\hbox {C}$, in turn, model-predicted friction coefficients underestimate the measured counterparts, and this might indicate that the surface roughness characterized at $-5\,^{\circ }\hbox {C}$ is not highly representative for $-13\,^{\circ }\hbox {C}$. This discussion provides high motivation for future studies to carry out roughness characterization of ice surfaces at different temperatures.

4.3 Rubber Friction on Ice and on Asphalt: Implications for Rubber Characterization

Since the measured friction values range up to $\mu =0.7$, and because this is reminiscent of friction values on asphalts, we discuss expected similarities and differences between rubber friction on ice and on asphalt, as well as related implications on rubber characterization. When it comes to rubber friction on ice or on asphalt, respectively, we expect in both cases that rubber strains will be large at the length scale which is important for the viscoelastic contribution to friction. In this context, it is noteworthy that the viscoelastic modulus for large strain—which we have used in the present paper—is significantly less sensitive with respect to changes in the strain amplitude than it is the case for very small strain. Therefore, the same mode of large-strain characterization of rubber appears to be useful also for asphalt.

4.4 How Was the Nonlinear Viscoelastic Behavior of Rubber Incorporated into the Model?

Also in the context of rubber characterization, we emphasize that the nonlinear viscoelastic behavior of rubber—as presented in Fig. 2—was incorporated in two approximate ways into our theoretical analysis.

• In the first method, we have multiplied the low strain viscoelastic modulus by the scaling factor shown in Fig. 2. Notably, this scaling factor is the result of averaging strain data obtained at different temperatures.

• In a second method, we took into account that the strain sweep data are temperature dependent. To this end, we have shifted strain data obtained at different temperatures (but fixed frequency) along the frequency axis using the small strain shift factor $a_{\mathrm{T}}$.

Notably, both procedures give—in the present case—similar results.

4.5 Assessment of Model Predictions Regarding the Influence of Sliding Velocity

While the test series was carried out at one specific sliding velocity, the Persson rubber friction and contact mechanics theory allows for predicting the dependency of rubber friction on ice as a function of sliding velocity (see Figs. 10, 11, and 13). Model predictions obtained under consideration of flash temperature show a maximum of friction coefficient for sliding velocities amounting to several hundred millimeters per second. These result are in very satisfactory qualitative agreement with results from a former indoor friction test series, during which friction coefficients were also studied as a function of sliding velocity [19] (see Fig. 16). Notably, both the rubber specimen and the ice surface involved in this former study were different from the materials tested and analyzed in the present paper.

Fig. 16

Results from a former indoor tests series regarding rubber friction on ice, carried out at $-5\,^{\circ }{{\mathrm{C}}}$ using sliding velocity ranging from 1 to 1000 mm/s and nominal contact pressures amounting to: 0.2 MPa ($*$), 0.3 MPa ($\circ$), 0.4 MPa ($+$), and 0.5 MPa ($\times$) (Color figure online)

4.6 The Microscopic Origin of the Cutoff Wavenumber

In the Persson rubber friction theory enters a cutoff wavenumber $q_1$. That is, when calculating rubber friction, only surface roughness components with wavenumbers smaller than $q_1$ (or wavelength larger than $\lambda _1 = 2 \pi /q_1$) are included. There may be different physical origins of the cutoff wavenumber $q_1$, but for rubber on ice, we believe it is related to plastic flow (or fracture) or melting of the ice surface, resulting in a smoothing the ice surface at short length scales, i.e., removing roughness components with wavenumbers $q>q_1$.

Our first attempt was to model the initiation of ice smoothing based on temperature-dependent ice indentation hardness values taken from the open literature, but this turned out to overestimate friction coefficients. This indicated that smoothing of the ice surface starts at a local pressure which is smaller than the indentation hardness, because also a tangential force (the friction force) acts on the surface asperities. However, a yield criterion for ice, which considering both pressure and shear, is to the best of our knowledge out of reach. As a remedy, we stayed with a pressure-dependent yield criterion, but we lowered the yield stress, while preserving its temperature dependency. Notably, the temperature-dependent yield stress was treated as an intrinsic ice property, independent from the rubber properties.

Cutoff wavenumbers are determined as follows. Considering a perfectly flat rubber body and starting theoretically with a vanishing wavenumber of ice, the area of real contact is equal to the nominal macroscopic contact area and the real contact pressure is equal to the nominal contact pressure. Considering all ice wavenumbers smaller than a nonzero threshold q, results in a decreased real contact area and, hence, in an increased real contact pressure. Progressively increasing the threshold, results in a progressively increasing contact pressure. Once the contact pressure reaches the intrinsic yield stress of ice, the threshold represents the cutoff wavenumber. Notably, the sliding speed (here: 0.65 m/s) and the viscoelastic properties of rubber intervene in the calculation of the real contact area, see [23]. This explains why we have ended up with compound-specific cutoff wavenumbers. Finally, it is noteworthy that our treatment of this problem does not yet include how the frictional heating (which depends on the nominal contact pressure) influences smoothing of ice and, hence, the cutoff wavenumber $q_1$. We plan to study this important problem in a future publication.

5 Conclusions

We have measured the friction force acting on rubber blocks sliding along ice surfaces at different background temperatures, different nominal contact pressures, and at a sliding speed which is representative for braking with an antilock braking system. The used Linear Friction Tester is a conditionable indoor test facility which makes it possible to conduct a large number of friction tests under well-controlled and reproducible conditions, in a relatively short period of time.

The experimental results have been analyzed using the Persson rubber friction and contact mechanics theory. We have shown that under the present sliding conditions (sliding speed $v=0.65\,\hbox {m/s}$), the largest contribution to the friction force arises from the viscoelastic deformations of the rubber surface by the ice asperities. The analysis indicates that the ice-rubber contact regions are covered by a few nanometer thin meltwater layer and that the contribution to the friction force from shearing the water film is very small.

We have found that different rubber compounds exhibit very different dependency of the friction coefficient on the nominal contact pressure. In the absence of frictional heating of the rubber, the theory predicts that the viscoelastic contribution to the friction coefficient is independent of the nominal contact pressure (or normal load), unless the pressure is so large as to give rise to a contact area approaching complete contact [29], which is not the case in the present study. However, including frictional heating results in a rubber friction coefficient which depends on the nominal contact pressure. The theory predictions for the dependency of the friction coefficient on the nominal contact pressure agree very well with what we observe experimentally, and in particular, it explains why one compound (R1) exhibits nearly no dependency of $\mu$ on $p_0$, while another compound (R3) exhibits a strong pressure dependency. This is a very important result, suggesting that the theory presents an accurate description of rubber friction on ice.