Big End Bearing Losses with Thermal Cavitation Flow Under Cylinder Deactivation

Abstract

The paper presents a mixed thermo-hydrodynamic analysis of elliptic bore bearings using combined solution of Navier–Stokes, continuity and energy equations for multi-phase flow conditions. A vapour transport equation is also included to ensure continuity of flow in the cavitation region for the multiple phases as well as Rayleigh–Plesset to take into account the growth and collapse of cavitation bubbles. This approach removes the need to impose artificial outlet boundary conditions in the form of various cavitation algorithms which are often employed to deal with lubricant film rupture and reformation. The predictions show closer conformance to experimental measurements than have hitherto been reported in the literature. The validated model is then used for the prediction of frictional power losses in big end bearings of modern engines under realistic urban driving conditions. In particular, the effect of cylinder deactivation (CDA) upon engine bearing efficiency is studied. It is shown that big-end bearings losses contribute to an increase in the brake specific fuel consumption with application of CDA contrary to the gains made in fuel pumping losses to the cylinders. The study concludes that implications arising from application of new technologies such as CDA should also include their effect on tribological performance.

1 Introduction

The main considerations in modern engine development are fuel efficiency and compliance with progressively stringent emission directives. Within the pervading global competition there is also a requirement to address customer demands for maintaining adequate output power. These often contradictory attributes have led to the downsizing concept and higher output power-to-weight ratio engines. Additionally, there is a growing trend towards the use of emerging technologies such as variable valve actuation and cylinder deactivation (CDA) [1–3]. There is also progressively an interest in the concept of stop-start in congested urban environments. The adoption of these technologies is primarily based on the direct reduction of brake specific fuel consumption. However, there are also indirect repercussions such as thermal and frictional losses, as well as poor noise, vibration and harshness (NVH) refinement issues with generally light weight and poorly damped power train structures, subjected to engine power torque fluctuations [4]. With the application of CDA a greater degree of engine torque fluctuations would result [5], which is likely to lead to further deterioration in NVH refinement.

There is a dearth of analysis with respect to thermal and frictional losses, when considering CDA. A recent study by Mohammadpour et al. [6] showed that CDA makes only marginal differences in parasitic frictional losses in engine bearing performance and that any significant gain would depend only on the brake specific fuel consumption. However, the analysis did not take into account some important issues such as multi-phase lubricant flow through the contact and the occurrence of cavitation. These affect the load carrying capacity of the bearing as well as the conjunction friction, viscous heat generation and heat transfer to the solid boundaries. Brewe et al. [7] have shown that Swift [8], Stieber [9] boundary conditions can only predict accurately the film rupture point for steadily loaded bearings, which is not suitable for engine bearings, particularly with exacerbated dynamic loading under CDA. Therefore, to include the effect of cavitation, it is essential to employ realistic conjunctional outlet boundary conditions rather than the traditional Swift–Stieber [8, 9] assumptions, used by Mohammadpour et al. [6]. This paper strives to improve upon Mohammadpour’s approach, through the combined solution of Navier–Stokes equations for fluid flow and the energy equation for heat balance.

The occurrence and complex nature of lubricant cavitation in journal bearings has received much attention since the pioneering works of Skinner [10] through a series of experiments. Later, Dowson and Taylor [11] reported the earlier predictive analyses of the cavitation phenomenon in bearings. They discussed three main modelling approaches, based on contact outlet boundary conditions. One is the traditional lubricant film rupture boundary conditions, proposed by Reynolds/Swift–Stieber [8, 9], the others being the JFO (Jakobsson–Floberg [12], Olsson [13]) boundary conditions and Coyne and Elrod’s separation condition [14, 15]. The JFO boundary conditions are based upon the principle of conservation of mass flow beyond the point of lubricant film rupture point into a cavitation region in the form of striations. It is a significant improvement upon the traditional Swift–Stieber [8, 9] boundary conditions (which do not adhere to the principle of mass flow continuity beyond the lubricant film rupture). However, the JFO [12, 13] boundary conditions require consideration of any reverse flow, viscous dissipation and heat transfer within the contact in order to determine the temperature distribution within the conjunction. Therefore, proper implementation of the JFO [12, 13] boundary conditions is quite difficult in a numerical solution using Reynolds equation. Elrod’s separation boundary conditions are a simplification of the JFO approach, which are based on the definition of a fractional film content and the continuity of Couette flow beyond the lubricant rupture point. Dowson and Taylor [11] pointed out that although for different working conditions, one or more of the above mentioned boundary conditions may determine the location of the lubricant film rupture with reasonable accuracy, the physics underlying the cavitation phenomenon remains mostly unknown. At the same time they also emphasised the importance of accurately predicting lubricant film reformation, especially in the case of journal bearings because of its influence, not only on the load carrying capacity, but also on the mechanism of heat transfer from the bearing.

Dowson and Taylor [11] concluded that for lightly loaded lubricated contacts, represented by a cylinder-on-plane conjunction, flow separation is the major mechanism determining the cavity location. For lightly loaded journal bearings, operating at low eccentricity ratios, the use of Coyne and Elrod [14, 15] separation boundary condition appears to lead to better predictions. At lower eccentricity ratios, there is considerable lubricant flow between cavities and hence Floberg’s rupture conditions show better agreement with experimental observations.

Dowson et al. [16] used the Elrod [17] cavitation algorithm in a numerical study in order to predict the location of lubricant film rupture and reformation boundaries in a plain journal bearing. They also conducted an experimental study [18] in order to investigate the validity of their numerical analysis. Their tests included investigation of the effect of varying eccentricity ratio, supply pressure and shaft rotational speed on the film rupture and reformation points. They obtained good correlation between their numerical predictions and their experimental results for the side leakage flow. They noted that the inclusion of film reformation through use of the Elrod [17] cavitation algorithm is crucial for accurate prediction of the side leakage flow. On the other hand, the use of Swift–Stieber [8, 9] boundary conditions resulted in some errors. However, at lower eccentricity ratios (<0.6) and supply pressures a significant difference between the experimental results and the numerical predictions was observed with the Elrod boundary conditions. In addition, there was poor correlation between the numerical predictions and the experimental results for the location of the film reformation point. Dowson and Taylor [11] attributed this to the inadequacy in the utilised rupture process model which does not allow for negative gauge pressures to be generated in the lubricant film.

The Elrod [17] cavitation model was later modified to improve its computational stability by Vijayaraghavan and Keith [19], Paydas and Smith [20], Hirani et al. [21], Payvar and Salant [22], and Xiong and Wang [23]. Alternative models, including the mass-conserving flow through the cavitation region have also been developed, such as that of Giacopini et al. [24].

The development of computational fluid dynamics (CFD) approach enabled solution of Navier–Stokes equations for multi-phase flow to be achieved, whilst retaining the principle of conservation of mass and momenta. Some of the underlying limitations of Reynolds equation could also be removed. Tucker and Keogh [25] employed a 3D CFD approach for thermo-hydrodynamic analysis of steady-state motion of journal bearings. They used an Elrod [17] type cavitation model which allowed for the existence of the sub-ambient pressures. In this approach, the vapour fraction becomes a function of the film thickness. However, as Tucker and Keogh [25] also note for non-Couette or unsteady flows a time-dependent continuity equation should be used to determine the vapour fraction. In their analysis continuity of heat flux and compatibility of temperature was assured at the solid–fluid interface.

This paper presents a full 3D CFD approach for thermo-hydrodynamic analysis of big-end bearings. No artificial boundary conditions are set at the exit from the conjunction. This means that the lubricant rupture and reformation boundaries are determined by the combined solution of Navier–Stokes equations, the energy equation and continuity of flow conditions (in terms of conservation of mass and momenta). In addition, the cavitation phenomenon is taken into account through solution of a vapour transport equation including the Rayleigh–Plesset source terms to take into account the growth and collapse of cavitation bubbles. The developed method is validated against experimental results of Dowson et al. [26]. The validated model is then used for analysis of a big-end engine bearing subjected to dynamic loading under normal engine operation as well as with the application of CDA; an approach not hitherto reported in the literature.

2 Big End Bearing Model

2.1 Big End Bearing Geometry

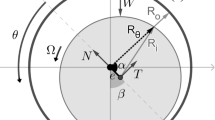
A schematic of the big end bearing used in IC engines is shown in Fig. 1. In a conventional internal combustion (IC) engine, the crank-pin acts as the journal and the bearing bushing is located at the bottom end of the connecting rod. The big end bearings are usually groove-less and are pressure-lubricated using a single hole drilled through the crank pin [27]. Although in most applications a simple circular profile is used to describe the geometry of the big end bearing, in practice, an elliptic (or ‘lemon shape’) bore profile is used. To study the effect of CDA, the engine studied here was a high performance four-stroke naturally aspirated engine with the specifications provided in Table 1.

Fig. 1

An elliptic big end bearing configuration

Table 1 Engine and bearing data

The film profile for such an elliptic bore bearing is defined as (Mishra et al. [28]):

$$h = c\,(1 + G\,\cos^{2} \theta + \varepsilon \,\cos \theta ) + \varDelta$$

(1)

where, the non-circularity is defined as: G = (c _maj − c _min)/c. The parameters c, ɛ, θ are the average clearance, eccentricity ratio and the angular position respectively (Fig. 1). The localised deflection of the Babbitt overlay, Δ is obtained using the column method contact mechanics approach [29], where: $\varDelta = \frac{(1 - 2\nu )(1 + \nu )d}{E\,(1 - \nu )}p$.

2.2 Applied Loads

Big-end bearings are designed to withstand the transmitted transient forces through the connecting rod. These are the result of combustion pressure and inertial imbalance [4].

For a typical four-cylinder four-stroke engine, the inertial imbalance force acting through the connecting rod along the axis of the piston is [4] (Fig. 2):

$$F_{\text{in}} \approx m_{1} r_{\text{c}} \omega^{2} \left( {\cos \omega \,t + \frac{{r_{\text{c}} }}{l}\cos 2\omega \,t} \right)$$

(2)

where, engine order vibrations up to the second engine order are considered here for the four-stroke engine under consideration. The mass m ₁ is the equivalent mass in translation, comprising that of the piston, the gudgeon pin and a proportion of the mass of the connecting rod in pure translation: m ₁ = m _p + m _g + m _c in a two degrees-of-freedom representation of piston-connecting rod-crank sub-system, where according to Thomson [30]:

$$m_{\text{c}} = \frac{{W_{\text{c}} }}{g}\left( {1 - \frac{C}{l}} \right)$$

(3)

where, W _c is the weight of the connecting rod and C denotes centre of mass of the connecting rod measured from its small end.

Fig. 2

Schematic of the piston–crank system with the applied loads

The applied vertical combustion force acting upon the piston crown area is:

$$F_{\text{com}} = p_{\text{com}} A_{\text{p}}$$

(4)

where, p _com is the instantaneous in-cylinder pressure and A _p is the piston crown surface area.

Therefore, the total transient load applied on the big end bearing at any instant of time, expressed in terms of the instantaneous connecting rod obliquity angle, φ is (Fig. 2) [4]:

$$F = \frac{1}{\cos \varphi }\left( {F_{\text{in}} + F_{\text{com}} } \right)$$

(5)

where:

$$\cos \varphi \approx 1 - \frac{1}{2}\left( {\frac{{r_{\text{c}} }}{l}\sin \omega \,t} \right)^{{}}$$

(6)

and ϑ = ωt, ϑ is the crank angle.

It should be noted that smaller moment loading from adjacent cylinders also exists, which is ignored in this analysis. More information is provided in Rahnejat [31].

3 Theory

3.1 General Navier–Stokes and Energy Equations

The general form of mass and momentum continuity (Navier–Stokes) equations for the flow of a compressible viscous fluid can be described as (White [31]):

$$\frac{{{\text{D}}\rho }}{{{\text{D}}t}} + \rho \vec{\nabla }\, \cdot \vec{V} = 0$$

(7)

$$\rho \frac{{{\text{D}}\vec{V}}}{{{\text{D}}t}} = - \vec{\nabla }p + \vec{\nabla } \cdot \,(\bar{\tau }_{\text{ij}} ) + \vec{F}$$

(8)

where D/Dt is the material covariant derivative operator. The parameters ρ and p are scalar quantities and represent the density and pressure of the fluid. $\vec{F}$ and $\vec{V}$ are the body force field and velocity vectors, and $\bar{\tau }_{ij}$ is the second order viscous shear stress tensor.

The only body force in the current analysis is the gravitational force due to the weight of the fluid. Although this has a negligible effect in comparison with the shear and pressure induced forces in lubrication studies, it has been taken into account in the current analysis for the sake of completeness.

In addition, $\vec{V} = u\hat{i} + v\hat{j} + w\hat{k}$ is the velocity vector expressed in the Cartesian frame of reference in which u is the component of velocity in the direction of axial lubricant flow entrainment (along the x-axis), v is that in the transverse or side-leakage direction along the y-axis and w is the velocity component in the direction perpendicular to the contacting surfaces (squeeze film action) along the z-axis.

Furthermore, the viscous shear stress tensor, $\bar{\tau }_{ij}$, can be expressed as spatial derivatives of the velocity field vector components for an isotropic fluid. In Einstein’s notation this becomes:

$$\bar{\tau }_{ij} = \eta \left( {\frac{{\partial u_{i} }}{{\partial x_{j} }} + \frac{{\partial u_{j} }}{{\partial x_{i} }} - \varDelta_{ij} \frac{2}{3}\frac{{\partial u_{k} }}{{\partial x_{k} }}} \right)$$

(9)

where, u is the general representation of (scalar) velocity components, η is the effective dynamic viscosity of the lubricant and Δ _ij is the Kronecker delta, defined as:

$$\varDelta_{ij} = \left\{ \begin{gathered} 0\quad {\text{if}}\;\;i \ne j \hfill \\ 1\quad {\text{if}}\;\;i = j \hfill \\ \end{gathered} \right.$$

(10)

Finally, the energy conservation equation in the most general form can be stated as (White [32]):

$$\rho \frac{{{\text{D}}H}}{{{\text{D}}t}} = \,\,\frac{{{\text{D}}p}}{{{\text{D}}t}} + \vec{\nabla } \cdot (k\vec{\nabla }T) + \bar{\tau }_{ij} \frac{{\partial u_{i} }}{{\partial x_{j} }}\,\,\,$$

(11)

where H is the fluid enthalpy, T is the fluid temperature and k is its thermal conductivity. It is noted that the last term on the right hand side of the equation is the sources term which takes into account the heat produced due to viscous shear of the fluid.

3.2 Cavitation Model

The full cavitation model proposed by Singhal et al. [33] is used here, where the transport equation for the vapour mass fraction is expressed as:

$$\frac{\partial }{\partial t}(\rho f_{\text{v}} ) + \vec{\nabla } \cdot \,(\rho f_{\text{v}} \vec{V}_{\text{v}} ) = \vec{\nabla } \cdot \,(\varGamma \,\vec{\nabla }f_{\text{v}} ) + R_{\text{e}} - R_{\text{c}}$$

(12)

where, Γ is the diffusion coefficient, $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {V}_{\text{v}}$ is the velocity vector of the vapour phase and f _v is the vapour mass fraction defined as:

$$f_{\text{v}} = \frac{{\rho - \rho_{\text{l}} }}{{1 - (\rho_{\text{l}} /\rho_{\text{v}} )}}$$

(13)

where, the subscripts l and v denote the liquid and vapour phases respectively.

In addition, R _e and R _c are the source terms which account for vapour generation and condensation rates, respectively. Singhal et al. [33] defined these phase change rates, based on the generalised Rayleigh–Plesset equation, thus:

$$R_{\text{e}} = C_{\text{e}} \frac{{V_{\text{ch}} }}{{\sigma_{\text{s}} }}\rho_{\text{l}} \,\rho_{\text{v}} \sqrt {\frac{{2(p_{\text{sat}} - p)}}{{3\rho_{\text{l}} }}} (1 - f_{v} ),\quad {\text{for}}\quad p \le p_{\text{sat}}$$

(14)

$$R_{\text{c}} = C_{\text{c}} \frac{{V_{\text{ch}} }}{{\sigma_{\text{s}} }}\rho_{\text{l}} \,\rho_{\text{v}} \sqrt {\frac{{2(p - p_{\text{sat}} )}}{{3\rho_{\text{l}} }}} \,f_{\text{v}} ,\quad {\text{for}}\quad p > p_{\text{sat}}$$

(15)

where, σ _s denotes the surface tension of lubricant and V _ch is a characteristic velocity associated with the local relative velocity between the liquid and vapour phases. In these models it is assumed that the bubble pressure, p equates to the saturation (vapour) pressure, p _sat, at a given temperature which is the case if one assumes that no dissolved gases are present. In addition, C _e and C _c are empirical constants which are considered to be 0.02 and 0.01 respectively according to Singhal et al. [33].

3.3 Boundary Conditions for the Fluid Flow

The flow boundary conditions are set, based on the conditions for a typical IC engine big-end bearing.

The cavitation (vaporisation) pressure is set at the atmospheric pressure of 101 kPa. Since the occurrence of cavitation in the current CFD analysis is treated through solution of transport equation for the vapour mass fraction alongside the general Navier–Stokes equations, there is no need to impose any particular boundary conditions for either lubricant film rupture or reformation. This is a significant fundamental improvement upon the imposed assumptions such as those of JFO [12, 13] or Elrod [17] cavitation models.

In addition to the fact that the solid boundaries were considered to be impermeable, the lubricant/solid interface is also assumed to follow the no-slip condition.

The bearing shell is modelled as a stationary wall, whilst the journal is modelled as a moving body with an absolute rotational velocity.

At the inlet hole supply orifice to the bearing the lubricant is fed into the contact at a constant pressure of 0.5 MPa as already assumed by Mohammadpour et al. [6].

Finally, at the bearing’s axial extremities the lubricant is assumed to leak to ambient (atmospheric) pressure.

3.4 Conduction Heat Transfer in the Solid Bodies (Journal and Bearing)

In order to proceed with full thermal analysis of the journal–lubricant–bearing bushing system, one needs to take into account the conduction of the generated heat to the solid boundaries using the energy equation. The conduction of heat into the rotating journal is governed by the transient form of the heat conduction equation as:

$$\frac{1}{\alpha }\frac{\partial T}{\partial t} = \nabla^{2} T$$

(16)

where, α is the thermal diffusivity for the journal’s material. The convective (time dependent term) on the left hand side of the equation takes into account the rotational effect.

On the other hand, the steady-state form of the heat conduction equation is used for the stationary bushing as:

$$\nabla^{2} T = 0$$

(17)

3.5 Thermal Boundary Conditions

The thermal boundary conditions are set for a typical IC engine big- end bearing (Fig. 3). At the lubricant–solid interface these conditions ensure the continuity of heat flux and compatibility of evaluated temperatures.

Fig. 3

Thermal boundary conditions

After lubricant enters the contact through the oil feed hole, its temperature is increased from that in the bulk due to the heat produced in the contact as the result of shearing. The generated heat is transferred by convection through lubricant side leakage and conducted through the bounding solid surfaces. In the experiments conducted by Dowson et al. [26], the journal’s extremities were exposed to the ambient air. Therefore, convection cooling would take place at these interfaces. However, for the engine conditions, it is assumed that the journal is not exposed to the ambient air and thus, any heat transfers to the journal increases its core temperature. Finally, a portion of the heat is conducted through the bearing bushing to the surrounding ambient air. Of course, for journal bearings, convective heat transfer by the lubricant film is most significant [34–36]. In both the validation process and engine running conditions, it was assumed that the bearing’s outer surface is exposed to the ambient temperature. Thus, the temperature of the outer surface of the bearing bushing (for the case of engine simulations) is set at 50 °C. The temperature of the inner surface of the bushing, T _bl is assumed to be that of the lubricant obtained through solution of energy equation. In reality, the temperature of lubricant would be slightly higher than the interface temperature of the solids. Figure 3 illustrates thermal boundary conditions in the journal bearing. A list of the assumed engine compartment temperature, lubricant and material data for the engine running conditions is provided in Table 2.

Table 2 Lubricant and material data

In solving the coupled energy and heat conduction equations, the temperature of the entrant lubricant is computed from the initial solid component temperatures and heat fluxes at the solid interfaces. The heat produced in the lubricant is allowed to increase the journal’s temperature whilst the transferred heat to the journal bushing can be convected away through ambient air. To include the effect of journal temperature a detailed thermal model for the entire crankshaft system would be required, which is outside the scope of the paper. This would necessitate a full engine model including the effect of all the adjacent cylinders. This is the reason for assuming no axial temperature gradient for the journal in the current analysis. The temperature of the oil at the inlet hole was set to T _i = 42 °C in the case of the validation procedure (Dowson et al. [26]). For the engine conditions this was set at 50 °C. The lubricant thermal properties such as thermal conductivity and specific heat are calculated at the engine compartment temperature of 50 °C under steady engine running condition and 40 °C for the validation case study.

3.6 Lubricant Rheology

Density and viscosity of the lubricant are the two most important rheological properties that need to be defined for the operating pressures and temperatures.

A density model proposed by Dowson and Higginson [37], modified for temperature variation by Yang et al. [38] provides:

$$\rho = \rho_{0} \left( {1 + \frac{{6.0 \times 10^{ - 10} (p - p_{\text{atm}} )}}{{1 + 1.7 \times 10^{ - 9} \,(p - p_{\text{atm}} )}}} \right)\,\left[ {1 - 0.65 \times 10^{ - 3} (T - T_{0} )} \right]$$

(18)

in which p _atm is the atmospheric pressure and T ₀ is the reference temperature with density ρ ₀. Table 2 provides the data associated with the lubricant properties.

Variation of lubricant dynamic viscosity with pressure and temperature is given by Houpert [39] as:

$$\eta = \eta_{0} \,\exp \left\{ {\left( {\ln (\eta_{0} ) + 9.67} \right)\left[ {\left( {\frac{T + 135}{{T_{0} + 135}}} \right)^{{ - S_{0} }} \left( {1 + \frac{{p - p_{\text{atm}} }}{{1.98 \times 10^{8} }}} \right)^{Z} - 1} \right]} \right\}$$

(19)

where, η ₀ is the lubricant dynamic viscosity at atmospheric pressure and reference temperature T ₀, and Z and S ₀ are constants (Gohar and Rahnejat [40]):

$$Z = \frac{{1.96 \times 10^{8} \alpha_{0} }}{{\ln (\eta_{0} ) + 9.67}}\,\quad {\text{and}}\quad S_{0} = \frac{{\beta_{0} (T_{0} + 135)}}{{\ln (\eta_{0} ) + 9.67}}$$

(20)

where, α ₀ and β ₀ are constants at ambient conditions (Table 2). It should be noted that the rheological parameters used are for a fresh lubricant. In practice, the lubricant is subject to shear thinning, oxidation and contamination (Lee et al. [41]).

3.7 Asperity Contact Model for Mixed/Boundary Regime of Lubrication

Journal bearings are designed to ideally operate in the hydrodynamic regime of lubrication. Therefore, ordinarily, it is expected that a coherent film of lubricant is maintained, guarding against direct contact of ubiquitous asperities on the contiguous surfaces. However, this may not be the case in applications such as those encountered in the big-end bearings of IC engines due to the transient nature of engine operations. The large variations in the applied load, as well as stop-start running conditions, contact of asperities on the contiguous surfaces is unavoidable. Consequently, some of the applied load can be carried by the direct contact of surfaces at asperity level. Therefore, the applied load is carried by a combination of hydrodynamic reaction and direct asperity contact as:

$$F = W_{\text{h}} + \,W_{\text{a}}$$

(21)

where, the hydrodynamic reaction is obtained by integration of the hydrodynamic contact pressure obtained through solution of Navier–Stokes equations:

$$W_{\text{h}} = \iint {p\left( {\theta ,z} \right)}\,r{\text{d}}\theta {\text{d}}z$$

(22)

The asperity load is a function of surface roughness and material properties. For an assumed Gaussian distribution of asperities the load supported by the asperity tips can be expressed as (Greenwood and Tripp [42]):

$$\,W_{\text{a}} = \frac{ 1 6\sqrt 2}{ 1 5}\pi \left( {\xi \beta \sigma } \right)^{2} \sqrt {\frac{\sigma }{\beta }} E^{{\prime }} AF_{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0pt} 2}}} (\lambda )$$

(23)

where, A is the apparent area of contact and E′ is the composite modulus of elasticity. The statistical function F _5/2(λ) is a function of the Stribeck oil film parameter $\lambda = \frac{h}{\sigma }$, where σ is the composite root mean square roughness of the contiguous surfaces. This statistical function can be represented by a polynomial-fit function as (Teodorescu et al. [43]):

$$\,F_{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0pt} 2}}} \left( \lambda \right) = \left\{ {\begin{array}{*{20}l} { - 0.004\lambda^{5} + 0.057\lambda^{4} - 0.296\lambda^{3} + 0.784\lambda^{2} - 1.078\lambda + 0.617;} \hfill & {{\text{for}}\;\;\lambda \le \lambda_{\text{cr}} } \hfill \\ {0;} \hfill & {{\text{for}}\;\;\lambda > \lambda_{\text{cr}} } \hfill \\ \end{array} } \right.$$

(24)

where, for the current analysis a critical film ratio of λ _cr ≈ 3 is assumed, below which mixed regime of lubrication (including asperity interactions) is deemed to occur. This value of critical Stribeck oil film parameter depends on the surface topographical asperity distribution and the chosen statistical parameter. Some researchers have used lower or slightly higher values for the transition boundary between mixed and full fluid film regimes of lubrication. In particular, Guanteng and Spikes [44] used thin film interferometry and showed that full film lubrication is only realised when λ > 2. They noted that there is no clear-cut demarcation boundary between mixed and boundary regimes of lubrication, based on the Stribeck’s oil film parameter. As already noted above, λ _cr > 3 is assumed for fluid film lubrication in the current analysis.

According to Greenwood and Williamson [45] and Greenwood and Tripp [42], the roughness parameter ξβσ is reasonably constant with a value in the range of 0.03–0.07 for steel surfaces. The ratio σ/β which is a representation of the average asperity slope (Gohar and Rahnejat [40]) is in the range 10⁻⁴–10⁻² according to Teodorescu et al. [43]. In the current study it is assumed that σ ₁ = σ ₂, ξβσ = 0.055 and σ/β = 0.001. Since a thin smooth hard layer of bismuth is applied as the outer layer of the shell overlay with a thickness of 3 μm, the boundary friction is assumed to largely depend on the rougher surface of the steel crank pin.

3.8 Friction Force and Power Loss

The total friction force in mixed regime of lubrication is obtained as:

$$f_{\text{t}} = f_{\text{vis}} + f_{\text{b}}$$

(25)

where, the viscous friction, f _vis, is obtained by integrating the generated shear stress over the lubricant-surface interface as:

$$f_{\text{vis}} = \iint \tau {\text{d}}A$$

(26)

The boundary component of friction takes into account the direct dry asperity contact as well as the non-Newtonian shear of pockets of lubricant entrapped between the asperity tips, as (Teodorescu et al. [43]):

$$f_{\text{b}} = \tau_{0} A_{\text{a}} + \varsigma W_{\text{a}}$$

(27)

where, the parameter ς is the pressure coefficient for boundary shear strength of asperities on the softer counterface. In the case of the big-end bearing this is the steel surface of the journal. A value of ς = 0.17 is obtained using an atomic force microscope. The procedure followed is the same as that described by Buenviaje et al. [46] and Styles et al. [47]. In addition, limiting Eyring shear stress [48] for the engine oil is τ ₀ = 2 MPa.

The underlying hypothesis in the use of Eq. (27) is that the asperities are wetted by adsorption of an ultra-thin film of boundary active molecules within the lubricant. Briscoe and Evans [49] assume that a thin Langmuir–Blodgett [50] layer of adsorbed of boundary active lubricant species are formed at the tip of asperities and entrapped in their inter-spatial valleys. This layer is subject to non-Newtonian Eyring shear [48]. An alternative hypothesis would be that the opposing asperities form adhesive junctures which are submerged in the menisci formed between them. Therefore, boundary friction may be considered as the effort required to break such meniscus bridges (Bowden and Tabor [51]) in addition to overcoming the adhesion of cold welded asperity junctures themselves. Such an approach is reported by Teodorescu et al. [43]. A shortcoming of the approach reported in [50] is the need to specify the proportion of contact in dry contact of asperities. On the other hand the approach in [43] makes use of asperity contact area A _a, based on the assumption of asperity distribution, which is considered to follow a Gaussian distribution as in [42].

The cumulative area of asperity tips, A _a, is found as (Greenwood and Tripp [42]):

$$A_{\text{a}} = \pi^{2} (\zeta \kappa \sigma )^{2} \sqrt {\frac{\sigma }{\kappa }} AF_{2} (\lambda )$$

(28)

where F ₂(λ) is a function representative of the Gaussian distribution of asperities in terms of λ as:

$$\,F_{2} (\lambda ) = \left\{ {\begin{array}{*{20}l} { - 0.0018\lambda^{5} + 0.0281\lambda^{4} - 0.1728\lambda^{3} + 0.5258\lambda^{2} - 0.8043\lambda + 0.5003;} \hfill & {{\text{for}}\;\;\lambda \le \lambda_{\text{cr}} } \hfill \\ {0;} \hfill & {{\text{for}}\;\;\lambda > \lambda_{\text{cr}} } \hfill \\ \end{array} } \right.$$

(29)

The total frictional power loss from the bearing, due to both viscous and boundary contributions to the overall friction, is calculated as follows:

$$P_{\text{f}} = f_{\text{t}} r\omega$$

(30)

4 Method of Solution

The governing equations described in Sect. 3.1 were solved in the environment of ANSYS FLUENT 14.5, where a computational mesh is generated. For the conjunctional fluid domain (the lubricant) was meshed with hexahedral cells (element size 50 μm and 20 division for film thickness direction), whilst the bounding solid surfaces were discretised using tetrahedral elements with 2 mm elements. There is no need for finer solid elements as there is no local deformation of surfaces at the expected generated pressures, since αp _m ≪ 1 for the conformal contact of the contiguous surfaces as in journal bearings [40]. The interfaces between the solid surfaces and the lubricant zone were defined by face meshing method. The total number of computational control volume elements was 2,533,165. A grid independency test for the result was performed, which showed that the number of elements used in excess of that stated did not significantly alter the results of the analyses (see “Appendix”). Since the gap between the two solid surfaces is subject to transience with variations in applied load and speed, a dynamic mesh model was employed to calculate the lubricant film thickness at any instant of time. Boundary Layer Smoothing Method and Local Cell Remeshing are used for the dynamic mesh model.

In order to be able to include the described cavitation model (Sect. 3.2), a mixture model was employed to take into account the two-phase flow nature of the problem [52]. In this method, the mass continuity, momentum and energy equations are solved for the mixture while a mass/volume fraction equation (Eq. 12) is solved for the secondary (gas or vapour) phase.

The velocity–pressure coupling is treated using the standard semi-implicit method for pressure-linked equations (SIMPLE algorithm) and the second-order upwind scheme is used for the momenta in order to reduce any discretisation-induced errors. A pressure-based segregated algorithm is employed in which the equations are solved sequentially.

For greater accuracy, an error tolerance of 10⁻⁴ is used for the residual terms of mass and momentum conservation and the volume fraction, whilst a tolerance value of 10⁻⁶ is employed for energy conservation and heat conduction equations (see “Appendix”).

5 Model Validation

Prior to any analysis of engine conditions under normal operating mode or with application of CDA, it is necessary to validate the developed numerical model. A two-stage validation process is undertaken.

Firstly, the model predictions are compared with the experimental measurements reported by Dowson et al. [26], which have been used for the same purpose by other research workers, including Tucker and Keogh [25], and Wang and Zhu [53]. Dowson et al. [26] measured the lubricant pressure distribution in a restricted grooved journal bearing (Fig. 4). A lubricant inlet supply hole with diameter d was drilled radially through the bearing on its central plane. A distribution groove with width d was cut axially into the inner surface of the bearing with the length, L _i. The attitude angle δ is measured from the location of the axial groove to the line of centres. The journal bearing variables used in the computation are listed in Table 3. Dowson et al. [26] noted a build-up of pressure with the passage of lubricant through the converging gap to support the applied load. In the diverging gap of the conjunctional outlet, the fall in the generated pressures resulted in the fluid film cavitating into a series of streamers below the saturation pressure of the dissolved gases.

Fig. 4

Schematic of journal bearing geometry used in Dowson et al. [26]

Table 3 Journal bearing variables used in the validation exercise (Dowson et al. [26])

Secondly, further numerical predictions were made using Reynolds equation and Elrod’s cavitation algorithm [17]. In the Elrod’s approach the fractional film content is the proportion of the conjunctional gap which attains generated pressures in excess of the cavitation vaporization pressure of the lubricant for a given conjunctional temperature (indicated by its bulk modulus, β), thus [17]:

$$p = \psi \beta \ln \gamma + p_{\text{cav}}$$

(31)

where, ψ is a switching function: ψ = 1, γ > 1, P > p _cav represents regions of a coherent fluid film and ψ = 0, γ < 1. P = p _cav represents the cavitation region, with clearly γ = 1 defining the lubricant film rupture point.

Dowson et al. [26] operated their experimental journal bearing rig at a steady speed of 1,500 rpm, an applied load of 9,000 N and with an attitude angle of δ = 18°. This yielded a journal operating eccentricity ratio of ɛ = 0.5. Figure 5 shows the numerically predicted pressure distribution in isobaric form using the current method. The position of the inlet groove is designated as θ = 0° in the circumferential direction. The maximum pressure occurs at θ = 206° and the lubricant film ruptures just beyond the position θ = 270°.

Fig. 5

Contours of pressure (MPa) for ɛ = 0.5 at N = 1,500 rpm

Figure 6 shows the cross-section through the 3D pressure distribution in the central plane of the bearing, where pressure tappings were made by Dowson et al. [26]. The experimental measurements are shown, as well as the numerical predictions made by Wang and Zhu [53], which are based on Elrod’s cavitation model [17] and those from the current CFD analysis. The area under all the pressure distributions, being the lubricant reaction remains the same. Both the predictive analyses employed the same convergence tolerance limit of 10⁻⁶. All the pressure distributions commence from the supplied inlet pressure of 0.5 MPa with an assumed fully flooded inlet boundary. The outlet boundary conditions differ between the numerical analyses. Those for the Elrod cavitation boundary are based on the lubricant film rupture point, γ = 1, whereas the current CFD analysis has an open exit boundary condition (not an imposed boundary condition) for the lubricant film rupture point. The different exit boundary conditions, as well as the embodied assumption of a constant pressure gradient into the depth of the lubricant film with a constant dynamic viscosity through its thickness made by Wang and Zhu [53] yield slightly different pressure profiles. Clearly, lack of artificially imposed assumptions with the CFD analysis yields results which conform more closely to the experimental measurements.

Fig. 6

Comparison of experimental result and current analysis on pressure distribution in the centre plane for ɛ = 0.5 at N = 1,500 rpm

Figure 7 shows the contours of temperature distribution for the journal and the bearing bushing surfaces obtained from the current analysis. For the journal surface the maximum temperature occurs close to the high pressure zone. The maximum temperature in the stationary bearing bushing occurs in the cavitation zone due to the high vapour volume fraction residing there with clearly poor convection cooling due to the lack of lubricant flow. Comparison of the experimental result, that from Tucker and Keogh [25] and that of the current model for journal and bearing surfaces are shown in Figs. 8 and 9, respectively. As it can be seen, the result of the current analysis shows closer agreement with the experimental measurements. The main difference between the Tucker and Keogh’s analysis [25] and the current model is in the treatment of the flow in the cavitation region. The former uses the fraction of vapour Φ in the cavitation region, similar to the Elrod’s approach [17]:

$$\varPhi = 1 - \frac{{h_{\text{c}} }}{h}$$

(32)

where h _c is the film height at the start of the cavitation region. Equation (32) is based only on steady state Couette flow continuity. This ignores the mass flow continuity, which includes the vapour phase and any changes in the Poiseuille flow in a divergent gap. The current model takes these issues into account using the time-dependent continuity equation (Eq. 12).

Fig. 7

Contours of temperature (°C) for a circumferential journal surface, b circumferential bearing surface for ɛ = 0.5 at N = 1,500 rpm

Fig. 8

Comparison of experimental result and current analysis for the circumferential journal surface temperatures for ɛ = 0.5 at N = 1,500 rpm

Fig. 9

Comparison of experimental result and current analysis for circumferential bearing bushing surface temperatures for ɛ = 0.5 at N = 1,500 rpm

Figure 10 shows the lubricant temperature into the depth of the lubricant at circumferential position, θ = 180°. It shows that the temperature of the lubricant is higher than the temperatures of both the journal and the bearing bushing surfaces. As the temperature varies through the thickness of the lubricant film its viscosity alters locally, which indicates that the thermal flow through the contact is in the form of streamlines at different temperatures and viscosity (with different phases), thus a pressure gradient exists into the depth of the film. Hence, for an accurate prediction of flow a combined solution of Navier–Stokes equation with Rayleigh–Plesset equation is essential as is the case in the current analysis.

Fig. 10

Lubricant temperature along the film depth at θ = 180°

6 Engine Big End Bearing Analysis with CDA

It is expected that introduction of CDA would affect the thermal conditions in engine big-end bearings and influence frictional power loss. The occurrence of cavitation and its extent would also affect friction. Therefore, it is necessary to develop the validated multi-phase flow methods with realistic boundary conditions such as that adopted in the current method.

Now with the validated model, realistic predictions under engine operating conditions with all-active fired cylinders and alternatively with some deactivated cylinders can be carried out. The analysis reported here corresponds to a four-cylinder four-stroke engine under city driving condition at the speed of 25 km/h with 25 % throttle action and engaged in second gear (ratio 1:2.038). The final drive differential ratio is 1:4.07. The engine speed for this condition is 2,200 rpm. All the necessary data used in the analysis are listed in Table 1. The results are presented for a deactivated cylinder as well as a fired cylinder. Figure 11 shows the combustion gas force for an active cylinder under engine normal operation, as well as that for an active cylinder under CDA. It also shows the gas force for a deactivated cylinder, caused by the trapped air/charge with closed valves, subjected to swept volumetric changes. Note that the gas force is increased in the active cylinders of a partially deactivated engine with the same flow rate through a common rail supply. The effect is higher temperature combustion which improves upon thermal efficiency and also enhances the operation of the catalytic converter, operating at a higher temperature, thus reducing hydrocarbon emission levels. The pumping losses can also be reduced whilst higher cylinder temperatures in active cylinders would reduce the lubricant viscosity, thus the frictional losses. This effect is not investigated here, but Morris et al. [54] using a control volume thermal mixing model showed that the average temperature of the lubricant, thus its viscosity, is primarily determined by the bore surface temperature. Therefore, there are fuel efficiency advantages in terms of reduced thermal losses as well as decreased active cylinder viscous frictional losses.

Fig. 11

Transmitted combustion gas forces for full and partially deactivated engine operations

When periodic steady state conditions are reached the interfacial temperature T _bl (defined in Fig. 3) reaches a maximum value of 145 °C when the engine is operating under normal conditions (no CDA). For an engine under CDA operating mode, the maximum interfacial temperature reached in the bearing of an active cylinder is 160 °C and for the big end bearing of the deactivated it reaches 135 °C. Although the deflection of the 100 µm thick Babbitt overlay is included in the analysis, the maximum conjunctional pressure reached (maximum of 20 MPa), under the investigated conditions yields an inappreciable value (<0.02 µm). However, under more severe operating conditions (higher engine speed and a greater throttle input), this may not be the case.

Cavitation occurs in the big-end bearings under low applied loads, resulting in reduced conjunctional pressures. Figures 12 and 13 show the generated pressure distribution and the corresponding volume fraction in the journal-bushing conjunction at the crank angle of ϑ = 180°, corresponding to the piston position at the bottom dead centre at the end of the power stroke with very low transmitted applied gas force (Fig. 11). The volume fraction of unity indicates a gap filled purely by vapour.

Fig. 12

Contours of pressure (MPa) at crank angle ϑ = 180° (piston at BDC) with all active cylinders

Fig. 13

Contours of volume fraction at crank angle ϑ = 180° with all active cylinders

The pressure profile through the circumferential centre line of the isobaric plot of Fig. 12 is shown in Fig. 14, also including that for the big-end bearing of an active cylinder in a partially deactivated engine, as well as for a deactivated cylinder’s connecting rod bearing. It can be seen that the lubricant film ruptures earlier in the case of an active cylinder in the partially deactivated engine, ahead of that for a normal engine operation, which in turn ruptures ahead of the deactivated cylinder’s bearing. This occurs because of progressively reduced applied bearing load at the same crankshaft speed, which is an expected outcome. The reverse trend is discernible for the lubricant film reformation boundary. Therefore, the extent of the cavitation region alters in accord with the cylinder operating condition and has direct implications for bearing load carrying capacity, film thickness and frictional losses.

Fig. 14

Pressure distribution in the circumferential centre line of the bearing at crank angle of ϑ = 180° for various cylinder conditions

Figure 15 shows the minimum film thickness during two engine cycles under steady state operating condition for the big-end bearings under various cylinder conditions. In all the cases, the absolute minimum film thickness occurs a few degrees after the top dead centre position within the engine power stroke, where the maximum chamber pressures are encountered. The demarcation boundaries between the prevailing instantaneous regime of lubrication are indicated by the Stribeck’s oil film parameter; $\lambda = \frac{h}{{\sigma_{\text{rms}} }}$, where h is the film thickness and σ _rms the root mean square roughness of the counterfaces (journal and the bearing bushing/shell). When, 1 < λ < 3 a mixed regime of lubrication is encountered and λ ≤ 1 indicates a boundary regime of lubrication. Therefore, the inclusion of direct boundary interactions for determination of friction (as in Sect. 3.8) is essential in any analysis of engine big-end bearings. An important point to note is the incidence of boundary interactions in the in-take stroke as well as the power stroke of the engine cycle for the deactivated cylinder because the valves remain closed and a residual bearing load is retained due to cylinder swept volume. This means that with CDA the big-end bearing contributes to boundary friction in parts of the engine cycle that is unexpected in the case of normal engine operation. This is because of the trapped air/charge volume with closed valves. This contributes to the overall frictional power loss of the engine operating under CDA as shown in Fig. 16.

Fig. 15

Minimum film thicknesses for various cylinder conditions

Fig. 16

Frictional power loss for various cylinder conditions

Figure 16 shows the frictional power loss in the deactivated cylinder’s big-end bearing is in fact larger than that for an engine under normal operation mode in a typical engine cycle 0° ≤ ϑ ≤ 720°. The results also show that active cylinders operating at higher pressures under CDA apply higher loads, thus increasing their bearings’ frictional power loss. Therefore, overall the bearing losses are increased under CDA, although this is more than offset by the efficiency gains through higher temperature combustion and reduced pumping losses accounting for 20 % lower fuel consumption for the engine under consideration (a four-cylinder four-stroke c-segment vehicle). The findings of the analysis agree with those of Mohammadpour et al. [6] using mixed thermohydrodynamic analysis, using Reynolds equation.

7 Conclusions

One of the main conclusions of the current study is the importance of determining the correct boundary conditions in the study of journal bearing lubrication. In particular, it is important to include mass conserving flow dynamics through the conjunction. This requires the solution of Navier–Stokes equation, also including vapour transport and energy equations. In this manner the effects of shear heating, multi-phase and any reverse flow conditions are automatically included for the determination of lubricant film rupture point and its subsequent reformation. The results obtained show closer conformance to the experimental measurements than other methods reported in literature, which impose cavitation algorithms such as the Elrod’s algorithm [17].

With respect to the application of CDA as one of the rapidly emerging engine technologies, the analysis shows that unlike the gains made through application of CDA in reduced pumping losses and fuel consumption, the big-end bearing frictional losses are actually increased. This is particularly concerning as the results of analysis corresponds to low speed city driving conditions where application of CDA is seen to be most effective. Of course gains made through reduced pumping losses and fuel consumption outweigh the increased frictional losses shown here. Nevertheless, the findings here indicate that tribological conditions should also be considered in more detail, whilst adopting new technologies.

The area under the power loss curve for a typical cycle 0° ≤ ϑ ≤ 720° corresponds to the enregy consumed within a bearing at the stated operating conditions. With the four-cylinder engine studied, under CDA condition, two cylinders are deemed to be deactivated simultaneously with the other two operating as active cylinders. The reason for this operating configuration is to reduce the engine crankshaft torsional oscillations which can be exacerbated through increased imbalances induced by applied combustion torque fluctuations [5] with CDA. Taking these points into account, the area under the power loss curve for the various big-end bearing conditions and the calorific value of fuel, the equivalent fuel consumed by the big-end bearings under normal engine operation at the city driving speed of 25 km/h for 100 km is 65.8 g, whilst that under CDA condition amounts to 87.5 g. This represents an increase in brake specific fuel consumption of nearly 25 % by the big-end bearings under CDA, which stands in contrast to the gains made in pumping losses to the cylinders. A main conclusion of the study is that tribology of engine conjunctions should be taken into account with application of new technologies such as CDA. Hitherto, the approach most commonly used disregards any detailed analysis, opting to evaluate more direct gains in fuel efficiency through control of combustion and determination of fuel injection rates.

Appendix

The number of control volumes was varied in order to determine the optimum for convergence and numerical accuracy. Figures 17, 18 and 19 show the effect of an increasing number of control volumes as well as numerical convergence error tolerance upon for some key computed parameters and at different crank-angle locations.

Fig. 17

Power loss versus different numbers of control volume

Fig. 18

Lubricant maximum temperature versus different convergence criteria for energy conservation

Fig. 19

Power loss versus different convergence criteria for mass and momentum conservation and the vapour volume fraction