A Macro-scale Approximation for the Running-in Period

Abstract

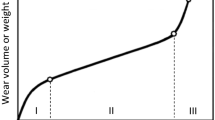
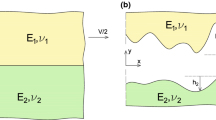
The article presents asymptotic modeling of the running-in wear process with fixed contact zone under a prescribed constant normal load or an imposed contact displacement. The wear contact problem is formulated within the framework of the two-dimensional theory of elasticity in conjunction with Archard’s law of wear. The running-in process is considered at the macro-scale level, while the micro-processes associated with roughness changes, tribomaterial evolution, and microstructural alteration in the subsurface layers as a first approximation are neglected. The setting of the steady-state regime for the macro-contact pressure evolution is chosen as the criterion to characterize the completion of running-in. Simple closed-form approximations are derived for the running-in period and running-in sliding distance. The obtained results can be used for estimating the running-in period in wear processes where the evolution of the macro-shape deviations at the contact interface plays a dominant role.

Appendix: Determining Eigenvalues in the Wear Contact Problem with Prescribed Displacement

Following Aleksandrov et al. [16], we employ the biorthogonal expansion

$$ \ln {\frac{2}{{\left| {x^{\prime} - \xi^{\prime}} \right|}}} + C = 2\left[ {\ln 2 + \mathop \sum \limits_{l \,=\, 1}^{\infty } {\frac{{T_{l} (\xi^{\prime})T_{l} (x^{\prime})}}{l}}} \right] + C $$

where $T_{l} \left( {x^{\prime}} \right) = \cos (l { \arccos } x)\,,l = 1, 2, \ldots ,$ are the Chebyshev polynomials.

Using the representation

$$ \varphi_{2r} \left( {x^{\prime}} \right) = \mathop \sum \limits_{m \,=\, 0}^{\infty } a_{m}^{\left( r \right)} \tilde{P}_{2m} \left( {x^{\prime}} \right),\quad \tilde{P}_{2m} \left( {x^{\prime}} \right) = \sqrt {{\frac{4m + 1}{2}}} \,P_{2m} \left( {x^{\prime}} \right) $$

where P _2m (x′) are the Legendre polynomials, one can derive the following infinite linear algebraic system for determination of the coefficients a ^(r) _m :

$$ a_{m}^{\left( r \right)} = \alpha_{2r} \mathop \sum \limits_{l \,=\, m}^{\infty } {\frac{{b_{mn} }}{{l^{*} }}}\mathop \sum \limits_{s \,=\, 0}^{l} b_{sl} a_{s}^{\left( r \right)}\quad (m = 0,1, \ldots ) $$

(26)

Here we used the notation

$$ l^{*} = l \ge 1,\quad 0^{*} = (2\ln 2 + C)^{ - 1} ,\quad b_{ml} = \mathop \int \limits_{ - 1}^{1} \tilde{P}_{2m} \left( {\xi^{\prime}} \right)T_{2l} \left( {\xi^{\prime}} \right)\,\rm{d}\xi^{\prime} $$

Finally, we transform the system (26) into the following one:

$$ \begin{gathered} \alpha_{2r}^{ - 1} a_{0}^{\left( r \right)} = \left( {\left( {2\ln 2 + C} \right)b_{00}^{2} + \mathop \sum \limits_{n \,=\, 1}^{\infty } {\frac{{b_{0l}^{2} }}{l}}} \right)a_{0}^{\left( r \right)} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \mathop \sum \limits_{s \,=\, 1}^{\infty } a_{s}^{\left( r \right)} \mathop \sum \limits_{l \,=\, s}^{\infty } {\frac{{b_{0l} }}{l}}\,b_{sl} \hfill \\ \end{gathered} $$

(27)

$$ \begin{gathered} \alpha_{2r}^{ - 1} a_{m}^{\left( r \right)} = \mathop \sum \limits_{l \,=\, m}^{\infty } {\frac{{b_{ml} }}{l}}b_{0l} a_{0}^{\left( r \right)} + \mathop \sum \limits_{s \,=\, 1}^{m} a_{s}^{\left( r \right)} \mathop \sum \limits_{l \,=\, m}^{\infty } {\frac{{b_{ml} }}{l}}b_{sl} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \mathop \sum \limits_{s \,=\, m + 1}^{\infty } a_{s}^{\left( r \right)} \mathop \sum \limits_{l \,=\, s}^{\infty } {\frac{{b_{ml} }}{n}}b_{sl}\quad (m \ge 1) \hfill \\ \end{gathered} $$

(28)

The results of numerical calculations based on the homogeneous system (27), (28) are presented in Table 1. We note the computational misprints in article [16].