1 Introduction

Hard disk drives (HDDs) are not free of particles, which are generated due to different causes such as manufacturing debris, the slider’s loading/unloading process, and its occasional contact onto the disk. These particles range in size from several nanometers to several micrometers. In the present article, we focus on the particle’s motion in the head–disk interface (HDI), which is the region between the slider and the disk, as shown in Fig. 1. Since the slider’s flying height, h, at the leading edge is around 200 nm, only particles smaller than this value can enter the HDI, and they are the ones of concern here. The slider carries the read–write transducer at its trailing edge which has a much smaller spacing, and the particles entering the HDI may stick to this region and affect the transducer’s effectiveness. Other particles might accumulate on the slider and increase the possibility of the slider’s contact with the disk, which could further cause the loss of data stored on the disk. Thus particle contamination on the slider can be critical to the HDDs’ reliability [1–4].

Fig. 1
figure 1

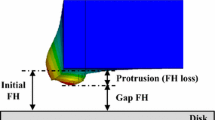
The head–disk interface is the region between the slider and the disk. The slider’s flying height, h, at the leading edge is around 200 nm while that at the trailing edge can be as low as 10 nm. A heating element is embedded near the read–write transducer located at the trailing edge. When power is applied to the heating element, the slider protrudes correspondingly. A coordinate system is set up with the z axis perpendicular to the disk. Note: This figure is not to scale

Full size image

To increase the HDDs’ linear data density on a track, it is necessary to reduce the slider’s flying height at the read–write transducer. To achieve this goal, the thermal flying-height control (TFC) slider has been developed and implemented in current commercial HDDs [5]. In these sliders, a heating element is integrated near the read–write transducer. When power is applied to this heating element, the slider protrudes near the transducer due to its thermomechanical expansion properties, which decreases the slider’s flying height at the transducer. In this approach, the slider’s temperature is raised higher than that of the disk, and therefore the temperature in the HDI is not uniform. This non-uniform temperature field induces a force, the so-called thermophoretic force, on particles moving in the HDI. This force points opposite to the temperature gradient direction and is due to the different mobility of gas molecules on different parts of the surface of the particle since the temperature is a macroscopic manifestation of the gas molecules’ speeds [6, 7].

Particle contamination on traditional sliders without a heating element has been thoroughly investigated. Zhang and Bogy [1, 2] studied the effect of lift force on the motion of particles in the HDI, and they showed that lift force is important only for particles with sizes larger than 200 nm. Shen and Bogy [3] extended Zhang and Bogy’s work to include the air flow perpendicular to the disk, and they showed that this flow is important for particles entering the recess region. The agreement of their results with experiments is better than that of Zhang and Bogy’s. Liu and Bogy [4] further considered the presence of the flow boundaries, i.e., the slider and the disk, on the drag force on the particle and concluded that the results obtained from Shen and Bogy’s particle contamination simulator did not change much with this new feature introduced. In all of the above work the air flow in the HDI is assumed to be isothermal since the slider and the disk are at the same temperature and no non-uniform temperature field exists in the HDI according to the linearized Boltzmann equation [8]. For the TFC slider, the non-uniform temperature field in the HDI induces a thermophoretic force on the particles, and its effect on a particle’s motion in the HDI and particle contamination on the slider has not yet been explored. The present article serves to fill this gap and clarify the applicability of the current CML particle contamination simulator [3] to the TFC slider. This paper is organized as follows. In Sect. 2, we discuss the calculation of the temperature field in the HDI, derive the thermophoretic force on the particle, and show how to simulate the particles’ motions in the HDI. The simulation results of a particle’s motion in the HDI are presented and discussed in Sect. 3. A summary and conclusion is given in Sect. 4.

2 Theory

2.1 Temperature Field in the HDI

Since the air gap thickness in the HDI ranges from several nanometers to around 1 μm and the mean free path of the air is about 65 nm, the air in the HDI is rarefied and the air flow in the HDI is described by the Boltzmann equation or its equivalents instead of the traditional continuum Navier–Stokes equation [8]. The exact approach to obtain the temperature field in the HDI is to solve the Boltzmann equation for the air flow between the slider and the disk whose temperatures are different. This approach is difficult and can not give results that are easy to implement in the CML particle contamination simulator. Since the temperature difference between the slider and the disk is much smaller than that of the slider or the disk, and the air flow speed is much less than the average thermal speed of the air molecules, which is of the same order as the speed of sound in air, the linearized Boltzmann equation is suitable for characterizing the air flow in the HDI. Based on this equation, it can be shown that the air flow problem and the temperature problem are decoupled [8], i.e., we can neglect the air flow when calculating the temperature field in the HDI.

Due to the complexity of the (linearized) Boltzmann equation, it is still difficult to solve for the temperature field in the HDI, and an approximate approach, the method of moments [9], is adopted here. This method can give analytical formulae, which compare well with experiments. Based on this method and the assumption that the accommodation coefficients of both the slider and the disk are equal to 1, which is a common practice in simulations related to the HDI [1–4], the temperature in the HDI is [9]:

$$ {\frac{T}{T_{\text{d}}}}={\frac{\alpha_2} {2}}\sqrt{\alpha_4-4\beta{\frac{\alpha_3}{\alpha_2}}{\frac{z}{h}}} $$
(1)

and

$$ \begin{aligned} \alpha_2 & = {\frac{\sqrt{(1+\beta)(L^4+2L^3+\beta)+L^2}-(L^3+2L^2-\beta-1)} {1+\beta-L^2}}\\ \alpha_3 & =2-\alpha_2\\ \alpha_4 & =1-2(1+\beta){\frac{\alpha_3} {\alpha_2}}+\left({\frac{\alpha_3}{\alpha_2}}\right)^2\\ \end{aligned} $$

where \(L=\sqrt{T_{\text{s}}/T_{\text{d}}},\) T s is the slider’s local temperature, T d is the disk’s temperature, β = h/λ, h is the air gap thickness, λ is the mean free path of air at T d, and z = 0 corresponds to the disk while z = h corresponds to the slider, as shown in Fig. 1. A typical temperature profile in the HDI is shown in Fig. 2.

Fig. 2
figure 2

A typical temperature profile in the head–disk interface. Here λ = 65 nm, h = 1μm, T s = 40 °C and T d = 20 °C. Due to the discontinuity of temperature at the boundary, the temperature near the disk is different from the temperature of the disk

Full size image

2.2 Thermophoretic Force

The thermophoretic force is induced by the non-uniformity of the temperature field. One classical example where this force is present is in the accumulation of carbon particles on a kerosene lantern. The temperature difference between the flame and the globe produces the force which drives the particles into the globe. Since Maxwell’s first investigation [6], extensive work has been done on this topic. Brock [10] solved the Navier–Stokes equation and the energy equation supplemented with the first order velocity and temperature slip boundary conditions, and he obtained an analytical formula for the thermophoretic force on a sphere in a non-uniform temperature field with a constant gradient. Due to its underlying assumption of using the first order slip theory, this formula is not guaranteed to hold for a highly rarefied gas. However, when Brock’s formula is applied to the latter case, it gives almost the same result as that derived by Waldmann [11] for the case of a highly rarefied gas and only differs by 3% [6]. Talbot [6] further applied Brock’s formula to an arbitrarily rarefied gas, and showed this formula agrees with experiments when appropriate values are chosen for the parameters involved in Brock’s formula. For our case, Brock’s formula gives [6, 7]

$$ F_{\text{T}}=-C_{\text{T}}{\frac{1}{T}}{\frac{\partial{}T}{\partial{}z}} $$
(2)

and

$$ C_{\text{T}}={\frac{14.04\pi\mu\nu{}R\left(k_{\text{g}}/k_{\text{p}}+2.18\lambda/R\right)} {\left(1+3.42\lambda/R\right)\left(1+2k_{\text{g}}/k_{\text{p}}+4.36\lambda/R\right)}} $$

where μ is the air viscosity, ν = μ/ρ, ρ is air density, R is particle radius, and k g and k p are the thermal conductivity of the gas and the particle, respectively.

Using Eq. 1 in Eq. 2, we get the thermophoretic force on a particle moving in the HDI:

$$ F_{\text{T}}=2\beta{}C_{\text{T}}{\frac{(1/h)(\alpha_3/\alpha_2)} {\alpha_4-4\beta(z/h)(\alpha_3/\alpha_2)}} $$
(3)

2.3 Simulation of a Particle’s Motion in the HDI

Since the volume density of particles in the HDI is much smaller than 1, collisions between particles can be neglected, and the motion of the particles is described by Newton’s second law:

$$ m{\frac{\text{d}^{2}{x}}{\text{d}t^2}={F}_{\text{total}}={F}_{\text{drag}}+{F}_{\text{Saffman}}+{F}_{\text{T}}} $$
(4)

where m is the mass of the particle and x is the particle’s location. The first term in the right hand side of Eq. (4) is the drag force, which resists the motion of the particle, and the second term is the Saffman lift force, which is induced by the non-uniformity of the air flow and points in the gradient direction of the air flow. In view of the particles’ small size, which is less than 1μm, other forces than those considered here can be neglected. To follow the particle’s location in time, the Runge–Kutta method is used to integrate Eq. 4, and a suitable integration time step is chosen to ensure the convergence of the numerical method [4].

3 Results and Discussions

The temperature of a TFC slider during operation only rises by less than 1 °C higher than that of the disk except in the region near the transducer where the temperature can locally rise as much as 10 °C [12, 13]. Despite this fact, we consider here an extreme case where the slider’s temperature is assumed to be uniformly 10 °C higher than that of the disk, and we explore the effect of this temperature rise on the motion of particles in the HDI. For each particle moving in the HDI, two trajectories are calculated: one with the thermophoretic force and the other one without it, the latter of which corresponds to a traditional slider without the heating element.

The profile of an air bearing surface, which is the surface of the slider facing the disk, is shown in Fig. 3 and is used in the following calculations. The numerical results presented in Fig. 4, show that these two trajectories essentially coincide with each other, which implies that the thermophoretic force is negligible even for this extreme case. To understand the reason behind this finding, we perform an order analysis and investigate the relative importance of the thermophoretic force and the Saffman force.

Fig. 3
figure 3

The profile of the air bearing surface used in the calculation of particle trajectories in the head–disk interface

Full size image
Fig. 4
figure 4

Typical particle trajectories in the head–disk interface. The two trajectories superpose on each other. Here h m is a nominal flying height used as a reference value to normalize z

Full size image

Since the slider’s flying height at the leading edge is about 200 nm and we are considering particles’ motion in the HDI, only those particles with size below 200 nm are of concern. Since k g/k p ∼ 0.024/30.9 ≪ 1 and Kn = λ/R > 0.3, the k g/k p term can be neglected in Eq. 2, and Eq. 3 becomes

$$ F_{\text{T}}\sim{\frac{192\mu\nu} {\left(1+3.42\lambda/R\right)\left(1+4.36\lambda/R\right)}}\,{\frac{\alpha_3/\alpha_2} {\alpha_4-4(\alpha_3/\alpha_2)(z/h)}} $$
(5)

From Refs. [1, 14], the Saffman force is

$$ F_{\text{Saffman}}\sim6.46\mu{}R^2\Updelta{}U\sqrt{G/\nu} $$
(6)

where G is the magnitude of the gradient of the non-uniform air flow and ΔU is the magnitude of the speed of the air flow relative to the center of the sphere.

From Eqs. 5 and 6, we obtain the ratio between the thermophoretic force and the Saffman force

$$ {\frac{F_{\text{T}}}{F_{\text{Saffman}}}}\sim{\frac{192}{6.46}}\left({\frac{\nu} {U}}{\frac{h^{1/3}}{R^{4/3}}}\right)^{3/2} {\frac{1} {\left(1+3.42\lambda/R\right)\left(1+4.36\lambda/R\right)}}{\frac{\alpha_3/\alpha_2} {\alpha_4-4\alpha_3/\alpha_2}} $$
(7)

where we take z = h to get an estimation of the order of F T, and we use U/h as an estimate of G, U as an estimate of ΔU and U is the disk’s speed. Equation 7 further requires an estimation of α2, α3, and α4, which involve β = h/λ and \(L=\sqrt{T_{\text{s}}/T_{\text{d}}}=\sqrt{1+l}\) where l = (T s−T d)/T d ≪ 1.

Due to the dependence of the mean free path on the local pressure, the mean free path decreases with the slider’s flying height, which means β ≫ 1 or β ∼ 1. For either of these two cases, α2 ∼ 2 and α4 ∼ 1 − (1 + β)α3, and

$$ \begin{aligned} \alpha_3 & = {\frac{-\sqrt{(\beta+2)^2+(1+\beta)\left[2l+l^2+2\left((1+l)^{3/2}-1\right)\right]+l}+ (1+l)^{3/2}+\beta+1}{\beta-l}}\\ & ={\frac{-(\beta+2)\sqrt{1+{\frac{1+\beta}{(2+\beta)^2}}\left[2l+l^2+ 2\left((1+l)^{3/2}-1\right)\right]+{\frac{l}{(2+\beta)^2}}}+ (1+l)^{3/2}-1+\beta+2}{\beta-l}}\\ & \sim{\frac{-(\beta+2)-{\frac{1+\beta}{2(2+\beta)}}\left[2l+l^2+ 2\left((1+l)^{3/2}-1\right)\right]-{\frac{l} {2(2+\beta)}} +{\frac{3}{2}}l+(\beta+2)}{\beta-l}}\\ & \sim -{\frac{\beta}{\beta+2}}l\\ \end{aligned} $$

Then α3/α2 ≪ 1 and α3/(α2α4) ≪ 1. Given that the kinematic viscosity for air ν ∼ 10−6 m2/s and the disk speed U ∼ 10 m/s, it can be shown from Eq. 7 that the thermophoretic force is always smaller than the Saffman force, and it is therefore negligible since the Saffman force itself is negligible for particles smaller than 200 nm [1]. Thus, we do not need to consider the thermophoretic force for calculation of a particle’s trajectory in the HDI between a TFC slider and a disk, and, accordingly, for studies of particle contamination on a TFC slider.

4 Summary and Conclusion

The particle contamination on a TFC slider is investigated in the present article. The temperature difference between the slider and the disk, due to local heating in the slider, induces a thermophoretic force on particles moving in the HDI. By incorporating results for the temperature field in the HDI based on the method of moments, we obtain an analytical formula for the thermophoretic force on the particles moving in the HDI. We then solve the governing equation for the particle’s motion and obtain the particle’s trajectory. It is found numerically that the effect of the thermophoretic force is negligible. This is further confirmed by an order analysis of the magnitude of the thermophoretic force and Saffman force. We show that the thermophoretic force is always smaller than the Saffman force and is therefore negligible since in our case they act along the same direction. The present study thus validates the use of the current CML particle contamination simulator for the investigation of particle contamination on a TFC slider.