Abstract
The paper offers a critical examination of a prominent, “quasi-deflationist” argument advanced in the contemporary debate on the semantic paradoxes against non-naive and non-transparent theories of truth. The argument claims that truth unrestrictedly fulfils certain expressive functions, and that its so doing requires the unrestricted validity of naivety and transparency principles. The paper criticises the quasi-deflationist argument by considering some kinds of cases in which transparency and naivety arguably fail. In some such cases truth still fulfils the relevant expressive functions without being transparent or naive; in some other such cases, truth does not fulfil the relevant expressive functions and other conceptual resources must be called upon. Thus, in different ways, all such cases belie the quasi-deflationist argument’s insistence that naivety and transparency should be unrestrictedly valid for truth unrestrictedly to fulfil the relevant expressive functions. There might however be other reasons for solving the semantic paradoxes by revising classical logic, and the paper in effect closes by offering versions of the liar paradox that rely on compelling but opacity-friendly truth-theoretic principles.
Similar content being viewed by others
Notes
For example, in the supervaluationist theory of truth of McGee (1991), (A) and (D) hold but (I) fails, and so the traditional principle of intersubstitutability of logical equivalents fails. Somewhat surprisingly, in many theories in which (I) too holds, this is not because it follows from (A) and (D) plus intersubstitutability of logical equivalents, since the latter principle still fails in those theories. For example, in many theories accepting (I) but rejecting the Liar sentence [see for instance Field (2008)], the latter is logically equivalent with but not intersubstitutable with \(0\ne 0\), while, in many theories accepting (I) and accepting the Liar sentence [see for instance Beall (2009)], the latter is logically equivalent with but not intersubstitutable with \(0= 0\). I think that the envisaged failures of intersubstitutability of logical equivalents raise some serious issues about the notion of logical equivalence (and of entailment) at work in all these theories: if \(\varphi \) and \(\psi \) are not intersubstitutable, they must differ in logical strength (by, for example, \(\varphi \) being in some respect logically stronger than \(\psi \)), and shouldn’t such a difference be reflected in a lack of entailment from \(\psi \) to \(\varphi \)? It is thus important to note that acceptance of (I) does not necessarily imply the implausible rejection of intersubstitutability of logical equivalents [see Zardini (2011, 2013a, b, 2014a, c, d, g) for an example of a consistent theory accepting (I) as well as intersubstitutability of logical equivalents].
The most developed version of quasi-deflationism is Field (2008), on whose claims I’ll thus mostly focus (Field is of course also one of the most prominent advocates of deflationism). Another important position favourable to quasi-deflationism is the one represented by Beall (2009). Although this paper is largely devoted to a criticism of the quasi-deflationist argument against non-naive or non-transparent theories of truth, I cannot emphasise enough how much my own thinking about truth has been shaped by reading and discussing with these two authors.
To take a somewhat extreme example, one might argue that neither ‘EZ will lift his left arm’ nor ‘It is not the case that EZ will lift his left arm’ are true (that is, true now) because, if either were, its present truth would rob me of the freedom, which I apparently have, to lift my left arm. I think this argument deserves much deeper considerations than those concerning the expressive functions of truth. As I’m mostly focussing on Field’s works, I should add that, in his specific case, those considerations are indeed grounded in a more fundamental deflationist outlook, which is in turn motivated by a deeply rooted scepticism about semantic properties.
Notice that, while the problem cannot be generated by relying purely on naivety, it can be generated without relying on the full power of transparency. For what is really needed to generate the problem is the principle of contraposed ascent:
-
(CA)
‘\(\ulcorner \varphi \urcorner \) is not true’ entails ‘It is not the case that \(\varphi \)’,
which would do the work done by the first application of (I) in the argument in the text, whereas the second such application is immediately licenced by (A). [Notice that, just as truth-value gaps make problems for (CA), truth-value gluts may be thought to make problems for its converse, as argued by Priest (2006), pp. 78–80.] Of course, given contraposition for logical consequence (if \(\varphi \) entails \(\psi \), ‘It is not the case that \(\psi \)’ entails ‘It is not the case that \(\varphi \)’), naivety [in particular, (A)] implies (CA). In turn, contraposition for logical consequence is arguably a valid principle even in the presence of the semantic paradoxes. I’ve argued this much already in Zardini (2014c), but I’d now wish to provide a further argument relying on intersubstitutability of logical equivalents (which I’ve in turn defended in fn 1). Suppose that \(\varphi \) entails \(\psi \). Then, for at least some broadly conjunction-like connective \(\wedge \), \(\varphi \) is equivalent with \(\varphi \wedge \psi \). But, by anyone’s lights, ‘It is not the case that \(\psi \)’ entails ‘It is not the case that \(\varphi \wedge \psi \)’, and so, by intersubstitutability of logical equivalents, ‘It is not the case that \(\psi \)’ entails ‘It is not the case that \(\varphi \)’. Having noted that, contraposition for logical consequence is unfortunately not acceptable in many non-classical theories of truth (although it unsurprisingly is in the theory developed in my works referenced in fn 1), and so I’ll continue to keep (CA) separate from (A).
-
(CA)
Beall (2002) argues that the contradiction is only apparent as one can understand the negation connected with falsity as choice negation (henceforth subscripted with ‘ch’) and the negation denying truth and falsity as exclusion negation (henceforth subscripted with ‘exc’). I find Beall’s proposal very interesting, but also multiply problematic. Firstly, some candidate types of gappy sentences are such that, if indeed gappy, they would also include gappy sentences governed by negation exc (for example, there are borderline cases of non\(_{\mathrm {exc}}\)-baldness), and, for such cases, Beall’s proposal is equally affected by the argument in the text (given that ‘It is not\(_{\mathrm {ch}}\) the case that it is not\(_{\mathrm {exc}}\) the case that \(\varphi \)’ is intersubstitutable with ‘It is not\(_{\mathrm {exc}}\) the case that it is not\(_{\mathrm {exc}}\) the case that \(\varphi \)’). Secondly, I’ll discuss below in the text how the kinds of truth-value gaps exemplified by certain sentences are compatible with acceptance of those sentences (for example, someone thinking that ‘Santa Claus doesn’t exist’ is not true because it suffers from reference failure may well nevertheless accept that sentence as reporting the non-existence of Santa Claus). But the argument in the text can still infer from the gappiness of any such sentence \(\varphi \) to ‘It is not\(_{\mathrm {exc}}\) the case that \(\varphi \)’, and so one would still be stuck with accepting a contradiction (‘\(\varphi \) and it is not\(_{\mathrm {exc}}\) the case that \(\varphi \)’), just as the original argument in the text would have it. Thirdly, I take it that, on a typical truth-value-gap approach, it is supposed to be false (rather than neither exc true nor exc false) that \(\varphi \) is both gappy and either true or false. [After all, every sentence is supposed to have exactly one status, and gappiness is supposed to be a third status: it follows from the first assumption that, if \(\varphi \) is gappy and true (false), gappiness is identical with truth (falsity), and so gappiness and truth are one and so not\(_{\mathrm {ch}}\) two, which is false given the second assumption]. But, if one accepts this, and accepts that \(\varphi \) is gappy, one should presumably infer that it is false that \(\varphi \) is either true or false—that is, infer that \(\varphi \) is neither\(_{\mathrm {ch}}\) true nor\(_{\mathrm {ch}}\) false, which reinstates the original argument in the text. Fourthly, Beall’s proposal is variously at odds with typical arguments in favour of truth-value gaps. On the one hand, such arguments proceed by identifying a necessary condition for truth (for example, that speakers’ practices determine a sufficient condition for ‘bald’ to apply to Harry and Harry satisfies the condition) and contending that this is not ch met by the relevant type of sentences: if at all sound, such arguments establish, by contraposition for implication (‘If \(\varphi \), then \(\psi \)’ entails ‘If it is not\(_{\mathrm {ch}}\) (not\(_{\mathrm {exc}}\)) the case that \(\psi \), then it is not\(_{\mathrm {ch}}\) (not\(_{\mathrm {exc}}\)) the case that \(\varphi \)’), that the relevant type of sentences are not\(_{\mathrm {ch}}\) true over and above being not\(_{\mathrm {exc}}\) true. On the other hand, such arguments proceed by identifying a broadly semantic feature of the relevant type of sentences (for example, suffering from reference failure) and contending that such feature is the root of the gappiness of those sentences. But the feature in question is typically not preserved under ascent (for example, while ‘Santa Claus doesn’t exist’ suffers from reference failure, ‘‘Santa Claus doesn’t exist’ is true’ does not), and so such arguments provide no support for thinking that gappiness is preserved under ascent, contrary to what is required by Beall’s proposal. Thanks to an anonymous referee for recommending a discussion of Beall’s proposal.
Throughout, an attitude expresses (or is associated with) an attitude iff they have the same correctness conditions. Thus, as I understand them, the expressive functions of truth concern its enabling one virtually to entertain a problematic attitude by non-virtually entertaining another, less problematic attitude, rather than its enabling one to voice one’s attitudes in conversation: as I understand them, the expressive functions of truth are functions of thought rather than communication. Thanks to an anonymous referee for urging these clarifications.
Field (2008), pp. 138–139 mainly uses ‘disagree’ and its relatives, but, focussing purely for simplicity on the case of a single sentence, I take it that, in the relevant sense of disagreeing with a sentence \(\varphi \) (rather than with a person), what he means is rejection of \(\varphi \) (which in turn in this debate is understood as a fairly sui generis attitude consisting, roughly, in ruling out the truth of \(\varphi \)). A possibly alternative interpretation would be that what he means is acceptance of ‘It is not the case that \(\varphi \)’. But, in a framework (such as Field’s) in which these two are indeed alternative interpretations (as I explain below in the text), the latter is arguably a very unnatural and rather uninteresting understanding of disagreement, since, under such understanding, one should not disagree with ‘Harry is bald’ if Harry is borderline bald. Indeed, Field (2008), p. 208 himself remarks that it is more natural to understand disagreement as rejection. For this reason, I assume throughout such understanding. Thanks to an anonymous referee for pointing out the need for this clarification.
One might object that that is not equally legitimate, since, while acceptance of \(\{ \varphi , \psi \}\) can be reduced to acceptances of individual sentences (namely, to acceptance of \(\varphi \) and acceptance of \(\psi \)), rejection of \(\{ \varphi , \psi \}\) cannot be reduced to rejections of individual sentences (namely, to rejection of \(\varphi \) or rejection of \(\psi \)). But, even granting for the sake of argument such a dubious reducibility constraint on legitimacy, in my view the objection crucially overlooks the fact that, as I explain in fn 15, there are two different kinds of acceptance and rejection, and that the weaker kind of acceptance—which is the one that is reducible to acceptances of individual sentences—has as corresponding exclusive kind of rejection the stronger one that is reducible to (conditional) rejections of individual sentences [in fact, just as the weaker kind of acceptance is reducible to a sum of acceptances of individual sentences, the stronger kind of rejection is reducible to a sum of (conditional) rejections of individual sentences]. Thanks to Sergi Oms for discussion of this point.
It seems to me clear that, quite generally, just as one can accept or reject, say, gifts without knowing exactly which gifts they are, one can straightforwardly accept or reject sentences without knowing exactly which sentences they are (rather than simply expressing such acceptance or rejection by using, for example, truth). For one thing, were this not so virtually no one could straightforwardly accept all the terms and conditions of many contracts, or the whole periodic table, or everything said by any past or future Pope etc. (Notice that, once we naturally extend this point from sentences to propositions, a casualty of the resulting view is arguably the implication from accepting the proposition that \(P\) to believing that \(P\).) However, since the quasi-deflationist framework is not particularly hospitable to such considerations, I’ll henceforth set them aside. Thanks to Sergi Oms for raising this issue.
An analogous point could have been made about conditional acceptance. Taking on board the rationale just mentioned in the text, for every \(\varphi \) and \(\psi \) there is some (possibly metalinguistic) context \(\mathcal {C}_{\varphi,\,\psi}(\ldots \cdot \ldots \cdot \ldots )\) such that conditional acceptance of \(\psi \) on \(\varphi \) is expressed by \(\mathcal {C}_{\varphi,\,\psi}(\ldots \varphi \ldots \psi \ldots )\). Moreover, \(\mathcal {C}_{\varphi,\,\psi}(\ldots \varphi \ldots \psi \ldots )\) both together with \(\varphi \) entails \(\psi \) and follows from \(\varphi \) ’s entailing \(\psi \) (since conditional acceptance of \(\psi \) on \(\varphi \) forces \(\psi \) given \(\varphi \) and is licenced by \(\varphi \)’s entailing \(\psi \)). But no standard (i.e., for the cognoscenti, non-substructural) transparent theory can allow for a notion with those two features [see Zardini (2013b, 2014a, c, d) for more details].
Keeping fixed that, at least in the case of the semantic paradoxes, attributions of untruth are always correlated with rejection, since the Liar sentence is tantamount to ‘The Liar sentence is not true’ it surprisingly but straightforwardly follows, under plausible assumptions about acceptance and rejection, that one should neither accept nor reject the Liar sentence. While in conflict with many theories of truth, that result is very much congenial to the theory I’ve developed in my works referenced in fn 1.
‘Certain’ because, arguably, the kind of truth-value gap exemplified by many other sentences suffering from reference failure (for example, ‘Santa Claus is 1.76 cm tall’) is rather of the malign variety. It is beyond the scope of this paper to offer an account of the distinction between malign and benign kinds of truth-value gaps, although it may at least be noted that it seems to correlate with the presence or absence of what may to a first approximation be described as indeterminacy in principle.
At least given the assumption justified in fn 7, Field (2008), pp. 206–208 disagrees, in effect claiming, about another example equally supposed for the sake of argument to be gappy, that one should reject the sentence in question. As I’ve briefly argued in the text, such claim is very problematic. In any event, the fact that attributions of untruth are not always correlated with rejection is probably even more clear-cut with other candidate types of gappy sentences: someone thinking on 06/10/2171 that ‘There will be a sea-battle on 07/10/2171’ is not true because it is not completely settled on 06/10/2171 may well nevertheless accept that sentence as describing what one has overwhelming reasons for thinking will be the case (or at the very least may on those grounds not reject that sentence); someone thinking that ‘If Italy played the final of the 2010 World Cup, they won’ is not true because it is only endowed with acceptability conditions relative to epistemic states, may well nevertheless accept that sentence as having a consequent that, on one’s evidence, is extremely likely given its antecedent (or at the very least may on those grounds not reject that sentence); someone thinking that ‘Abortion is wrong’ is not true because it expresses an evaluation may well accept that sentence as expressing one’s own evaluation (or at the very least may on those grounds not reject that sentence). To take philosophically somewhat less loaded cases, someone thinking that ‘If \(P\), then \(P\)’ is not true because it contains schematic expressions with no specific content may well accept that sentence as stating the valid law of reflexivity for implication (or at the very least may on those grounds not reject that sentence); someone thinking that ‘It might be black’ (understood as anaphoric on ‘A sheep might come in’) is not true because it contains a pronoun with no specific referent may well accept that sentence (under the relevant understanding) as contributing a further specification to an overall correct discourse (or at the very least may on those grounds not reject that sentence). (Since schematic or anaphoric sentences plausibly do not express propositions, there arguably are no beliefs corresponding to their acceptance, thus providing another kind of example, in addition to that discussed in fn 9, of failure of implication from acceptance to belief.) Notice that Field does actually agree that attributions of untruth are not always correlated with rejection, as with non-indicative sentences (and in many other more degenerated cases as well). As I understand it, the idea is that one can still express rejection by a suitably strengthened attribution of untruth along the lines of ‘‘\(\varphi \)’ is meaningful, indicative and not true’. It is actually very unclear whether something along these lines can by itself adequately deal with the problem posed by non-indicative sentences in all its respects, for it would seem that, for example, one can accept imperative sentences just as well as indicative ones, but acceptance of imperative \(\varphi \) cannot be expressed by either ‘‘\(\varphi \)’ is true’ (as that is not true of any imperative sentence) or ‘‘\(\varphi \)’ is not true because non-indicative’ (as that is true of every imperative sentence). (Since imperative sentences plausibly do not express propositions, there arguably are no beliefs corresponding to their acceptance, thus providing yet another kind of example, in addition to those discussed in fn 9 and above in this fn, of failure of implication from acceptance to belief. With respect to the last two kinds of examples, one may well suspect that the quasi-deflationist argument illicitly conflates the general kind of acceptance that is at issue in considerations concerning the expressive functions of truth with a specific kind of acceptance for whose instances there are corresponding beliefs.) Setting aside (as I generally mean to do in this paper) the problem of non-indicative sentences, what I’d wish to stress here is rather that one cannot further strengthen the attribution of untruth along the lines of, say, ‘‘\(\varphi \)’ is meaningful, indicative, not about the future and not true’, for that is not always correlated with rejection of \(\varphi \) now in the other direction (for example, if \(T\) consists of ‘There will be peace talks on 07/10/2171’, one should never accept and should actually always reject ‘Some members of \(T\) are meaningful, indicative, not about the future and not true’ although, on 06/10/2171, one may reject \(T\) as misdescribing what one has overwhelming reasons for thinking will be the case). Thanks to Enric Casaban, José Martínez, Sergi Oms, Gonçalo Santos and Jordi Valor for discussions of some of these issues.
In fact, even setting aside the important issue represented by “mixed sentences”, as noted more accurately in fn 12 whether an untrue sentence is acceptable will sometimes be a question with a finer mesh than what type that sentence is a token of. Thanks to an anonymous referee for raising the issues discussed in this paragraph.
In fact, by the quasi-deflationist’s own lights, by doing so one necessarily accepts as a whole the sentences belonging to \(T\) over and above accepting individually each of them [as Field (2008), p. 139 himself notes]. That there is an important difference between these two kinds of acceptance is brought out by the preface paradox [introduced by Makinson (1965)]. But that means that, by the quasi-deflationist’s own lights, truth only expresses the former, stronger kind of acceptance and not the latter, weaker kind. However, in many contexts, the only relevant kind of accepting \(T\) is arguably the weaker one (when there is good but non-conclusive evidence for each of the many independent sentences belonging to \(T\)), and truth will not help to express it. (Notice that to fall back on accepting something along the lines of ‘Every member of \(T\) is likely to be true’ would be on the contrary too weak, for such acceptance does not commit one to accepting individually each sentence belonging to \(T\), which is certainly involved even by the weaker kind of accepting \(T\)—in fact, such acceptance does not even commit one to accepting individually any sentence belonging to \(T\)!) An analogous distinction can be drawn for rejection: in a stronger sense, rejection of \(T\) consists in, for some non-empty \(U\subseteq T\), rejecting individually each sentence belonging to \(U\) conditional on accepting individually each other such sentence (the sense in which the author of a book cannot rationally reject the theory of her book), while in a weaker sense it consists in rejecting as a whole the sentences belonging to \(T\) (the sense in which the author of a book can rationally reject the theory of her book). (Thus, thinking of oneself as one’s body of beliefs, while, in the weaker sense, one necessarily accepts oneself, in the stronger sense one can rationally not accept oneself, and, while, in the stronger sense, one cannot rationally reject oneself, in the weaker sense one can rationally reject oneself.) And an analogous point applies concerning the fact that truth does not express the former, stronger kind of rejection. Having said that, I should like to note that, in certain non-contractive logics, a distinction can be drawn between the standard universal quantifier ‘every’ and a weaker universal quantifier ‘any’, and that the latter quantifier may well offer a solution to the expressive problem pointed out in this fn [see Zardini (2014g) for more details]. Thanks to an anonymous referee for an observation that led to this fn.
Richard (2008), whose general outlook is broadly congenial to the arguments of this section, in effect explicitly notices on p. 44 that some benign kinds of truth-value gaps prevent truth from always fulfilling the function of expressing acceptance, but does not bring this observation to bear on the quasi-deflationist argument [oddly, Richard (2008), p. 68 also claims that a close kin of (A) and (D) holds unrestrictedly, which, as far as I can see, is inconsistent with the existence of benign kinds of truth-value gaps]. Thanks to an anonymous referee for alerting me to the relevance of Richard’s work.
For cases along the lines of some of those discussed in fn 13, the relevant members of \(T\) should be systematically massaged into sentences that embed as expected under \(\lnot _{\mathcal {B}}\) (for example, schematic sentences should be massaged into the universally quantified sentences suggested at the end of Sect. 3). It is not clear that this is always possible (for example, in the case of imperative sentences).
Given how really expansive the envisaged substitutional quantification will turn out to be supposed to be (see especially fn 30), it is to some extent misleading to label it as ‘substitutional’, as this suggests that, contrary to objectual propositional quantification, its range is in some sense tied to the expressive resources of the language, while it is not (in fact, in this respect, as far as I can see the sentences that come out true under my substitutional reading of the quantifiers are the same as those that come out true under an objectual reading). For a variety of reasons (which I’ll list in decreasing order of importance), for our purposes I still prefer the substitutional way of doing things: it is not subject to the vicissitudes that may prevent meaningful sentences from expressing propositions, it makes the ascent required by a quotation device like \([ \cdot ]\) smoother and it has a semantics that is more naturally extended to reach the suitable expansiveness.
I should remark in passing that that requirement (properly understood) and the justification that I’ve given for it are not at all affected by the possible limits of the scheme I’ve proposed that I’ve emphasised in the last paragraph, so that that scheme perfectly fits the requirement and optimally embodies the justification that I’ve given for the requirement. To make this explicit with respect to the two possible limits considered so far, the kind of case discussed in fn 15 does not involve a single state of mind in the first place, and so falls outside the scope of the justification that I’ve given for the requirement and outside the scope of the requirement itself understood as concerning only the stronger kind of acceptance and the weaker kind of rejection; the relevant kind of case discussed in fn 17 does not involve a representational state of mind in the first place, and so falls outside the scope of the justification that I’ve given for the requirement and outside the scope of the requirement itself understood as concerning only indicative sentences.
Throughout, an utterance of \(\langle \varphi \rangle \) refers to the proposition expressed in the utterance’s context by \(\varphi \).
Such propositions are often labelled as ‘singular’, but that strikes me as a very misleading label, since the object-dependence feature mentioned in the text is universally agreed to be supposed to be exemplified for exactly the same reason by \(\langle \)Socrates and Plato are wise\(\rangle \), which has little “singular” about it. Thanks to Nasim Mahoozi for prompting this fn.
Since, necessarily, languages are conventional, it is very plausible that, necessarily, they are the product of rational beings (a sort of abstract artifact); if so, it follows that, necessarily, ‘Socrates is wise’ (just as well as any other sentence, whether semantically individuated or not) exists only if there are rational beings.
I should note that the simple-present tense in these arguments is meant in the familiar sense of ‘at some time in the present, past or future’. I should also note that I’m not inclined to run analogous arguments for temporality: for example, I’m inclined to reject the claim that \(\langle \)Socrates is wise\(\rangle \) now is partly the proposition it is because (and so now exists only if) it now refers to Socrates (it might suffice that it referred to Socrates).
The latter claim could be derived from the former by necessitation, but it enjoys independent high plausibility (even more so for the weaker claim that, necessarily, Socrates is wise or Socrates is not wise, which is all is needed by the argument to follow in the text).
The interaction of quantification with modality unsurprisingly generates issues of scope. In this respect, the obvious, scope-inverting alternative acceptance of which might be thought to express acceptance of the necessity of \(T\) is ‘Necessarily, every member of \(T\) is true’. However, as I explain in fn 26, although it might behave interestingly differently with respect to our dialectic I don’t think that this alternative is ultimately more tenable than the sentence I focus on in the text.
To come back to the alternative mentioned in fn 25, notice that, in the example in the text, on a standard understanding of the sentence and under a very plausible metaphysical assumption about theories, one should not accept ‘Necessarily, every member of \(T\) is true’ either. For, on a standard understanding of the sentence, that is true only if, necessarily, \(T\) exists, and, under a very plausible metaphysical assumption about theories, necessarily \(T\) exists only if all its members exist. I suppose however that someone (probably brainwashed by the formalisation methods learnt in Logic 101) could so view ‘Every member of \(T\) is true’ as to count it as vacuosuly true at worlds in which no members of \(T\) exist. On this scheme, in the example in the text, ‘Necessarily, every member of \(T\) is true’ would be true. But it would still not express acceptance of the necessity of \(T\): for example, if \(T\) merely consists of \(\langle \)Socrates exists\(\rangle \), on this scheme one should accept ‘Necessarily, every member of \(T\) is true’ although one should not accept the necessity of \(T\) (and should actually reject it and accept its contradictory).
Curiously, Field (1994a), pp. 250–251 does note truth-bearer contingency while apparently assuming (at least officially) that, contrary to what I’ve just argued in the text, it does not create problems for truth to fulfil the function of expressing acceptance of necessity [see however Field (1994a), p. 264, fn 18 for a hint that Field is probably aware of the complexities generated by truth-bearer contingency].
It is well-known that (A), (D) and (I) fail in hyper-intensional contexts such as propositional attitudes and implications: the nominalist believes that snow is white without believing that \(\langle \)Snow is white\(\rangle \) is true; if the nominalist were right, snow would be white without \(\langle \)Snow is white\(\rangle \) being true. Sometimes, (A), (D) and (I) even come with an explicit proviso concerning such contexts [see e.g. Field (1994a), p. 251]. The proviso is of course completely legitimate and does not in the least detract from the validity of those principles. However, the broad kinds of expressive functions emphasised by quasi-deflationists also concern these contexts. Thus, although the failures of (A), (D) and (I) in hyper-intensional contexts do not tell against their validity (contrary to their other failures discussed in this paper), they do tell against the quasi-deflationist argument in favour of them.
In conformity with the argument in favour of truth-bearer contingency set out at the beginning of this section, I don’t assume that ‘\(es\)’ actually refers to anything. But I do assume, at least in the official formulation of the claim made in the text, that this does not prevent \(es\) from functioning in a natural way when embedded in suppositional contexts—in particular, that, when embedded in a suppositional context, ‘\(es\)’ can be used to pick out the unique witness of an existential claim occurring at the same or less deep level of embedding. I recognise however that this may be controversial, and observe that the gist of the claim made in the text and that of similar claims remains unaltered if we so reformulate them as to replace ‘Possibly, for some \(x\), \(x\) is the unique person \(es\) generated by \(e\) and \(s\) and ...\(es\)...’ with ‘Possibly, for some \(x\), \(x\) is the unique person generated by \(e\) and \(s\) and \( \ldots x \ldots \)’.
For this to make sense, substitutional quantification must be really expansive: specifically, it must be the case that a particular substitutional quantification is true if (and only if), possibly, there is an expansion of the language such that some sentence in the relevant substitution class is true at the relevant world of evaluation (in our case, the relevant sentence could be something like ‘\(es\) does not exist’—which, individuated semantically, could exist even if it actually doesn’t—and the relevant world is the actual world). Notice that the previous clause only requires, as usual, truth at a world rather truth in a world (and that, in our case, there is no problem for something like ‘\(es\) does not exist’ to be true at the actual world even if it is not true in it). One might wonder whether the envisaged kind of expansive substitutional quantification is legitimate, but it’s hard to see why it shouldn’t be: the explanation just given seems perfectly coherent (although it could certainly use some more precision), and we clearly seem to have a notion of something being the case under which, for example, something is the case with respect to the specific non-existence of the unique person that would have been generated by \(e\) and \(s\).
In many of the cases discussed in Sect. 2 and in this section, what emerges is that our thought is diaphanous in the sense that, in accepting (for certain purposes) \(\varphi \), we simply think that things are such-and-such (full stop), typically without any direct bearing on \(\varphi \) itself, whose truth might then be prevented by factors that do not prevent things from being such-and-such. For example, in accepting ‘Santa Claus doesn’t exist’, we simply think that Santa Claus doesn’t exist (full stop), without any direct bearing on ‘Santa Claus doesn’t exist’ itself, whose truth might then be prevented by factors that do not prevent things from being such that Santa Claus doesn’t exist. In all these cases, it is precisely the diaphanousness of our thought that, by enabling us to appreciate the gaps between how things are and which truth bearers are true, enables us to appreciate the opacity of truth.
Notice that the justification that I’ve given in Sect. 2 for a broadly related requirement does not apply in the case of supposition of a theory, for that justification relies on the assumption that the state of mind in question is supposed to represent a way things are, which supposition clearly isn’t. However, the obvious modification of that justification relying on the assumption that the state of mind in question is supposed to represent a way things could be does apply to the case of supposition of a theory, and yields as conclusion that every supposition is expressed by supposition of a certain sentence.
Heck (2004), pp. 322–329 also takes up the challenge of Field (1994a), pp. 265–266 concerning how to express acceptance of the necessity of \(T\). Keeping fixed a non-deflationist conception of truth, he grants Field that it would not be adequate to accept ‘Every sentence member of \(T\) is necessarily true’, for that would involve issues about the representational properties of sentences that are intuitively foreign to the issue whether \(T\) is necessary. Heck’s proposal is rather to accept ‘Every proposition expressed by any member of \(T\) is necessarily true’. Keeping fixed a non-deflationist conception of truth as applied to propositions too, it is not clear to me why acceptance of the latter sentence does not incur in the analogous problem of involving issues about the representational properties of propositions that are intuitively foreign to the issue whether \(T\) is necessary. Be that as it may, the proposal is subject to the problem from truth-bearer contingency that I’ve explored in this section. I should add though that Heck also says things (as on p. 327) suggesting to me that he wouldn’t be hostile to developing further his proposal along lines similar to those of my own proposal in the text.
For, at least under the assumption of temporalism (very roughly, the doctrine that propositions typically change their truth value over time), that proposition is true (that is, true now) iff I’m now not hungry, which however I am. Granted, even under temporalism, some remotely related proposition is true, like \(\langle \)I was not hungry (on 10/07/2013)\(\rangle \). However, firstly, that proposition does not seem relevant to the intuition that there’s something true about me saying “I’m not hungry” in yesterday’s entry of my diary, as it never gets expressed by anyone in the envisaged circumstances; secondly, at least under the further assumption of tensism (very roughly, the doctrine that propositions are tensed and that their truth value is sensitive to such tense), that proposition was false yesterday, while the intuition in question is also an intuition to the effect that there’s something that was true yesterday and is true today about me saying “I’m not hungry” in yesterday’s entry of my diary.
In general, I resist the automatic inference from the premise that instances of kind \(k\) can only be \(F\) as considered under a certain aspect to the conclusion that instances of \(k\) cannot be, in the relevant cases, the sole bearers of \(F\) ness (for example, from the premise that people can only vote for people when considered as electors and candidates respectively for a particular post to the conclusion that people cannot be, in the relevant cases, the sole bearers of the relation of voting). In fact, in Zardini (2014b) I’ve resisted precisely that inference in the similar case of the question of the bearers of logical consequence. But I think that, in the case of the question of the bearers of truth discussed in the text, several auxiliary considerations are available to licence the inference. Firstly, contrary to the cases which motivate the idea that the inference might fail, it is not at all intuitive to think that ‘I’m not hungry’ or \(\langle \)I’m not hungry\(\rangle \) as used by me yesterday are true (in contrast to its being intuitive to think that they were true). Secondly, contrary to the cases which motivate the idea that the inference might fail, ‘I’m not hungry’ and \(\langle \)I’m not hungry\(\rangle \) are unqualifiedly not true (and so not unqualifiedly true), while the intuition in question is also an intuition to the effect that there’s nothing unqualifiedly not true (and, indeed, something unqualifiedly true) about me saying “I’m not hungry” in yesterday’s entry of my diary. Thirdly, what’s intuitively true about me saying “I’m not hungry” in yesterday’s entry of my diary is the record I produced yesterday: something that was made with paper and ink, that is evidence of what was the case yesterday, that in two thousand years will be exhibited in an archeology museum etc. All those are not properties that ‘I’m not hungry’ or \(\langle \)I’m not hungry\(\rangle \) can plausibly exemplify, even as used by me yesterday.
In other work [for example, Zardini (2008)], I’ve rather used ‘utterance’ to refer to assertoric speech acts and I've focussed on those as the operative truth bearers. But utterances understood along those lines would be unsuitable to account for the intuition discussed in the text, for the only assertoric speech act made in the envisaged circumstances is the act performed by inscribing ‘I’m not hungry’ in my diary: that act only existed yesterday, and so, given the plausible assumption that something is true only if it exists, it is not true (that is, true now), and so cannot account for the intuition that there’s something true about me saying “I’m not hungry” in yesterday’s entry of my diary.
True, given truth-condition context dependence, it is also the case that there is no proposition that is uniquely associated with a sentence (for example, uttered by Rajoy ‘I’m hungry’ expresses something along the lines of \(\langle \)Rajoy is hungry\(\rangle \), while uttered by Merkel ‘I’m hungry’ expresses something along the lines of \(\langle \)Merkel is hungry\(\rangle \)). But the dialectic of Sect. 3 did not require considering context-dependent sentences, and many sentences that are not context dependent do have a proposition that is uniquely associated with them. Indeed, even if the relevant sentence referred to in (A), (D) and (I) is context dependent, one could take ‘\(\ulcorner \varphi \urcorner \)’ as it occurs in an utterance of any of those principles as standing for the proposition expressed in the context of that utterance by any utterance of the value of ‘\(\varphi \)’. [Notice that such understanding would not have the crippling effects that a similar move would have in the case of utterances (which would take \(\ulcorner \varphi \urcorner \) as it occurs in an utterance of any "quoting instantiation" of those principles as standing for the utterance of \(\varphi \) that is correlated with it in the utterance of the principle), as it still yields versions of (A), (D) and (I) that govern attributions of truth also to propositions expressed by utterances made in a context different from the context in which (A), (D) and (I) are uttered (as long as those propositions are also expressed by some utterance made in the latter context).]
Utterances, even more clearly than other kinds of truth bearers, are contingent. Therefore, similarly to what was observed in Sect. 3, (A) fails in a possible world \(w\) (including the actual world), if, as it will so often be the case, \(\varphi \) is true at \(w\) but there are no utterances of \(\varphi \) in \(w\). Points similar to those made in Sect. 3 thus apply if utterances are assumed to be the operative truth bearers.
A failed attempt is to replace ‘\(\ulcorner \varphi \urcorner \)’ with a simple variable ‘\(u\)’ and conditionalise (A), (D) and (I) with the clause ‘if \(u\) expresses \(\langle \varphi \rangle \)’ [see for example Williamson (1998)]. For, as per the beginning of this section, yesterday’s entry in my diary expresses \(\langle \)I’m not hungry\(\rangle \), but it is true although I’m hungry [see Zardini (2008) for further discussion of this attempt in the slightly different framework mentioned in fn 36].
For example, merely material implication will not do, for, in that sense, if, for instance, \(u_{0}\) is an utterance of ‘Rajoy promotes regressive policies’ and \(u_{1}\) is an utterance of ‘Merkel promotes regressive policies’, \(u_{0}\) is true iff \(u_{1}\) is (in which way I’ll leave it to you to decide), but, clearly, one may accept ‘\(u_{0}\) is true’ without accepting ‘\(u_{1}\) is true’.
To ward off a likely rejoinder, an utterance of something along the lines of ‘The hair referred to by that utterance of ‘this’ by Rajoy is grey’ will not work for at least two reasons. Firstly, Rajoy’s utterances might be just as inextricable as his hairs are, in which case I won’t be able to use ‘that utterance of ‘this’ by Rajoy’ to single out the relevant utterance (and so won’t be able to use ‘the hair referred to by that utterance of ‘this’ by Rajoy’ to single out the relevant hair). Secondly, the device envisaged by the rejoinder is anyways inadmissible in the quasi-deflationist framework. For it would seem that the quasi-deflationist argument about truth, if it is any good, should be extendable to similar semantic properties like reference, in which case the rejoinder would simply push the problem to the one of getting ‘the hair referred to by that utterance of ‘this’ by Rajoy’ to behave as expected (that is, roughly, to be intersubstitutable with a singular term standing for the relevant hair) in virtue of some sort of correlation principle about reference. If this problem were dodged, and so if it were in effect conceded that ‘the hair referred to by that utterance of ‘this’ by Rajoy’ behaves as expected even in the absence of a suitable correlation principle, that would open the flood gates to opacity: if a singular term like ‘the object referred to by \(\tau \)’ behaves as expected even in the absence of a suitable correlation principle, given that the quasi-deflationist should have no objection to a predicate like ‘satisfies \(\tau \)’ behaving as expected (whether in virtue of some sort of correlation principle about satisfaction or not) one could accept any utterance \(u\) of any atomic sentence simply by accepting, roughly, ‘The objects referred to by the singular terms of \(u\) as they are used in \(u\) satisfy the predicate of \(u\) as it is used in \(u\)’, without need of any correlation principle about truth (with this extending in the usual way to cover utterances of compound sentences). (Notice that any fuss about satisfaction still needed to be naive or transparent would be quite out of place, since any predication can be rephrased as an identification: for example, ‘Rajoy admires Merkel’ can be rephrased as ‘Rajoy is the Rajoy admirer of Merkel’. Reference and identity can ground truth without need of satisfaction.)
At this point of the dialectic, the problem has really become the more general one—stretching beyond the domain of truth-condition context dependence—of how, using correlation principles, to account for the fact that attributions of truth to utterances one cannot understand express acceptance of the relevant utterances just as well as attributions of truth to utterances that one does understand. Field (2001), pp. 147–151 proposes an interesting new strategy for solving that problem from a deflationist perspective. Adapted to the present dialectic, Field’s idea is that, even if one cannot understand an utterance \(u\) of \(\varphi \), by attributing truth to \(u\) one in some sense borrows \(\varphi \) and uses it (or, if \(\varphi \) is context dependent, uses some suitable relative of it) deferentially to \(u\), in such a way that one in some sense accepts ‘\(\varphi \) iff \(u\) is true’. Interesting as it is, I think that there is a dilemma for this broad kind of strategy at least when it is supposed to help in the present dialectic (and I hasten to note that Field does not say that it does). On the one hand, if the strategy is understood so that \(\varphi \), as one uses it, has a virtually completely indeterminate content (which I think is how Field intended the proposal), then, since one accepts ‘\(\varphi \) iff \(u\) is true’, the content of ‘\(u\) is true’, as one uses that sentence, will be forced to be virtually completely indeterminate too. But then one will not accept the theory expressed by \(u\) by accepting ‘\(u\) is true’, for the content of the latter, as one uses it, will be virtually completely indeterminate, and so will fall short of entailing virtually any interesting theory. On the other hand, if the strategy is understood so that \(\varphi \), as one uses it, has the same content as it has in \(u\), then the underlying ultraliberal conception of how one can use sentences as having certain contents, in addition to being totally implausible (at least under standard assumptions concerning the relation between use of sentences and grasp of their contents), will suffice all by itself for fulfilling the expressive functions emphasised by quasi-deflationists. For that conception amounts in effect to the idea that it is sufficient for using a sentence as having a certain content that one be in a fairly remote relation to that content (plus, of course, that one intend to use that sentence as having that content). Thus, if \(T\) contains infinitely many sentences, or if one does not know exactly which sentences belong to \(T\), whereas one was supposed to accept \(T\) by accepting ‘Every member of \(T\) is true’, it will now be sufficient that one simply intend to use \(\varphi \) so that it has the content of \(T\) (to which one is surely at least in a fairly remote relation). This discussion actually helps to bring out yet another expressive function for truth to fulfil [one which, unsurprisingly, is not emphasised by quasi-deflationists since it has little to do with (A), (D), (I) or any other correlation principle]: that of expressing attitudes towards what one cannot understand (when such attitude is acceptance, the etymologies of ‘truth’ and veritas, in stark contrast to the Heideggerian fanfare about
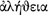 , become both very suggestive). [Notice that, if what one cannot understand are sentences or propositions, in view of the limitations on truth explored in Sects. 2 and 3 the suitably expansive substitutional quantification fulfils such function even better (since, for every sentence or proposition one cannot understand, there is presumably an expansion of the language that contains a sentence synonymous with the sentence one cannot understand or a sentence expressing the proposition one cannot understand). However, if what one cannot understand are utterances, I’ll point out at the end of this section that, in an important respect, truth fulfils such function better than the suitably expansive substitutional quantification. Thanks to an anonymous referee for a question that prompted this last comment.]
, become both very suggestive). [Notice that, if what one cannot understand are sentences or propositions, in view of the limitations on truth explored in Sects. 2 and 3 the suitably expansive substitutional quantification fulfils such function even better (since, for every sentence or proposition one cannot understand, there is presumably an expansion of the language that contains a sentence synonymous with the sentence one cannot understand or a sentence expressing the proposition one cannot understand). However, if what one cannot understand are utterances, I’ll point out at the end of this section that, in an important respect, truth fulfils such function better than the suitably expansive substitutional quantification. Thanks to an anonymous referee for a question that prompted this last comment.]True, in our particular example it might be thought that one does have the end of committing oneself to accepting a different common-or-garden-variety truth-free sentence: ‘Rajoy is hungry’ (or a similar sentence). But, as the discussion in the last paragraph makes clear, there are many cases in which that cannot be the case given that it is totally plausible that there are no relevant common-or-garden-variety truth-free sentences one can understand, and so no relevant common-or-garden-variety truth-free sentences one can, in the relevant sense, commit to accepting.
Ironically, in the case of truth-condition context dependence, it is exactly because all of (A), (D) and (I) fail that truth fulfils the expressive functions emphasised by the quasi-deflationist.
(A), (D) and (I) are sometimes appealed to in justifying the mantra that logical consequence requires necessary truth preservation [see for example Field (2008), pp. 42–43, 284–286 for a perceptive reconstruction of such justification; Field himself rejects the justification and indeed the mantra for the reason I adumbrate in fns 10 and 49]. In Zardini (2012), I’ve criticised the justification and its underlying conception of necessary truth preservation mainly relying on considerations concerning context dependence (of a different kind though from those I’m exploiting in this section). To the (restricted) extent that logical consequence does require necessary truth preservation, the real grounds for such requirement are opaque. Notice that the requirement is actually of great relevance for the debate on the semantic paradoxes (see fn 49).
Notice that, while I’ve variously argued against each of (A), (D) and (I), and against several putative connections between acceptance/rejection of \(T\) and acceptance of ‘Every member of \(T\) is true’/‘Some member of \(T\) is not true’, no consideration in this paper tells against the idea that, if one accepts ‘Every member of \(T\) is true’, one thereby accepts \(T\) [and so against the point made by Field (2008), pp. 148–149 against certain specific theories rejecting (D)]. Thanks to an anonymous referee for pointing this out.
Setting aside those cases in which truth itself does not fulfil certain expressive functions, I’ve argued in Zardini (2014e) that a suitable development of the hierarchical theory of truth might well provide all the resources needed in the remaining cases. If so, even if some sort of revamped quasi-deflationist argument could pull off the magic trick of justifying a restriction that leaves out all the counterexamples offered in this paper and nevertheless leaves in paradoxical sentences, such argument would still break down at the further step assuming that truth only fulfils the relevant expressive functions concerning paradoxical sentences if the paradoxical instances of (A), (D) and (I) hold. [With its replacement of the property of truth with a hierarchy of truth-like properties, the hierarchical theory may also not be overly impressed by the two arguments in favour of revising classical logic that I’ll run below in the text. For what it’s worth, I’ve argued in Zardini (2014e) that the hierarchical theory cannot account for a kind of generalising use of truth which is different from the expressive one and which consists, roughly, in using truth to attribute a unifying feature to all instances of certain kinds of sentences, and, by doing so, to be able to speak for the first time about general principles and notions.]
Thanks to an anonymous referee for recommending this discussion.
I find this second argument insightful, among other things, because it is easily generalisable to cover paradoxes concerning properties other than truth for which some sort of quasi-deflationist argument would seem to be a non-starter and for which there are no plausible instances of correlation principles that suffice for generating a conflict with classical logic. Such are the properties of necessity, knowledge, justified belief etc. In particular, those properties completely fail to satisfy ascent principles (and some of them even descent principles). But they do arguably satisfy consistency, iteration and soundness principles. Opaque necessity, knowledge, justified belief etc. are in conflict with classical logic just as truth is. The second argument is also easily generalisable to cover paradoxes concerning sentences other than Liar sentences, such as for example Curry sentences (in which case the relevant interaction of truth is with implication in the form of the preservation principle to the effect that, if an implication is true, then, if its antecedent is true, so is its consequent). In fact, these generalisations suggest that the general principle yielding as special cases all the relevant interaction and soundness principles is an abstract principle of closure under logical consequence suitably understood. Closure and iteration suffice for paradox. And, since closure in turn suffices for iteration “at level \(\omega \)” [see e.g. Field (2007), p. 115, fn 41], in the end closure alone suffices for paradox [in fact, as I’ve argued in Zardini (2013b, 2014a), it suffices for forcing not only a revision of classical logic, but also a revision of the traditional structural properties preserved by many non-classical logics, thus pointing in the direction of the theory of truth developed in my works referenced in fn 1].
References
Beall JC (2002) Deflationism and gaps: untying ‘not’s in the debate. Analysis 62:299–305
Beall JC (2009) Spandrels of truth. Oxford University Press, Oxford
David M (2005) Some T-biconditionals. In: Armour-Garb B, Beall JC (eds) Deflationary truth. Open Court, Chicago, pp 382–419
Dummett M (1959) Truth. Proc Aristot Soc 59:141–162
Field H (1994a) Deflationist views of meaning and content. Mind 103:249–285
Field H (1994b) Disquotational truth and factually defective discourse. Philoso Rev 103:405–452
Field H (2001) Postscript to “Deflationist views of meaning and content”. In: Truth and the absence of fact. Oxford University Press, Oxford, pp 141–156
Field H (2007) Solving the paradoxes, escaping revenge. In: Beall JC (ed) Revenge of the Liar. Oxford University Press, Oxford, pp 78–144
Field H (2008) Saving truth from paradox. Oxford University Press, Oxford
Fine K (1977) Prior on the construction of possible worlds and instants. In: Prior A, Fine K, Worlds, times and selves. Duckworth, London, pp 116–161
Heck R (2004) Truth and disquotation. Synthese 142:317–352
Makinson D (1965) The paradox of the preface. Analysis 25:205–207
McGee V (1991) Truth, vagueness, and paradox. Hackett, Indianapolis
Priest G (2006) In contradiction, 2nd edn. Oxford University Press, Oxford
Prior A (1957) Time and modality. Clarendon Press, Oxford
Richard M (2008) When truth gives out. Oxford University Press, Oxford
Stalnaker R (2010) Merely possible propositions. In: Hale B, Hoffmann A (eds) Modality: metaphysics, logic, and epistemology. Oxford University Press, Oxford, pp 21–34
Williamson T (1998) Indefinite extensibility. Grazer Philos Stud 55:1–24
Zardini E (2008) Truth and what is said. Philoso Perspect 22:545–574
Zardini E (2011) Truth without contra(di)ction. Rev Symb Log 4:498–535
Zardini E (2012) Truth preservation in context and in its place. In: Dutilh-Novaes C, Hjortland O (eds) Insolubles and consequences. College Publications, London, pp 249–271
Zardini E (2013a) It is not the case that [\(P\) and ‘It is not the case that \(P\)’ is true] nor is it the case that [\(P\) and ‘\(P\)’ is not true]. Thought 1:309–319
Zardini E (2013b) Naive modus ponens. J Philos Log 42:575–593
Zardini E (2014a) Naive truth and naive logical properties. Rev Symb Log 7:351–384
Zardini E (2014b) Context and consequence. An intercontextual substructural logic. Synthese
Zardini E (2014c) Getting one for two, or the contractors’ bad deal. Towards a unified solution to the semantic paradoxes. In: Achourioti T, Fujimoto K, Galinon H, Martínez J (eds) Unifying the philosophy of truth. Springer, Dordrecht
Zardini E (2014d) Restriction by non-contraction. Notre Dame J Formal Log
Zardini E (2014e) The general missing from the hierarchy. In: Bacchini F, Caputo S, Dell’Utri M (eds) New frontiers in truth. Cambridge Scholars Publishing, Cambridge
Zardini E (2014f) The role of utterances in Bradwardine’s theory of truth. Recherches de théologie et philosophie médiévales
Zardini E (2014g) \(\forall \) and \(\omega \). ms
Author information
Authors and Affiliations
Corresponding author
Additional information
This paper continues in the tradition of promoting the forces of darkness that I’ve initiated with Zardini (2008, 2012). Earlier versions of the material in the paper have been presented in 2012 at the LOGOS Semantic Paradoxes and Vagueness Seminar (University of Barcelona); in 2013, at the LOGOS Philosophy of Logic Seminar; in 2014, at a research seminar at the University of Valencia. I’d like to thank all these audiences for very stimulating comments and discussions. Special thanks go to JC Beall, Philipp Blum, Enric Casaban, Hartry Field, Joost Joosten, Nasim Mahoozi, José Martínez, Sergi Oms, David Ripley, Sven Rosenkranz, Gonçalo Santos, Jordi Valor, Timothy Williamson and several anonymous referees. I’m also grateful to the editors Massimiliano Carrara and Julien Murzi for inviting me to contribute to this special issue and for their support and patience throughout the process. At different stages during the writing of the paper, I’ve benefitted from an AHRC Postdoctoral Research Fellowship and from the FP7 Marie Curie Intra-European Research Fellowship 301493 on A Non-Contractive Theory of Naive Semantic Properties: Logical Developments and Metaphysical Foundations (NTNSP), as well as from partial funds from the project CONSOLIDER-INGENIO 2010 CSD2009-00056 of the Spanish Ministry of Science and Innovation on Philosophy of Perspectival Thoughts and Facts (PERSP), from the FP7 Marie Curie Initial Training Network 238128 on Perspectival Thoughts and Facts (PETAF), from the project FFI2011-25626 of the Spanish Ministry of Science and Innovation on Reference, Self-Reference and Empirical Data and from the project FFI2012-35026 of the Spanish Ministry of Economy and Competition on The Makings of Truth: Nature, Extent, and Applications of Truthmaking.
Rights and permissions
About this article
Cite this article
Zardini, E. The Opacity of Truth. Topoi 34, 37–54 (2015). https://doi.org/10.1007/s11245-014-9268-1
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11245-014-9268-1





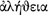 , become both very suggestive). [Notice that, if what one cannot understand are sentences or propositions, in view of the limitations on truth explored in Sects.
, become both very suggestive). [Notice that, if what one cannot understand are sentences or propositions, in view of the limitations on truth explored in Sects.