Abstract
This study shows the result of a simulation of a proposed kinetic reaction scheme of high-concentration (5000 ppm NO) and high-temperature (570–800 K) selective catalytic reduction of NO with NH3 on a commercial vanadia based catalyst at a system pressure of 2.2 bar. The simulations are performed with COMSOL Multiphysics ver. 5.1. Experimental data from a catalytic flow reactor can be nicely fitted to a system of kinetic expressions for the selective catalytic reduction (SCR) reaction and its side reactions. Especial attention is given to the formation of N2O. All reaction rate expressions contain an ammonia adsorption term. The value for its pre-exponential factor is 9e−9 and its activation energy is −139 kJ/mol. The fastest reaction is the standard SCR reaction with a pre-exponential factor of 5.28e7 s−1 and an activation energy of 85 kJ/mol. This reaction is affected by internal diffusion limitations. The oxidation of NH3 to NO is the second fastest reaction with parameters 5e12 mol/m3s and 200 kJ/mol. The NSCR of NH3 to N2O is the third fastest reaction with values of 7.5e5 s−1 and 110 kJ/mol. The oxidation of NH3 to N2O has the parameters 8e11 mol/m3/s and 190 kJ/mol. At 640 K inlet temperature the rate of the SCR reaction is about 1.3 mol/m3/s. The oxidation of NH3 to NO is 4.7e−4 mol/m3/s. The rate of the NSCR producing N2O is 1.63e−4 mol/m3/s. The rate of the direct oxidation of NH3 to N2O is 3.7e−5 mol/m3/s. Thus the rate of the SCR reaction is about 35,000 faster than the high temperature production of N2O at this temperature.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
The removal of NOX from flue gas via catalytic reduction using, for example, ammonia is today considered an established technology, referred to as selective catalytic reduction (SCR) of NOX. The catalysts used under normal operating conditions, such as for cleaning up combustion gases associated with electricity production, are normally vanadia based [1–4].
However, with the advent of power production methods, such as Oxyfuel combustion, as well as in niche applications, there is a need to treat effluent streams with higher NOX concentrations. Of the niche applications, nitric acid plants, cement calcination, and FCC catalyst re-generation may result in NOX levels in the 1000–2000 ppm range [3].
An experimental study of high-temperature and high-concentration (5000 ppm NO) SCR of NO was performed earlier in which performance of several catalysts used was determined [5].
The formation of N2O in the SCR has mostly been addressed in aftertreatment of diesel exhaust gases [6] and on other types of catalysts [7]. In this application NO2 is present causing much of the N2O formation at low temperatures. The renewed interest in N2O, which is normally present in the ppm range in the normal SCR reaction, is due to its high (298 times that of CO2) global warming potential [8]. A recent experimental study examines the formation of N2O over V2O5–WO3/TiO2 catalysts [9]. This thorough study covers a wide range of temperatures from 150 to 500 °C, NO contents up to 1000 ppm and V2O5 contents from 1 to 5 wt%. One measurement series is done in the presence of water showing the strong reducing effect of its presence on the formation of N2O. It also includes kinetic information. The formation of N2O and the reducing effect of water has been shown by us already in 1991 [10].
The main aim of this paper is to show possible reactions leading to the formation of N2O thereby giving ideas on how to reduce its formation. We also intend to show the strength of the presented simulation method when it comes to reactions with high reaction rates.
It is also interesting to see how the unusual conditions in the Oxyfuel process will result in e.g. high temperature rises in the catalytic bed. It would also be interesting to see if flow and temperature distributions in the reactor affect the performance. All these phenomena can be studied when a model of the finite element type is set up in COMSOL Multiphysics. The results from such a study is presented in this paper.
2 Materials and Methods
2.1 Experimental
Data for the simulation were obtained by measuring concentrations of NO and N2O according to the method described in paper [5]. In short, the data were obtained in a catalytic bed reactor made of stainless steel with an inner diameter of 8 mm and an outer diameter of 10 mm. The inside of this reactor was plated with gold to minimize ammonia oxidation reactions. The N2O was measured using a SICK/SIDOR NDIR gas analyzer, while NO was measured using an Eco Physics CLD 700 RE ht chemiluminescence instrument.
The reactor itself is 465 mm long with the bottom of the catalyst bed positioned 130 mm from the inlet. The catalyst bed, supported on quartz wool, is 30 mm high.
A thermocouple is positioned just after and in contact with the bed, measuring the outlet temperature. To avoid condensation of potential products, such as ammonium nitrate/nitrite, all sampling lines are insulated and heated to 465 K. The gas coming from the reactor is scrubbed with phosphoric acid to remove residual NH3 before entering the NOX analysis instrument in order to minimize cross sensitivity.
In this study a commercial vanadia based catalyst with around 0.4 wt% vanadia content was used. The catalyst amount was 1.5 cm3 with particle diameters between 0.71 and 0.80 mm.
In the data selected for the simulation study the concentration of NO was 5000 ppm and that of NH3 5500 ppm. The total gas flow was 3 LNTP min−1 and the pressure at the reactor inlet pressure was 1.2 bar gage. This resulted in a GHSV of 120,000 h−1. The temperature at the inlet to the reactor was varied between 570 and 800 K at 25° intervals. Temperatures are always reported as measured directly after and in direct contact with the catalyst bed. The activity was measured at steady state which was reach after about 45 min at the lowest temperature and after 10 min at the highest. The activity was measured at several time intervals before reaching steady state.
2.2 Reactor Geometry
The system studied in the simulation is shown in Fig. 1.
Reactor geometry used in the simulations. The measures are in m starting with 0 at the exit of the reactor. The mesh used. The number of degrees of freedom solved for is 82,195 (plus 35,514 internal DOFs). Only the important parts, with the catalyst section after 10 cm from the large tube, are shown
The reactor system consists of the large cylindrical reactor tube connected to a smaller inlet tube. In the simulations only one eight of the whole 3D system is used in order to get reasonable computation times. The large tube is a 465 mm long stainless steel tube with an outer diameter of 10 mm and an inner diameter of 8 mm. The gas flow enters through a 60 mm long tube with 4 mm inside diameter connected to the main tube from the left side in the Figure. The following numbering is used for different domains in the system as needed by the simulation program. The empty channel sections are numbered 2, 4, 6, 8 and 10 from the outlet of the reactor. The porous catalyst bed from 10 to 13 cm from the inlet side of the large tube is number 4. The wall sections are numbered 1, 3, 5, 7 and 9 from the outlet of the reactor.
The mesh used in the simulations is also shown in Fig. 1. The mesh is of a free triangular type and is swept from the inlet to the outlet of the reactor. The swept mesh is divided in five parts along with the domains described before. The inlet section (domains 9 and 10), 6 cm long, is given 40 elements. The connection between the large and the small tube (domains 7 and 8), 2 cm long, is given 20 elements. The inlet of the large tube (domains 5 and 6) is 10 cm long and is given 20 elements. The catalyst bed (domains 3 and 4) is 3 cm long and is given 40 elements since here the reactions are taking place and the accuracy should be largest. The outlet tube section, 33.5 cm long is given 20 elements. Both the wall and the empty section are given the same number of elements in the axial direction with a tighter mesh closer to the catalyst bed. The number of elements in each domain is set to create more accurate values where most of the changes are assumed to appear. This procedure is very important for the results.
2.3 Kinetic Model
The kinetic scheme used in the simulations is based on reactions between adsorbed ammonia and gaseous nitric oxide according to an Eley–Rideal model [11]. All oxidation reactions of ammonia are also based on adsorbed ammonia. In all cases the effect of oxygen, present in large excess (13.06%), is included in the rate constant presented since the effect on small variations of O2 will be small for 5000 ppm (0.5%) NO in the inlet. The effect of water (5.03%) is included in the same way.
The first two reactions included are based on the generally excepted scheme for the SCR reaction. The first reaction is the standard SCR reaction and the second is the oxidation of the surplus of ammonia by oxygen to NO and water and are given in Table 1. The formation of N2O is assumed to be from firstly a non selective catalytic reduction (NSCR) reaction forming N2O instead of N2. Secondly, N2O is also formed by a direct oxidation of NH3. The effect of the different activation energies leads to that the standard SCR reaction dominates at low temperatures. For the formation of N2O the reaction 3 (NSCR) is more important at lower temperatures than reaction 4. The value of the activation energy for the SCR reaction (See Table 5) is somewhat low because of diffusion limitations. No appreciable amounts of NO2 were present in the experimental data so the redactions of NO2 are omitted.
2.4 Application Model and Calculation Procedure
COMSOL Multiphysics version 5.1 is the software used in this work. The simulation includes diffusion, heat generation and transfer and flow characteristics along with kinetics of the chemical reactions. A stationary solution is generated. The behavior of the whole reactor length was simulated.
The model couples the interface “chemistry”, wherein the reactions in Table 1 are used, with “transport of dilute species”, “free and porous media flow” and “heat transfer in porous media”. All results in all interfaces are calculated simultaneously using a finite element method. “Transport of dilutes species”, which include all gaseous components in Table 1 as well as the solvent N2 is used in the whole reactor except for its walls. The result is the concentration of the species. “Free and porous media flow” deals with pressure and velocity in all open parts of the reactor. The chemical reactions produce heat and some heat is also transported in the catalyst walls. Both the heat generated by all reactions as the heat transported in the systems various parts is calculated in the module “heat transport in porous media”. The reactions are only taking place within the porous bed i.e. the catalyst layer (domain 4) which is the source for the heat of all reactions.
As shown above four different rate equations are used to represent the main reactions and the side reactions. The computations are performed using a parameter sweep of the inlet temperatures between 560 and 760 K. Measured data of the gas content of NO and N2O (at the exit of the reactor) as a function of the temperature at the exit of the bed are compared to simulated values.
Kinetic parameters were adjusted manually with starting values for the kinetic parameters and the ammonia adsorption parameters for the SCR reaction calculated from data given by Lietti [12]. The SCR reaction is by far the fastest reaction. Since the SCR reaction is dominating in the low temperature region fitting for this reaction is done primarily in this region (560–700 K). At high temperatures (780–800 K) increased concentrations of NO are experimentally observed. That phenomenon can be explained be either a decreased rate of reduction of NO or by a direct oxidation of NH3 to NO or by the combination of the two. It is common that the adsorption of NH3 decreases above 670 K. Adjustment of the pre-exponential factor in the coverage of ammonia (A0 × exp(−E0/(R × T) in the model) is used to reach a decreasing value of the ammonia coverage at inlet temperatures at around 670 K. The increased NO content at high temperatures is simulated by adjusting the parameters in the oxidation reaction of NH3 to NO. When the simulated values for the NO content (ppm NO) are close enough to the experimental ones for the whole temperature range the fitting of the data for N2O is performed using data in the low (560–720 K) temperature range. Finally, the increased N2O content at high temperatures is fitted by adjusting the parameters for the oxidation of NH3 to N2O.
Temperature dependent transport data for the gas are calculated by the program from the characteristic length of each component in the gas flow, its Lennard-Jones potential, the energy minimum of the Lennard–Jones potential and its dipole moment. From these values an automatic calculation yields the values of the thermal conductivity and the viscosity of the gas as well as the diffusivity of the different species in the solvent gas N2. These data are then used, as needed, in the various modules. The original parameters for these calculations are taken from [13]. Some other data are given by the author and are shown below.
The program need definition of material properties for all parts of the system. The materials used in the model are presented in Table 2. Nitrogen is by far the most abundant species in the gas domain. The program needs this definition for calculation of various properties of the gas. Similarly, the reactor wall is stainless steel and its properties is calculated from formulas in the program.
2.5 Subdomain and Boundary Settings
The subdomain and boundary settings for each application node are presented below.
The “chemistry”, “transport of diluted species” and “free and porous media flow” nodes are active in the domains where nitrogen is set as the solvent gas.
The “chemistry” node contains all the kinetic information for the system. It is also used to calculate physical data for the gas mixture.
Symmetry is given on all surfaces in the partial model which is the result of splitting of the 3D model in order to make the calculations less time consuming.
In the “transport of diluted species” node the species are transported by convection. The equations governing is shown below:
The diffusion coefficients for the components, \({D_i}\), are calculated by the program based on nitrogen as solvent. The initial concentrations in the system, needed for the computations, at the start of the simulation are calculated as mol/m3 by the gas law from the inlet ppm and % values given in Table 3 and the respective inlet temperatures. The results of the computations in this module is the concentrations.
The inflow conditions are the same as the initial values as below. The equation for the concentration of NO is:
Similar equations are used for all components. The outflow condition is:
The symmetry condition is:
In the “free and porous media flow” node the species are transported by convection. It is used to determine the velocity and pressure in the system. The equations governing are shown below:
The inlet linear velocity \(\left( {{v_{in}}} \right)\) is varying with the inlet temperature and is calculated from the volume flow, which is constant, the area inside the tube and the gas law. The density and the viscosity of the solvent is calculated as functions of temperature by the program and used in simulations. The porosity of the catalyst layer is measured in a glass cylinder to 0.4 and the permeability is calculated as shown below and both are constant values. A laminar inflow condition is used in the inlet tube and the governing equation is:
U is \({v_{in}}\) and \({L_{entr}}\) is 0.01 m. \({L_{entr}}\) is the length of turbulent flow assumed in the inlet tube.
At the outlet the pressure is set to \({p_{tot}}\), the pressure in the experiments.
The symmetry condition in this node is:
At the wall no slip conditions (no flow through the wall) are given:
The initial value for u in the X direction is \({v_{in}}\). In the Y and Z directions the value is set to 0. The initial pressure value is \({p_{tot}}\) (2.2 bar).
The “heat transfer in porous media” node is active in all domains. Inside this node there are separate parts for the heat transfer in the porous media (catalyst bed), the wall and the open gas channel. Heat Transfer in the catalyst bed is active in domain 4 and values for physical constants used are given in Table 4. The inlet gas temperature is used as initial value for the temperature of the bed.
The equations are:
Thermal insulation is defined on the outside of the reactor (adiabatic conditions) for the large diameter section.
Heat flux is used for the inlet tube which is situated outside of the oven in an insulated package.
Convective heat flux is used with q0 = h×(Text − T) where h is set to 0.2 W/m2 and Text is the temperature outside of the inlet tube set equal to \({T_{in}}\).
The outflow and symmetry conditions are:
The heat source is:
The heat source is the chemical reactions.
The heat transfer in the wall is:
and is active in domains 1, 3, 5, 7, and 9. Values for thermal conductivity, density and heat capacity are taken from the material in these domains.
Heat transfer in fluids is used in domains 2, 6, 8, and 10 (i.e. the open channel). The condition is:
Values for thermal conductivity, density, heat capacity and ratio of specific heats are taken from the material in these domains.
The inlet temperature is the same as above and is defined at both the wall and the channel inlet boundaries 43 and 44. The conditions at the outflow boundaries (1 and 4) are temperature gradients which are 0. The heat source is active in domain 4 (the catalyst bed) and is calculated as “heat source of reactions” in the “chemistry” node.
The porosity of the bed \(\left( {{{e}_{{bed}}}} \right)\) has been experimentally determined, by filling a glass cylinder with the catalyst particles, and was found to be 0.4. The permeability (K) was calculated from the particle diameter (dp) and the bed porosity by a method given by [14]. The formula used is:
The value obtained is shown in Table 4.
The bed density is calculated from bed porosity and particle apparent density by:
The density of the particles is calculated in steps given by [15]:
First the porosity of the catalyst particles is calculated:
Vpor was measured by N2 physisorption to 0.275 cm3/g [5] and 0.05 cm3/g was added, from earlier measurements, as macro pore volume. This yielded a total pore volume of 0.325 cm3/g. The solid density of the catalyst was set to the value of TiO2 (anatase) of 3.84 g/cm3 [16].
Then the particle density was calculated from:
The density of the porous particle calculated was 1.71 g/cm3, and the bed density 1.03 g/cm3.
The thermal conductivity of the bed was calculated from Gonzo [17]. The method calculates the effective thermal conductivity of the bed \(\left( {{k_{eff}}} \right)\) from values of the particles \(\left( {{k_{part}}} \right)\) and the gas phase \(\left( {{k_{gas}}} \right)\).
with \({\theta _p}\) = 0.6 and
A mean value of \({k_{gas}}\) of 0.104 W/(m/K) was obtain from COMSOL in the temperature range of the simulations. The value for \({k_{part}}\) (0.33 W/(m/K)) was obtained from Fig. 5 and the porous solid model for air in [18] using the value for ks for Rutile of 3.2 W/(m/K) [16]. The calculated value of the \({k_{eff}}\) for the bed thus obtained was 0.209 W/(m/K).
2.6 Study Settings
A stationary solution is used solving all four nodes simultaneously. An auxiliary temperature sweep is used to generate solutions at various inlet temperatures warranted. Large steps in temperature (40 K) are used in early simulations and smaller (10 K) at the end to reduce computation time. The simulations are performed on a Hp Z620 work station with 2 Xeon E5-2630 v2, 2.6 GHz processors with six cores each and with 32 GB of 1600 MHz RAM. A relative tolerance of 0.001 is used. The solver is a direct one called PARDISO. The variables u and p, T and concentrations are solved in three different segregated modes.
The equations which are compiled are:
-
the velocity field and the pressure
-
the temperature
-
the concentration for each gas component except the solvent
3 Results
The experimental data can very nicely be represented by a reaction scheme consisting of the SCR reaction (reaction 1) as well as the ammonia oxidation to NO (reaction 2) and the formation of N2O from reactions 3 and 4.
3.1 Fitted Kinetic Parameters
The parameters determined are presented in Table 5. More details of this below.
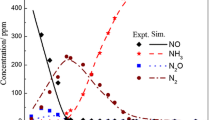
The proposed reaction scheme with four reactions can represent the experimental data of the content of NO (ppm) very well as shown in Fig. 2. There are some deviations at the lowest temperatures (below 620 K). Simulation results of this type has not been presented before and could be of great help in constructing SCR units in connection with cleaning of exhaust gases with high NO contents and also at elevated pressures. It is especially useful for reactions where large temperature gradients are expected.
It is also possible to predict the formation of N2O with the reaction scheme of this paper (Fig. 3). This is possible by using reactions forming N2O from NO, NH3 and O2 (the NSCR reaction 3) in combination with the direct oxidation of NH3 to N2O (reaction 4) at higher temperatures.
3.2 The Temperature Distribution
The maximal temperature in the system is 796 K, i.e. a temperature increase of 76° is simulated at 720 K inlet temperature. In the figure isothermal data are given at ten levels. It is observed how the maximum temperature (794 K) is present in the catalyst bed. It is also observed how the good heat conduction of the wall causes preheating of the gas before entering the catalyst section. Even in the inlet gas tube the temperature has increased by 4°. There also a gradient of temperatures across the bed with higher temperatures closer to the wall. This will of course effect the chemical reactions which are very sensitive to the temperature (Fig. 4).
Figure 5 shows that the major temperature increases appear in the catalyst bed (from 0.335 to 0.365 m). The figure shows the temperature in the middle of the reactor along its axis. All temperature increases caused by the rapid SCR reaction yield an overshoot in temperature with a maximum somewhere inside the catalyst bed. he higher the inlet temperature the closer to the inlet the maximum appears. The maximal temperature in the simulations is 796 K. Very large temperature increases are observed so analyzing the kinetics using simpler models would not result in the right values of the parameters.
3.3 Pressure Drop in the Reactor
The pressure drop is only present to a noticeable extent in the catalyst bed. At 720 K inlet temperature the pressure decreases from 2.2228 to 2.2 bar at the reactor exit (boundary condition). Thus the pressure drop is only 0.0228 bar (1.03% of the total pressure). There are also no noticeable differences between values of the pressure in the center of the bed and at the wall which was expected since the velocities were different (Fig. 6).
3.4 The Velocity Distribution in the Reactor
The inlet is to the right in Fig. 7. In the small inlet tube values up to 9.5 m/s are obtained at the very inlet in the center of the channel at 720 K inlet temperature. The velocity drops somewhat along the inlet tube even if the temperature increases somewhat. In the large tubes inlet section, the velocity drops linearly with the distance along the axis of the reactor down to about 4.3–5.2 m/s. At the inlet of the bed the velocity drops sharply. In the catalyst bed the velocities are of the order of 1 m/s. In the outlet tube the velocity increases close to the bed and levels out to constant values at each temperature in the range1.8–2.7 m/s.
The figure shows how the low permeability of the catalyst bed causes a warranted evening out of the velocity over its radius. Before the bed there is quite a large variation of the velocity with the radial position with a relatively thick stagnant layer along the wall. Re numbers are in the 1–8.6 range so the flow behaves as a laminar one. A laminar inlet condition was also assumed for the inlet condition in the small tube.
The results show that most of the catalyst bed has an even linear velocity, of course varying with the inlet temperature. The stagnant region is very small in the bed at only 3% of the radius. Thus there should not be a large effect on the conversion of NO observed because of the variation in the linear velocity (Fig. 8).
3.5 Concentration of the Nitric Oxide and its Conversion
Figure 9 shows how NO decreases rapidly from 0.187 mol/m3 to about 0.04 mol/m3 in about 1/3 of the length of the bed.
The details in Fig. 9 indeed show that the concentration decreases faster closer to the wall where the velocity is lower. Therefore, the time for reaction is longer at this position yielding a larger conversion as is expected.
There is only 0.9% difference between the largest and the smallest conversion of NO across the catalyst at the exit of the bed. Values are from 96.7 to 97.6% conversion of NO at an inlet temperature of 720 K.
Earlier presented changes in pressure, velocity and most importantly the temperature causes rapid decrease of the concentrations of the limiting reactant NO (Fig. 10).
3.6 The Coverage by Ammonia
The coverage by ammonia ((KNH3 × CNH3)/(1 + KNH3 × CNH3)) is very close to 1 at low temperatures and only decreases somewhat at temperatures above 680 K at the inlet of the bed (Fig. 11). The temperature increase in the bed is very large and this causes the rapid decline in coverage above 680 K. This in turn decreases all reaction rates towards the exit of the bed since all of them contain the coverage term. At high temperatures this also leads to desorption of ammonia from the catalyst causing lower conversions of NO. This effect is not very large but can be seen as an upward trend in the NO concentration at high temperatures in Fig. 2.
3.7 The Reaction Rates
In the process of determining the kinetic parameters it is very useful to see which reactions are the most important ones at a given temperature (Fig. 12). It is especially important in fitting the concentration of N2O. At 640 K inlet temperature the rate of the SCR reaction is about 1.3 mol/m3/s. The oxidation of NH3 to NO is 4.7e−4 mol/m3/s. The third fastest reaction at this temperature is the NSCR producing N2O. Its rate is 1.63e−4 mol/m3/s. The rate of the direct oxidation of NH3 to N2O is 3.7e−5 mol/m3/s. Thus the rate of the SCR reaction is about 35,000 faster than the high temperature production of N2O at this temperature. All these rates are given per volume of reactor bed including the empty space and must be recalculated for calculation of the Weisz modulus (see below).
4 Discussion
The most valuable contribution of this work is that the detail of the formation of N2O is shown. Also the values of concentration, velocity, pressure and most importantly temperature are shown on a local scale in the reactor. When using the SCR reaction process under high concentration, high pressure conditions the reaction rates are very fast. Thus unusually high temperatures are produced in the catalyst when almost all of the incoming NO is reduced in the first part of the catalyst bed.
The purpose of the experimental study [5] was to elucidate the possibility to use the SCR process for removing nitrogen oxides in the Oxyfuel process. It was not our aim to determine accurate experimental data for a kinetic investigation. Therefore e.g. the particle size of the catalyst was by far too large to exclude internal diffusion problems. All other experimental parameters were in a normal range for the Oxyfuel process.
It should not be possible to evaluate the kinetics using a fixed bed model of the usual type. This is typically so because of the high temperature gradients within the catalyst bed.
By using the method presented here it was possible to fit the experimental data of both the NO and the N2O concentrations obtained at various temperatures to a model consisting of the four reactions described above.
When starting the simulation work a simpler model of the reactor was used consisting of only the 0.465 long large diameter part of the reactor (See Fig. 1). It was suspected that the inlet section should create a much high linear velocity for the gas flow in the inlet section so this part was included. Indeed, as shown above (Fig. 7) very large values (about 9 m/s) were obtained. This is true even for the large inlet tube 10 cm ahead of the catalyst bed (about 5 m/s). Because of the very small value of the permeability of the bed the linear velocity decreases at the inlet of the bed to values around 1 m/s.
Also at first the concentrations and the temperatures at the exit of the reactor were used. Then it was appreciated that the temperature was actually measured at the exit of the catalyst bed. The model was thus changed to take this fact into consideration. So in the final model the concentrations at the exit of the reactor, which is even across the tube, is correlated to the temperature measured at the exit of the bed. The temperature is measured by a thermocouple at the exit of and in contact with the catalyst bed.
In [19] Koebel and Elsener determined the kinetics over commercial V2O5–WO3/TiO2 catalysts similar to the one presented here. Their catalyst D21 with 1% V2O5 was tested with particles 0.16–0.20 mm diameter. The effectiveness factor at 470 K was estimated to 1.00 and 0.57 at 670 K. They measured rates at 1000 ppm NO, 5% water, 10% O2 and GHSV 550 000 h−1. Our values were 5000 ppm NO, 5.03% water, 13.06% oxygen and GHSV 120,000 h−1. The main difference is in the content of NO. The rates are usually independent on the oxygen and water at these levels. They used very small catalyst particles of 0.16–0.20 mm compared to ours of 0.70–0.81 mm. They corrected for internal diffusion limitations by calculation of effectiveness factors and got values of between 0.98 at 525 K and 0.49 at 700 K. The activation energy, for the rate constant determined by a plug flow model first order in NO, was determined to be 83.2 kJ/mol between 475 and 625 K. They also determined the parameters for the adsorption of ammonia. The heat of adsorption in their study was −144 kJ/mol while we used a value of −139 kJ/mol. We did not change this value which was taken from [20].
At higher temperatures the effect of diffusion is larger as will be the case in these experiments because of the higher rates and the larger particle size used. The presented value of 85 kJ/mol is similar to theirs though. Our effectiveness factors are in the range 0.99 at 560 K inlet temperature to 0.7 at 760 K when calculated from the Weisz-Prater modulus. The effectiveness factor (η) was, in this work, calculated from the the following formulas (Nw−p = R × rp 2/(Cs × Deff) < 3β and η = 1 − β/4) [21] for a first order isothermal reaction. Since our conditions are non-isothermal the comparison to other data might be erroneous. The apparent activation energy for the SCR reaction is 60 kJ/mol in our experimental data [5]. This is a rather high value and the rate should not be completely hindered by internal diffusion or could be enhanced by internal temperature gradients in the catalyst particles. Realistic values of the intrinsic activation energy for this kind of kinetics for the SCR are in the range 97.3 [22] to 101.9 kJ/mol [23].
There has been one publication on the simulation of the SCR of NO by NH3 using COMSOL published on ResearchGate [24]. That paper did not consider the formation of N2O though. Hee Je Soong used kinetic data from Chae [25] in their simulation. The reactions used were the SCR, the oxidation of NH3 to N2 and the oxidation of NH3 to NO. They used an isothermal model for a 0.07 m long by 0.1 m wide bed. There is insufficient data in the paper for a valuable comparison to the results presented here. The current model represents the geometric data of the reactor where our experimental data were determined. Most importantly we used a non-isothermal model for the whole system and we have seen the large temperature gradients present in the reactor.
In another paper a simulation using a CFD program (Ansys 14.5 Fluent) was presented [26]. They only used the SCR reaction and the oxidation of NH3 to N2 but did have an adsorption term for NH3 in the model. They simulated a monolith instead of a fixed bed as presented here. Concentrations were in the 1000 ppm range. Parameters were too different to make a reasonable comparing between the two results.
There have been publications on the formation of N2O on a similar catalyst as the one used here before as described in the introduction. In an early study we determined the amounts of N2O formed on vanadia model catalysts (10–30% V2O5/SiO2–TiO2) containing large amounts of crystalline vanadia [10]. We found that up to 143 ppm N2O was formed when oxidizing 700 ppm of NH3 with 2% O2 at 686 K in the absence of water. With 1% water the amount was reduced to 55 ppm.
Kim [27] studied the vanadia content and its effect on the formation of N2O over V2O5–WO3/TiO2 catalysts with 1–8% vanadia. They observed increasing selectivity for the formation of N2O with an increased content of vanadia reaching 7.5% at 670 K for the 8% catalyst. In separate experiments it was shown that N2O was also formed in the oxidation of NH3 over the catalyst. The maximal selectivity was 9% in that case. Their results support the proposal of a direct oxidation reaction of NH3 to NO as used here.
Kim et al. [28] showed the 54 ppm N2O was formed on 1.68% V2O5–WO3/TiO2 catalyst at 745 K. In another study [29] on a commercial catalyst with 1.43% V2O5 and 7.56% WO3 the formation of 20 ppm N2O at a NO conversion of 85% at 750 K was presented. Similar results were obtained by [30].
Lietti [31] also showed similar results but stated that 10 ppm was formed in the oxidation of NH3 at 750 K. For this reaction no effect of water was seen. The three oxidation reactions of NH3 yielding N2, N2O and NO were used to explain their data.
Yates et al. [32] studied catalyst with 90% TiO2 and 0–10% V2O5 or WO3 or combinations of the two latter ones. At 615 K the selectivity to N2O was 76% in 1000/1000 ppm NO/NH3 and 3% O2. When V2O5 was below 5% the selectivity was only 10%. In the NH3 oxidation the selectivity was <5%. They assumed that the N2O was formed from two NO molecules without the involvement of NH3. This is not in line with results from many others. They presented similar results in another publication later [33].
In our earlier study [10] the maximal content was 15 ppm with 5% water at 790 K. In this study a commercial catalyst, which was manufactured in order not to produce large amounts of N2O, was used. Our earlier study confirms the new results that N2O is formed by two reactions. One low temperature reaction of NH3 with NO and O2 (NSCR) and one high temperature one by direct oxidation of NH3 to N2O.
The formation of N2O as a side product in the SCR reaction and from the oxidation of NH3 was also studied in [20]. This paper also deals with situations where the gas contains NO2 shown to lead to low and medium temperature formation of N2O. When 1000 ppm NH3 was oxidized by 10% O2 in the presence of 5% water N2O was formed at 350 C and its selectivity increased to 15% at 450 C. In the Reaction of 300 ppm NO with 300 ppm NH3 with 10% O2 in the presence of 5% water the selectivity to N2O increased from 0.3% at 350 C to 5.4% at 450 C (16 ppm). The values in this study are much lower at 0.3 and 3 ppm respectively. This can be explained by the low content of V2O5 (0.4%) in our catalyst and the absence of NO2 in the gas.
It has not been possible to find a study describing the complete non-isothermal kinetics of the SCR including the formation of N2O in the literature. Therefore, this study contributes to an increased understanding of this important issue since N2O is a much more potent greenhouse gas than CO2 and its formation should be avoided where possible.
Xiong [9] completed a thorough kinetic study of the SCR system and included the NSCR and the deep oxidation of NH3 to NO. They showed that higher amounts of NO and NH3 (in equimolar ratios) produced less N2O. There was no effect of the GHSV (30,000–480,000 cm3/g,h) on the selectivity to N2O. At 720 K kNSCR/kSCR was 118e−6 for a 1% V2O5 catalyst. Addition of 5% water, for a 5% catalyst, decreased the amount of N2O formed to only 3% of the value in the dry system. The activation energies were 51.6 and 100.7 kJ/mol for the SCR and the NSR respectively. These values are not too far from our apparent activation energy (60 kJ/mol) and the value for the NSCR (110 kJ/mol) used in the simulations. They also state that the formation of N2O requires the following reactions:
\({N}{{H}_{3}}\left( {g} \right)\,+\,{{V}^{{5}\,+}}{=O=> }{{V}^{{4}+}} - {OH}\,+\,{N}{{H}_{2}}\)
\({N}{{H}_{2}}\,+\,{{V}^{{5}\,+}}{=O=> }{{V}^{{4}+}} - {OH}\,+\,{NH}\)
\({NH}\,+\,{{V}^{{5}\,+}}{=O}\,+\,{NO}\left( {g} \right)=>{{V}^{{4}+}} - {OH}\,+\,{{N}_{2}}{O}\left( {g} \right)\)
It is very interesting to see the large effect of the high thermal conductivity of the stainless steel reactor tube on the temperature gradient in the reactor (Fig. 5) and how it contributes to preheating the reactant gases. The heat formed by the reactions in the catalyst bed is conducted in the wall towards the inlet of the reactor. At least a temperature of 763 K is reached in the wall close to the inlet of the bed at an inlet temperature of 720 K. Even in the small inlet tube at temperature of 724 K is obtained. This can be expected because of the god heat conductivity of steel.
It is also expected to get the major pressure drop in the dense catalyst bed. We have suspected to see some small pressure drop in other sections also (Fig. 6) but did not.
5 Conclusions
The concentrations of nitric oxide and nitrous oxide reported in high temperature and high centration reduction of NOx by NH3 [5] can be nicely represented by a system of four reactions. They are: the SCR reaction, the NSCR formation of N2O, the formation of N2O from NH3, and at higher temperature the oxidation of NH3 to NO. In a 3D model, using COMSOL Multiphysics, much has been learnt about the details of the processes taking place in a laboratory reactor operating under adiabatic conditions. Kinetic parameters can be determined but the presented reactions might not be the only ones possible since we have shown that the replacing the oxidation of NH3 to NO with the oxidation to N2 give similar results. Luckily enough the SCR reaction is by far the fasted one at low temperatures making it fairly easy to fit its parameters first. Then the formation of N2O is dealt with. Finally, at the highest temperatures the increased NO concentrations caused by the desorption of NH3, and therefore decreased rate of SCR reaction, is accounted for.
The importance of using a reactor with a long part after the catalyst bed, for the evening out of the concentrations in order to obtain correct data, is also shown.
Abbreviations
- Ain :
-
Cross sectional area of the inlet tube (m2)
- Ci :
-
Molar concentration of specie i (mol/m3)
- Cp :
-
Specific heat capacity at constant pressure (J/kg/K)
- dp :
-
Diameter of the catalyst particle (m)
- F:
-
Volume force (N)
- Di :
-
Molecular diffusivity of specie i (m2/s)
- Ftot :
-
Total molar flow in inlet (mol/s)
- kdisp :
-
Dispersive thermal conductivity (W/m/K)
- keff :
-
Effective thermal conductivity (W/m/K)
- kgas :
-
Thermal conductivity of the gas phase (W/m/K)
- kp :
-
Thermal conductivity of the porous bed (W/m/K)
- K:
-
Constant in the symmetry condition of the free and porous media flow module
- n:
-
Boundary normal pointing out of the domain
- NOfrac :
-
Molar fraction of NO in inlet
- Ni :
-
Flow of specie i over the boundary surface (mol/m2/s)
- q:
-
Heat flux (W/m2)
- Q:
-
Heat source (W/m3)
- Qbr :
-
Mass creation in domain (kg/s)
- Qted :
-
Thermoelastic damping heat source (W/m3)
- Qvd :
-
Viscous dissipation term (W/m3)
- q0 :
-
The heat flux that enters the domain (W/m2)
- Qp :
-
Point heat source (W/m3)
- Ri :
-
Rate of formation of specie i (mol/m3/s)
- T:
-
Temperature (K)
- u:
-
Velocity field (m/s)
- vin :
-
Linear velocity in inlet (m/s)
- Vpor :
-
Pore volume of the catalyst (cm3/g)
- βF :
-
Forcheimer coefficient (kg/s)
- εp :
-
Bed porosity (−)
- εpart :
-
Porosity of the catalyst particle (−)
- Κ:
-
Permeability (m2)
- µ:
-
Dynamic viscosity (Pa×s)
- ρ:
-
Density (kg/m3)
- ρbed :
-
Density of the catalyst bed (kg/m3)
- ρpart :
-
Density of the catalyst particle including pores (g/cm3)
- ρsolid :
-
Density of the solid part of the catalyst particle (kg/m3 or g/cm3)
- θp:
-
Fraction of catalyst particles in the bed (−)
References
Bosch H, Janssen F (1988) Preface. Catal Today 2:369–531
Heck RM (1999) Catal Today 53:519–523
Gabrielsson P, Pedersen HG (2008) In: Ertl G, Knözinger H, Schüth F, Weitkamp J (eds) Handbook of Heterogeneous Catalysis, Wiley, Weinheim, pp 2345–2385
Satterfield CN (1996) Heterogeneous catalysis in industrial practice, 2nd edn. Krieger Publishing Company, Malabar
Brandin J G M, Hulteberg CP, Odenbrand C U I (2012) Chem Eng J 191:218–227
Colombo M, Nova I, Tronconi E (2012) Catal Today 197:243–255
Colombo M, Nova I, Tronconi E (2010) Korean J Chem Eng 27(6):1730–1737
Cho CP, Pyo YD, Jang JY, Kim GC, Shin YJ, (2017) Appl Therm Eng 110:18–24
Xiong S, Xiao X, Liao Y, Dang H, Shan W, Yang S (2015) Ind Eng Chem Res 54:11011–11023
Odenbrand CUI, Gabrielsson PLT, Brandin JGM, Andersson LAH (1991) Appl Catal 78:109–123
Nova I, Tronconi E (eds) (2014) Urea-SCR technology for deNOx after treatment of diesel exhausts, fundamental and applied catalysis. Springer, New York
Lietti L, Nova I, Camurri S, Tronconi E, Forzatti P (1997) AI ChE J 43:2559–2570
Gordon S, McBridge B J (1971) Computer program for calculating of complex chemical equilibrium compositions, rocket performance, incident and reflected shocks, and champman-jouquet detonations, NASA-SP-273
Amiri A, Vafai K (1994) Int J Heat Mass Transf 37:939–954
Smith JM (1981) Chemical engineering kinetics. McGraw-Hill Book Company, New York
Weast R C (1975) Handbook of chemistry and physics, 56th edn. CRC Press, Cleveland
Gonzo EE (2002) Chem Eng J 90:299–302
Harriot P (1975) Chem Eng J 10:65–71
Koebel M, Elsener M (1998) Chem Eng Sci 53:657–669
Roduit B, Baiker A, Bettoni F, Baldyga J, Wokaun A (1998) AIChE J 44:2731–2744
Froment GF, Bischoff K B (1990) Chemical reactor analysis and design, 2nd edn. Wiley, Hoboken
Tronconi E (1997) Catal Today 34:421–427
Roduit B, Wokaun A, Baiker A (1998) Ind Eng Chem Res 37:4577–4590
Soong HJ (2015). http://www.researchgate.net/publication/239592194
Chae HJ, Choo ST, Choi H, Nam I, Yang HS, Song SL (2000) Ind Eng Chem Res 39:1159–1170
Madia G, Koebel M, Elsener M, Wokaun A (2002) Ind Eng Chem Res 41:4008–4015
Kim J-H, Choi J-H (2013) Korean Chem Eng Res 51(3), 313–318
Kim DW, Kim MH, Ham S-W (2010) Korean J Chem Eng 27(6):1730–1737
Kim MH, Lee HS (2014) In: 8th Conference on Environmental Catalysis, Asheville, NC, USA, EC-P-60, 24–27 Aug 2014
Lee Y-H, Kim MH, Ham S-W (2013) In: 23rd North American Conference on Catalysis, Louiseville, Kentucky, USA, 2–7 June 2013
Lietti L, Nova I, Forzatti P (2000) Top Catal 11/12:111–122
Yates M, Martín JA, Martin-Luego MA, Suarez S, Blanco J (2005) Catal Today 107–108:120–125
Martin JA, Yates M, Avila P, Suarez S, Blanco J (2007) Appl Catal B 70:330–334
Acknowledgements
The experimental part of the project was financed by the Swedish Research Council Formas, Vattenfall AB and Hulteberg Chemistry & Engineering AB. Catalyst materials were kindly supplied by Johnson Matthey Ltd., BASF AG, CRI/Criterion Catalyst Company Ltd., Haldor Topsoe A/S and Hulteberg Chemistry & Engineering AB. The experimental investigation of the SCR reaction was performed by Mr. Robert Almqvist.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Odenbrand, C.U.I. High Temperature and High Concentration SCR of NO with NH3 for the Oxyfuel Combustion Process: Fitting of Kinetics to Data from a Laboratory Reactor Experiment. Top Catal 60, 1317–1332 (2017). https://doi.org/10.1007/s11244-017-0817-x
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11244-017-0817-x