Convective Plume Spreading in Model Transparent Porous Media

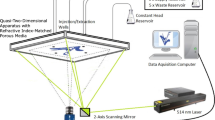
Abstract

Visualising fluid flow in porous media using optical techniques is challenging due to the inability to see through the medium. Here, we present an experimental methodology based on shadowgraphy to investigate the dynamic spreading of convective plumes in saturated transparent porous media made of glass beads. The saturated porous medium can be tuned transparent by matching the refractive index of the solid glass beads to that of the saturating fluid mixture. The proposed technique allows to investigate the essential elements of convective mixing within a porous medium using miscible fluids. We also describe a method to determine the velocity of convective plumes as they propagate. Our experimental results show that the density difference achieved during convection significantly affects the convective front velocity of the plumes. This is significant because it allows to quantitatively predict the intensity of convective mixing in porous media from the speed of the convective front.

Article Highlights

• Shadowgraphy has been successfully used to investigate fluid flow in transparent porous media.

• Convective front velocities are used to evaluate quantitatively convective mixing in porous media.

• In the fluid flow regime of our experiment, we observed a super-linear scaling of the convective front velocity and density difference.

Appendices

Appendix A: Density of Fluid Mixtures

In the study of the thermodynamic mixing of toluene and 1-hexanol, (Almasi 2021) conducted density and viscosity measurements using a scanning voltage microscopy (SVM) 3000 Stabinger viscometer. For all the compositions and a temperature of 293.2 K, we plotted the density data as shown in Fig. 9a and fitted them through a density equation as follows:

$$\rho =3.795{x}_{tol}^{4}-5.307{x}_{tol}^{3}+11.965{x}_{tol}^{2}+37.481{x}_{tol}+818.7$$

(8)

The Bias $=\frac{1}{N}\sum_{i=1}^{{N}_{c}}100\left(1-\frac{{\rho }_{calc}}{{\rho }_{exp}}\right)$, the mean absolute deviation $AAD=\frac{1}{N}{\sum }_{i=1}^{{N}_{c}}100\left|1-\frac{{\rho }_{calc}}{{\rho }_{exp}}\right|$ and the maximum deviation ${\Delta }_{\max}=\max\left(100\left|1-\frac{{\rho }_{calc}}{{\rho }_{exp}}\right|\right)$ were estimated from a total of N = 12 experimental points and the results are reported in Table 5. The relative deviations of our calculations from the experimental measurements are shown in Fig. 9b.

Fig. 9

a Density of the toluene/1-hexanol mixtures and their fit to the fourth-order polynomial at 293.2 K. b Relative deviations, in percentage, between calculations and measurements

Table 5 Relative deviations between the calculations of the density of the Toluene/1-hexanol mixture and the experimental data from the literature (Almasi 2021)

Appendix B: Calculation of the Molecular Diffusion Coefficient

A correlation for the computation of the mass diffusion coefficient for binary mixtures of n-alkanes and systems involving gases dissolved in alcohols at infinite dilution was proposed by (Wu et al. 2019). The correlation was generated using more than 300 datasets from various light-scattering experiments and equilibrium molecular simulations. Below is the correlation for determining the molecular diffusion coefficient of a liquid mixture.

$${D}_{m}=5.249\times {10}^{-17}\times \frac{T{\left(\psi {M}_{2}\right)}^{0.5}}{{v}_{2}^{0.8}{\left[{M}_{1}\left(0.45+{\omega }_{1}\right)\right]}^{0.25}}$$

(9)

$$\psi =1+1.338\times {10}^{6}\times \frac{{v}_{2}^{0.3}{\mu }_{2}}{{M}_{2}T}$$

(10)

where $\psi$ is the association factor, T is the temperature (K), ${M}_{1}$ and ${M}_{2}$ are the molar masses of the solute and solvent (g mol⁻¹), respectively, ${v}_{2}$ is the kinematic viscosity of the pure solvent (m² s⁻¹), ${\omega }_{1}$ is the acentric factor of the solute, and ${\mu }_{2}$ is the total dipole moment of the solvent (Debye). When a fluid's thermodynamic state changes, the dipole moment of the molecule must also change; this information is frequently unavailable.

The uncertainty in using this correlation comes from the value of the dipole moment because it is assumed that the liquid structure is independent of the systems, and the association factor does not contain any information about the solute.

In this study, we used the acentric factor of toluene for the composition of the injected fluids (toluene/1-hexanol mixtures) during the diffusion coefficient calculation, because the wt% of toluene was higher than 80% in all cases. The total dipole for the mixtures was taken to be equal to 1, and the dynamic viscosity was derived from the fitting of the experimental data from Almasi (2021). The density data used to calculate the kinematic viscosity were also obtained from the fitting of experimental data from Almasi (2021). The average molecular weight was calculated using the formula $\sum ({x}_{i}{M}_{i})/{n}_{i}$, where ${x}_{i}$= wt% of i component; ${M}_{i}$ = molar mass of i component; ${n}_{i}$ = number of i component.