1 Introduction

Carbon sequestration, particularly geological sequestration, plays a pivotal role in addressing global carbon emissions and is a vital tool in the battle against climate change. As carbon dioxide levels in the atmosphere continue to rise, finding reliable and effective methods to store it becomes necessary. One such method is by injecting carbon dioxide deep into geological formations. In geological sequestration, carbon dioxide is injected in deep formations either as a brine–gas-saturated mixture or as supercritical phase \(\left( {{\text{ScCO}}_{{2}} } \right)\). It can be sequestered in various types of formations, such as sandstone, saline aquifers, dolomite, coal, and basalt formation. Chemical reactions are typically induced, and the type and intensity of the reaction depend on the formation type and carbon dioxide phase (brine/\({\text{CO}}_{{2}}\) mixture or \({\text{ScCO}}_{{2}}\)). Mineral carbonation can occur, resulting in the formation of new minerals, such as iron, magnesium, and calcium ions, affecting the porosity and permeability of the rock. This process is known as mineral trapping.

Each formation reservoir undergoes chemical reactions based on the primary minerals present. Chemical reaction coupling is complex. It includes dissolution and precipitation, which affect energy, fluid flow, porosity, and solid deformation. When dissolution occurs, the resulting ions may react with other minerals and acidic solutions to produce carbonate species (precipitation). The temperature and carbon dioxide solubility in the fluid directly affect the precipitation/dissolution process because they are related to the pH level of the fluid (Luo et al. 2012; Rathnaweera et al. 2017). Chemical reactions can change the physical properties, such as porosity and permeability, of the solid matrix and affect fluid transport, in which mass flow is added to the liquid. The stress/strain ratio is also affected by this process.

The effect of the chemical reactions between injected carbon dioxide and surrounding rocks on formation porosity has been investigated in previous studies; however, most reactive models consider only the effect of changing porosity on permeability (Xu et al. 2005; Fischer et al. 2013; Klein et al. 2013; Ilgen and Cygan 2016; Wolf et al. 2016; Zhou et al. 2016; Dai et al. 2020).

Although several hydro-mechanic-chemical reactive models have been introduced in recent years, a knowledge gap in mechanical-chemical coupling relations, specifically the effect of the dissolution/precipitation process on the applied stress/strain on the solid matrix, still exists. Some researchers such as Olivella et al. (1994) tried to develop a comprehensive thermo-hydro-mechanical (THM) framework for the multi-phase flow of brine and gas through saline media, which incorporated salt species dissolution, precipitation, and deformation via a pressure solution. However, the framework lacked coupling between strain–stress and chemical reactions. Guimarães et al. (2007) attempted to create a fully coupled model by combining the model introduced by Olivella et al. (1994) and the approach of Gens et al. (2002) with reactive transport equations. However, this model only accounted for the change in porosity (dynamic porosity) and thus permeability due to chemical reactions, neglecting the effect of chemical dissolution on the governing equations for deformation and stress. Yin et al. (2011) used a mathematical model derived by Lewis and Schrefler (1998) to describe the two-phase transport of fluids. Subsequently, the general transport of the solute equation was incorporated into the model. However, the hydromechanical-chemical coupling was limited to the changes in porosity and permeability without the governing equations for solid, liquid, and gas being modified.

Some researchers attempted to create a coupling between chemical reaction and stiffness of the material and the induced stresses, such as Mehrabi and Atefi-Monfared (2022). The author introduced a model that predicts the spatial distribution of bio-cementation and the resulting enhanced characteristics of microbially induced carbonate precipitation (MICP) treated soils. However, the presented model can handle one phase flow only and more advanced model is required for applications such as carbon capture and storage.

In addition to the work of Mehrabi and Atefi-Monfared (2022), other researchers, including Gawin et al. (2003), Kuhl et al. (2004), Gawin et al. (2008), Haxaire and Djeran-Maigre (2009), Karrech (2013), Zhang and Zhong (2018) have explored the coupling of chemical reactions with solid/stress equations. Recently, Yue et al. (2022) proposed a single-phase transport model that includes dissolution and chemically reactive processes (i.e., changes in porosity due to dissolution). They introduced the concept of ‘solid affinity’ to couple the dissolution reactions with the hydro-mechanical framework. Although this model addresses the gap in the studies on mechanical-chemical coupling, it only considers one-phase transport, limiting its usefulness for multi-phase flow applications such as carbon sequestration. Moreover, the numerical simulation in that study was simplistic and did not show the effect of the added term on the strain.

One approach that promises to address the shortcomings of traditional models is rooted in a method known as the mixture coupling theory (Chen et al. 2018). This method, which was first presented by Heidug and Wong (1996), provides a unique interpretation of fluid-filled rocks or soils. Rather than treating them as separate entities, it views them as a unified whole. This shift in perspective addresses some challenges seen in standard mechanics methodologies and presents clear advantages. While classical mechanics typically hinges on the principles of stress–strain tensor and the balance of linear momentum, the mixture coupling theory turns to the realms of non-equilibrium thermodynamics, focusing on an energy and entropy-centric approach. This method has been distinguished and differentiated from others in several scholarly contributions, with some pointing out its strategic omission of the momentum conservation balance equation.

With such advancements in modeling frameworks, we still face two pivotal questions:

  • How can chemical reactions be effectively integrated into a multi-phase hydro-mechanical-chemical system for carbon dioxide sequestration?

  • How can the influence of these reactions on the hydromechanical framework be accurately captured?

To address this research gap, this study presents a novel approach for modeling a reactive multi-phase hydro-mechanical-chemical system for carbon dioxide sequestration using coupling mixture theory. The proposed model is simulated under isothermal conditions, and a theoretical carbon dioxide injection test into limestone sample rock is performed, considering only the chemical reactions that lead to mineral dissolution. The extent of the reaction and solid affinity is applied to the model to capture the coupled effects of chemical reactions on the hydromechanical framework. Finally, objectives of this study can be set clear as:

  • To present a novel approach for modeling a reactive multi-phase hydro-mechanical-chemical system for carbon dioxide sequestration using coupling mixture theory by applying the extent of reaction and solid affinity to the model, ensuring the coupled effects of chemical reactions on the hydromechanical framework are effectively captured.

  • To simulate the proposed model under isothermal conditions by performing a theoretical carbon dioxide injection test into limestone sample rock, focusing on chemical reactions that lead to mineral dissolution.

2 Mathematical Model

When carbon dioxide is injected into a rock formation containing saline water, a considerable amount of the carbon dioxide fluid dissolves in the water to create carbonic acid. In the proposed model, a two-phase system consisting of a supercritical (Sc) fluid and liquid saline/carbonic water is considered. An immiscible system where the change in mass due to carbon dioxide solubility in saline water is not considered is assumed (carbon dioxide is assumed to be already dissolved in saline water). Additionally, the system is assumed to be isotropic under isothermal conditions.

In this paper, the model is defined by selecting an arbitrary microscopic domain of arbitrary size that encompasses all phases, along with a surrounding surface boundary that contains the domain. Fluids are the only substances allowed to pass through this boundary. The subscripts “Sc”, “l”, “w”, and “c” refer to supercritical fluid, saline water, water, and chemical solute (salt), respectively.

The volumes of saline water and supercritical fluid flows are identified as \(V^{l}\) and \(V^{{{\text{Sc}}}}\), respectively. The relationship between the pore space volume, \(V^{{{\text{pore}}}}\), and these volumes can be expressed as follows (Biot 1955; Lewis and Schrefler 1987; Bear 2013):

$$\begin{aligned} & V^{{{\text{pore}}}} = V^{{{\text{Sc}}}} + V^{l} , \\ & \phi = \phi^{{{\text{Sc}}}} + \phi^{l} , \\ & S^{{{\text{Sc}}}} + S^{l} = 1. \\ \end{aligned}$$
(1)

where \(\phi = {{V^{{{\text{pore}}}} } \mathord{\left/ {\vphantom {{V^{{{\text{pore}}}} } V}} \right. \kern-0pt} V}\) is the volume fraction (porosity); \(\phi^{{{\text{Sc}}}} = {{V^{{{\text{Sc}}}} } \mathord{\left/ {\vphantom {{V^{{{\text{Sc}}}} } V}} \right. \kern-0pt} V}\) is the volume fraction of the \({\text{ScCO}}_{{2}}\); \(\phi^{l} = {{V^{l} } \mathord{\left/ {\vphantom {{V^{l} } V}} \right. \kern-0pt} V}\) is the volume fraction of saline water; the saturation of the \({\text{ScCO}}_{{2}}\) is denoted by \(S^{{{\text{Sc}}}} = {{V^{{{\text{Sc}}}} } \mathord{\left/ {\vphantom {{V^{{{\text{Sc}}}} } {V^{{{\text{pore}}}} }}} \right. \kern-0pt} {V^{{{\text{pore}}}} }}\); while the saturation of saline water is represented by \(S^{l} = {{V^{l} } \mathord{\left/ {\vphantom {{V^{l} } {V^{{{\text{pore}}}} }}} \right. \kern-0pt} {V^{{{\text{pore}}}} }}\).

The relationship between the mixture density (mass over the volume of mixture) and the phase density (mass over the volume of the phase) can be written as (Chen 2013)

$$\begin{aligned} & \rho^{l} = \phi^{l} \rho_{l}^{l} , \\ & \rho^{{{\text{Sc}}}} = \phi^{{{\text{Sc}}}} \rho_{{{\text{Sc}}}}^{{{\text{Sc}}}} . \\ \end{aligned}$$
(2)

where the symbols \(\rho^{l}\), \(\rho^{{{\text{Sc}}}}\) denote the mixture density, and \(\rho_{l}^{l}\), \(\rho_{{{\text{Sc}}}}^{{{\text{Sc}}}}\) denote the phase density.

Based on the above relation, the water, chemical solute, and liquid mixture density can be expressed as:

$$\begin{aligned} & \rho^{w} = \phi^{l} \rho_{l}^{w} , \\ & \rho^{c} = \phi^{l} \rho_{l}^{c} , \\ & \rho^{l} = \rho^{w} + \rho^{c} . \\ \end{aligned}$$
(3)

The variables \(\rho_{l}^{w}\) and \(\rho_{l}^{c}\) denote the mass ratios of water and chemical, respectively, to the total volume of the liquid phase.

2.1 Flux and Diffusion

The mass flux of \(\beta\), where \(\beta\) represents either the saline water flow ‘l’, or the supercritical flow ‘Sc’, or any of the sub-constituents in saline water (i.e., water ‘w’ and chemical ‘c’), is defined as (Chen 2013)

$${\mathbf{I}}^{\beta } = \rho^{\beta } \left( {{\mathbf{v}}^{\beta } - {\mathbf{v}}^{s} } \right),$$
(4)

\({\mathbf{I}}^{\beta }\) represents the fluid mass flux, \(\rho^{\beta }\) denotes the mixture density of \(\beta\), and \({\mathbf{v}}^{\beta }\) and \({\mathbf{v}}^{s}\) refer to the velocities of \(\beta\) and the solid, respectively. To express the diffusion flux \({\mathbf{J}}^{\beta }\) in terms of the barycentric velocity, the following equations can be used (Ma et al. 2021):

$$\begin{aligned} & {\mathbf{J}}^{\beta } = \rho^{\beta } \left( {{\mathbf{v}}^{\beta } - {\mathbf{v}}^{l} } \right),\quad \beta \in l, \\ & {\mathbf{J}}^{\beta } = \rho^{\beta } \left( {{\mathbf{v}}^{\beta } - {\mathbf{v}}^{{{\text{Sc}}}} } \right),\quad \beta \in {\text{Sc}}{.} \\ \end{aligned}$$
(5)

The barycentric velocity of saline water is denoted by \({\mathbf{v}}^{l} = \frac{{\rho^{w} }}{{\rho^{l} }}{\mathbf{v}}^{w} + \frac{{\rho^{c} }}{{\rho^{l} }}{\mathbf{v}}^{c}\). The supercritical flow, since it is considered to be composed of a single constituent, then the diffusion flux of the supercritical flow is 0.

Nether less, saline water flow contains water and chemical, \({\mathbf{v}}^{w} \ne {\mathbf{v}}^{l}\) and \({\mathbf{v}}^{c} \ne {\mathbf{v}}^{l}\), therefore, by using Eq. (4) and (5) the diffusion flux can be written as

$${\mathbf{J}}^{\beta } = {\mathbf{I}}^{\beta } - \rho^{\beta } \left( {{\mathbf{v}}^{l} - {\mathbf{v}}^{s} } \right).$$
(6)

2.2 Chemical Reaction and Dissolution

In this study, the dissolution rate is incorporated in the model through chemical affinity, which is directly related to the extent of the reaction. Solute c is only transported in the liquid and does not react chemically. The reaction occurs only between the rock minerals and carbonic acid.

The dissolution reaction can be expressed as (Katchalsky and Curran 1965)

$$v_{x} X_{(s)} + v_{y} Y_{{({\text{aq}})}} \to v_{z} Z_{{({\text{aq}})}} ,$$
(7)

where \(X,\,Y\) are the reactants and \({\text{Z}}\) is the product, \(v_{x} ,\,v_{y}\), and \(v_{z}\) are the stoichiometric coefficient for \(X,\,Y,\) and \({\text{Z}}\).

There is a direct relation between the extent of reaction and the moles changes \(\frac{{{\text{d}}n_{i} }}{V} = \chi v_{i} {\text{d}}\xi ,\)

where \(\xi\) is extent of reaction, \({\text{d}}n_{i}\) is the change in number of moles, \(V\) pore volume. \(\chi\) equals to 1 for products Z and − 1 for reactants \(X,\,Y\) and 0 for anything that does not join the reaction. Furthermore, the driving force reaction (affinity) can be written as (Kondepudi and Prigogine 2014; Yue et al. 2022)

$$A = - \sum \chi v_{i} M^{i} \mu^{i} = v_{x} M^{X} \mu^{X} + v_{y} M^{Y} \mu^{Y} - v_{z} M^{Z} \mu^{Z} ,$$
(8)

where \(A\) is the affinity, \(M\) is the molar mass, and \(\mu\) is the chemical potential.

2.3 Energy, Entropy, and Phenomenological Equations

2.3.1 Helmholtz Free Energy Balance Equation

The Helmholtz free energy balance equation in a mixture system comprising saline water, \({\text{ScCO}}_{{2}}\), and chemical solutes can be expressed as (Katchalsky and Curran 1965; Heidug and Wong 1996)

$$\frac{D}{Dt}\left( {\int\limits_{V} {\psi {\text{d}}V} } \right) = \int\limits_{\Gamma } {{\mathbf{\sigma v}}^{s} \cdot {\mathbf{n}}{\text{d}}\Gamma } - \left( {\int\limits_{\Gamma } {\mu^{w} {\mathbf{I}}^{w} } + \int\limits_{\Gamma } {\mu^{{{\text{Sc}}}} {\mathbf{I}}^{{{\text{Sc}}}} } + \int\limits_{\Gamma } {\mu^{c} {\mathbf{I}}^{c} } } \right) \cdot {\mathbf{n}}{\text{d}}\Gamma - T\int\limits_{V} {\gamma {\text{d}}V} .$$
(9)

In the above equation, the Helmholtz free energy density \(\psi\) is analyzed in the context of the Cauchy stress tensor \({{\varvec{\upsigma}}}\), the outward unit normal vector (n), and the chemical potentials for water \(\mu^{w}\), supercritical fluid \(\mu^{{{\text{Sc}}}}\), and chemical solute \(\mu^{c}\), at a fixed temperature \(T\), while considering the entropy production per unit volume \(\gamma\).

The balance equation of the free energy density can be presented in differential form as follows (Chen et al. 2018):

$$\dot{\psi } + \psi \nabla \cdot {\mathbf{v}}^{{\mathbf{s}}} - \nabla \cdot \left( {{\mathbf{\sigma v}}^{{\mathbf{s}}} } \right) + \nabla \cdot \left( {\mu^{w} {\mathbf{I}}^{w} + \mu^{{{\text{Sc}}}} {\mathbf{I}}^{{{\text{Sc}}}} + \mu^{c} {\mathbf{I}}^{c} } \right) = - T\gamma \le 0.$$
(10)

It should be mentioned that the term \(\mu^{c} {\mathbf{I}}^{c}\) here represent the energy change caused by the chemical mass exchanging with the surroundings.

2.3.2 Fluid Mass Balance Equation

The balance equation for the fluid component can be expressed as (Katchalsky and Curran 1965)

$$\frac{D}{Dt}\left( {\int\limits_{V} {\rho^{\beta } {\text{d}}V} } \right) = - \int\limits_{\Gamma } {{\mathbf{I}}^{\beta } \cdot {\mathbf{n}}{\text{d}}\Gamma } + \int\limits_{V} {\chi \nu^{\beta } M^{\beta } \dot{\xi }{\text{d}}V} ,$$
(11)

where the last term in the above equation, i.e., \(\int\limits_{V} {\chi \nu^{\beta } M^{\beta } \dot{\xi }{\text{d}}V}\), represents the change of fluid components due to the chemical reaction.

The balance equation for the fluid component in the local form is (Chen et al. 2018):

$$\dot{\rho }^{\beta } + \rho^{\beta } \nabla \cdot {\mathbf{v}}^{s} + \nabla \cdot {\mathbf{I}}^{\beta } - \chi \nu^{\beta } M^{\beta } \dot{\xi } = 0.$$
(12)

2.3.3 Entropy Production Equation

The dissipation in the mixture including solid/fluid friction can be expressed as (Katchalsky and Curran 1965; Ma et al. 2022)

$$0 \le T\gamma = - {\mathbf{I}}^{w} \cdot \nabla \mu^{w} - {\mathbf{I}}^{{{\text{Sc}}}} \cdot \nabla \mu^{{{\text{Sc}}}} - {\mathbf{I}}^{c} \cdot \nabla \mu^{c} + A\dot{\xi },$$
(13)

where \({\mathbf{I}}^{w} \cdot \nabla \mu^{w} ,\;{\mathbf{I}}^{{{\text{Sc}}}} \cdot \nabla \mu^{{{\text{Sc}}}}\), and \({\mathbf{I}}^{c} \cdot \nabla \mu^{c}\) are the entropy productions caused by the mass flow of the liquid (water), supercritical fluid, and transport of the diluted chemical, respectively. \(A\) denotes affinity, and \(A\dot{\xi }\) represents the entropy generated by the chemical reaction.

The Darcy velocity, \({\mathbf{u}}\), is for both liquids (including the chemicals), and supercritical phase can be expressed as (Whitaker 1986; Lewis and Schrefler 1987)

$$\begin{aligned} & {\mathbf{u}}^{l} = S^{l} \phi \left( {{\mathbf{v}}^{l} - {\mathbf{v}}^{s} } \right), \\ & {\mathbf{u}}^{{{\text{Sc}}}} = S^{{{\text{Sc}}}} \phi \left( {{\mathbf{v}}^{{{\text{Sc}}}} - {\mathbf{v}}^{s} } \right). \\ \end{aligned}$$
(14)

The Gibbs–Duhem equation for the liquid and supercritical phases can be used to express the pore liquid pressure and supercritical phase pressure as (Chen et al. 2016)

$$\begin{aligned} & \nabla p^{l} = \rho_{l}^{w} \nabla \mu^{w} + \rho_{l}^{c} \nabla \mu^{c} , \\ & \nabla p^{{{\text{Sc}}}} = \rho_{{{\text{Sc}}}}^{{{\text{Sc}}}} \nabla \mu^{{{\text{Sc}}}} . \\ \end{aligned}$$
(15)

The relationships in Eqs. (3), (6), (14), and (15) can be applied to describe the diffusion of chemical c as \({\mathbf{J}}^{c} = - {\mathbf{J}}^{w}\), and Eq. (13) can be revised as

$$0 \le T\gamma = - {\mathbf{u}}^{l} \cdot \nabla p^{l} - {\mathbf{J}}^{c} \cdot \nabla \left( {\mu^{c} - \mu^{w} } \right) - {\mathbf{u}}^{{{\text{Sc}}}} \cdot \nabla p^{{{\text{Sc}}}} + A\dot{\xi },$$
(16)

where \(- {\mathbf{u}}^{l} \cdot \nabla p^{l}\) represents the liquid flow driven by the internal liquid potential difference, \({\mathbf{J}}^{c} \cdot \nabla \left( {\mu^{c} - \mu^{w} } \right)\) represents the chemical diffusion in the liquid saline water driven by chemical potential gradient, \(- {\mathbf{u}}^{{{\text{Sc}}}} \cdot \nabla p^{{{\text{Sc}}}}\) represents the supercritical flow driven by the supercritical flow pressure difference, and \(A\dot{\xi }\) represent the chemical reaction that causes the dissolution of solid minerals.

Equation (16) describes the entropy production through thermodynamics fluxes and their corresponding driving forces. The phenomenological equation concept can be used to describe the interaction between flows and driving forces by assuming a linear relationship between each flow and its driving forces (Chen et al. 2018).

Several assumptions have been proposed in this model: (I) the chemical solute is present only in the liquid phase (saline water) and does not chemically react; (II) the carbon dioxide in the supercritical phase is considered chemically non-reactive; (III) the system is immiscible, i.e., no exchange of mass between the liquid and supercritical phases via dissolution occurs; (IV) some of the carbon dioxides are already dissolved in the saline water to form carbonate acid and can react with solid minerals (dissolution of solid minerals); (V) the process is under isothermal conditions; (VI) the porous media exhibits completely isotropic behavior (isotropic material).

2.3.4 Phenomenological Equations

Due to the interdependence of fluxes in a coupled system, the relationship between flow and driving forces can be expressed through linear dependence equations, also known as phenomenological equations. In the context of mass transport in an isotropic medium, the calculation of the three major flows (\(\rho_{l}^{l} {\mathbf{u}}^{l} ,\rho_{{{\text{Sc}}}}^{{{\text{Sc}}}} {\mathbf{u}}^{{{\text{Sc}}}} ,\) and \({\mathbf{J}}^{c}\)) is dependent on their corresponding driving forces (\(\nabla p^{l} ,\,\nabla p^{{{\text{Sc}}}}\), and \(\nabla \left( {\mu^{c} - \mu^{w} } \right)\)) as (Heidug and Wong 1996; Chen et al. 2018):

$$\rho_{l}^{l} {\mathbf{u}}^{l} = - \frac{{L_{11} }}{{\rho_{l}^{l} }}\nabla p^{l} - \frac{{L_{12} }}{{\rho_{{{\text{Sc}}}}^{{{\text{Sc}}}} }}\nabla p^{{{\text{Sc}}}} - L_{13} \nabla \left( {\mu^{c} - \mu^{w} } \right),$$
(17)
$$\rho_{{{\text{Sc}}}}^{{{\text{Sc}}}} {\mathbf{u}}^{{{\text{Sc}}}} = - \frac{{L_{21} }}{{\rho_{l}^{l} }}\nabla p^{l} - \frac{{L_{22} }}{{\rho_{{{\text{Sc}}}}^{{{\text{Sc}}}} }}\nabla p^{{{\text{Sc}}}} - L_{23} \nabla \left( {\mu^{c} - \mu^{w} } \right),$$
(18)
$${\mathbf{J}}^{c} = - \frac{{L_{31} }}{{\rho_{l}^{l} }}\nabla p^{l} - \frac{{L_{32} }}{{\rho_{{{\text{Sc}}}}^{{{\text{Sc}}}} }}\nabla p^{{{\text{Sc}}}} - L_{33} \nabla \left( {\mu^{c} - \mu^{w} } \right),$$
(19)

where \(L_{ij}\) are phenomenological coefficients, and \(\rho_{l}^{l}\) is the liquid phase density.

The equations presented above assume that the affinity is a scalar quantity and that the system is isotropic. As a result, there is no coupling between the scalar term and the other vectorial quantities, in accordance with the Curie–Prigogine principle. While this allows the scalar term to be ignored, it also means that the coupling between diffusion and chemical reactions cannot be accounted for in the phenomenological equations for an isotropic system, as noted by Katchalsky and Curran (1965).

Equations (17)–(19) describe the coupled diffusion flux and liquid water/flow, along with the liquid/supercritical fluid pressures and chemical potential differences. Because chemical potential is not common in the geomechanics field, it would be preferred to replace it with chemical concentration \(c^{\alpha }\). The relation between the chemical potential and the solute mass fraction can be described as (Chen et al. 2018):

$$\frac{{\partial \mu^{c} }}{{\partial c^{c} }} = \frac{RT}{{M^{c} c^{c} }}.$$
(20)

The following coefficients are defined.\(k_{{{\text{abs}}}} \frac{{k_{rl} }}{{v^{l} }} = \frac{{L_{11} }}{{\left( {\rho_{l}^{l} } \right)^{2} }},r_{1} = - \frac{{L_{12} }}{{L_{11} }},r_{2} = - \frac{{L_{13} }}{{L_{11} }},r_{3} = - \frac{{L_{21} }}{{L_{22} }},r_{4} = - \frac{{L_{23} }}{{L_{22} }},L^{l} = - \frac{{L_{31} p^{l} }}{{\left( {\rho_{l}^{l} } \right)^{2} }},L^{g} = - \frac{{L_{32} p^{{{\text{Sc}}}} }}{{\left( {\rho_{{{\text{Sc}}}}^{{{\text{Sc}}}} } \right)^{2} }},D = \frac{{L_{33} }}{{c^{w} \rho_{l}^{l} }}\frac{{\partial \mu^{c} }}{{\partial c^{c} }}\)

$${\mathbf{u}}^{l} = - k_{{{\text{abs}}}} \frac{{k_{rl} }}{{v^{l} }}\left( {\nabla p^{l} - r_{1} \frac{{\rho_{l}^{l} }}{{\rho_{{{\text{Sc}}}}^{{{\text{Sc}}}} }}\nabla p^{{{\text{Sc}}}} - r_{2} \rho_{l}^{l} \left( {\frac{1}{{c^{w} }}\frac{{\partial \mu^{c} }}{{\partial c^{c} }}\nabla c^{c} } \right)} \right),$$
(21)
$${\mathbf{u}}^{{{\text{Sc}}}} = - k_{{{\text{abs}}}} \frac{{k_{{r{\text{Sc}}}} }}{{v^{{{\text{Sc}}}} }}\left( { - r_{3} \frac{{\rho_{{{\text{Sc}}}}^{{{\text{Sc}}}} }}{{\rho_{l}^{l} }}\nabla p^{l} + \nabla p^{{{\text{Sc}}}} - \rho_{{{\text{Sc}}}}^{{{\text{Sc}}}} r_{4} \left( {\frac{1}{{c^{w} }}\frac{{\partial \mu^{c} }}{{\partial c^{c} }}\nabla c^{c} } \right)} \right),$$
(22)
$${\mathbf{J}}^{c} = - \left( {\frac{{L^{l} \rho_{l}^{l} }}{{p^{l} }}} \right)\nabla p^{l} - \left( {\frac{{L^{{{\text{Sc}}}} \rho_{{{\text{Sc}}}}^{{{\text{Sc}}}} }}{{p^{{{\text{Sc}}}} }}} \right)\nabla p^{{{\text{Sc}}}} - D\rho^{l} \nabla c^{c} ,$$
(23)

where \(v^{l}\) is the viscosity of the liquid saline water and \(v^{{{\text{Sc}}}}\) is the viscosity of the supercritical flow, \(k_{{{\text{abs}}}}\) is the absolute permeability of the porous media.

2.4 Constitutive Relations

Assuming mechanical equilibrium in the solid/rock, in which, \(\nabla \cdot {{\varvec{\upsigma}}} = 0\), Helmholtz free energy density equation can be derived by utilizing Eqs. (13) and (10) as:

$$\dot{\psi } + \psi \nabla \cdot {\mathbf{v}}^{s} - \left( {{{\varvec{\upsigma}}}:\nabla {\mathbf{v}}^{s} } \right) + \mu^{w} \nabla \cdot {\mathbf{I}}^{w} + \mu^{{{\text{Sc}}}} \nabla \cdot {\mathbf{I}}^{{{\text{Sc}}}} + \mu^{c} \nabla \cdot {\mathbf{I}}^{c} + A\dot{\xi } = 0.$$
(24)

Equation (24) outlines the free energy density in the current configuration. By applying Fundamental principles of continuum mechanics (Wriggers 2008) along with Eq. (12), the equation can be transformed to its reference configuration as (Heidug and Wong 1996; Chen and Hicks 2011):

$$\dot{\Psi } = tr\left( {{\mathbf{T\dot{E}}}} \right) + \mu^{w} \dot{m}^{w} + \mu^{{{\text{Sc}}}} \dot{m}^{{{\text{Sc}}}} + \mu^{c} \dot{m}^{c} - A_{s} \dot{\varsigma }.$$
(25)

where \(\Psi = J\psi ,m^{\beta } = J\rho^{\beta } = JS^{\beta } \phi \rho_{\beta }^{\beta } ,\varsigma = J\xi .\) \(\Psi\) is the free energy in the reference configuration, while \(m^{\beta }\) represents the mass density of liquid, supercritical and chemical flow in the reference configuration, and \(\varsigma\) is the extent of the reaction in the reference configuration. Furthermore, \({\mathbf{T}}\) is the second Piola–Kirchhoff stress tensor, \({\mathbf{E}}\) is the Green strain, \(A_{S}\) is the solid affinity and be expressed as \(A_{s} = v_{x} M^{X} \mu^{X} .\) \(J\) is the Jacobian and can be expressed as \(J = \frac{{{\text{d}}V}}{{{\text{d}}V_{0} }},\,\dot{J} = J\nabla \cdot {\mathbf{v}}^{s}\), where \(dV\) is the volume in the current configuration, and \(dV_{0}\) is the volume in the reference configuration.

2.4.1 Helmholtz Free Energy Density of Pore Space

The Helmholtz free energy density denoted as \(\psi^{{{\text{pore}}}}\) pertains to a pore containing supercritical \({\text{CO}}_{{2}}\) and saline water. In compliance with classic thermodynamics:

$$\psi^{{{\text{pore}}}} = - p^{p} + S^{l} \sum\limits_{k} {\rho_{l}^{k} } \mu^{k} + S^{{{\text{Sc}}}} \rho_{{{\text{Sc}}}}^{{{\text{Sc}}}} \mu^{{{\text{Sc}}}} ,$$
(26)

\(p^{p}\) is the average pressure in the pore space, and \(k\) is the chemical species (e.g.,\(w\), \(c\)). If \(p^{p}\) can be expressed as (Lewis and Schrefler 1987)

$$p^{p} = p^{l} S^{l} + p^{{{\text{Sc}}}} S^{{{\text{Sc}}}} = p^{l} S^{l} + p^{{{\text{Sc}}}} - S^{l} p^{{{\text{Sc}}}} ,$$
(27)

then Eq. (26) can be revised as

$$\psi^{{{\text{pore}}}} = - p^{l} S^{l} - p^{{{\text{Sc}}}} S^{{{\text{Sc}}}} + S^{l} \left( {\mu_{l}^{w} \rho_{l}^{w} + \mu_{l}^{c} \rho_{l}^{c} } \right) + S^{{{\text{Sc}}}} \mu_{{{\text{Sc}}}}^{{{\text{Sc}}}} \rho^{{{\text{Sc}}}} .$$
(28)

2.4.2 Free Energy Density of the Solid Matrix

To calculate the free energy density stored in a solid matrix the free energy of the pore liquid/supercritical \(J\phi \psi^{{{\text{pore}}}}\) is subtracted from the total free energy of the combined rock/liquid/supercritical system, \(\Psi\) (e.g., \(\Psi - J\phi \psi^{{{\text{pore}}}}\)). If the pore volume fraction of the reference configuration is represented as \(\upsilon = J\phi\), the differential term can be expressed as follows:

$$\left( {\left. {\Psi - J\phi \psi^{{{\text{pore}}}} } \right)} \right.^{ \cdot } = \dot{\Psi } - \left( {J\phi \psi^{{{\text{pore}}}} } \right)^{ \cdot } = \dot{\Psi } - \left( {J\phi } \right)^{ \cdot } \psi^{{{\text{pore}}}} - J\phi \dot{\psi }^{{{\text{pore}}}} .$$
(29)

Equations (25) and (28) can be used to convert Eq. (29) to

$$\left( {\left. {\Psi - J\phi \psi^{{{\text{pore}}}} } \right)} \right.^{ \cdot } = tr\left( {{\mathbf{T\dot{E}}}} \right) + p^{p} \dot{\upsilon } - A_{s} \dot{\varsigma }.$$
(30)

The dual potential can be expressed as

$$W = \left( {\Psi - J\phi^{w} \psi_{{\text{pore }}} } \right) - p^{p} \upsilon .$$
(31)

By substituting Eq. (30) into the time derivative of Eq. (31), we obtain

$$\dot{W}\left( {{\mathbf{E}},p^{p} ,\varsigma } \right) = tr\left( {{\mathbf{T\dot{E}}}} \right) - \dot{p}^{p} \upsilon - A_{s} \dot{\varsigma }.$$
(32)

The total deformation energy including reaction-induced energy can be written as:

$$\dot{W}\left( {{\mathbf{E}},p^{p} ,\varsigma } \right) = \left( {\frac{\partial W}{{\partial E_{ij} }}} \right)_{{p^{p} ,\varsigma }} \dot{E}_{ij} + \left( {\frac{\partial W}{{\partial p^{p} }}} \right)_{{E_{ij} ,\varsigma }} \dot{p}^{p} + \left( {\frac{\partial W}{{\partial A_{s} }}} \right)_{{E_{ij} ,p^{p} }} \dot{\varsigma },$$
(33)

where

$$T_{ij} = \left( {\frac{\partial W}{{\partial E_{ij} }}} \right)_{{p^{p} ,\varsigma }} ,\upsilon = - \left( {\frac{\partial W}{{\partial p^{p} }}} \right)_{{E_{ij} ,\varsigma }} ,A_{s} = - \left( {\frac{\partial W}{{\partial \varsigma }}} \right)_{{E_{ij} ,p^{p} }} .$$
(34)

The above equations can be considered as an extension of Maxwell's relations, where Maxwell’s relations are a set of equations that relate the partial derivatives of thermodynamic state functions with respect to their conjugate variables.

The equation frameworks for the stress, pore volume fraction, and chemical potential can be written as

$$\dot{T}_{ij} = L_{ijkl} \dot{E}_{kl} - M_{ij} \dot{p}^{p} - H_{ij} \dot{\varsigma },$$
(35)
$$\dot{\upsilon } = M_{ij} \dot{E}_{ij} + Q\dot{p}^{p} + D\dot{\varsigma },$$
(36)
$$\dot{A}_{s} = H_{ij} \dot{E}_{ij} + D\dot{p}^{p} + Y\dot{\varsigma },$$
(37)

where parameters \(L_{ijkl} ,\,M_{ij} ,H_{ij} ,Y,D\), and \(Q\) are coefficients and can be expressed as

$$\begin{aligned} & L_{ijkl} = \left( {\frac{{\partial T_{ij} }}{{\partial E_{kl} }}} \right)_{{p^{p} ,\varsigma }} = \left( {\frac{{\partial T_{kl} }}{{\partial E_{ij} }}} \right)_{{p^{p} ,\varsigma }} , \\ & M_{ij} = - \left( {\frac{{\partial T_{ij} }}{{\partial p^{p} }}} \right)_{{E_{ij} ,\varsigma }} = \left( {\frac{\partial \upsilon }{{\partial E_{ij} }}} \right)_{{p^{p} ,\varsigma }} , \\ & Q = \left( {\frac{\partial \upsilon }{{\partial p^{p} }}} \right), \\ & H_{ij} = - \left( {\frac{{\partial T_{ij} }}{\partial \varsigma }} \right)_{{E_{ij} ,p^{p} }} = \left( {\frac{\partial A}{{\partial E_{ij} }}} \right)_{{p^{p} ,\varsigma }} , \\ & D = \left( {\frac{\partial \upsilon }{{\partial \varsigma }}} \right)_{{E_{ij} ,p^{p} }} = \left( {\frac{\partial A}{{\partial p^{p} }}} \right)_{{E_{ij} ,p^{p} }} , \\ & Y = \left( {\frac{\partial A}{{\partial \varsigma }}} \right)_{{E_{ij} ,p^{p} }} . \\ \end{aligned}$$
(38)

2.5 Governing Equation for the Mechanical Behavior

Assuming small strain condition yields

$$E_{ij} \approx \varepsilon_{ij} ,\,\,T_{ij} \approx \sigma_{ij} .$$
(39)

Assuming mechanical equilibrium, it can be inferred that \(\frac{{\partial \sigma_{ij} }}{{\partial x_{j} }} = 0\). Moreover, \(L_{ijkl} ,\,M_{ij}\), and \(Q\) are assumed to be material-dependent constants. Moreover, additionally, it is assumed that the material is fully isotropic, and therefore \(M_{ij}\) is diagonal and can be expressed as

$$M_{ij} = \zeta \delta_{ij} ,\,H_{ij} = \omega_{R} \delta_{ij} ,$$
(40)

where \(\zeta\) is Biot’s coefficient. \(Q\& \zeta\) can be expressed as (Heidug and Wong 1996):

$$Q = \frac{\zeta - \phi }{{K^{s} }}\,,\,\,\,\,\zeta = 1 - \frac{K}{{K^{s} }}.$$
(41)

where K and \(K_{s}\) are the bulk modulus and the bulk modulus of the solid matrix, respectively. It is worth mentioning that when the compressibility of the rock matrix is significantly lower than that of the bulk rock (i.e., \(\frac{K}{{K^{s} }} = 0\)), \(\zeta\) can be assumed to be 1.

\(L_{ijkl}\) is the elastic stiffness, and it can be described as a fourth-order isotropic tensor as:

$$L_{ijkl} = G\left( {\delta_{ik} \delta_{jl} + \delta_{il} \delta_{jk} } \right) + \left( {K - \frac{2G}{3}} \right)\delta_{ij} \delta_{kl} ,$$
(42)

where \(G\) is the rock shear modulus. From the assumptions and Eqs. (40) and (42),

$$\dot{\sigma }_{ij} = \left( {K - \frac{2G}{3}} \right)\dot{\varepsilon }_{kk} \delta_{ij} + 2G\dot{\varepsilon }_{ij} - \zeta \dot{p}^{p} \delta_{ij} - \omega_{R} \dot{\xi }\delta_{kl} ,$$
(43)

where \(\omega_{R}\) can be expressed in terms of the bulk modulus, \(K\), as \(\omega_{R} = \omega_{r} K\), where the dissolution-induced stress can be expressed as

$$\dot{\sigma }_{r} = \omega_{r} K\dot{\xi }.$$
(44)

Then,

$$\dot{\sigma }_{ij} = \left( {K - \frac{2G}{3}} \right)\dot{\varepsilon }_{kk} \delta_{ij} + 2G\dot{\varepsilon }_{ij} - \zeta \dot{p}^{p} \delta_{ij} - \omega_{r} K\dot{\xi }\delta_{kl} .$$
(45)

The volumetric strain due to dissolution can be expressed as (Tao et al. 2019)

$$\omega_{r} = \frac{{V^{s} }}{{V_{0}^{s} }} - 1 = \frac{{M^{x} }}{{\rho_{x}^{x} \left( {1 - \phi } \right)}},$$
(46)

where \(V^{s}\) is the current solid volume (i.e., the remaining solid matrix), \(V_{0}^{s}\) is the initial solid volume (before dissolution), \(M^{x}\) is the molar mass of the solid mineral, and \(\rho_{x}^{x}\) is the phase density of the solid mineral.

Then, the governing equation for the solid phase can be described as:

$$G\nabla^{2} {\dot{\mathbf{d}}} + \left( {\frac{G}{1 - 2\theta }} \right)\nabla (\nabla \cdot {\dot{\mathbf{d}}}) - \zeta \nabla \dot{p}^{p} - \omega_{r} \nabla \dot{\xi } = 0,$$
(47)

\(c^{s} = \frac{{\partial S^{l} }}{{\partial p^{c} }}\) is the specific moisture capacity and \(p^{c} = p^{{{\text{Sc}}}} - p^{l}\) is the capillary pressure. The final equation is:

$$G\nabla^{2} {\dot{\mathbf{d}}} + \left( {\frac{G}{1 - 2\theta }} \right)\nabla \left( {\nabla \cdot {\dot{\mathbf{d}}}} \right) - \zeta \nabla \left[ {\left. {\left( {S^{l} + c^{s} p^{c} } \right)\dot{p}^{l} } \right] - \zeta \nabla \left[ {\left( {S^{{{\text{Sc}}}} - c^{s} p^{c} } \right)\dot{p}^{{{\text{Sc}}}} } \right.} \right] - \frac{{M^{x} }}{{\rho_{x}^{x} \left( {1 - \phi } \right)}}\nabla \dot{\xi } = 0.$$
(48)

It is important to note that if the mineralogy changes due to chemical reactions, the overall stiffness of the rock may change including its shear modulus. However, in this research, it is assumed that the shear modulus \(G\) is a constant value and does not change during the chemical dissolution.

Note that the volumetric strain is negative because the solid volume decreases (dissolution). A change in the solid matrix can result in a change in porosity. This relation can be expressed as

$$\dot{\upsilon } = \zeta \dot{\varepsilon }_{ii} + Q\dot{p}^{p} + D\dot{\xi }.$$
(49)

where D can be expressed as

$$D = \frac{{M^{x} }}{{\rho_{x}^{x} }}.$$
(50)

A change in porosity can be expressed as

$$\dot{\upsilon } = \zeta \dot{\varepsilon }_{ii} + \frac{\zeta - \phi }{{K^{s} }}\left[ {\left( {S^{l} + c^{s} p^{c} } \right)\dot{p}^{l} + \left( {S^{{{\text{Sc}}}} - c^{s} p^{c} } \right)\dot{p}^{{{\text{Sc}}}} } \right] + \frac{{M^{x} }}{{\rho_{x}^{x} }}\dot{\xi }.$$
(51)

2.6 Governing Equation for the Fluid Phase Transport

Equation (12) can be used to describe the balance equation for the liquid fluid itself as

$$\left( {\phi S^{l} \rho_{l}^{l} } \right)^{ \cdot } + \phi S^{l} \rho_{l}^{l} \nabla \cdot {\mathbf{v}}^{s} + \nabla \cdot {\mathbf{I}}^{l} - \sum\limits_{\beta \in l} {\chi \nu^{\beta } M^{\beta } \dot{\xi }} = 0.$$
(52)

Equation (52) represents the change in density for the liquid phase, the summation part at the end of the equation take in account the change in density due to chemical reaction (aqueous reactants and products) where \(\beta\) accounts for liquid reactant/product only.

Equations (4) and (14) can be applied to express the Jacobian and Euler identities as \(\dot{J} = J\nabla \cdot {\mathbf{v}}^{s} ,\,\upsilon = J\phi\). Moreover, Eq. (21) can be used to obtain the following equation:

$$\begin{aligned} & \dot{S}^{l} \upsilon \rho_{l}^{l} + S^{l} \left( {\zeta \dot{\varepsilon }_{ii} + Q\dot{p}^{p} + D\dot{\xi }} \right)\rho_{l}^{l} + S^{l} \upsilon \dot{\rho }_{l}^{l} \\ & \quad + \nabla \cdot \rho_{l}^{l} \left[ { - k_{abs} \frac{{k_{rl} }}{{v^{l} }}\left( {\nabla p^{l} - r_{1} \frac{{\rho_{l}^{l} }}{{\rho_{Sc}^{Sc} }}\nabla p^{Sc} - r_{2} \rho_{l}^{l} \left( {\frac{1}{{c^{w} }}\frac{{\partial \mu^{c} }}{{\partial c^{c} }}\nabla c^{c} } \right)} \right)} \right] - \left( {v_{y} M^{Y} \mu^{Y} - v_{z} M^{Z} \mu^{Z} } \right) = 0. \\ \end{aligned}$$
(53)

The displacement variables, \(d_{i} \left( {i = 1,2,3} \right)\), through \(\varepsilon_{ij} = \frac{1}{2}\left( {d_{i,j} + d_{j,i} } \right)\) can be revised as

$$\delta_{ij} \dot{\varepsilon }_{ii} = \nabla \cdot {\dot{\mathbf{d}}}.$$
(54)

Using Eqs. (27), (49), and (54) yields

$$\begin{aligned} & \zeta S^{l} \rho_{l}^{l} \nabla \cdot {\dot{\mathbf{d}}} + \frac{\zeta - \phi }{{K^{s} }}S^{l} \rho_{l}^{l} (S^{l} + c^{s} p^{c} )\dot{p}^{l} + \frac{\zeta - \phi }{{K^{s} }}S^{l} \rho_{l}^{l} (S^{{{\text{Sc}}}} - c^{s} p^{c} )\dot{p}^{{{\text{Sc}}}} + S^{l} \rho_{l}^{l} D\dot{\xi } + \dot{S}^{l} \upsilon \rho_{l}^{l} + S^{l} \upsilon \rho_{l}^{l} \frac{1}{{K^{w} }}\dot{p}^{l} \\ & \quad + \;\nabla \cdot \rho_{l}^{l} \left[ { - k_{{{\text{abs}}}} \frac{{k_{rl} }}{{v^{l} }}\left( {\nabla p^{l} - r_{1} \frac{{\rho_{t}^{l} }}{{\rho_{{{\text{Sc}}}}^{{{\text{Sc}}}} }}\nabla p^{{{\text{Sc}}}} - r_{2} \rho_{l}^{l} \left( {\frac{1}{{c^{w} }}\frac{{\partial \mu^{c} }}{{\partial c^{c} }}\nabla c^{c} } \right)} \right)} \right] - J\left( {v_{y} M^{Y} \mu^{Y} - v_{z} M^{Z} \mu^{Z} } \right) = 0. \\ \end{aligned}$$
(55)

Finally, if \(J = 1\) (small deformation), the final liquid governing equation for the liquid is given as

$$\begin{aligned} & \zeta S^{l} \nabla \cdot {\dot{\mathbf{d}}} + \left( {\frac{\zeta - \phi }{{K^{s} }}S^{l} S^{l} + S^{l} \frac{\phi }{{K^{w} }}} \right)\dot{p}^{l} + \frac{\zeta - \phi }{{K^{s} }}S^{l} S^{{{\text{Sc}}}} \dot{p}^{{{\text{Sc}}}} + \left( { - \frac{\zeta - \phi }{{K^{s} }}S^{l} p^{c} + \phi } \right)\dot{S}^{l} + \frac{{M^{x} }}{{\rho_{x}^{x} }}S^{l} \dot{\xi } \\ & \quad + \left[ { - k_{{{\text{abs}}}} \frac{{k_{rl} }}{{v^{l} }}\left( {\nabla^{2} p^{l} - r_{1} \frac{{\rho_{l}^{l} }}{{\rho_{{{\text{Sc}}}}^{{{\text{Sc}}}} }}\nabla^{2} p^{{{\text{Sc}}}} - r_{2} \rho_{l}^{l} \frac{1}{{c^{w} c^{c} }}\frac{RT}{{M^{c} }}\nabla^{2} c^{c} } \right)} \right] - \frac{{\left( {v_{y} M^{Y} \mu^{Y} - v_{z} M^{Z} \mu^{Z} } \right)}}{{\rho_{l}^{l} }} = 0. \\ \end{aligned}$$
(56)

Similarly, for the supercritical phase,

$$\begin{aligned} & \zeta S^{{{\text{Sc}}}} \nabla \cdot {\dot{\mathbf{d}}} + \left( {\frac{\zeta - \phi }{{K^{s} }}S^{{{\text{Sc}}}} S^{{{\text{Sc}}}} + S^{{{\text{Sc}}}} \frac{\phi }{{K^{{{\text{Sc}}}} }}} \right)\dot{p}^{{{\text{Sc}}}} + \frac{\zeta - \phi }{{K^{s} }}S^{{{\text{Sc}}}} S^{l} \dot{p}^{l} + \left( {\frac{\zeta - \phi }{{K^{s} }}S^{{{\text{Sc}}}} p^{c} + \phi } \right)\dot{S}^{{{\text{Sc}}}} + \frac{{M^{x} }}{{\rho_{x}^{x} }}S^{l} \dot{\xi } \\ & \quad + \;\left[ { - k_{{{\text{abs}}}} \frac{{k_{{r{\text{Sc}}}} }}{{v^{{{\text{Sc}}}} }}\left( {\nabla^{2} p^{{{\text{Sc}}}} - r_{3} \frac{{\rho_{{{\text{Sc}}}}^{{{\text{Sc}}}} }}{{\rho_{l}^{l} }}\nabla^{2} p^{l} - r_{4} \rho_{{{\text{Sc}}}}^{{{\text{Sc}}}} \frac{1}{{c^{w} c^{c} }}\frac{RT}{{M^{c} }}\nabla^{2} c^{c} } \right)} \right] = 0. \\ \end{aligned}$$
(57)

Equation (57) disregards the chemical reaction between carbon dioxide and solid phases because previous studies have shown that such reactions are slow and limited in the presence of gaseous or supercritical carbon dioxide (Lackner et al. 1995; André et al. 2007; Han et al. 2015). Instead, this study focuses solely on the chemical reaction between the fluid phase and solid phase, assuming that the reaction occurs only between the aqueous and solid phases when carbon dioxide dissolves in water to form carbonic acid. As a result, the direct chemical reaction between carbon dioxide in its supercritical phase and solid minerals can be neglected. Nevertheless, while the chemical reaction does not change the gaseous mass or density, it changes the porosity and hence affect the gas transport.

2.7 Governing Equation for the Chemical Phase Transport

Using Eq. (12), we obtain

$$\left( {\phi^{k} \rho_{l}^{k} } \right)^{ \cdot } + \phi^{k} \rho_{l}^{k} \nabla \cdot {\mathbf{v}}^{s} + \nabla \cdot {\mathbf{I}}^{k} - \chi \nu^{k} M^{k} \dot{\xi } = 0,$$
(58)

for small deformation (\(J = 1\)), with Eq. (6),

$$\left( {\phi S^{l} \rho_{l}^{k} } \right)^{ \cdot } + \nabla \cdot {\mathbf{J}}^{k} + \nabla \cdot \left( {\rho_{l}^{k} {\mathbf{u}}^{l} \, } \right) - \chi \nu^{k} M^{k} \dot{\xi } = 0,$$
(59)

The liquid phase is assumed to be incompressible, if the mass fraction is defined as \(c^{k} = \frac{{\rho_{l}^{k} }}{{\rho_{l}^{l} }}\), then the chemical transport governing equation for the solute can be expressed as

$$\phi S^{l} \rho_{l}^{l} \dot{c}^{k} + \nabla \cdot {\mathbf{J}}^{k} + \rho_{l}^{l} {\mathbf{u}}^{l} \cdot \nabla c^{k} - \chi \nu^{k} M^{k} \dot{\xi } + c^{k} \sum\limits_{k} {\chi \nu^{k} M^{k} \dot{\xi }} = 0.$$
(60)

where the superscript is the different chemical solutes in general form.

The key novelty of this study lies in the incorporation of additional terms into the mechanical, liquid, and gas/supercritical phases. To the best of our knowledge, these terms have never been used in two-phase flow governing equations to couple chemical reactions to a hydromechanical model for carbon capture and storage applications.

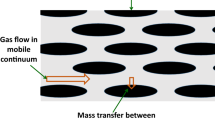
For the mechanical Eq. (48), the term \(\frac{{M^{x} }}{{\rho_{x}^{x} \left( {1 - \phi } \right)}}\nabla \dot{\xi }\) represents the effect of chemical reactions on the strain, providing relief for the strain in dissolution cases. In the liquid and gas/supercritical phases, \(\frac{{M^{x} }}{{\rho_{x}^{x} }}S^{l} \dot{\xi }\) is derived from \(D\dot{\xi }\), which is the coupling effect of chemical reactions on porosity. This term reflects the impact of chemical reactions on liquid and gas/supercritical flows through changes in porosity. Equation (51) shows that porosity is also affected by changes in pressure and strain. For the liquid phase, \(\left( {v_{y} M^{Y} \mu^{Y} - v_{z} M^{Z} \mu^{Z} } \right)\) represents the chemicals added to the aquatic phase resulting from solid dissolution in liquid flow. Figure 1 demonstrates some of the cross-coupling relations of the HMC coupled model.

Fig. 1
figure 1

Cross couplings relations of the HMC model: 1. Change due to strain term \(\zeta \dot{\varepsilon }_{ii}\), 2. Effect the mechanical properties, 3. Change due to pore pressure term \(Q\dot{p}^{p}\), 4. Effect the pore pressure, 5. Change due to chemical reaction term \(D\dot{\xi }\), 6. Change in reactive surface area

Full size image

3 Validation and Comparison with Other Models

The final governing Eq. (48) for the solid, Eq. (56) for the liquid, and Eq. (57) for the supercritical phases present more comprehensive framework based on a rigorous mathematical derivation. This is in contrast to the equations presented by Abdullah et al. (2022), which serve as a special case of the present study, excluding considerations of dissolution and dynamic porosity. When compared with the renowned two-phase transport model by Schrefler and Scotta (2001), the fluid equations exhibit similarities. However, their model omits the effects of chemical reactions (dissolution), solute transport, and energy losses due to friction between the two-phase flow; barring these elements, the equations appear congruent Notably, the chemical dissolution term in the equations parallels that in the governing equation of (Yue et al. 2022), where one-phase transport dissolution effects are captured. This is also in line with the governing equation modeled by (Karrech 2013). Fall et al. (2014) did account for a two-phase flow but regrettably overlooked the chemical reaction aspect. Their governing equation resonates with the one proposed in this study, but it lacks the chemical reactive term. Conversely, their model can manage the effects of plasticity, which is not considered in the present model. In summary, the governing equation introduced in this study incorporates basic two-phase flow coupling terms, as validated in previous research by Lewis and Schrefler (1987), Schrefler and Scotta (2001), and Abdullah et al. (2022). Additionally, this equation integrates chemical dissolution effects, which have been partially addressed in single-phase flow studies such as those by Karrech (2013) and (Ma et al. 2022). For further refinement, it would be beneficial to test these equations against empirical data in future studies, enhancing our understanding of the coefficients' empirical values.

The following simulation investigates the fully coupled effect, focusing on the coupling effect of pressure, strain, and chemical dissolution on porosity change.

4 Numerical Simulation

Numerical simulations will be used for the demonstration purpose of the novel coupled equations derived in this paper. In the numerical section, the focus will be on how the chemical reaction will affect the two-phase pressure, saturation, strain and porosity. To simplify the discussion, only one chemical reaction leading to dissolution is considered. Additionally, as the objective of the simulation is to emphasize the novel aspects of the equations, and since the presence of salt in saline water does not significantly affect the chemical reaction, the simulation will employ pure water instead of saline water to exclude any potential confounding effects of salt. The primary chemical reaction has been described in Zerai et al. (2006) as follows:

$${\text{CaCO}}_{{3}} + {\text{H}}_{{2}} {\text{O}} + {\text{CO}}_{{2}} \Rightarrow {\text{Ca}}^{{{2} + }} + {\text{2HCO}}_{{3}}^{ - } .$$
(61)

In addition to the term \(\frac{{M^{x} }}{{\rho_{x}^{x} \left( {1 - \phi } \right)}}\nabla \dot{\xi }\) in the general governing equation for the solid phase, three primary coupling terms have a direct implication on two-phase flow through porosity change, as described in Eq. (51). These terms are mechanical strain, pore pressure, and chemical reaction.

4.1 Study Subject and Geometry

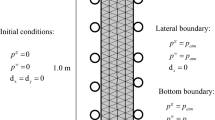
To investigate the effects of these terms, a conceptual model, consisting of a block of carbonate rock that contained calcite, with dimensions of 50 cm in length and 20 cm in height, has been created. \({\text{CO}}_{{2}}\) under supercritical conditions is injected through the semi-saturated sample rock that has an initial water saturation of \(\left( {S^{w} } \right)_{i}\) = 61.9% for a time \(t\). The system is assumed to be under isothermal condition with a temperature of \(T = 350\;{\text{K}}\). Figure 2 shows the initial and boundary conditions of the system and the mesh geometry/ horizontal cross-section line along with cut point 1.

Fig. 2
figure 2

Initial and boundary conditions for two-phase flow into carbonate rock sample

Full size image

The dissolution of calcite by carbon dioxide has been extensively investigated (Plummer and Wigley 1976; Gaus et al. 2005; Kaufmann and Dreybrodt 2007; Izgec et al. 2008; Matter et al. 2009; Xu et al. 2010; Van Pham et al. 2012; Peng et al. 2015; Gray et al. 2016; Siqueira et al. 2017). Calcite usually exists widely in limestone formation but not in other formations with less quantity, such as in shale formations (Gaus et al. 2005), carbonate deep saline aquifers (Izgec et al. 2008), and basaltic rocks (Van Pham et al. 2012). This model is assumed to be a calcite-rich rock. The parameters used in the model are listed in Table 1. A finite element general solver (COMSOL Multi-Physics®) is used to solve the system. The reaction rate (dissolution rate) is highly dependent on the temperature and pH level in the fluid (Matter et al. 2009). The kinetics of the reaction rate is expressed as (Steefel and Lasaga 1994)

$$r = k_{{{\text{rate}}}} {\text{Area}}\left( {1 - \left( {\frac{Q}{{K_{{{\text{eq}}}} }}} \right)^{\theta } } \right)^{n} ,$$
(62)
Table 1 Physical parameters used in the conceptional model (Hart and Wang 1995; Parkhurst and Appelo 2013; Zhou and Burbey 2014)
Full size table

The variable \(r\) in the equation above represents the rate of dissolution in moles per unit volume of porous media, \({\text{Area}}\) is the reaction surface area, \(Q\) is the \(C_{{\text{a}}}^{ + }\) ions activity product, \(K_{{{\text{eq}}}}\) is the equilibrium constant, \(\theta\) and \(n\) are constants, which are set as 1, and \(k_{{{\text{rate}}}}\) is the dissolution rate constant defined as (Steefel and Lasaga 1994)

$$k_{{{\text{rate}}}} = k_{r25} \exp \left[ { - \frac{{E_{{\text{a}}} }}{R}\left( {\frac{1}{T} - \frac{1}{298.15}} \right)} \right],$$
(63)

where \(k_{r25}\) is the rate constant at \(25\;^{ \circ } {\text{C}}\), \(E_{{\text{a}}}\) is the activation energy, \(R\) is the gas constant, and \(T\) is the temperature (\(T =\) 350 K). The following correlation can be used to calculate the equilibrium constant for calcite minerals at given temperature (Plummer and Busenberg 1982):

$$\log \left( {K_{{{\text{eq}}}} } \right) = - 1228.732 - 0.299444\left( T \right) + \frac{35512.75}{T} + 485.818 \times \log (T).$$
(64)

According to (Lee and Morse 1999; Gaus et al. 2005), the reactive surface area for calcite in limestone \({\text{Area}}\) is approximately \(6.71 \times 10^{ - 2} \;{\text{m}}^{2} /{\text{g}}.\) The molar volume of calcite is \(36.93 \times 10^{ - 6} \,{\text{m}}^{3} /{\text{mol}}.\) \(E_{{\text{a}}}\) and \(k_{r25}\) have been extracted from literature as \(k_{r25} =\)\(1.6 \times 10^{ - 9} \;{\text{mol}}\;{\text{m}}^{2} \;{\text{s}}^{1}\) and \(E_{{\text{a}}} =\) 41.87 kJ/mol (Xu et al. 2003).

For liquid saturation calculations, the Van Genuchten relationship is used. This relationship is a widely used model in soil science and hydrology that describes the relationship between the volumetric water content of soil and soil water potential. It can be used to predict water movement in soils and rocks, estimate soil hydraulic properties, and simulate soil–water–plant interactions, as in the following (Ma et al. 2020):

$$k_{rl} = (S^{l} )^{0.5} \times \left[ {1 - \left( {1 - \left( {S^{l} } \right)^{\frac{1}{m}} } \right)^{m} } \right]^{2} ,$$
(65)
$$k_{{r{\text{Sc}}}} = (1 - S^{l} )^{0.5} \times \left[ {1 - \left( {1 - \left( {1 - S^{l} } \right)^{\frac{1}{m}} } \right)^{m} } \right]^{2} ,$$
(66)
$$S^{l} = \left[ {\left( {\frac{{\left| {p^{c} } \right|}}{M}} \right)^{{\frac{1}{1 - m}}} + 1} \right]^{ - m} ,$$
(67)

where \(M\) and m are Van Genuchten parameters related to pore size and shape. For this simulation, the values have been estimated as \(M = 500\,{\text{kPa}}\) and \(m = 0.43\) (Van Genuchten 1980; Rutqvist et al. 2002).

Finally, the change in permeability can be obtained using Kozeny–Carman relation (Bitzer 1996; Xu et al. 2003):

$$k_{{{\text{abs}}}} = \left( {k_{{{\text{abs}}}} } \right)_{i} \times \left( {\frac{\phi }{{\phi_{i} }}} \right)^{3} \left( {\frac{{1 - \phi_{i} }}{1 - \phi }} \right)^{2}$$
(68)

where \(\left( {k_{{{\text{abs}}}} } \right)_{i}\) and \(\phi_{i}\) are the initial instinct permeability and initial porosity, respectively.

4.2 Simulation Assumptions

For the simulation, assumptions are made to ensure stability and simplify some computational issues: (I) the rock is assumed to have a high percentage of calcite, which maintains the dissolution reaction for the entire simulation time; (II) the energy dissipation due to solute transport and the friction between the two-phase flow are zeros (\(r_{1} ,\,r_{2} ,\,r_{3}\), and \(r_{4}\) in Eqs. (56) and (57) are zeros); (III) because the sample is small in size and reaches the equilibrium phase rapidly, the initial intrinsic permeability is assumed to be extremely small \(\left( {k_{{{\text{abs}}}} = 1.4 \times 10^{ - 17} \;{\text{m}}^{2} } \right)\) in order to hold back the pressure for a longer time; (IV) although the liquid in the formation is assumed to contain dissolved carbon dioxide (carbonic acid), the properties of the liquid have been approximated as those of liquid water.

4.3 Results and Discussion

This study simulates the two-flow injection for 2000 h. Figures 3, 4 and 5 show the liquid pressure, supercritical pressure, and solid deformation, respectively, across the sample distance. Because the sample size is relatively small, the simulation time is approximately 2000 h or 83.3 d. The liquid and supercritical pressures show the increase in the pressure across the sample rocks before it stabilizes. Because of the assumed chemical reaction in Eq. (61), part of the solid matrix is dissolved, suggesting that the porosity will continue to increase until the solubility equilibrium is reached. Figure 5 presents the horizontal displacement within the cross-section line (shown in Fig. 2) of the sample rock. The displacement starts at a higher value and decreases with time, this is because the differential pressure is high at the beginning especially at the left boundary, then, the pressure starts to equalize through the pores of the specimen and therefore the displacement decrease. Furthermore, the deformation is relatively small because the Young’s modulus is high (33 GPa).

Fig. 3
figure 3

Liquid pressure across the horizontal distance of the sample rock

Full size image
Fig. 4
figure 4

\({\text{CO}}_{{2}}\) pressure across the horizontal distance of the sample rock

Full size image
Fig. 5
figure 5

Horizontal displacement across the horizontal distance of the sample rock

Full size image

Figure 6 displays the concentration of calcium ions that dissolve in the sample rock at different time spans. The initial value of the concentration on the left boundary was assumed to be zero. Thus, the concentration started at zero and increased while moving to the right side of the sample. As expected, the concentration increased with time during the chemical reaction and calcium ions increased. Figures 7 and 8 depict the liquid and supercritical \({\text{CO}}_{{2}}\) saturation distribution across the sample rock cross section at different times. At the start of the simulation, the water/liquid saturation starts at 61.9% and then the \({\text{CO}}_{{2}}\) starts to flow from the left side to the right, and the liquid saturation starts to decrease. The liquid saturation in this study is completely dependent on the capillarity pressure, \(p^{c}\), as per Van Genuchten (1980) relations shown in Eqs. (65)–(67). Figure 9 shows the change in porosity and permeability over time at Point 1, which is located in the middle of the sample. The results show that the permeability at this point will almost double within 2000 h.

Fig. 6
figure 6

Concentration of \({\text{Ca}}^{ + }\) across the horizontal distance of the sample rock

Full size image
Fig. 7
figure 7

Liquid saturation across the horizontal distance of the sample rock

Full size image
Fig. 8
figure 8

\({\text{ScCO}}_{{2}}\) saturation across the horizontal distance of the sample rock

Full size image
Fig. 9
figure 9

Porosity and permeability change at Point1 of 2D sample rock

Full size image

Figures 10 and 11 show the three primary factors influencing porosity change according to Eq. (49). Compared with pressure and mechanical strain, the chemical reaction has the greatest impact on porosity. Fig. 10 presents a comparison between the chemical coupling term and the strain term, \(\zeta \dot{\varepsilon }_{ii}\), indicating that the chemical reaction has a more significant impact on porosity change than mechanical strain. Similarly, Fig. 11  presents a comparison between the chemical term and the pressure term, \(Q\dot{p}^{p}\),showing that the chemical reaction has a greater effect on porosity than pressure. The effects of the pressure and strain terms are relatively similar. Figure 12 compares the effects of liquid pressure, supercritical pressure, and the extent of reaction on the volumetric strain at Point 1 in the 2D rock sample. As the strain increases, the extent of reaction undergoes exponential changes, emphasizing the importance of considering the coupling between chemical reactions and mechanical behavior. In Fig. 13, it can be seen that the dissolution rate at across the horizontal section of the sample decreases as it approaches kinetic equilibrium. While the simulation results from this model are insightful, assumptions underpinning the model introduce certain limitations. Key among these is the presumption that the chemical solute exists solely in the liquid phase (saline water) and remains chemically inert, with the supercritical phase of carbon dioxide also being treated as non-reactive. This implies that any interactions between the supercritical and solid phases are not captured by the model. Further, the system is considered immiscible, meaning that there's no mass exchange between the liquid and supercritical phases via dissolution. This phenomenon, which is anticipated to be prevalent in actual carbon sequestration processes, is interlinked with temperature changes and variations in the pH levels of the liquid phase, both of which influence the rate of chemical reactions. An additional limitation arises from the model's assumption of isothermal conditions and treating the porous medium as an isotropic material, potentially deviating from real-world scenarios.

Fig. 10
figure 10

Comparison between the porosity change due to strain term and chemical reaction term across the horizontal distance of the sample rock

Full size image
Fig. 11
figure 11

Comparison between the porosity change due to pressure term and chemical reaction term across the horizontal distance of the sample rock

Full size image
Fig. 12
figure 12

Effects of liquid pressure, supercritical pressure, and the extent of reaction on the volumetric strain at Point 1 in the 2D rock sample

Full size image
Fig. 13
figure 13

Dissolution rate at across the horizontal section of the sample rock

Full size image

5 Conclusion

In this study, a novel approach for modeling a reactive multi-phase hydro-mechanical chemical system for carbon dioxide sequestration using coupling mixture theory was presented. Addressing the gap in the coupled relationship between chemical and mechanical properties, we linked it to stress/strain. The extent of the reaction and solid affinity were employed in the model, spotlighting the interplay of chemical reactions within the hydromechanical framework.

Simulations under isothermal conditions on limestone rock samples highlighted the significant role of chemical reactions in dictating changes in porosity and mechanical strain within geological formations. Observable changes in liquid pressure, supercritical pressure, solid deformation, and porosity over time emphasized the primary influence of chemical reactions. This research serves as a foundational benchmark for the carbon sequestration domain. Offering a holistic lens, it enables professionals and researchers to better understand chemical reactions' influence on the hydromechanical attributes of geological formations, paving the way for more strategic carbon sequestration decisions.

While promising, the proposed model operates under certain constraints, notably assumptions of zero energy dissipation due to solute transport, friction between the two-phase flow, and the approximation of liquid properties to water. Future research should delve into integrating thermal coupling, precipitation processes, and accounting for mass transfer between gas and the liquid phase to further refine the model's precision and applicability.