1 Introduction

In situ recovery (ISR), also known as in situ leaching, is a technically and commercially feasible method for the extraction of minerals from high-grade ore bodies in a radically different way to conventional mining (Paul 1989; Seredkin et al. 2016; Vargas et al. 2020). ISR is the circulation of lixiviants through subsurface mineralized ore fractures to dissolve valuable minerals, especially metal minerals, without physically destroying ore formations (Ahlness and Pojar 1983; Bates and Jackson 1987; Council et al. 2002; Sinclair and Thompson 2015). Compared with conventional mining, ISR has several advantages: (1) it eliminates mining costs, costs for removing ores and fragments to surface dumps, and costs of storage/disposal of tailings (Seredkin et al. 2016; (2) it exhibits reduced noise levels and lower greenhouse gas emissions (Sinclair and Thompson 2015), and (3) it creates a safer working environment for mine workers. Starting in the early 1970s, ISR was developed and applied for uranium extraction from roll-front sandstone deposits, particularly in Kazakhstan and Uzbekistan (Seredkin et al. 2016; Kuhar et al. 2018; Lagneau et al. 2019; Zhou et al. 2020). To date, ISR has been extensively applied in the production of other metals, such as copper, gold, and lithium (O’Gorman et al. 2004; Seredkin et al. 2016). Unlike sandstone deposits that contain many pores and fractures, the host formations for many metallic minerals are mainly low-permeability consolidated hard rocks. Therefore, it is difficult to inject lixiviant into hard rock formations by hydraulic force, which presents challenges for ISR and results in low recovery rates (Sinclair and Thompson 2015).

To resolve the issue of the limited permeability of hard rock formations, electrokinetic (EK) ISR (EK-ISR) has been proposed to enhance ion transportation within low-permeability formations via the application of an external electric potential (Martens et al. 2018, 2018, 2021). EK is a mature technology that has been applied in many engineering fields, including soil remediation (Virkutyte et al. 2002), wastewater treatment (Yuan and Weng 2006), and mine tailing remediation (Baek et al. 2009). For conventional ISR, flow is governed by hydraulic pressure gradients, whereby only a few preferential flow paths can be swept, which makes ISR highly unstable and unpredictable, as these preferential flow paths may host only a small fraction of the total metals (Sinclair and Thompson 2015; Martens et al. 2021). In EK-ISR, electric potential induces a more homogeneous flow through the heterogeneous ore. Therefore, EK-ISR is currently considered a promising method for the recovery of various metals, including gold and copper, from intact hard rocks (Martens et al. 2018, 2018, 2021). EK-ISR, however, has not yet been applied in any mining project and thus requires further experimental and numerical work to better understand its efficacy for specific physicochemical subsurface environments and rock surface properties. Until recently, several researchers experimentally and numerically studied EK transport in porous media and EK-ISR (Chowdhury et al. 2017; Alizadeh et al. 2019; Sprocati et al. 2019; Tripathi et al. 2020; Martens et al. 2021; Gill et al. 2021; Sprocati and Rolle 2022; Karami et al. 2022). Particularly, (Chowdhury et al. 2017; Gill et al. 2021) studied the electrokinetic permanganate delivery in low-permeable porous media and found that electrokinetics significantly enhanced fluid permanganate delivery. (Karami et al. 2022) conducted lab-scale experiments on EK-ISR with different voltage and pressure fields and (Martens et al. 2021) used COMSOL Multiphysics coupled with Phreeqc to perform a continuum-scale simulation of EK-ISR. However, to our best knowledge, the pore-scale study of EK-ISR is still lacking. Considering that hard rock is a low-permeable system where lixiviant can only flow through fractures, the pore-scale characterization of the process is non-trivial. The pore-scale study can be potentially performed with micro-CT imaging that captures the 3D information of the fractures and metal minerals as well as a large-domain pore-scale direct simulation for modeling the flow in real porous media obtained by micro-CT image (McClure et al. 2014; Da Wang et al. 2019; Ali et al. 2020; Xiao et al. 2021). The information extracted from the digital twin study can be used for the upscaling study.

The main transport mechanisms of EK-ISR include (1) electromigration, which involves the displacement of charged species towards an electrode of opposite charge, and (2) electroosmotic flow (EOF), which represents the net movement of fluid flow as a result of the excess charge adhered to the mineral surface (Acar and Alshawabkeh 1993). For traditional ISR, the ore body is subjected to external hydrostatic pressure, which causes a pressure gradient between the inlet and outlet. This gradient propels the fluid through the pore space, carrying the ions. Conversely, for EK-ISR, an external electric potential is applied to the ore body. Instead of fluid flow, the ions near the naturally charged solid surface start to move under the electric potential gradient. The ion migration generates the local net charge, and the charged solid surface creates EOF at the solid–fluid interface. Both of these local flows contribute to the overall fluid flow.

The electrical double layer (EDL) plays a key role in EOF. The EDL consists of a charged solid surface and a thin layer of counter ions in an aqueous solution. As counter ions in the EDL move towards the oppositely charged electrode, momentum is transferred to the surrounding fluid molecules, thereby inducing flow (Acar and Alshawabkeh 1993). The Helmholtz–Smoluchowsky equation (HS) is commonly used to determine EOF in porous media, and its application depends on the thickness of the EDL (Acar and Alshawabkeh 1993; Wang and Chen 2007; Zhang and Wang 2017). Most studies in the literature assume a thin double layer, which means that the thickness of the EDL is considerably smaller than the pore size (Wang and Chen 2007; Zhang and Wang 2017). The counter ions of the EDL screen the wall charge within a region that scales with Debye length (Pennathur and Santiago 2005). In addition, the thickness of the EDL varies with the electric potential at the particle surface. The zeta potential is a way to characterize the EDL based on the ionic concentration in the EDL and the pH as a result of the protonation/deprotonation reactions that occur at the particle surface (Vane and Zang 1997; Lima et al. 2008; Zhang and Wang 2017; Khoso et al. 2019; Liu et al. 2010). Other essential procedures and parameters for EK including geochemical reaction and local pH distribution as well as some larger-scale factors such as tortuosity and porosity were characterized for fluid-solid systems (Mattson et al. 2002; Appelo and Wersin 2007; Al-Hamdan and Reddy 2008; Storey and Bazant 2012; Zhang and Wang 2017; Sprocati et al. 2019; Sprocati and Rolle 2020; Priya et al. 2021). Geochemical reactions change ion composition and concentration and therefore, changes the thickness of EDL and zeta potential (Pengra and Wong 1996; Al-Hamdan and Reddy 2008). The dissolution of the mineral during the reaction will change the porous structure and flow pattern. These changes due to geochemical reactions influence the electroosmotic permeability and electromigration. Considering EK-ISR, the ionic concentration is high and its effect on the ion transport becomes non-trivial. Meanwhile, the local pH heterogeneity causes the heterogeneity of zeta potential and results in a nonlinear response of the electroosmotic velocity. With a significant change of pH, the zeta potential might be reversed and results in the reversed electroosmotic velocity (Zhang and Wang 2017). Tortuosity and porosity provide the morphological information of the porous ore and provide the bridge to study the micro-scale and macro-scale relationship for future upscaling (Yeung 1994; Pengra and Wong 1995; Pengra et al. 1999). (Pengra et al. 1999) compared the permeability estimated by EK and generated from flow experiments, the two permeability values are consistent after reconciling through the hydraulic tortuosity. (Alizadeh et al. 2019; Sprocati and Rolle 2022) studied the effect of the heterogeneity porosity on the EK and found that the porous heterogeneities play an important role in EK and the coupling to hydraulic process.

Most of the metal ore formation for ISR is presumably composed of a low porosity-permeability hard rock system, with only thin fractures presented (Seredkin et al. 2016; Lagneau et al. 2019). However, it is still unclear what are the sizes of the fractures in the underground ore formation and whether it overlaps with EDL thickness or not. Considering that the Debye length can vary from a few nanometers to a few micrometers, we presume that both unresolved and resolved regions would exist in the system. For those connected thin fractures (mainly connected to larger fractures), the velocity front for the lixiviant changes from plug-shape into parabolic-shape (Zhang and Wang 2017). For a negatively-charged mineral surface in the fracture, the flow velocity toward the cathode is lower near the mineral surface. Therefore, to understand EOF in EK-ISR, the thickness of the EDL and zeta potential must be characterized based on the chemical condition of the ore. EOF in microchannels has been extensively studied because of its significant applications in EK remediation (Acar et al. 1995; Alshawabkeh et al. 1999; Pamukcu and Kenneth Wittle 1992; Reddy and Saichek 2004). However, most studies are based on simplified pore-structure models (Wang and Chen 2007; Wang et al. 2006; Zhang and Wang Jan. 2017; Alizadeh et al. 2021). (Wang et al. 2006) developed a numerical method to simulate electroosmotic flow in a 2D microchannel, which consisted of the combination of nonlinear Poisson equation for the electric potential with lattice Boltzmann method (LBM) for fluid flow (Wang et al. 2006; Yoshida et al. 2014; Basu et al. 2020; Li et al. 2021). Most EK studies using LBM are based on simultaneously solving the Poisson, Nernst–Planck, and Navier–Stokes equations in a self-consistent scheme. (Wang et al. 2006) studied the effect of electrically-driven and pressure-driven flows on flow velocity, electro-viscous effect, and electroosmosis in homogeneous microchannels. The LBM has also been used to study EOF in a heterogeneous pore structure reconstructed using random porous structures (Zhang and Wang 2017). They studied the effects of the heterogeneous zeta potential at the mineral-liquid interface at different pH values and reported that for a small electric potential strength, the effect of the electrical force on the distribution of pH causes a nonlinear response in the electroosmotic velocity. Such studies are examples of the successful application of numerical schemes based on the LBM to analyze EK flows. However, these studies mainly focused on the fundamental physical perspective of EOF and used manually generated porous media as the study domain. At the same time, the effect of EOF on the flow behavior in a realistic 3D porous media has not yet been investigated.

Herein, we developed an EK model for the simulation of the physical transport of fluid and ions for EK using the lattice Boltzmann–Poisson method (LBPM) based on the fundamental principles of surface chemistry and EK transport. Compared to COMSOL Multiphysics, our EK model with LBPM has the ability to handle complex geometry (3D porous media generated by micro-CT in this study), unlike the previous studies using COMSOL Multiphysics that only used simple geometries (Sprocati et al. 2019; Martens et al. 2021; Sprocati and Rolle 2022). The model is also highly parallelizable and distributed across GPUs, enabling faster simulations and scalability to larger domains. The governing model includes three coupled equations: (1) Poisson equation, (2) Nernst–Planck equation, and (3) Navier–Stokes equation. In this study, we describe the main workflow of our model and validation in terms of electroosmosis. Meanwhile, a more complex chalcopyrite-silica system is investigated and the efficacy of ion transport under various EK conditions and mineral distributions is evaluated. Specifically, the EK model based on LBPM was first validated against COMSOL Multiphysics in terms of EOF in cases where the EDL is both resolvable and unresolvable in a 2D microchannel. After validation, a chalcopyrite-silica system was created by mixing silica and chalcopyrite powders. The synthetic ore was imaged using high-resolution X-ray micro-computed tomography (micro-CT), which allowed the visualization of the 3D structure and mineral distribution within the system and subsequent direct simulation with LBPM. Overall, the proposed model was designed to investigate the transport of fluid/ions to the target metals under electric potential at the pore scale. For future work, considering the importance of surface potential in this study, a surface complexation model is planned to be introduced to characterize zeta potential at liquid–solid interfaces. The proposed model can be coupled with a geochemical solver such as PhreeqcRM (Parkhurst 1995; Parkhurst and Appelo 1999; Parkhurst and Wissmeier 2015) for the full characterization of the physical-chemical process in the EK-ISR.

2 Materials and Methods

2.1 Numerical Methods

The governing model of the EK flow includes three coupled equations: Poisson equation for the electric potential, Nernst–Planck equation for ion transport driven by chemical and electric potentials, and Navier–Stokes equation for the flow of an electrolyte solution carrying ions.

2.1.1 Mathematical Models

The flow of the electrolyte solution is governed by the incompressible conservation of mass and Navier–Stokes equations:

$$\begin{aligned} \begin{aligned} \nabla \cdot {\varvec{u}}&= 0, \\ \rho _0 \frac{\partial {\varvec{u}}}{\partial t} + \rho _0 {\varvec{u}} \cdot \nabla {\varvec{u}}&= -\nabla p + \mu \nabla ^2 {\varvec{u}} + {\varvec{F}}, \end{aligned} \end{aligned}$$
(1)

where \({\varvec{u}}\) is the fluid velocity vector, \(\rho _0\) is the fluid density, p is the fluid pressure, \(\mu\) is the dynamic viscosity, and \({\varvec{F}}\) is the body force, which in this study is primarily caused by an external electric potential. The Navier–Stokes equations were solved in pore spaces, whereas a standard nonslip boundary condition was applied to the solid spaces. In the case where the thickness of the EDL was much smaller than the characteristic length of the simulation, an electroosmotic velocity boundary condition was introduced in the EDL which excluded the detailed flow field between the solid and slipping plane, and analytically calculated the velocity at the solid according to the local zeta potential of the solid surface. Herein, we adopted the commonly used HS equation:

$$\begin{aligned} {\varvec{u}} = - \frac{\epsilon \zeta }{\mu } \nabla _T \psi ,\;\; \text {for}\; {\varvec{x}} \in \partial \Omega , \end{aligned}$$
(2)

where \(\Omega\) denotes the fluid domain, \(\psi\) is the electric potential within the electrolyte, \(\zeta\) is the local zeta potential of the solid surface, \(\epsilon\) is the permittivity of the electrolyte solution, and \(\nabla _T\) is the tangential part of the gradient operator, perpendicular to the solid surface orientation. When the electroosmotic velocity boundary condition is applied as the driving force of the flow, the electric body force in Eq. 1 is set to zero, because the EDL is below resolution and the bulk fluid is considered electrically neutral (Zhang and Wang 2017). The key assumption of the HS boundary condition, besides the thin EDL assumption, is that the surface potential is small. Thus, the local conductivity and electric field due to surface ion distribution are only slightly perturbed. The HS boundary condition has two inputs: the externally applied electric field and the zeta potential, where the latter can be seen as a lumped parameter that characterises the electric properties of the Stern layer (i.e. the thin layer of immobile surface-induced charges). It strongly depends on the liquid and solid interfacial properties, including the material types and impurities of the solid surface and its solubility in the solvent, pH, electrolyte concentration and valence, and the specific types of chemical reactions performed at the interface. In our solver, one can adjust the relative strength due to the charged surface with respect to that due to the externally applied field by varying zeta potentials. Meanwhile, the zeta potential setting is flexible and supports either user-defined voxel-by-voxel mapping of experimentally measured zeta potentials or incorporations of sophisticated surface complexation models (Zhang and Wang 2017) that can compute localized zeta potentials as a function of pH and ion concentrations at the solid surface.

Ion transport is governed by the Nernst–Planck equation, which incorporates electrochemical migration as an extra drift term into the mass flux under the assumption that the short-range interactions among ions were negligible since the probability of two ions getting close is relatively small:

$$\begin{aligned} \frac{\partial C_i}{\partial t} + \nabla \cdot \left[ \left( {\varvec{u}} - \frac{z_i D_i}{V_T} \nabla \psi \right) C_i \right] = D_i \nabla ^2 C_i, \end{aligned}$$
(3)

where \(C_i\) is the concentration of the ith ion, \(z_i\) is the ion algebraic valency, and \(V_T=k_B T/e\) is the thermal voltage, where \(k_B\) is the Boltzmann constant and e is the electron charge. The ion mass flux is affected by three factors: the first and second terms on the left-hand side of Eq. 3, which are the convection and electrochemical migration, respectively; the term on the right-hand side is the diffusion where \(D_i\) is the diffusivity of the ith ion.

A non-flux boundary condition at the fluid-solid interface was applied to the ions:

$$\begin{aligned} {\varvec{n}}_s \cdot {\varvec{J}}_i = 0,\;\; \text {for}\; {\varvec{x}} \in \partial \Omega , \end{aligned}$$
(4)

where \({\varvec{n}}_s\) is the unit normal vector of the solid surface, and \({\varvec{J}}_i = -D_i \nabla C_i + ({\varvec{u}}-z_i D_i/V_T \nabla \psi ) C_i\) is the flux of the ith ion.

The electric potential of the distribution of excess ions was solved by the Poisson equation:

$$\begin{aligned} \nabla ^2 \psi = - \frac{\rho _e}{\varepsilon _r \varepsilon _0}, \end{aligned}$$
(5)

where \(\varepsilon _0\) is the permittivity of vacuum, and \(\varepsilon _r\) is the dielectric constant of the electrolyte solution. The net charge density \(\rho _e\) (C/m\(^3\)) is related to the ion concentration as follows:

$$\begin{aligned} \rho _e = \sum _i F z_i C_i, \end{aligned}$$
(6)

where the sum runs over all ionic species and F is Faraday’s constant given by \(F=e N_A\), where \(N_A\) is Avogadro’s number. The force on the body owing to the net charge density in the Navier–Stokes equation is given by:

$$\begin{aligned} {\varvec{F}}_e = \rho _e {\varvec{E}} =- \rho _e \nabla \psi . \end{aligned}$$
(7)

The fluid–solid boundary condition for the electric potential is typically specified in two forms: 1) the surface charge density \(\sigma _e\) and 2) surface potential \(\psi _s\) at the solid surface (when the EDL is unresolved, the surface potential is equivalent to the zeta potential). The former is a Neumann-type boundary condition given by

$$\begin{aligned} {\varvec{n}}_s \cdot \nabla \psi = - \frac{\sigma _e}{\varepsilon _r \varepsilon _0}, \;\; \text {for}\; {\varvec{x}} \in \partial \Omega , \end{aligned}$$
(8)

whereas the latter is a Dirichlet-type boundary given by

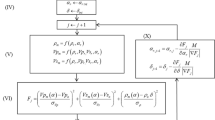
$$\begin{aligned} \psi ({\varvec{x}}) = \psi _s,\;\; \text {for}\; {\varvec{x}} \in \partial \Omega , \end{aligned}$$
(9)

where \(\psi _s\) is the user-specified electric potential of the solid surface. A detailed flowchart of how these equations were solved is shown in Fig. 1.

Fig. 1
figure 1

Flow chart for the proposed EK model. Debye length was calculated and compared with voxel length to check if the EDL is resolvable

Full size image

2.1.2 Lattice Boltzmann Methods

To solve the coupled transport and electric equations (mentioned above) in porous media, we adopted the commonly used LBM because of its inherent scalability of parallel computation and efficient handling of complex boundary conditions. Several coupled lattice Boltzmann (LB) frameworks dedicated to EK flow have been developed and studied over the past decade (Wang et al. 2006; Yoshida et al. 2014; Zhang and Wang 2017; Basu et al. 2020). Herein, we adopted the method proposed by Wang and Kang (2010), which was modified by Yoshida et al. (2014); Zhang and Wang (2017), to incorporate an electroosmotic velocity boundary condition.

The LB method naturally suits parabolic partial differential equations. The Poisson equation, however, is elliptical, and thus an artificial time-dependent term is usually added so that the LBM yields a steady-state solution of the ‘transient’ Poisson equation of the following form:

$$\begin{aligned} \frac{\partial \psi }{\partial t} = \nabla ^2 \psi + \frac{\rho _e}{\varepsilon _r \varepsilon _0}. \end{aligned}$$
(10)

We deployed the D3Q7 lattice to solve the Poisson equation. The corresponding LB evolution equation for the distribution function \(h_q\) of the electric potential \(\psi\) is given by

$$\begin{aligned} h_q({\varvec{x}}+{\varvec{\xi _q}} \triangle x, {\tilde{t}} + 1) - h_q({\varvec{x}}, {\tilde{t}}) = -\frac{1}{\tau _\psi } \Big [h_q({\varvec{x}}, {\tilde{t}}) -h_q^{eq}({\varvec{x}}, {\tilde{t}}) \Big ] +\omega _q \frac{\rho _{e}}{\varepsilon _r \varepsilon _0}, \end{aligned}$$
(11)

with

$$\begin{aligned} \psi = \sum _{q=0}^{6} h_q, \end{aligned}$$
(12)

and the equilibrium distribution is

$$\begin{aligned} h^{eq}_q = \omega _q \psi , \end{aligned}$$
(13)

where \({\varvec{\xi }}_q\) and \(\omega _q\) are the D3Q7 lattice velocity vector and weighting coefficient, respectively, with \(\omega _0=1/4\) and \(\omega _{1-6}=1/8\); and \(\triangle x\) is the spatial resolution of the simulation domain. It should be noted that the time in the LB Poisson equation is denoted as \({\tilde{t}}\); thus, it should be differentiated from the LB time t in the Navier–Stokes and Nernst–Planck equations to be covered later because only the steady-state solution of Eq. 10 is of interest. Within each main evolution step (Fig. 1 for flow chart), Eq. 11 is executed iteratively until the standard mean squared error over a certain amount of timestep, \({\tilde{t}}'\), is smaller than the user-specified tolerance:

$$\begin{aligned} \frac{1}{N} \sum _{{\varvec{x}}} \left[ \psi ({\varvec{x}},{\tilde{t}}) - \psi ({\varvec{x}},{\tilde{t}}-{\tilde{t}}') \right] ^2 < \epsilon _{\text {err}}, \end{aligned}$$
(14)

where N is the total number of fluid nodes, and \(\epsilon _{\text {err}}\) is the prescribed tolerance.

The LB relaxation time parameter \(\tau _{\psi }\) in Eq. 11 is given by:

$$\begin{aligned} \tau _{\psi } = \frac{1}{2}+ \frac{1}{c_s^2}, \end{aligned}$$
(15)

where \(c_s^2\) is the LB speed of sound; for the D3Q7 lattice \(c_s^2=1/4\).

For the boundary condition, we adopted the formulation developed by Yoshida et al. (2014), which is a completely localized scheme that is more suitable for complex porous media. For the Neumann-type boundary condition, where a surface charge density \(\sigma _e\) is specified, after the LB collision, the normal streaming step is replaced by the following equation:

$$\begin{aligned} h_q({\varvec{x}}+{\varvec{\xi _q}} \triangle x, {\tilde{t}} + 1) = h'_{\overline{q}}({\varvec{x}}+{\varvec{\xi _q}} \triangle x, {\tilde{t}}) + \sigma _e/ \left( \varepsilon _r \varepsilon _0 \right) , \end{aligned}$$
(16)

where \(h'_q({\varvec{x}},t)\) is the post-collision distribution, and the index \(\overline{q}\) indicates the direction opposite to q. The Dirichlet-type boundary condition, where the surface potential is specified, is given by:

$$\begin{aligned} h_q({\varvec{x}}+{\varvec{\xi _q}} \triangle x, {\tilde{t}} + 1) = -h'_{\overline{q}}({\varvec{x}}+{\varvec{\xi _q}} \triangle x, {\tilde{t}}) + c_s^2 \psi _s. \end{aligned}$$
(17)

Incidentally, the electric field \({\varvec{E}}\) is given by the gradient of the electric potential, that is \({\varvec{E}} = -\nabla \psi\). According to Yoshida et al. (2014), the gradient can be calculated locally as

$$\begin{aligned} E_{\alpha } = \frac{1}{\tau _{\psi } c_s^2 \triangle x} \sum _q \xi _{q,\alpha } h_q, \end{aligned}$$
(18)

where the index \(\alpha\) denotes Cartesian coordinates.

For ion transport, the LB evolution equation was also solved for the D3Q7 lattice and is given by

$$\begin{aligned} g_q({\varvec{x}}+{\varvec{\xi _q}} \triangle x, t +\triangle t_{D_i}) - g_q({\varvec{x}}, t) = -\frac{1}{\tau _{D_i}} \left[ g_q({\varvec{x}}, t) -g_q^{eq}({\varvec{u}}, {\varvec{u}}_{EP,i}, t)\right] , \end{aligned}$$
(19)

for the ion distribution function \(g_q\). The equilibrium distribution function is given by

$$\begin{aligned} g_q^{eq} = \omega _q C_i \left[ 1+ \frac{\triangle t_{D_i}}{\triangle x} \frac{{\varvec{\xi }}_q \cdot \left( {\varvec{u}} + {\varvec{u}}_{EP,i} \right) }{c_s^2} \right] , \end{aligned}$$
(20)

where \(\triangle t_{D_i}\) is the time resolution; the method of determining \(\triangle t_{D_i}\) is covered further on; \(C_i=\sum _q g_q\) is the ion concentration of ith species; and \({\varvec{u}}_{EP,i}\) is the electrophoretic velocity of the ith ion in response to applied electric potential. The electrophoretic velocity is given by

$$\begin{aligned} {\varvec{u}}_{EP,i} = \frac{z_i D_{i,\text {LB}}}{V_T} {\varvec{E}} =-\frac{z_i D_{i,\text {LB}}}{V_T} \nabla \psi , \end{aligned}$$
(21)

where \(D_{i,\text {LB}}\) is the diffusivity of the ith ion species in the LB unit; it is related to the relaxation parameter \(\tau _{D_i}\) as follows:

$$\begin{aligned} \tau _{D_i} = \frac{1}{2} + \frac{D_{i,\text {LB}}}{c_s^2}. \end{aligned}$$
(22)

For the Dirichlet-type boundary condition, that is, if the surface ion concentration \(C_s\) is specified, the normal streaming step after LB collision is replaced by

$$\begin{aligned} g_q({\varvec{x}}+{\varvec{\xi _q}} \triangle x, t + \triangle t_{D_i}) = -g'_{\overline{q}}({\varvec{x}}+{\varvec{\xi _q}} \triangle x, t) + c_s^2 C_0. \end{aligned}$$
(23)

Here, \(g'_q\) denotes the post-collision distribution. For the non-flux boundary condition in Eq. 4, it has been proved in Yoshida et al. (2014) that it is equivalent to the half-way bounce-back boundary condition widely used in the LB method, which ensures no ion flux across the solid boundary:

$$\begin{aligned} g_q({\varvec{x}}+{\varvec{\xi _q}} \triangle x, t + \triangle t_{D_i}) = g'_{\overline{q}}({\varvec{x}}+{\varvec{\xi _q}} \triangle x, t). \end{aligned}$$
(24)

Regarding the LB Navier–Stokes solver for the electrolyte solution, because it has been extensively studied and used in numerous publications, the details of the formulation are not repeated here. Therefore, we implemented the formulation by McClure et al. (July 2014, 2020, 2021), where a multi-relaxation LB method is deployed, and incorporated the slipping velocity boundary condition proposed by Ladd (1994) and Zhang and Wang (2017) into model cases in which the EDL is not resolved.

When solving a multi-physics problem where each transport equation has its own time scale and internal LB timestep, it is important to ensure that all of the coupled equations are synchronized in terms of a physical time scale. In other words, the relationship

$$\begin{aligned} N_{t_u} \triangle t_u = N_{t_{D_1}} \triangle t_{D_1} = N_{t_{D_2}} \triangle t_{D_2} =... = N_{t_{D_n}} \triangle t_{D_n} \end{aligned}$$
(25)

must be maintained, where \(N_{t_u}\) and \(N_{t_{D_i}}\) are the internal LB timestep relative to the main timestep for the Navier–Stokes and ion transport solvers, respectively; \(\triangle t_u\) and \(\triangle {t_{D_i}}\) are the time conversion factors (for example, a unit of [s/l.t.], where l.t. denotes the LB timestep) for the fluid and ith ion species, respectively.

The time conversion factor \(\triangle t_u\) for fluid flow is determined by the following relation:

$$\begin{aligned} \nu _{\text {phys}} = \frac{\triangle x^2}{\triangle t_u} \nu _{\text {LB}}, \end{aligned}$$
(26)

where \(\nu _{\text {phys}}\) and \(\nu _{\text {LB}}\) are the fluid kinematic viscosities in the physical and LB units, respectively. Notably, \(\nu _{\text {LB}}\) is linked to the Navier–Stokes LB relaxation time by \(\nu _{\text {LB}} = (\tau _u-0.5)/3\), where \(\tau _u\) is usually taken between 0.5 and 2 for numerical stability.

The time conversion factor \(\triangle t_{D_i}\) for ion transport is determined using the following relation:

$$\begin{aligned} D_{i,\text {phys}} = \frac{\triangle x^2}{\triangle t_{D_i}} D_{i,\text {LB}}, \end{aligned}$$
(27)

where \(D_{i,\text {phys}}\) and \(D_{i,\text {LB}}\) are the diffusivities of the ith ion in physical and LB units, respectively. Note that \(D_{i,\text {LB}}\) is related to the LB relaxation time through Eq. 22, where \(\tau _{D_i}\) is set to 1.0 for numerical stability.

In summary, using the image resolution \(\triangle x\), the input physical parameters (\(\nu _{\text {phys}}\), \(D_{i,\text {phys}}\)) and user-specified LB relaxation time (\(\tau _u\) and \(\tau _{D_i}\)), the time conversion factor for each solver was determined; this step was performed using a multi-physics controller in LBPM. The internal LB timestep of each solver was also subsequently determined based on \(\triangle t_u\) and \(\triangle t_{D_i}\). For example, if \(\triangle t_u\) is the largest among the sets \(\{\triangle t_u, \triangle t_{D_1}, \triangle t_{D_2},...,\triangle t_{D_n} \}\), then \(N_{t_u}\) is set to 1 and \(N_{t_{D_i}}\) can be determined using \(N_{t_{D_i}}=\triangle t_u/\triangle t_{D_i}\), rounded up to the nearest integer. The open-source code for our EK model is accessible on GitHub (https://github.com/OPM/LBPM).

Our EK model was first benchmarked with COMSOL Multiphysics for EOF under both conditions, where the EDL is resolvable and unresolvable in a two-dimensional microchannel. The validation results can be found in Supplementary Materials Section 3. After validation, we use a simple EK model to evaluate the benefits of EK transport compared to pressure-driven flow in a simple heterogeneous system. EK simulations were then performed on the chalcopyrite-silica system to evaluate the effect of the zeta potential and electric potential on the feasibility of EK transport for EK-ISR. All simulation parameters are listed in Table S1 in Supplementary Materials Section 3. Simulations were performed on a local workstation with a 64-core CPU, 24 GB of GPU memory, and 256 GB of RAM. Simulations were computed on the GPU with a much faster computational speed than the CPU.

2.2 Micro-CT Imaging and Image Processing

A chalcopyrite-silica system, which is a mixture of a Cu mineral (chalcopyrite) and gangue mineral (silica), was prepared to obtain a copper-rich porous system. This chalcopyrite-silica system was imaged using micro-CT to generate a digital 3D model for simulation. The chalcopyrite powder was obtained from Kremer Pigments (Germany) with a particle size of approximately 80 \(\mu\)m. The mineral and elemental contents of the chalcopyrite powder were quantified using X-ray diffraction (XRD) analysis and X-ray fluorescence (XRF), and the results are shown in Table 1. The XRF results show that the major elements are Fe\(^{+3}\) and Cu\(^{+2}\) which are the main elements in chalcopyrite (CuFeS\(_2\)). It can be further confirmed from XRD that the powder contained over 72% chalcopyrite. To prepare the synthetic ore system, SiO\(_2\) (2.5g) and copper ore (40 mg) were mixed in NaCl solution (1.37mL, 0.1M) in a beaker (50 mL). The mixture was stirred for 5min to ensure complete saturation of the system. The saturated mixture was moved to a container (height: 3 cm; inner diameter: 1 cm; outer diameter: 1.2 cm) for micro-CT scanning, as shown in Fig. 2a. Cotton cloth was used to cover the top of the chalcopyrite-silica system, ensuring minimal powder movement during the micro-CT scanning. The micro-CT image of the chalcopyrite-silica system is shown in Fig. 2b. The voxel size was \(2013 \times 2013 \times 2970\) with a resolution of 5.4 \(\mu\)m.

Fig. 2
figure 2

a Micro-CT image of the wet chalcopyrite-silica system. The system is a mixture of silica and chalcopyrite powders saturated with sodium chloride solution. b 4-phase segmentation, including void, solution, silica, and chalcopyrite. The solution used herein is 0.1M NaCl. Multi-phase segmentation is based on CNN. c Segmented 3D synthetic ore system. d 3D distributions of silica and chalcopyrite in the system

Full size image
Table 1 XRF and XRD results of the chalcopyrite powder. For XRF, the powder was preoxidized before being fused into the glass bead. Therefore, the XRF results show the element oxide weight percent. The XRD pattern shows the minerals occurring in the powder. Both results confirm that the most abundant mineral in the powder is chalcopyrite
Full size table

Identifying the mineral composition and distribution in the synthetic ore system was a pre-process for EK modeling using LBPM. Therefore, the first step was to perform multiphase segmentation of the synthetic ore system. The synthetic ore system was a mixture of silica, chalcopyrite, NaCl solution, and unsaturated voids. To segment these four phases, we used trainable WEKA segmentation (Arganda-Carreras et al. 2017) to generate a training dataset of registered images that were then fed to a U-ResNet convolutional neural network(CNN) (Tang et al. 2022; Wang et al. 2021; Tang et al. 2022, 2022). The workflow is outlined as follows.

  1. 1.

    A 2D grayscale image was selected, and its pixels were manually clustered into the 4 phases as training data for the WEKA segmentation.

  2. 2.

    After training, the WEKA segmentation generated a 2D segmented slice of the input 2D grayscale image which works as ground truth for CNN training.

  3. 3.

    Once the CNN was trained, it could segment the entire 3D image of the synthetic ore system. The detailed U-ResNet architecture and training schedule can be found in Supplementary Materials Section 1.

Figure 2c–d shows the 3D segmentation result of the 4-phase synthetic ore system, and Fig. 2e shows the 3D distribution of silica and chalcopyrite, which are homogeneously distributed throughout the system.

3 Results and Discussion

3.1 EK Versus Hydraulic Pressure Driven Transport

To understand the difference between single-phase flow behavior under either solely EK or hydraulic pressure, a single-phase flow simulation was performed using the validated EK model in a \(100 \times 100\) 2D multi-microchannel system with a resolution of 4\(\mu\)m. The system contains only one type of solid phase with \(\zeta = -0.02\,{\rm V}\). Three microchannels with aperture sizes of 8, 20, and 40\(\mu\)m were established in the system. The hydraulic pressure \(\Delta\) was 3000 kPa/m, and the electric field \(\psi\) was 2.5 V/m. The simulation settings of the lixiviant and diffusion coefficient are listed in Table S1 in Supplementary Materials and Table 2. The ionic concentration range from \(1\times 10^{-7}\,{\rm M}\) to 1.7M still belongs to the category of dilute species. For pressure-driven simulation, the external electric potential is set to zero and only a pressure difference is applied. The velocity profile results are shown in Fig. 3. With only \(\Delta\)P, the flow was different in the three microchannels, because with a large channel size, the capillary entry pressure for fluid flow is lower than that of a smaller channel size (Lake 1989). Therefore, fluid prefers to enter the largest-sized channel owing to less hydraulic resistivity, as shown in Fig. 3a. Consequently, the flow velocities were greater in the larger channel. For ISR, only minerals that resided in the larger pores and fractures with the preferential flow would be recovered efficiently, whereas minerals in the smaller pores would be transported less efficiently. On the other hand, a promising flow behavior was obtained when applying an electric potential, as shown in Fig. 3b. The velocity in all three channels is the same, and the velocity profile is sharp, indicating that all minerals in the pores or fractures can be efficiently exposed to lixiviant, independent of the pore size. Based on these results, it can be seen that flow driven by the EK mechanism enables the minimization of the effect of pore-scale heterogeneity, thus promising a higher mineral recovery efficacy during ISR.

Table 2 Settings for numerical simulation, which are the same as the previously reported experimental conditions (M represents molarity). At the inlet and outlet, the numerical settings are the boundary conditions, and in the system, the numerical settings are the initial condition
Full size table
Fig. 3
figure 3

Single-phase flow of lixiviant in a micro-channel system under only a hydraulic pressure gradient or b electric field. The velocity profile shows that an uneven flow is obtained with hydraulic pressure, whereas a uniform flow is obtained with the electric field due to the EOF

Full size image

3.2 EK in a Chalcopyrite-Silica System

Lixiviants are chemical substances used to selectively dissolve target metals. For the dissolution of chalcopyrite, we use the ferric chloride (\({\rm FeCl}_{3}\)) to simulate the \({\rm Fe}^{3+}\) flow in the system. \({\rm FeCl}_{3}\) is relatively environmentally benign compared to sulfuric acid (Martens et al. 2021) but still has potential environmental impacts, such as water pollution and persistence in the environment (Crane and Sapsford 2018). These environmental impacts are suggested to minimize by designing hydrogeological models prior to the commencement of ISR and cleaning aquifers after ISR (Seredkin et al. 2016). When \({\rm FeCl}_{3}\) is dissolved into water, hydrated ferric ions (\({\rm Fe}^{3+}\)) and chloride ions (\({\rm Cl}^{-}\)) are formed and stabilized. The reaction between chalcopyrite with dissolved \({\rm Fe}^{3+}\) is described as follows:

$$\begin{aligned} {\hbox {CuFeS}_{2} + 4\hbox {Fe}^{3+} -> \hbox {Cu}^{2+} + 5\hbox {Fe}^{2+} + 2\hbox {S}^{0}}. \end{aligned}$$
(28)

The oxidative dissolution of chalcopyrite occurs due to the reaction with \({\rm Fe}^{3+}\) ions present in the lixiviant. To apply EK-ISR, the migration of Fe\(^{3+}\) through the ore system must be ensured for the dissolution of chalcopyrite into the fluid phase. Therefore, the discussion of Fe\(^{3+}\) ion is focused on in this section. Based on the validation results, the EK model in LBPM showed good agreement with COMSOL and was thus used for studying the EK transport in a complex chalcopyrite-silica system. To reduce the computational time for the simulation, a representative 256 cubic voxels subdomain was cropped from the original domain, as shown in Fig. S2 in Supplemental Materials, Section 2. Representative elementary volume analysis of the chalcopyrite-silica system was also performed, and the results are provided in the Supplemental Materials. The typical chalcopyrite content in the sulfide ore is around 0.3–5 % (Agar 1991; Ikiz et al. 2006; Velásquez-Yévenes et al. 2018). The mineral composition of the representative sub-domain that is used in the following simulation is 96.3% silica and 3.7% chalcopyrite, which is in the typical range. Moreover, to check the physical accuracy of the proposed EK model, and also consider the heterogeneous distribution of chalcopyrite in the small sub-section of the whole sample, two manually generated subdomains that have chalcopyrite concentrations of 15.6% and 63.3 % were created and used to check the physical accuracy of the model and study the effect of zeta potential for different percentages of chalcopyrite. These subdomains were obtained by changing the silica grains to chalcopyrite grains. The material compositions for all simulated representative sub-domains are listed in Table 3. The following numerical studies were conducted on these sub-domains.

Table 3 Mineral compositions of all three sub-domains used in this study. Domain 1 is the real scanned sub-domain. Domain2 and Domain3 are manually generated sub-domains
Full size table

3.2.1 EK Under Different Zeta Potentials

The simulation settings were set to match the EK-ISR laboratory-scale experimental settings in Martens et al. (2021), as shown in Table 2. At the inlet and outlet, 0.2M HCl is set as the boundary condition. In the system, \(1\times 10^{-7}\,{\rm M}\) is set as the initial condition. During the simulation, \({\rm H}^{+}\) is transported into the system under diffusion and electromigration. Under an electric field, \({\rm Fe}^{3+}\) moves from the source reservoir to the copper-bearing reservoir, where \({\rm Cu}^{2+}\) is leached. The dissolved \({\rm Cu}^{2+}\) and other cations are then transported to the target reservoir via electromigration. The reactive surface area plays a fundamental role in the mineral dissolution and reactive transport processes. The porous media properties such as tortuosity, porosity, and permeability evolve as the mineral dissolution takes place. Such changes in the pore structure alter the magnitude of the velocity field and control the flow pattern. Moreover, mineral dissolution modifies the local pH in the system, affecting the zeta potential which has a great influence on the electroosmotic permeability. Therefore, understanding \({\rm Fe}^{3+}\) transport in the domain is non-trivial. The pH at the inlet and outlet was set to 0.7 (initial strongly acidic conditions). Other settings are listed in Table S1. The zeta potential \(\zeta\) for silica and chalcopyrite is another important factor that controls the fluid/ion flow behavior. Moreover, transport is sensitive to the pH of the solution. For silica and chalcopyrite, experimental measurements of \(\zeta\) at various pH values have been reported in Xu et al. (2006) and Runqing et al. (2010). Under pH around 0.7, the \(\zeta\) value for silica was approximately \(-0.005\,{\rm V}\). For chalcopyrite, \(\zeta\) was approximately 0.002V, whereas \(\zeta\) of chalcopyrite after the treatment with ferric chromium lignin sulfonate is approximately \(-0.03\,{\rm V}\). To further investigate the effect of \(\zeta\) on EK, three simulations using three subdomains (3.7, 15.6, and 63.3% chalcopyrite) with \(\zeta = 0.002\,{\rm V}\) were compared.

Fig. 4
figure 4

Simulation results for Domain1: a electric potential; b fluid velocity difference between chalcopyrite \(\zeta\) of 0.002V and \(-0.03 \,{\rm V}\); c fluid velocity profile of \(\zeta = 0.002 \,{\rm V}\); d fluid velocity profile of \(\zeta = -0.03 \,{\rm V}\)

Full size image

At the set ionic concentration and image voxel size, the EDL fell into the unresolvable regime; therefore, Eq. 2 was used to compute the flow velocity. Using the HS equation, the velocity rapidly converged. The stopping criterion for the steady-state condition was the average velocity difference between these two timesteps is less than \(10^{-9} m/s\). Figure 4 shows the electric potential, velocity profiles for \(\zeta = 0.002\,{\rm V}\) and \(\zeta = -0.03\,{\rm V}\), and the difference between the resulting velocity profiles. Electroosmosis is related to the \(\zeta\) value of each mineral. For a negative \(\zeta\), the fluid moves towards the cathode, whereas for a positive \(\zeta\), the fluid moves towards the anode. The major mineral in the subdomain was silica with \(\zeta = -0.005 \,{\rm V}\). The fluid surrounding the silica flowed toward the cathode (positive velocity value). For \(\zeta\) of chalcopyrite of 0.002 V, the fluid flowed towards the anode (negative velocity value), indicating that electroosmosis acted in the opposite direction to electromigration. However, when \(\zeta\) for chalcopyrite was \(-0.03\,{\rm V}\), the fluid surrounding the chalcopyrite flowed at a higher velocity than that surrounding the silica, indicating that the effects of electroosmosis and electromigration were codirectional. The average velocities and electroosmotic permeabilities are listed in Table 4. The average velocity for \(\zeta = -0.03\,{\rm V}\) was slightly higher than that for \(\zeta = 0.002\,{\rm V}\), owing to the EOF. The electroosmotic permeability governs the fluid flow under the electric potential similarly to how the hydraulic conductivity governs the flow under a hydraulic gradient. Therefore, a larger electroosmotic permeability was obtained for a more negative \(\zeta\). The difference is 7.28% because the amount of chalcopyrite in Domain1 is small compared to that in silica.

To investigate the effect of chalcopyrite occurrence, Domain2 and Domain3 were compared with Domain1 under the same conditions, where \(\zeta = 0.002 \,{\rm V}\). The results are presented in Table 5. Ion flux owing to advection, diffusion, and electromigration are also reported. With an increase in chalcopyrite fraction, the average velocity decreases significantly (up to 76.21% difference between Domain1 and Domain3) because the lixiviant near the chalcopyrite moves towards the anode (negative velocity) owing to the positive zeta potential. Consequently, the overall movement of the lixiviant from the anode to the cathode decreases, resulting in a reduction in average velocity. For \({\rm Fe}^{3+}\) ion flux, with an increase in chalcopyrite fraction, the advective flux decreases because advection is related to fluid velocity. However, the diffusive flux remained almost constant for all three domains, whereas the electrical flux slightly decreased. Comparing the ionic flux, the flux of advection due to EOF is four orders of magnitude less than electromigration and diffusion. Overall, the results reveal that for EK-ISR, where an external electric potential is applied, electromigration is the dominant ion transport mechanism. The diffusive flux is the second important transport mechanism in our simulation settings because the domain initially contained no \({\rm Fe}^{3+}\), resulting in high diffusive flux. EOF contributes less to ion transport. The EOF at the solid–fluid interface is the main transport mechanism for fluid flow than the ion interactions and their influence on the bulk fluid.

Table 4 Electroosmotic permeability results at \(\zeta = 0.002 \,{\rm V}\) and \(-0.03 \,{\rm V}\) for Domain1. The average velocity at \(\zeta = -0.03 \,{\rm V}\) is greater than at \(\zeta = 0.002 \,{\rm V}\). Because the same external electric potential is applied, the electroosmotic permeability at \(\zeta = -0.03 \,{\rm V}\) is greater than at \(\zeta = 0.002 \,{\rm V}\)
Full size table
Table 5 Average velocity and ferric ion flux under advection, diffusion, and electromigration for Domain1, Domain2, and Domain3 with \(\zeta =0.002\,{\rm V}\) for chalcopyrite and \(\zeta =-0.005\,{\rm V}\) for silica
Full size table

Under an external electric potential, positively charged ions move toward the cathode, and negatively charged ions move toward the anode owing to electromigration. Fe\(^{3+}\), therefore, moves from the anode to the cathode, as shown in Timesteps 1–3 in Fig. 5a, b. The physical time corresponding to them is 3.6, 9.6, and 14.5 s, respectively. which illustrates the transport of Fe\(^{3+}\) ions under applied electric potential,. As Fe\(^{3+}\) moves into the ore system, a larger region of chalcopyrite is exposed, which is essential for the reaction and recovery of Cu\(^{2+}\). Figure 5c calculates the differences in Fe\(^{3+}\) distribution between Fig. 5a, b, and shows the different Fe\(^{3+}\) concentration due to different zeta potential at mineral surface. Different zeta potential results in different velocity profile calculated from Eqs. 1 and 2. This velocity causes the difference in Fig. 5c by the advection flow shown in Eq. 3. Overall, pH and the geochemical reactions involved with \(\zeta\) for different minerals in the ore are essential parameters affecting the EK performance and therefore need to be comprehensively characterized.

Fig. 5
figure 5

Fe\(^{3+}\) distribution in Domain1 under different \(\zeta\) of chalcopyrite: a \(\zeta = 0.002 \,{\rm V}\); b \(\zeta = -0.03 \,{\rm V}\). c Differences in Fe\(^{3+}\) distribution between (a) and (b)

Full size image

3.2.2 EK Under Different Electric Potentials

Based on previous results, electromigration is the main transport mechanism in EK-ISR. Therefore, simulations with different electric potentials (\(\psi = 0.4 \,{\rm V}\) and \(\psi = 1.2 \,{\rm V}\)) were computed at \(\zeta = -0.03 \,{\rm V}\) for chalcopyrite and \(\zeta = -0.005 \,{\rm V}\) for silica. Figure 6a, b show the electric potential for both cases. Figures 6c, d show the z-component velocity for the two cases. The velocity towards the cathode under a higher electric potential was greater than that under a lower electric potential at negative \(\zeta\) for both silica and chalcopyrite. This can be explained using Eq. 2, where the velocity is proportional to the electric potential. The average velocity exhibited the same trend, as listed in Table 6. Notably, if \(\zeta\) is positive for chalcopyrite, under a higher electric potential, the average velocity towards the cathode becomes smaller than that under a lower electric potential. This is because at positive \(\zeta\), electroosmosis leads to flow in the opposite direction (negative velocity) towards the anode at the locations surrounding chalcopyrite. Additionally, the electroosmotic permeability is the same in both cases, which indicates that the electroosmotic permeability is independent of the external electric potential. This condition is valid for this case because a constant of 0.2M HCl was applied at the inlet and outlet, resulting in a homogeneous pH distribution in the system. However, this condition is not met when there is a variation in pH. For example, (Zhang and Wang 2017) found that electroosmotic permeability can change under heterogeneous pH conditions.

Fig. 6
figure 6

Simulation results for Domain1: a electric potential at \(\psi = 0.4 \,{\rm V}\); b electric potential at \(\psi = 1.2 \,{\rm V}\). c Velocity profile of \(\psi = 0.4 \,{\rm V}\). d Velocity profile of \(\psi = 1.2 \,{\rm V}\)

Full size image
Table 6 Electroosmotic permeability results at \(\psi = 1.2 \,{\rm V}\) and 0.4V for Domain1. The average velocity at \(\psi =1.2\,{\rm V}\) is greater than at \(\psi = 0.4 \,{\rm V}\). The electroosmotic permeability, however, is the same for both \(\psi\)
Full size table

Although the electric potential has no effect on electroosmotic permeability, it dominates the distribution of \({\rm Fe}^{3+}\) in the system. Figure 7a, b show the distributions of \({\rm Fe}^{3+}\) concentration at three different timesteps under electric potentials of \(\psi = 0.4 \,{\rm V}\) and \(\psi = 1.2 \,{\rm V}\), respectively. Figure 7c shows the difference between the concentration fields. From timestep 1 to 3, \({\rm Fe}^{3+}\) ions under \(\psi = 1.2 \,{\rm V}\) flowed faster from the anode to the cathode than those under \(\psi = 0.4 \,{\rm V}\). This resulted in a broader distribution of \({\rm Fe}^{3+}\) ions in the sample, which is beneficial for chalcopyrite dissolution.

Fig. 7
figure 7

\({\rm Fe}^{3+}\) distribution in Domain1 under different external \(\psi\): a \(\psi = 0.4 \,{\rm V}\); b \(\psi = 1.2 \,{\rm V}\). c Differences in \({\rm Fe}^{3+}\) distributions between (a) and (b)

Full size image

Figure 8 shows the relationship between \({\rm Fe}^{3+}\) and chalcopyrite at different timesteps. When \(\psi = 0.4 \,{\rm V}\), at an early timestep, the majority of \({\rm Fe}^{3+}\) concentration near the chalcopyrite is in the range of 0 to 20 \({\rm mol}/{\rm m}^{3}\), and only one voxel has an \({\rm Fe}^{3+}\) concentration of \(>501\,{\rm mol}/{\rm m}^{3}\). At the late timestep, the number of voxels in the range 0 to 20 \({\rm mol}/{\rm m}^{3}\) decreases, whereas the number of voxels in other ranges increases, which is especially significant for the \({\rm Fe}^{3+}\) concentration of \(>501\,{\rm mol}/{\rm m}^{3}\) (from 1 to 2278). When \(\psi\) increases to 1.2V, as the simulation progresses, more voxels have \({\rm Fe}^{3+}\) concentration higher than 21 \({\rm mol}/{\rm m}^{3}\), particularly with an increase in \({\rm Fe}^{3+}\) concentration greater than 401 \({\rm mol}/{\rm m}^{3}\). \({\rm Fe}^{3+}\) moves faster at higher \(\psi\). In both cases, as the timestep increases, more \({\rm Fe}^{3+}\) flows into the system and contacts the chalcopyrite body.

Fig. 8
figure 8

\({\rm Fe}^{3+}\) distribution is divided into seven concentration ranges. The voxel frequency refers to the number of voxels that are connected to the voxels of chalcopyrite and also fall into the satisfied concentration range. The results in early and late timesteps are compared for \(\psi = 0.4 \,{\rm V}\) and \(\psi = 1.2 \,{\rm V}\). For the range \(>501\,{\rm mol}/{\rm m}^{3}\), except for the late timestep for \(\psi = 1.2 \,{\rm V}\), the voxel frequency for others are 1

Full size image

4 Conclusions

In this study, we propose a pore-scale EK model built with LBPM to describe the advection/diffusion, electromigration, and electroosmosis of fluid and charged species in the complex porous media. Key features of the proposed model are: (1) capable of simulating EK on complex porous media of images; (2) characterise the fluid/ion flow under both conditions when EDL is resolvable and unresolvable; (3) supports GPU acceleration (McClure et al. 2014, 2021) and therefore, can be used for large domain simulation as a digital twin study with of experiments results; and (4) the model that solves the transport of fluid and charged species can be coupled to PhreeqcRM in Python and MATLAB for reactive transport. The EK model was validated against COMSOL Multiphysics in terms of EOF in a 2D microchannel. The thickness of the EDL and its effect on the numerical model were discussed and validated. Specifically, at the thickness of EDL comparable to the domain size, the EDL can be fully resolved by the EK model, whereas at the thickness of EDL smaller than the domain size, the EDL is unresolvable by the model. Therefore, the HS equation was used to compute the slip boundary velocity. Good agreement was obtained between the EK model and COMSOL Multiphysics.

Subsequently, a chalcopyrite-silica system consisting of chalcopyrite and silica powder was prepared and imaged with micro-CT. The simulation with the chalcopyrite-silica system provides a more complex porous structure for characterising fluid and ions flow under the EK condition. The simulation application studied the EK processes under various mineral occurrences, zeta potential, and electric potential. The results highlight the important influence of mineral occurrence, zeta potential, and electric potential on electroosmosis and electromigration for EK. The flexibility of the model opens the opportunity to couple the surface complexion model for local pH characterization, such as 1-pk model (de Lima et al. 2010) and triple layer model (Revil and Leroy 2004), coupling with a geochemical model, such as PhreeqcRM to fully capture the reactive transport under electric potential (Parkhurst and Wissmeier 2015) and simulating large domain ore sample which is used in experiments. With the geochemical reaction of minerals, the change of effective conductivity of the fluid phase also needs to be considered, because it results in potential implications such as changing fluid chemical properties, local pH, and solubility. Overall, such model application can be applied for EK-ISR where the low permeability-porosity system is presented (Martens et al. 2021).