Room-Scale CO₂ Injections in a Physical Reservoir Model with Faults

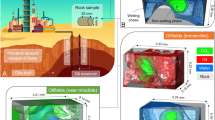
Abstract

We perform a series of repeated CO₂ injections in a room-scale physical model of a faulted geological cross-section. Relevant parameters for subsurface carbon storage, including multiphase flows, capillary CO₂ trapping, dissolution and convective mixing, are studied and quantified. As part of a validation benchmark study, we address and quantify six predefined metrics for storage capacity and security in typical CO₂ storage operations. Using the same geometry, we investigate the degree of reproducibility of five repeated experimental runs. Our analysis focuses on physical variations of the spatial distribution of mobile and dissolved CO₂, multiphase flow patterns, development in mass of the aqueous and gaseous phases, gravitational fingers and leakage dynamics. We observe very good reproducibility in homogenous regions with up to 97% overlap between repeated runs, and that fault-related heterogeneity tends to decrease reproducibility. Notably, we observe an oscillating CO₂ leakage behavior from the spill point of an anticline and discuss the observed phenomenon within the constraints of the studied system.

1 Introduction

In its simplest form, geological carbon storage (GCS) involves the injection of captured carbon dioxide (CO₂) into deep subsurface porous and permeable sedimentary rocks, overlain by an impermeable sealing layer. The migration of the buoyancy-driven CO₂ is determined by: (i) the intrinsic rock and fluid properties (e.g., porosity, permeability, fluid density and viscosity) and (ii) the distribution and properties of geological structures such as faults and fracture networks that are inherent to both reservoir and seal rocks. Faults are discontinuities that form at a range of scales; they can act as conduits or barriers for flow, and they generally have directionally dependent flow properties (Bastesen and Rotevatn 2012). Large sealing faults control storage site geometries and compartmentalization, whereas networks of small faults and fractures may affect reservoir flow and seal integrity (Ogata et al. 2014).

1.1 Faults, Fractures and Flow

The properties of the fracture networks (i.e., topology, connectivity and permeability) that form damage zones around faults as they evolve (Nixon et al. 2020) are particularly important to CO₂ flow. Subsurface faults are discerned from reflection seismic data, but descriptions suffer from limitations in seismic resolution and coverage. Geologically analogous outcrops and dedicated laboratory experiments provide a means to investigate smaller structures around faults and shed light on flow and sealing properties. Being able to identify and forecast the behavior of potential subsurface bypass structures during GCS operation is essential; understanding the interplay between multiphase flow and fault evolution is critically needed for carbon storage projects. Despite this, the flow properties of faults and their damage zones remain insufficiently understood, and little is known about how their flow behavior evolves in the different stages of a carbon storage project. Our current understanding of large-scale CO₂ plume migration is mainly from time-lapse seismic surveys with limited a priori knowledge (Furre et al. 2017). With increases in reservoir pressures during CO₂ injection, there is a greater risk of reactivation and potential generation of new fracture networks that can enhance seal permeability and capillary flow and provide pathways for fluid escape to shallower reservoirs or the surface (e.g., Ogata et al. 2014; Karstens and Berndt 2015; Karstens et al. 2017).

1.2 The Laboratory FluidFlower Rig

The FluidFlower concept links research and dissemination through a new experimental rig constructed at University of Bergen (UiB) that enables repeatable, meter-scale, multiphase, quasi-two-dimensional (2D) flow on model geological geometries with high-accuracy data acquisition. Intermediate-scale (decimeter to meter) quasi-2D laboratory experiments are widely used to study multiphase porous media flow, including gravity unstable flows in the presence of heterogeneity (Glass et al. 2000; Van De Ven and Mumford 2018, 2020; Krishnamurthy et al. 2022) and CO₂ migration and dissolution (Kneafsey and Pruess 2010; Trevisan et al. 2017; Rasmusson et al. 2017). These approaches enable visualizing and studying a range of porous media flow dynamics in engineered representative porous media using beads or sand grains. For the present study, we built a multi-scale heterogenous geometry motivated by geological features found on the Norwegian Continental Shelf (cf. Fig. 1). A key feature of the FluidFlower rig is the ability to repeat experiments in the same geometry, without the need to remove the sands between repeated runs. The five repetitions reported here are defined as ‘physical ground truth’ in a double-blind validation benchmark study (outlined below and detailed in Flemisch et al. 2023). Structurally, the benchmark geometry is characterized by broad open folds and normal faults: a major normal fault breaches the lower reservoir-seal system and terminates upward at the base of the upper reservoir. A broad open anticline, in the footwall of the fault, forms the main trap to the lower reservoir-seal system and has a spill point in the immediate footwall of the fault. The broad open anticline is also the main trap geometry for the upper reservoir-seal system, but this is affected by a graben bounded by two oppositely dipping normal faults.

1.3 The FluidFlower Validation and Forecasting Study

Accurate modeling and simulation of multiphase flow in porous media is central to GCS operation, risk assessment and mitigation strategies. Forecasts of large-scale GCS deployment, including injectivity, field-scale CO₂ migration and reservoir pressure response, heavily rely on modeling and numerical simulation studies. Only a few dozen large-scale GCS projects are currently active globally (Steyn et al. 2022), and none of these are in a post-injection phase following a multi-decadal injection period. Hence, the modeling and simulation community does not have robust datasets to assess their forecasting skill, and significant uncertainty is associated with our ability to accurately capture the dominant physical GCS processes. As a partial remedy to this, several code comparison studies have been conducted (Pruess et al. 2004; Class et al. 2009; Nordbotten et al. 2012), none of which, however, were conducted in the presence of a physical ground truth. The FluidFlower forecasting and validation study (Flemisch et al. 2023) aims to provide a first assessment of the predictive skills of the GCS modeling and simulation community. Active academic GCS research groups around the world were invited to participate in a double-blind forecasting study. The participants of the forecasting study were asked to provide independent forecasts and then subsequently invited to update their forecasts in view of group interactions. The forecasts were compared to each other and to the experimental FluidFlower data (‘physical ground truth’) by means of various indicative qualitative and quantitative measures with relevance to both the CO₂ injection and post-injection dynamics of the GCS operations.

1.4 Relevance to Subsurface GCS

While the present study is set at ambient conditions at intermediate (meter) scale, the most important subsurface CO₂ trapping mechanisms are present in the laboratory experiment: structural trapping occurs under the sealing sand layers and within different reservoir zones; dissolution trapping occurs almost instantaneously when the injected CO₂ dissolves into the water phase initially saturating the porous media; residual trapping is observed in regions with intermediate water saturation, but is temporary because of rapid dissolution; convective mixing occurs when the CO₂-saturated water migrates downward and generate gravitational fingers. Mineral trapping is by design not part of the current study for increased control of active chemistry (using silica sand rendered inert by hydrochloric acid, with the pressure and temperature conditions set outside mineralization thresholds in the experimental time series). The fundamental physical processes of multiphase, multi-component flows and trapping behavior in the FluidFlower rig to a large degree represents the porous media physics in a subsurface system, even if the petrophysical properties like porosity, permeability and small-scale heterogeneity, as well as the pressure and temperature conditions, are not directly comparable to subsurface conditions. Furthermore, we remark that the structural trapping in the FluidFlower relies more on capillary entry pressure and less on permeability contrast, than expected at the field scale. Overall, we argue that the findings and observations in this study are indicative of field-scale simulation, although several observed phenomena scale differently in the FluidFlower compared with subsurface systems. The proper identification of key scaling parameters for a 2D flow in a complex geology is non-trivial and is detailed elsewhere (see Kovscek et al. 2023, this issue).

Despite the physical similarities, actual field-scale simulation will deviate from this study in several important aspects, of which we highlight (see Flemisch et al. 2023 for a comprehensive discussion):

• Heterogeneity. The facies in the benchmark geometry were built with a single sand type aiming for homogenous petrophysical properties and, hence, emphasizing larger-scale structural heterogeneities. On the field scale, it is expected that there will be significant subscale heterogeneity also within each geological structure.

• Quality of geological characterization. A high-resolution image of the geological geometry, with accompanying thicknesses before CO₂ injections, was issued to the benchmark participants (cf. Nordbotten et al. 2022). At the field scale, the initial geological characterization will be associated with higher uncertainty and lower spatial resolution data from seismic surveys.

• Pressure and temperature conditions. The laboratory conditions in the reported study yield a gaseous CO₂ phase when injected, compared with liquid or supercritical phase at field conditions in typically reservoirs. The difference in phase condition has a minor impact on viscosity, but leads to a denser and less compressible CO₂ phase at the field scale.

The importance of forecasting, risk assessment and mitigation strategies for carbon storage, with many of the critical coupled subsurface processes remaining poorly understood, merits a continued broad interdisciplinary engagement. The utility of numerical modeling and simulation as a key decision-making tool for industrial application of CO₂ storage is scrutinized in the FluidFlower validation benchmark study for the storage of CO₂  (Flemisch et al. 2023).

2 Materials and Methods

This section briefly describes the key operational considerations and methodology developed to perform the experimental part of the forecasting study. It provides an overview of all procedural steps, a description of the geological geometry and parameters. The description is not exhaustive, and the reader is referred to supplementary materials (SM) and cited work for more detailed descriptions.

2.1 Fluids

The main fluids and their composition and usage are listed in Table 1.

Table 1 Fluid compositions and role in benchmark study

Throughout the article we refer to the gaseous form of CO₂ as ‘gas’- the dry gas injected will partially partition into the aqueous phase saturating the porous media and will have a positive, nonzero water content due to solubility of water in CO₂. The water content in CO₂ was not explicitly quantified in this work. We refer to the aqueous phase partially saturated with dissolved CO₂ as the ‘CO₂-saturated water’, and the aqueous phase without CO₂ as ‘formation water’. The aqueous, pH-sensitive solution (‘formation water’) was in equilibrium with the atmosphere when injected and contained dissolved atmospheric gases (predominantly nitrogen and oxygen). The presence of other gases influences the CO₂-to-water mass transfer due to differences in gas-to-water Henry’s constant (Van De Ven and Mumford 2020): the CO₂ mass transfer to the formation water releases nitrogen and oxygen into the gaseous phase. Hence, over time the gaseous phase in the system becomes deprived of CO₂, with reduced solubility in water. This effect was predominately observed toward the later-life of the gas accumulation under the anticlines and is discussed more below.

2.2 Sand Handling and Porous Media Flow Properties

Danish quartz sand was purchased (in total 3.5 tons) and systematically treated to achieve the required properties. Six different sand types were used (see Table 2). Before use, each sand was manually sieved from the supplied sand stock and treated with a strong acid (HCL) to remove impurities (predominately calcite). The acid was neutralized with sodium hydroxide, rinsed with tap water while manually agitating to remove precipitates and dust until no visible particles and then rinsed in tap water multiple times until clear solution without particles. The sand was then dried at 60 °C until dry and stored in cleaned plastic containers with lid until use. The absolute permeability was measured for each sand, all with nominal porosity 0.44. Detailed sand description, properties and procedural steps are outlined in (Haugen et al. 2023, this issue).

Table 2 Key parameters for each of the six sand types

2.3 The FluidFlower rig and Building the Geometry

The FluidFlower enables meter-scale, multiphase, quasi-two-dimensional flow experiments on model geological geometries with quantitative data acquisition. Time-lapsed images are acquired to monitor dynamic, multiphase flow patterns with high spatial resolution where single sand grains may be identified. CO₂-saturated water is distinguished from formation water by a color shift of aqueous pH sensitive solution, whereas the gas phase is observed by reduction in colored aqueous phase (formation or CO₂-saturated water). The design allows for repeated injections tests with near identical initial conditions, allowing physical uncertainty and variability to be addressed using the same geological geometry. The model geological geometry is constructed using unconsolidated sands (cf. Table 2) and held in place between an optically transparent front panel and an opaque back panel. The rig has 56 perforations that enable a range of well configurations (injector, producer, monitoring, or plugged) for porous media flow studies.

The FluidFlower rig is curved to sustain internal forces and capable of porous media up to approximately 6 m² (3 m length x 2 m height). The validation benchmark and forecasting study (Flemisch et al. 2023) monitored four wells (two for CO₂ injection and two for pressure measurements), but several other wells were active during the experiments. Technical wells/ports at the bottom and top enabled resetting the fluids between CO₂ injections and to maintain a fixed water column during experiments. Technical considerations and mechanical properties of the FluidFlower rig are detailed elsewhere (Eikehaug et al. 2023a, this issue). The FluidFlower has no-flow boundaries at the bottom and both sides, whereas the top is open with a fixed free water column (constant hydrostatic head). Relevance for subsurface carbon storage processes is maintained as dominant multiphase flow parameters and trapping mechanisms are present in the room-scale laboratory flow rig, including capillarity, dissolution and convective mixing.

The dry, unconsolidated sands were manually poured from the top into the water-filled void between the front and back panels. Each layer (consisting of one sand type, except the heterogeneous fault) was constructed from the bottom and upward, and faults and large dipping angle were created by manipulating the layer during pouring using guiding polycarbonate rectangles, funnels and plastic hoses. Mechanical manipulation (raking/scratching) was kept to a minimum and only in some areas in the vicinity of the faults. Faults were constructed though an iterative process, detailed in (Haugen et al. 2023, this issue), and the sealed fault was created using a silicone rubber rectangle. The hydrostatic pressure during geometry assembly was 100 mm above operating conditions. When the geometry was complete, the water-level was lowered to operating water-level (kept constant during all injections). Multiple flushing sequences using injection rates 10% higher than the injection protocols (cf. SM 4) were performed to achieve an initial, pre-injection sand settling to improve conditions for reproducibility during CO₂ injections. The nominal porous media depth was 19 mm, but depth variations were observed and accounted for with a spatially resolved depth map (cf. SM 2).

2.4 The Rationale Behind the Benchmark Geometry

The geological geometry of the physical room-scale model (cf. Fig. 1) was motivated by typical North Sea reservoirs. It was developed in close interdisciplinary collaboration between UiB researchers from reservoir physics, earth science and applied mathematics based on the following four principles:

• 1. Incorporate relevant features frequently encountered in subsurface geological carbon sequestration.

• 2. Enable realistic CO₂ flow patterns and trapping scenarios with increasing modeling complexity.

• 3. Sufficiently idealized for the sand facies to be reproduced numerically with high accuracy.

• 4. Be able to operate, monitor and reset the fluids within a reasonable time frame.

The geometry was designed to achieve realistic CO₂ flow and trapping mechanisms to evaluate the modeling capability of the porous media community. The anticipated CO₂ flow, migration and phase behavior from each of the two CO₂ injection wells are described below, along with a geological interpretation of the benchmark geometry where geological features described are found in Fig. 1 and highlighted in italic below.

2.5 Geological interpretation of benchmark geometry

The benchmark geometry is a compromise between geological realism, building a physical model from unconsolidated sand, and accurate gridding for numerical simulations of the geometry. The benchmark geometry comprises two stacked reservoir-seal systems, each capped by regional seals (represented by sand ESF). The lower reservoir is a homogeneous, high permeability reservoir (sand F) overlain by a laterally continuous seal. In contrast, the upper reservoir is stratigraphically more heterogeneous, forming an overall upward fining succession, but with permeability variations within the coarse sand layers (alternation of sands E, F, D and C), and additional stratigraphic complexity around a sealed fault associated with the local development of sands C and D.

Structurally, the benchmark geometry is relatively simple, characterized by broad open folds and normal faults. The major left-dipping normal fault (heterogeneous fault) breaches the lower reservoir-seal system and terminates upward at the base of the upper reservoir (within sand F). A broad open anticline, in the footwall of the fault, forms the main trap to the lower reservoir-seal system and has a spill point in the immediate footwall of the fault. The broad open anticline is also the main trap geometry for the upper reservoir-seal system, but this is affected by a graben bounded by two oppositely dipping normal faults; one sealed fault and one open fault. An additional, subtle, low relief anticline forms an additional trap in the footwall of the graben-bounding sealed fault. The graben-bounding faults tips-out downdip into the basal layer of the upper reservoir (sand E) and updip into the base of the top regional seal (the uppermost sand layer in the model), as such they only affect the stratigraphy in the uppermost reservoir. The sealed and open faults have different properties and sealing potential: the sealed fault is designed as a sealing fault with a low permeability fault core, whereas the open fault has a high permeability fault core and would potentially act as a conduit for cross-formational fluid flow.

Anticipated flow from well [9,3]. The buoyant gas phase flows upward and reaches the anticline sealing layer (sand ESF) above the injection point [9,3]. CO₂-saturated water is observed in the near-well region directly after onset of CO₂ injection. The anticline dipping angle facilitates gas migration into Box A and accumulation at the highest point of the CO₂ trap. The trap fills with gas and a layer with CO₂-saturated water forms underneath the downward expanding gas accumulation. The CO₂-saturated water flows downward into Box C over time due to (i) the positive pressure gradient from the expanding gas and (ii) convection because of the increased density relative to formation water. The gas accumulation increases upon continued injection until the gas-water interface aligns with the spill point; the excess gas flows through the heterogeneous fault and into Box B containing the fining upward sequence and upper fault zone. The layered sequence (sands F, E, D and C, bottom to top) temporarily traps buoyant gas and laterally spreads the gas phase at the capillary barriers between layers. The increased density of CO₂-saturated water relative to the formation water leads to gravitational fingers. The CO₂ injection ends (after 305 min) when the gas reaches the upper sand layer (sand C) under the seal, and CO₂ in all forms is contained between the left no-flow boundary and the sealed fault.

Anticipated flow from well [17,7]. The gas phase (injected in sand F) flows upward and spreads laterally at layer boundaries in the fining upward sequence (except between sand F and E, cf. Table 2). The gas phase advances upward sequentially when it exceeds the capillary entry pressure in each layer. The CO₂-saturated water flows downward due to increased density and the pressure gradient of the gas accumulation—its flow pattern is influenced by the permeability variations in the layered sequence. The gas phase accumulates under the top seal above the injection well and migrates laterally until CO₂ injection is terminated (after 165 min). Depending on the volume of CO₂ injected, the gas phase will reach the open fault, and CO₂ in all forms will be contained between the open fault and the right no-flow boundary.

Fig. 1

The benchmark geometry with color enhanced layers for facies identification. Each sand type (ESF, C, D, E, F and G; cf. Table 2) has a separate color indicated to the left. Sand/color correlation: ESF/yellow; C/light blue; D/light brown; E/red; F/green; G/dark blue. The geometry includes three faults: sealed (silicone strip), open (sand G) and heterogeneous (sands G, F, D and C). Total length of visible porous media is 2800 mm, and porous media height is nominally 1300 mm. Edge shadows visible on the left and right, and the active porous extends 30 mm behind the black metal frame on each side. The three no-flow boundaries (left, right and bottom) are indicated gray, whereas the open boundary is blue (top). A 100 × 100 mm Cartesian grid with the origin [0,0] in the lower left corner with the x-axis positively oriented toward the right and the y-axis positively oriented toward the top aids the following coordination. Four monitored ports: two CO₂ injection well (red circles, coordinates [9,3] and [17,7]) and pressure ports (purple circles, coordinates [15,5] and [17,11]). Areas for reporting (Box A, B and C) are defined with the following coordinates (top right = TR; top left = TL; bottom right = BR; bottom left = BL): Box A: TL [11,6] -> TR [28,6], BL [11,0] -> BR [28,0]; Box B: TL [0,12] ->TR [11, 12], BL [0,6] -> BR [11,6]; Box C: TL [11, 4] ->TR [26,4], BL [11,1] ->BR [26,1]

2.6 Image Acquisition and Analysis

The camera (Sony A7III, lens SAMYANG AF 45 mm F1.8) used the following settings (kept constant through all injections): shutter speed 1/30 sec; F number F2.8; ISO 100; color temperature 4100 K; and manual focus. The camera was positioned in the curve focal point with a 3.6 m distance from the center point in the rig, halfway up the window height. Images were captured at high spatial (7952 × 4472 pixels, for a total of 35.5 megapixels) and temporal (between 10 s and 5 min intervals, depending on active experimental phase) resolution to capture displacement and mass transfer dynamics. Each run consists of more than 1000 images; a subset that captures key events, displacement processes and mass transfer dynamics is available for open-access download (Eikehaug et al. 2023b). The subset contains 137 high-resolution images with the following intervals: 10 images before CO₂ injection at 20 s intervals; images every 5 min during the first 360 min (6 h) of the experiment (73 images); images every hour until 48 h (42 images); images every 6 h until end of experiment (12 images).

2.6.1 Phase Identification

The image analysis toolbox was used to separate between the different CO₂ phases (gaseous and aqueous) present in the experiments, and a set of assumptions enabled the quantification of each phase to be calculated during the CO₂ injection and associated mixing. Four main phases are anticipated:

• 1. Free gas (potentially flowing gas phase with nonzero gas permeability, referred to as mobile gas).

• 2. Trapped gas (residually trapped CO₂ with zero gas permeability, referred to as immobile gas).

• 3. CO₂-saturated water (aqueous phase with a nonzero CO₂ content).

• 4. Formation water (aqueous solution with zero CO₂ content).

Several assumptions were needed to quantitatively describe the observed multiphase flow phenomena during repeated CO₂ injections in the physical flow rig (these and further assumptions required for the data processing are discussed in more detail in SM 3):

• SM3.I we assume that gas-filled regions are 100% saturated with the gas (CO₂).

• SM3.II we assume a constant CO₂ concentration in the CO₂-saturated water.

• SM3.III we do not account for the dynamics of the gas partitioning in the gas accumulation.

Based on these assumptions, a two-staged geometric separation of the formation water from any CO₂ in the system and of the gaseous CO₂ from the CO₂-saturated water is sufficient. This separation was possible due to the use of the pH-indicator mix (cf. Table 1; Fig. 2). Through pixel-wise image comparison to the image corresponding to the injection start, a thresholding approach first in the CMYK color space restricted to the key (black) channel, indicating any sort of change, and subsequently in the blue channel of the RGB color space, highlighting the gaseous phase, accomplishes the separation. The threshold parameters are carefully tuned through visual identification of the respective distinct plumes and their boundaries, based on several calibration images from all experimental runs. The heterogeneous nature of the geometry is considered in the analysis by choosing facies-based threshold parameters and thereby allows for tailored and relatively accurate phase segmentation, cf. Fig. 2. The parameters are chosen such that transition zones are included as demonstrated. In addition, further techniques are used to convert the resulting thresholded scalar images to Darcy-scale quantities, cf. (Nordbotten et al. 2023). The same unified setup has been used for analyzing all experimental runs.

Fig. 2

Resulting phase identification of formation water, CO₂-saturated water and free gas using DarSIA, at injection stop; two plumes are identified, containing free gas regions (yellow contour) and CO₂-saturated water (green contour). Subfigure B: The pH-indicator mix (left and right, with and without contours, resp.) allows for visual separation of the different phases based on color spectra. Subfigure C: Detection of free gas in the open fault. Subfigure D: Due to the use of regularization in the upscaling, DarSIA smears out fingers and thus merely detects fingertips for fingers that are closer than a few grain diameters

It must be noted that based on the choice of the assumptions and the resulting image analysis, the identification of gaseous phases for which assumption SM 3.I is not satisfied may be erroneous; transition zones smear out and the saturation decays which leads to a sudden disappearance of the post-processed gaseous phase due to the use of fixed threshold parameters. In all experimental runs, two gaseous regions are detected, cf. Fig. 2, and the described effect takes place for the upper gaseous region, whereas the lower region is detected stably. While the upper region fully dissolves, the lower region results in remaining gas, cf. SM 3.III, which is detected as gaseous CO₂. Consequently, the subsequent quantitative analysis reports on a small amount of non-vanishing gas accumulation toward the end of the experimental runs.

2.6.2 Procedure in the Quantitative Analysis

The subsequent quantitative analysis results from post-processing the phase identification. We briefly elaborate on the procedure of key computations.

• 1. Mass calculations and concentration maps. Total CO₂ mass of dissolved and mobile CO₂ are determined through integration of the pixel-wise defined areal densities of mobile CO₂, $m_{{{\text{CO}}_{2} }}^{g} = \varphi \cdot d \cdot s_{g} \cdot \chi _{c}^{g}$, and dissolved CO₂, $m_{{{\text{CO}}_{2} }}^{w}=\varphi \cdot d \cdot {s}_{w} \cdot {\chi }_{c}^{w}$, with the single components determined as follows. Based on assumption SM 3.V, the porosity $\varphi$ and the depth $d$ can be accurately determined. Resulting from assumption SM 3.I, the phase identification provides saturation maps ${s}_{g}$ for the gaseous phase and ${s}_{w}$ for the aqueous phase, taking values either 0 or 1. It remains to quantify the mass concentrations of CO₂, ${\chi }_{c}^{g}$ and ${\chi }_{c}^{w}$ in gaseous and aqueous phases, respectively. Based on assumption SM 3.I, ${\chi }_{c}^{g}$ is provided as the density of gaseous CO₂ under operational conditions, cf. SM 1, obtained from the NIST database (Lemmon et al. 2022). With that, the pixel-wise areal density $m_{{{\text{CO}}_{2} }}^{g}$ is known. Assumption SM 3.II allows now for obtaining the remaining mass concentration ${\chi }_{c}^{w}$ through sparsification, as follows. As illustrated in Fig. 2, two CO₂ plumes originating from the two injection ports remain unconnected throughout almost the entire run time (until 84 h). The total CO₂ mass in each plume is known at any point in time based on the injection protocol, cf. SM 4, while the respective total mass of mobile CO₂ is determined through integration of $m_{{{\text{CO}}_{2} }}^{g}$ over the area of the plumes. Subtraction of both provides the total mass of dissolved CO₂ for each plume. Finally, by assumption SM 3.II, ${\chi }_{c}^{w}$set to be 0 in the formation water; constant and equal to the proportionality constant between the total volume and the total mass of dissolved CO₂ in each connected region of CO₂-saturated water ${\chi }_{c}^{w}$; and not relevant for the mass calculations, yet for the discussion of convective mixing, in the remaining gaseous regions, ${\chi }_{c}^{w}$ is set to ${\chi }_{c,\,{\rm max}}^{w}$ =1.8 kg/m³.

• 2. Physical variability. Given a set of phase segmentations, associated to different configurations, the intersections and complements of phase segmentations can be directly determined. Furthermore, we introduce metrics based on volume-weighted ratios of these, to quantify corresponding overlap and unique appearances of detected regions.

• 3. Fronts and fingers. When restricted to a region of interest, the internal interface between the detected water formation and the CO₂-saturated water can be interpreted as propagating front. Its length can be determined by making use of the Cartesian coordinate system attached to the images. Extremal points can be identified as fingertips, allowing to count them over time. Due to the use of regularization in DarSIA, when converting grain-scale data to Darcy scale, fingers are slightly smeared out. This affects the detection of the free space in between fingers, cf. Fig. 2. Thus, in these regions the resulting interface between the formation water and CO₂-saturated water can be understood as approximating non-convex hull of the fingers with its length being a lower estimate to the actual contour length of the fingers. The detection of single fingertips is, however, not affected resulting in lower uncertainty.

2.7 Image Analysis Toolbox

To use the high-resolution images as measurement data, image analysis is required. As part of the benchmark study, the open-source image analysis software DarSIA (short for Darcy Scale Image Analysis, Both et al. 2023a) has been developed, detailed in [Nordbotten et al. 2023, this issue]. DarSIA provides the capability to extract physically interpretable data from images for quantitative analysis of the image sequences of the time-lapsed CO₂ injection and storage experiments. In particular, DarSIA includes preprocessing tools to align images; project suitable regions of interest of images onto two-dimensional Cartesian coordinate systems; correcting for geometrical discrepancies due to, e.g., the curved nature of the physical asset; as well as correcting white balance fluctuations and perform color correction utilizing the color checker attached to the physical asset, overall, resulting in unified image sequences. Furthermore, additional analysis tools are available to, e.g., determine spatial deformation maps comparing different configurations and extract concentration profiles or identify phases, to mention a few. The latter aims at a Darcy-scale interpretation of the high-resolution images taken of the physical asset, effectively, removing sand grains and upscaling fluid quantities.

3 Results and Discussion

This section is divided into two parts: Part 1 relates to the sparse dataset requested in the benchmark study (Flemisch et al. 2023) and includes a discussion on temporal behavior for studied parameters across repeated runs; Part 2 expands our analysis and focuses on physical variability between repeated injections and drivers for the observed variability.

3.1 The Benchmark Sparse dataset

The sparse dataset (defined in Nordbotten et al. 2022) requested six data points to assess the ability of the participating modeling groups to forecast relevant properties of the physical system. The CO₂ phase was to be reported in the following three categories: mobile free phase (gas at saturations with a positive gas relative permeability), immobile free phase (gas at saturations with zero gas relative permeability), dissolved (mass of CO₂ in CO₂-saturated water). The sum of the mobile, immobile and dissolved phases equals the total mass of CO₂. The sparse dataset is included for completeness here, but the reader is referred to (Flemisch et al. 2023) for comprehensive analysis and discussion.

The following sparse data were requested (cf. Fig. 1 for described regions and pressure ports):

• 1. As a proxy for assessing risk of mechanical disturbance of the overburden: Maximum pressure [N/m²] at pressure port (a) [15,5] and (b) [17,11].

• 2. As a proxy for when leakage risk starts declining: Time [s] of maximum mobile CO₂ [g] in Box A.

• 3. As a proxy for our ability to accurately forecast near-well phase partitioning: CO₂ mass [g] of (a) mobile; (b) immobile; (c) dissolved; and (d) total in seal in Box A at 72 h after injection start.

• 4. As a proxy for our ability to handle uncertain geological features: CO₂ mass [g] of (a) mobile; (b) immobile; (c) dissolved; and (d) total in seal in Box B at 72 h after injection start.

• 5. As a proxy for our ability to capture onset of convective mixing: Time [s] for which the quantity.

$$M\left(t\right)\equiv {\int }_{C}\left|\nabla \left(\frac{{\chi }_{c}^{w}\left(t\right)}{{\chi }_{c,\text{m}\text{a}\text{x}}^{w}}\right)\right| dx$$

first exceeds 110% of the width of Box C, where ${\chi }_{c}^{w}$ is the mass fraction of CO₂ in the CO₂-saturated water.

• 6. As a proxy for our ability to capture migration into low-permeable seals: Total mass of CO₂ [g] in the top seal facies (sand ESF) at final time within Box A.

Here we report laboratory sparse dataset (cf. Table 3) using the dataset (Eikehaug et al. 2023b) and dedicated DarSIA scripts (Both et al. 2023b) with assumptions (cf. SM 3). The CO₂ distribution after 72 h with locations of Box A, Box B and Box C is included to aid interpretation (see Fig. 3).

Table 3 Benchmark Sparse dataset

Fig. 3

Distribution of CO₂ after 72 h for run C3. The positions of Box A (green, dashed line), Box B (white, dashed line) and Box C (blue, dashed line) are used to populate the sparse benchmark dataset. The shaded regions in the benchmark geometry (top right and bottom left) are outside the defined boxes. CO₂ (in any form) in the shaded regions was not included in the analysis for the sparse dataset

3.1.1 Maximum Pressure at Ports [15,5] and [17,11] (parameters 1a and 1b)

The maximum pressures at the pressure ports ([15,5] and [17,11]) located in the sealing structures (sand ESF, cf. Fig. 1) were initially recorded with five pressure transducers (ESI, GSD4200-USB, -1 to 2 bara) because single digits millibar pressure gauges were not available for the benchmark study. The results were, however, discarded because 75% of the transducers recorded pressures less than the atmospheric pressure in the room. Hence, we use historical atmospheric pressure data reported from a nearby meteorological weather station (here Geophysical Institute, SM 1) and adjust for differences in elevation between the two locations. We then added the calculated hydrostatic pressures (see Table 3) to the recorded atmospheric pressure to get an estimate for the maximum value in each port. We apply an uncertainty of ± 1 mbar, five times stated instrument accuracy, to account for the possible overpressure during CO₂ injections.

3.1.2 Time of Maximum Mobile CO₂ in Box A (parameter 2)

The development in mobile gas in Box A for all five runs (cf. Fig. 4) increased linearly with the injection until the gas accumulation aligned with the spill point (defined in Fig. 1). On average, the maximum mass of mobile gas was observed after 4.11 ± 0.17 h. While there appears to be some noise in the identification of the maximum mobile gas, the time of maximum value is a clearly defined peak in the time series. Seen together with temporal resolution of the image series (20 s per frame), we expect identification of the time for maximum mobile CO₂ have an uncertainty of no more than three frames, i.e., ± 1 min. The nature behind the fluctuating mass after the initial spill (cf. black rectangle, Fig. 4) is discussed in more detail in Section 3.2.

3.1.3 Mobile, Immobile and Dissolved CO2 in Box A and Box B (parameters 3, 4 and 6)

The mass of mobile gas in Box A (parameter 3a in Table 3) was on average 0.232 ± 0.047 g and is considered an upper bound for this parameter. The lower bound was found indirectly from the observation of nonzero mass of mobile gas at the end of the experiments (cf. Fig. 4), related to atmospheric gases in the formation water due to insufficient degassing (cf. Chapter 2.1 and Haugen et al. 2023 ). Based on our physical understanding of the studied system, we anticipate that the mass of mobile CO₂ should be zero at the end of the experiment. Hence, we subtract the end point mass from the upper bound to find an estimate of the lower bound, cf. Table 3. An alternative, but also physically plausible, lower bound for parameter 3a is zero, where all the mobile gas (CO₂) is dissolved in the CO₂-saturated water. The mass of mobile gas in Box B after 72 h (parameter 4a) is reported as zero because mobile gas was not observed in the segmented images.

The mass of immobile gas in Box A and Box B (parameters 3b and 4b in Table 3) were reported as zero because the formation water did not generate a unique and characteristic color for immobile gas. Hence, DarSIA and its color-based segmentation (cf. Section 2.5) are not able to distinguish immobile gas from the other phases. Careful visual inspection identified small amounts of immobile gas at early times, but visual inspection at 72 h did not identify any immobile gas. This is consistent with our physical understanding of the system, where isolated bubbles of CO₂ are expected to dissolve quickly.

The mass of dissolved gas in the CO₂-saturated water in Box A and Box B after 72 h (parameters 3c and 4c in Table 3) were 3.10 ± 0.07 g (Box A) and 0.778 ± 0.066 g (Box B), see Fig. 5. The mass calculations use the known injected CO₂ mass in well [9,3] for Box A and well [17,11] for Box B and apply DarSIA to segment the separate plumes originating from each well to calculate the mass of mobile and dissolved gas (cf. Section 2.5). The two plumes remain unconnected throughout almost the entire run time (until 84 h), and the total CO₂ mass in each plume is known at any point in time based on the injection protocol. After 84 h the plumes merge and the plots are extrapolated to 120 h (end of experiment) based on current trends. The mass of CO₂ in the sealing structures in Box A and Box B after 72 h (parameters 3d and 4d in Table 3) were 0.382 ± 0.012 (Box A, cf. Fig. 5) and 0.00 (Box B). Mobile and dissolved gas did not enter the top regional seal confined within Box B, but minute amounts of dissolved gas (in the order of 10⁻³ g) entered the sealing structure in the lower, right corner of Box B after 72 h. Hence, the final mass of CO₂ in the sealing structure confined within Box A (parameter 6, cf. Fig. 6) was on average 0.567 ± 0.035. For the parameters discussed here (3c, 3d, 4c, 4d and 6), we attribute a nominal measurement uncertainty of ± 20% based on the limitations and influence of underlying assumptions (cf. SM 3), stated weakness in the analysis of the color scheme (cf. Section 2.5), extrapolating trends and operational difficulties with mineralization of methylene red.

Fig. 4

Development in mass (g) of mobile gas in Box A for the whole experimental time (120 h) for all five runs (C1–C5) and the average (black, dashed line). The mass increased linearly with the injection rate until spill time (cf. Table 3) and then decreased because the mobile gas dissolved into the formation water. The development in mobile mass associated with the spill point (black rectangular) is discussed in detail below

Fig. 5

The development in mass of dissolved CO₂ (g) in CO₂-saturated water in Box A (open circles) and Box B (crosses) for runs C1–C5 during the whole experimental time (120 h). All mass curves increase from the onset because mobile gas dissolved into the formation water to form CO₂-saturated water and reach plateau values when most of the gas within each box is dissolved. The curves in Box B remain zero until the gas exceeds the spill point and flow into the fault (after approximately 4 h). The somewhat different development for run C1 in Box A (blue circles) and run C5 in Box B (purple crosses) relates to the inconsistencies for these runs, discussed in Section 3.2. Note that the average curves (black, dashed lines) are calculated until 84 h

Fig. 6

Development of CO₂ (in any form) in sealing layer (sand ESF) confined within Box A during the whole experimental time (120 h) for all five runs (C1–C5). Only CO₂-saturated water (no gas) was observed in the sealing layer in Box A, and advection from the underlaying gas was the main driving force for increased mass initially. After gas injection stopped (after approximately 5 h), there was a slight decrease of CO₂ mass in the sealing layer, explained by gravity of the denser CO₂-saturated water and diminishing advective forces due to a reducing gas cap under the anticline. After approximately 20 h, the mass increases again because CO₂-saturated water from injector [17,7] flows downward and enters the top boundary of Box A (cf. Fig. 4 after 72 h)

3.1.4 Development in M (t) Relative to the Width of Box C (parameter 5)

The $M\left(t\right)$ (parameter 5 in Table 3) is a measure of the total variation of the concentration field. As such, it is related to the contour lengths of the density-driven fingers, and we normalize it relative to the length of Box C, so that a value of ${M}_{\rm norm}\left(t\right)=1$ corresponds to no fingers below a gas cap spanning the whole length of the top of Box C. As CO₂-saturated water migrated downward due to gravity, the contour lines and the ${M}_{\rm norm}\left(t\right)$ increase (see Fig. 7). On average for the five runs ${M}_{\rm norm}\left(t\right)$ exceeds 110% of the width of Box C after 4.14 ± 0.4 h, where the stated times for each run may be considered as an upper bound due to the assumption that the concentrations are constant, which decreases the measure of the gradient in the integral. A lower bound is the time when ${M}_{\rm norm}\left(t\right)$ reached 100% of the length of Box C, which is closely correlated to gas filling the upper boundary of Box C, a necessary prerequisite for ${M}_{\rm norm}\left(t\right)$ exceeding 110%.

Fig. 7

Development in ${M}_{\rm norm}\left(t\right)$ for all five runs from injection start until end of experiment (120 h). For the initial state of a zero CO₂ concentration within Box C, ${M}_{\rm norm}\left(t\right)$ takes the value 0. Run C1 (blue) is ahead of the other runs, both in the start and at the end (fingers start to leave Box C). The rapid increase between 3 and 4 h arises because the mobile gas fills the top of Box C. The reverse is true after approximately 10 h (6 h for run C1) when the gas accumulation (due to shrinking by dissolution) exits the upper boundary of Box C and the parameter ${M}_{\rm norm}\left(t\right)$ rapidly decreases. This is counterbalanced to some extent by the further development of the density-driven fingers, as seen around 20 h, until dissolution and diffusion eventually leads to a more uniform distribution of dissolved CO₂, and ${M}_{\rm norm}\left(t\right)$ approaches 0 again

3.2 Physical Repeatability of Multiphase flow During Laboratory Carbon Sequestration runs

The benchmark study consisted of five operationally identical CO₂ injection experiments using the same geological geometry and initial conditions. The experiments were designed to generate physical data for model comparison, with the motivation to achieve a physical ‘ground truth’. Here we discuss physical repeatability between the five runs (C1–C5) by comparing the degree of areal sweep overlap incorporating all forms of CO₂ (mobile, immobile, dissolved) in three regions (Box A, Box B’ and Box D, cf. Fig. 8) with increasing geological complexity. We quantify the degree of overlap of runs C2, C3 and C4 and discuss the uniqueness of each run.

Fig. 8

Degree of physical overlap and description of Box A, Box B’ and Box D with increasing geological complexity. Box A is identical to Fig. 1; Box B’ is an extension of Box B (cf. Fig. 1) and includes the lower part of the geometry left to the heterogenous fault; Box D includes the fining upward sequence associated with injector [17,7] and the open fault (cf. Fig. 1). The CO₂ distribution (all forms) for all five runs (C1–C5) in three boxes (Box A, Box B’ and Box D) after 155 min of CO₂ injection is shown. Spatially distributed overlap for all runs, with the following color scheme: gray (overlap C2 + C3 + C4); blue (unique C1); orange (unique C2); green (unique C3); red (unique C4); purple (C5 unique); brown (combinations all runs with at least one of C2, C3 or C4), white (other combinations). The reader is referred to SM 5 for additional time steps

3.2.1 Physical Reproducibility with Increasing Reservoir Complexity

We investigate the reproducibility between five runs in the same geometry, with the hypothesis that increased reservoir complexity tends to reduce the degree of physical reproducibility. As mentioned above, our motivation to achieve a physical “ground truth” was not fully achieved. This was because our ‘identical’ experiments indeed were not truly identical, even if the gas injection protocol was (within measurement uncertainty, cf. SM 4). Next, we describe the two known variables that influence the displacement patterns:

• 1. Inconsistent water chemistry. The formation water (cf. Table 1) in run C1 unintentionally used tap water instead of deionized water. The inconsistent water chemistry for C1 resulted in a unique dissolution rate and convective mixing behavior (cf. Figure SM.3). Run C1 is thus omitted from the analysis of physical reproducibility.

• 2. Atmospheric pressure variations. The atmospheric pressure variations in Bergen (cf. Figure SM.1) resulted in a low-pressure outlier for run C5 (968 mbar) compared with the other runs (on average 999 mbar during the injection period, cf. Table SM 1). Hence, the larger volume of the injected CO₂ (equal mass injected for all runs) influenced key parameters in the experiment (most prominently parameter 2 in Table 3, but also rate of dissolution). Run C5 is thus omitted from the analysis of physical reproducibility.

The described operational (water chemistry) and environmental (atmospheric pressure) inconsistencies provide the rationale for excluding C1 and C5 in our analysis of physical reproducibility for operationally identical experiments with comparable pressure and temperature conditions. An analysis of sand settling between runs showed only minor changes (cf. SM 6). Hence, we focus on runs with comparable system parameters and report the development in overlap between runs C2, C3 and C4 (cf. Fig. 9). To compute the overlap percentages, we first weight all pixels in the segmented images with their corresponding volume (see SM 2). Then, the ratio between the number of volume-weighted pixels where CO₂ (gas and dissolved) in C2, C3 and C4 overlap and the number of volume-weighted pixels where CO₂ (gas and dissolved) in any of the three runs appear is reported. Next, we describe the development in physical overlap within Box A, Box B’ and Box D.

The development in physical overlap in Box A may be divided into four intervals: i. pre-spilling; ii. gravitational fingers, iii. dissolution-driven flow and iv. homogenization. The pre-spilling interval (from the injection start to approximately 4 h) occurred before the gas column height exceeded the spill point. The onset of gravitational fingers occurred in this interval, but they were still only minor and did not develop into pronounced gravitational fingers. The overlap increased from injection start and reached a global maximum (97% overlap) after approximately 4 h, with an average 92% C_2,3,4 overlap for the whole interval. The uniqueness of runs C2, C3 and C4 were on average 0.14% (cf. Figure SM.4) during the pre-spilling period. The gravitational fingers interval (approximately 4 to 30 h) was characterized by development of pronounced gravitational fingers in  the gas accumulation under the anticline trap in Box A. The physical overlap of C_2,3,4 decreased from 97 to 79% (local minimum), dominated by the differences in number of fingers and individual finger dynamics (discussed in more detail below). The dissolution-driven flow interval (approximately 30 to 70 h) describes the period when the gravitational fingers reached the no-flow at the lower Box A boundary, and fingers started to move lateral and merge as the gas accumulation dissolved and pulled aqueous phase from surrounding regions into Box A. The physical overlap increased to above 95% in this period. The homogenization interval (approximately 70 to 120 h) was characterized by a constant physical overlap (above 95%) with only minor movement of aqueous phases confined in Box A.

Box B’ generally follows the overall behavior of Box A in the four intervals defined above. Importantly, the reduction in physical overlap observed in the gravitational fingers interval (after approximately 4 h) was related to variable spilling times for runs C2, C3 and C4, not related to finger development (cf. parameter 2, Table 3 that approximates the spilling time for each run). The variation in spill times resulted initially in reduced overlap with slight variation in fault migration and displacement patterns for runs C2,C3 and C4. The sustained reduction of physical overlap stems from an apparent stochastic variation for run C3 (cf. Figure SM.3; 10 h), corroborated with development of the uniqueness for each run (cf. Figure SM.4; middle). The physical explanation for the observed variation in run C3 is not clear, but this only occurred for that single run, with subsequent runs (C4 and C5) reverting to the flow patterns seen for the earlier runs (C1 and C2). Hence, we do not expect the deviation in run C3 to stem from any physical alterations within the experiment (sand settling or chemical alterations). Remaining explanations could be related to variations in atmospheric pressure, or factors outside our experimental control.

The development in Box D was delayed in time relative to Box A and Box B’ due to the later injection start of well [17,11], but follows the overall trend: initially increasing overlap, slight reduction due to finger development and convective mixing, then increase through homogenization. Small amounts of dissolved gas were observed in a localized point the top regional seal contained in Box D for most runs (cf. Figure SM 3). The seal breach occurred around a plugged port (CO₂ migrated along the sealing silicone), resembling a of CO₂ leakage scenario along a poorly abandoned well.

Fig. 9

Degree of physical reproducibility between operationally identical CO₂ injection runs with comparable pressure and temperature conditions (runs C2, C3 and C4). Box A (green line) represents the most homogenous case; Box B’ (red line) represents the case with the heterogenous fault zone and fining upward sequence; Box D (purple line) represents the middle case with a fining upward sequence. Overlap considering the whole geometry (dashed line) is included for comparison

3.2.2 Dynamics of Gravitational Fingers in Box C

Box C is the homogenous zone under the lower anticline under the main gas accumulation and where most of the gravitational fingers emerged during and after CO₂ injection. From image analysis it was possible to extract the development of fingers as a function of time for all runs (cf. Fig. 10). Noticble fingers appear after an onset time of approximately 3 h, and the number was reasonably stable around 25–30, which corresponds to a characteristic spacing of about 5–6 cm. The stability of the number of fingers was an indication that the system is near the regime of the “maximally unstable” fingers spacing, predicted by theoretical considerations (see, e.g., Riaz et al. 2006; Elenius et al. 2012). This observation is supported by the finger lengths, which indicated a linear growth regime after onset. Repeatability was observed in terms of onset location and finger dynamics, even at time significantly after onset (cf. Figure SM.5 and Table SM.3).

Fig. 10

Dynamics of convective mixing and gravitational fingers in Box C for all runs C1–C5. Left: Number of gravitational fingers, all runs follow the general trend: a rapid increase until a maximum is reached, followed by a declining number as some fingers merge. Right: The length (m) of the boundary of the phase segmentation, also identifying (an approximation) of the fingers. Note that the contour length only considers the boundary inside Box C. Both graphs end when the first finger reached the lower boundary of Box C (20 h)

3.2.3 Oscillating CO₂ Leakage from Anticline

The benchmark geometry and injection protocol were designed to achieve realistic displacement processes relevant for subsurface carbon storage, where most observed phenomena and mass transfer dynamics were anticipated; showcased in the description of expected behavior (cf. Section 2.4) and benchmark description (Nordbotten et al. 2022). An oscillating CO₂ spilling event from the lower anticline was observed in our study, something that was not anticipated. Non-monotonic leakage behavior has previously been suggested in the literature (Preuss 2005) and in natural analogues (Shipton et al. 2004), attributed to the interplay between multiphase flow, Joule–Thomson cooling and heat transfer effects in the fault plane. Pulsating non-wetting CO₂ invasion has also been studied experimentally in tanks with heterogeneous geometries (Glass et al. 2000), focusing on buoyant-driven flow through capillary barriers. Intermittent non-wetting flows with repeated fragmentation (snap-off) and reconnection during buoyancy-driven flows (Wagner et al. 1997; Islam et al. 2014), with pulsation in the capillary pressure (Geistlinger et al. 2006; Mumford et al. 2009) has previously been discussed. Flow pulsation in fingers under buoyancy can occur regardless of grain sizes, with stepwise invasion of the non-wetting phase as new pathways form (Geistlinger et al. 2006). To our knowledge, oscillating CO₂ leakage behavior from an anticline spill point into a fault zone in the absence of thermal effects has not previously been observed experimentally nor received attention in the literature. Below we discuss the displacement dynamics during multiphase flow in the fault plane generating the observed oscillating anticline CO₂ leakage behavior.

The mass of mobile gas in Box A oscillated after the initial spilling event for all runs (cf. Fig. 11). The gas escapes the anticline trap in bursts and flows into the narrow restriction at the bottom of the fault (aligned in height with the spill point). When gas migrates upward in the fault zone (essentially a localized permeable pathway) it displaces resident aqueous fluids downward. The inflow of aqueous phase effectively reduces and ultimately blocks the upward migration of gas. This is in essence because the localized pathway in the inlet region of the fault cannot accommodate stable counter-current flow (upward gas flow and downward water flow), possibly due to viscous coupling effects (see, e.g., the review paper by Ayub and Bentsen 1999). When the upward migration of gas is temporarily blocked, the anticline gas column height increases again with continued CO₂ injection. The process then repeats itself when the aqueous phase flow dissipates. A secondary effect is that the inflowing aqueous phase increases the local water saturation between the spill point and the inlet point of the fault and traps gas. The gas quickly dissolves into aqueous phase, and the subsequent spilling events (up to four events per run) are essentially local drainage processes, characterized by oscillating mass of mobile gas under the anticline (Box A). Interestingly, the process appears hysteretic in nature, with decreasing peak mass values for each event, most likely related either to increased gas relative permeability between the spill point and the fault, or changes in the local CO₂ concentration in the aqueous phase. The fluctuations stopped when the CO₂ injection terminated (after approximately 300 min, cf. SM 4), and the gas column height (and, hence, the mass of mobile gas) decreased under the spilling point.

To generalize the underlying causes for the observed phenomenon is difficult based on the reported experiments alone, but pulsation behavior of buoyant gas accumulations underneath capillary barriers has been observed in similar tank experiments (Glass et al. 2000). In their work, pulsation occurs when the gas breaks through the capillary barrier through a finger that cannot be sustained (due to reinvasion of the wetting phase in the capillary barrier) when the gas column height decreases. The cycle repeated itself with continued CO₂ injection as the gas accumulation height increased again. Although Glass et al. (2000) concluded that the pulsation behavior would not significantly impact large-scale CO₂ flow, the pulsation behavior may accelerate upward plume migration through capillary barriers, especially in a relatively homogeneous formation with sparse capillary barriers (Ni and Meckel 2021). In our work, the observations are to some degree influenced by the physical system (no-flow boundaries in the vicinity of the spill point and fault, and the fault geometry aligned with the spill point acting as a restriction of upward migration of gas) and presence and shape of the gas accumulation effectively reducing the area available for water flow. A systematic evaluation of the cyclic behavior including coupled processes and parameters of the problem remains a task for future work.

Fig. 11

Fluctuations in mass of mobile gas (g) in Box A after initial spilling event. The mass curves all demonstrate oscillations due to recurring spilling events from the anticline to the adjacent fault. For all runs, the maximum mass was observed before the initial gas escape. The lower atmospheric pressure for run C5 (purple circles) results in a lower initial spilling time

4 Concluding Remarks

The open-access, high-quality laboratory dataset, accompanied with dedicated analysis tools, represents an asset and opportunity for the carbon storage community to expand the current analysis in future studies. The physical data, describing many of the relevant processes for subsurface carbon storage, may also be used for model validation, comparison and data-driven forecasts for different stages of a carbon storage operation. Blueprints of the experimental infrastructure enhance reproducibility of scientific research and enable the porous media community at large to build physical assets and collectively join our efforts.

Our outlook, based on the observations identified in this study, is to probe the origin and premises for establishing non-thermally induced oscillating flows and to broaden the understanding of at what length scales and to what accuracy multiphase flows in porous media are deterministic.

In conclusion, the observed processes and phenomena qualitatively corroborate the physical understanding and knowledge within the carbon storage community. This supports the assertion that we have a sufficient understanding to claim that industrial carbon storage operations can be conducted in an efficient and safe manner.