1 Introduction

Carbon capture, utilization, and storage (CCUS) has been prioritized by many countries and international agencies as part of a strategy to lower CO2 emissions and mitigate climate change effects. The aim of CCUS generally is to capture CO2 from a variety of emitting sources and use it for many purposes (i.e., fuels, chemicals production, enhanced oil recovery, geological storage) to reduce atmospheric greenhouse gas emissions. Many studies have identified several challenges related to implementation of CCUS which can be classified broadly into political, cross-chain, economic, and technical issues (Muslemani et al. 2020). Poor injectivity is one of the technical issues often encountered during CO2 injection and storage in subsurface geological structures (Andre et al., 2014). Injectivity problems may be caused by a variety of reasons including asphaltene precipitation (Srivastava et al. 1999; Darabi et al. 2014; Cho et al. 2016), water blockage (Ford et al. 1988; Mahadevan & Sharma 2003; Arjomand et al. 2020b), salt precipitation (Giorgis et al. 2007; Pruess & Müller 2009; Andre et al. 2014; Ott et al. 2015) and fines migration (Sayegh et al. 1990; Mohamed et al. 2012; Iglauer et al. 2014; Yusof et al. 2022).

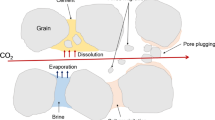
When CO2 is injected into saline aquifers, evaporation of liquid water into the CO2 phase leads to a process where the dissolved salts precipitate. This phenomenon is broadly called “salting-out”; in this context, salts can precipitate in the wellbore vicinity (Kleinitz et al. 2001; Lorenz & Müller 2003; Peysson et al. 2011). The dissolution of CO2 alone is not expected to cause a significant decrease in the solubility of sodium chloride in water at elevated pressure/temperature (Sawamura et al. 2007; Zhao et al. 2015). However, the solubility of other salts (e.g., calcium carbonate) are strongly related to pH resulting from CO2 dissolution into an aqueous phase. Regardless, precipitated salts are predominantly a result of water evaporation and cause a decrease in porosity resulting in potentially poor injectivity. The impact of salt precipitation is most prominent when capillary-driven backflow is also present. Under this condition, formation water (with dissolved salts) flows back toward the injection well due to capillary suction. As evaporation continues, further accumulation of localized salt precipitates near the wellbore takes place (Giorgis et al. 2007; Pruess & Müller 2009; Andre et al. 2014).

However, other studies found that injectivity impairment was insignificant in the presence of salt precipitation (Roels et al. 2014; Ott et al. 2015). In these experiments, precipitation formed homogenously indicating the absence of capillary-driven back flow. This causes CO2 to flow essentially as a single-phase when the porous media is virtually devoid of a water phase and the gas relative permeability increases to near unity. In other words, this overall mobility improvement results from the increase in relative permeability despite the effects of salt precipitation on absolute permeability. This specific phenomenon occurs only when CO2 injection rate exceeds a certain critical rate (Andre et al. 2014; Ott et al. 2015; Miri and Hellevang 2016). Below this critical rate, local precipitation due to capillary backflow can occur and the impact on mobility is more deleterious. However, the authors did not observe the phenomena in low permeability samples in which the formation of solid is supposed to affect the permeability significantly. Ott et al. (2021) conducted studies in a multi-porosity rock (i.e., dolomite) as opposed to Berea in their previous study showing that salt precipitation in this case strongly affects permeability.

For numerical simulations, evaporation of water into the CO2 phase is typically described as a kinetic phenomenon instead of local equilibrium partitioning. This kinetics approach was first investigated by Roels et al. (2014) in their study which coupled experimental results with numerical modeling. They found that using local equilibrium partitioning in a computational simulation for evaporation overestimated salt precipitation near the wellbore. With a kinetics model, the salt precipitation both near the well bore and further away from the well is more accurately simulated. On the other hand, Ott et al. (2015) identified that evaporation may take place weakly during viscous force displacement until the brine is immobile within the pores. After a couple of hours of injection, brine saturation changes only slightly. After a longer period where the water saturation remains constant, salt precipitation begins to dominate suggesting that evaporation is strong. Based on this study, solid saturation should not exceed irreducible water saturation even though capillary driven backflow takes place.

Though water blockage is more common in hydrocarbon reservoirs (particularly tight gas reservoirs (Bennion 2002)), water blockage can also take place when CO2 is stored in deep saline aquifers. Water blockage occurs when the formation water forms a thin film on the rock surface and occupies smaller pores leaving limited pore space for CO2 to flow necessitating a high injection pressure. In other words, water blockage reduces gas relative permeability (Mahadevan and Sharma 2003; Arjomand et al. 2020b; Lopez et al. 2021). The issue is common under strongly water-wet conditions (i.e., rocks composed predominantly of quartz) in sandstone reservoirs with invaded fluids which are used during drilling, completion, and fracturing activities (Holditch 1979; Bennion et al. 1996; Al-Anazi et al. 2003). Those activities may use water-based fluids and considering that water is strongly wetting toward sandstone an increase in irreducible water saturation near the perforation can occur. This issue is usually unpredicted as core analysis in laboratory may show low connate water saturation. In fact, the core sample may have been cleaned/restored which diminishes the observed impact of operating fluids during drilling, completion, or hydraulic fracturing activities.

Several remediation methods have been proposed to overcome the above-mentioned injectivity issues. Salt precipitation can be alleviated temporarily by pre-injecting low salinity water into the well reducing brine salinity around the wellbore (Pruess and Müller 2009). However, this method may only temporarily solve the problem by delaying or moving the location of the precipitation. As evaporation keeps taking place, immobile brine will extend causing salt precipitation albeit a bit later. Furthermore, injecting low salinity water can induce clay mineral activity causing other forms of damage (i.e., fines migration, and clay swelling). Another effort recently proposed and tested at the Quest CCS facility located in Alberta, Canada (Smith et al. 2022) used a water-based fluid to dissolve precipitated salts near the wellbore. This method succeeded in repairing the injectivity index to twice the pre-treatment value. However, there is no further evaluation regarding the possibility of water blockage following the treatment and fines migration induced by the water injection into the formation.

Regardless, it is worth noting that injection of CO2 could vaporize trapped brine (causing salt precipitation) as well as induce water blockage (Bennion et al. 1996). Generally, injectivity worsens with salt precipitation deteriorating the absolute permeability (Zuluaga and Monsalve 2003). In some caes, a high drawdown pressure remediates this issue (Bennion et al. 1996). Another approach is to use a chemical treatment to change the rock wettability and hence permanently impact the extent of water blockage. This includes injecting supercritical CO2 with an organo-alkoxysilane component (i.e., sc-CO2 based silylation) to chemically functionalize the rock surface and change the formation wettability toward less water wet thereby addressing water blockage (Arjomand et al. 2020b). This technique even outperforms conventional silylation using organic solvents by accelerating the kinetic reaction rate (i.e., the sc-CO2 based accomplishes the reaction within 30 min compared to 24 h for conventional method under otherwise similar conditions) (Sánchez-Vicente et al. 2014); a modest increase in coverage is also observed with this approach. Silane reagents have the general chemical formula RnSiX4-n, where “R” represents a non-hydrolysable organic group and “X” represents hydrolysable groups (typically halides or alkoxy groups). During the silylation process, organo-alkoxysilane modifies the rock surface by reacting with the hydroxyl groups on the rock surface (through a hydrolysis/condensation process) to form covalent bonds. Several studies which performed sc-CO2 based silylation on mesoporous silica found that silane reaches up to 1.6 molecules per nm2 of surface (Staroverov & Fadeev 1991; Cao et al. 2001; López-Aranguren et al. 2012). A recent study that used N,N-dimethylaminopropyl)trimethoxysilane (DMAPTS) in a sc-CO2 based method on mesoporous silica reached a bonding density of approximately 2.5 molecules/nm2 (Sánchez-Vicente et al. 2014).

To date, there have been several studies coupling experimental data with numerical simulations to evaluate formation damage due to salt precipitation during CO2 injection (Roels et al. 2014; Andre et al. 2014; Ott et al. 2015; Roels, et al. 2016; Ott et al. 2021). Also, water blockage has been observed frequently in gas reservoirs particularly with the development of low permeability gas reservoirs; the impact of CO2 injection on water blockage has been examined as well (Ford et al. 1988; Bennion et al. 1996; Bennion 2002; Mahadevan & Sharma 2003; Arjomand et al. 2020b; Lopez et al. 2021, 2023). However, such studies have only these issues on their own and not examined how they are coupled. This study attempts to simulate both water blockage and salt precipitation in a single numerical reservoir simulation and to analyze the impact of surface wettability (i.e., changes induced by the silylation process) when both take place in situ. The purpose of this study is to develop a deeper understanding of the corresponding phenomena during CO2 underground storage and well preparation before the implementation of a chemical treatment.

2 Numerical Simulation Model

2.1 Component Transport Equations

This work uses the same conservation equations that were used by Kohse and Nghiem (2004) to model the deposition of solid asphaltene from crude oil within a reservoir. This includes the basic components flow, asphaltene deposition rate (in this study, replaced by salt precipitation rate), and a materials balance of the deposited solids with the asphaltene present in crude oil. We use a similar model here noting that supercritical CO2 will be treated as the gas phase. Silane injection is simulated under miscible condition with CO2. Silane then will be adsorbed on rock surface as an outcome of silylation process where it will have minimal impact on the porosity and assumed to only affect the wettability characteristics (i.e., the multi-phase relative permeability behaviour). As silane acts like polymer within a porous media, transport equation normally used in polymer enhanced oil recovery is applied in this work. The accumulation terms of the flowing components and the adsorbed silane can be written as (Druetta and Picchioni 2019; CMG 2020):

$$\frac{\partial }{\partial t}\left[V{\phi }_{f}\left({\rho }_{g}{S}_{g}{y}_{i}+{\rho }_{w}{S}_{w}{w}_{i}\right)+V{\phi }_{v}{c}_{sil}\right]$$
(1)

where \(V\) is the grid block volume, \(\rho \) and \(S\) are the phase molar density in mol/m3 and phase saturation, respectively, \({c}_{sil}\) is the moles of adsorbed silane within the void pore volume in moles/m3, \({y}_{i}\) and \({w}_{i}\) are moles fraction of component-i—which are water, CO2, and dissolved salt—in the gas and water phases, respectively. \({\phi }_{v}\) and \({\phi }_{f}\) are void porosity and fluids-contained porosity, respectively. The relationship between \({\phi }_{v}\) and \({\phi }_{f}\) are proposed to consider the presence of solid salt (denoted as “salt”) and/or adsorbed silane. They are related following this formula:

$$ \phi _{f} = \phi _{v} \left[ {1 - \left( {c_{{sil}} /\rho _{{sil}} + c_{{salt}} /\rho _{{salt}} } \right)} \right] $$
(2)

where \(c\) and \(\rho \) are the moles of the component per void pore volume and their molar density. When there is no solid and/or adsorbed component, then \({\phi }_{f}={\phi }_{v}\). In this simulation, the small concentration of silane used has an insignificant impact on porosity with salt precipitation being the only solid which appreciably affects porosity.

The conservation equation for solid salt formation is written below (Parvin et al. 2020; CMG 2020):

$$\frac{\partial }{\partial t}\left({\phi }_{v}{c}_{salt}\right)={r}_{salt}$$
(3)

where \({r}_{salt}\) is a volumetric rate of salt formation in moles/day.m3.

2.2 Fluids and Mechanistic Models

2.2.1 Salt Precipitation Model

For this study (and similar to prior studies), the aquifer brine is assumed to be composed of only halite (i.e., sodium chloride) and water. The effects of minor impurities on salt precipitation due to evaporation are not considered here. The modified black oil (MBO) fluid model within the reservoir simulator Computer Modelling Group (CMG) was used with the STARS module. This simulator can also implement the kinetics of the evaporation process.

Experimental results obtained by Ott et al. (2015) with a 20 wt.% NaCl aqueous solution and numerical simulations results by Roels et al. (2014) were used to generate the salt precipitation kinetic model. A non-equilibrium phase partitioning was applied for the evaporation of water from the aqueous phase. This process results in an increase of salt precipitation which induces the precipitation. The mass transfer of water toward CO2 phase was simulated with a closer match between experimental results of salt precipitation distribution and subsequent numerical simulations, using kinetic approach following the reaction rate as follow (Pinder & Celia 2006; Roels et al. 2014):

$$r=k^{\prime}{\phi }_{v}\left({c}_{H2O,e}-{c}_{H2O}\right)$$
(4)

where \(r\) and \(k{\prime}\) are the evaporation rate (units of moles·day−1·grid volume−1) and reaction rate constant (units of day−1 for a first order reaction), respectively. \({c}_{H2O}\) and \({c}_{H2O,e}\) are the concentration factor (moles per void pore volume) of H2O in the CO2 phase at any time and its equilibrium concentration (moles per pore volume), respectively. Under these conditions, the maximum (or equilibrium) mole fraction of water in the CO2 phase was set at 0.004 (Ji et al. 2005; Spycher and Pruess 2005; Miri and Hallevang 2016). CO2 solubility in water is important during the CO2 injection into saline aquifer as it is responsible for the solubility trapping mechanism. However, within this context, the role of dissolved CO2 does not appreciably affect salt precipitation and as such is not considered in this work. Dissolved CO2 may induce mineralization near the wellbore such as Calcite precipitation. However, the amount of Calcite precipitation is negligible compared to that of Halite precipitation as shown in simulation results by Cui et al. (2018). The STARS module in the CMG simulators uses a specific factor “\(f\)” designed to explain weak evaporation processes when viscous forces are dominant. This factor is a function of water velocity and governed by the following equations (CMG 2020):

$$f={\left[\frac{v-{v}_{crit}}{{v}_{ref}}\right]}^{m}$$
(5)
$$k^{\prime}={k^{\prime}}_{ref}.f$$
(6)

where \(v\), \({v}_{crit}\), and \({v}_{ref}\) are the current, critical and reference velocities of water, respectively (see Table 1). The constant \(m\) is set negative resulting in a smaller factor for larger water velocities. Due to a non-zero rule for \({v}_{ref}\), it was fixed at a very low water velocity. This number was obtained from the water velocity near the residual water saturation in a traditional coreflood simulation performed before defining onset of the evaporation process. Then, the reaction rate constant varies based on the velocity of water following Eqs. (5) and (6). \({k{\prime}}_{ref}\) is the reaction rate constant at \({v}_{ref}\) which is a fitting-parameter in this case. \({k{\prime}}_{ref}\) is assumed to be the maximum reaction rate constant and is applied to trapped brine up to \({v}_{ref}\)+\({v}_{crit}\).

Table 1 Parameters used in the simulation describing the salt precipitation modeling based on the experiment conducted by Ott et al. (2015)
Full size table

Once salt saturation is reached in the aqueous phase, salt precipitation will commence. In fact, halite solubility in water is only moderately sensitive to temperature changes up to 80 °C and pressures up to 10 bar (Pinho and Macedo 2005; Sawamura et al. 2007). As such, a constant salt solubility of 26.5 wt.% (or 0.1 mol fraction) was utilized to simplify the numerical simulation. During the evaporation process, once saturation is reached the solid salt is assumed to instantly form until the brine has been completely dried. For this simulation, however, the mass transfer of the salt from aqueous solution to solids uses a kinetic approach with a large rate constant as described by Eq. (4). Kohse and Nghiem (2004) used a value of 50,000 day−1 to represent the equilibrium process of a mass transfer for asphaltene deposition which is assumed to be very fast in their simulation; we use the same value here.

2.2.2 Permeability Reduction Model Due to Salt Precipitation

Salt precipitation definitively reduces the porosity of the rock formation; with a strong positive correlation between permeability and porosity, the permeability is also expected to drop. A variable resistance factor (\({R}_{f}\)) is introduced to quantify the permeability reduction induced by salt precipitation. The relationship is written by (CMG 2020):

$${R}_{f}=\frac{{k}_{0}}{k}$$
(7)
$${R}_{f}=max\left[1,g\left({c}_{salt}\right)\right]$$
(8)

where \({c}_{salt}\), \({k}_{0}\) and \(k\) is the moles of solid salt within the void pore volume, initial and salt deposition-induced permeability values, respectively. \({R}_{f}\) will not be less than 1 and increase as the salt precipitation increases. The function \(g\left({c}_{salt}\right)\) can be defined with any porosity–permeability relationship (e.g., Kozeny-Carman, Verma-Pruess or a regression model based on results from core flooding experiments). Higher incremental \({R}_{f}\) over a change in porosity is supposed to be applied on low permeability formations as the change is very sensitive in this characteristic. Several studies utilized critical porosity, at which permeability drops to zero due to solid deposition, in a range of 85–90% of the original porosity (Pruess and Müller 2009; Andre et al. 2014; Ott et al. 2015; Ott et al. 2021). Giorgis et al. (2007) performed a simulation study in relatively high permeability by using a critical porosity of 50% of the original porosity.

To determine the fitting parameters in Table 1 and an approximation to \(g\left({c}_{salt}\right)\), a 1-D simulation (with the grid model shown in Fig. 1, each cell has dimensions of 0.5 (length) × 1 (width) × 1 (thickness) cm) was performed based on the experiment results obtained by Ott et al., (2015). These fitting parameters were then used in the larger scale simulation for this study. CO2 injection is simulated at a rate of 0.0062 m3/day (4.4 cm3/min) into a water-saturated model. It is assumed that \({v}_{ref}\) = \({v}_{crit}\) to represent a low water velocity in which the evaporation rate is maximum. Salt saturation and differential pressure obtained in the simulation show good agreement with the experimental results, as can be seen in Figs. 2 and 3. Ott et al. (2015) used porosity–permeability relationship proposed by Verma & Pruess (1988) to describe these results at it has more flexible fitting parameters. The function \(g\left({c}_{salt}\right)\) used in this work is described by Eq. (9) (Wang and Liu 2014; Choi et al. 2015; CMG 2020) and the comparison with experimental data from Ott et al. (2015) is shown by Fig. 4.

$$ g\left( {c_{{salt}} } \right) = 1 + \left( {rrf - 1} \right)c_{{salt}} /c_{{salt,max}} $$
(9)

where \(rrf\) is a resistance factor constant and \({c}_{salt,max}\) is the maximum amount of salt expected present in a pore volume (moles/m3.pore volume). \(rrf\) is a fitting parameter and is adjusted to obtain a qualitative best-match of the porosity–permeability reduction relationship with the experimental data. In this work, 60 was used for the \(rrf\). \({c}_{salt,max}\) is obtained from the maximum salt precipitation observed in the experiment. The maximum salt saturation is 0.4 which equates to 14,784 mol/m3. The latter number was used in this simulation as \({c}_{salt,max}\).

Fig. 1
figure 1

Grid model employed in this work representing the core used by Ott et al. (2015)

Full size image
Fig. 2
figure 2

a Salt concentration yielded from simulation and b salt saturation in the simulation results () which is calculated by using Eq. 8 compared to that in the experimental results () which the data taken from work conducted by Ott et al. (2015)

Full size image
Fig. 3
figure 3

Pressure difference obtained in the simulation results () compared to that in experimental results ()

Full size image
Fig. 4
figure 4

permeability reduction model between reference study () which the data taken from work conducted by Ott et al. (2015) and this work ()

Full size image

Evaporation also decreases the trapped brine saturation causing an increase in the relative permeability for CO2. When the formation becomes completely dry, CO2 flows as a single phase. In this work, gas relative permeability beyond the connate water saturation (Swc) was modelled linearly increasing from its endpoint at Swc towards unity. This is also applied to cases where water blockage takes place. The relative permeability curves used in the simulation can be seen in Fig. 9 and the extrapolation during drying-out is annotated as a dashed line in Figs. 9 and 10.

2.3 Water Blockage Model

Water blockage is a severe decrease in the relative permeability of water due to a strongly water wet formation characteristic. This issue is particularly exacerbated in low permeability reservoirs and restricts the flow of CO2 due to high amount of remaining brine within the pore space limiting the ability for CO2 to flow (Bennion 2002). Consequently, the impact of this issue decreases as water saturation reduces. Water blockage is most common after using water-based fluids or muds for drilling or completion activities; there will be an unusual condition characterizing the invaded zone near the wellbore. This is modelled by separating the invaded zone from the rest of the reservoir (see Fig. 9). This zone should be very strongly water-wet compared to the original formation wettability with a higher Swc and lower krg (gas/CO2 relative permeability) at Swc. Relative permeability curves used to represent the water blockage are shown by Fig. 5a. The curve was constructed based on the flooding results from a core that exhibited water blockage issue as performed by Arjomand et al. (2020b) (as core GB.4). Figure 5b was synthetically constructed using the empirical correlations (Eqs. 10–11) (Benson et al., 2013) for a typical sandstone formation which has Swc = 0.2 (common value for Berea sandstone), exponents of 1.6 for ng and 2.7 for nw, krw’ (water relative permeability end-point) = 1, and krg’ (krg end-point) = 0.66 (Bennion & Bachu 2008; Krause et al. 2011; Krevor et al. 2012).

Fig. 5
figure 5

Relative permeability of a the zone affected by water blockage (RT-1) and b original condition (RT-2)

Full size image
$${k}_{rw}={{k}_{rw}}{\prime}{\left(\frac{{S}_{w}-{S}_{wc}}{1-{S}_{wc}}\right)}^{{n}_{w}}$$
(10)
$${k}_{rg}={{k}_{rg}}{\prime}{\left(\frac{1-{S}_{w}}{1-{S}_{wc}}\right)}^{{n}_{g}}$$
(11)

2.3.1 Silylation Process Model

The experimentally determined impacts of sc-CO2 based silylation on the rock wettability (therefore relative permeability curves) was implemented to remediate water blockage. The type of silane used in this work has a formula of R1SiX3, where R is a un-hydrolysable organic group and X is a hydrolysable group such as halogen, alkoxy, etc. (Combes et al. 1999). Experimental results obtained by Arjomand et al. (2020b) for core GB.4 using silane reagent of (3-chloropropyl)triethoxysilane (CPTS) were integrated into this study. Other properties of this chemical and core sample are listed in Tables 2 and 3, respectively. The experiment was operated at 21 MPa and 60 °C.

Table 2 Basic properties of silane reagent used in the experiment performed by Arjomand et al. (2020a)
Full size table
Table 3 The properties of Core GB.4 used in the experiment performed by Arjomand et al. (2020b)
Full size table

In the simulation, CPTS is co-injected with CO2 under a miscible state at the operating condition. Two processes are included for silylation process, i.e., hydrolysis and condensation. In fact, those processes are very sensitive depending on many conditions such as pH of brine, presence of catalyst, chemical properties of the silane, brine salinity, silane concentration, etc. (Issa and Luyt 2019). The kinetics of this process will be complicated to model at the field-scale of these numerical simulations. In this study, hydrolysis and condensation of CPTS were assumed to occur instantly once CPTS interacts with brine. This assumption was taken since silylation takes less than a day to complete which is very short compared to the whole simulation period. Considering the economic aspect, silane may not be injected continuously for long time. In this work, silane injection was simulated for 2 days from the beginning of injection to affect a wettability change in the near wellbore region most affected by water blockage.

Mechanistically, water is detached from the rock surface following the condensation leading to a more hydrophobic surface. However, this microscale process was simplified considering the wellbore-drainage-scale used in this work. The release of water component after condensation was coupled with wettability alteration triggered by silylation. In this work, once the silane invades the water blockage impacted zone, the relative permeability curves shift toward less water-wet instantly. This process infers the reduction of connate water saturation due to silylation as described in Fig. 6.

Fig. 6
figure 6

Modified from results obtained by Arjomand et al. (2020b)

Relative permeability of pre- (impacted by water blockage, RT-1) and post-treatment of silylation.

Full size image

2.4 Radial Single-Well Model

The results obtained from the experiments is scaled up to a larger radial single-well model. The schematic and properties of the radial model can be seen in Fig. 7. The grid size is increased logarithmically away from the injector towards the outer radius. The vertical layering is composed of 10 grids with identical thickness. The injector is perforated in the first-six grids (indicated by arrows, see Fig. 8) from the formation top. The model edge was set to open flow to represent an infinite boundary. The top and bottom boundaries of the model were set closed (no-flow). A temperature and pressure of 58.9 °C and 16 MPa, respectively, were applied to represent a deep saline aquifer.

Fig. 7
figure 7

Schematic of radial single well model and the rock properties. Color scale is referred to Fig. 8

Full size image
Fig. 8
figure 8

Cross-section of radial single well model

Full size image

In Fig. 9, two rock types were assigned to represent an invaded zone (i.e., zone RT-1 which is characterized by water blockage). This zone extends to 1.34 m measured from the injector as shown by Fig. 9. Figure 5 shows the different characteristics of both rock types in terms of relative permeability. Relative permeability of treated zone by silylation is provided in Fig. 6. If silane invades RT-2, it is assumed to have no effect on the relative permeability characteristics.

Fig. 9
figure 9

Schematic of zone affected by water blockage where silylation takes place (RT-1; blue colored zone) and original characteristics (RT-2; red colored zone)

Full size image

Six cases including a base case were developed to elucidate the impacts of silylation on a reservoir impacted by water blockage/salt precipitation. Cases 1 to 3 are designed to observe the impacts of water blockage and salt precipitation both separately and simultaneously. Case 4 and 5 are designed to examine the role of silylation reducing the severity of injectivity loss caused by these issues. A similar constraint toward injection well is used for all cases, i.e., constant injection rate of 193.4 tonnes/day. The simulation ends after 455 days. The information summarizing the cases is shown in Table 4.

Table 4 Detail of case studies developed in this study
Full size table

3 Results and Discussion

3.1 Scaling-up Well Injectivity Issues Simulation

The primary aim of this study is to elucidate qualitatively the efficacy of a silylation treatment (causing a wettability changes) to address the impacts of water blockage and salt precipitation on CO2 injectivity. With that in mind, for the purposes of simulation scale-up, some adjustment regarding the process parameters needs to be considered. The simulation parameters used for salt precipitation were derived from experimental results obtained at a lower pressure and temperature (i.e., 10 MPa and 45 °C, respectively) compared to those which used for radial single-well simulation (i.e., 16 MPa and 58.9 °C, respectively) here. Increasing the temperature improves the solubility of water in the CO2 phase leading to enhanced evaporation. On the other hand, the higher pressure slows the evaporation rate of water (Zuluaga and Monsalve 2003). For the simulation in this study, the solubility (mole fraction) of water in CO2 is assumed to be 0.007 for the selected conditions (Ji et al. 2005; Spycher and Pruess 2005; Miri and Hallevang 2016). For the purposes of this qualitative assessment, no other parameters were adjusted. This work is considered as the worst case of precipitated salt while specific experimental work can be conducted to obtain representative parameters at higher pressure conditions. On the other hand, the water blockage model does not employ process parameters that are generally sensitive to pressure and temperature. Therefore, parameter adjustment is not necessary for this issue in terms of simulation scale-up from core-scale toward radial single-well.

Analysis is conducted toward injectivity index (\(J\)) (akin to permeability) of each case study. In this case, injectivity index is defined as the amount of CO2 which can be injected for a unit of pressure drop (i.e., pinjection–paquifer, as described in Eq. 12). Injectivity loss as the impacts in the case studies are evaluated as the relative injectivity change (RIC) as represented by Eq. 13 (Sokama-Neuyam et al. 2017; Yusof et al. 2022). Both parameters are mathematically defined as:

$$J=\frac{{q}_{inj}}{\Delta p}$$
(12)
$$RIC=1-\frac{{J}_{i}}{{J}_{bc}}$$
(13)

where \({q}_{inj}\) and \(\Delta p\) are injection rate in tonnes/day and pressure drop in MPa, respectively. Subscripts -i and bc refer to case-i to which the results are evaluated and the base case, respectively. In this work, the CO2 injection rate is the same and constant for all cases. Since the boundary is infinite, paquifer is assumed unchanged during over the entirety of simulated time-period. For comparison purposes, the pressure at bottom of the well is used for these calculations.

Injection pressure in the early period (i.e., initial 10 days) of case 1 is up to 0.14 MPa higher than that of the base case as depicted in Fig. 10. This is caused by the condition in which CO2 remains static until gas saturation reaches 0.15 (the so-called critical gas saturation) as can be shown by Fig. 5a. Gas mobility is also dropped due to high amount of immobile water around the vicinity of perforation. Limited space for gas flowing causes higher pressure during the injection. As shown by Fig. 10, injection pressure of case 1 stays higher than that of base case throughout the first 10 days of the simulation. At the end of this period, a high amount of water is still trapped near the well bore area as shown in Fig. 11a thus reducing CO2 mobility.

Fig. 10
figure 10

Injection pressure for base case (), case 1: water blockage exists (), case 2: salt precipitation exists (), and case 3: both issues exist ()

Full size image
Fig. 11
figure 11

Distribution of water saturation at the end of simulation which shown in full scale model for a) case 1: water blockage exists and b) base case

Full size image

Injection pressure of case 2 is noticeably higher than that of base case after a certain period of injection due to the initiation of salt precipitation. This indicates that the water has been displaced around the perforation close to the irreducible saturation. Under this condition, evaporation is at its maximum rate. However, water blockage (represented by case 1) deteriorates the well injectivity worse than that caused by salt precipitation (represented by case 2) during this early injection period. Over this period, salt precipitation continues causing an ever-increasing damage to the well injectivity (as indicated by a pressure difference between case 2 and the base case). Thus, the bottom-hole pressure of case 2 is higher than that of case 1 after 4 days of injection (see Fig. 10).

Case 3 (which simulates the combined effects of water blockage and salt precipitation) yields higher injection pressure than those of base case, case 1 and case 2 at the early period of injection. The impacts of water blockage, which should be dominant during this period, are combined with the effects of evaporation which cause decreasing water saturation. The injection pressure for case 3 becomes higher than those of other cases after the first day of injection. Since the amount of trapped brine in this case is higher than that of case 2, the resulting salt precipitation is also larger, resulting in a more severe impact on injectivity.

For the base case, the injectivity index continuously increases (with the rate of increase tapering with time) throughout the longer 455 day simulation (see Fig. 12). For this case, the pseudo-steady state might have not been reached within this period. This is presumably caused by the open system used in this simulation to represent the infinite lateral boundary. Similar behavior was observed by Meng et al. (2015) who studied the effect of boundaries affecting pressure profile buildup and salt precipitation distribution. From their study, for the case of an open boundary system, the pressure buildup near the wellbore keeps decreasing gently (i.e., inverse relationship to injectivity index) although salt has been precipitated. This pattern is also observed at the infinite-acting flow regime before pseudo-steady state takes place.

Fig. 12
figure 12

Injectivity index for base case (), case 1: water blockage exists (), case 2: salt precipitation exists (), and case 3: both issues exist ()

Full size image

On the other hand, water blockage (case 1, which the simulation limits to a distance of less than 1.34 m from injector) deteriorates the injectivity up to 32.9% after 455 days of injection period, as shown by Table 5 and Fig. 12. That considerable injectivity loss is caused by only a higher injection pressure required due to the large amount of water trapped near the wellbore. More severe damage is identified when salt precipitation takes place either in case 2 or 3 with an injectivity collapses up to 58% and 68.6% for cases 2 and 3, respectively.

Table 5 Summary of relative injectivity change for all studied cases
Full size table

The distribution of precipitated salt for case 2 at the end of the 455 day simulation is shown in Fig. 13a with precipitated solid extending approximately 6.1 m from the well. A nearly identically affected distance is observed in case 3. However, as shown in Fig. 13b, the solid saturation in the water blockage zone of case 3 lies between 0.06 and 0.18 while that in case 2 lies between 0.03 and 0.05. A sharp decrease in the solid saturation in case 3 is identified between the invaded and uninvaded zones (see Fig. 13b); the irreducible water saturations are substantially different as described by kr curves in Fig. 5a and b. This variation of immobile saturation provides different amounts of prospective salt which can then precipitate. However, the amount of solid deposited (i.e., very little) within the uninvaded zone in case 3 seems to be similar to that in case 2.

Fig. 13
figure 13

Distribution of solid saturation for a Case 2: salt precipitation exists and b Case 3: water blockage and salt precipitation exist, at the end of simulation

Full size image

An accumulation of salt is captured at the bottom of the perforation in both cases. Capillary-driven backflow of brine, which was also modeled in the simulation, supported by buoyant effects causes the accumulation of salt at the bottom of perforation. Due to those processes, brine flows downward to the injection well direction. The resistance factor for case 2 varies from 6 to 11.5 (which means the permeability for case 2 is 8.7–16.7% of its original number in the base case) and indicative of the impact of solid salt precipitation on injectivity (see Fig. 14a). The impact of salt combined with water blockage results in an increase in the resistance factor to between 10.7 to 50 (i.e., a permeability of 2–9.3% of the original permeability in the base case) (see Fig. 14b).

Fig. 14
figure 14

Resistance factor applied on a Case 2: salt precipitation exists and b Case 3: water blockage and salt precipitation exist, at the end of simulation

Full size image

As previously elaborated in Sect. 2, injecting CO2 may help to alleviate water blockage as the water component within the invaded zone is evaporated by continuous stream of injected CO2. At the simulation end for case 3, the CO2 relative permeability (see Fig. 15) is near unity in the invaded zone showing that the pore space has been effectively dried completely (i.e., CO2 flows as a single fluid within the pore space). Thus, the CO2 relative permeability is increased under this condition where water blockage is insignificant. However, evaporated water turns the brine more saline; eventually, the solution becomes saturated resulting in precipitate formation with further evaporation. The damage to the injectivity for case 3 is even worse than that caused by either case 1 or 2. From this condition, the relationship between water blockage and salt saturation becomes clear. Water blockage diminishes when evaporation takes place; however, this also induces salt precipitation. In this strongly water wet formation, the zone impacted by water blockage exhibits enhanced salt precipitation. Furthermore, intensive salt precipitation occurs in the volume near the well perforation since brine remains immobile behind the front and fresh CO2 invades that zone rigorously. Below the well perforation, evaporation is minimal resulting in dramatically less salt precipitation in this zone (see Fig. 13).

Fig. 15
figure 15

kr,CO2 at the end of simulation of Case 3: water blockage and salt precipitation exist

Full size image

3.2 Simulation of Cases Applying Silylation

For this study, silylation is applied to remediate water blockage around the wellbore by changing the wettability characteristics. The injection pressure for case 4 (representing water blockage and silylation) is slightly decreased compared to case 1 (representing water blockage only) (see Fig. 16). This may be due to some reasons. Basically, this results from the CO2 relative permeability decreasing due to this treatment (see Fig. 6). The CO2 relative permeability for the post-treatment state remains lower than that of pre-treatment up to the original irreducible brine saturation. However, the injection pressure for case 4 is lower since some trapped brine near the wellbore has been displaced due to the treatment. As a consequence, the gas saturation enlarges which, in turn, increases the end-point CO2 relative permeability. The effect of the silylation treatment is more noticeable for brine mobility as indicated by Arjomand et al. (2020b). Similar comparisons between cases 3 and 5 can be made.

Fig. 16
figure 16

Injection pressure for Case 1: water blockage exists (), Case 3: water blockage and salt precipitation exist (), Case 4: silane treats Case 1 (), and Case 5: silane treats Case 3 () in the early period

Full size image

Comparing cases 1 and 4 or cases 3 and 5, the application of alkoxysilane co-injected with sc-CO2 decreases the severity of injection loss as shown by Figs. 16 and 17. As the silylation is assumed to occur instantly over the simulation timescale, a lower injection pressure is observed from the beginning of the simulation. On an absolute basis, this method counteracts the injectivity index by approximately 5–7%. This number when silylation shifts the wettability represented by a decrease in irreducible water saturation from approximately 0.55 to 0.40 (see Fig. 6). The improvement in injectivity seems unchanged beyond 90 days. The role is supposed to be more significant when dealing with strong water-wet and wider invaded zones in the targeted aquifer formation.

Fig. 17
figure 17

Injectivity Index for Case 1: water blockage exists (), Case 3: water blockage and salt precipitation exist (), Case 4: silane treats Case 1 (), and Case 5: silane treats Case 3 ()

Full size image

During the early period (i.e., up to 10 days), comparing case 5 with case 3, a reduction in the injection pressure is observed (see Fig. 16). Comparing cases 4 and 5, the effects of salt precipitation on injection pressure are not evident until after 2 days (as indicated by nearly coincident lines); salt precipitation then acts dominantly after that period which is indicated by the lines becoming separated (see red circle symbols in Fig. 16 indicating turnover point). Comparing cases 3 and 5 (see Fig. 18), after both 90 days and 455 days, the silylation treatment decreases the salt precipitation immediately around the wellbore leading to precipitation further from the wellbore. After 90 days of injection in case 3, the invaded zone has been dried and 6–15% of pore has been filled by precipitated salt; following silylation, salt precipitation decreases to 5–7.5% of pore space albeit over a larger volume (see Fig. 18a and b). Similar behaviour is observed at the simulation end (see Figs. 18c and d).

Fig. 18
figure 18

Distribution of salt precipitation in a case 3: water blockage and salt precipitation exist, at day 90, b case 5: silane treats Case 3, at day 90, and c case 3 and d case 5 at the end of simulation

Full size image

Comparing salt distribution in the perforation middle for cases 3 and 5 (see Fig. 19), silylation seems to decrease the severity of salt precipitation encouraged by water blockage. The salt saturation of case 5 in the invaded zone (representing a distance of 1.34 m from injector) is reduced compared to case 3 and nearly the same as in case 2. The salt accumulated in case 3 is slightly elevated just before the edge of the invaded zone (i.e., a distance of 0.6–1.22 m from the injector). This high localized precipitation is induced by early capillary suction which occurs at a high irreducible water saturation. Under this condition, the brine in uninvaded zone is still moveable. Some brine from the uninvaded zone flows back to the invaded zone providing more salt to be precipitated. A similar pattern is shown by case 5; additionally, the brine previously trapped within invaded zone is displaced further into the uninvaded zone. In case 2, the salt precipitates homogenously as there is no water blockage (i.e., different relative permeability curves). This different capillary behavior should be well noticed during the plan of full-field scale CO2 storage in a saline aquifer.

Fig. 19
figure 19

Solid saturation profiles at the middle of perforation after 90 days of injection forecast

Full size image

Based on the simulation work, water blockage impact (red color in Fig. 20) decreases as salt forms within the pores (see top panels in Fig. 20). When the maximum salt precipitation has been reached (blue color), gas mobility is improved because it flows as a single phase. Silane co-injected with CO2 has been simulated and it decreases the severity of both issues as indicated by a lower impact level compared to that without silane injection (see top panels in Fig. 21). Wettability shift induced by silylation reduces the trapped water within the pores to alleviate water blockage negative impact. In the meantime, lower connate water saturation also depreciates the amount of salt that will be precipitated.

Fig. 20
figure 20

Schematic of injection pressure in case of salt precipitation and water blockage taking place at the same system

Full size image
Fig. 21
figure 21

Schematic of injection pressure in case of sc-CO2 based silylation depressing negative impact of salt precipitation and water blockage

Full size image

One thing should be noted that both case 3 and 5 are not in sequence (see Figs. 20 and 21). Silylation must be applied as early as possible to reduce the severity of salt precipitation. The formation of solid salts covering the pore surface may halt the silylation process in altering wettability. Silane may fail to access quartz which is already covered by salt. This happens only when the aquifer has been injected for a certain period with pure CO2. This phenomenon was recognized by Arjomand and his research team (Arjomand et al. 2020b) during their experiment. Under this condition, silane treatment may be ineffective. On the other hand, specific experiments are required to investigate the effects of evaporation and silylation when they take place simultaneously. The evaporation rate of water component in the presence of silane in CO2 phase may not be the same as that in the pure CO2 injection. There could be another wettability alteration taking place and needed to be modelled due to salt precipitation which has been investigated as a hydrophilic micro-porous crystal (Kim et al., 2013; Miri et al., 2015; Miri & Hallevang, 2016). The suction of brine toward evaporation front under capillary force may be stronger. This phenomenon can be a future simulation work in a larger scale as unconsidered in this work.

4 Conclusions

According to the simulation result, a decrease in injectivity due to salt precipitation is more significant than that due to water blockage. Salt precipitation decreases pore space by forming additional solid in it, while water blockage affects the mobility of CO2 due to relatively high irreducible water saturation. The negative impact of water blockage gradually diminishes (as the water evaporates) while salt starts growing within the pore space. With a high level of trapped brine, the injectivity is deteriorated more severely (up to 68.6% of relative injectivity change (RIC)) when both salt precipitation and water blockage occur. Different capillary behavior may induce localized precipitation considering the heterogeneity either caused by water blockage or naturally employed in the geological structure of a deep saline aquifer.

Beside the ability of sc-CO2 based silylation in altering wettability, applying this method reduces the severity of salt precipitation indirectly. The alteration turns some trapped brine moveable and thus decreases irreducible water saturation. This phenomenon prevents large accumulation of salt near perforation of the injection well. In case of salt precipitation endorsed by water blockage, this method counteracted the injectivity around 5 to 7% of RIC (absolute basis). In addition, this method is encouraged to be implemented before continuous CO2 injection for the geological sequestration because the expected mechanism will not work when salt precipitation comes up covering the pore surface.