1 Introduction

Foam improved (or enhanced) oil recovery, also known as foam IOR, is a tertiary oil extraction technique which aims to sweep the remaining oil trapped in porous media (Shan and Rossen 2004). Within the reservoir or porous medium, foam can be created either by co-injection of a liquid surfactant solution and gas, or via surfactant alternating gas (SAG) injection (Li et al. 2010), which is the mechanism to be considered in this study. Upon contacting the liquid filled region (containing both liquid oil and liquid surfactant solution), the injected gas produces foam.

Foam tends to have a high effective viscosity and therefore low mobility (maybe even orders of magnitude lower than other fluids within the medium, often with surprisingly low mobility in more permeable parts of a medium where foam is difficult to break (Zhou and Rossen 1995)). As a result, foam can penetrate through low permeability regions and hence offer a more uniform sweep, avoiding fluid escaping preferentially through high permeability regions, and in addition avoiding fingering phenomena (Grassia et al. 2014). The entire system’s dynamics can then be controlled by controlling the flow of foam (Farajzadeh et al. 2012; de Velde Harsenhorst et al. 2014). The foam then propagates pushing the liquid (oil and surfactant solution) to an extraction well. Although originally considered for IOR, several industrial applications involving flow through porous media take advantage of foam properties, including processes like remediation of contaminated aquifers, clean up of polluted soils, and subsurface sequestration of foamed CO2, to name a few (Ma et al. 2015; Shen et al. 2011; Wang and Mulligan 2004; Zhong et al. 2010; Farajzadeh et al. 2020; Gong et al. 2020; Skauge et al. 2020; Boeije et al. 2020).

In foam IOR via SAG, the propagating foam front (or the region where the gas and the liquid surfactant solution meet), can usually be identified as the region with lowest mobility along the direction of flow (see Fig. 1). Lower mobilities are associated with finely textured foam, since a higher resistance to motion is encountered when more films are present (Kovscek and Bertin 2003; Khatib et al. 1988). Texture is however a function of liquid saturation, because liquid saturation influences the pore scale processes that create and destroy foam films. It is then possible to make a direct link between liquid saturation and foam mobility, bypassing the need to determine texture explicitly (Ma et al. 2015). Low mobility (and by implication fine texture, even if not determined explicitly) tend to be associated with a fairly narrow domain of liquid saturations (Shan and Rossen 2004). In a system with very low liquid saturation, foam collapses due to capillary effects, and unfoamed gas is usually much more mobile than foamed gas. In a system with substantially higher liquid saturations, the overall mobility of the system is dominated by the mobility of the liquid rather than any contribution from the much smaller mobility of foamed gas. Thus low overall mobilities correspond to a window of liquid saturations in which gas is foamed, but liquid relative permeability and hence liquid mobility likewise are not so high (Shan and Rossen 2004).

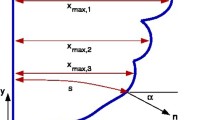
Once mobilities for foamed gas and for liquid are specified, driving injection pressures are imposed and flow propagates forward through the porous medium at a well-defined rate. Flows are then often determined (Majid Hassanizadeh and Gray 1993) based on Darcy’s law or multiphase extensions thereof. Consequently pressure gradients are necessarily highest where overall mobilities are lowest. In view of this, models such as the so called pressure-driven growth model have been used to capture a forward propagating foam front considering that essentially all the pressure drop is tied to the aforementioned low mobility region (Shan and Rossen 2004; Grassia et al. 2014, 2017; Torres-Ulloa and Grassia 2021). Note that in the 2-D pressure-driven growth model (see Fig. 1) the low mobility region as a whole is often considered to represent the foam front, since pressure-driven growth does not attempt to resolve the internal structure of this region, merely where it is located.

However, the imposed injection pressure is not the only pressure that is relevant. Hydrostatic pressures arise due to the density difference between the liquid-filled region and the region filled with foamed gas. What matters is then the net driving pressure difference, namely the difference between the imposed injection pressure and the hydrostatic one (Shan and Rossen 2004). There is moreover a certain depth at which imposed pressure and hydrostatic pressure balance: the foam front as it moves forward can penetrate no deeper than that (Grassia et al. 2014).

If the imposed injection pressure subsequently falls below the hydrostatic pressure at depth, the process goes from injecting gas into liquid to injecting liquid into foamed gas. This is known as flow reversal (Eneotu and Grassia 2020), and is the main process studied in this work (see Fig. 1). Flow reversal would take place, as described in Eneotu and Grassia (2020), if the injection pressure is suddenly reduced, or if due to external factors, the pressure field downstream of the front is increased: e.g. new gas injection wells are brought online downstream, or indeed if a gas injection well is shut in. It can also be relevant when porous media are used for gas storage in energy applications (e.g. hydrogen storage (Heinemann et al. 2021)): relatively immobile foamed gas can be readily stored in a medium, but eventually the gas needs to be extracted for energy generation and so must flow back out of the medium again.

Regardless of the underlying reason causing flow reversal, in a typical situation (Eneotu and Grassia 2020) on the upper part of the foam front we may still have forward flow, while it is at depth where hydrostatic pressure is larger that the flow starts reversing (see Fig. 1). The sketch of the 2-D process shown in Fig. 1 here is merely however for illustrative purposes to motivate the study. In the present work we focus just on understanding 1-D dynamics along particular flow paths in detail, rather than obtaining the full 2-D solution for an entire collection of flow paths.

Fig. 1
figure 1

Illustrative definition sketch: foam front propagation across a vertical domain Y and a horizontal domain X. At time zero, the front is located along the Y axis. It then propagates forward under the influence of an imposed injection pressure \(P_{\textrm{inj}}\) but offset by a hydrostatic pressure \(P_{\textrm{hyd}}\). After time \(t^*\), the injection pressure is reduced from a value \(P_{\textrm{inj}}^{\textrm{before}}\) to a value \(P_{\textrm{inj}}^{\textrm{after}}\). Some points on the front keep moving forward even after this happens, but others switch to reverse flow: the focus here is upon these latter points. Specifically the front starts backtracking at any points below the depth at which \(P_{\textrm{hyd}}=P_{\textrm{inj}}^{\textrm{after}}\), where as mentioned \(P_{\textrm{hyd}}\) denotes hydrostatic pressure

Full size image

Figure 1 as drawn is a 2-D sketch indicating the foam front location, but (as already alluded to) does not resolve what happens in detail within the foam front itself. There is however a 1-D fractional flow theory (Buckley and Leverett 1942; Zhou and Rossen 1995; Ashoori et al. 2010) that underlies the 2-D pressure-driven growth theory: the 1-D theory resolves the detailed structure of front in a manner made precise by Eneotu and Grassia (2020). Essentially the 1-D theory follows the flow paths executed by each of the elements constituting the 2-D foam front. The 1-D theory allows us to interrogate the mobility at any point on the flow path and hence to assign a thickness to the front along the flow direction: as will be discussed in detail later on, the assigned thickness represents the size of the region that is at or near the lowest mobility on each flow path.

What the 1-D theory predicts more specifically is a discontinuous jump in liquid saturation at the front location (Eneotu and Grassia 2020): the liquid saturation however ultimately governs the mobility, and it is indeed those liquid saturations at the front which turn out to have lowest mobility. This situation arises both in forward flow and in reverse flow (Eneotu and Grassia 2020), but details differ (see Sect. 2 later on). What the 2-D model is trying to capture as the foam front is therefore the location of this discontinuous jump in liquid saturation on each flow path. The 1-D model however captures details around this discontinuity.

The way the 1-D theory itself proceeds (Buckley and Leverett 1942) is discussed further in Sect. 2, but briefly is as follows. Based on the mobilities of foamed gas and of liquid, it determines what proportion of the flow is foamed gas and what proportion of it is liquid. Conservation equations can then be solved to determine how liquid saturations are distributed in space and time (Buckley and Leverett 1942; Eneotu and Grassia 2020), and likewise how mobilities are distributed. It is these conservation equations that admit the aforementioned discontinuous jumps in saturations in their solutions.

For either forward flow (when gas is pushed into liquid) (Shan and Rossen 2004) or upon flow reversal (liquid pushed into foamed gas) (Eneotu and Grassia 2020), the liquid saturation and foam mobility specifically at these discontinuous jumps can be obtained using fractional flow theory. This information can then feed into the pressure-driven growth model, which has even been reformulated so as to predict the foam front behaviour as the flow is reversed. A key result of the reformulated theory (Eneotu and Grassia 2020) (discussed in more detail later) was that the mobility in reverse flow could be substantially lower than that in forward flow.

Now we return to the question of front thickness measured along the flow direction. Fractional flow theory recognises that the thickness (or extent) of the region with low mobilities will be some fraction, denoted \(\epsilon\) say, of the distance travelled by the foam front (Shan and Rossen 2004; Grassia et al. 2014; Eneotu and Grassia 2020). Front thickness, in particular, is relevant to front propagation since it is across this region (with low mobility) where it is assumed that the majority of the pressure drop occurs. The thinner the region, the higher the pressure gradient, and the faster the front propagates. Remember, as alluded to earlier, that to evaluate \(\epsilon\) we only need here to discuss a 1-D theory, since the 1-D result for \(\epsilon\) will inform the 2-D theory. Thus here we are considering just one spatial coordinate plus time. In the 1-D model, the foam front at any given time has propagated a certain distance along that spatial coordinate, and adjacent to the front, a fraction \(\epsilon\) of the distance covered corresponds then to a region of low mobility.

This value \(\epsilon\) (the front’s thickness to displacement ratio) is generally assumed to be small compared to unity (Shan and Rossen 2004; Grassia et al. 2014), regardless of whether forward or reverse flow is considered (Eneotu and Grassia 2020). However, what Eneotu and Grassia (2020) did not consider is that different values of \(\epsilon\) might still apply as we switch from injecting gas into liquid, to pushing liquid into foamed gas as flow starts reversing at depth. In the present work therefore we obtain formulae to compute \(\epsilon\) for both cases (forward and reverse flows) and we compare the \(\epsilon\) values in relative terms. We have already mentioned that reverse flow mobility is rather lower than forward flow mobility. If the front thickness in reverse flow also happens to exceed the front thickness in forward flow that merely exacerbates the effect.

Another important issue that we address here is to query the assumption that \(\epsilon\) is small compared to unity. Having small \(\epsilon\) simplifies modelling because it means than all pressure gradients are confined close to the front location with pressures close to uniform everywhere else: this then has been the basis under which the 2-D pressure-driven growth model attempts to track foam fronts without needing to resolve their detailed structure (Shan and Rossen 2004; Grassia et al. 2014). However, the underlying assumption of \(\epsilon\) being small was based on the fact that low mobilities tend to be associated with just a small domain of liquid saturations. There is no guarantee that this small domain of liquid saturations necessarily translates to a small thickness domain over space. If \(\epsilon\) is not small, then pressure gradients are distributed over a wide domain of space, and knowing a front location alone may then be insufficient to determine how the entire 2-D flow proceeds. The underlying 1-D fractional flow theory itself (which is what we study here) has no difficulty dealing with \(\epsilon\) values that are not small. The concern is instead about future impact on a 2-D model which is fed information from the 1-D solution: that is why establishing the value of \(\epsilon\) (as is to be done here) is of such interest.

The rest of this work is structured as follows. In Sect. 2 we start by reviewing fractional flow theory and its application to the present study. In Sect. 3 we review the theory used to compute pressure drops, and then extend that theory to derive novel formulae determining the thickness of the low mobility region. In Sect. 4 we use those formulae to evaluate front thicknesses in both forward and reverse flow. That then determines the region across which the bulk of the driving pressure is dissipated in each flow scenario, as well as the size of the pressure drop when forward and reverse flows are combined. Finally in Sect. 5 we offer conclusions.

2 Modelling foam IOR via SAG

As mentioned in Sect. 1, fractional flow theory (Buckley and Leverett 1942; Zhou and Rossen 1995; Ashoori et al. 2010) can be used to determine how liquid saturation and hence foam mobility evolve in space and time in porous media, for both forward and reverse flow. Fractional flow theory incorporating reverse flow after an initial forward flow has already been modelled in detail by Eneotu and Grassia (2020). However since not all readers might be familiar with the models in that work, we have provided an in depth discussion within an appendix (see Sect. A in supplementary material). Some readers may prefer to consult that appendix immediately, but in what follows we give just a brief description of what it covers.

As the appendix explains, what fractional flow theory tells us (Eneotu and Grassia 2020; Fisher et al. 1990) is how liquid saturation \(S_{\textrm{l}}\) evolves with position x and time t when liquid and gas flow together with a total overall fluid flux q in a medium of porosity \(\phi\) and permeability k. To achieve this, it is first necessary (Buckley and Leverett 1942) to determine (as a function of \(S_{\textrm{l}}\)) what fraction of the flow \(f_{\textrm{l}}\) is liquid, with the remaining fraction being flowing gas. Increasing \(S_{\textrm{l}}\) leads to \(f_{\textrm{l}}\) increasing also, but the relationship is nonlinear (see Fig. A2(a) in the appendix for an example). Once \(f_{\textrm{l}}\) is known though, a conservation equation (Buckley and Leverett 1942; Zhou and Rossen 1995; Ashoori et al. 2010) coupled to the method of characteristics (Courant and Friedrichs 1999; Laney 1998), then allows us to determine how \(S_{\textrm{l}}\) varies with x and t. Some typical examples of how \(S_{\textrm{l}}\) varies with x are plotted in Fig. 2 later on, albeit specifically with the x coordinate normalised in Fig. 2 to collapse together data at different times. The way figures such as these are determined is that so called characteristic lines each with a specified \(S_{\textrm{l}}\) value propagate through x versus t space, with a well-defined velocity \((q/\phi ) \textrm{d}f_{\textrm{l}}/\textrm{d}S_{\textrm{l}}\) for each line. Different \(S_{\textrm{l}}\) values however have different \(\textrm{d}f_{\textrm{l}}/\textrm{d}S_{\textrm{l}}\) values and hence different velocities associated with them, so in x versus t space, the characteristics spread out in the form of a fan (Shan and Rossen 2004): see e.g. Fig. A1 in the appendix, particularly the left side of the figure, for a schematic indication of what such a fan might look like.

In order to determine the form of the function \(f_{\textrm{l}}(S_{\textrm{l}})\), it is necessary to know viscosities of liquid and gas, \(\mu _{\textrm{l}}\) and \(\mu _{\textrm{g}}\), respectively (with gas remaining rather less viscous than liquid under typical reservoir conditions (Shan and Rossen 2004)). We also need so called relative permeabilities (Brooks 1965) of liquid and gas \(k_{\textrm{r,l}}\) and \(k_{\textrm{r,g}}^{0},\) respectively. These relative permeabilities and are often treated as power law functions of \(S_{\textrm{l}}\) or \(1-S_{\textrm{l}},\) respectively (Shi 1996; Brooks 1965): see Sect. A.2.1 in the appendix for details of the functions we assume. Specifically we will consider both quadratic and quartic power laws here, see equations (A2)–(A3). Ratios between relative permeabilities and viscosities give so called relative mobilities. A total relative mobility \({\mathcal {M}}_{\textrm{tot}}\) is defined here as the sum of the liquid and gas relative mobilities, and a dimensionless analogue \(M_{\textrm{tot}}\equiv \mu _{\textrm{l}}{\mathcal {M}}_{\textrm{tot}}\) can also be defined. The quantity \(M_{\textrm{tot}}\) (see equation (A5) for the formal definition) is then a well-defined function of \(S_{\textrm{l}}\) (Buckley and Leverett 1942; Fisher et al .1990).

We are interested here however, not merely in gas, but specifically in foamed gas. Foam causes a very large reduction in the mobility of gas in particular (Shan and Rossen 2004; Eneotu and Grassia 2020). Towards this end, we identify a maximum mobility reduction factor \(R_{\textrm{f}}\), which is the maximum factor by which the mobility of foamed gas can be reduced relative to unfoamed gas. The value of \(R_{\textrm{f}}\) is often very large (Ashoori et al. 2010), up to tens of thousands (Zeng et al. 2016; Ma et al. 2013; Rossen and Boeije 2014). Following Eneotu and Grassia (2020) we will consider values \(R_{\textrm{f}}=[185,1850,18{,}500]\).

The mobility of foamed gas does not always reduce by quite so much at the maximum mobility reduction factor \(R_{\textrm{f}}\) suggests (see equation (A4) in the appendix for example). Even more importantly, total mobilities do not always reduce by quite so much as the maximum reduction factor \(R_{\textrm{f}}\) either (Ma et al. 2013). The reasons have already been mentioned in Sect. 1. At very high liquid saturations, total mobilities tend to be dominated by the mobility of liquid, so any reduction in gas mobility is less relevant. Meanwhile, at very low liquid saturations, foam collapses (Zeng et al. 2016), so we deal then with high mobility unfoamed gas, rather than low mobility foamed gas. It is for intermediate saturations therefore that \({\mathcal {M}}_{\textrm{tot}}\) or equivalently \(M_{\textrm{tot}}\) tend to be lowest. Often there can be quite deep minima in \(M_{\textrm{tot}}\) at intermediate liquid saturations, such that very low \(M_{\textrm{tot}}\) values correspond to a rather narrow domain of saturations: see Fig. A2(b) for an example. What is evident here is that the presence of foamed gas influences the functional form of \(M_{\textrm{tot}}(S_{\textrm{l}})\). It also consequently influences the function \(f_{\textrm{l}}(S_{\textrm{l}})\), because this turns out to be nothing more than the ratio between liquid mobility and total mobility: see the definition in equation (A6). As is then seen in Fig. A2(a), when \(S_{\textrm{l}}\) rises meaning that foamed gas is present, flow is primarily liquid, and so \(f_{\textrm{l}}\) rises.

Turning now back to consider the liquid saturation \(S_{\textrm{l}}\), the aforementioned method of characteristics admits discontinuous jumps in solutions for \(S_{\textrm{l}}\). During so called forward flow (Shan and Rossen 2004), gas is pushed into liquid, and a discontinuity (called a contact discontinuity (Courant and Friedrichs 1999; Laney 1998)) appears at a location \(x_{\textrm{s}}\), with this location \(x_{\textrm{s}}\) moving over time t at a well-defined velocity. Remember we are dealing with a 1-D problem here, so \(x_{\textrm{s}}\) is propagating here along just a single spatial coordinate.

At the discontinuity, liquid saturation jumps from a value \(S_{\textrm{l,fwd}}\) to unity (we ignore here complications associated with having irreducible gas saturation and/or irreducible liquid saturation (Attia et al. 2008), but they can be handled merely by rescaling the definition of \(S_{\textrm{l}}\)). Likewise during pure reverse flow (without any prior forward flow occurring), liquid is pushed into gas. Once again a contact discontinuity appears (Eneotu and Grassia 2020) at a certain 1-D location \(x_{\textrm{s}}\) and again this location moves with a well-defined velocity. At the discontinuity, liquid saturation now jumps from a value \(S_{\mathrm {l,rev,\infty }}\) to zero. Note that \(S_{\mathrm {l,rev,\infty }}\) exceeds \(S_{\textrm{l,fwd}}\): see e.g. Fig. A2(a) which identifies values of \(S_{\textrm{l,fwd}}\) and \(S_{\mathrm {l,rev,\infty }}\), and see also Table A1. Consider also that the slope of the fractional flow curves themselves in Fig. A2(a) indicates the velocity of characteristics, whereas the slope of the various straight lines constructed upon Fig. A2(a) indicates instead the velocity of the discontinuity. The fact that, both in forward flow and in pure reverse flow, we can identify specific liquid saturations at which these slopes match is what implies in each case the existence of a contact discontinuity. This property relies in turn on the fractional flow curve exhibiting a point of inflection.

Thus far we have considered liquid saturation itself at the discontinuities. Now we consider instead mobility, which as we have noted is just a function of saturation. The total mobility (in dimensionless form) at the saturation adjacent to each discontinuity will be denoted \(M_{\textrm{tot,fwd}}\) and \(M_{\mathrm {tot,rev,\infty }},\) respectively. Typically we find that \(M_{\mathrm {tot,rev,\infty }}\) is rather smaller than \(M_{\textrm{tot,fwd}}\), which was one of the key results of Eneotu and Grassia (2020): see also Fig. A2(b) and Table A1 in the appendix.

In both cases forward flow or reverse flow however, moving away from the discontinuity causes mobility \(M_{\textrm{tot}}\) to increase (Shan and Rossen 2004; Grassia et al. 2014). It can happen though that \(M_{\textrm{tot}}\) is less sensitive to liquid saturation \(S_{\textrm{l}}\) for the reverse flow case than the forward flow case, owing to the reverse flow case being close to a local minimum in the \(M_{\textrm{tot}}\) versus \(S_{\textrm{l}}\) curve (see Fig. A2(b)). Here however we consider instead how mobility \(M_{\textrm{tot}}\) increases not with liquid saturation \(S_{\textrm{l}}\) moving away from the discontinuity, but rather how \(M_{\textrm{tot}}\) increases with position x moving away.

In x versus t space it has been mentioned already that characteristics spread out like a fan (Shan and Rossen 2004) (again see Fig. A1 in the appendix, particularly the left side of the figure). It follows then that characteristics in parts of the fan that are far away from the discontinuity should have rather higher mobility than the mobility at the discontinuity itself. There will however be regions of the fan very close to the discontinuity at which \(M_{\textrm{tot}}\) still remains close to either \(M_{\textrm{tot,fwd}}\) or \(M_{\mathrm {tot,rev,\infty }}\). In a sense to be made precise later, these regions are assumed (Shan and Rossen 2004; Grassia et al. 2014; Eneotu and Grassia 2020) to extend (as alluded to in Sect. 1) over a fraction \(\epsilon\) of the distance \(\mid x_{\textrm{s}} \mid\) that the discontinuity itself displaces, remembering throughout here that we are working in 1-D. Specifically we define values \(\epsilon _{\textrm{fwd}}\) for forward flow and \(\epsilon _{\textrm{rev}}\) for reverse flow and these values need not be the same. Indeed computing these quantities is one of the contributions of the present work.

Thus far we have considered forward flows and reverse flows separately. Now we consider these together, namely a forward flow followed immediately by a reverse flow (Eneotu and Grassia 2020). This is what appendix A.1 discusses, and an illustration of what is happening here in x versus t space is shown in Fig. A1: this figure captures the essence of what Eneotu and Grassia (2020) discovered. The sign convention we adopt is that the initial forward flow is in the negative x direction, seen towards the left of Fig. A1. Moreover, the forward flow is assumed to last for a duration \(t^{*}\), so we focus now on times \(t\ge t^{*}\) once reverse flow has already begun, which is seen now towards the right of Fig. A1.

For times \(t\ge t^{*}\), it turns out that a discontinuity in liquid saturation is still present. However, it is no longer a contact discontinuity (which would have a constant velocity), but instead is now a shock (with variable velocity, as the right of Fig. A1 also indicates) (Courant and Friedrichs 1999; Laney 1998; Eneotu and Grassia 2020). We still however continue to denote its location by \(x_{\textrm{s}}\) as a function of t.

Initially when it appears at time \(t^{*}\), the shock is at a specific location \(x_{\textrm{switch}}\): it inherits the same location as the predecessor contact discontinuity had at the instant when the flow direction switches. The shock’s subsequent locations at later times can be computed, knowing liquid saturations on either side of the discontinuity (Eneotu and Grassia 2020).

The liquid saturation at the shock jumps from a higher value \(S_{\textrm{l,high}}\) on the upstream side of the shock to a lower value \(S_{\textrm{l,low}}\) on the downstream side. These values can be identified using the method of characteristics recognising that there is no longer just a single fan of characteristics, but rather a double fan (Eneotu and Grassia 2020): again see the right of Fig. A1. One characteristic fan, which is downstream of the shock is just a reflection of the characteristic fan that was present in the original forward flow. A second fan however, with a different (i.e. higher) set of liquid saturations now appears upstream of the shock. One of the issues that Eneotu and Grassia (2020) considered was which of these two fans presents more resistance to the motion: this is a point we will return to discuss later on.

The saturations \(S_{\textrm{l,high}}\) and \(S_{\textrm{l,low}}\) at the shock evolve with time (Eneotu and Grassia 2020). Specifically \(S_{\textrm{l,high}}\) begins with a certain value \(S_{\textrm{l,rev,0}}\) and grows over time towards \(S_{\mathrm {l,rev,\infty }}\). The value of \(S_{\textrm{l,rev,0}}\) is typically only slightly less than \(S_{\mathrm {l,rev,\infty }}\) (see Fig. A2(a)), so the growth in \(S_{\textrm{l,high}}\) is quite modest. Meanwhile \(S_{\textrm{l,low}}\) begins with a value \(S_{\textrm{l,fwd}}\) and falls over time.

At a certain time that we call the cross-over time \(t_{\textrm{cross}}\), the shock has moved back in reverse flow through exactly the same distance that the discontinuity originally moved in forward flow. Moreover, at time \(t_{\textrm{cross}}\), it turns out that the value of \(S_{\textrm{l,low}}\) has fallen to zero, and thereafter downstream of the shock we have only gas, rather than a mixture of liquid and gas together. Moreover, at very long times after \(t_{\textrm{cross}}\), the shock asymptotes back towards the same contact discontinuity as arises in pure reverse flow, without any initial forward flow period (Eneotu and Grassia 2020).

This then provides a description of the findings of Eneotu and Grassia (2020) insofar as they impact on the present work. Further details of what Eneotu and Grassia (2020) achieved are presented in appendix (see Sect. A), along with parameter values that need to be used within models for forward-and-reverse flows of liquid and gas in porous media. Based on all this information, we can now proceed in what follows to determine pressure drops associated with such flows.

3 Pressure drop across the flow and thickness of low mobility region

As shown in Eneotu and Grassia (2020) (by invoking Darcy’s law), the pressure drop \(\Delta P\) across a region of variable liquid saturation \(S_{\textrm{l}}\) extending in the x direction can be computed as

$$\begin{aligned} \Delta P=\int \dfrac{q}{k {\mathcal {M}}_{\textrm{tot}}(S_{\textrm{l}}(x))}\,\textrm{d}x=\int \dfrac{q\mu _\textrm{l}}{k M_{\textrm{tot}}(S_{\textrm{l}}(x))}\,\textrm{d}x, \end{aligned}$$
(1)

with k as the permeability of the medium, q as the total fluid flux (liquid and gas together), \(\mu _{\textrm{l}}\) as liquid viscosity and \(M_{\textrm{tot}}\) being the dimensionless analogue of mobility \({\mathcal {M}}_{\textrm{tot}}\). Note that \(\Delta P\) here is always defined in the sense from upstream to downstream, so ought to be a positive quantity. In the present work, we are interested in both forward flows and reverse flows, so the direction of upstream and downstream relative to the x coordinate is liable to change. The sign of q is likewise liable to change. Integration limits for equation (1) are omitted for now to give the flexibility to maintain \(\Delta P\) positive regardless of the sign convention for how x and q are defined. It is only in later equations that we will invoke a definite sign convention for x and for q, and we will ensure that \(\Delta P\) is positive once that is done.

We now proceed to use equation (1) to develop novel formulae to compute the ratio \(\epsilon\) between front thickness and displacement for two situations, namely forward flow and pure reverse flow (both processes discussed in Sect. 2). These situations lead to formulae for ratios \(\epsilon _{\textrm{fwd}}\) and \(\epsilon _{\textrm{rev}}\), respectively, see Sects. 3.1–3.2. These values are later used in Sect. 3.3 to obtain a formula for pressure drop applicable to the case of flow reversal immediately after forward flow.

3.1 Forward flow

When considering just forward flow, and looking at the pressure drop just across the region containing foamed gas (the region between 0 and \(x_\textrm{s}\)), the pressure drop \(\Delta P\) can be represented as

$$\begin{aligned} \Delta P \approx \dfrac{{\mid q \mid } \, \mu _\textrm{l}\epsilon _{\textrm{fwd}} \mid x_{\textrm{s}}\mid }{k\, M_{\textrm{tot,fwd}}}, \end{aligned}$$
(2)

where absolute value signs are included on the right hand side of the equation to remind us that \(\Delta P\) measured upstream to downstream is positive. Here the factor \(\epsilon _{\textrm{fwd}}<1\) represents that across this region of size \(\mid x_{\textrm{s}}\mid\), mobility is at least \(M_\textrm{tot,fwd}\), and typically higher. Via combining equations (1) and (2) the value of \(\epsilon _{\textrm{fwd}}\) can therefore be computed as

$$\begin{aligned} \epsilon _\textrm{fwd}=\int _{- \mid x_{\textrm{s}}\mid }^{0} \dfrac{M_\textrm{tot,fwd}}{\mid x_{\textrm{s}}\mid M_\textrm{tot}} \,\textrm{d}{x} = \int _{0}^{S_{\textrm{l,fwd}}} \dfrac{M_\textrm{tot,fwd}}{\mid x_{\textrm{s}}\mid M_\textrm{tot}(S_\textrm{l})} \left| \dfrac{\textrm{d}x}{\textrm{d}S_\textrm{l}} \right| \textrm{d}S_\textrm{l}, \end{aligned}$$
(3)

integration limits here being obtained remembering the aforementioned convention that forward flow corresponds to the negative x direction. Now substituting in \(x = (q\, t/\phi ) \textrm{d}f_\textrm{l}/\textrm{d}S_\textrm{l}\) (the equation for a characteristic line) and also \(x_\textrm{s} = (q \, t/\phi ) \textrm{d}f_\textrm{l}/\textrm{d}S_\textrm{l}\mid _{S_\textrm{l}=S_\textrm{l,fwd}}\) (with the convention that \(q<0\) in forward flow) gives

$$\begin{aligned} \epsilon _\textrm{fwd} = \dfrac{M_\textrm{tot,fwd}}{\textrm{d}f_\textrm{l}/\textrm{d}S_\textrm{l}\mid _{S_\textrm{l}=S_\textrm{l,fwd}}}\int _{0}^{S_{\textrm{l,fwd}}} \dfrac{1}{M_\textrm{tot}(S_\textrm{l})} \dfrac{\textrm{d}^2 f_\textrm{l}}{\textrm{d}S_\textrm{l}^2} \,\textrm{d}S_\textrm{l}. \end{aligned}$$
(4)

The smaller the value of \(\epsilon _{\textrm{fwd}}\), the faster \(M_\textrm{tot}\) rises above \(M_\textrm{tot,fwd}\) as we move away from the front, and hence as x becomes smaller in magnitude than \(x_{\textrm{s}}\). The value we compute for \(\epsilon _{\textrm{fwd}}\) depends of course on the functional forms for \(f_{\textrm{l}}\) and \(M_{\textrm{tot}}\). Typical formulae used to determine these are provided in Sect. A.2.1 in the appendix (see equations (A2)–(A6)), but the actual formulae would need to be validated in any specific system.

Equations (3)–(4) assume that the dominant pressure drop is occurring across regions in which \(M_{\textrm{tot}}\) is varying (with \(S_{\textrm{l}}\) also varying specifically in the domain \(S_{\textrm{l}}<S_{\textrm{l,fwd}}\)), but is ignoring regions in which \(M_{\textrm{tot}}\) is spatially uniform (far upstream or far downstream, where \(S_{\textrm{l}}\) is spatially uniform). In particular, we are explicitly excluding pressure drop across any regions filled with pure liquid. This is based on the notion that regions containing foamed gas should be rather less mobile than regions containing pure liquid (by definition \(M_\textrm{tot}=1\) for pure liquid). As data provided in the appendix make clear, however (see Table A1), this is not actually the case for forward flows with quadratic power laws (as per equation (A2)) for relative permeability: the mobility at \(S_{\textrm{l}}=S_{\textrm{l,fwd}}\) exceeds that at \(S_{\textrm{l}}=1\). Neglecting the pressure drop across spatially uniform regions as we do here is not such a good approximation in that case. In pure reverse flow however (again based on Table A1), the mobilities within the region containing foamed gas are much lower than those in the region containing foamed gas in forward flow. Hence in pure reverse flow, the assumption that the region containing foamed gas is rather less mobile than any spatially uniform regions containing pure gas (mobility \(M_{\textrm{tot}}=\mu _\textrm{l}/\mu _\textrm{g} = 10\)) is now a rather good one, so we go on to consider that case next.

3.2 Pure reverse flow

Pure reverse flow consists of the injection of liquid (which subsequently forms foamed gas and liquid), into a pure gas phase. Such a flow can also be considered to take place at an asymptotically long time when a front is made to backtrack following forward flow. The formula for pressure drop \(\Delta P\) via equation (1) still applies and the subsequent analysis is analogous to what is already presented in Sect. 3.1. For brevity we have relegated details to appendix B.1 in supplementary material. A formula for \(\epsilon _{\textrm{rev}}\) eventually results (see equation (B3) in the appendix). Whereas equation (4) for forward flow requires integrating over a characteristic fan involving liquid saturations from 0 to \(S_{\textrm{l,fwd}}\), the analogous equation (B3) for reverse flow requires integrating over a characteristic fan involving saturations from \(S_{\mathrm {l,rev,\infty }}\) to 1. As was also the case for \(\epsilon _{\textrm{fwd}}\), the actual \(\epsilon _{\textrm{rev}}\) value is sensitive to formulae used to obtain \(f_{\textrm{l}}\) and \(M_{\textrm{tot}}\). Typical formulae used to determine these have been provided in Sect. A.2.1, but actual formulae are subject to validation in any specific system.

3.3 Flow reversal immediately after forward flow

Having considered the situation of forward flow and the situation of pure reverse flow, we now consider the case of flow reversal immediately after forward flow. We need now to account for the double fan structure of the flow (Eneotu and Grassia 2020) mentioned in Sect. 2 and sketched in Fig. A1. Again full details are relegated to an appendix (Sect. B.2) in supplementary material, being largely analogous to what we have already discussed before in Sects. 3.1–3.2. A summary of the situation is given below.

There is now a shock present, which forms at time \(t^{*}\) when the flow switches direction. It forms at first at a location \(x_{\textrm{switch}}\). Later on, the shock propagates to location \(x_{\textrm{s}}\), with \(x_{\textrm{s}}\) varying with time. Our sign convention is such that \(x_{\textrm{switch}}\) is negative, and (at least to start with) \(x_{\textrm{s}}\) is negative also.

As mentioned a double fan structure develops around the shock. As per Fig. A1, one fan appears downstream of the shock between spatial locations \(x_{\textrm{s}}\) and 0. The other fan appears upstream of the shock between spatial locations \(x_{\textrm{switch}}\) and \(x_{\textrm{s}}\). As far as pressure drops are concerned, spatially uniform regions of pure gas (which are even further downstream than the downstream fan) or pure liquid (which are even further upstream than the upstream fan) are neglected altogether, on the basis that pure gas or pure liquid should be more mobile than the regions within the fans containing liquid and foamed gas. To obtain the resulting pressure drop \(\Delta P\) then, equation (1) is broken up into just two pieces, one for each fan, and that is what the pressure drop equation (B4) in the appendix shows.

Within the double fan structure, the downstream fan is inherited from the initial forward flow stage and involves comparatively low liquid saturations in a domain from 0 to a value \(S_{\textrm{l,low}}\). The upstream fan is newly formed after flow reversal begins and involves comparatively high liquid saturations in a domain from a value \(S_{\textrm{l,high}}\) and 1. Recall from Sect. 2 that both \(S_{\textrm{l,low}}\) and \(S_{\textrm{l,high}}\) vary with time. We need to know \(S_{\textrm{l,low}}\) and \(S_{\textrm{l,high}}\) at each time in order evaluate \(\Delta P\) via equation (B4). However, it turns out that estimates of \(\Delta P\) can still be proposed even without all that information, as we now discuss.

3.3.1 Estimate of pressure drop

It has been proposed (Eneotu and Grassia 2020) that a reasonable estimate for pressure drop (that we call \(\Delta P_{\textrm{estimate}}\)) might result if we approximate the double fan as being composed of two separate fans as follows. The downstream fan is replaced by a fan having the same spatial extent but resulting from forward flow. The upstream fan is again replaced by a fan having the same spatial extent but resulting from pure reverse flow.

The domain of liquid saturations covered by the downstream fan is now estimated to be 0 to \(S_{\textrm{l,fwd}}\) (where \(S_{\textrm{l,fwd}}\) is fixed over time, unlike \(S_{\textrm{l,low}}\) which varies). The domain of liquid saturations covered by the upstream fan is now estimated to \(S_{\mathrm {l,rev,\infty }}\) to 1 (where \(S_{\mathrm {l,rev,\infty }}\) is fixed over time, unlike \(S_{\textrm{l,high}}\) which varies). Mobilities can likewise be estimated. The liquid saturation \(S_{\textrm{l,fwd}}\) is associated with a mobility \(M_{\textrm{tot,fwd}}\) and the liquid saturation \(S_{\mathrm {l,rev,\infty }}\) is associated with a mobility \(M_{\mathrm {tot,rev,\infty }}\).

Knowing these mobilities (see e.g. values in Table A1), and coupling together solutions for forward flow and pure reverse flow, an estimate for pressure drop across the full domain of interest is obtained (Eneotu and Grassia 2020). It is considered that the total mobility \(M_{\textrm{tot}}\) remains in effect close to \(M_{\textrm{tot,fwd}}\) over a region of extent \(\epsilon _{\textrm{fwd}} \mid x_{\textrm{s}}\mid\) on the low liquid saturation side of the shock (low liquid saturation fan with \(S_{\textrm{l}}\) values close to \(S_{\textrm{l,low}}\)), and remains in effect close to \(M_{\mathrm {tot,rev,\infty }}\) over a region of extent \(\epsilon _{\textrm{rev}} \mid x_{\textrm{s}}-x_{\textrm{switch}}\mid\) on the high liquid saturation side of the shock (high liquid saturation fan with \(S_{\textrm{l}}\) values close to \(S_{\textrm{l,high}}\)). The pressure drop across these regions as determined in Eneotu and Grassia (2020), can then be estimated as

$$\begin{aligned} \Delta P_{\textrm{estimate}}\approx \dfrac{q \mu _\textrm{l}}{k}\left( \dfrac{\epsilon _{\textrm{fwd}}\mid x_{\textrm{s}}\mid }{M_{\textrm{tot,fwd}}}+\dfrac{\epsilon _{\textrm{rev}}\mid x_{\textrm{s}}-x_{\textrm{switch}}\mid }{M_{\mathrm {tot,rev,\infty }}} \right) . \end{aligned}$$
(5)

We emphasise that this is an estimate, and need not be identical to the \(\Delta P\) computed by equation (1) using the actual distribution of \(M_{\textrm{tot}}\) around the shock during a reverse flow following immediately after a forward flow, i.e. it need not be identical to equation (B4).

The question now arises also as to which region, the downstream side of the shock (the first term on the right hand side of equation (5)) or the upstream side of the shock (the second term on the right hand side of equation (5)) makes the dominant contribution to \(\Delta P\). It is already established (Eneotu and Grassia 2020), that \(M_{\mathrm {tot,rev,\infty }}\) is smaller than \(M_\textrm{tot,fwd}\) (mentioned in Sect. 2; see also Table A1 for instance), and moreover immediately after flow reversal starts, the shock can move quite quickly, meaning that the magnitude of \(x_\textrm{s}\) can also decrease quickly (as incidentally Fig. A1 shows). Both these effects give more weight to the second term in equation (5).

What Eneotu and Grassia (2020) did not do however was establish the values of \(\epsilon _{\textrm{fwd}}\) and \(\epsilon _{\textrm{rev}}\). We do not know definitively which side of the shock makes the dominant contribution to driving pressure difference unless \(\epsilon _\textrm{fwd}\) and \(\epsilon _\textrm{rev}\) are known. What Eneotu and Grassia (2020) did instead was assume \(\epsilon _\textrm{fwd}\) and \(\epsilon _\textrm{rev}\) were equal, and it set them both to an arbitrarily chosen small value (much smaller than unity). Small values of \(\epsilon _\textrm{fwd}\) and \(\epsilon _\textrm{rev}\), i.e. greater increases in mobility moving away from the shock, would tend to give a lower pressure drop for a given propagation rate or equivalently faster propagation for a given imposed pressure. The assumption of \(\epsilon _{\textrm{fwd}}\) and \(\epsilon _{\textrm{rev}}\) being small, and the assumption of equality between them, will however be relaxed here. Instead these quantities will be computed as we have said.

Obtaining values of \(\epsilon _\textrm{fwd}\) and \(\epsilon _\textrm{rev}\) as we do here is also expected to be important eventually in moving from 1-D model to 2-D models (Eneotu and Grassia 2020). In 1-D we often set flow rates, and then from those flow rates we determine a posteriori pressures required to maintain that flow. In 2-D however we typically know driving pressure difference and could use equation (5) to deduce flow rate, and hence foam front propagation rate, which clearly depends on \(\epsilon _\textrm{fwd}\) and \(\epsilon _\textrm{rev}\). Moving the front location in 2-D however modifies the hydrostatic pressure and hence modifies the driving pressure difference, which then impact back on how the front propagates.

3.3.2 Discontinuity that moves further in reverse flow than in forward flow

Before proceeding further with any calculations, we first consider a discontinuity which propagates in reverse flow at least as far as it travelled in forward flow, a situation which can happen in 1-D flows (and also in 2-D flows like those sketched in Fig. 1 if points are considered that start off just slightly above what was originally the bottom of the front). Full discussion of this in the 1-D context considered here is again relegated to supplementary material, on the basis that it is developed using arguments about pressure drops across characteristic fans analogous to those we have already seen. Essentially what happens (as Sect. 2 also alludes to) is that there is a certain time \(t_{\textrm{cross}}\) after which the front has backtracked during reverse flow at least as far as it originally propagated in forward flow. In the context of Fig. A1 for instance, the downstream fan has now disappeared and only the upstream fan survives.

Exactly at time \(t_{\textrm{cross}}\), there is a pressure drop \(\Delta P_{\textrm{cross}}\) and a formula for determining it is presented in equation (B9). At this same time, we can also identify a region within the surviving upstream fan within which mobility \(M_{\textrm{tot}}\) remains in effect close to \(M_{\mathrm {tot,rev,\infty }}\). The ratio between the size of this region to the full extent of the upstream fan is a quantity \(\epsilon _{\textrm{cross}}\), a formula for which is given in equation (B11). Although the formula for \(\epsilon _{\textrm{cross}}\) looks somewhat similar to that for \(\epsilon _{\textrm{rev}}\) (arising in pure reverse flow, see equation (B3)) the two formulae are not quite the same. In particular the domain of liquid saturations covered by the surviving upstream fan at time \(t_{\textrm{cross}}\) is not the same as the domain of saturations corresponding to pure reverse flow.

This completes our review of the formulae (Eneotu and Grassia 2020) to compute pressure drops \(\Delta P\) and as well as our extension of those formulae to determine relative thicknesses (\(\epsilon _{\textrm{fwd}}\), \(\epsilon _{\textrm{rev}}\) and \(\epsilon _{\textrm{cross}}\)) of low mobility regions that result in the flow domain. All this material discussed in Sects. 2–3 is now used in Sect. 4 to generate the main novel results of this work. Parameter values utilised are provided in appendix A.2.2.

4 Results: Foam front thickness to displacement ratio & pressure drop

In Sect. 4.1 we first determine liquid saturation profiles over position. Then Sects. 4.2–4.3 use that information to obtain \(\epsilon _{\textrm{fwd}}\) and \(\epsilon _{\textrm{rev}},\) respectively. Recall that if these values are small, then low mobility regions are localised close to foam fronts, but if they are not small, then low mobility regions are more extended spatially. The final section here, namely Sect. 4.4 goes on to consider pressure drops when flow reversals take place.

4.1 Liquid saturation over the x domain

Once we know fractional flow curves (see Fig. A2(a) in the appendix), we can now proceed to solve for the spatial distribution of liquid saturations. In Fig. 2 we show \(S_{\textrm{l}}\) versus \(x/x_{\textrm{s}}\), first in Fig. 2a for forward flow with \(S_{\textrm{l}}\in [0,S_{\textrm{l,fwd}}]\), and then in Fig. 2b for pure reverse flow (without previous forward flow, i.e. with \(x_{\textrm{switch}}\equiv 0\)). In both figures we see that much of the domain of x corresponds to \(S_{\textrm{l}}\) values close to either \(S_{\textrm{l,fwd}}\) or \(S_{\mathrm {l,rev,\infty }}\). This immediately implies that the extent of the low mobility region along x is considerably larger than what was assumed in previous studies (Grassia et al. 2014; Torres-Ulloa and Grassia 2021). The only exception is seen for the quartic power laws for relative permeability with \(R_\textrm{f}=185\). Here \(S_\textrm{l}\) changes away from \(S_\mathrm {l,rev,\infty }\) more quickly than for any of the other cases, and the reason is actually discussed in Sect. A.2.3 in the appendix. The effect arises due to the gradual change in slope in the \(f_\textrm{l}\) versus \(S_\textrm{l}\) curve for this particular case (see Fig. A2(a)), so that a significant change in \(S_{\textrm{l}}\) is needed to impact on \(\textrm{d}f_\textrm{l}/\textrm{d}S_\textrm{l}\) and hence on distance that a given characteristic will propagate. Aside from this exceptional case, the results with low mobilities extending over a significant x domain suggest that the bulk of the pressure drop, is not confined to a limited portion of the solution spatial domain, despite what has been assumed before (Grassia et al. 2014; Torres-Ulloa and Grassia 2021).

Fig. 2
figure 2

a Values of \(x/x_{\textrm{s}}\) vs \(S_{\textrm{l}}\) for forward flow. Note that at \(x/x_{\textrm{s}}=1\), the value of \(S_{\textrm{l}}\) undergoes a discontinuous jump to unity. b Values of \(x/x_{\textrm{s}}\) vs \(S_{\textrm{l}}\) for pure reverse flow, without previous forward flow. Note that at \(x/x_{\textrm{s}}=1\), the value of \(S_{\textrm{l}}\) undergoes a discontinuous jump to zero. Note also that even though \(x_{\textrm{s}}\) formally switches sign between forward flow and pure reverse flow, the domain of x values upon which we focus likewise switches sign, so the domain of \(x/x_{\textrm{s}}\) is positive in both instances

Full size image

4.2 Computing \(\epsilon _{\textrm{fwd}}\)

Here we compute the value of the front’s thickness to displacement ratio, in the first instance for forward flow (i.e. \(\epsilon _{\textrm{fwd}}\)). As mentioned before, the propagating foam front in a porous medium can be captured as the region where the foam is finely textured, and therefore is, in principle at least, less mobile than in other regions within the medium (Shan and Rossen 2004; Grassia et al. 2014; Torres-Ulloa and Grassia 2021). The thickness of this region is taken to be a fraction \(\epsilon _{\textrm{fwd}}\) of the front’s total travelled distance \(\mid x_\textrm{s}\mid\), and the value of \(\epsilon _{\textrm{fwd}}\) can then be determined by using equation (4).

By using the various formulae for \(f_\textrm{l}\) and \(M_{\textrm{tot}}\) (as discussed in Sect. A.2 in the appendix), and the two different relative permeability approaches (quadratic and quartic) along with selected values for the maximum mobility reduction factor \(R_{\textrm{f}}\), we can determine various values of \(\epsilon _\textrm{fwd}\): these are reported in Table 1. Clearly the \(\epsilon _\textrm{fwd}\) values are smaller than unity (as they must be) but are not orders of magnitude smaller than unity. In addition in Fig. 3a, we plot \(M_{\textrm{tot,fwd}}/M_{\textrm{tot}}\) against the scaled distance over which the front is propagating \(x/x_{\textrm{s}}\). Moving back from the contact discontinuity, the value \(M_\textrm{tot,fwd}/M_\textrm{tot}\) does not decay remarkably quickly, which means that \(\epsilon _\textrm{fwd}\) (which is the area under the curve in Fig. 3a) is not terribly small. Note that \(M_\textrm{tot,fwd}/M_\textrm{tot}\) is relatively insensitive to \(R_\textrm{f}\) but there are some differences depending on whether we consider a quartic or quadratic power law for relative permeability. The quartic power law has a slightly faster decay of \(M_\textrm{tot,fwd}/M_\textrm{tot}\) moving back from the front (hence a slightly smaller \(\epsilon _\textrm{fwd}\), remembering this is the area under the curve in Fig. 3a).

In Fig. 3b, on the other hand, we show a plot of the function \((M_{\textrm{tot,fwd}}/(\mid \textrm{d}f_{\textrm{l}}/\textrm{d}S_{\textrm{l}}\mid _{S_{\textrm{l}}=S_{\textrm{l,fwd}}}M_{\textrm{tot}}))\textrm{d}^2f_\textrm{l}/\textrm{d}S_{\textrm{l}}^2\) versus \(S_{\textrm{l}}\). Here we can see that this function is sharply peaked near \(S_{\textrm{l}}=S_{\textrm{l,fwd}}\). Once again however, the value of \(\epsilon _\textrm{fwd}\) is just the area under the curve. The main contribution to this is from \(S_\textrm{l}\) values close to \(S_{\textrm{l,fwd}}\). This narrow domain of \(S_\textrm{l}\) values might however map to a fairly wide domain of x values (as Fig. 2a makes clear). In other words, the majority of the pressure drop needed to drive the flow arises from a narrow domain of \(S_\textrm{l}\) values, but this does not correspond to a narrow domain of x values.

Fig. 3
figure 3

a Mobility ratio \(M_{\textrm{tot,fwd}}/M_{\textrm{tot}}\) versus \(x/x_{\textrm{s}}\). This quantity integrates to \(\epsilon _{\textrm{fwd}}\). b Function \((M_{\textrm{tot,fwd}}/ ( \mid \textrm{d}f_{\textrm{l}}/\textrm{d}S_{\textrm{l}}\mid _{S_{\textrm{l}}=S_{\textrm{l,fwd}}} M_{\textrm{tot}}))\,\textrm{d}^2f_\textrm{l}/\textrm{d}S_{\textrm{l}}^2\) versus \(S_{\textrm{l}}\) with \(S_{\textrm{l}}\in [0,S_{\textrm{l,fwd}}]\)

Full size image

Returning to consider Table 1, we can see how different values of \(\epsilon _{\textrm{fwd}}\) are obtained for different power laws for the liquid and (unfoamed) gas relative permeabilities \(k_{\textrm{r,l}}\) and \(k_{\textrm{r,g}}^0\), respectively and for different maximum mobility reduction factors \(R_{\textrm{f}}\). As Fig. 3a also suggests (considering the area under the curves), \(\epsilon _{\textrm{fwd}}\) decreases monotonically with \(R_{\textrm{f}}\), but the decreases are only slight. In addition, lower values of \(\epsilon _{\textrm{fwd}}\) are observed for quartic power laws, in comparison with quadratic ones. None of the \(\epsilon _{\textrm{fwd}}\) values are however orders of magnitude smaller than unity. Of course establishing which of the various \(\epsilon _{\textrm{fwd}}\) values in Table 1 is most appropriate for a given system relies on validating the various formulae proposed in Sect. A.2.1. Even if some adjustments to those formulae were to be made however, it seems unlikely that \(\epsilon _{\textrm{fwd}}\) would ever become orders of magnitude smaller than unity.

Table 1 Ratio between foam front thickness and displacement for forward flow \(\epsilon _{\textrm{fwd}}\). This is computed for different power laws for relative permeability \(k_{\textrm{r,l}}\) and \(k_{\textrm{r,g}}^0\), and in addition for different maximum mobility reduction factors \(R_{\textrm{f}}\)
Full size table

4.3 Computing \(\epsilon _{\textrm{rev}}\)

As mentioned already (see Sects. 1 and 2), when flow is reversed, the thickness of the low mobility region near the front might not necessarily be the same as in forward flow. We are now pushing liquid into gas, not gas into liquid. Here we compute the value of the front’s thickness to displacement ratio, i.e. \(\epsilon _{\textrm{rev}}\), under conditions of pure reverse flow. This is given by equation (B3), and is evaluated for the quadratic and quartic power laws for relative permeability and for different values of maximum mobility reduction factor \(R_\textrm{f}\). Relevant data are reported in Fig. 4 and Table 2.

In Fig. 4a, we plot \(M_{\mathrm {tot,rev,\infty }}/M_{\textrm{tot}}\) against rescaled distance \(x/x_{\textrm{s}}\). Here we can see that moving back from the front, the value of \(M_\textrm{tot}\) decays only rather gradually (even when different power laws or mobility reduction factors are considered). This implies that the value of \(\epsilon _{\textrm{rev}}\) (which is the integral under these curves) is not extremely small, despite what was assumed previously (Shan and Rossen 2004; Grassia et al. 2014). On the contrary, \(\epsilon _{\text {rev}}\) can be rather close to unity (see Table 2). This is partly the effect of \(S_\textrm{l}\) being insensitive to x (see Fig. 2b), and partly the effect of \(M_\textrm{tot}\) being insensitive to \(S_\textrm{l}\) (as it is near a global minimum, see Fig. A2(b)). In the case of forward flow, we had the first effect but not the second.

In Fig. 4a we also observe some sensitivity of \(M_\mathrm {tot,rev,\infty }/M_\textrm{tot}\) to \(R_\textrm{f}\) (higher \(R_\textrm{f}\) gives higher \(M_\mathrm {tot,rev,\infty }/M_\textrm{tot}\)). There is also sensitivity to whether a quartic or quadratic power law is used for relative permeability: \(M_\mathrm {tot,rev,\infty }/M_\textrm{tot}\) is smaller for the quartic. The exception which differs from the other curves is (as already noted) the case \(R_\textrm{f} = 185\) for the quartic power law, which shows \(M_\mathrm {tot,rev,\infty }/M_\textrm{tot}\) decaying faster as \(x/x_\textrm{s}\) decreases. The reasons have already been discussed: \(S_\textrm{l}\) shows more sensitivity to \(x/x_\textrm{s}\) than any of the other reverse flow cases (see Fig. 2b), and \(M_\textrm{tot}\) incidentally shows more sensitivity to \(S_\textrm{l}\) also (see Fig. A2(b)).

Changing now to consider Fig. 4b, we show a plot of the function \((M_{\mathrm {tot,rev,\infty }}/( \mid \textrm{d}f_{\textrm{l}}/\textrm{d}S_{\textrm{l}} \mid _{S_{\textrm{l}}= S_{\mathrm {l,rev,\infty }}} M_{\textrm{tot}})) \mid \textrm{d}^2f_\textrm{l}/\textrm{d}S_{\textrm{l}}^2\mid\) versus \(S_{\textrm{l}}\). As \(S_{\textrm{l}}\) increases above \(S_{\mathrm {l,rev,\infty }}\), the value of this function falls considerably. This implies that, when considering the area under the curve to obtain \(\epsilon _{\textrm{rev}}\), the majority of the contribution arises from saturations close to \(S_\mathrm {l,rev,\infty }\), although these do not necessarily correspond to x values close to \(x_\textrm{s}\).

Fig. 4
figure 4

a Mobility ratio \(M_{\mathrm {tot,rev,\infty }}/M_{\textrm{tot}}\) versus \(x/x_{\textrm{s}}\). This quantity integrates to \(\epsilon _{\textrm{rev}}\). b Function \((M_{\mathrm {tot,rev,\infty }}/ ( \mid \textrm{d}f_{\textrm{l}}/\textrm{d}S_{\textrm{l}} \mid _{S_{\textrm{l}}=S_{\mathrm {l,rev,\infty }}} M_{\textrm{tot}}))\,\mid \textrm{d}^2f_\textrm{l}/\textrm{d}S_{\textrm{l}}^2\mid\) versus \(S_{\textrm{l}}\) with \(S_{\textrm{l}}\in [S_{\mathrm {l,rev,\infty }},1]\)

Full size image

In Table 2 we summarise the different values of \(\epsilon _{\textrm{rev}}\), for different power laws for the liquid and gas relative permeabilities \(k_{\textrm{r,l}}\) and \(k_{\textrm{r,g}}^0\), respectively, and different maximum mobility reduction factors \(R_{\textrm{f}}\). As Fig. 4 also suggests (considering the area under the curves), \(\epsilon _{\textrm{rev}}\) tends to increase monotonically with \(R_{\textrm{f}}\). A different behaviour was observed for \(\epsilon _{\textrm{fwd}}\) (see Fig. 3, and also Table 1), where \(\epsilon _{\textrm{fwd}}\) tended to decrease as \(R_{\textrm{f}}\) increases. This difference between the effect of \(R_\textrm{f}\) on forward and reverse flows can be traced back to the shape of the mobility curve (see Fig. A2(b)). The point \(S_\textrm{l,fwd}\) is well away from the global minimum of the \(M_\textrm{tot}\) versus \(S_\textrm{l}\) curve and increasing \(R_\textrm{f}\) makes the slope of that curve steeper around \(S_\textrm{l,fwd}\). This makes \(M_\textrm{tot}(S_\textrm{l,fwd})/M_\textrm{tot}(S_\textrm{l})\) smaller and hence \(\epsilon _\textrm{fwd}\) becomes smaller. However, \(S_\mathrm {l,rev,\infty }\) is much closer to the global minimum and the \(M_{\textrm{tot}}\) versus \(S_{\textrm{l}}\) curve is not so steep there. Increasing \(R_\textrm{f}\) however moves \(S_\mathrm {l,rev,\infty }\) slightly closer to the global minimum (again see Fig. A2(b)), the \(M_\textrm{tot}\) curve is slightly less steep making \(M_\textrm{tot}(S_\mathrm {l,rev,\infty })/M_\textrm{tot}(S_\textrm{l})\) slightly larger, and \(\epsilon _\textrm{rev}\) increases. Moreover, as Table 3 makes clear, \(\epsilon _\textrm{fwd}\) is consistently less than \(\epsilon _\textrm{rev}\), which is presumably associated with \(M_\textrm{tot}\) being more sensitive to \(S_\textrm{l}\) in the neighbourhood of \(S_\textrm{l,fwd}\) than in the neighbourhood of \(S_\mathrm {l,rev,\infty }\). Determining the actual \(\epsilon _\textrm{fwd}\) and \(\epsilon _\textrm{rev}\) in a given system requires validation of the various formulae in Sect. A.2.1, but the result that \(\epsilon _\textrm{fwd}\) is less than \(\epsilon _\textrm{rev}\) appears robust.

In summary, lower values of both \(\epsilon _{\textrm{fwd}}\) and \(\epsilon _{\textrm{rev}}\) are observed for quartic power laws, in comparison with quadratic power laws. Increasing \(R_{\textrm{f}}\) has two effects. It makes the slope of the \(M_{\textrm{tot}}\) versus \(S_{\textrm{l}}\) curve steeper around \(S_{\textrm{l,fwd}}\), even though the slope is rather shallow around \(S_{\mathrm {l,rev,\infty }}\). This in turn makes \(M_{\textrm{tot}}(S_{\textrm{l,fwd}})/M_{\textrm{tot}}(S_{\textrm{l}})\) smaller and hence \(\epsilon _{\textrm{fwd}}\) becomes smaller. Increasing \(R_{\textrm{f}}\) also turns out however to compress the domain of \(S_\textrm{l}\) values that account for most of the x values. This keeps \(M_{\textrm{tot}}(S_{\mathrm {l,rev,\infty }})/M_{\textrm{tot}}(S_{\textrm{l}})\) larger for most x, hence \(\epsilon _{\textrm{rev}}\) becomes larger. The former effect seems to dominate in the case of \(\epsilon _{\textrm{fwd}}\), while the latter effect seems to dominate in the case of \(\epsilon _{\textrm{rev}}\).

Table 2 Ratio between foam front thickness and displacement for reverse flow \(\epsilon _{\textrm{rev}}\). This is computed here for different power laws for relative permeability \(k_{\textrm{r,l}}\) and \(k_{\textrm{r,g}}^0\), as well as for different maximum mobility reduction factors \(R_{\textrm{f}}\)
Full size table

In Table 3, we compute not just the ratio between \(\epsilon _{\textrm{rev}}\) and \(\epsilon _{\textrm{fwd}}\), but also the ratio between \(M_{\textrm{tot,fwd}}\) and \(M_{\mathrm {tot,rev,\infty }}\). Even though the latter ratio is clearly far away from unity, the former ratio is not. This suggests that it is not really necessary to consider \(\epsilon _{\textrm{rev}}\) and \(\epsilon _{\textrm{fwd}}\) (i.e. the thicknesses of the low mobility regions relative to front displacement) as unequal values. What is more important as a finding here is that neither \(\epsilon _{\textrm{rev}}\) nor \(\epsilon _{\textrm{fwd}}\) is very small compared to unity. As a result, even though low mobilities account for only a small fraction of the \(S_{\textrm{l}}\) domain, they actually account for a fairly large fraction of the x domain (as Fig. 2 makes apparent). Hence the notion proposed previously (Shan and Rossen 2004; Grassia et al. 2014) of low mobilities being confined spatially (as opposed to confined merely in \(S_{\textrm{l}}\)) is actually not such a good one.

Table 3 Ratios between \(\epsilon _{\textrm{rev}}\) and \(\epsilon _{\textrm{fwd}}\) and between \(M_{\textrm{tot,fwd}}\) and \(M_{\mathrm {tot,rev,\infty }}\)
Full size table

4.4 Pressure drop data for forward-and-reverse flow

Now that \(\epsilon _{\textrm{fwd}}\) and \(\epsilon _{\textrm{rev}}\) have been determined, we proceed to calculate the pressure drop across the full 1-D domain, considering forward-and-reverse flow, i.e. reverse flow following immediately after forward flow. The pressure drop is then as given by equation (B4). This is then compared with the estimated pressure drop across the low mobility regions on both sides of the shock as given by equation (5), which effectively combines together a fan from a forward flow and a fan from a pure reverse flow. This is what we plot in Fig. 5. In Fig. 5a specifically we show the ratio between the estimated pressure drop (\(\Delta P_{\textrm{estimate}}\)), as computed by equation (5), and (neglecting any regions of pure liquid or pure gas) the actual pressure drop (now denoted \(\Delta P_{\textrm{actual}}\)) given by equation (B4). This is plotted against \(t/t^*\). Figure 5b corresponds to a zoomed view of Fig. 5a at small times shortly after \(t^*\).

Fig. 5
figure 5

a Pressure drop \(\Delta P_{\textrm{estimate}}\) given by equation (5) divided by actual pressure drop \(\Delta P_{\textrm{actual}}\) given by equation (B4). The value \(t_{\textrm{cross}}/t^{*}\) is indicated via \(\circ\). For relative permeability given by a quadratic power law, \(t_{\textrm{cross}}/t^*\) corresponds to 1.1476, 1.1254, and 1.1176, while for the quartic power law it corresponds to 1.1463, 1.1101, and 1.1019, in each case for \(R_{\textrm{f}}=[185,1850,18{,}500]\), respectively. b Zoom in of (a) at small times

Full size image

Unsurprisingly perhaps, the ratio between estimated pressure drop and the actual pressure drop remains close to unity. At times close to \(t^*\) and also at later times \(t\gg t_{\textrm{cross}}\) this is actually guaranteed by construction. However, after \(t^*\), the ratio between estimated and actual pressures decreases up to time \(t= t_{\textrm{cross}}\) (see “\(\circ\)” in Fig. 5), and then starts increasing again. The minimum value of \(\Delta P_{\textrm{estimate}}/\Delta P_{\textrm{actual}}\) is given in Table 4, for each case.

Table 4 Minimum value of \(\Delta P_{\textrm{estimate}}/\Delta P_{\textrm{actual}}\) for each case. The minimum itself. Occurs at time \(t_{\textrm{cross}}\). The corresponding \(S_{\textrm{l,high}}\) values which are required here in order to determine \(\Delta P_{\textrm{actual}}\) are 0.3713, 0.3503 and 0.3290 for the quadratic power law, and also 0.3798, 0.3597 and 0.3400 for the quartic power law, in each case for \(R_{\textrm{f}}=[185,1850,18{,}500]\), respectively
Full size table

From Table 4, we notice that larger \(R_\textrm{f}\) gives less deviation between the estimated and actual pressure drops (which is useful because in realistic problems often \(R_\textrm{f}\) is on the order of tens of thousands (Ma et al. 2013)). The quartic power law however gives more deviation than the quadratic. It is clear from Fig. 4 that the maximum deviation happens at time \(t_\textrm{cross}\), which is an effect of the estimate in equation (B6) (with \(x_{\textrm{s}}= 0\) by definition at \(t=t_{\textrm{cross}}\)) underestimating the actual pressure drop. In other words \(\epsilon _{\textrm{rev}}\) is smaller than the quantity \(\epsilon _{\textrm{cross}}\) appearing in equations (B8) and (B11). In order to elucidate how this occurs, the liquid saturation profile and mobility along x at time \(t_\textrm{cross}\) can be examined: for brevity though, these results and discussion of them are relegated to Sect. C in the appendix.

5 Conclusions

We have studied the process of foam IOR via SAG injection. This has been done using 1-D fractional flow theory. In particular, we have analysed the flow reversal process, which takes place at depth as the imposed injection pressure is reduced. Although the case of interest is reverse flow after forward flow, these two individual flow directions are studied in the first instance separately. Thus forward flow, i.e. injecting gas into liquid (oil plus surfactant solution), and pure reverse flow, i.e. injecting liquid into a pure gas phase (without prior forward flow) have been studied in order to determine the profile of liquid saturation and foam mobility in each case.

Via fractional flow theory it is found that the mobility of foamed gas falls by orders of magnitude in the neighbourhood where the gas and liquid meet. In the particular systems we study, there is a discontinuous jump in the liquid saturation at some point in the flow field, and mobilities tend to be low in the neighbourhood of that discontinuity, but can be higher away from that discontinuity. The extent of the low mobility region in relation to the distance travelled by the discontinuity is then computed as \(\epsilon _{\textrm{fwd}}\) and \(\epsilon _{\textrm{rev}}\) for forward and reverse flow, respectively. What we found is that the relative differences between \(\epsilon _{\textrm{fwd}}\) and \(\epsilon _{\textrm{rev}}\) are actually relatively modest, certainly far less than differences between forward and reverse mobilities \(M_\textrm{tot,fwd}\) and \(M_\mathrm {tot,rev,\infty }\). In principle, given a shock location, to determine which side of the low mobility region dominates the pressure drop associated with forward-and-reverse foam front motion, we need to know the ratios \(\epsilon _{\textrm{fwd}}/M_\textrm{tot,fwd}\) and \(\epsilon _{\textrm{rev}}/M_\mathrm {tot,rev,\infty }\), respectively downstream and upstream of the shock. Given the very modest difference between \(\epsilon _{\textrm{fwd}}\) and \(\epsilon _{\textrm{rev}}\) what matters then for judging which side of the low mobility region dominates pressure drop during foam propagation in porous media are the different mobilities \(M_\textrm{tot,fwd}\) and \(M_\mathrm {tot,rev,\infty }\) for forward and reverse flow. Generally \(M_\mathrm {tot,rev,\infty }\) is the smaller of the two, so the upstream side dominates the pressure drop as indeed Eneotu and Grassia (2020) suggested.

We found that even though low mobilities account for only a small fraction of the liquid saturation \(S_{\textrm{l}}\) domain, they actually account for a fairly large fraction of the x domain. Hence the notion of low mobilities being confined spatially (as opposed to confined to a small domain of \(S_{\textrm{l}}\)) is not a good assumption. Indeed, \(\epsilon _{\textrm{rev}}\) and \(\epsilon _{\textrm{fwd}}\) although smaller than unity, are not orders of magnitude smaller than unity. Results from forward flow and from pure reverse flow were subsequently combined to consider foam fronts and associated discontinuities in liquid saturation that arise during flow reversal, i.e. when a forward flow is followed by a reverse flow. Based on estimates of the thicknesses of the low mobility regions either side of a discontinuity, and estimates of the mobilities within such regions, we have obtained reasonably reliable estimates of the pressure drop that results as the discontinuity propagates.

In this work, we have focussed on 1-D modelling in which we specify flow rate and compute pressure drop. The findings in principle however carry over to 2-D (and more generally 3-D) models, in which we typically know imposed injection pressures and wish to compute flow rate. The 1-D modelling work we have done here provides the necessary parameters to insert into a 2-D pressure-driven growth model, which can then in principle be used to predict evolving front shape and front location. A question remains however regarding how accurate such predictions might be. Pressure-driven growth as originally conceived by Shan and Rossen (2004) and Grassia et al. (2014) envisaged that low mobilities and hence significant pressure gradients were confined just to thin regions adjacent to a foam front: the front location was then evolved on that basis. Nonetheless, given that low mobility regions are now expected to be quite extended spatially, what we have found is that specifying just a propagating foam front location alone provides limited information about how pressures are distributed in space. Whether 1-D information along flow paths that then feeds into a 2-D pressure-driven growth model can adequately predict front location for a pressure field that is in effect fully 2-D still remains to be determined. In other words, establishing whether pressure-driven growth predictions for foam front propagation are still validated by a fully 2-D Darcy type flow remains an important outstanding task.