Early- and Late-Time Prediction of Counter-Current Spontaneous Imbibition, Scaling Analysis and Estimation of the Capillary Diffusion Coefficient

Abstract

Solutions are investigated for 1D linear counter-current spontaneous imbibition (COUSI). It is shown theoretically that all COUSI scaled solutions depend only on a normalized coefficient ${\Lambda }_{n}\left({S}_{n}\right)$ with mean 1 and no other parameters (regardless of wettability, saturation functions, viscosities, etc.). 5500 realistic functions ${\Lambda }_{n}$ were generated using (mixed-wet and strongly water-wet) relative permeabilities, capillary pressure and mobility ratios. The variation in ${\Lambda }_{n}$ appears limited, and the generated functions span most/all relevant cases. The scaled diffusion equation was solved for each case, and recovery vs time $RF$ was analyzed. RF could be characterized by two (case specific) parameters $RFtr$ and $lr$ (the correlation overlapped the 5500 curves with mean ${R}^{2}=0.9989$): Recovery follows exactly $\mathrm{RF}={T}_{n}^{0.5}$ before water meets the no-flow boundary (early time) but continues (late time) with marginal error until $RFtr$ (highest recovery reached as ${T}_{n}^{0.5}$) in an extended early-time regime. Recovery then approaches 1, with $lr$ quantifying the decline in imbibition rate. $RFtr$ was 0.05 to 0.2 higher than recovery when water reached the no-flow boundary (critical time). A new scaled time formulation ${T}_{n}=t/\tau {T}_{\mathrm{ch}}$ accounts for system length $L$ and magnitude $\overline{D }$ of the unscaled diffusion coefficient via $\tau ={L}^{2}/\overline{D }$, and ${T}_{\mathrm{ch}}$ separately accounts for shape via ${\Lambda }_{n}$. Parameters describing ${\Lambda }_{n}$ and recovery were correlated which permitted (1) predicting recovery (without solving the diffusion equation); (2) predicting diffusion coefficients explaining experimental recovery data; (3) explaining the challenging interaction between inputs such as wettability, saturation functions and viscosities with time scales, early- and late-time recovery behavior.

Article Highlights

• The solution of all 1D linear counter-current problems only depends on a scaled diffusion coefficient with mean 1

• Accurate recovery correlation characterized by highest root of time recovery and subsequent rate decline parameter

• The behavior of all relevant COUSI systems is investigated for trends, prediction and experiment interpretation

1 Introduction

Spontaneous imbibition is a process where capillary forces cause uptake of wetting fluid (referred to as water) into a porous medium and simultaneous displacement of less or non-wetting fluid (referred to as oil). In the subsurface it is especially relevant for oil and gas recovery in naturally fractured reservoirs (Mason and Morrow 2013) and water uptake during hydraulic fracturing in shale (Makhanov et al. 2014; Li et al. 2019). In the former, injected water displaces oil from disconnected matrix blocks by spontaneous imbibition and gravity (Xie and Morrow 2001; Karimaie et al. 2006), while advective flow occurs in the permeable fracture network.

There are two main modes of spontaneous imbibition (Morrow and Mason 2013). The first is counter-current spontaneous imbibition (COUSI) where water and oil flow in opposite directions. That happens when water surrounds a homogeneous matrix on all open sides and capillarity is dominant: e.g., the Amott test (Amott 1959) with imbibition of (cylindrical) core plug samples with all faces open (Fig. 1a), or some faces closed (Fig. 1 b, c). COUSI is the focus of this work, where 1D linear flow is considered. Such flow can be obtained by closing the radial face of a core (yielding symmetrical flow from two sides) or by closing the radial face and one flat face (yielding flow from one side toward the closed face). The second mode is co-current spontaneous imbibition which occurs where parts of the open surface are exposed to water and the rest to oil (Hamon and Vidal 1986; Bourbiaux and Kalaydjian 1990), see Fig. 1d. Then both phases flow mainly co-currently toward the oil-exposed surfaces (Pooladi-Darvish and Firoozabadi 2000; Andersen 2021b). The oil production is predominantly co-current, but less favorable mobility ratio or higher oil-wetness can reduce this dominance (Andersen and Ahmed 2021).

Fig. 1

Some common boundary conditions applied on a cylindrical core plug to generate spontaneous imbibition of water (W) displacing oil (O). Flow through open faces is indicated with arrows, the other faces are closed. Setups a-c give COUSI, while setup d gives co-current imbibition. In setup d only oil flows through (out) the oil-exposed top face while both fluids pass the water-exposed bottom face

Spontaneous imbibition is a strong indicator of wettability in the sense that the water uptake, and hence oil production, is limited by the degree of water-wetness (Kovscek et al. 1993; Zhou et al. 2000). If the rock is strongly oil-wet there is no uptake, while stronger water-wetness means more uptake (Anderson 1987a). A strongly water-wet (SWW) rock will produce as much oil by COUSI as forced imbibition. Capillarity is the driving force, which vanishes when zero capillary pressure has been reached. Capillary diffusion can also impact estimation of relative permeabilities and residual saturations in core flooding experiments (Rapoport and Leas 1953; Andersen 2021a, 2022) by liquid holdup from capillary forces.

Significant efforts have been made to understand how various properties affect COUSI and to upscale lab experiments (see Mason and Morrow (2013) and Abd et al. (2019) for reviews on the subject). This has been done particularly considering the nonlinear partial differential equation describing COUSI. Permeability, porosity, block dimensions and shape and fluid properties such as viscosities and interfacial tension have been studied and built into time scales, usually considering a fixed rock type and wettability (Mattax and Kyte 1962; Hamon and Vidal 1986; Ma et al. 1997; Standnes 2006; Mason et al. 2009; Standnes and Andersen 2017). Relative permeability and capillary pressure functions also play an important role coupled with the viscosities. Zhou et al. (2002) included characteristic mobility end points in the time scale. Other works have included the role of viscosity or viscosity ratio using correction factors relative to established time scales (Fischer et al. 2008; Standnes 2009; Mason et al. 2010; Meng et al. 2017). The focus has also here usually been for SWW systems, scaling experiments and limited theoretical cases rather than solving the mathematical problem in general. At high Bond numbers, fluid densities and block height can also matter (Schechter et al. 1994; Xie and Morrow 2001; Bourbiaux 2009). Bourbiaux and Kalaydjian (1990) found that fluid mobilities during COUSI were necessarily lower than during co-current flow to explain experimental observations. Qiao et al. (2018) simulated their observations consistently by accounting for viscous coupling. Gravity and viscous coupling are not considered within the scope of this work.

Aronofsky et al. (1958) suggested that experimental imbibition recovery could be modeled as exponential with time. COUSI is usually not 1D and linear (in lab or field), but approximated so by introducing a characteristic length (Ma et al. 1997). This can affect the functional relation between recovery and time although Mason et al. (2009) indicated that the deviation from square root of time trends was not very significant. General solutions for 1D linear COUSI by McWhorter and Sunada (1990) accounted for arbitrary saturation functions and showed that the solution depends on a self-similar variable $x/{t}^{0.5}$, which implies that recovery follows a square root of time profile. The solution was only valid until the no-flow boundary was reached (called the critical time). Their solution was later used by Schmid and Geiger (2013) to scale experimental imbibition data for all wetting conditions. It was extended by Andersen et al. (2020) to account for viscous coupling. It was also demonstrated that late-time recovery (defined as after the critical time) generally does not scale to one curve. Ruth et al. (2007) estimated a self-similar variable as function of saturation and predicted square root of time recovery at early time. Khan et al. (2018) compared the semi-analytical solution with simulations from a commercial simulator.

Imbibition recovery at late time has been a challenge to predict without numerical simulation. Tavassoli et al. (2005) assumed Corey relative permeabilities and a saturation profile as polynomial function of distance with time dependent coefficients. They derived recovery solutions at early and late time, the former following the square root of time. However, they did not get continuous slope in recovery at the transition time (set as the critical time). Their solution was also independent of capillary pressure except its derivative at the inlet saturation (we will show that to be incorrect). March et al. (2016) approximated the late-time behavior with an exponential profile. They optimized the transition time by extending the square root of time period (which is considered a good approximation) and ensuring equal recovery and slope at the transition to exponential behavior. However, the exponential model did not represent late-time recovery well in many of the cases. Andersen (2021c) studied shale gas recovery with mathematically same type equation as COUSI. It was shown that the linear trend between recovery and square root time could last until recovery levels were 0.2 to 0.4 higher than the recovery at the critical time (the final recovery was 1 by definition). Velasco-Lozano and Balhoff (2021) modified the method by Tavassoli et al. (2005). They assumed the saturation profile maintained its early-time shape as long as recovery was linear with square root of time. To account for the boundary, mass conservation was used to keep water inside the core. They tuned four parameters in a polynomial saturation profile to fit the true profile at early time and to obtain continuous slope in recovery at the transition to the finite-acting regime. That allowed predicting late-time saturation profiles and recovery with time. Momeni et al. (2022) derived asymptotic late-time solutions for SWW cases.

From the above review we observe a few knowledge gaps: (a) Little has been said about possible distinctions between SWW and mixed-wet (MW) media regarding early- and late-time behavior; (b) existing solutions for all-time recovery are either numerical; use non-general correlations (e.g., derived under limiting assumptions) with poor and unjustified transition to late time; and lack clear descriptions of what controls the late-time behavior and its variations; (c) the only truly general solution is semi-analytical in integral form, thus lacking intuitive explanatory power and is valid only until the no-flow boundary is met; (d) existing late-time correlations suffer from poor transition from early to late time or ability to follow the numerical solutions.

In this work we investigate recovery during COUSI accounting for ‘all’ conditions (parameters related to wettability/saturation functions, core and fluid parameters, but not heterogeneity or dynamic changes in the stated parameters). It is shown that only a normalized capillary diffusion coefficient (CDC) function ${\Lambda }_{n}$ with mean 1 is needed to determine scaled solutions (Sect. 2), while specific case solutions follow from unscaling. Recovery behavior is investigated based on solving the diffusion equation with 5500 ${\Lambda }_{n}$ different functions, expected to cover most possible scenarios. A correlation for early- and late-time recovery containing two tuning parameters (Sect. 3) is found to represent scaled recovery very well for the simulated cases and is used to describe a given recovery profile. We give a definition of transition time that matches visual observation and allows few parameters to describe the data. Three parameters describing the shape of ${\Lambda }_{n}$ (Sect. 4) are correlated with the two recovery parameters, all of which are intuitive, even allowing visual interpretation. That allows estimating recovery directly from a given ${\Lambda }_{n}$, and opposite; estimate ${\Lambda }_{n}$ from experimental recovery data, as illustrated on literature data (Sect. 5). Besides the stated knowledge gaps, we address: How does a given capillary diffusion coefficient, wettability and viscosities affect imbibition recovery; How can we use experimental recovery data from COUSI to estimate the CDC; What determines when recovery no longer acts proportional to the square root of time?.

2 Mathematical Description of COUSI

2.1 Geometry and Mass Balance Equations

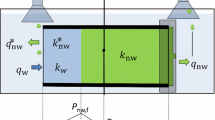
We consider 1D linear, incompressible, immiscible flow of oil ($o$) and water ($w$), Fig. 2, expressed with phase saturations ${s}_{i}$ and phase pressures ${p}_{i}$ $\left(i=o,w\right)$. The variables are constrained by volume conservation and the imbibition capillary pressure function ${P}_{c}\left({s}_{w}\right)$:

$${s}_{w}+{s}_{o}=1, {p}_{o}-{p}_{w}={P}_{c}\left({s}_{w}\right)$$

(1)

Fig. 2

Illustration of the 1D linear COUSI system and the boundary conditions. Water and oil flow counter-currently through the open boundary at $x=0$ by spontaneous imbibition while the system is closed at $x=L$ (which can be due to symmetrical flow opposite this boundary or that the porous medium is sealed/impermeable at that point)

Fluid fluxes ${u}_{i}$ are described by Darcy’s law. Gravity is ignored, and the system has constant porosity $\phi$, absolute permeability $K$ and wettability (represented by saturation functions). The system is open to water at $x=0$ and closed at $x=L$. The open side has zero capillary pressure ${P}_{c}$ corresponding to a fixed saturation ${s}_{w}^{eq}$, defined such that ${P}_{c}\left({s}_{w}^{eq}\right)=0$ (Hamon and Vidal 1986; Bourbiaux and Kalaydjian 1990). The system is saturated with oil and immobile water, yielding a positive capillary pressure driving COUSI.

Under the stated assumptions, the COUSI system is described by the well-known nonlinear capillary diffusion equation (McWhorter and Sunada 1990; Tavassoli et al. 2005):

$$\phi \frac{\partial {s}_{w}}{\partial t}=-K\frac{\partial }{\partial x}\left({\lambda }_{o}{f}_{w}\frac{\partial {P}_{c}}{\partial x}\right),\, \left(0<x<L\right).$$

(2)

${f}_{w}$ is the fractional flow function, related to fluid mobilities ${\lambda }_{i}$ (relative permeability ${k}_{ri}$ divided by viscosity ${\mu }_{i}$) by:

$${f}_{w}=\frac{{\lambda }_{w}}{{\lambda }_{w}+ {\lambda }_{o}}, {\lambda }_{i}=\frac{{k}_{ri}}{{\mu }_{i}}, \left(i=o,w\right).$$

(3)

The initial condition is uniform residual water saturation ${s}_{wr}$. This and the boundary conditions are expressed as:

$$s_{w} \left( {x,t = 0} \right) = s_{wr} , s_{w} \left( {x = 0,t} \right) = s_{w}^{eq} , u_{i} \left( {x = L,t} \right) = 0$$

(4)

Capillary diffusion causes the saturations to approach ${s}_{w}^{eq}$ throughout the system after infinite time.

2.2 Scaled Representation

We introduce scaling of saturation, spatial axis and time:

$$S=\frac{{s}_{w}-{s}_{wr}}{\Delta {s}_{w}},\Delta {s}_{w}=1-{s}_{or}-{s}_{wr}, X=\frac{x}{L}, T=\frac{t}{\tau }$$

(5)

${s}_{or}$ is residual oil saturation, $\Delta {s}_{w}$ the range of mobile saturations and $\tau$ a time scale to be defined soon. The imbibition saturation functions are monotonous functions of $S$. Capillary pressure is expressed using the dimensionless $J$-function (Dullien 1992):

$${P}_{c}={\sigma }_{ow}\sqrt{\phi /K}J\left(S\right),$$

(6)

In line with Young–Laplace’ equation, it states that capillary pressure increases with interfacial tension ${\sigma }_{ow}$ and inverse (characteristic) pore radius. From (2) we obtain a scaled transport equation:

$$\frac{\partial S}{\partial T}=\frac{\tau }{{L}^{2}}\frac{\partial }{\partial X}\left(D\left(S\right)\frac{\partial S}{\partial X}\right),$$

(7)

where $D\left(S\right)$ is a CDC with one part containing known constant parameters (unit m²/s), and a dimensionless saturation dependent part $\Lambda \left(S\right)$.

$$D\left(S\right)=\frac{{\sigma }_{ow}\sqrt{K/\phi }}{{\mu }_{m}\Delta {s}_{w}}\Lambda \left(S\right), {\mu }_{m}={\left({\mu }_{o}{\mu }_{w}\right)}^{0.5}$$

(8)

$$\Lambda \left(S\right)={\mu }_{m}{\lambda }_{o}{f}_{w}\left(- \frac{dJ}{dS}\right)=\frac{{k}_{rw}{k}_{ro}\left(- \frac{dJ}{dS}\right)}{{\left({\mu }_{o}/{\mu }_{w}\right)}^{0.5}{k}_{rw}+{\left({\mu }_{w}/{\mu }_{o}\right)}^{0.5} {k}_{ro}}$$

(9)

$\Lambda \left(S\right)$ contains the saturation function terms multiplied by the mean viscosity. The latter makes $\Lambda \left(S\right)$ dimensionless and independent of ${\mu }_{m}$ (but dependent on the viscosity ratio ${\mu }_{w}/{\mu }_{o}$). The scaled initial and boundary conditions become:

$$S\left( {X = 0,T} \right) = S_{eq} = \frac{{s_{w}^{eq} - s_{wr} }}{{\Delta s_{w} }}, \frac{\partial S}{{\partial X}}\left. \right|_{X = 1} = 0, S\left( {X,T = 0} \right) = 0$$

(10)

Although the saturation functions span $0<S<1$, the relevant range for spontaneous imbibition is $0<S<{S}_{eq}$. ${S}_{eq}$ can be less than 1 for cases that are not SWW and it is convenient to rescale the saturation:

$${S}_{n}=\frac{S}{{S}_{eq}}=\frac{{s}_{w}-{s}_{wr}}{{s}_{w}^{eq}-{s}_{wr}}$$

(11)

Only saturations with positive capillary pressure, $0<{S}_{n}<1$, affect the solution. We update the transport Eq. (7):

$$\frac{\partial {S}_{n}}{\partial T}=\frac{\tau }{{L}^{2}}\frac{\partial }{\partial X}\left(D\left({S}_{n}\right)\frac{\partial {S}_{n}}{\partial X}\right),$$

(12)

Now we select the time scale $\tau$ to account for the length $L$ and magnitude of $D$:

$$\tau ={L}^{2}/\overline{D }=\frac{{\mu }_{m}\Delta {s}_{w}{L}^{2}}{{\sigma }_{ow}\sqrt{K/\phi }\overline{\Lambda } },$$

(13)

$$\overline{D }={\int }_{{S}_{n}=0}^{1}D\left({S}_{n}\right)d{S}_{n}, \overline{\Lambda }={\int }_{{S}_{n}=0}^{1}\Lambda \left({S}_{n}\right)d{S}_{n}$$

(14)

Earlier imbibition time scales may be found in Mattax and Kyte (1962), Ma et al. (1997), Zhou et al. (2002). $\overline{D }$ and $\overline{\Lambda }$ denote averaged dimensional and dimensionless CDCs, respectively, over the saturation range with positive capillary pressure. Dividing either of the two CDCs by their mean gives the same normalized function ${\Lambda }_{\mathrm{n}}\left({S}_{n}\right)$ with mean 1.

$${\Lambda }_{\mathrm{n}}\left({S}_{n}\right)=\frac{D\left({S}_{n}\right)}{\overline{D} }=\frac{\Lambda \left({S}_{n}\right)}{\overline{\Lambda } }.$$

(15)

With the time scale (13), we obtain the final scaled system of equations:

$$\frac{\partial {S}_{n}}{\partial T}=\frac{\partial }{\partial X}\left({\Lambda }_{\mathrm{n}}\left({S}_{n}\right)\frac{\partial {S}_{n}}{\partial X}\right),$$

(16)

$${S}_{n} \left(X=0,T\right)=1, \frac{\partial {S}_{n}}{\partial X}{\left. \right|}_{X=1}=0, {S}_{n} \left(X,T=0\right)=0$$

(17)

In this system we have normalized the independent variables space $0<X<1$ and time $T>0$ and the dependent saturation variable $0<{S}_{n}<1$. The boundary conditions are the same for all cases. The only parameter affecting the scaled solution is the saturation dependent and normalized CDC ${\Lambda }_{\mathrm{n}}\left({S}_{n}\right)$ which is positive, has mean 1, is zero at ${S}_{n}=0$ (and ${S}_{n}=1$ for SWW cases) and is independent of mean viscosity. This represents all 1D linear counter-current imbibition problems, for any input and wetting states.

Oil recovery factor $RF$ (the fraction of oil that can be produced by COUSI) is given by:

$${\mathrm{RF}}\left(T\right)={\overline{S} }_{n}\left(T\right), {\overline{S} }_{n}={\int }_{X=0}^{1}{S}_{n}\left(X,T\right)dX, 0\le RF\left(T\right)\le 1.$$

(18)

RF starts at 0 and ends at 1 (regardless of wettability and residual and initial oil saturation).

3 Theory Motivated Characterization of COUSI

3.1 Semi-analytical Solution for Early Time

McWhorter and Sunada (1990) developed a semi-analytical solution to 1D COUSI under the limitation that the no-flow boundary had not been reached by imbibing water. Their solution was adapted to our normalized Eqs. (16) and (17). For a full derivation, see Supp Mat Section A. Mainly, the position $X$ of saturation ${S}_{n}$, and recovery factor, are both proportional to ${T}^{0.5}$:

$$\mathrm{X}\left({S}_{n},T\right)=2A{F}^{\mathrm{^{\prime}}}\left({S}_{n}\right){T}^{0.5}, RF=2\mathrm{A}{T}^{0.5}$$

(19)

where ${F}^{^{\prime}}\left({S}_{n}\right)=dF/d{S}_{n}$. The function $F\left({S}_{n}\right)$ and the parameter $A$ can be calculated when ${\Lambda }_{n}$ is provided but they are defined implicitly in integral form and require numerical evaluation:

$$F\left({S}_{n}\right)=1-\left[{\int }_{\beta ={S}_{n}}^{1}\left(\beta -{S}_{n}\right)\frac{{\Lambda }_{n}\left(\beta \right)}{F\left(\beta \right)}d\beta \right]\cdot {\left[{\int }_{\beta =0}^{1}\beta \frac{{\Lambda }_{n}\left(\beta \right)}{F\left(\beta \right)}d\beta \right]}^{-1}$$

(20)

$${A}^{2}=\frac{1}{2}{\int }_{\beta =0}^{1}\beta \frac{{\Lambda }_{n}\left(\beta \right)}{F\left(\beta \right)}d\beta$$

(21)

$\beta$ is an integration variable. The solution (19) to (21) is valid until the critical time ${T}_{cr}$ when the fastest saturation ${S}_{n}=0$ meets the no-flow boundary $X\left({S}_{n}=0,{T}_{cr}\right)=1$:

$${T}_{\rm{cr}}=\frac{1}{4{A}^{2}}\frac{1}{{\left[{F}^{\mathrm{^{\prime}}}\left({S}_{n}=0\right)\right]}^{2}}$$

(22)

We next scale $T$ with a factor ${T}_{ch}$, to yield same recovery when plotted against the resulting normalized time ${T}_{n}$:

$$RF={T}_{n}^{0.5}, {T}_{n}=\frac{T}{{T}_{ch}}=\frac{t}{\tau {T}_{ch}}, {T}_{ch}=\frac{1}{4{A}^{2}}$$

(23)

${T}_{n}$ represents a similar normalized time as Schmid and Geiger (2013) derived from McWhorter and Sunada (1990). However, it sorts the scaling contributions into the magnitude of the diffusion coefficient and length through $\tau$ and the contribution of the shape of the diffusion coefficient through ${T}_{ch}$ (which again only depends on viscosity ratio and the shape of the saturation functions, but not other parameters due to the definition of ${\Lambda }_{n}$). It also does not assume modification of the saturation functions to treat MW cases. $RF$ equals ${T}_{n}^{0.5}$ at early time for all cases. From (22) and (23), recovery at the critical time is:

$${\mathrm{RF}}_{\rm{cr}}={T}_{n,cr}^{0.5}=\sqrt{\frac{{T}_{cr}}{{T}_{ch}}}=\frac{1}{{F}^{\mathrm{^{\prime}}}\left({\mathrm{S}}_{\mathrm{n}}=0\right)}$$

(24)

Equations (23) are valid at early time, but do not explain what happens at later time, or give an intuitive link between ${\Lambda }_{n}$ and the parameters $A$ and RF_cr. We will relate $A$ and $R{F}_{cr}$ quantitatively with ${\Lambda }_{n}$ and offer extensions from the early-time solution.

3.2 Transition from Early to Late Time

Early-time recovery RF equals ${T}_{n}^{0.5}$ and obeys $\frac{\mathrm{dRF}}{d\sqrt{{T}_{n}}}=1$ until ${T}_{n}={T}_{n,cr}$. Considering recovery trends after critical time, this linear behavior appears to last significantly longer (March et al. 2016; Andersen 2021c). To capture this, we define a transition time ${T}_{n,tr}>{T}_{n,cr}$ when the slope of the full time solution deviates ‘enough’ from 1, here selected as when the slope has decreased to 0.9:

$$\frac{\mathrm{d}RF}{d\sqrt{{T}_{n}}}{\left.\right|}_{{T}_{n}={T}_{n,tr}}=0.9,$$

(25)

The value 0.9 represented well where the numerically calculated recovery curves appeared to intersect the extended straight line $\left(RF=\sqrt{{T}_{n}}\right)$, illustrated in Sect. 5.3, and improved the overall match of the investigated dataset compared to values such as 0.95 and 1 (no transition).

Since recovery until this point is well approximated by the straight line, we formulate it mathematically as:

$${\mathrm{RF}}={T}_{n}^{0.5}, \left(0<{T}_{n}<{T}_{n,tr}\right)$$

(26)

and we define recovery at the transition point $R{F}_{tr}$ as:

$${\mathrm{RF}}_{\rm{tr}}={T}_{n,tr}^{0.5}$$

(27)

After ${T}_{n,tr}$ recovery deviates from the linear trend. For convenience we from now refer this as late time, but remind that late time generally includes the transition after ${T}_{n,cr}$. The time before ${T}_{n,tr}$ can be considered (extended) early time.

3.3 Late-Time Recovery

The correlation derived by Tavassoli et al. (2005) for late-time recovery will be assumed except in general form below with arbitrary constants ${c}_{0},{c}_{1},{c}_{2},r$. We determine the constants to our own constraints.

$${\mathrm{RF}}\left({T}_{n}\right)={c}_{0}-\frac{{c}_{1}}{{\left({T}_{n}+{c}_{2}\right)}^{r}}$$

(28)

Upon time differentiation, the expression is equivalent to Arp’s harmonic decline curve (Arp 1945). We require that RF equals 1 at infinite time; RF is on the square root profile at ${T}_{n,tr}$; and the derivative of recovery wrt. $\sqrt{{T}_{n}}$ is 0.9 at ${T}_{n,tr}$:

$${\mathrm{RF}}\left({T}_{n}\to \infty \right)=1, \mathrm{RF}\left({T}_{n,tr}\right)=R{F}_{tr}, \frac{\mathrm{d}RF}{d\sqrt{{T}_{n}}}{\left.\right|}_{{T}_{n}={T}_{n,tr}}=0.9$$

(29)

These constraints applied to (28) eliminate ${c}_{0},{c}_{1},{c}_{2}$, yielding the following late-time expression:

$${\mathrm{RF}}\left({T}_{n}\right)=1-{\left[1+\frac{0.9}{2r} \frac{{T}_{n}-{\left[R{F}_{tr}\right]}^{2}}{R{F}_{tr}-{\left[R{F}_{tr}\right]}^{2}}\right]}^{-r}\left(1-{\mathrm{RF}}_{tr}\right), \left({T}_{n,tr}<{T}_{n}<\infty \right)$$

(30)

Given ${\mathrm{RF}}_{tr}$, $r$ is the only tuning parameter for recovery between ${T}_{n,tr}$ and ${T}_{n}\to \infty$. For convenience, we will refer to the logarithmic value of $r$, called $lr$:

$$lr={\mathrm{log}}_{10}r$$

(31)

Sensitivity analysis showed that the correlation (30) converges to an exponential profile for $lr>1.5$ (regardless value of ${\mathrm{RF}}_{tr}$):

$$\mathrm{RF}=1+\left(R{F}_{tr}-1\right)\frac{\mathrm{exp}\left(C{T}_{n}\right)}{\mathrm{exp}\left(C{T}_{n,tr}\right)}, C=\frac{0.9}{2\left(R{F}_{tr}-1\right){\rm{RF}}_{tr}}$$

(31)

3.4 Summarized Parameterization of Recovery

Based on the previous discussion, two parameters are used to describe scaled recovery $\mathrm{RF}\left({T}_{n}\right)$: ${\rm{RF}}_{tr}$ defines (extended) early-time recovery with (26), and $lr$ is used to describe the continued late-time profile using (30). The combined correlation is illustrated in Fig. 3 for a low and high RF_tr and three choices of $lr$ each. At higher lr, the late-time recovery more quickly reaches 1. The case with $lr=1.5$ is indistinguishable from an exponential correlation. To get RF against $T$, we need the factor ${T}_{ch}$ (equivalently $A$). RF against regular time $t$ further requires $\tau$, see (23). We will also calculate RF_cr (RF when the no-flow boundary is encountered) mainly for comparing with RF_tr.

Fig. 3

Plot of the recovery correlation against ${T}_{n}^{0.5}$ for various RF_tr and lr. At $lr>1.5$ the curve converges to an exponential function (yellow points)

3.5 Estimate of Spatial Saturation Profiles Before Critical Time

Before critical time, saturation positions are proportional to ${T}_{n}^{0.5}$ and a function ${F}^{^{\prime}}\left({S}_{n}\right)$, see (19). ${S}_{n}=1$ has zero speed, while ${S}_{n}=0$ travels the fastest and reaches $X=1$ at critical time, see (22). The following expression suggests a function ${F}^{^{\prime}}\left({S}_{n}\right)$ (the factor to ${T}_{n}^{0.5}$) with an exponent $m$ determining the shape:

$$X=\frac{1}{2}\left[\left(1-{S}_{n}^{m}\right)+{\left(1-{S}_{n}\right)}^\frac{1}{m}\right]\frac{{T}_{n}^{0.5}}{{\rm{RF}}_{cr}}, \left(0<{T}_{n}<{T}_{n,cr}\right)$$

(33)

The averaged saturation profile must equal recovery, see (18). In particular, at critical time when $X\left(0\right)=1$, we obtain $\mathrm{RF}={\mathrm{RF}}_{cr}$. That allows to determine $m$ from the parameter RF_cr:

$$m = \frac{{{\text{R}}{{\text{F}}_{{\text{cr}}}}}}{{1 - {\text{R}}{{\text{F}}_{{\text{cr}}}}}}$$

(34)

Thus, from estimates of $\mathrm{RF}$ and ${\mathrm{RF}}_{\rm{cr}}$ we can estimate a saturation profile with correct amount imbibed water and front position.

4 Parameters Characterizing the Scaled Diffusion Coefficient ${{\varvec{\Lambda}}}_{{\varvec{n}}}$

By reducing the COUSI problem to (16) and (17) through scaling, the function ${\Lambda }_{n}$ is the only input affecting the solution. For a simple description of a given function ${\Lambda }_{n}\left({S}_{n}\right)$, we introduce a few parameters quantifying its shape. Define ${z}_{a,b}$ as the fraction area of ${\Lambda }_{n}$ on the interval $a<{S}_{n}<b$ which is on the upper half of that interval:

$${z}_{a,b}=\frac{{\int }_{{S}_{n}=\frac{a+b}{2}}^{b}{\Lambda }_{\mathrm{n}}\left({S}_{n}\right)d{S}_{n}}{{\int }_{{S}_{n}=a}^{b}{\Lambda }_{\mathrm{n}}\left({S}_{n}\right)d{S}_{n}}, \left(0<{z}_{a,b}<1\right)$$

(35)

A higher ${z}_{a,b}$ means ${\Lambda }_{n}$ is shifted more toward $b$ than $a$ on the interval. As the fraction only indicates shape, we could replace ${\Lambda }_{n}$ with $D$ in (35) and get the same answer. Three fractions ${z}_{\mathrm{0,1}},{z}_{\mathrm{0,0.5}},{z}_{\mathrm{0.5,1}}$ are used to characterize each function ${\Lambda }_{n}$ in this work, see Fig. 4. Andersen (2021c) showed that ${z}_{\mathrm{0,1}}$ correlated strongly with the solution output for a shale gas problem.

Fig. 4

Illustration of how ${z}_{\mathrm{0,1}},{z}_{\mathrm{0,0.5}},{z}_{\mathrm{0.5,1}}$ are calculated for a function ${\Lambda }_{n}\left({S}_{n}\right)$ with values indicated for this specific example

5 Results and Discussion

5.1 Workflow and Implementation

We have proven that $\mathrm{RF}\left(T\right)$ only depends on ${\Lambda }_{n}\left({S}_{n}\right)$. A set of recovery parameters A, RF_tr, lr and ${\mathrm{RF}}_{\rm{cr}}$ will be shown is a highly accurate description of all relevant curves RF(T). Further, we have proposed describing ${\Lambda }_{n}$ with the three fractions ${z}_{\mathrm{0,1}},{z}_{\mathrm{0,0.5}},{z}_{\mathrm{0.5,1}}$ (see Fig. 4). Assuming ${z}_{\mathrm{0,1}},{z}_{\mathrm{0,0.5}},{z}_{\mathrm{0.5,1}}$ give a sufficiently detailed representation of ${\Lambda }_{n}$ we can expect them to provide an accurate prediction of early- and late-time recovery in terms of $A, {\rm{RF}}_{\rm{cr}}, {\rm{RF}}_{\rm{tr}}$ and $lr$ (as will be demonstrated). We will also show that normalized recovery parameters ${\rm{RF}}_{\rm{tr}}$ and $lr$ allow to estimate $A$ and ${z}_{\mathrm{0,1}},{z}_{\mathrm{0,0.5}},{z}_{\mathrm{0.5,1}}$, thus resulting in prediction of the diffusion coefficient ${\Lambda }_{n}$. The analyses are based on creating a database of 5500 ${\Lambda }_{n}$ functions (which can be considered to span all relevant cases), the resulting recovery solutions and their characterizing parameters. Accordingly, the relations we obtain are general for all COUSI behavior. Unscaling allows connecting to standard data formats including experimental data.

Relative permeability and $J$-functions, combined with mobility ratio in (9) and (15), yield realistic ${\Lambda }_{n}$ (Sect. 5.2). For a given ${\Lambda }_{n}\left({S}_{n}\right)$ we calculate $\mathrm{RF}\left(T\right)$ numerically by solving the PDE (16), but also semi-analytically until critical time. Recovery is characterized with ${\rm{RF}}_{\rm{cr}}$ and $A$ from (20), (21) and (24) in the semi-analytical solution; and RF_tr (defined by where $\frac{dRF}{d\sqrt{{T}_{n}}}=0.9$) and $lr$ by fitting (30) to RF(T_n) > RF_tr from the numerical solution (see their role in Fig. 3). The input ${\Lambda }_{n}$ is characterized by ${z}_{\mathrm{0,1}},{z}_{\mathrm{0,0.5}},{z}_{\mathrm{0.5,1}}$. The ability of correlation (26) and (30) to describe recovery, and the link between ${\Lambda }_{n}$ and recovery are discussed with an example (Sect. 5.3). The database and the recovery correlation performance are described (Sect. 5.4). Relations between ${\Lambda }_{n}$ parameters and recovery parameters are demonstrated and quantified (Sect. 5.5 and Supp Mat D). Recovery is predicted (without solving the PDE) for two literature data cases (Sect. 5.6); and we estimate CDCs explaining experimental recovery data (Sect. 5.7). The approaches are validated by comparing estimated recovery with the numerical solution.

The numerical solution was implemented fully implicit in-house in MATLAB as described in Supp Mat Section B. We used 500 equal grid cells and 50000 time steps (equal on a square root axis) until $\sqrt{{T}_{n}}=5$ (2 orders of magnitude higher than when RF = 0.5, and 3.4 orders higher than when $\mathrm{RF}=0.1$ in the linear regime). See convergence analyses in Supp Mat Section C.

The quality of the correlations in predicting parameters and recovery profiles is evaluated using $\mathrm{RMSE}$ and ${R}^{2}$:

$${RMSE}=\sqrt{\frac{1}{n}{\sum }_{i}{\left({y}_{i}^{p}-{y}_{i}^{obs}\right)}^{2}}, {R}^{2}=1-\frac{{\sum }_{i}{\left({y}_{i}^{p}-{y}_{i}^{obs}\right)}^{2}}{{\sum }_{i}{\left(\overline{{y }_{i}^{obs}}-{y}_{i}^{obs}\right)}^{2}}, \overline{{y }_{i}^{obs}}=\frac{1}{n} {\sum }_{i}{y}_{i}^{obs}$$

(36)

where $n$ indicates the number of (data) points, ${y}_{i}^{p}$ the prediction and ${y}_{i}^{obs}$ the observation (or true value) of point$i$. RMSE has the same unit as$y$. If there is a constant prediction error $\left|{y}_{i}^{p}-{y}_{i}^{obs}\right|>0$, RMSE will equal that value. ${R}^{2}$ indicates how much scatter there is compared to explanative power. ${R}^{2}=1$ indicates perfect prediction, while ${R}^{2}=0$ means no predictive power.

5.2 Saturation Function Correlations and Normalized Diffusion Coefficients

We use extended Corey function correlations (Brooks and Corey 1966) for relative permeability:

$${k}_{ri}={k}_{ri}^{*}{S}_{i}^{{n}_{i}}, {n}_{i}={n}_{\mathrm{i}1}S+{n}_{\mathrm{i}2}\left(1-S\right), \left(i=o,w\right)$$

(37)

The exponents ${n}_{i}$ vary linearly with $S$ from ${n}_{i1}$ to ${n}_{i2}$ for flexibility. The $J$-function is a modified Bentsen and Anli (1976) correlation, where we have incorporated $J\left({S}_{eq}\right)=0$:

$$J\left(S\right)=-{J}_{1}\mathrm{ln}\left(\frac{S}{{S}_{eq}}\right)+{J}_{2}\mathrm{ln}\left(\frac{1-S}{1-{S}_{eq}}\right)$$

(38)

The resulting CDC $\Lambda \left(S\right)$, defined by (9), becomes:

$$\Lambda \left(S\right)=\frac{{J}_{2}{k}_{ro}^{*}}{{\left(\frac{{\mu }_{o}}{{\mu }_{w}}\right)}^{0.5}}\frac{{S}^{{n}_{w}-1}{\left(1-S\right)}^{{n}_{o}}\left(\frac{{J}_{1}}{{J}_{2}}\right)+{S}^{{n}_{w}}{\left(1-S\right)}^{{n}_{o}-1}}{{S}^{{n}_{w}}+\left(\frac{{k}_{ro}^{*}}{{k}_{rw}^{*}}\frac{{\mu }_{w}}{{\mu }_{o}}\right){\left(1-S\right)}^{{n}_{o}}}$$

(39)

At the end saturations $S=0$ and $S=1$, $\frac{dJ}{dS}$ goes to negative infinity, but $\Lambda \left(S\right)$ goes to 0 for typical Corey exponent values ${n}_{i}\left({S}_{i}=0\right)>1$. The parameters ${J}_{1},{J}_{2},{k}_{rw}^{*},{k}_{ro}^{*},{\mu }_{w},{\mu }_{o}$ affect the function shape through the two parameter ratios, $\frac{{J}_{1}}{{J}_{2}}$ and $\frac{{k}_{ro}^{*}}{{k}_{rw}^{*}}\frac{{\mu }_{w}}{{\mu }_{o}}$, while they only affect the magnitude if the ratios are kept constant. The factor $\frac{{J}_{2}{k}_{ro}^{*}}{{\left(\frac{{\mu }_{o}}{{\mu }_{w}}\right)}^{0.5}}$ cancels during normalization to ${\Lambda }_{\mathrm{n}}\left({S}_{n}\right)=\Lambda \left({S}_{n}\right)/{\int }_{{S}_{n}=0}^{1}\Lambda \left({S}_{n}\right)d{S}_{n}$ and does not need specification to predict scaled solutions against ${T}_{n}$.

5.3 Imbibition Behavior from Normalized Diffusion Coefficients

Saturation functions from Kleppe and Morse (1974) were adapted to correlations (37) to (38), Fig. 5. Function and system parameters are listed in Table 1 (tables are at the end of the paper). Assuming five oil viscosities ${\mu }_{o}$ (0.01 to 100 cP) gives $D\left({S}_{n}\right)$ and after normalization ${\Lambda }_{n}\left({S}_{n}\right)$, Fig. 5. Increasing ${\mu }_{o}$ four orders of magnitude reduces $\overline{D }$ and $\tau$ increases accordingly, by a factor 12 (Table 2). The peak shifts to lower ${S}_{n}$.

Fig. 5

Input relative permeabilities (a) and J-function (b) based on Kleppe and Morse (1974) (points), adapted to correlations (lines) (37) to (38). Corresponding $D\left({S}_{n}\right)$ in (c) and normalized versions ${\Lambda }_{n}\left({S}_{n}\right)$ in (d) for different oil viscosities

Table 1 Input parameters characterizing the system and saturation functions from Kleppe and Morse (1974)

Table 2 ‘Recovery parameters’ were calculated from the semi-analytical (${T}_{\rm{ch}}$ and $R{F}_{\rm{cr}}$) and numerical ($R{F}_{\rm{tr}}$ and $r$) recovery solution. ${J}_{1}/{J}_{2}=10$ while $\frac{{k}_{ro}^{*}{\mu }_{w}}{{k}_{rw}^{*}{\mu }_{o}}$ is 1070 at 0.01 cP oil viscosity and reduces to 0.107 at 100 cP. Values without units are dimensionless. ‘Matching metrics’ describe the correlation fit to the numerical recovery profile

Considering ${\Lambda }_{n}$ (same mean of 1), only the shape is shifted, from having most of the coefficient collected around a high saturation peak (the 0.01 cP case) to more even distributions at high viscosity. The change is quantified by lower ${z}_{\mathrm{0,1}}$ and ${z}_{\mathrm{0.5,1}}$ (${z}_{\mathrm{0,0.5}}$ did not change much) as ${\Lambda }_{n}$ shifts to lower saturations (Table 2).

Numerical solutions of $RF\left({T}^{0.5}\right)$ are shown in Fig. 6a based on each ${\Lambda }_{n}\left({S}_{n}\right)$. In all cases $RF$ is linear with ${T}^{0.5}$ initially and then falls below the extended straight line. For ${\Lambda }_{n}\left({S}_{n}\right)$ with higher ${z}_{\mathrm{0,1}}$ (lower oil viscosity) the early-time recovery goes faster (higher slope 2A and equivalently lower ${T}_{\rm{ch}}$) and lasts longer in terms of both RF_cr and RF_tr (marked with circles and triangles, respectively), quantified in Table 2. RF_tr is clearly higher than RF_cr (by ~ 0.15 units) and visually better represents the deviation from straight line behavior. In Fig. 6b we plot RF against ${T}_{n}^{0.5}$. All curves fall on the same line $RF={T}_{n}^{0.5}$ at early time but deviate from the line at different RF_tr.

Fig. 6

Recovery RF against ${T}^{0.5}$ (a) and ${T}_{n}^{0.5}$ (b) based on ${\Lambda }_{n}$ with five choices of oil viscosity (0.01 cP to 100 cP). RF_cr (circles), and RF_tr (triangles) are marked. Dashed lines indicate extended early-time solutions (equivalent to $\rm{RF}={T}_{n}^{0.5}$)

In Fig. 7, RF is plotted against time (hours) together with the correlation proposed to describe recovery. The lowest ${R}^{2}$ of the five cases was 0.9999, and the highest RMSE was 0.0021. The applied characterization thus appears to describe recovery well. The 10 cP case in Fig. 7 was also simulated using IORCoreSim (Lohne 2013, Lohne et al. 2017), for validation of the numerical code.

Fig. 7

Numerically calculated (full lines) RF against time with corresponding correlations (dashed lines) and RF_tr indicated (red triangles). The 10 cP case was also simulated with an independent software (circles)

Numerically calculated saturation profiles are shown in Fig. 8. Estimated profiles based on (33) are also provided, at and before critical time. At low oil viscosity 0.01 cP (high ${z}_{\mathrm{0,1}}$) saturations are high behind the front (given by a large m = 3.1), while at high oil viscosity 100 cP (low ${z}_{\mathrm{0,1}}$) the saturations fall quickly near the inlet (reflected by a low $m=0.588$). The estimated profiles follow the numerical solution profiles reasonably and capture that at higher ${z}_{\mathrm{0,1}}$ a higher recovery is obtained when the no-flow boundary is reached, or equivalently that at high ${z}_{\mathrm{0,1}}$ the fastest saturation ${S}_{n}=0$ is not very fast compared to the remaining profile. Note that our main focus is on recovery (which is well predicted), and not the saturation profiles (where better prediction is possible).

Fig. 8

Profiles ${S}_{n}\left(X\right)$ at different levels of RF for ${\mu }_{o}=0.01$ cP (high ${z}_{\mathrm{0,1}}$) (a) and 100 cP (low ${z}_{\mathrm{0,1}}$) (b). Full lines are calculated numerically, while dashed lines are shown at or before critical time based on (33)

5.4 Simulation Database

We generate 5500 functions ${\Lambda }_{\mathrm{n}}\left({S}_{n}\right)$ from 5500 random combinations of the seven parameters ${n}_{w1},{n}_{w2},{n}_{o1},{n}_{o2},{S}_{eq},{\mathrm{log}}_{10}\left(\frac{{J}_{1}}{{J}_{2}}\right),{\mathrm{log}}_{10}\left(\frac{{k}_{ro}^{*}}{{k}_{rw}^{*}}\frac{{\mu }_{w}}{{\mu }_{o}}\right)$, see Table 3. Half the cases were SWW by setting ${S}_{eq}=0.999$, while the others had random values down to ${S}_{eq}=0.2$. ${\mathrm{log}}_{10}\left(\frac{{J}_{1}}{{J}_{2}}\right)$ was positively correlated with ${S}_{eq}$ since the positive $J$-term should be more dominant in more water-wet systems.

Table 3 Random selection of input parameters to generate normalized CDCs ${\Lambda }_{\mathrm{n}}\left(S\right)$ using uniform distributions with limits indicated. ^aHalf the cases were SWW by setting ${S}_{eq}$ equal to 0.999. ^b $\frac{{J}_{1}}{{J}_{2}}$ was correlated with ${S}_{eq}$ such that ${\mathrm{log}}_{10}\left(\frac{{J}_{1}}{{J}_{2}}\right)=\frac{{S}_{eq}-0.2}{0.8}+rand\left(-\mathrm{1,1}\right)$

Based on each ${\Lambda }_{n}\left({S}_{n}\right)$, we solved the model numerically and semi-analytically to calculate $RF$ at early and late scaled times $T$ and ${T}_{n}$ and quantified ${z}_{\mathrm{0,1}},{z}_{\mathrm{0,0.5}},{z}_{\mathrm{0.5,1}}$ (for the coefficient shape, see Fig. 4) and $A,{\rm{RF}}_{\rm{cr}},{\rm{RF}}_{\rm{tr}},lr$ (characterizing recovery, see Fig. 3).

Each curve $\rm{RF}\left({T}_{n}\right)$ described by the correlation (26) and (30) with ${\rm{RF}}_{\rm{tr}}$ and $lr$ was compared with the curve (numerical solution) it was approximating. The mean $\mathrm{RMSE}$ was 0.0045 and the mean ${R}^{2}$ was 0.9989. The histograms in Fig. 9 indicate that $\mathrm{RMSE}<0.01$ for 90% of the cases and ${R}^{2}>0.995$ for 95% of the cases and good match also on the outliers. We thus find the correlation to be an accurate representation of COUSI recovery.

Fig. 9

Quantitative description of how well the correlation (26) and (30) matches numerically calculated recovery profiles for the 5500 simulations

5.5 Parameter Correlations

Nonlinear regression correlations referred to in the following were obtained using multivariable polynomials. Expressions and performance metrics are found in Supp Mat Section D.

5.5.1 Estimation of Recovery Curve Parameters $\left(\mathbf{A},\mathbf{R}{\mathbf{F}}_{\mathbf{tr}},\mathbf{RF}_{\mathbf{cr}},\mathbf{lr}\right)$ from ${{\varvec{\Lambda}}}_{\mathbf{n}}$

Based on the 5500 simulations, $A,{\rm{RF}}_{\rm{tr}}$ and ${\rm{RF}}_{\rm{cr}}$ were plotted against ${z}_{\mathrm{0,1}}$ in Fig. 10. They all predominantly increase with ${z}_{\mathrm{0,1}}$, in line with Sect. 5.3, but also show scatter for a fixed ${z}_{\mathrm{0,1}}$. The data for $A$ and ${\rm{RF}}_{\rm{tr}}$ could be sorted vertically (at fixed ${z}_{\mathrm{0,1}}$) by ${z}_{\mathrm{0,0.5}}$ when ${z}_{\mathrm{0,1}}<0.35$, while ${\rm{RF}}_{\rm{cr}}$ was sorted by ${z}_{\mathrm{0,0.5}}$ for ${z}_{\mathrm{0,1}}<0.85$. Similarly, $A$ and ${\rm{RF}}_{\rm{tr}}$ were sorted by ${z}_{\mathrm{0.5,1}}$ when ${z}_{\mathrm{0,1}}>0.35$ while ${\rm{RF}}_{\rm{cr}}$ was sorted by ${z}_{\mathrm{0.5,1}}$ for ${z}_{\mathrm{0,1}}>0.85$.

Fig. 10

$A$ (a), RF_tr (b) and RF_cr (c) plotted against ${z}_{\mathrm{0,1}}$ and sorted by their values of ${z}_{\mathrm{0,0.5}}$ for low ${z}_{\mathrm{0,1}}$ and their values of ${z}_{\mathrm{0.5,1}}$ for high ${z}_{\mathrm{0,1}}$. In (d) a histogram of the differences RF_tr–RF_cr

These trends directly state that higher RF is obtained in the square root regime, whether defined by critical time recovery (with ${\rm{RF}}_{\rm{cr}}$) or transition time recovery (${\rm{RF}}_{\rm{tr}}$), when ${\Lambda }_{n}$ is shifted to higher saturations (quantified by increased ${z}_{\mathrm{0,1}}$ or increase in the second fraction at a fixed ${z}_{\mathrm{0,1}}$). ${\rm{RF}}_{\rm{tr}}$ was consistently higher than ${\rm{RF}}_{\rm{cr}}$, by 0.05 to 0.2 units for 90% of the cases (Fig. 10d), indicative that the transition period after critical time is significant.

The early-time imbibition rate coefficient $A$, similarly increases as ${\Lambda }_{n}$ is shifted to higher saturations. $A$ spanned a narrow range from 0.2 to 0.7. Thus, ${\Lambda }_{n}$ determines $A$ within a factor 3.5, and ${T}_{\rm{ch}}=1/4{A}^{2}$ within a factor of 12. $A$ only contains the contribution from the shape of $D$ on time scale. The remaining contribution is from $\tau ={L}^{2}/\overline{D }$.

Correlations were developed for $A,{\rm{RF}}_{\rm{tr}}$ and ${\rm{RF}}_{\rm{cr}}$ as function of $\left({z}_{\mathrm{0,1}},{z}_{\mathrm{0,0.5}}\right)$ or $\left({z}_{\mathrm{0,1}},{z}_{\mathrm{0.5,1}}\right)$ on the stated ranges of ${z}_{\mathrm{0,1}}$, with ${R}^{2}$ varying from 0.989 to 0.998. See Fig. 12 a–c for cross plots of correlation values vs dataset values.

The parameter $lr$ is plotted in Fig. 11a against ${z}_{\mathrm{0.5,1}}$ and sorted into water-wet cases (WW) in blue and mixed-wet (MW) cases in red defined by whether ${S}_{eq}>0.99$ or not, respectively. This sorting was selected and found useful since it appears late-time behavior is controlled by the diffusion coefficient at the highest saturations, which is described particularly by ${z}_{\mathrm{0.5,1}}$ and wetting state. The MW values at a given ${z}_{\mathrm{0.5,1}}$ are significantly higher than the WW values, and for both cases $lr$ increases with ${z}_{\mathrm{0.5,1}}$.

Fig. 11

The $lr$ data plotted against ${\rm{RF}}_{\rm{tr}}$ sorted into MW and WW (a). Maps of ${z}_{\mathrm{0,1}}$ and ${\rm{RF}}_{tr}$ with specific value ranges of $lr$ for MW (b) and WW (c) data. Dashed lines indicate the transition to points with $lr>1.5$

Both these trends relate to fluid mobility at the highest saturations ${S}_{n}\approx 1$ (giving larger values of the coefficient): MW cases have ${\Lambda }_{n}>0$ at ${S}_{n}=1$, while WW cases have a zero value (since the oil mobility terminates). Higher ${z}_{\mathrm{0.5,1}}$ indicates how much of ${\Lambda }_{n}$ at high saturations is located at the very highest saturations. Thus, if there is high fluid mobility (giving high ${\Lambda }_{n}$) at the highest saturations, $lr$ is high and RF quickly approaches 1 at late time. On the other hand, low mobility at the highest saturations gives low $lr$ and RF more slowly approaches 1.

For an illustration of this phenomena, consider the CDCs ${\Lambda }_{n}$ in Fig. 5d. The 100 cP oil case is almost flat at high saturations and $lr$ takes the low value of $-0.23$ (Table 2), while as viscosity reduces ${\Lambda }_{n}$ is shifted to higher saturations, and $lr$ changes accordingly reaching $1.5$ at the lowest viscosity. Figure 7 demonstrates that this difference in $lr$ results in several orders of magnitude longer time in the late-time regime for the high oil viscosity case.

In order to build predictive correlations estimating $lr$, the MW and WW data were treated separately and plotted in Fig. 11b and c as $\rm{RF}_{\rm{tr}}$ and ${z}_{\mathrm{0,1}}$ points taking specific values of $lr$. $lr$ varied systematically with ${z}_{\mathrm{0,1}}$ for a given $\rm{RF}_{\rm{tr}}$. That was used as a criterion (dashed lines) for whether $lr>1.5$ (blue points in Fig. 11b and c) which would result in an exponential recovery profile. Specifically, we could draw a line $q:={z}_{\mathrm{0,1}}-2.1{\rm{RF}}_{\rm{tr}}$ through the data (dashed black line) such that 98.5% of the MW points with $q<-0.85$ and 89.2% of the WW points with $q<-0.98$ had $lr>1.5$ (the blue points). The variable $q$ was also found to be a very good input for predicting $lr$. At high $\rm{RF}_{\rm{tr}}$ and $q$ below the stated limit, $lr$ was set to 1.5. Continuous correlations were provided for low $\rm{RF}_{\rm{tr}}$ and for high $\rm{RF}_{\rm{tr}}$ with high $q$.$lr$ was well predicted at $\rm{RF}_{\rm{tr}}<0.6$ with $RMSE\sim 0.03$ (blue points in Fig. 12d, e), while at high $\rm{RF}_{\rm{tr}}>0.6$ the prediction was less accurate with $RMSE\sim 0.2$ (small compared to $lr$ varying from −1 to 1.5). Accurate $lr$ prediction at low $\rm{RF}_{\rm{tr}}$ is however considered more important since a greater portion of recovery then is in the late-time regime which is determined by $lr$. The smaller amount of late-time recovery data for high $\rm{RF}_{\rm{tr}}$ may explain why $lr$ becomes more uncertain. Increased uncertainty in $lr$ at higher $lr$ values (> 0.5) is explained by the recovery curve becoming less sensitive to $lr$, see Fig. 3. Hence, inaccuracy in $lr$ does not cause inaccuracy in recovery calculations.

Fig. 12

Cross plots showing estimated recovery parameter values against dataset values from the 5500 simulations for $A$ (a), $\rm{RF}_{\rm{tr}}$ (b), RF_cr (c), MW lr (d) and WW lr (e). Based on correlations a to l in Table S1 using fractions ${z}_{a,b}$ as input. Note that inputs $\rm{RF}_{\rm{tr}}$ and $q={z}_{\mathrm{0,1}}-2.1{\rm{RF}}_{\rm{tr}}$ in (d) and (e) are also based on estimates of $\rm{RF}_{tr}$ from fractions ${z}_{a,b}$, while $zr={z}_{\mathrm{0.5,1}}/{z}_{\mathrm{0,1}}$

5.5.2 Estimation of Diffusion Coefficient Parameters (${{\varvec{z}}}_{\mathrm{0,1}},{{\varvec{z}}}_{\mathrm{0.5,1}},{{\varvec{z}}}_{\mathrm{0,05}}$) and ${\varvec{A}}$ from Scaled Recovery Parameters

The parameters $A,{z}_{\mathrm{0,1}},{z}_{\mathrm{0.5,1}},{z}_{\mathrm{0,05}}$ are plotted against $\rm{RF}_{tr}$ in Fig. 13. Estimated values from correlations vs dataset values are shown in Fig. 14.

Fig. 13

Plot of $A$ (a), ${z}_{\mathrm{0,1}}$ (b), ${z}_{\mathrm{0.5,1}}$ (c) and ${z}_{\mathrm{0,05}}$ (d) against $\rm{RF}_{\rm{tr}}$, the latter three sorted by $lr$

Fig. 14

Cross plots showing estimated values against dataset values for the 5500 simulations for $A$ (a), and CDC parameters ${z}_{\mathrm{0,1}}$ (b), ${z}_{\mathrm{0.5,1}}$ (c), ${z}_{\mathrm{0,0.5}}$ (d). Based on correlations m to s in Table S1 with scaled recovery parameters RF_tr and lr as input

$A$ did not display significant scatter and could be estimated accurately as a correlation of $\rm{RF}_{\rm{tr}}$ (${R}^{2}=0.9996$). The fractions ${z}_{a,b}$ generally increase with $\rm{RF}_{\rm{tr}}$, predicting a coefficient shifted to higher saturations. They show scatter for a given $\rm{RF}_{\rm{tr}}$ but were relatively well sorted by $lr$. ${z}_{\mathrm{0,1}}$ and ${z}_{\mathrm{0.5,1}}$ appeared well defined given $\rm{RF}_{\rm{tr}}$ and $lr$. ${z}_{\mathrm{0.5,1}}$ depended mainly on $\rm{RF}_{\rm{tr}}$ at $\rm{RF}_{\rm{tr}}>0.8$ and mainly on $lr$ at $\rm{RF}_{\rm{tr}}<0.6$. For all three parameters, but especially ${z}_{\mathrm{0,05}}$, the data were better sorted by $lr$ at $\rm{RF}_{\rm{tr}}<0.6$ than at $\rm{RF}_{\rm{tr}}>0.6$. Correlations for the ${z}_{a,b}$ fractions were developed as function of $(\rm{RF}_{\rm{tr}}, lr$ on the two intervals. Data values of $lr>1.5$ were set as 1.5 since the recovery curve becomes the same.

The prediction performance was good for ${z}_{\mathrm{0,1}}$ and ${z}_{\mathrm{0.5,1}}$ at low $\rm{RF}_{\rm{tr}}<0.6$ (red points in Fig. 14b,c) with $RMSE\sim 0.01$ for both. At high $\rm{RF}_{\rm{tr}}>0.6$ (blue points) the error of both increased to $RMSE\sim 0.03$. ${z}_{\mathrm{0,05}}$ was estimated less accurately ($RMSE\sim 0.06$ for $\rm{RF}_{\rm{tr}}<0.6$ and $RMSE\sim 0.07$ for $\rm{RF}_{\rm{tr}}>0.6$). Based on recovery parameters $\rm{RF}_{\rm{tr}}$ and $lr$, we are thus able to determine $A$ and CDC parameters ${z}_{a,b}$. That is applied on experimental data in Sect. 5.7 to obtain full diffusion coefficients.

5.6 Estimation of Recovery from the Capillary Diffusion Coefficient

We illustrate estimation of recovery based on diffusion coefficients $D$. Consider the coefficients in Fig. 5c, based on Kleppe and Morse (1974). They were scaled by $\overline{D }$ to obtain ${\Lambda }_{n}$. The three fractions ${z}_{a,b}$ for each were used to estimate $A,\rm{RF}_{\rm{tr}},lr$ (correlations in Supp Mat Section D) giving $RF\left({T}_{n}\right)$. To calculate RF against time $t$ we use that $t=\tau {T}_{ch}{T}_{n}$ where $\tau ={L}^{2}/\overline{D }$ and ${T}_{\rm{ch}}=1/4{A}^{2}$. The estimated curves are plotted against numerically simulated results in Fig. 15a.

Fig. 15

Predicted RF(t) using correlations (dashed lines) with $A,\rm{RF}_{\rm{tr}},lr$ based on diffusion coefficient fractions ${z}_{a,b}$ and numerically calculated $\rm{RF}\left(t\right)$ (full lines). Five cases are shown with different oil viscosity and input from Kleppe and Morse (1974) (a) and Behbahani and Blunt (2005) (b)

Additionally, we consider MW relative permeabilities and $J$-function from Behbahani and Blunt (2005) (Fig. 16a). They ran pore scale simulation of wetting conditions and matched experiments by Zhou et al. (2000) with upscaled functions. We vary oil viscosity (from 0.1 to 1000 cP), obtain ${\Lambda }_{n}$ (Fig. 16b), calculate $z{}_{a,b}$, estimate $A,\rm{RF}_{\rm{tr}}$ and $lr$ (Tables 4 and 5), unscale ${T}_{n}$ to get $\rm{RF}\left(t\right)$ and compare with numerical simulations in Fig. 15b (the two cases with lowest viscosity are similar).

Fig. 16

Saturation functions from Behbahani and Blunt (2005) (a) and resulting ${\Lambda }_{n}\left({S}_{n}\right)$ for different oil viscosities (b)

Table 4 System and saturation function input from Behbahani and Blunt (2005)

Table 5 Calculated parameters based on MW data from Behbahani and Blunt (2005)

For both datasets $\rm{RF}\left(t\right)$ is well predicted: $RMSE$ and ${R}^{2}$ spanned 0.001–0.009 and 0.999–1.000 for the WW example and 0.001–0.005 and 0.999–1.000 for the MW example, respectively.

5.7 Estimation of Capillary Diffusion Coefficients from (experimental) Recovery Data

Assume data $\rm{RF}\left(t\right)$ for an imbibition experiment. The data can be plotted against square root of normalized time such that early-time data lay on the straight line $\rm{RF}={T}_{n}^{0.5}$. Based on the plot of RF against ${T}_{n}^{0.5}$, we determine $\rm{RF}_{\rm{tr}}$ where RF deviates from the straight line. Fitting $\rm{RF}>\rm{RF}_{\rm{tr}}$ (late-time data) to (30) provides the value of $lr$. The factor between time $t$ and ${T}_{n}$ from scaling equals the product of $\tau$ and ${T}_{\rm{ch}}$, which are both unknown. ${T}_{\rm{ch}}$ is estimated from the correlation $A\left(R{F}_{tr}\right)$ and using ${T}_{\rm{ch}}=1/4{A}^{2}$. After, $\tau$ can be calculated. The only unknown parameter in $\tau$, $\overline{\Lambda }$, is calculated subsequently. The fractions ${z}_{\mathrm{0,1}},{z}_{\mathrm{0,0.5}},{z}_{\mathrm{0.5,1}}$ characterizing ${\Lambda }_{n}$ are estimated from $\rm{RF}_{\rm{tr}}$ and $lr$. We then have information about the shape and magnitude of ${\Lambda }_{n},\Lambda$ and $D$.

5.7.1 Interpretation of Experimental Data

Fischer et al. (2008) conducted one-end-open COUSI experiments on SWW Berea sandstone core plugs. ${\mu }_{o}$ was either 3.9 or 63.3 cP and wetting phase viscosity was varied from 1.0 to 494.6 cP in five tests each. Recovery was scaled by the highest observed value (48.7%) and plotted against square root of ${T}_{n}=\frac{t}{\tau {T}_{\rm{ch}}}$ in Fig. 17 by selecting values of $\tau {T}_{\rm{ch}}$ for each test.

Fig. 17

Experimental data from Fischer et al. (2008) plotted against ${T}_{n}^{0.5}$, with varied wetting phase viscosity for oil viscosity of 3.9 cP (a) and 63.3 cP (b)

The early data overlapped as $\mathrm{RF}={T}_{n}^{0.5}$. For the 3.9 cP oil tests all the data appear linear, with abrupt deviations at $\mathrm{RF}\ge 0.95$, which could be from variation in residual saturation. The high ${\mathrm{RF}}_{tr}$ is consistent with relatively low or similar oil viscosity compared to water viscosity. Water-wet systems tend to have much lower ${k}_{rw}$ than ${k}_{ro}$ (Mungan 1972; Kleppe and Morse 1974; Anderson 1987b; Bourbiaux and Kalaydjian 1990; Andersen et al. 2022) so the oil-to-water mobility ratio is high, shifting ${\Lambda }_{n}$ to high saturations and ${\mathrm{RF}}_{\mathrm{tr}}$ to high values. In the 63.3 cP oil tests, the oil-to-water mobility ratios are lower, and the curves deviate from the linear trend between ${\mathrm{RF}}_{\mathrm{tr}}=$ 0.75 and 0.9. Only a few tests have significant amounts of late-time data. For some such tests we estimate CDCs to explain the observed recovery.

Three tests with ${\mu }_{o}=63.3$ cP and ${\mu }_{w}=1, 4.1$ and 27.8 cP were matched with ${\mathrm{RF}}_{\mathrm{tr}}$ and $lr$, see Fig. 18. Straight line behavior, deviation from the straight line and late-time trends are well captured. The factor $\tau {T}_{\rm{ch}}$ was found from time normalization. $A$ and thus ${T}_{\rm{ch}}$ were estimated from ${\mathrm{RF}}_{\mathrm{tr}}$. Knowing the constants in $\tau$ and ${T}_{\rm{ch}}$ we calculate $\overline{\Lambda }$ from $\tau {T}_{\rm{ch}}$. Fractions ${z}_{a,b}$ are calculated from ${\mathrm{RF}}_{\mathrm{tr}}$ and $lr$. See matched and estimated parameters in Table 6.

Fig. 18

Experimental RF (points) from Fischer et al. (2008) with same oil viscosity and different water viscosities plotted against ${T}_{n}^{0.5}$ and matched to the recovery correlation

Table 6 Parameters matched to experimental recovery data from Fischer et al. (2008) and resulting estimated parameters to determine the CDC and time scales

A function ${\Lambda }_{n}$ fitting the fractions ${z}_{a,b}$ of an experiment can be determined tuning (39) freely (we set ${S}_{eq}=0.999$). However, as the three experiments were performed under same conditions (apart from ${\mu }_{w}$) we assume wettability, and hence saturation functions are fixed. We thus require fixed parameters ${n}_{w1},{n}_{w2},{n}_{o1},{n}_{o2},\frac{{J}_{1}}{{J}_{2}},\frac{{k}_{ro}^{*}}{{k}_{rw}^{*}},{J}_{2}{k}_{ro}^{*}$ when matching the three tests. The last product appears in $\Lambda \left({S}_{n}\right)$ and controls $\overline{\Lambda }$. Initial water saturation was zero such that ${k}_{ro}^{*}=1$. We could thus determine ${J}_{1},{J}_{2},{k}_{rw}^{*}$ separately, Table 7. The mean relative error of the matched fractions was 2 to 12% for the three experiments, i.e., the functions were well adapted (better match is possible by tuning each experiment freely). The estimated ${\Lambda }_{n}$ are shown in Fig. 19. Under the constraint of fixed saturation functions, higher ${\mu }_{w}$ shifts ${\Lambda }_{n}$ to higher saturations and $\overline{\Lambda }$ to lower values.

Table 7 Saturation function parameters used to calculate CDCs with correct fractions and correct $\overline{\Lambda }$ values. Time scales are consistent with calculated saturation functions

Fig. 19

Estimated ${\Lambda }_{n}\left({S}_{n}\right)$ (a) and comparison of estimated vs experimental mean of coefficients $\Lambda \left({S}_{n}\right)$ (b). The coefficients are based on estimated fractions ${z}_{a,b}$ and time scaling from Fischer et al. (2008)’s experiments, constrained by assuming same saturation functions

For validation, $\rm{RF}\left(T\right)$ is calculated solving the PDE with the determined ${\Lambda }_{n}$. $\tau$ uses $\overline{\Lambda }$ corresponding to the determined saturation functions and viscosities, $A$ follows analytically from ${\Lambda }_{n}$. $\mathrm{RF}$ against $t$ and ${T}_{n}^{0.5}$ compared with experimental data is shown in Fig. 20. The forward simulations overlap the experimental data very well, but late-time estimated $\mathrm{RF}$ is higher than experimental points for the 4.1 cP test. Higher water viscosity consistently leads to higher ${\mathrm{RF}}_{\mathrm{tr}}$ when simulated, but the 4.1 cP test did not follow this experimentally (like the other two tests), which is attributed to experimental variation (e.g., residual saturation). We should expect monotonous trends when the same input are used except only the oil viscosity is varied.

Fig. 20

Comparison of RF from forward simulation of estimated coefficients ${\Lambda }_{n}$ and RF data from Fischer et al. 2008, plotted against log time (a) and against ${T}_{n}^{0.5}$ (b)

6 Conclusions

The 1D linear COUSI problem was normalized, showing that all systems only depend on a normalized diffusion coefficient ${\Lambda }_{n}\left({S}_{n}\right)$ with mean 1. By investigating how variations of ${\Lambda }_{n}$ impacts recovery we determine what controls COUSI. Based on theory and running 5500 cases spanning all expectedly relevant shapes of ${\Lambda }_{n}\left({S}_{n}\right)$ and investigating the resulting recovery curves, the following findings were made:

• (1) Scaled recovery for all cases could be described highly accurate (mean ${R}^{2}=0.9989$ on dataset) with only two parameters $\rm{RF}_{\rm{tr}}$ and $lr$. Before water meets the no-flow boundary (early time, until $\mathrm{RF}={\mathrm{RF}}_{\mathrm{cr}}$) $\rm{RF}=\sqrt{{T}_{n}}$ (exactly), and stays a very good approximation in an extended early-time regime until $\mathrm{RF}={\mathrm{RF}}_{\mathrm{tr}}$. The time after is described by an Arps equation with $lr$ controlling imbibition rate decline. Our definition of extended early time explains the good match compared to previous works.

• (2) $\rm{RF}_{\rm{tr}}$ (when deviation is seen from root of time trend) is significantly higher than $\rm{RF}_{\rm{cr}}$ (recovery at critical time), mainly between 0.05 and 0.2.

• (3) ${T}_{n}$ is a universal scaled time for COUSI. It relates to regular time via the mean of the diffusion coefficient $D$ divided by squared system length, and a factor ${T}_{\rm{ch}}$ depending only on the coefficient shape, i.e., $t=\tau {T}_{\rm{ch}}{T}_{n}$ and $\tau ={L}^{2}/\overline{D }$. ${T}_{\rm{ch}}$ varied between 0.5 and 6 meaning $\tau$ alone gives correct time scale for COUSI within approximately one order of magnitude.

• (4) Since $\rm{RF}_{\rm{tr}}$ and $lr$ take many different values, full imbibition profiles do not scale/overlap. They do scale the extended early time period (longer than early time).

• (5) It was possible to associate the shape of ${\Lambda }_{n}$ with different early- and late-time behavior of the recovery profiles and make accurate qualitative and quantitative predictions matching numerically calculated solutions. Diffusion coefficients ${\Lambda }_{n}$ that are shifted to higher saturations (e.g., if oil-to-water mobility ratio increases) have high $\rm{RF}_{\rm{tr}}$ (recovery acts proportional to square root of time until this value) and low ${T}_{\rm{ch}}$ (faster imbibition rate due to coefficient shape). ${\Lambda }_{n}$ shifted toward higher saturations also have more rapid late-time recovery (higher $lr$, giving fewer time orders of magnitude in that regime).

• a) Lower oil mobility (e.g., higher oil viscosity) increases $\tau$ and shifts ${\Lambda }_{n}$ to low saturations. That increases the time scale via both $\tau$ and ${T}_{\rm{ch}}$, reduces the recovery obtained as root of time $\rm{RF}_{\rm{tr}}$ and also reduces $lr$ making the late-time regime approach more slowly toward full recovery.

• b) Lower water mobility (e.g., higher water viscosity) increases $\tau$ and shifts ${\Lambda }_{n}$ to high saturations. That increases the time scale via $\tau$ but is compensated by a reduction of ${T}_{\rm{ch}}$. Higher recovery is obtained as root of time $\rm{RF}_{\rm{tr}}$ and $lr$ is increased making the late-time regime approach faster toward full recovery.

• c) Mixed-wet cases have coefficients ending at nonzero values ${\Lambda }_{n}\left({S}_{n}=1\right)>0$ since both fluids have mobility at zero capillary pressure. Their coefficients are therefore shifted more toward high saturations than water-wet cases, resulting in higher square root of time recovery $\rm{RF}_{\rm{tr}}$ and less severe decline in late-time imbibition rate (they have higher $lr$) than water-wet cases. The time scale may, however, be longer due to, e.g., weaker capillary pressure.

• (6) Experimental recovery data could be fitted with recovery parameters $\rm{RF}_{\rm{tr}}$ and $lr$ (which quantify early- and late-time regimes). Accurate correlations allowed determining ${\Lambda }_{n}$. It is indicated that high ${\mathrm{RF}}_{\mathrm{tr}}$ means ${\Lambda }_{n}$ is shifted to higher saturations, while a high $lr$ means ${\Lambda }_{n}$ is shifted toward the highest saturations.