Sequence-to-Sequence Change-Point Detection in Single-Particle Trajectories via Recurrent Neural Network for Measuring Self-Diffusion

Abstract

A recurrent neural network is developed for segmenting between anomalous and normal diffusion in single-particle trajectories. Accurate segmentation infers a distinct change point that is used to approximate an Einstein linear regime in the mean-squared displacement curve via the transition density function, a unique physical descriptor for short-lived and delayed transiency. Through several artificial and simulated scenarios, we demonstrate the compelling accuracy of our model for dissecting linear and nonlinear behaviour. The inherent practicality of our model lies in its ability to substantiate the self-diffusion coefficient through offline trajectory segmentation, which is opposed to the common ‘best-guess’ linear fitting standard. Additionally, we show that the transition density function has fundamental implications and correspondence to underlying mechanisms that influence transition. In particular, we show that the known proportionality between salt concentration and diffusion of water also influences delayed anomalous behaviour.

Article Highlights

• Recurrent neural network is developed to identify diffusive change points in single-particle trajectories

• RNN predictions are accurate in a variety of synthetic and experimental scenarios simulated by molecular dynamics

• Particle trajectory transitions follow a distribution that can be affected by salinity in the context of CO₂ storage

1 Introduction

In an effort for global carbon neutrality, carbon capture and storage (CCS) has been regarded as a promising method for minimising the atmospheric effects of greenhouse gases (GHG). In practice though, CCS remains to be a significant challenge due to a myriad of technical, financial and logistic factors. More specifically, the efficacy and safety of carbon injection in depleted oil reservoirs and saline aquifers continue to be scrutinised as it is difficult to predict the long-term influent status and its associated effect(s) on geological conditions. This ambiguity poses potential environmental risks like leakage, eco-toxicity and even catastrophic releases (Bruant et al. 2002; Deng et al. 2017; Vinca et al. 2018). Consequently, many recent efforts have been directed towards the simulation and modelling of molecular GHG, brine and impurities at various aquifer/reservoir conditions to inform macroscopic predictions of storage capacity, injectivity and trapping mechanisms (Moultos et al. 2016; Omrani et al. 2022; Tung et al. 2011; Kadoura et al. 2016). Critical to these predictions is an accurate and reliable assessment of long-term molecular transport via the self-diffusion coefficient, $d_\textrm{s}$. Single-particle tracking (SPT) is a powerful tool for observing the trajectories of particles in a given environment. $d_\textrm{s}$ is frequently assessed via an ensemble averaged mean-squared displacement, MSD, of many individual trajectories in both experimental and simulated conditions (Ghosh and Krishnamurthy 2018; Trinh et al. 2013; Bullerjahn et al. 2020):

$$\begin{aligned} MSD(\textit{t}) = \frac{1}{\textit{N}} \sum _{\textit{i}=1}^{\textit{N}} \left( X^{(\textit{i})}(\textit{t}) - X^{(\textit{i})}(0) \right) ^2 , \end{aligned}$$

(1)

where x, N and t denote the position vector, number of particles and time, respectively. The self-diffusion coefficient is then computed using the familiar Einstein formulation (Einstein 1905)

$$\begin{aligned} \lim _{t \rightarrow \infty } MSD(\textit{t}) = 2 \textit{N}_\textrm{D} d_\textrm{s} \textit{t} , \end{aligned}$$

(2)

where $N_\textrm{D}$ is the number of spatial dimensions. In many cases, Eq. 2 is realised by fitting the MSD curve for a region where anomalous diffusion, MSD$\, \propto t^{\alpha \ne 1}$, has passed and linearity is arbitrarily observed (Fogelmark et al. 2018; Riahi et al. 2019). Although easy to implement and extensively used, such methodology adheres to no concrete justification and is consistently prone to errors. This is particularly true for cases of short trajectories, small sample size and multi-behavioural diffusion characteristics (Muñoz-Gil et al. 2020) where the change point from nonlinear to linear behaviour may be obfuscated. This can lead to data misinterpretations and inconsistencies, as $d_\textrm{s}$ is highly sensitive to the chosen fitted MSD region (Michalet 2010; Riahi et al. 2019; Kepten et al. 2015). Thus, the need for a new systematic approach to quickly and accurately quantifying nonlinear/linear behaviour in bulk systems is warranted.

In this work, we investigate a data-driven approach for the sequence-to-sequence (seq2seq) classification of anomalous and normal diffusion regimes in the MSD curve. More specifically, a recurrent neural network (RNN) model is developed for identifying the change point in single-particle trajectories. Through several synthetic examples, we demonstrate the predictive capabilities of RNN. We then apply our developed model to molecular dynamics (MD) case studies of brine and $\hbox {CO}_2$ with brine. We expect that this tool can be particularly useful in future MD investigations for estimating if and when normal diffusion has been reached. As well, quantifying a distinct changeover may inform fundamental investigations regarding transition mechanics and origin of anomalous behaviour.

1.1 Anomalous Diffusion

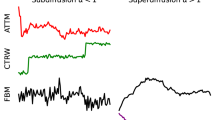
As mentioned prior, anomalous diffusion is generalised for instances where MSD $\,\propto t^{\alpha \ne 1}$. This phenomenon can be further decomposed into sub- and super-diffusive regimes where $\alpha <1$ and $\alpha >1$, respectively, as depicted in Fig. 1. This is in direct contrast to pure Brownian motion where a particle’s movement is impartial to its environment and is allowed to wander freely (Loch-Olszewska and Szwabinski 2020).

Fig. 1

Anomalous versus normal diffusion

In the context of carbon capture, utilisation and storage (CCUS), the tortuous environment and heterogeneity of commonly investigated materials like zeolites can delay the onset of normal diffusion (Hu et al. 2010). In fact, the MSD curve may undergo several major transitions until reaching linearity. Kummali et al. (2021) illustrated such a tendency for the diffusion of $\hbox {CO}_2$ in ZSM-22, a high silica zeolite, where the MSD curve traverses an initial ballistic ($\alpha \ge 2$) and sub-diffusive regime prior to reaching normal diffusion. Alternatively, $\hbox {CH}_4$ in supercritical water was shown to exhibit short-term ballistic diffusion where particles rapidly advanced to pure Brownian motion (Zhao and Jin 2020). It is clear that accurately quantifying the change point(s) in a particle’s motion is critical for further sequence segmentation, classification and analyses. Particular to this work, an automated change-point detection from anomalous to normal diffusion can supplant the existing ‘best-guess’ fitting of an MSD curve. As well, it can help grant valuable insight into the environmental influence on a particle’s motion.

1.2 Change-Point Detection

Change-point detection considers the task of identifying an abrupt change in statistical properties of time series data. This is used to quantify distinct behavioural switches in many applications, including but not limited to electrocardiographs (Fotoohinasab et al. 2020), stock market fluctuations (Takayasu 2015) and electrical grid activity (He et al. 2010). Two commonly implemented strategies for segmentation are by mean and variance change-point detection, respectively (Lavielle 1999). The mean change-point process aims to identify where the local mean between segments is drastically different. Therefore, an approximate change-point location can be inferred from such dissimilarity, as represented in Fig. 2.

Fig. 2

Mean change point

Fig. 3

Variance change point

A second approach is by variance change-point detection, where one can quantify dissimilar segments based on local variances, as shown in Fig. 3. Many case-specific strategies exist for change-point detection, but typically rely on some a priori knowledge, such as the number of change points and stationarity. This obvious limitation has motivated us to develop machine learning techniques for more robust and comprehensive methods in both offline and online applications. Aminikhanghahi and Cook (2017) provided an excellent review of unsupervised and supervised strategies for change point detection in a variety of real-world test cases. They indicated superior performance of supervised change-point detection methods for cases where ample training data exist and test data are stationary.

1.3 Machine Learning for Anomalous Diffusion

Recently, characterising anomalous diffusion in single-particle trajectories has been addressed via machine learning. Gajowczyk (2021) classified protein trajectories between sub-diffusive, super-diffusive and normal diffusive behaviour. They demonstrated exceptional performance on synthetic test trajectories, albeit predictions on real data ‘confusing’ due to classification discrepancies. Granik et al. (2019) classified cell trajectory data as fractional Brownian motion, Brownian motion or continuous time random walk, but indicated the potential issue of transient behaviour in single-particle trajectories. Kirichenko et al. (2020) accurately classified synthetic multi-fractional Brownian motion realisations at moderate-to-long trajectory lengths. Much work has demonstrated astonishing performance of machine learning on synthetic trajectories but complicated predictions on experimental data. One enduring challenge is the ability to predetermine change points for neural network models whose outputs produce singular label probabilities. That is, one class is assigned to an entire trajectory input. Without such tandem cooperation between these two objectives, switching behaviour can be overlooked and further consolidated into an overall imprecise classification.

The AnDi Challenge (http://andi-challenge.org) recently shed light on the advantages and disadvantages of various methods for the inference, segmentation and classification of anomalous diffusion in both synthetic and experimental data. The objective comparison of individual groups’ efforts indicated the potential of machine learning for accurately characterising the behaviour of individual particle trajectories (Muñoz-Gil et al. 2021). In particular, RNN was ranked amongst top performers in this challenge for all three tasks. Once more, the switching behaviour of individual trajectories remains difficult to evaluate if discrete change points are not identified beforehand. To address this issue, we investigate the potential of a simplified change-point model that generalises non-Brownian motion as anomalous. In this case, transient behaviour can then be classified into one bulk category as to provide a coherent dissection of anomalous and normal diffusive motion. The novelty of our model builds upon considerable prior success of neural networks for identifying and classifying anomalous behaviour in single-particle trajectories. Specifically, we target the practical application of RNN for substantiating $d_\textrm{s}$ via MSD piecewise fitting. Again, this is directly opposed to the error prone standard of observing linearity via eyesight.

2 Recurrent Neural Network Model

2.1 Training Data and Pre-Processing

Here, our training, validation and test sets reflect a unique and simplified labelling scheme based on three limiting features: (1) Non-Brownian motion is classified as anomalous. (2) The change point from anomalous to normal diffusion follows a piecewise formulation (Yin et al. 2018). 3) The system eventually evolves to pure Brownian motion. Figure 4 illustrates several training examples where the locations of fabricated change points are uniformly distributed as a ratio of trajectory length (L), $0 \le CP/L \le 0.82$. This construction method spans a wide but non-exhaustive range of possible trajectory paths and artificial scenarios for our model to ‘learn’ from. The location of these change points is simply the interface between generated anomalous and Brownian trajectories, as highlighted by blue and orange paths.

Fig. 4

Training data examples

The success of supervised machine learning methods is inherently dependant on the quality, representation and size of training set. Furthermore, machine learning-based models are inherently data-hungry, requiring a large training set to prevent model overfitting. Several previously mentioned authors considering the segmentation, inference or classification of anomalous behaviour in single-particle trajectories have reported training sets on the order of $\sim 10^5$ as a lower bound for sufficient model convergence (Argun et al. 2021; Granik et al. 2019). Naturally, current practical limitations dissuade the dependency of training on real-world experimental data due to the scarcity of available data. More so, inducing a behavioural switch can be difficult to impose without understanding the transitional influences in transport phenomena exhibiting multi-scalar or multi-fractional Brownian motion. Instead, it is often suitable to utilise simulated trajectories as both a computationally cheap and representative alternative to describe the stochastic dynamics of a given system/object under consideration.

The anomalous diffusion models we consider in our training data are fractional Brownian motion and scaled Brownian motion, as these are particularly relevant to the particle migration in porous media (Chang and Sun 2018) and transport in bundles (Bodrova et al. 2015). Fractional Brownian motion (FBM) is an ergodic, Gaussian, random processes where correlated incremental steps are either persistent ($1< \alpha < 2$) or anti-persistent ($0< \alpha < 1$) (Yerlikaya-Özkurt et al. 2014). Realisations of FBM can be simulated for training data via wavelet synthesis as proposed by Abry and Sellan (1996). Scaled Brownian motion (SBM) is a weakly non-ergodic Gaussian process that reflects the case of increasing ($1< \alpha < 2$) or decreasing ($0< \alpha < 1$) diffusion coefficient with time (Jeon et al. 2014). Here, we consider a power law time dependency for the synthesised anomalous training data where the anomalous exponent is maintained between $0.2 \le \alpha \le 0.75$ and $1.25 \le \alpha \le 1.8$ for SBM and FBM. Naturally, $\alpha = 1$ is only applied for the case of pure Brownian motion. Table 1 provides a summary of the constraints we utilise for constructing our training, validation and test sets, where trajectory lengths were determined in coordination with the expected simulation time of our molecular dynamics test samples.

Table 1 Training data constraints

2.2 Model Architecture

Recurrent neural networks have proven to be exceedingly effective at interpreting trends that exist in time series data (Hüsken and Stagge 2003; Hewamalage et al. 2021). In particular, long short-term neural networks (LSTM) have even demonstrated success for cases where time series exhibit nonlinear or non-stationary tendencies (Preeti 2019). The effectiveness of LSTM is primarily due to its ability to preserve long-term contextual trends in sequential data. In part, this is accomplished by looping sequence inputs to imitate natural human recollection. Unlike the generalised RNN though, LSTM units address the ‘vanishing error problem’ (Gers et al. 2000) by regulating relevant information via an input gate, forget gate and output gate (Graves et al. 2009). Simply put, these gates allow for the addition or removal of information in the current cell state, a comprehensive encoding of previously introduced data. This encoding is then used to appropriately weight the prediction at time = t, i.e. the hidden state. An unwrapped visual schematic for a single LSTM unit is shown in Fig. 5, where x, C and h refer to the input, cell state and hidden state, respectively. Gates are identified by regions within the bounding red boxes for clarity.

Fig. 5

Unwrapped LSTM unit schematic

Here, we implement an LSTM neural network for the sequence-to-sequence segmentation of individual trajectories. This is opposed to some previously discussed methods that classified entire trajectories by a singular label probability. An architecture schematic of our model is shown in Fig. 6, where numbers indicate layer units (width). We use a dropout layer to prevent overfitting by randomly setting neural units and their connections to zero (Srivastava et al. 2014). A softmax activation layer is then used to output a likelihood probability over $k = 2$ classes prior to computing the cross-entropy loss between predicted and ground truth labels.

Fig. 6

Architecture schematic

Our model accepts one-dimensional (1D) trajectory displacement vectors of length, L, where data are standardised with mean, $\mu = 0$, and standard deviation, $\sigma = 1$. Though LSTM networks have shown to be capable of accurately interpreting input data of dissimilar length to the training set, we adopted an equivalent strategy to Argun et al. (2021) where separate neural networks are developed for different trajectory lengths, $L = 1700, 2000, 2300$. Their method minimises the burden of padding or slicing data while still covering a wide range of multi-length possibilities. For the sake of clarity though, we restrict our remaining results and discussion to the case of $L = 1700$ as shorter trajectories pose as an inherent limiting factor in model prediction (Granik et al. 2019).

2.3 Model Training and Validation

The following tasks dictate the proposed trajectory segmentation procedure: (1) The particle displacement signal, $\Delta x$, $\Delta \textit{y}$ or $\Delta z$, is fed as a univariate time series to our neural network model. (2) The output layer assigns a label probability at each displacement, $\Delta x(t)$, indicating either anomalous or normal diffusion (2 or 1). This labelling mask is applied to its corresponding particle trajectory given by the cumulative summation of individual displacements. (3) The change point is directly inferred from labelling switch. (4) Steps 1, 2 and 3 are repeated for all individual particles in the system. A case example highlighting all four tasks is shown in Fig. 7 for a single particle, one degree of freedom, system traversing an enforced transition between SBM at $\alpha = 1.5$ and BM. Implicated by the red step change at time step = 900, a familiar orange and blue mask is applied to the particle trajectory indicating a distinct behavioural shift. For a larger system where $N_\textrm{particles} \gg 1$, this same procedure can also be utilised to infer a switch in the MSD curve by tracking the distribution of individual change points. We will demonstrate this probabilistic approach for segmenting the MSD curve in Sect. 3.1.

Fig. 7

Automated trajectory segmentation strategy

Computed as the labelling difference between ground truth and predicted segmentation, our final training results indicated an expected performance on both training and validation sets, 97.41% and 97.25%, respectively. This capacity is the result of iteratively refining our model to a final, best-fit scenario. We utilised a learning rate of 0.005 to reduce training time while still maintaining high validation accuracy. Different learning rates, $LR = 0.01, 0.001$, were shown to give comparable end results at the expense of significantly higher training times. This is illustrated in Fig. 8 where the adaptive moment estimation (ADAM) optimiser is used for all cases due to its fast convergence (Kingma and Ba 2014). Random shuffling was imposed at the beginning of training to prevent any kind of learning bias like memorising change-point location, $\alpha$, or anomalous diffusion model. This strategy helps to generalise supervised learning methods by eliminating any kind of routine order to the training data. In many cases, it can be advantageous to reshuffle every epoch (Nguyen et al. 2022) for further network refinement. However, our model tends to converge within 1 epoch, indicating no obvious training order dependence. Finally, a batch size of 128 samples was used based upon validation accuracy and training time. A comparison of various batch sizes of form $2^n$ is shown in Fig. 9 with LR $=\,0.005$.

Fig. 8

Learning rate

Fig. 9

Batch size

From Figs. 8 and 9, we can see that a learning rate, LR $= 0.005$, and batch size of 128 is appropriate for training our model as it converges quickly and maintains the highest overall validation accuracy. We present a summary of neural network training parameters, hyperparameters and hardware used for our final model deployment in Table 2.

Table 2 Neural network development parameters

3 Results and Discussion

In this section, we analyse the predictive capabilities of our model for synthetic test scenarios and two molecular dynamics case studies: brine and $\hbox {CO}_2$ + brine. These scenarios reflect distinct behaviours to demonstrate our model’s performance on highly contrasting particle motion, namely rapid, delayed and long-term anomalous diffusion. For all MD set-up parameters and background, see Appendix A. We demonstrate how to effectively implement RNN for labelling individual trajectories, segmenting the MSD curve and quantifying the transition density from anomalous to normal motion. Note that, amongst prior investigations, it is difficult to assess the reliability of our model on unlabelled experimental or simulated cases. Thus, the expectation of our model is largely based on the accuracy of our synthetic test set.

3.1 Test Set and Model Performance

RNN performed very well on our test set with an overall classification accuracy of 95.2%. As the test and validation sets exhibit analogous statistical characteristics, this was an expected result. A second, equivalently distributed test set was generated to assess the false positive/negative segmentation concerning respective models. This is to measure our model’s labelling preference and associated error that is common for classification tasks. Figure 10 shows the confusion matrices for individual models, SBM, FBM and BM, for 5,000 test samples.

Fig. 10

Confusion matrices for RNN

Our model tends to slightly underperform when classifying fractional Brownian motion trajectories. This would indicate a potential over-prediction of normal diffusive behaviour when classifying real-world data that exhibits fractal dynamics. Figure 11 demonstrates the performance of our model for a randomly selected test example where ground truth is juxtaposed against our raw and filtered label prediction. Our segmentation procedure follows an equivalent application of our aforementioned strategy in Figs. 4 and 7.

Fig. 11

Trajectory segmentation of test sample

It is clear that RNN is capable of segmenting between anomalous and normal diffusion behaviour in synthetically derived trajectories. However, a change-point over-prediction can be observed in our labelling subplot. This is a non-physical artefact of filtering our raw model prediction (yellow) by a 30-time step moving window average so that segmented regions can appear more distinguishable. The cost of this aesthetic procedure is a modest over-prediction of change point while allowing for an easier interpretation of real-world data. This post-processing technique can be appreciated for cases where the transition from anomalous to normal diffusion is non-instantaneous or highly obscured such that RNN erroneously oscillates between labelling.

To demonstrate our procedure for segmenting the MSD curve, we consider a hypothetical scenario where particles are initially restricted by some semi-rigid boundary. At a prescribed time, these particles break free and are allowed to diffuse freely with $d_\textrm{s}$. The change-point times from confined to normal diffusion obey the following preparations a) Gaussian distribution with $\mu$ = 1,100 ps, $\sigma$ = 150 ps. b) Continuous uniform distribution on interval $700 \le t \le 1,500$ ps. RNN is then used to track all N = 2,000 change points for estimating a best-fit linear region in both respective cases. Different percentiles for our transition density function (TDF), 25th, 50th, 75th, etc., can provide a discretionary indicator for where to piecewise fit the MSD curve as shown by the segmented orange regions in Figs. 12 and 13, respectively. Naturally, as t approaches 100th, linearity becomes more apparent, indicating where $d_\textrm{s}$ should be measured. However, as we recall RNN has a slight tendency to over-predict these change points, a conservative bound for practical applications falls between 75th and 85th. This over-prediction can also be observed via the juxtaposition between ground truth (blue) and predicted (purple) TDFs.

Fig. 12

Gaussian TDF segmentation

Fig. 13

Uniform TDF segmentation

Our model is capable of estimating the TDF, granting useful insight into transitional influences and an expected linear MSD region. As we will demonstrate in coming sections, surrounding environmental factors can greatly affect the stretching, shifting and scaling of the TDF. Indeed, this corresponds to varying degrees of transiency and delays that further warrants the usefulness of our model and segmentation procedure. While we acknowledge the uncertain physicality of a Gaussian or uniform TDF, it is anticipated that different scenarios, environments and conditions can give rise to equally diverse distributions.

3.2 Brine Case Study—Fleeting and Delayed Anomalous Behaviour

In this section, we evaluate the relationship between salt ion concentration and transition time to highlight the disparity between arbitrary and endorsed piecewise fitting. RNN was used to identify the change points of $\hbox {H}_2$O for 9 different salt concentrations using discussed methods. Interestingly, Fig. 14 illustrates an exponential transition from anomalous to normal diffusion. Figure 15 indicates the exponential decay rate, $\kappa$, increases as a function of salt concentration, while the initial transition density, $\lambda$, decreases. More plainly, salt ions significantly affect the delayed transiency of molecular $\hbox {H}_2$O, i.e. stretching of the TDF. This consequence can dictate the computational minimum for cases that transition beyond the simulation lifetime (dashed). That is, if a complete transition is not identifiable, the molecular dynamics simulation should be computed for longer times to observe linearity.

Fig. 14

Exponential TDF comparison of H$_2$O for varying salt concentrations

Fig. 15

Exponential decay rate ($\kappa$) and initial transition density versus salt concentration

These results share a comparable tendency to previous works that have identified an inverse relationship between $d_\mathrm {s,H_2O}$ and salt concentration (Yao et al. 2015; Ben Ishai et al. 2013). This suggests that $\hbox {Na}^+$ and $\hbox {Cl}^-$ ions in bulk water not only affect the diffusion coefficient, $d_\mathrm {s,H_2O}$, but also the expected transition time from anomalous to normal diffusion. More precisely, the decrease in $\lambda$ indicates a persistent transient behaviour likely ascribed to a ‘many-body’ polarisation effect (Yao et al. 2015; Ding et al. 2014) that hinders the movement of water molecules. This delayed transiency can be exaggerated by salt ions well beyond the saturation limit, approximately 26.3 wt.% NaCl at 330 K (Farnam et al. 2014), as shown in Fig. 16. Again, these metrics can provide valuable insight as to an approximate linear MSD regime. We segregate diffusive and non-diffusive behaviour based on computed 85th percentiles as per the methodology illustrated in Figs. 12 and 13. For all MSD curves, the segmented anomalous and normal diffusion regions are identified by the areas below and above our computed curve fitting boundary, respectively.

Fig. 16

MSD of H$_2$O for various salt concentrations

Intuitively, our extrapolated boundary provides a good estimate as to where nonlinear behaviour ends and linear begins. This dissection indicates that, for salt concentrations greater than or equal to the solubility limit, the molecular dynamics simulations may need to run for much longer times to adequately observe linearity. This infers that the reliability of arbitrarily piecewise fitting MSD is, at best, speculative. Conversely, RNN can accurately estimate when normal diffusion has been reached for a quantitative corroboration of $d_\textrm{s}$.

3.3 $\hbox {CO}_2$ with Brine Case Study—Lingering Anomalous Behaviour

In this section, we examine the case where a particle’s movement is continuously obstructed. Such a tendency is apparent for the molecular dynamics simulation of multiphase flow ($\hbox {CO}_2$-aqueous brine) where strong interfacial tension (IFT) is known to exist at low pressure and high salinity conditions over a wide range of temperatures 298– 375 K (Amooie et al. 2019; Pereira et al. 2017). This is demonstrated in Fig. 17, where randomly selected salt ions, $\hbox {Na}^+$ and $\hbox {Cl}^-$, remain bundled due to hydration (Mountain 2007) and high $\hbox {CO}_2$-brine IFT (Mutailipu et al. 2019). Compared to the wandering $\hbox {CO}_2$ molecule highlighted by an orange trajectory path, it can be observed that salt ions remain corralled throughout the simulation lifetime.

Fig. 17

Trajectories of CO$_2$, Na$^+$ and $\hbox {Cl}^-$

The expected crowding and confinement of hydrated ions leads to highly sub-diffusive behaviour akin to ‘soft’ reflections in a bounding sphere (Bickel 2007). This is affirmed by our model prediction in Figs. 18 and 19, where we compare the diffusion behaviour of $\hbox {Na}^+$ and $\hbox {Cl}^-$, respectively. Again, the inputs to our model are individual displacements $\Delta x$, $\Delta y$ and $\Delta z$, shown by blue, yellow and purple signals, respectively.

Fig. 18

RNN prediction for Na$^+$ ion

Fig. 19

RNN prediction for Cl$^-$ ion

The anomalous labelling of selected salt ions is likely due to a power law scaling of $\Delta x$, $\Delta y$ and $\Delta z$, similar to scaled Brownian motion under confinement (Jeon et al. 2014). As there are no intervening physical or chemical mechanisms that allow for the salt ions to escape, our model recognises this confinement as non-freely diffusive behaviour in 94% of tracked particles. We confirm that this attribute remains consistent over different concentrations to demonstrate the statistical reliability of RNN. This is demonstrated in Fig. 20 where brine nano-droplets are shown to persist for varying salt concentrations.

Fig. 20

Salt concentration dependency on anomalous behaviour

In line with an expected nonlinear behaviour, our model validates the presence of sub-diffusion motion within the brine nano-droplets. Furthermore, the varying concentration of salt ions does not dissuade this prediction as confinement and bundling are evident throughout all simulated cases.

4 Conclusions

In this work, we demonstrated a data-driven method for segmenting anomalous and normal diffusive behaviour in single-particle trajectories that exhibit fractional and scaled Brownian dynamics. In particular, an LSTM-based recurrent neural network was shown to be exceedingly capable of detecting change points over an assortment of synthetic and experimental scenarios. Through simple, effective formulation, our labelling and segmentation scheme provides powerful implications regarding both practical and fundamental investigations. (1) The self-diffusion coefficient $d_\textrm{s}$ can be quantitatively corroborated by dissecting linearity in the MSD curve. (2) Predicting the transition density function provides a novel description of transient behaviour that can inform how physical and chemical influences affect transition. We provided a thorough investigation of various artificial and molecular dynamics simulated scenarios to assess the practicality and accuracy of the RNN. Despite the origin or type of anomalous diffusion represented in our simulated test cases, our model is always able to generate coherent and meaningful change-point predictions. These predictions were substantiated by insight regarding known and observed physical mechanics associated with anomalous behaviour. Specifically, we focused on delayed transiency (brine case study) as an increase in salt ion concentration highlighted an intuitively recognisable disparity between anomalous and normal diffusion. Our model was used to predict the TDF at different salt concentrations to show how transiency can persist due to hydration. By following a consistent segmentation strategy, we were able to derive an empirical boundary that can be used for estimating when/if normal diffusion has been reached. For the case of $\hbox {CO}_2$ in brine, our model implicated an obvious confinement and bundling of salt ions throughout the simulation lifetime. This phenomenon was shown to remain independent of salt concentration. One limiting factor of this model is its tendency to oscillate between anomalous and normal labelling near change points. This was addressed via window average filtering that better emphasised a terminal change-point time.

Appendix A: Molecular Models and Case Set-up

The potential energy in this study includes the non-bonded energy of Coulombic and van der Waals (vdW) forces and the intramolecular energy of bond stretch and angle bend:

$$\begin{aligned} E = \frac{q_i q_j}{4\pi \varepsilon _0 r_{ij}} + 4 \varepsilon _{ij} \left[ \left( \frac{\sigma _{ij}}{r_{ij}} \right) ^{12} - \left( \frac{\sigma _{ij}}{r_{ij}} \right) ^6 \right] + \frac{k_r}{2} (r_{ij} - r_0)^2 + \frac{k_\theta }{2} (\theta _{ijk} - \theta _0)^2 , \end{aligned}$$

(A1)

where q is the charge of an atom, $\varepsilon _0$ is the vacuum permittivity, $\varepsilon$ is the depth of the Lennard–Jones (LJ) potential well, $\sigma$ is the inter-particle distance where the potential energy is zero, $k_r$ and $k_\theta$ are the energy constants, r is the distance between atoms, $r_0$ is the equilibrium bond distance, $\theta$ is the angle of two bonds, and $\theta _0$ is the equilibrium angle.

The interactions between different species are described by the Lorentz–Berthelot (LB) combining rules for both size and energy parameters: $\sigma _{ij} = (\sigma _{ii} + \sigma _{jj})/2$ and $\varepsilon _{ij} = (\varepsilon _{ii} \varepsilon _{jj})^{1/2}$.

For $\hbox {H}_2$O, the SPC/E (extended simple point charge) rigid model is used. The $\hbox {CO}_2$ molecular model is adopted from the work of Cygan et al. (2012). It is an accurate and fully flexible set of interatomic potentials for $\hbox {CO}_2$, which is developed and combined with clay potentials to help evaluate the intercalation mechanism and examine the effect of molecular flexibility on the diffusion rate of $\hbox {CO}_2$ in water. The latest Madrid-2019 force field (Zeron et al. 2019) for ion simulation is used, which is developed for seawater simulation. The force field parameters of $\hbox {H}_2$O, $\hbox {CO}_2$ and ions are listed in Tables 3 and 4.

Table 3 Atomic force field parameters for H$_2$O, CO$_2$ and ions

Table 4 Geometry and potential parameters for H$_2$O and CO$_2$

All the MD simulations are performed with LAMMPS (Large-scale Atomic Massively Parallel Simulator) package (Thompson et al. 2022). The cut-off distances for LJ interactions and Coulombic interactions are set to be 1.2 nm. The long-range Coulombic interactions are calculated using the particle–particle–particle mesh (PPPM) solver with a desired relative error in forces of 10$^{-4}$. Periodic boundary conditions are applied in three directions for all simulations. The SHAKE algorithm (Ryckaert et al. 1977) was used to keep water molecules rigid. The initial velocities are assigned following a Maxwell–Boltzmann distribution at each temperature.

The molecules are randomly distributed in the box with a larger edge length to avoid overlap. The isobaric–isothermal ensemble (to control the number of atoms, pressure and temperature, i.e. NPT) is used with time step of 1 fs to compress the box towards the desired density (see Fig. 21). Another 1 ns simulation is followed in NVT ensemble (constant number, volume and temperature) for the production run with time step of 1 fs. The temperature and pressure damping factors equal 100 and 1000 times of the time step, respectively. The atom trajectories and properties are output every 1 ps.

Fig. 21

A representative MD system to show the compression process in NPT simulation, which contains 1000 CO$_2$, 3000 H$_2$O, 100 Na$^+$ and 100 $\hbox {Cl}^-$; T = 330 K, P = 100 bar