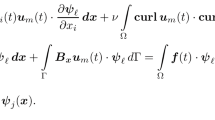1 Introduction

Porous flow problems are found in many physical phenomena, including hydraulic engineering (Chellam and Wiesner 1993), ultrafiltration membranes (Singh and Laurence 1979), gasesous diffusion (Wang et al., 1990), biological organisms (Majdalani et al. 2002) and ablation cooling (Dauenhauer and Majdalani 2003), and thus the challenge of understanding solutions to these problems have continued to interest the scientific research community.

A seminal study on porous flow problems is due to Berman (1953), who analyzed the velocity field of a homogeneous fluid that was laminarly flowing in a channel formed by two porous walls. Therein, Berman assumed a non-slip (or zero tangential velocity) boundary condition at the porous walls, which characterizes flows with solid bounding walls (Singh and Laurence 1979). However, the work of several authors (Beavers and Joseph 1967; Kohler 1973; Saffman 1971) suggests that laminar flow problems with porous surfaces do exhibit a slip boundary condition. For example, when the fluid contains smaller particles that pass through the porous wall material, and larger particles that accumulate near the porous boundaries, it creates a so-called “slip" boundary effect. For instance, the physical phenomena of concentration polarization (Blatt et al. 1970 [p. 47.]; Michaels 1968 [p.297]), involves anisotropic ultrafiltration membranes and an accumulation of solutes that forms “a polarized gel-layer” (Singh and Laurence 1979 [p.721]). As such, flow problems with slip conditions have been examined subsequently by many authors, such as Chellam et al. (1993, 1992); Ullah et al. (2021); Bhat and Katagi (2021); Balhoff et al. (2010); Ullah et al. (2020); Siddiqui et al. (2020); Varunkumar and Muthu (2020); Ullah et al. (2019); Farooq et al. (2018); Ashwini et al. (2017); Cox and Hill (2011); El-Genk and Yang (2009); Nazari Moghaddam and Jamiolahmady (2016); Nishiyama and Yokoyama (2017); Sparrow et al. (1974); Rasoulzadeh and Panfilov (2018); Skjetne and Auriault (1999); Taherinejad et al. (2021).

We analyze the following nonlinear, ordinary differential equation

$$\begin{aligned} f{^{(iv)}} + {\mathcal {R}}(f'f'' - f f''') = 0, \ \ \ \eta \in [0,1], \end{aligned}$$
(1.1)

with \(f= f(\eta )\) a part of a stream function associated with the components of the fluid’s velocity, \({\mathcal {R}}\) is a Reynolds number and [0, 1] covers half of the width of the channel (a more detailed explanation will be given in Sect. 2). The differential equation (1.1) is coupled with the boundary conditions:

$$\begin{aligned} f(0)=0, \ f''(0) = 0, \ f(1) = 1, \ f'(1)=-\gamma f''(1), \end{aligned}$$
(1.2)

where \(\gamma\) is a non-negative constant that we refer to as the slip coefficient. If \(\gamma = 0\) then (1.1), (1.2) collectively reduce to the classical non-slip case of Berman (1953).

Several scholars (Singh and Laurence 1979; Chellam et al. 1992; Chellam and Wiesner 1993; Chellam et al. 1993; Chellam and Lui 2006; Guo et al. 2020) have developed approximations to solutions to porous flow problems that include type (1.1), (1.2) with suction (\(\mathcal{R} >0\)) through perturbation techniques, numerical integration and Runge-Kutta schemes. For instance, a polynomial approximation is generated by constructing a perturbation expansion, with standard practice to usually consider two terms or less. The expansions are done in terms of a parameter, in this case \({{{\mathcal {R}}}}\), the Reynolds number. Essentially, this involves starting with a solution for \({{{\mathcal {R}}}} = 0\) and then constructing approximative (but low degree) polynomials, see, for example, Singh and Laurence (1979). The problem (1.1), (1.2) has also been transformed via a substitution so that the Reynolds numbers was transferred to one of the boundary conditions (Chellam and Wiesner 1993) and then Runge-Kutta methods were used to approximate solutions. Shooting methods via numerical integration have also been applied to develop insight into the solutions of (1.1), (1.2), for example, in Chellam and Lui (2006).

However, a firmer and more precise mathematical understanding of the solutions to porous flow problems with slip conditions and their properties is yet to be fully developed. For example, it is unknown if (1.1), (1.2) is well-posed for the slip case \(\gamma > 0\), the location of the solution(s) remains unknown, it is yet to be known if and how approximations converge to this solution, and what the estimates for errors in the approximations are. Herein we formulate a new mathematical foundation regarding solutions, including existence; uniqueness; location; approximation; convergence and error estimates. Our strategy involves developing new and interesting connections between solutions to (1.1), (1.2) and the theory of fixed points of operators, and cover both suction cases \(({{{\mathcal {R}}}}>0)\) and injection cases \((\mathcal{R}< 0)\).

A real valued function on [0, 1] with a continuous fourth order derivative is called a solution to the BVP (1.1), (1.2) if it satisfies both (1.1) and (1.2) for some value of \({\mathcal {R}}\) and some value of \(\gamma \ge 0\).

Recently, Almuthaybiri and Tisdell (2022) analyzed the non-slip case (\(\gamma = 0\)) of (1.1), (1.2) and employed a contractive mapping technique to better understand the nature of solutions. They established existence, uniqueness and approximation of solutions under the assumptions

$$\begin{aligned} \gamma = 0, \ \ \ |{{{\mathcal {R}}}}| < \frac{ 2000\sqrt{65}}{19500 + 4901 \sqrt{65}} \approx 0.2732360884. \end{aligned}$$
(1.3)

Their work naturally raises questions regarding solutions to the more accurate slip case \(\gamma > 0\), such as: for what values of \({{{\mathcal {R}}}}\) and \(\gamma >0\) does (1.1), (1.2) have a unique solution? Where is this solution located? How can we approximate this solution? We address these questions herein through the use of fixed point methods, in particular, via contractive mappings. We discover that for all slip coefficients \(\gamma >0\), the BVP (1.1), (1.2) has a unique solution for sufficiently small values of \(|{{{\mathcal {R}}}}|\), and we determine a location for this solution. Furthermore, we construct a sequence of approximating functions whose limit is the above solution to (1.1), (1.2). The convergence rate is shown to be linear, and we establish error estimates on the approximative sequence, which generates approximations to any prescribed level of accuracy. We also compare our results with that of the non-slip problem to shed light on connections and differences between the two.

The layout of this article is as follows. In Sect. 2 we briefly derive the problem (1.1), (1.2) to introduce notation and to provide context. We also formulate an equivalent integral equation to the BVP (1.1), (1.2). In Sect. 3 we construct new bounds on the integrals of various Green’s functions for (1.1), (1.2) and relate them to the non-slip case. In Sect. 4 we synthesize the equivalent integral representation and our bounds to enable an application of fixed point theory to a suitable operator that yields new existence, uniqueness and approximation results. In Sect. 5 we discuss an open problem.

2 Problem Derivation and an Integral Form

Let us briefly derive the problem (1.1), (1.2) under consideration. For additional details see, for example, Singh and Laurence (1979) or Chellam and Wiesner (1993).

Consider steady, laminar flow of fluid containing macro-molecular solutes in a two-dimensional channel with porous walls in the form of two parallel and flat ultrafiltration membranes, where the walls are separated by a distance of 2h, see Fig. 1. We assume the fluid has constant density \(\rho\) and kinematic viscosity \(\nu\). The fluid is subject to either injection or suction with constant velocity \({\mathcal {V}}\) through the walls, with each wall having equal permeability. This implies the flow will be symmetrical about the midplane of the channel.

Fig. 1
figure 1

Flow Within Parallel Flat Membranes: Suction at Walls (\({{{\mathcal {R}}}}>0\))

Full size image

Choose a coordinate system with its origin located at the center of the channel. We let x denote the co-ordinate axis that is parallel to the channel walls, and let y be the axis that is perpendicular to the channel walls. Also, let \(u=u(x,y)\) represent the velocity component of the fluid in the x direction and let \(v=v(x,y)\) represent the velocity component of the fluid in the y direction. Let p denote the pressure.

Introduce the normalized variable

$$\begin{aligned} \eta =\frac{y}{h} \end{aligned}$$

and form the Navier-Stokes equations

$$\begin{aligned} u \frac{\partial u}{\partial x} + \frac{v}{h} \frac{\partial u}{\partial \eta }= & {} - \frac{1}{\rho } \frac{\partial p}{\partial x} + \nu \left( \frac{\partial ^2 u}{\partial x^2} + \frac{1}{h^2} \frac{\partial ^2 u}{\partial \eta ^2}\right) \\ u \frac{\partial v}{\partial x} + \frac{v}{h} \frac{\partial v}{\partial \eta }= & {} - \frac{1}{h \rho } \frac{\partial p}{\partial \eta } + \nu \left( \frac{\partial ^2 v}{\partial x^2} + \frac{1}{h^2} \frac{\partial ^2 v}{\partial \eta ^2}\right) .\end{aligned}$$

The continuity equation is

$$\begin{aligned} \frac{\partial u}{\partial x} + \frac{1}{h} \frac{\partial v}{\partial \eta } = 0 \end{aligned}$$

and the associated boundary conditions are

$$\begin{aligned} u(x,\pm 1) = -\frac{\sqrt{k}}{\alpha h}\frac{\partial u}{\partial \eta },{} & {} \ \ \ v(x,0)=0 \\ v(x,\pm 1) = \pm {\mathcal {V}},{} & {} \ \ \ \frac{\partial u}{\partial \eta }(x,0) = 0. \end{aligned}$$

Note that the slip boundary condition captures the assumption that the slip velocity at the porous boundaries is proportional to the wall shear rate (Chellam and Wiesner 1993). Here \(k \ge 0\) is the permeability of the membrane matrix and \(\alpha >0\) is a dimensionless constant that depends on the surface characteristics of the membrane (Singh and Laurence 1979). Throughout this paper, the constant \(\gamma\) will represent the slip coefficient associated with the slip condition at the boundaries, namely

$$\begin{aligned} \gamma = \frac{\sqrt{k}}{\alpha h}. \end{aligned}$$

Due to symmetry, we can focus our attention on (say) the upper half-channel of thickness h. Since our attention is on the upper half channel from \(\eta = 0\) to \(\eta = 1\), we disregard the boundary conditions involving \(u(x,-1)\) and \(v(x,-1)\) from what follows.

A stream function \(\psi\) exists with

$$\begin{aligned} u(x,\eta ) = \frac{1}{h} \frac{\partial \psi }{\partial \eta }, \ \ \ v(x,\eta ) = \frac{\partial \psi }{\partial x} \end{aligned}$$
(2.1)

with the continuity equation holding.

Drawing on Berman’s assumption (Berman , 1953) that the velocity component v is independent of x, we can introduce a stream function, \(\psi\), that takes the form

$$\begin{aligned} \psi (x,\eta ) := [h{{{\bar{u}}}}(0) - {\mathcal {V}} x]f(\eta ). \end{aligned}$$

Above, f is a function of \(\eta\) which is to be determined later, and \({{{\bar{u}}}}(0)\) is an arbitrary velocity at \(x = 0\) that is managed away.

From (2.1) we can derive the velocity components in terms of f

$$\begin{aligned} u(x,\eta ) = \left[ {{{\bar{u}}}}(0) - {\mathcal {V}} \frac{x}{h} \right] f'(\eta ), \ \ \ v(x,\eta ) = v(\eta )= {\mathcal {V}} f(\eta ). \end{aligned}$$
(2.2)

Our u and v in (2.2) are expressed in terms of f and \(f'\), with the equations of motion then leading to (1.1) with \({{{\mathcal {R}}}} = {\mathcal {V}} h / \nu\) a Reynolds number. Furthermore, if we consider (2.2) at the boundaries of the half-channel bounded by \(\eta = 0\) and \(\eta = 1\) then we obtain (1.2).

Let us establish a new result that links the equivalency between the slip BVP (1.1), (1.2) and an integral equation. The integral equation will be drawn upon in Sect. 3 to leverage our main results.

Theorem 2.1

For all \(\gamma \ge 0\), the BVP (1.1), (1.2) is equivalent to the integral equation

$$\begin{aligned} f(\eta ) = \int _0^1 G(\eta ,s) {\mathcal {R}}\left( f'(s)f''(s) - f(s)f'''(s) \right) \ ds + \phi (\eta ), \ \ \ \eta \in [0,1]. \end{aligned}$$
(2.3)

Above, \(G(\eta ,s)\) is the Green’s function

$$\begin{aligned}{} & {} G(\eta ,s) \nonumber \\{} & {} := \left\{ \begin{array}{lr} \dfrac{s(1-\eta )^2 [(s^2-3)\eta + 2s^2] + 6\gamma (1-\eta )s(\eta ^2+s^2-2\eta )}{12(1+3\gamma )}, &{} \text{ for } \ 0 \le s \le \eta \le 1, \\ \\ \dfrac{ \eta (1-s)^2 [(\eta ^2-3)s + 2\eta ^2] + 6\gamma (1-s)\eta (\eta ^2+s^2-2s)}{12(1+3\gamma )}, &{} \text{ for } \ 0 \le \eta \le s \le 1; \end{array}\right. \end{aligned}$$
(2.4)

and \(\phi\) is given by

$$\begin{aligned} \phi (\eta )=\dfrac{-\eta ^3+3(1+2\gamma )\eta }{2(1+3\gamma )}. \end{aligned}$$
(2.5)

Proof

The proof is motivated by that of Almuthaybiri and Tisdell (2022) for the non-slip case and we make the appropriate modifications to incorporate the slip conditions (1.2). Consider the form

$$\begin{aligned} f(\eta ) = \phi _1(\eta ) + \phi (\eta ) \end{aligned}$$

where \(\phi\) is a solution to

$$\begin{aligned} \phi {^{(iv)}} = 0; \ \ \phi (0) = 0, \ \phi ''(0) = 0, \ \phi (1)=1, \ \phi '(1)= -\gamma \phi ''(1); \end{aligned}$$
(2.6)

and \(\phi _1\) is a solution to

$$\begin{aligned} \phi _1{^{(iv)}} + {\mathcal {R}}(\phi _1'\phi _1'' - \phi _1 \phi _1''') = 0; \ \phi _1(0) = 0, \ \phi _1''(0) = 0, \ \phi _1(1)=0, \ \phi _1'(1)=-\gamma \phi ''(1). \end{aligned}$$
(2.7)

Direct differentiation of f and substitutions into (1.1), (1.2) shows that our f satisfies these equations and thus is of a suitable form.

The general solution to the homogeneous differential equation in (2.6) can be constructed via integration, forming a general polynomial of degree three, namely

$$\begin{aligned} \phi (\eta ) = A_0 \eta ^3 + B_0 \eta ^2 + C_0 \eta + D_0. \end{aligned}$$

The associated boundary conditions in (2.6) are then applied to determine the coefficients. For example, \(\phi (0)=0\) yields \(D_0=0\), and \(\phi ''(0) = 0\) yields \(B_0=0\). Furthermore, the remaining boundary conditions produce

$$\begin{aligned} \phi (1) = 1 = A_0 + C_0, \ \ \ \phi ' (1) = 3A_0+C_0 = -\gamma \phi ''(1) = 6\gamma A_0 \end{aligned}$$

which are solved for \(A_0 = -1/[2(1 + 3\gamma )]\) and \(C_0= 3(1+2\gamma )/[2(1 + 3\gamma )]\) to obtain

$$\begin{aligned} \phi (\eta ) = \dfrac{-\eta ^3+3(1 + 2\gamma )\eta }{2(1+3\gamma )}. \end{aligned}$$

Consider the nonhomogeneous differential equation for \(\phi _1\) in (2.7). We integrate both sides from \(s = 0\) to \(s=\eta\) four times to produce

$$\begin{aligned} \phi _1(\eta ) = -\frac{1}{6} \int _0^\eta (\eta -s)^3 {\mathcal {R}}\left( \phi _1'(s)\phi _1''(s) - \phi _1(s)\phi _1'''(s) \right) \ ds + A\eta ^3 + B\eta ^2 +C \eta + D \end{aligned}$$
(2.8)

where A, B, C, D are arbitrary constants of integration which we determine from the boundary conditions in (2.7). The boundary data \(\phi _1(0)=0\) leads to \(D=0\) and \(\phi _1''(0)=0\) produces \(B=0\). If we now draw on the right-hand boundary data, then we obtain

$$\begin{aligned} \phi _1(1)= & {} 0= -\frac{1}{6} \int _0^1 (1-s)^3 {\mathcal {R}}\left( \phi _1'(s)\phi _1''(s) - \phi _1(s)\phi _1'''(s) \right) \ ds + A +C; \\ \phi _1'(1) + \gamma \phi _1''(1)= & {} 0 = -\frac{1}{2} \int _0^1 (1-s)^2 {\mathcal {R}}\left( \phi _1'(s)\phi _1''(s) - \phi _1(s)\phi _1'''(s) \right) \ ds + 3 A +C \\{} & {} \ - \ \gamma \int _{0}^{1} (1-s) {\mathcal {R}}(\phi _1'(s)\phi _1''(s)-\phi _1(s)\phi _1'''(s)) \; ds + 6A\gamma . \end{aligned}$$

The above simultaneous equations are solved for A and C to obtain

$$\begin{aligned} A= & {} \frac{1}{12(1+3\gamma )} \left[ \int _0^1 \left[ 6\gamma (1-s) + 3(1-s)^2 - (1-s)^3\right] {\mathcal {R}}\left( \phi _1'(s)\phi _1''(s) - \phi _1(s)\phi _1'''(s) \right) \ ds\right] \\= & {} \frac{1}{12(1+3\gamma )}\left[ \int _0^\eta (1-s)[6\gamma + (1-s)(s+2) ]{\mathcal {R}}\left( \phi _1'(s)\phi _1''(s) - \phi _1(s)\phi _1'''(s) \right) \ ds \right. \\{} & {} \left. + \int _\eta ^1 (1-s)[6\gamma + (1-s)(s+2) ] {\mathcal {R}}\left( \phi _1'(s)\phi _1''(s) - \phi _1(s)\phi _1'''(s) \right) \ ds \right] ;\\ C= & {} \dfrac{1}{6} \int _{0}^{1} (1-s)^3 {\mathcal {R}}(\phi _1'(s)\phi _1''(s)-\phi _1(s)\phi _1'''(s)) ds - A \\= & {} \dfrac{1}{12(1+3\gamma )}\int _{0}^{1}[(1-s)^2(-3s)+6\gamma (1-s)s(s-2)]{\mathcal {R}}(\phi _1'(s)\phi _1''(s)-\phi _1(s)\phi _1'''(s)) \; ds \\= & {} \dfrac{1}{12(1+3\gamma )}\left[ \int _{0}^{\eta }3(1-s)s[2\gamma (s-2) - (1-s)]{\mathcal {R}}(\phi _1'(s)\phi _1''(s)-\phi _1(s)\phi _1'''(s)) \; ds \right. \\{} & {} \left. +\int _{\eta }^{1}3(1-s)s[2\gamma (s-2) - (1-s)]{\mathcal {R}}(\phi _1'(s)\phi _1''(s)-\phi _1(s)\phi _1'''(s)) \; ds \right] . \end{aligned}$$

Substituting these expressions into (2.8) and collecting like terms leads us to the form (2.3).

If we differentiate our f with the above values of A and C, then we obtain the differential equation (1.1). If we evaluate our integral representation for f and its derivatives at the boundary points, then we see that the boundary conditions (1.2) also hold. \(\square\)

Remark 2.1

Our derived formulae for the Green’s function G in (2.4) and \(\phi\) in Theorem 2.1 extends the result of Almuthaybiri and Tisdell (2022) from \(\gamma = 0\) to \(\gamma \ge 0\).

3 Bounds on the Green’s Functions

In this section we develop new bounds on the integral involving the absolute value of the Green’s function in (2.4) and its derivatives. These bounds will be applied in Sect. 4 to help generate our theorems on existence, uniqueness and approximation of solutions to (1.1), (1.2).

Before we calculate new bounds, we notice an important connection between our Green’s function (2.4) for the slip case, and the Green’s function for the non-slip problem derived by Almuthaybiri and Tisdell (2022). For all \((\eta ,s) \in [0,1] \times [0,1]\) and \(\gamma \ge 0\), we have

$$\begin{aligned} G(\eta ,s) = \dfrac{1}{1+3\gamma } \left[ H(\eta ,s) + \dfrac{\gamma }{2} F(\eta ,s) \right] , \end{aligned}$$
(3.1)

with

$$\begin{aligned} H(\eta ,s) := \dfrac{1}{12} {\left\{ \begin{array}{ll} s(1-\eta )^2[(s^2-3)\eta +2s^2], \ \text {for} \; 0 \le s \le \eta \le 1,\\ \eta (1-s)^2[(\eta ^2-3)s+2\eta ^2], \ \text {for} \; 0 \le \eta \le s \le 1; \end{array}\right. } \end{aligned}$$
(3.2)

and

$$\begin{aligned} F(\eta ,s) := {\left\{ \begin{array}{ll} (1-\eta )s(\eta ^2+s^2-2\eta ), \ \text {for} \; 0 \le s \le \eta \le 1,\\ (1-s)\eta (\eta ^2+s^2-2s), \ \text {for} \; 0 \le \eta \le s \le 1.\\ \end{array}\right. } \end{aligned}$$
(3.3)

Here, \(H(\eta ,s)\) is the Green’s function for the non-slip problem when \(\gamma = 0\) that was derived by Almuthaybiri and Tisdell (2022), and \(F(\eta ,s)\) is an additional component that arises from the slip condition.

If we apply the triangle inequality to (3.1) then for all \(\gamma \ge 0\) we can deduce the inequality

$$\begin{aligned} | G (\eta ,s)|\le & {} \dfrac{1}{1+3\gamma } \left[ |H(\eta ,s)| + \dfrac{\gamma }{2} |F(\eta ,s)| \right] \\\le & {} |H(\eta ,s)| + \frac{1}{6} |F(\eta ,s)|. \end{aligned}$$

Similarly, for the partial derivatives, we have

$$\begin{aligned} \left| \dfrac{\partial ^i}{\partial \eta ^i}G(\eta ,s) \right|= & {} \dfrac{1}{1+3\gamma } \left| \dfrac{\partial ^i}{\partial \eta ^i}H(\eta ,s) +\dfrac{\gamma }{2}\dfrac{\partial ^i}{\partial \eta ^i}F(\eta ,s) \right| \nonumber \\\le & {} \dfrac{1}{1+3\gamma }\left( \left| \dfrac{\partial ^i}{\partial \eta ^i}H(\eta ,s) \right| +\dfrac{\gamma }{2}\left| \dfrac{\partial ^i}{\partial \eta ^i}F(\eta ,s) \right| \right) \nonumber \\\le & {} \left| \dfrac{\partial ^i}{\partial \eta ^i}H(\eta ,s) \right| +\dfrac{1}{6}\left| \dfrac{\partial ^i}{\partial \eta ^i}F(\eta ,s) \right| . \end{aligned}$$
(3.4)

Integrating both sides of (3.4) from 0 to 1 gives, for all \(\eta \in [0,1]\) and \(\gamma \ge 0\),

$$\begin{aligned} \int _0^1 \left| \dfrac{\partial ^i}{\partial \eta ^i}G(\eta ,s) \right| \ {\rm d}s= & {} \dfrac{1}{1+3\gamma } \int _0^1 \left| \dfrac{\partial ^i}{\partial \eta ^i}H(\eta ,s) +\dfrac{\gamma }{2}\dfrac{\partial ^i}{\partial \eta ^i}F(\eta ,s) \right| \ {\rm d}s \nonumber \\\le & {} \dfrac{1}{1+3\gamma }\left( \int _0^1 \left| \dfrac{\partial ^i}{\partial \eta ^i}H(\eta ,s) \right| \ {\rm d}s +\dfrac{\gamma }{2}\int _0^1 \left| \dfrac{\partial ^i}{\partial \eta ^i}F(\eta ,s) \right| \ {\rm d}s \right) \nonumber \\\le & {} \int _0^1 \left| \dfrac{\partial ^i}{\partial \eta ^i}H(\eta ,s) \right| \ {\rm d}s +\dfrac{1}{6}\int _0^1 \left| \dfrac{\partial ^i}{\partial \eta ^i}F(\eta ,s) \right| \ {\rm d}s. \end{aligned}$$
(3.5)

Using the above connections to the non-slip problem, our strategy is to analyze the integrals involving |F| and |H| separately, and to synthesize them with Almuthaybiri and Tisdell (2022) results to produce new bounds. This strategy streamlines some of the calculations and essentially reduces the problem of constructing bounds to only working with F, which has nice symmetric properties and is relatively easy to differentiate, integrate and analyze. In doing so, we hope to lead the reader to the heart of the problem without experiencing significant departures. Our method of analyzing integrals involving |F| and |H| separately means that our bounds may not be the sharpest possible.

Our new bounds are formulated in terms of the slip coefficient \(\gamma\), and then independently of \(\gamma\). Including \(\gamma\) in our estimates illustrates the connection between the slip and non-slip cases, while excluding \(\gamma\) enables the bounds to be of less complex nature, and perhaps more user-friendly.

Theorem 3.1

For all \(\gamma \ge 0\), the Green’s function G in (2.4) satisfies \(G\le 0\) on \([0,1]\times [0,1]\) and

$$\begin{aligned} \int _0^1 |G(\eta ,s) | \ {\rm d}s< & {} \frac{1}{1 + 3\gamma }\left( \frac{3}{500} + \frac{5}{64} \left( \frac{\gamma }{2} \right) \right) \nonumber \\\le & {} \frac{3}{500} + \frac{5}{384} = \frac{913}{48000} =:\beta _0 , \ \ \ \text {for all} \ \eta \in [0,1]. \end{aligned}$$
(3.6)

Proof

From Almuthaybiri and Tisdell (2022), we have our H in (3.2) satisfying \(H\le 0\) on \([0,1]\times [0,1]\) and

$$\begin{aligned}&\int _0^1 |H(\eta ,s) | \ {\rm d}s = -\int _0^1H(\eta ,s) \; {\rm d}s\le \frac{39 + 55\sqrt{33}}{65536} < \frac{3}{500}. \end{aligned}$$

Now, we claim that for F in (3.3), we have \(F\le 0\) on \([0,1]\times [0,1]\). If we consider the case \(0 \le s \le \eta \le 1\) then we have \(1-\eta \ge 0\) and \(s\ge 0\), and

$$\begin{aligned} \eta ^2+s^2-2\eta&\le \eta ^2+\eta ^2-2\eta \\&=2\eta (\eta -1)\\&\le 0. \end{aligned}$$

Hence,

$$\begin{aligned} (1-\eta )s(\eta ^2+s^2-2\eta ) \le 0, \ \text {for all} \ 0 \le s \le \eta \le 1. \end{aligned}$$

Employing a similar technique, but interchanging s and \(\eta\), we have

$$\begin{aligned} (1-s)\eta (\eta ^2+s^2-2s)\le 0, \ \text {for all} \ 0 \le \eta \le s \le 1. \end{aligned}$$

Combining the above two cases, we conclude that \(F\le 0\) on \([0,1]\times [0,1]\). Thus, the form (3.1) gives us \(G \le 0\) on \([0,1]\times [0,1]\) as claimed.

Consequently, for all \(\eta \in [0,1]\) we have

$$\begin{aligned} \int _0^1 |G(\eta ,s)| \; {\rm d}s&= - \int _0^1G(\eta ,s) \; {\rm d}s \nonumber \\&=- \dfrac{1}{1+3\gamma }\left[ \int _0^1H(\eta ,s) \; {\rm d}s+\dfrac{\gamma }{2} \int _0^1F(\eta ,s) \; {\rm d}s \right] . \end{aligned}$$
(3.7)

And for all \(\eta \in [0,1]\),

$$\begin{aligned} \int _0^1F(\eta ,s) \; {\rm d}s&= \int _0^\eta (1-\eta )s(\eta ^2+s^2-2\eta ) \; {\rm d}s + \int _\eta ^1(1-s)\eta (\eta ^2+s^2-2s) \; {\rm d}s \\&= -\dfrac{\eta ^3}{4}(3\eta ^2-7\eta +4)+\dfrac{\eta }{4}(3\eta +1)(\eta -1)^3\\&=- \dfrac{1}{4}(\eta ^4-2\eta ^3+\eta ). \end{aligned}$$

This quadric function achieves its minimum of \(-5/64\) on [0, 1] at \(\eta = 1/2\), and so for all \(\eta \in [0,1]\) we have

$$\begin{aligned} -\int _0^1F(\eta ,s) \; {\rm d}s\le \dfrac{5}{64}. \end{aligned}$$

Thus, (3.7) leads to

$$\begin{aligned} \int _0^1 |G(\eta ,s)| \; {\rm d}s&=\dfrac{1}{1+3\gamma }\left[ \left( -\int _0^1H(\eta ,s) \; {\rm d}s\right) +\dfrac{\gamma }{2}\left( -\int _0^1F(\eta ,s) \; {\rm d}s\right) \right] \\&< \dfrac{1}{1+3\gamma } \left[ \dfrac{3}{500}+\frac{\gamma }{2} \left( \dfrac{5}{64}\right) \right] \\&< \frac{3}{500} + \frac{5}{384} = \frac{913}{48000}. \end{aligned}$$

\(\square\)

Let us continue the momentum of the previous theorem, but now focusing on \(|\partial G/\partial \eta |\).

Theorem 3.2

For all \(\gamma \ge 0\), the Green’s function G in (2.4) satisfies

$$\begin{aligned} \int _0^1 \left| \frac{\partial }{\partial \eta }G(\eta ,s) \right| \ {\rm d}s< & {} \dfrac{1}{1+3\gamma }\left( \dfrac{1}{25} + \dfrac{415}{324} \left( \frac{\gamma }{2} \right) \right) \nonumber \\\le & {} \dfrac{1}{25} + \dfrac{415}{1944} = \frac{12319}{48600} =:\beta _1 , \ \ \ \text {for all} \ \eta \in [0,1]. \end{aligned}$$
(3.8)

Proof

Let us work with (3.5) for the case \(i=1\). By Almuthaybiri and Tisdell (2022), we have

$$\begin{aligned} \int _0^1 \left| \frac{\partial }{\partial \eta }H(\eta ,s) \right| \ {\rm d}s < \frac{1}{25}, \ \text {for all} \ \eta \in [0,1]. \end{aligned}$$
(3.9)

Thus, our attention turns to establishing an estimate on \(\int _0^1 |\partial F/\partial \eta | \ {\rm d}s\). Differentiating F in (3.3) with respect to \(\eta\) gives:

$$\begin{aligned} \dfrac{\partial }{\partial \eta }F(\eta ,s) = {\left\{ \begin{array}{ll} -s(3\eta ^2+s^2-6\eta +2), \quad &{}\text {for} \; 0 \le s \le \eta \le 1,\\ (1-s)(3\eta ^2+s^2-2s), \quad &{}\text {for} \; 0 \le \eta \le s \le 1. \end{array}\right. } \end{aligned}$$

Thus, for all \(\eta \in [0,1]\) we have

$$\begin{aligned} \int _0^1 \left| \dfrac{\partial }{\partial \eta }F(\eta ,s) \right| \; {\rm d}s&=\int _0^\eta \left| -s(3\eta ^2+s^2-6\eta +2) \right| \; {\rm d}s + \int _\eta ^1 \left| (1-s)(3\eta ^2+s^2-2s) \right| \; {\rm d}s \\&\le \int _0^\eta s(3\eta ^2+s^2+6\eta +2) \; {\rm d}s + \int _\eta ^1(1-s)(3\eta ^2+s^2+2s) \; {\rm d}s\\&= \left( 6\eta ^3-\dfrac{\eta ^4}{4}+2\eta \right) + \left( \dfrac{\eta ^2}{2} - \dfrac{8\eta ^3}{3} +\dfrac{7\eta ^4}{4} +\dfrac{5}{12}\right) \\&= \dfrac{3\eta ^4}{2} - \dfrac{10\eta ^3}{3} + \dfrac{\eta ^2}{2} + 2\eta +\dfrac{5}{12}. \end{aligned}$$

This quadric function achieves its maximum value on [0, 1] of 415/324 at \(\eta = 2/3\) and so

$$\begin{aligned} \int _0^1\left| \dfrac{\partial }{\partial \eta }F(\eta ,s) \right| \; {\rm d}s \le \dfrac{415}{324}, \ \text {for all} \ \eta \in [0,1]. \end{aligned}$$
(3.10)

Substituting the estimates (3.9) and (3.10) into (3.5) with \(i=1\) establishes our estimate (3.8). \(\square\)

We now develop bounds involving higher order derivatives of G as follows.

Theorem 3.3

For all \(\gamma \ge 0\), the Green’s function G in (2.4) satisfies

$$\begin{aligned} \int _0^1 \left| \frac{\partial ^2}{\partial \eta ^2} G(\eta ,s) \right| \ {\rm d}s \le \dfrac{1}{1+3\gamma }\left( \dfrac{9}{8} + \dfrac{3}{4} \left( \frac{\gamma }{2} \right) \right) \le \frac{5}{4} =:\beta _2, \ \ \ \text {for all} \ \eta \in [0,1]. \end{aligned}$$
(3.11)

Proof

From Almuthaybiri and Tisdell (2022), we have

$$\begin{aligned} \int _0^1 \left| \frac{\partial ^2}{\partial \eta ^2} H(\eta ,s) \right| \ {\rm d}s \le \frac{9}{8}. \end{aligned}$$

Thus, our challenge is to construct a bound on the remaining integral in (3.5) when \(i=2\). Differentiating F in (3.3) with respect to \(\eta\) twice gives:

$$\begin{aligned} \dfrac{\partial ^2}{\partial \eta ^2}F(\eta ,s) = {\left\{ \begin{array}{ll} 6s(1-\eta ), \quad &{} \text {for} \ 0 \le s \le \eta \le 1,\\ 6\eta (1-s), \quad &{}\text {for} \ 0 \le \eta \le s \le 1. \end{array}\right. } \end{aligned}$$

Clearly we have \(\dfrac{\partial ^2}{\partial \eta ^2}F(\eta ,s) \ge 0\) for all \((\eta ,s) \in [0,1] \times [0,1]\) and so

$$\begin{aligned} \int _0^1 \left| \dfrac{\partial ^2}{\partial \eta ^2}F(\eta ,s) \right| \ {\rm d}s&= \int _0^1 \dfrac{\partial ^2}{\partial \eta ^2}F(\eta ,s) \ {\rm d}s \\&= \int _0^\eta 6s(1-\eta ) \ {\rm d}s + \int _\eta ^1 6\eta (1-s) \ {\rm d}s \\&= 3\eta - 3\eta ^2 . \end{aligned}$$

This above quadratic function achieves its maximum of 3/4 on [0, 1] at \(\eta = 1/2\) and thus for all \(\eta \in [0,1]\) we have

$$\begin{aligned} \int _0^1\left| \dfrac{\partial ^2}{\partial \eta ^2}F(\eta ,s) \right| {\rm d}s \le \dfrac{3}{4} = \left[ \int _0^1\left| \dfrac{\partial ^2}{\partial \eta ^2}F(\eta ,s) \right| \ {\rm d}s \right] _{\eta = 1/2}. \end{aligned}$$

If we now leverage the above two bounds then (3.5) when \(i=2\) yields (3.11). \(\square\)

Our final bound result is as follows.

Theorem 3.4

For all \(\gamma \ge 0\), the Green’s function G in (2.4) satisfies

$$\begin{aligned} \int _0^1 \left| \frac{\partial ^3}{\partial \eta ^3} G(\eta ,s) \right| \ ds \le \dfrac{1}{1+3\gamma }\left( \dfrac{5}{8}+3\dfrac{\gamma }{2}\right) \le \frac{7}{8}=:\beta _3, \ \ \ \text {for all} \ \eta \in [0,1]. \end{aligned}$$
(3.12)

Proof

From Almuthaybiri and Tisdell (2022), we know that

$$\begin{aligned} \int _0^1 \left| \frac{\partial ^3}{\partial \eta ^3} H(\eta ,s) \right| \ {\rm d}s \le \frac{5}{8}. \end{aligned}$$

Differentiating F with respect to \(\eta\) three times gives:

$$\begin{aligned} \dfrac{\partial ^3}{\partial \eta ^3}F(\eta ,s) = {\left\{ \begin{array}{ll} -6s, \quad &{}\text {for} \ 0 \le s \le \eta \le 1,\\ 6(1-s), \quad &{}\text {for} \ 0 \le \eta \le s \le 1. \end{array}\right. } \end{aligned}$$

It clear that \(\dfrac{\partial ^3}{\partial \eta ^3}F(\eta ,s) \le 0\) for \(0 \le s \le \eta \le 1\) and \(\dfrac{\partial ^3}{\partial \eta ^3}F(\eta ,s) \ge 0\) for \(0 \le \eta \le s \le 1\), and

$$\begin{aligned} \int _0^1 \left| \dfrac{\partial ^3}{\partial \eta ^3}F(\eta ,s) \right| \ ds&= \int _0^\eta |-6s| \ ds + \int _\eta ^1 |6(1-s)| \ ds \\&= \int _0^\eta 6s \ ds + \int _\eta ^1 6(1-s) \ ds \\&= 6\eta ^2 - 6 \eta + 3. \end{aligned}$$

This quadratic function achieves its maximum at the boundaries \(\eta = 0\) and \(\eta = 1\), so that for all \(\eta \in [0,1]\) we have

$$\begin{aligned} \int _0^1 \left| \dfrac{\partial ^3}{\partial \eta ^3}F(\eta ,s) \right| \ {\rm d}s \le 3. \end{aligned}$$

Substituting our two bounds into (3.5) when \(i=3\) yields (3.12). \(\square\)

4 Existence, Uniqueness and Approximation

This section contains our main theorems regarding the existence, uniqueness, location and approximation of solutions.

4.1 Complete Metric Space, Bound and Lipschitz Constants

We will work in the context of a complete metric space. Let \(C^3([0,1])\) denote the set of real-valued functions that are defined on [0, 1] and have a continuous third order derivative. Consider the following metric on \(C^3([0,1])\):

$$\begin{aligned} {\rm d}(f,g) := \max _{i \in \{0,1,2,3\}}\left\{ W_i \max _{\eta \in [0,1]} |f^{(i)}(\eta )-g^{(i)}(\eta )|\right\} , \ \text {for all} \ f,g \in C^3([0,1]); \end{aligned}$$

where

$$\begin{aligned} W_0=1, \ W_1 = \frac{\beta _0}{\beta _1}= \frac{73953}{985520}, \ W_2 = \frac{\beta _0}{\beta _2} = \frac{913}{60000}, \ W_3 = \frac{\beta _0}{\beta _3} = \frac{913}{42000} \end{aligned}$$

and each \(\beta _i\) is defined in (3.6), (3.8), (3.11) and (3.12). The metric space \((C^3([0,1]),d)\) is known to be complete (see (Almuthaybiri and Tisdell 2022)).

Let \(R>0\) be a constant and let \(\phi\) be defined in (2.5). In our main results, it will be shown that the following set provides a suitable location for the graph of the unique solution to (1.1), (1.2)

$$\begin{aligned} B:= & {} \left\{ (\eta ,u,v,w, z) \in {{\mathbb {R}}}^5: \eta \in [0,1], \ |u - \phi (\eta )| \le R, \right. \\{} & {} \ \ \ \left. |v - \phi '(\eta )| \le \frac{\beta _1}{\beta _0}R, \ |w - \phi ''(\eta )| \le \frac{\beta _2}{\beta _0}R, \ |z - \phi '''(\eta )| \le \frac{\beta _3}{\beta _0}R \right\} . \end{aligned}$$

We note that for all \(\gamma \ge 0\), our \(\phi\) in (2.5) satisfies

$$\begin{aligned} |\phi | \le 1, \ |\phi '| \le \frac{3(1+2\gamma )}{2(1 + 3\gamma )}\le \frac{3}{2}, \ |\phi ''| \le \frac{3}{1+3\gamma }\le 3, \ |\phi '''|\le \frac{3}{1+3\gamma } \le 3. \end{aligned}$$
(4.1)

To enable the invariance of an appropriate operator between sets, the following result will be helpful by establishing a bound on (1.1) on B.

Theorem 4.1

Let

$$\begin{aligned} h(u,v,w,z):= {\mathcal {R}}(vw - uz). \end{aligned}$$

We claim that for all \(\gamma \ge 0\) our |h| is bounded on B by

$$\begin{aligned} M:=|{\mathcal {R}}|\left[ \frac{20745742000}{22506363} R^2 + \frac{4623473}{24651}R + \frac{15}{2} \right] . \end{aligned}$$

Proof

The proof is similar to that of Almuthaybiri and Tisdell (2022) with appropriate modifications made to accommodate the more general bounds from (4.1). For \((\eta ,u,v,w,z) \in B\) consider

$$\begin{aligned}{} & {} |h(u,v,w,z)| = |{\mathcal {R}}(vw - uz)| \\\le & {} |{\mathcal {R}}|\left( |v| \ |w| + |u| \ |z| \right) \\= & {} |{\mathcal {R}}| \left[ |(v - \phi '(\eta )+\phi '(\eta )|)(|w- \phi ''(\eta ) +\phi ''(\eta )|) \right. \\{} & {} + \left. (|u - \phi (\eta ) + \phi (\eta )|) (|z - \phi '''(\eta ) + \phi '''(\eta )|) \right] \\ \\\le & {} |{\mathcal {R}}| \left[ |(v - \phi '(\eta )| + |\phi '(\eta )|)(|w- \phi ''(\eta )| + |\phi ''(\eta )|) \right. \\{} & {} + \left. (|u - \phi (\eta )| + |\phi (\eta )|) (|z - \phi '''(\eta )| + |\phi '''(\eta )|)\right] \\ \\\le & {} |{\mathcal {R}}| \left[ \left( \frac{\beta _1}{\beta _0}R + \frac{3}{2} \right) \left( \frac{\beta _2}{\beta _0}R + 3 \right) + \left( R + 1 \right) \left( \frac{\beta _3}{\beta _0}R + 3 \right) \right] \\ \\= & {} |{\mathcal {R}}|\left[ \frac{20745742000}{22506363} R^2 + \frac{4623473}{24651}R + \frac{15}{2} \right] . \end{aligned}$$

\(\square\)

The following result constructs new Lipschitz constants for (1.1) on B for the non-slip case.

Theorem 4.2

For given \(R>0\), \({{{\mathcal {R}}}}\) and \(\gamma \ge 0\), the function

$$\begin{aligned} h(u,v,w,z):= {\mathcal {R}}(vw - uz) \end{aligned}$$

satisfies

$$\begin{aligned} |h(u_0,u_1,u_2,u_3)- & {} h(v_0,v_1,v_2,v_3)| \le \sum _{i=0}^3 L_i |u_i - v_i|, \nonumber \\{} & {} \text {for all} \ (\eta ,u_0,u_1,u_2,u_3), (\eta ,v_0,v_1,v_2,v_3) \in B \end{aligned}$$

for some constants \(L_i\).

Proof

Here we take a slightly different approach than Almuthaybiri and Tisdell (2022) who produced different Lipschitz constants for the case \(\gamma = 0\). We opt for algebraic techniques, rather than constructing bounds on the partial derivatives of h on B. One important reason for including some of the details of this proof is to illustrate the precise form of the Lipschitz constants \(L_i\).

For all \((\eta ,u_0,u_1,u_2,u_3), (\eta ,v_0,v_1,v_2,v_3) \in B\) consider

$$\begin{aligned}{} & {} |h(u_0,u_1,u_2,u_3) - h(v_0,v_1,v_2,v_3)| = | {\mathcal {R}}(u_1 u_2 - u_0 u_3) - {\mathcal {R}}(v_1 v_2 - v_0 v_3)| \nonumber \\= & {} |{{{\mathcal {R}}}}| \left| v_3(v_0-u_0) + u_2(u_1-v_1) + v_1(u_2-v_2) + u_0 (v_3-u_3) \right| \nonumber \\\le & {} |{{{\mathcal {R}}}}| \left[ (|v_3 - \phi '''| + |\phi '''|) \ |v_0-u_0| + u_2 (u_1-v_1) + v_1(u_2-v_2) + u_0 (v_3-u_3) \right] . \end{aligned}$$
(4.2)

Now, on B,

$$\begin{aligned} |{\mathcal {R}}| [ |v_3 - \phi '''(\eta )| +|\phi '''(\eta )|] \le |{\mathcal {R}}| \left[ \frac{42000}{913}R + 3 \right] =: L_0. \end{aligned}$$

Also, we can continue this algebraic process for each of the remaining terms in (4.2) to obtain

$$\begin{aligned} |{\mathcal {R}}| [ |u_2 - \phi ''(\eta )| +|\phi ''(\eta )|]\le & {} |{\mathcal {R}}| \left[ \frac{60000}{913}R + 3\right] =: L_1 \nonumber \\ |{\mathcal {R}}| [ |v_1 - \phi '(\eta )| +|\phi '(\eta )|]\le & {} |{\mathcal {R}}| \left[ \frac{985520}{73953}R + \frac{3}{2}\right] =: L_2 \nonumber \\ |{\mathcal {R}}| [ |u_0 - \phi (\eta )| +|\phi (\eta )|]\le & {} |{\mathcal {R}}| \left[ R +1\right] =: L_3. \end{aligned}$$

\(\square\)

4.2 Contraction Mapping Approach

We will employ the following well known fixed point theorem found in Zeidler (1986)[Theorem 1.A] to generate a unique fixed point of an operator connected with (1.1), (1.2).

Theorem 4.3

Let X be a nonempty set and let d be a metric on X such that (X, d) forms a complete metric space. If the mapping \(T:X \rightarrow X\) satisfies

$$\begin{aligned} d(Tf,Tg) \le c d(f,g), \ \text {for some} \ 0< c <1 \ \text {and all} \ f,g\in X; \end{aligned}$$
(4.3)

then there is a unique \(z\in X\) such that \(Tz = z\). In addition, for any \(z_0\in X\) we have \(d(z_n,z) \rightarrow 0\) where \(z_n\) is a recursively defined sequence defined via \(z_{n+1} :=Tz_n\).

Armed with the integral equation of Sect. 2, the bounds of Sect. 3, and the Lipschitz constants and bound of Sect. 4, we are now ready to formulate our main theorems.

Theorem 4.4

If there is a \(R>0\) and \({\mathcal {R}}\) such that

$$\begin{aligned} |{\mathcal {R}}|\left[ \frac{20745742000}{22506363} R^2 + \frac{4623473}{24651}R + \frac{15}{2} \right] \frac{913}{48000}\le & {} R; \end{aligned}$$
(4.4)
$$\begin{aligned} |{\mathcal {R}}| \left[ \frac{17044598093}{486019116}R + \frac{4623473}{1296000} \right]< & {} 1; \end{aligned}$$
(4.5)

then for all \(\gamma \ge 0\) the slip BVP (1.1), (1.2) has a unique solution f such that

$$\begin{aligned} (\eta ,f(\eta ),f'(\eta ),f''(\eta ),f'''(\eta )) \in B, \ \ \ \text {for all} \ \eta \in [0,1]. \end{aligned}$$

Proof

The structure of the proof follows similar lines as that of Almuthaybiri and Tisdell (2022) and so is only sketched, highlighting the distinctions.

Choose a suitable value of \(R>0\) to form B, with R and \({\mathcal {R}}\) satisfying (4.4) and (4.5).

Consider the set

$$\begin{aligned} {{{\mathcal {B}}}}_R:= \{ f \in C^3([0,1]): d(f,\phi ) \le R\} \subset C^3([0,1]). \end{aligned}$$

with \(({{{\mathcal {B}}}}_R,d)\) forming a complete metric space.

Consider the operator \(T:{{{\mathcal {B}}}}_R \rightarrow C^3([0,1])\) that we define by

$$\begin{aligned} (Tf)(\eta ) := \int _0^1 G(\eta ,s) {\mathcal {R}}(f'(s)f''(s) - f(s)f'''(s)) \ ds + \phi (\eta ), \ \ \ \eta \in [0,1]. \end{aligned}$$

Let us show that T has a unique fixed point in \({{{\mathcal {B}}}}_R\), by illustrating that the assumptions of Theorem 4.3 hold with \(X={{{\mathcal {B}}}}_R\).

Firstly, we claim \(T:{{{\mathcal {B}}}}_R \rightarrow {{{\mathcal {B}}}}_R\). For \(f\in {{{\mathcal {B}}}}_R\) and \(\eta \in [0,1]\), we have

$$\begin{aligned} |(Tf)(\eta ) - \phi (\eta )|\le & {} \int _0^1 |G(\eta ,s)| \ |{\mathcal {R}}(f'(s)f''(s) - f(s)f'''(s))| \ {\rm d}s \nonumber \\\le & {} M \int _0^1 |G(\eta ,s)| \ {\rm d}{\rm d}s \\\le & {} M \beta _0 \\= & {} |{\mathcal {R}}|\left[ \frac{20745742000}{22506363} R^2 + \frac{4623473}{24651}R + \frac{15}{2} \right] \frac{913}{48000}. \end{aligned}$$

Furthermore, we have

$$\begin{aligned} |(Tf)'(\eta ) - \phi '(\eta )|\le & {} \int _0^1 \left| \frac{\partial }{\partial \eta } G(\eta ,s) \right| \ |{\mathcal {R}}(f'(s)f''(s) - f(s)f'''(s)))| \ ds \nonumber \\\le & {} M \int _0^1 \left| \frac{\partial }{\partial \eta } G(\eta ,s) \right| \ {\rm d}s \\\le & {} M \beta _1 \\= & {} |{\mathcal {R}}|\left[ \frac{20745742000}{22506363} R^2 + \frac{4623473}{24651}R + \frac{15}{2} \right] \frac{12319}{48600} \end{aligned}$$

and so

$$\begin{aligned} \frac{\beta _0}{\beta _1} |(Tf)'(\eta ) - \phi '(\eta )|\le & {} M \beta _0 \\= & {} |{\mathcal {R}}|\left[ \frac{20745742000}{22506363} R^2 + \frac{4623473}{24651}R + \frac{15}{2} \right] \frac{913}{48000}. \end{aligned}$$

A similar line of arguments also give

$$\begin{aligned} |(Tf)''(\eta ) - \phi ''(\eta )|\le & {} M\beta _2 \\= & {} |{\mathcal {R}}|\left[ \frac{20745742000}{22506363} R^2 + \frac{4623473}{24651}R + \frac{15}{2} \right] \frac{5}{4};\\ |(Tf)'''(\eta ) - \phi '''(\eta )|\le & {} M\beta _3 \\= & {} |{\mathcal {R}}|\left[ \frac{20745742000}{22506363} R^2 + \frac{4623473}{24651}R + \frac{15}{2} \right] \frac{7}{8}; \end{aligned}$$

so that

$$\begin{aligned} \frac{\beta _0}{\beta _2} |(Tf)''(\eta ) - \phi ''(\eta )|\le & {} M \beta _0 = |{\mathcal {R}}|\left[ \frac{20745742000}{22506363} R^2 + \frac{4623473}{24651}R + \frac{15}{2} \right] \frac{913}{48000}; \\ \frac{\beta _0}{\beta _3} |(Tf)'''(\eta ) - \phi '''(\eta )|\le & {} M \beta _0 =|{\mathcal {R}}|\left[ \frac{20745742000}{22506363} R^2 + \frac{4623473}{24651}R + \frac{15}{2} \right] \frac{913}{48000}. \end{aligned}$$

Combining the above inequalities, for all \(f\in {{{\mathcal {B}}}}_R\) we have

$$\begin{aligned} d(Tf,\phi )\le & {} \max \{ M \beta _0, M \beta _0, M \beta _0, M\beta _0\}\\= & {} M\beta _0 \\= & {} |{\mathcal {R}}|\left[ \frac{20745742000}{22506363} R^2 + \frac{4623473}{24651}R + \frac{15}{2} \right] \frac{913}{48000}\\\le & {} R \end{aligned}$$

where we have invoked (4.4). Thus, for all \(f\in {{{\mathcal {B}}}}_R\) we see that \(Tf \in {{{\mathcal {B}}}}_R\) and hence \(T:{{{\mathcal {B}}}}_R \rightarrow {{{\mathcal {B}}}}_R\).

Secondly, we claim that T is contractive on \({\mathcal {B}}_R\) in the sense of (4.3). For \(f,g \in {\mathcal {B}}_R\) and \(\eta \in [0,1]\), consider

$$\begin{aligned}{} & {} |(Tf)(\eta ) - (Tg)(\eta )| \\\le & {} \int _0^1 |G(\eta ,s)| \ |h(f(s),f'(s),f''(s),f'''(s)) - h(g(s),g'(s),g''(s),g'''(s)) | \ {\rm d}s \\\le & {} \int _0^1 |G(\eta ,s)| \ \left( \sum _{i=0}^3 L_i\ |f^{(i)}(s) - g^{(i)}(s)| \right) \ {\rm d}s \\\le & {} \beta _0 \left( L_0 + \sum _{i=1}^3 L_i \frac{\beta _i}{\beta _0} \right) {\rm d}(f,g) \\= & {} \left( \sum _{i=0}^3 L_i \beta _i \right) \ {\rm d}(f,g)\\= & {} |{\mathcal {R}}| \left[ \frac{17044598093}{486019116}R + \frac{4623473}{1296000} \right] {\rm d}(f,g) \end{aligned}$$

where we invoked the bound from Theorem 4.2.

In a similar fashion, we can also show

$$\begin{aligned} |(Tf)'(\eta ) - (Tg)'(\eta )|\le & {} \beta _1 \left( L_0 + \sum _{i=1}^3 L_i \frac{\beta _i}{\beta _0} \right) {\rm d}(f,g); \\ |(Tf)''(\eta ) - (Tg)''(\eta )|\le & {} \beta _2 \left( L_0 + \sum _{i=1}^3 L_i \frac{\beta _i}{\beta _0} \right) {\rm d}(f,g);\\ |(Tf)'''(\eta ) - (Tg)'''(\eta )|\le & {} \beta _3\left( L_0 + \sum _{i=1}^3 L_i \frac{\beta _i}{\beta _0} \right) d(f,g). \end{aligned}$$

Thus, for all \(f,g \in {\mathcal {B}}_R\) we have

$$\begin{aligned} d(Tf,Tg)= & {} \max _{i \in \{0,1,2,3\}} \left\{ W_i \max _{\eta \in [0,1]} |(Tf)^{(i)}(\eta ) - (Tg)^{(i)}(\eta )) \right\} \\ \\\le & {} \left( \sum _{i=0}^3 L_i \beta _i \right) d(f,g) \\ \\= & {} |{\mathcal {R}}| \left[ \frac{17044598093}{486019116}R + \frac{4623473}{1296000} \right] d(f,g). \end{aligned}$$

Due to our assumption (4.5) we see that T is a contractive map on \({\mathcal {B}}_R\).

Thus, the conditions of Theorem 4.3 are satisfied for our T and \(X={\mathcal {B}}_R\). We conclude that T has a unique fixed point in \({\mathcal {B}}_R\subset C^3([0,1])\). This is equivalent to proving that our slip BVP (1.1), (1.2) has a unique solution for all \(\gamma \ge 0\). \(\square\)

Let us delve deeper into our assumptions (4.4) and (4.5) by establishing some more concrete values for \({{{\mathcal {R}}}}\), R and \(\gamma\) that ensure (4.4) and (4.5) hold.

Theorem 4.5

For all \(\gamma \ge 0\) and

$$\begin{aligned} |{{{\mathcal {R}}}}| < \frac{4033081884314736000}{5113379427900 \sqrt{6223891796782} + 14387997838671531943} \approx 0.1485770398, \end{aligned}$$
(4.6)

the slip BVP (1.1), (1.2) admits a unique solution whose graph lies completely in B with

$$\begin{aligned} R = 3 \frac{\sqrt{6223891796782}}{82981960} \approx 0.09019211747. \end{aligned}$$

Proof

We see that (4.4) and (4.5) can be rewritten as

$$\begin{aligned} |{\mathcal {R}}|\le & {} R \left[ \left[ \frac{20745742000}{22506363} R^2 + \frac{4623473}{24651}R + \frac{15}{2} \right] \frac{913}{48000}\right] ^{-1} \end{aligned}$$
(4.7)
$$\begin{aligned} |{\mathcal {R}}|< & {} \left[ \frac{17044598093}{486019116}R + \frac{4623473}{1296000}\right] ^{-1}. \end{aligned}$$
(4.8)

The crossing of the graphs of the right hand sides in (4.7), (4.8) occurs when

$$\begin{aligned} R = 3 \frac{\sqrt{6223891796782}}{82981960} \approx 0.09019211747. \end{aligned}$$

The “value” of \(|{{{\mathcal {R}}}}|\) at this point is

$$\begin{aligned} \frac{4033081884314736000}{5113379427900 \sqrt{6223891796782} + 14387997838671531943} \approx 0.1485770398 \end{aligned}$$
(4.9)

and so, for values of \(|{\mathcal {R}}|\) strictly less than (4.9), both of our inequalities (4.4) and (4.5) will hold. Thus, for the above R and range of \({\mathcal {R}}\) the conclusion of Theorem 4.4 holds. \(\square\)

Remark 4.1

If we compare the bounds on \({{{\mathcal {R}}}}\) in (4.6) that includes the slip case \(\gamma >0\), with the bounds on \({{{\mathcal {R}}}}\) for the non-slip case of Almuthaybiri and Tisdell (2022) in (1.3), then we observe that the range of \(\mathcal{R}\) values in the non-slip BVP is about half of that in the slip BVP. However, in the slip case we have results for all \(\gamma > 0\) that also include the special case \(\gamma = 0\). So, to modify an old saying about swings and roundabouts, when comparing our results of the slip situation with that of the non-slip situation, it appears to be a case of: what you lose on the Reynolds number, you gain on the slip constant.

Theorem 4.5 also ensures insights into the approximation of solutions to the slip BVP (1.1), (1.2).

Theorem 4.6

Let the conditions of Theorem 4.5 hold. If we define a sequence of functions \(f_n = f_n(\eta )\) on [0, 1] via

$$\begin{aligned} f_0(\eta ):= & {} \phi (\eta ) = \dfrac{-\eta ^3+3(1+2\gamma )\eta }{2(1+3\gamma )} \\ \\ f_{n+1}(\eta ):= & {} \int _0^1 G(\eta ,s) {\mathcal {R}}(f_n'(s) f_n''(s) - f_n(s) f_n'''(s))\ {\rm d}s + f_0(\eta ), \ \ \ n=0,1,2,\cdots \end{aligned}$$

then for all \(\gamma \ge 0\), our \(f_n\) converges to the solution f of (1.1), (1.2) lying in B, and the rate of convergence is given by

$$\begin{aligned} d(f_{n+1},f) \le \left( \sum _{i=0}^3 L_i \beta _i \right) d(f_n,f) = |{\mathcal {R}}| \left[ \dfrac{17044598093}{486019116}R + \dfrac{4623473}{1296000} \right] d(f_n,f). \end{aligned}$$

In addition, for each n, an a priori estimate on the error is given by

$$\begin{aligned}{} & {} d(f_n,f) \le \dfrac{ \left( \sum _{i=0}^3 L_i \beta _i \right) ^n}{1 - \sum _{i=0}^3 L_i \beta _i}d(f_1,\phi ) \\= & {} \left[ |{\mathcal {R}}| \left[ \frac{17044598093}{486019116}R + \frac{4623473}{1296000} \right] \right] ^n \left[ 1 - |{\mathcal {R}}| \left[ \frac{17044598093}{486019116}R + \frac{4623473}{1296000} \right] \right] ^{-1} d(f_1,\phi ) \end{aligned}$$

and for each n, an a posteriori estimate on the error is given by

$$\begin{aligned}{} & {} d(f_{n+1},f) \le \dfrac{ \sum _{i=0}^3 L_i \beta _i }{1 - \sum _{i=0}^3 L_i \beta _i }d(f_{n+1},f_n) \\= & {} |{\mathcal {R}}| \left[ \frac{17044598093}{486019116}R + \frac{4623473}{1296000} \right] \left[ 1 - |{\mathcal {R}}| \left[ \frac{17044598093}{486019116}R + \frac{4623473}{1296000} \right] \right] ^{-1} d(f_{n+1},f_n). \end{aligned}$$

Proof

The style of proof is well known and follows from the conditions of Theorem 4.3 holding. For example, the (linear) rate of convergence can be shown in the following way. Since T satisfies \(Tf = f\) and \(f_{n+1} = Tf_n\) we have

$$\begin{aligned} d(f_{n+1},f) = d(Tf_n,Tf) \le |{\mathcal {R}}| \left[ \dfrac{17044598093}{486019116}R + \dfrac{4623473}{1296000} \right] d(f_n,f) \end{aligned}$$

where we have used the contraction property of T with

$$\begin{aligned} c = |{\mathcal {R}}| \left[ \dfrac{17044598093}{486019116}R + \dfrac{4623473}{1296000} \right] < 1. \end{aligned}$$

Furthermore, the a priori error on the estimate can be shown via repeatedly applying the triangle inequality and the contraction property of T:

$$\begin{aligned} d(f_n,f)\le & {} d(f_n,f_{n-1}) + \cdots + d(f_2,f_1) + d(f_1,f_0) \\\le & {} c^n d(f_1, \phi _0) + \cdots + c d(f_1,\phi _0) + d(f_1,\phi _0)\\= & {} \frac{c^n}{1-c} d(f_1,\phi _0). \end{aligned}$$

For brevity, we omit the proof of the a posteriori estimate on the error. \(\square\)

Remark 4.2

In fact, it is not necessary to start with the particular form of \(\phi _0\) in Theorem 4.6. We can begin our recursive sequence of approximations with any function \(f_0\in C^3([0,1])\) such that

$$\begin{aligned} (\eta ,f_0(\eta ), f_0'(\eta ), f_0''(\eta ), f_0'''(\eta )) \in B, \ \text {for all} \ \eta \in [0,1] \end{aligned}$$

and we will still have \(f_n\) converging on [0, 1] to the solution f in the sense of Theorem 4.6.

Let us briefly compare the approximation method using our integral form in Theorem 4.6 with that of the perturbation approach in Singh and Laurence (1979). Therein, the following equivalent form of (1.1) is considered

$$\begin{aligned} {\mathcal {R}} [(g')^2 - g'g''] + g''' = K \end{aligned}$$

with (1.2), where K is a constant of integration. Singh and Laurence (1979) sought a solution for small \({{{\mathcal {R}}}}\) in series form

$$\begin{aligned} g(\eta ) = g_0 + {\mathcal {R}}g_1(\eta ) +{\mathcal {R}}^2 g_2(\eta ) + \cdots +{\mathcal {R}}^n g_n(\eta ) + \cdots \end{aligned}$$

where

$$\begin{aligned} K = K_0 + {\mathcal {R}} K_1 + {\mathcal {R}}^2 K_2 + \cdots + {\mathcal {R}}^n K_n + \cdots \end{aligned}$$

and each \(g_i\) and \(K_i\) are assumed to be independent of \(\mathcal{R}\). They collected corresponding coefficients for powers of \({\mathcal {R}}\) and constructed \(g_0\) and \(g_1\). There appear to be limitations in this particular approach, in the sense that there are a significant number of constants to compute at each stage of the process, and the boundary conditions are drawn on at every iteration for each \(g_i\). For instance, keeping the constant K in the differential equation under consideration and expanding it as a power series means that there are many \(K_i\) to be found. In addition, for the zero order, \(g_0''' = K_0\) is solved easily, however there are now four separate boundary conditions to navigate. For the first order, \(g_1''' = K_1 - (g_0')^2 + g_0 g_0''\), there are again four separate boundary conditions to incorporate, and so on in each iteration. If we compare the perturbation approach with our scheme in Theorem 4.6, then we see that our scheme of approximations does not include the constant K or rely on repeated incorporation of boundary conditions at every step of the iteration process. Thus, we argue that our strategic use of an integral representation throughout this article forms a more streamlined approach than has been previously available for the slip problem (1.1), (1.2).

5 Opportunities and Conclusion

We note that the estimates used from Sect. 2 in Sects. 3 and 4 are independent of the slip coefficient \(\gamma\). This strategy has been done for simplicity, but raises the open question of what would happen if the results of Sects. 3 and 4 were formulated with the \(\gamma\)-dependent bounds of Section 2. We suspect that this would lead to extremely complex expressions involving \(\gamma\), but might improve the range of Reynolds numbers set in this paper, with the interval tending to that of Almuthaybiri and Tisdell (2022) when \(\gamma \rightarrow 0\).

We also note that the existence, uniqueness and approximation results of this paper apply to the bounded set B that contains the graph of the solution. The raises questions regarding what happens outside of the set B. Do more solutions exist there? How many, and what are their properties? This naturally aligns with the position of Kuo and Wang (2012) that a precise understanding of the multiplicity of solutions appears to be still open. As a very simple motivational example, consider the equation \(u = 1 + {{{\mathcal {R}}}} u^2\). For \(X = \{u \in R: |u-1| \le 1\}\) and \(T(u) = 1 + {{{\mathcal {R}}}}u^2\), Theorem 4.3 can be applied to show the existence and uniqueness of a solution to our equation for \(|{{{\mathcal {R}}}}| < 1/4\). However, for \(0<{{{\mathcal {R}}}} < 1/4\) there is a second solution \(u^*\) satisfying \(u^* > 2\). Thus, additional solutions can exist that do not lie in the original set under consideration.

The main contribution of the ideas in this paper involved constructing new understanding of solutions to the slip BVP (1.1), (1.2). We now have novel knowledge regarding the existence, uniqueness, location and approximation of the precise solution, including a specific range on the Reynolds number that guarantees this, for all slip coefficients.