Impact of Physical Heterogeneity and Transport Conditions on Effective Reaction Rates in Dissolution

Abstract

A continuous-time random walk (CTRW) reactive transport model is used to study the impact of physical heterogeneity on the effective reaction rates in porous media in a sample of length 15 cm over timescales up to 10$^8$ s (3 years). The model has previously been validated using nuclear magnetic resonance (NMR) measurements during dissolution of a limestone. The model assumes first-order reaction. We construct three domains with increasing physical heterogeneity and study dissolution at four Péclet numbers, Pe = 0.0542, 0.542, 5.42 and 54.2. We characterize signatures of physical heterogeneity in the three porous media using velocity distributions and show how these imprint on the signatures of particle displacement, namely particle propagator distributions. In addition, we demonstrate the ability of our CTRW model to capture the impact of physical heterogeneity on the longitudinal dispersion coefficient over several orders of magnitude in space and time. Reactive transport simulations show that the effective reaction rates depend on (i) initial physical heterogeneity and (ii) transport conditions. For all heterogeneities and Pe, the late-time reaction rate exhibits a time dependence $t^{-a}$ with $a \ne 0.5$ that indicates the persistence of incomplete mixing. We show that the higher the initial heterogeneity, the lower the late-time reaction rate. A decrease in Pe promotes mixing by diffusion over advection, resulting in higher reaction rates. The post-dissolution propagators indicate an increase in the degree of non-Fickian transport. Overall, we establish a framework to demonstrate and quantify the impact of physical heterogeneity on transport and effective reaction rates in porous media.

1 Introduction

Reactive transport in porous media is commonly encountered in contaminant hydrology (MacQuarrie and Sudicky 1990), reactive flow in batteries and fuel cells (Gayon Lombardo et al. 2019), nuclear waste disposal (Kenney et al. 2017), oil recovery (Egbe et al. 2021), carbon storage (Metz et al. 2010), and chemical reactor engineering (Fogler 1987). In some applications, such as well stimulation by acidization, reaction is required, while in others, such as in dissolution-induced compromised well integrity, reaction is detrimental. Common to all these applications is that effective reaction rates may depend strongly not only on the nature of the chemical reactants but also on the porous media structure and composition which makes design of reactive processes complex.

Fluid/solid reaction rates depend on the size and the connectivity of the pores. In this work we will call this physical heterogeneity. Despite its relevance and importance, the impact of physical heterogeneity on reactive transport in porous media is not fully understood. Furthermore, it is well known that reaction rates are scale dependent—in geological porous media; it is common to have orders of magnitude differences from pore to field scales (White and Brantley 2003). While some recent experimental work has tried to systematically characterize the impact of physical and/or chemical heterogeneity at the pore scale (Al-Khulaifi et al. 2017, 2018, 2019), more work is needed to address these important phenomena at the continuum scale.

This paper addresses the scientific challenge of determining the interaction of transport conditions and heterogeneity, from the pore scale upwards, on reaction rates over time. In particular, we will explore the role of incomplete mixing and examine how dissolution patterns evolve as a function of flow rate, intrinsic reaction rate and initial pore structure. We will use our previously developed reactive transport continuous-time random walk (CTRW) model that has accurately predicted the difference between effective and batch reaction rates (Oliveira et al. 2021).

At the continuum scale, in the context of predicting dissolution patterns, Hoefner and Fogler (1988) visualized channel formation in limestones and dolomites. They showed the rates of channel formation and growth depend on the fluid velocity and reaction rates. Later Daccord et al. (1993) took the observations further to model wormholing dissolution patterns. The authors described the flow properties of the wormhole in terms of its equivalent size and studied the influence of flow rate and the acid concentration. They recognized that more parameters are needed to completely describe the process. Bazin (2001) developed a laboratory method to study matrix-fracture systems under dissolution and evaluated the impact of a more complete set of parameters on the resultant dissolution patterns. Under similar conditions, Swoboda-Colberg and Drever (1993) observed effective reaction rates with two orders of magnitude difference between laboratory and field studies. Dentz et al. (2011) presented a thorough review on mixing, spreading and reaction in porous media from the pore to the field scale. The authors stressed the importance of modelling the interaction between diffusion and spatial fluctuations in the velocity field to account for mixing and spreading and to properly estimate effective reaction rates at continuum scales.

The physical heterogeneity of porous media impacts the flow field and solute transport. The complex arrangement of pores and grains subjects solute transport to a wide range of velocities; this is a wider range in carbonate samples compared to sandstones and beadpacks in most cases (Blunt et al. 2013; Bijeljic et al. 2013). The recognition of a wide span in the velocity distributions and hence physical heterogeneities has motivated the development of improved numerical models to properly model transport (Gouze et al. 2008; Bijeljic et al. 2013; Pereira Nunes et al. 2015; Bultreys et al. 2015; Weishaupt et al. 2019; Puyguiraud et al. 2019; Municchi and Icardi 2020; Ferreira and d. P., de Oliveira, T. D. S., Surmas, R., da Silva, M. A. P., and Peçanha, R. P. 2020) and reactive transport in porous media (Willmann et al., 2010; Edery et al., 2011; Alhashmi et al., 2015; Oliveira et al., 2020, Oliveira et al., 2021; Edery, 2021; Jia et al., 2021).

A signature of heterogeneity is obtained by quantifying molecular displacements or flow propagators. This can be measured using NMR (Callaghan 1993; Seymour and Callaghan 1997) to provide a quantitative description of non-Fickian solute transport in porous media (Scheven et al. 2005, 2005). Measuring molecular propagators can be time-consuming for dynamic systems, so under-sampling methods have been developed to accelerate the acquisitions (Scheven et al. 2005; Mitchell et al. 2008; Paulsen et al. 2011). Colbourne et al. (2016) developed a technique that significantly speeds up the recordings to observe the temporal evolution of the flow propagators during a dissolution experiment. This enabled the study of the impact of dissolution processes on the transport in fast channels and stagnant regions of a limestone by Muljadi et al. (2018). The authors observed the change of the heterogeneity parameter $\beta$ in the transport-only model as a proxy for the change in pore-scale heterogeneity during dissolution. Later, Oliveira et al. (2021) developed a new CTRW-based model for dissolution and validated it against NMR measurements by comparison of the effective reaction rates. They demonstrated a combined experimental and modelling workflow in which both the experimental measurements and the model predictions for Ketton limestone indicated reaction rates up to three orders of magnitude lower than the independently measured batch reaction rate for pure calcite (Peng et al. 2015). The considerable scale discrepancy in the reaction rates was ascribed to mass transfer limitations in the complex pore space. However, the impact of physical heterogeneity on the reaction rates has not been systematically investigated.

In this work we study the impact of increasing physical heterogeneity and flow conditions on reactive transport in porous media. We apply a CTRW model to examine the impact of physical heterogeneity and transport conditions on effective reaction rates at the continuum scale (15 cm in this paper). We model unresolved physical heterogeneity in a CTRW framework with a truncated-power law (TPL) transit-time distribution model containing the transport heterogeneity parameter (Dentz et al. 2004; Bijeljic and Blunt 2006; Rhodes et al. 2009; Edery et al. 2014; Oliveira et al. 2021; Edery 2021). We start with section 2 showing the details of the first-order reactive transport model. Then in section 3 we describe the porous media studied, showing their signatures of flow heterogeneity characterized by the velocity distributions and of transport heterogeneity characterized by flow propagators. Finally, we investigate the evolution of reaction rates and the capabilities of our CTRW reactive transport framework to capture changes in the heterogeneity signatures caused by dissolution.

2 Description of the CTRW Reactive Transport Model

At the macro-scale where Darcy’s law is valid, the Advection-Dispersion Reaction Equation (ADRE) is described as

$$\begin{aligned} \phi \frac{\partial c}{\partial t} = - \nabla \cdot \left( {\mathbf {v}} c\right) + \nabla \cdot \phi {\mathbf {D}} \nabla c + R, \end{aligned}$$

(1)

where $\phi$ is the porosity, c is the molar concentration of a given species, ${\mathbf {v}}$ is the Darcy velocity, ${\mathbf {D}}$ is the dispersion coefficient, and R is the reaction rate. The choice of R controls the reactions of the system, such that a value of $R=0$ makes Eq. 1 applicable for an inert system, without dissolution or precipitation of any species, or a value of $R = k_r c$, as adopted in the present study, makes it appropriate to model first-order kinetic reactions (Plummer et al. 1978; Gray et al. 2018; Oliveira et al. 2021).

We use the model described in Oliveira et al. (2021) and illustrated in Fig. 1. Instead of having the solute concentration modelled as a continuous field variable, we describe it using a Lagrangian framework with particles distributed on a lattice (Bijeljic and Blunt 2006; Le Borgne et al. 2008; Kang et al. 2011; Pereira Nunes et al. 2016a, b). Each particle contains a number of moles of aqueous calcium. Particles are not created or destroyed; instead the number of moles associated with a particle changes over time. The aqueous calcium concentration is defined as the sum of the moles associated with each particle in a given volume. Solute transport is then modelled as particle transitions on a lattice, carrying the chemical components from site to site. Reactions are then accounted for as interactions between the chemical components in the particles and the chemical components in the lattice nodes, representing the solid.

Fig. 1

Simplified illustration of (a) an ensemble of particles and (b) the detailed representation of a single particle (b) before and (c) after transiting and reacting through a lattice. The change in colour depicts an increase of the aqueous calcium concentration. A particle transits in the lattice with variable transit-time $\Delta \tau$ and displacement $\Delta x$, obtained from a locally defined transit-time distribution $\psi _{ij}$ and displacement probability $p_{ij}$. After each transition, the number of moles of aqueous calcium in a particle increases by $\Delta n$, as a consequence of the reaction within the node of origin, which in turn has its porosity increased by $\Delta \phi$. Modified from Oliveira et al. (2021)

The CTRW joint probability distribution $\psi ({\mathbf {x}},t)$ can be described in terms of the decoupled probabilities of spatial displacement $p({\mathbf {x}})$ and transition time $\psi (t)$, $\psi ({\mathbf {x}},t) = p({\mathbf {x}}) \psi (t)$. The particle transitions are then governed by the decoupled probability distributions for the transit-time and displacement of the particles. This concept is explored in Dentz et al. (2004) and Berkowitz et al. (2006).

The transit-time distribution $\psi _{ij}$ is represented by a TPL distribution which empirically matches experimental results (Levy and Berkowitz 2003) defined using two characteristic timescales (Dentz et al. 2004; Bijeljic and Blunt 2006) and an adjustable parameter

$$\begin{aligned} \psi (t) = A e^{-t/t_2} {(1+t/t_1)}^{-1-\beta }, \end{aligned}$$

(2)

where $t_1$ is the advective transit time, $t_2$ is the diffusive cut-off time, $\beta$ is a fitting parameter representing the heterogeneity of the medium, and A is a normalization constant such that $\int _{0}^{\infty } \psi (t') \mathrm {d}t' = 1$ meaning that $\psi$ can be used as a PDF. We sample transit times $\Delta \tau$ from Eq. 2 defined at the links between nodes i and j. The characteristic timescales $t_1$ and $t_2$ are locally defined at the link level, from the link velocity and using the molecular diffusion coefficient,

$$\begin{aligned} t_1&= \frac{l}{|v_{ij} |}, \end{aligned}$$

(3a)

$$\begin{aligned} t_2&= \frac{l^2}{D_m}, \end{aligned}$$

(3b)

where $v_{ij}$ is the velocity in the link between nodes i and j, $D_m$ is the molecular diffusion coefficient, and l is the length of the link. In this work we assume that l and $D_m$ are fixed; however, because the velocity in each link is different, the transit-time distribution will also vary from link to link.

The probability of transition from node i to node j is calculated from the asymptotic solution of the ADE developed in Rhodes and Blunt (2006) and generalized in Rhodes et al. (2008) as

$$\begin{aligned} p_{ij}&= G \frac{\textit{Pe}_{ij}}{1-e^{\textit{-Pe}_{ij}}},&\quad \forall v_{ij} > 0 \end{aligned}$$

(4a)

$$\begin{aligned} p_{ij}&= G \frac{\textit{Pe}_{ij}}{e^{\textit{Pe}_{ij}}-1},&\quad \forall v_{ij} < 0 \end{aligned}$$

(4b)

where $\textit{Pe}$ is the locally defined Péclet number, $\textit{Pe}_{ij} = l |v_{ij} |/ D_m$, in the link connecting node i to node j, and G is a normalization factor such that $\sum _j p_{ij} = 1$. At the sample scale, we define Péclet and Damköhler numbers as

$$\begin{aligned} \textit{Pe}&= \frac{v L}{D_m}, \end{aligned}$$

(5a)

$$\begin{aligned} \textit{Da}&= \frac{\pi r}{v c_n}, \end{aligned}$$

(5b)

where v is the average interstitial velocity through the sample in the flow direction ($v \equiv \langle v_x \rangle$), $L = 407$ $\mu$m is the characteristic length for Ketton limestone representing a typical distance between pores (Muljadi et al. 2018), r is the batch reaction rate constant of pure calcite measured in moles per unit area per unit time, and $c_n$ is the initial number of moles of calcite per unit volume of the porous medium.

Finally, dissolution occurs as particles containing acid, or H$^{+}$-rich particles, are injected in the domain and are allowed to react with the calcite-rich nodes in the lattice. We track the amount of calcium in the aqueous phase which is transported by the particles, following the approach of Pereira Nunes et al. (2016a, b). The main assumption in our reaction model is that dissolution is modelled with first-order kinetics in an ideal solution, such that

$$\begin{aligned} \frac{dn}{dt} = k_r \left( n_\text {eq} - n\right) , \end{aligned}$$

(6)

where n is the number of moles in a particle, $n_\text {eq}$ is the number of moles in a particle at equilibrium, $n_\text {eq} - n$ represents the departure from equilibrium, while $k_r$ is the reaction rate constant, estimated from the batch reaction rate r of calcite and the specific surface area (surface area per unit volume of the porous medium) $\sigma _A$ as $k_r = V \sigma _A r / n_\text {eq}.$ $V = l^3$ is the volume associated with a node. We assume that the specific surface area and hence $k_r$ are constant as dissolution proceeds.

We then relate the increase of porosity $\phi _i$ after a particle transition from node i with the amount of calcite $n_{i}$,

$$\begin{aligned} \Delta \phi _i = \Delta n_i \frac{M_{\text {CaCO}_3}}{V \rho _{\text {CaCO}_3}}, \end{aligned}$$

(7)

where $V = l^3$, $\rho$ is the density of calcite ($2.71 \times 10^{3}$ kg/m$^3$) and M the molar mass of calcite (0.1 kg/mol). We define the change of porosity $\Delta \phi _i$ during the time interval $\Delta \tau$ with the change of calcite moles in the node and the corresponding change in Ca$^{2+}$ moles in the particle during the same time as

$$\begin{aligned} \Delta \phi _i&= \phi _i^{t+ \Delta \tau } - \phi _i^t, \end{aligned}$$

(8a)

$$\begin{aligned} \Delta n_i&= n_i^{t+ \Delta \tau } - n_i^t = k_r \Delta \tau (n_{eq} - n_i^t). \end{aligned}$$

(8b)

$\Delta \tau$ is the time sampled from the transit-time distribution $\psi _{ij}$ (Eq. 2) locally defined at the links between nodes i and j for particles that have left node i and moved to node j. We remove moles from the particles at node i before their transition to a new node.

Next, we systematically demonstrate the impact of physical heterogeneity on transport and reactive flow signatures. We study this by creating three porous media of increasing heterogeneity and examining the emergent effective reaction rates. The three samples are used to show different initial porosity and velocity distributions and are subjected to four transport regimes, from diffusive to advective dominated, characterized by Péclet numbers of Pe = 0.0542, 0.542, 5.42 and 54.2. We will also compare the results obtained with our CTRW model with solutions described by the ADRE, Eq. 1, in a homogeneous system.

3 Signatures of Physical Heterogeneity

The samples studied are described in Sect. 3.1. Next we evaluate the velocity distribution and particle propagators as proxies for the physical heterogeneity of the samples, similarly to what is described in Bijeljic et al. (2011, 2013). Then in Sect. 3.2 we show the imprint of the regions available for flow on the velocity distributions. The signatures of transport heterogeneity are then shown in Sect. 3.3, where we consider the shape of the particle propagators as an indication of physical heterogeneity. The differences between stagnant and mobile particles are a direct consequence of the contrasts in the velocity distributions combined with the transport heterogeneity parameter $\beta$.

3.1 Description of the Porous Media

We build three samples with increasing heterogeneity: Het. 1, 2 and 3; see Appendix 1 for more details of the generation procedure. Each sample is built from a background 3D porosity field that is used to populate the properties of an underlying regular lattice, similarly to how the model for the Ketton limestone sample was constructed in Oliveira et al. (2021). The cell centres of the 3D porosity field cells are coincident with the node centres of the lattice. The lattice has $N_x = 150$, $N_y = N_z = 50$ nodes along the x, y and z directions and link size of $l = 10^{-3}$ m. Hence the total length of the sample is 0.15 m.

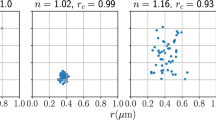
The 3D porosity field consists of a normally distributed porosity with mean $\langle \phi _\text {bg} \rangle = 0.3$ and standard deviation $\sigma _{\phi \text {bg}} = 0.1$. This is called here the background porosity not to be confused with the samples’ initial mean porosity. The heterogeneity is emulated by uniformly distributing solid spheres with $\phi _\text {spheres} = 0$ that are allowed to overlap, resulting in a sphere density of $7.03 \times 10^{6}$ spheres/m$^{3}$. The sphere radius for Het. 1, 2 and 3, is normally distributed with mean $\langle r_1 \rangle = 1.5 \times 10^{-3}$ m, $\langle r_2 \rangle = 3.0 \times 10^{-3}$ m and $\langle r_3 \rangle = 4.5 \times 10^{-3}$ m, respectively the standard deviation $\sigma _{r} = 0.2 \langle r \rangle$ and the sphere centres are the same. Figure 2 shows the distribution and radius of the solid spheres for all samples, and Table 1 summarizes the parameters used.

Table 1 Initial sample properties

The presence of solid spheres of different radius reduces the mean porosity of each sample from $\langle \phi _\text {bg} \rangle = 0.3$ to $\phi _1 = 0.29$, $\phi _2 = 0.25$ and $\phi _3 = 0.17$, respectively, for Het. 1, 2 and 3.

Fig. 2

Different radii for the solid spheres used to generate the initial porosity fields of samples Het. 1, 2 and 3. The porosity in the regions where the spheres are located is set to zero. The spheres are uniformly distributed in the domain and allowed to overlap. The mean radius for (a) Het. 1 is $\langle r_1 \rangle = 1.5 \times 10^{-3}$ m, for (b) Het. 2 $\langle r_2 \rangle = 3.0 \times 10^{-3}$ m and for (c) Het. 3 $\langle r_3 \rangle = 4.5 \times 10^{-3}$ m, and the standard deviation of radius is $\sigma _{r1} = \sigma _{r2} = \sigma _{r3} = 0.2 \langle r \rangle$ m

For Het. 1, the sphere radius and distribution makes the spheres very unlikely to overlap and the porosity of the sample is mostly driven by the background porosity such that for Het. 1 the mean porosity is $\phi = 0.29$. As the sphere radius increases, the domain of Het. 2 and Het. 3 becomes more irregular and the sample mean porosity is driven by the combination of the solid spherical inclusions and the background porosity. This significantly reduces the porosity and permeability when comparing Het. 1 to 2 and 3, as shown in Table 1. As an analogy, Het. 1 is related to beadpacks, Het. 2 to a mildly homogeneous carbonate, while Het. 3 to a highly heterogeneous carbonate. The heterogeneity of the samples lies on an observation scale that is larger than the link and node sizes, so we compare the choice of characteristic value of $\beta = 1.8$ for beadpacks, $\beta = 1.2$ for mildly homogeneous carbonates and $\beta = 0.6$ for heterogeneous carbonates, with a baseline of $\beta =1.8$ for all three porous media in Sect. 4. $\beta$ is an empirical parameter that captures the heterogeneity of the medium at a scale below the scale of a link (at the pore scale) which is not explicitly captured by the larger-scale heterogeneity in the model. The values of $\beta$ for Het. 1, 2 and 3 we choose are taken from previous studies of pore-scale transport in beadpacks and mildly heterogeneous media (Dentz et al. 2004; Bijeljic et al. 2011) and carbonates (Oliveira et al. 2021), respectively.

The permeability at the link k is calculated using a power-law correlation with the porosity,

$$\begin{aligned} K = a \phi ^b, \end{aligned}$$

(9)

where a and b are fitting parameters defined in Table 1. Such power-law correlations between porosity and permeability are widely used to model the evolution of permeability in dissolution experiments where the emergence of channels leads to a very rapid change in permeability with porosity (Menke et al. 2015; Honari et al. 2015). The initial porosity and permeability distribution are presented in Fig. 3. The more heterogeneous the sample, the smaller are the peaks at the mean porosity $\langle \phi \rangle = 0.3$ and the larger is the number of porosity values at the lower end of the distributions.

Fig. 3

Initial nonzero (a) porosity and (b) permeability distributions for Het. 1, 2 and 3. The mean porosity value for Het. 1 is $\langle \phi _1 \rangle = 0.29$, for Het. 2 $\langle \phi _2 \rangle = 0.25$ and for Het. 3 $\langle \phi _3 \rangle = 0.17$. The more homogeneous sample Het. 1 has a larger peak at $\phi = 0.3$, whereas the other samples are characterized by the tail of the distribution towards lower values of porosity. The porosity–permeability correlation factors are defined in Eq. 9 and listed in Table 1. The mean permeability value for Het. 1 is $\langle K_1 \rangle = 1.69$ D, for Het. 2 $\langle K_2 \rangle = 315$ mD and for Het. 3 $\langle K_3 \rangle = 4.50$ mD (1 D = 9.87 $\times 10^{-13}$ m$^2$). The heterogeneity of the samples extends the tail in the permeability distribution to lower-end values

3.2 Signatures of Flow Heterogeneity

At the scale of individual links we assume that the heterogeneity of the system is characterized by $\beta =$ 1.8, 1.2 and 0.6, respectively, for Het. 1, 2 and 3, as presented in Table 1. This hypothesis is further explored in Sect. 4, where we consider different values of $\beta$ in Eq. 2. To solve the velocity in the links, we impose a unit pressure gradient along the $x-$axis $\Delta P_x = 1 \text {Pa}$ and then scale the average velocity such that the Péclet number, Eq. 5a, is equal to $\textit{Pe}$ = 0.0542, 0.542, 5.42 and 54.2. These Péclet numbers represent different transport regimes, from diffusive dominated to advection dominated.

The resulting pressure fields alongside the porosity fields are displayed side-by-side in Fig. 4. The lower porosity values significantly restrict the regions available for flow, focusing the transport only to the regions of higher porosity.

Fig. 4

Initial porosity fields (a)–(c) and the corresponding calculated pressure fields for (d) to (f), respectively, for Het. 1, 2 and 3. The porosity field is constructed using zero porosity inclusions in a background porosity field of $\langle \phi \rangle = 0.3$ as shown in Fig. 2. The calculated pressure reflects the initial heterogeneity of the sample, gradually increasing the local pressure differences from Het. 1 to 3

From the pressure field, we calculate the normalized velocity distribution in the flow direction for each sample and plot it in Fig. 5. The shape of the normalized velocity distribution shows a sharp peak at $v_x / \langle v_x \rangle = 1$ with a narrow velocity distribution of only one order of magnitude of variation for Het. 1. This is markedly different than of Het. 2 and 3 that exhibit much wider distributions than Het. 1 and a smeared-out tail towards lower velocity values. The velocity distribution for Het. 2 spans over nearly 10 orders of magnitude, having very low velocities. The velocity distribution for Het. 3 is slightly wider than Het. 2, showing even more contrast between the low and high velocities. At the high end of the distribution, the velocity in the links of Het. 3 can reach nearly 20 times the mean velocity. This is likely due to the regions available for flow that are restricted by the presence of the spherical solid inclusions with larger radius than of Het. 1 and 2. Additionally both Het. 2 and 3 show significant amounts of slower velocities, or near-stagnant links, where solute transitions are mostly influenced by diffusion.

Fig. 5

Normalized velocity distribution for the different samples. The shape of the normalized velocity distribution shows a sharp peak at $v_x / \langle v_x \rangle = 1$ with a narrow velocity distribution for Het. 1. In contrast, Het. 2 and 3 have a much wider distribution with a smeared-out tail towards lower velocity values. The inset shows the same distributions but without the $\log$-$\log$ transformation

3.3 Signatures of Transport Heterogeneity

We calculate the probability of a longitudinal particle displacement, called the particle propagator, $P\left( \zeta \right)$ by observing the longitudinal particle displacements $\zeta$ over an observation time $\Delta$ and normalized by the mean displacement $\langle \zeta \rangle _0$. Particle propagators are calculated from the displacement of the particles and are analogues to molecular propagators. The calculated particle propagators in Fig. 6 are obtained by injecting 10$^6$ particles uniformly at $x = 0.02$ m, instead of at the inlet face to allow for back-diffusion through the inlet, and are tracked using observation times of $t/t_1 = 0.5$ and $t/t_1 = 1.0$. Here we define $t_1 = l/v$ where $v \equiv <v_x$ is the average velocity in the flow direction. The lower resolution of the propagators for $\textit{Pe} = 54.2$ is due to many produced particles within $t/t_1$, and consequentially, there are few particles left in the domain. The observation times are normalized by the mean advective time to display the different samples in a consistent time frame; at late times when $t / t_1 \gg 1$ the particle propagator is expected to be fully developed to a Gaussian profile (Dentz et al. 2004; Berkowitz et al. 2006).

Fig. 6

Initial particle propagators for Het. 1, 2 and 3 at $t/t_1 = 0.5$ and $t/t_1 = 1.0$, and Péclet numbers of $\textit{Pe}$ = 0.0542 (a) and (b), $\textit{Pe}$ = 0.542 (c) and (d), $\textit{Pe}$ = 5.42 (e) and (f), and $\textit{Pe}$ = 54.2 (g) and (h). As $\textit{Pe}$ increases, the contrast between the faster and the slower moving particles increases for Het. 2 and 3, showing a peak at $\zeta / \langle \zeta \rangle = 0$. The cut-off at the higher end of Het. 3 is due to particles exiting the domain, making them unavailable for the calculation

The porous media structure arising from the distribution of solid spherical inclusions significantly impacts the shape of the propagator distribution. The profiles in most cases are far from the expected Gaussian profile that results from the solution of the transport equation using Fick’s law, Eq. 1. For $\textit{Pe}$ = 0.0542, the propagator distributions for both samples Het. 1 and Het. 2 behave similarly, with little to no difference at early and late times. The propagator for Het. 3 is slightly asymmetrical at early times, showing higher probability of slow displacements ($\zeta / \langle \zeta \rangle < 1$) than for the other samples and takes longer to fully develop when compared to Het. 1 and 2. This is not the case for $\textit{Pe}$ = 0.542 that shows the signature of the pore space heterogeneity in all samples. Het. 1 shows little to no disturbance and is near Gaussian at both early and late times, and Het. 2 seems to behave similarly but with a longer delay. However Het. 3 is highly asymmetrical with a high probability at $\zeta / \langle \zeta \rangle = 0$, showing a significant amount of stagnant particles at early observation times. This effect is still evident at later times when the profile fails to achieve the expected Gaussian shape. For $\textit{Pe}$ = 5.42, the observations are similar to those at $\textit{Pe}$ = 0.542, but with enhanced non-Gaussian behaviour. The particle propagator distribution for Het. 3 does not change significantly from early to late times.

Links showing characteristic advective times $t_1$ of the same order of the diffusive cut-off times $t_2$, or lower, are likely considered as of part of a stagnant region. Figure 5 shows that Het. 2 and 3 have velocities several orders of magnitude lower than the mean velocity. For $\textit{Pe}$ = 0.0542, diffusion is sufficiently rapid to allow particles in these slow-flow domains to be transported quickly to neighbouring links. However for $\textit{Pe}$ = 0.542, 5.42 and 54.2, the differences in velocity arising from the heterogeneity of the sample are sufficient to strand a significant number of particles in stagnant regions.

Fig. 7

Longitudinal dispersion coefficient versus Péclet number. Numerical results for Het. 1, 2 and 3 and experimental measurements on beadpacks and sandpacks from Bijeljic et al. (2004) using the sources of Pfannkuch (1963), Seymour and Callaghan (1997), Kandhai et al. (2002), Khrapitchev and Callaghan (2003), and Stöhr (2003). The longitudinal dispersion coefficient is calculated from the variance of the particle horizontal travel distance as $D_L = 1/2 \frac{d \sigma ^2_L}{dt}$

Figure 7 shows the asymptotic normalized longitudinal dispersion coefficient $D_L/D_m$ results for Het. 1, 2 and 3 versus Péclet number. The longitudinal dispersion coefficient is calculated from the variance of the particle horizontal travel distance as $D_L = \frac{1}{2} \frac{d \sigma ^2_L}{dt}$. The numerical results are compared against the experimental data presented in Bijeljic et al. (2004). The CTRW model reproduces the observed experimental measurements for beadpacks and sandpacks with $\beta =1.8$ which describes fairly homogeneous media. For $\textit{Pe} \ll 1$, $D_L/D_m$ increases from Het. 3, 2 to 1 since the higher tortuosity in more heterogeneous media decreases the spread of solute by diffusion. However when advection is more dominant than diffusion, for $\textit{Pe} \gg 1$, this behaviour is inverted, and $D_L/D_m$ increases from most homogeneous Het. 1, to most heterogeneous Het. 3. This increase in physical heterogeneity is reflected in a decrease in $\beta$ with values 1.8, 1.2 and 0.6 for Het. 1, 2 and 3, respectively.

4 Impact of Physical Heterogeneity on Reactive Flow

We start in Sect. 4.1 showing the dissolution patterns and the evolving porosity profiles. Next in Sect. 4.2 we show the effects of the physical heterogeneity on the reaction rates. Finally in Sect. 4.3 we show the impact of reactive flow on the evolution of the transit-time distributions $\psi$ caused by the increase in porosity of the links and the post-dissolution particle propagators.

Each simulation runs for $t = 10^8$ s, $10^7$ s, $10^6$ s and $10^5$ s (timescales of approximately 3 years to 1 day) for $\textit{Pe}$ = 0.0542, 0.542, 5.42 and 54.2, respectively. This amounts to the injection of $V_\text {inj} = 7.3 \times 10^{-2}$ m$^3$ of acid, which is equivalent to injecting $6.74 \times 10^{2}$, $7.82 \times 10^{2}$, and $1.15 \times 10^{3}$ pore volumes, $\textit{PV}$, respectively, for Het. 1, 2 and 3. The characteristic reaction time $t_\text {reac} = 1/k_r = 1.59$ s is 21 times smaller than smallest characteristic advective time (Eq. 3a) of the fastest link in the lattice. This shows that reaction is fast when there is acid available. Figure 8 shows Pe and Da dimensionless numbers Eq. 5, and the expected dissolution regimes for each sample defined according to Golfier et al. (2002). For consistency with the definitions in Golfier et al. (2002), Pe and Da were calculated using the characteristic length scale of $l = \sqrt{K}$, where K is the mean permeability of the sample as defined in Table 1. This results in $l = 1.3 \times 10^{-6}$, $5.6 \times 10^{-7}$ and $6.7 \times 10^{-8}$ m, respectively, for Het. 1, 2 and 3, and different values of Pe and Da from the ones defined from Eq. 5 and used in the paper. The diagram highlights the Pe dependence when transitioning from the regimes of compact dissolution, conical wormholes and dominant wormholes, and the Da dependence when transitioning from the regimes of uniform dissolution, ramified wormholes and dominant wormholes.

Fig. 8

Péclet (Pe) and Damköhler (Da) dimensionless numbers, and the expected dissolution regimes for each sample defined according to Golfier et al. (2002). For consistency with the definitions in Golfier et al. (2002), the values of Pe and Da used in the figure were calculated using the characteristic length scale $l = \sqrt{K}$

4.1 Visualization of Dissolution and Porosity Evolution

As mentioned previously we choose $\beta$ = 1.8, 1.2 and 0.6 for Het. 1, 2 and 3, respectively, to represent a beadpack, a mildly homogeneous carbonate and a highly heterogeneous carbonate (Bijeljic and Blunt 2006; Bijeljic et al. 2011, 2013). However, we assume that all three solid structures can dissolve at the same batch rate. The assumption is that lowering the $\beta$ parameter increases the domain heterogeneity at the scale of the nodes and links. Ideally we would estimate the local distribution of $\beta$ from finer scales, such that each individual link would have a representative value, as described in Rhodes et al. (2008). However we keep the same assumption as in our previous work (Oliveira et al. 2021); $\beta$ is constant in time and space.

Figure 9 shows the emerging dissolution patterns for Het. 1 with $\beta = 1.8$, Het. 2 with $\beta = 1.2$ and Het. 3 with $\beta = 0.6$ for $\textit{Pe}=$ 0.0542, 0.542, 5.42 and 54.2. After each row characterised with the same $\textit{Pe}$ number we also repeat the results for $\beta = 1.8$ for the same $\textit{Pe}$ for comparison. We show snapshots when $t/t_1 = 1$ for $\textit{Pe} =$ 0.0542 and at $t/t_1 = 10$ for $\textit{Pe} =$ 0.542, 5.42 and 54.2. For $\textit{Pe} = 0.0542$ particle transport is more driven by diffusion and the majority of the dissolution happens at the inlet. The solid spherical inclusions play little role in restricting the available regions for dissolution for Het. 1, but have a significant impact for Het. 2 and 3, for which the dissolution front reaches further into the sample. The dissolution pattern resembles compact or face dissolution for Het. 1, but has some channelling for Het. 2 and dominant channelling for Het. 3, dependent on Pe, broadly consistent with the predictions of Fig. 8, but with some differences that will be discussed below. As Péclet number increases the particles are less likely to diffuse away from fast-flowing channels, while experiencing shorter resident time in the nodes. Hence for $\textit{Pe} =$ 0.542, 5.42 and 54.2 the dissolution forms a channelized pattern (Menke et al. 2015). The heterogeneity of the porous media does not allow a uniform dissolution, but leads to the formation of preferential channels. Table 2 shows the initial and final mean values for porosity and permeability of Het. 1, 2 and 3 and $\textit{Pe}=$ 0.0542, 0.542, 5.42 and 54.2.

The results in Fig. 8 highlight a predicted transition from compact dissolution towards uniform dissolution or ramified wormholes. The observed behaviour is more complex in Fig. 9 because of the interaction of reaction with heterogeneity. For instance the intermediate pattern of a conical wormhole is never observed in Fig. 9. Instead what we observe is a compact dissolution pattern for the lowest Pe numbers and Het. 1 and channel widening as we increase Pe with the emergence of channels in Het. 2 and 3 for even the smallest values of Pe. We observe that for the most heterogeneous material, Het. 3, we do not observe uniform dissolution, contrary to the predictions in Fig. 8. Instead, local variations in the flow field lead to a positive feedback in the dissolution process, leading to the formation of channels (Menke et al. 2017).

It is evident that when the transport heterogeneity increases ($\beta$ decreases), the emerging dissolution patterns change to a more channelized behaviour. This indicates that a wider distribution of transit times promotes higher contrast for dissolution rates in the channels compared to the stagnant regions. This leads to a positive feedback, with the channels taking most of the flow and the injected reactant, exacerbating the contrast with the stagnant regions, and further enhancing dissolution in the channels. This impact is observed most prominently for Het. 3 and at higher $\textit{Pe}$. The dissolved channels are formed earlier and reach further than for the other cases. Furthermore, this impact is more pronounced when the heterogeneity parameter $\beta$ used in the model is decreased for Het. 2 and Het. 3 compared to when it has a higher baseline value of $\beta =1.8$.

Fig. 9

Dissolution-induced porosity of the different samples at $t/t_1 = 1$ for Het. 1 using $\beta = 1.8$, Het. 2 using $\beta = 1.2$ and Het. 3 $\beta = 0.6$, and Péclet numbers of $\textit{Pe}$ = 0.0542, and at $t/t_1 = 10$ for $\textit{Pe}$ = 0.542, 5.42 and 54.2. Below each row characterised with the same $\textit{Pe}$ number the results for $\beta$ = 1.8 for the same $\textit{Pe}$ are presented for comparison. Smaller values of $\beta$, the upper figures, tend to result in greater channelling

Table 2 Mean, initial and final porosity and permeability dissolution simulations for Het. 1, 2 and 3 and Pe = 0.0542, 0.542, 5.42 and 54.2

The change in the mean porosity profiles along the flow direction is illustrated in Fig. 10 for Het. 1, 2 and 3 and $\textit{Pe}$ = 0.0542, 0.542, 5.42 and 54.2. For a common normalized advective time $t/t_1$, the samples with highest porosity increase are the ones subjected to the smallest local $\textit{Pe}$ number, as the particles have a longer resident time in the nodes. The profiles highlight the differences between the different dissolution patterns; for low $\textit{Pe}$ number the dissolution follows a compact dissolution pattern mostly occurring at the inlet, and progressing with a lower rate further down the sample. For higher $\textit{Pe}$ numbers, the change in porosity in the inlet is not as significant. Furthermore, the impact of heterogeneity is observed, with the highest porosity change at the inlet for Het. 3.

Fig. 10

Porosity profiles along the flow direction ($x-$axis) for Het. 1, 2 and 3, and Péclet numbers of (a) $\textit{Pe}$ = 0.0542, (b) $\textit{Pe}$ = 0.542, (c) $\textit{Pe}$ = 5.42 and (d) 54.2

Looking into the porosity distribution, Fig. 11 highlights the porosity intervals that were more effectively altered by dissolution. The regions of higher changes are in the vicinity of higher mean porosity, as these regions naturally focus flow and the transport of fresh reactants. Lower porosity regions have little to no influence at higher $\textit{Pe}$; it is only when $\textit{Pe}$ is low and diffusion is significant that noticeable dissolution can be observed.

Fig. 11

Histogram of porosity distributions for Het. 1, 2 and 3 with $\textit{Pe}$ = 0.0542, 0.542, 5.42 and 54.2 at different normalized advective times $t/t_1$. Dissolution is fastest in regions of high porosity, as these regions naturally focus flow and the transport of fresh reactants. Lower porosity regions have little to no influence at higher $\textit{Pe}$; only when diffusion is significant can such regions experience noticeable dissolution

4.2 Effect of Physical Heterogeneity on Reaction Rates

Figure 12 shows the normalized effective reaction rate calculated for all $\textit{Pe}$ and samples, and compares it to the reaction rate at late-time $r_\text {eff} \sim 1 / \sqrt{t}$ which would be observed for complete mixing and transport governed by ADRE, Eq. 1 (Dentz et al. 2011). This timescaling assumes that the reactant undergoes diffusive mixing over a length that scales as $\sqrt{t}$. The effective reaction rate is normalized with the batch reaction rate of calcite measured in Peng et al. (2015). The effective reaction rate obtained by the CTRW model increases with time, achieves a maximum value and then decreases towards but does not attain the complete mixing reaction rate given by the ADRE. At early times $t/t_1 \ll 1$, the CTRW model reaction rates are much smaller than would be predicted by a Fickian, ADRE, model. This is expected as the effective reaction rate given by the ADRE assumes that all reactants are perfectly mixed controlled by the asymptotic (and larger) value of the longitudinal dispersion coefficient $D_L$, whereas in fact the behaviour of $D_L$ is preasymptotic and much lower than its asymptotic late-time value (Alhashmi et al. 2016). However, even at late times $t/t_1 \gg 1$, when $D_L$ increases, the CTRW model effective reaction rates still deviate from the behaviour predicted assuming complete mixing for all $\textit{Pe}$ numbers studied and with a different scaling for each porous medium.

At late times, the effective reaction rate scales as $t^{-a}$ with $a \ne 0.5$ for all samples and $\textit{Pe}$ numbers, pointing out that $r_\text {eff}$ is still far from the complete mixing reaction rate even at late-times when the effective reaction rate could be expected to scale with $t^{-a}$ with $a = 0.5$ (Dentz et al. 2011). This is a result of the persistence of incomplete mixing. The late-time power-law scaling for each individual sample and $\textit{Pe}$ number are presented in Table 3. The scaling deviates further from the ideal value as $\textit{Pe}$ increases, for the most heterogeneous case, Het. 3.

The effective reaction rates exhibit a dependence on transport conditions. At early times, mixing in the fast flow channels dominates; hence, reaction rates are higher for $\textit{Pe}=54.2$ compared to the lower $\textit{Pe}$ numbers. However, by late times diffusion has mixed the reactants in both fast channels and stagnant regions, resulting in the higher reaction rates for the lowest $\textit{Pe} = 0.0542$, for which diffusion is most significant. The impact of physical heterogeneity on the reaction rates at $\textit{Pe}$=54.2 is manifested as the highest maximum at early times for the most heterogeneous medium Het. 3. At both intermediate $\textit{Pe}$=0.542 and low $\textit{Pe}$=0.0542, diffusion leads to better mixing of reactants and results in the higher reaction rates for more homogeneous medium Het. 1.

Fig. 12

Normalized effective reaction rate plotted against $1 / \sqrt{t}$ for Het. 1, Het. 2 and Het. 3, respectively, and $\beta$ = 1.8, 1.2 and 0.6, at $\textit{Pe}$ = 0.0542, 0.542, 5.42 and 54.2. The effective reaction rate is normalized with the batch reaction rate of calcite (Table 1). The black solid line is the 1:1 trend, highlighting the power-law scaling of $r_\text {eff} \sim t^{-a}$ with $a = 0.5$. The best-fit power-law scaling factors a at late time for each sample and $\textit{Pe}$ are shown in Table 3

Table 3 Estimated power-law scaling a for the effective reaction rate and the uncertainty in the estimated exponent $\sigma _{{\bar{a}}}$ for $\textit{Pe}$ = 0.0542, 0.542, 5.42 and 54.2 and for samples Het. 1, 2 and 3. The power-law scaling $t^{-a}$ with $a \ne 0.5$ is a result of the persistence of incomplete mixing

4.3 Transit-time Distributions and Particle Propagators

Figure 13 shows the locally defined transit-time distribution $\psi$ for Het. 1, 2 and 3 at $\textit{Pe} =$ 0.0542 and 54.2, at two times, $t/t_1 = 0$ and $t/t_1 = 10$ at the location near the inlet at ${\mathbf {x}}_1 =$ (0.5, 3.7, 3.0) $\times 10 ^{-3}$ m and near the outlet at ${\mathbf {x}}_2 =$ (12.0, 0.8, 3.0) $\times 10 ^{-3}$ m. The local $\psi$ functions are calculated using Eq. 2, $t_1$ is calculated from the velocity at the link, $t_2$ is calculated from the defined molecular diffusion coefficient, and using $\beta$ = 1.8, 1.2 and 0.6, respectively, for Het. 1, 2 and 3. When comparing the initial state $t/t_1 = 0$ to the final state $t/t_1 = 10$, the probability of shorter transitions increases for Het. 1 at both $\textit{Pe}$ numbers, more effectively for lower $\textit{Pe}$ = 0.0542 but is still significant for $\textit{Pe}$ = 54.2. The behaviour of the $\psi$ function of Het. 2 is similar. However, Het. 3 experiences the same increase in $\psi$ at both $\textit{Pe}$ = 0.0542 and 54.2. At lower $\textit{Pe}$ numbers, the solid at the inlet dissolves entirely, but at higher $\textit{Pe}$ numbers only the solid along the channels dissolves, such that the links there undergo the highest increase in velocity and change in $\psi$. When comparing the changes in the links near the inlet and near the outlet at the end of the dissolution simulation, Het. 1 shows little difference for $\textit{Pe}$ = 0.0542, and no difference for $\textit{Pe}$ = 54.2. This reflects the uniformity by which the pore space is dissolved at low $\textit{Pe}$ number and the lack of preferential channels at higher $\textit{Pe}$ number. Het. 2 shows a similar trend, but with a slightly bigger difference for $\textit{Pe}$ = 54.2. However Het. 3 shows a different behaviour: irrespective of the $\textit{Pe}$ number, the change at the inlet and outlet is similar as both locations are within the dissolved channel.

Fig. 13

(Top row) Local $\psi$ functions before ($t/t_1 = 0$) and after ($t/t_1 = 10$) dissolution defined at the links located near the inlet at ${\mathbf {x}}_1 =$ (0.5, 3.7, 3.0) $\times 10 ^{-3}$ m and (Bottom row) local $\psi$ functions at $t/t_1 = 10$ at ${\mathbf {x}}_1$ and near the outlet at ${\mathbf {x}}_2 =$ (12.0, 0.8, 3.0) $\times 10 ^{-3}$ m, for Het. 1, 2 and 3 at $\textit{Pe}$ = 0.0542 and 5.42

Figure 14 shows the propagators at $t/t_1 =$ 0.5 and 1.0, after dissolution processes takes place, compared against the propagators obtained at beginning of the simulation with the original porosity shown in Figure 6. The dissolution process significantly alters the particle propagator distribution and increases the contrast between slow and fast flow regions in all samples. At lower $\textit{Pe}$ number, the particle propagators are no longer able to recover a Gaussian-like distribution even at late times. The sharp cut-off in the high end of the propagator distribution is due to the fact that the particles exited the domain during the observation window $t / t_1$. At $\textit{Pe} = 5.42$ the distribution is marked by a strong stagnant peak and is asymmetrical for all samples. Het. 1 is the only sample that starts to recover a Gaussian-like shape at late times, but still far from the initially observed distribution. For $\textit{Pe} = 5.42$ and 54.2, the distribution mostly reflects the stagnant peak. Overall, the analysis of post-dissolution propagators indicates that dissolution results in heterogeneity signatures with a markedly higher degree of non-Fickian transport than observed initially.

Fig. 14

Particle propagators for (solid lines) Het. 1 with $\beta = 1.8$, Het. 2 with $\beta = 1.2$ and Het. 3 with $\beta = 0.6$ at $t/t_1$ = 0.5 and $t/t_1$ = 1.0, and Péclet numbers of $\textit{Pe}$ = 0.0542, 0.542, 5.42 and 54.2. The results are compared against the initial particle propagators from Figure 6 (dashed lines)

5 Discussion

When considering heterogeneity signatures, the velocity distributions shown in Fig. 5 are key to understanding the initial propagators in Fig. 6 (Bijeljic et al. 2013). The higher probability of transitions faster than the mean velocity increases as the heterogeneity increases from Het. 1 to 3. This is more evident in Het. 3 that shows more displacement for $\zeta / \langle \zeta \rangle > 1$. Furthermore, the velocities at the lower end of the distribution represent longer transit times and stagnant particles. Figure 15 shows the velocity distribution and the contribution of each individual region to the particle transitions at the pore scale associated with the links in the lattice. Bijeljic et al. (2013) showed a similar plot based on pore-scale direct numerical simulations of transport in different carbonate rock samples. As we increase the $\textit{Pe}$ number, we increase the number of links with faster velocity.

Fig. 15

Normalized velocity distributions for the different samples. The lower velocity values contribute to slow and diffusive only transitions. The high velocity values contribute to advective dominated transitions, responsible for the highly mobile tails and the formation of dissolution channels

The dissolution patterns formed for the samples using a constant transport heterogeneity parameter $\beta = 1.8$ are compared in Fig. 9 to the dissolution patterns formed when reducing the value of $\beta =$ 1.2 and 0.6, respectively, for Het. 2 and 3. This reduction is perceived as an increase in heterogeneity at the node and link scale; it increases the probability of a particle to experience slower time transitions. This is highlighted in Fig. 13.

6 Conclusions

We have demonstrated the impact of physical heterogeneity on the effective reaction rate during dissolution on samples of length 15 cm over timescales up to $10^8$ s. We constructed three samples, Het. 1, 2 and 3, characterised by increasing heterogeneity by uniformly distributing solid spheres of zero porosity in a heterogeneous domain. The heterogeneity is first characterized by the velocity distribution. Het. 1 has a narrow velocity distribution near $v_x / \langle v_x \rangle = 1$ reflecting the relative homogeneity of the sample, while Het. 2 and 3 have a wider distribution with a smeared-out tail towards lower velocity values. At the scale of the sample, these resemble a beadpack for Het. 1, a mildly homogeneous carbonate for Het. 2, and a highly heterogeneous carbonate for Het. 3. However, we assume that the solid dissolves with the same batch reaction rate for all three samples. At the scale of the nodes and links, to describe the local transit-time distributions, Eq. 2, we consider $\beta = 1.8$ for Het. 1, $\beta =1.2$ for Het. 2 and $\beta =0.6$ for Het. 3, to better represent difference in heterogeneity in the corresponding velocity fields. Each of these samples were subjected to fluid reactant injection under different advective dominated flow regimes, from low to strongly advective dominated regimes, by choosing Peclét numbers of $\textit{Pe}$ = 0.0542, 0.542, 5.42 and 54.2.

The different $\textit{Pe}$ numbers led to the appearance of two distinct dissolution patterns – a compact or face dissolution for $\textit{Pe}$ = 0.0542, and channelized dissolution for $\textit{Pe}$ = 0.542, 5.42 and 54.2. The emergence of preferential channels in heterogeneous media, as opposed to uniform dissolution, is consistent with experiments in carbonates (Menke et al. 2015, 2017). For all samples and advective regimes, the change in porosity is proportional to time at early times, while the effective reaction rate deviates from late-timescaling behaviour characterised by $1 / \sqrt{t}$, assuming complete mixing. Instead, at late-times we found a power-law scaling $t^{-a}$ with $a \ne 0.5$, as a result of the persistence of incomplete mixing.

The propagator distributions showed the imprint of heterogeneity on its asymmetrical shape, as well as the contrast between slow and fast regions that increased with the dissolution process. The variation in the velocity distribution of Het. 1 is very narrow, and there are almost no stagnant particles. However for Het. 2 and 3, the variation in the velocity distribution is orders of magnitude higher and this is perceived by the amount of stagnant particles for $\textit{Pe}$ = 0.542, 5.42 and 54.2 that experience the highest contrast between the characteristics advective time $t_1$ and diffusive cut-off time $t_2$. After the dissolution process, Het. 1 starts to recover a symmetrical shape at late times, but it is still far from the initial observed state. However Het. 2 and 3 have significant amount of stagnant particles and are asymmetric in shape. Overall, dissolution increases the degree of non-Fickianity on transport.

The more heterogeneous samples had lower late-time reaction rates, as reaction was eventually confined to a small subset of the pore space in preferential channels. An increase in $\textit{Pe}$ also exacerbated the effect of channelling and incomplete mixing, although at early time the reaction rates were higher, due to a greater degree of spreading by advection.

Future work could consider the coupling of a geochemical solver with our transport model, to consider nonlinear higher-order reactions. In addition, the application of this model to a wider range of porous media and flow conditions could be explored. In particular, the transition from incomplete to complete mixing at very long times could be simulated. Finally, the separate influence of sub-grid and macroscopic heterogeneity could be explored through a thorough sensitivity study to the parameters in the truncated power-law CTRW model.

Appendix A: Procedure to Generate Heterogeneous Domains

The 3D samples Het. 1, 2 and 3 used in this paper and described in Section 3.1 are constructed using a simple procedure detailed below and illustrated using a 2D representation of the image and lattice in Fig. 16.

• 1. Create a 3D image with $N_x = 150$ and $N_y = N_z = 50$ grid cells.

  • (a) Create a normally distributed porosity field with mean $\langle \phi _\text {bg} \rangle = 0.3$ and standard deviation $\sigma _{\phi \text {bg}} = 0.1$.

  • (b) Uniformly distribute solid spheres with centres $\left( x_c, y_c, z_c\right)$ and with normally distributed radius with mean $\langle r_1 \rangle = 1.5 \times 10^{-3}$ m, $\langle r_2 \rangle = 3.0 \times 10^{-3}$ m and $\langle r_3 \rangle = 4.5 \times 10^{-3}$ m and standard deviation $\sigma _{r} = 0.2 \langle r \rangle$.

  • (c) For all solid spheres, anywhere $(x-x_c)^2 + (y-y_c)^2 + (z-z_c)^2 < r^2$, the porosity in the grid cell of the image becomes $\phi = 0$.

• 2. Create a regular lattice nodes coincident with the 3D grid cell centres.

  • (a) Populate the porosity of the nodes with the porosity from the 3D image.

Fig. 16

Illustration of the procedure to create the samples Het. 1, 2 and 3. We start with (a) a 3D image with background porosity, (b) sample the radius and centres of several solid spheres, (c) use it to remove porosity from the background porosity image, (d) the original lattice with nodes centres coincident with the 3D image cell centres, (e) the highlighted nodes that will be modified and finally (d) the lattice with the porosity of the nodes mapped from the 3D image with the removed porosity