1 Introduction

The level of mixing of species strongly affects the overall rates of biogeochemical reactions in the subsurface. An appropriate characterization of mixing in geologic formations is of essential importance for the modeling of reactive transport processes in scientific and industrial applications, such as contaminant management in groundwater (Attinger et al. 2009), geological CO\(_2\) sequestration (Kong and Saar 2013; Tutolo et al. 2015; Ma et al. 2019; Grimm Lima et al. 2020), geothermal energy utilization (Spycher et al. 2014), reservoir characterization using tracer tests (Kong et al. 2018; Kittilä et al. 2019, 2020b, a), and miscible displacement in enhanced oil recovery (Terry 2001; Song et al. 2014), to name a few. In porous media, the transport of solutes is typically governed by advection, diffusion, and dispersion processes. Advection of solutes describes the movement of solutes that are carried along with the moving fluid. Diffusion and dispersion processes contribute to the reduction of the solute concentration gradients until a homogeneous concentration field is reached.

The presence of heterogeneity (such as fracture, heterogeneous permeability and porosity) in porous media results in flow heterogeneity (i.e. fluid velocity variation), enhancing the mass exchange across flow streamlines (Werth et al. 2006; Rolle et al. 2009; Chiogna et al. 2011; Yoon et al. 2021; Naets et al. 2022). Due to the non-uniform flow velocity, the non-Fickian transport is more common in heterogeneous media (Berkowitz et al. 2006; Berkowitz and Scher 2009), which has been observed in laboratory experiments (Silliman and Simpson 1987; Hatano and Hatano 1998; Bijeljic et al. 2013b), numerical simulations (Cortis et al. 2004; Klise et al. 2008; Zhang and Benson 2008; Bijeljic et al. 2013a; Yang and Wang 2019), and field studies (Mackay et al. 1986; Gelhar et al. 1992; Sidle et al. 1998; Birk et al. 2005). When the transport of solute is dominated by advection with strong fluid velocity contrasts, the solute plume may undergo stretching, squeezing, and folding (Chiogna et al. 2011; Le Borgne et al. 2013; Rolle et al. 2013; Cirpka et al. 2015), which greatly affects the physical mixing process (Weeks and Sposito 1998).

The mixing of solute can typically be quantified by the evaluation of the transport properties, such as the spatial moments of the solute concentration field (Güven et al. 1984; Mackay et al. 1986; Freyberg 1986; Amaral Souto and Moyne 1997; Ahkami et al. 2020). To delineate the transport properties, different parameters have been derived from the spatial moments, including the ensemble dispersion tensor (Gelhar and Axness 1983) and the effective dispersion coefficients (Dentz and Carrera 2003, 2005). Depending on the scale of measures, mixing can also be quantified locally and globally (Souzy et al. 2018; Wright et al. 2019). The local measures describe the deformation of the solute plume due to fluid velocity gradients, such as the Okubo-Weiss parameter (De Dreuzy et al. 2012), the Cauchy-Green strain tensor (Engdahl et al. 2014), the Lyapunov exponent (Engdahl et al. 2014), and the local strain matrix squared (Aquino and Bolster 2017). The global measures interpret the overall variation in the concentration field over the domain of interest, including the scalar dissipation rate (Le Borgne et al. 2010; Engdahl et al. 2013) and the dilution index (Kitanidis 1994; Rolle et al. 2009; Bolster et al. 2011a; Chiogna et al. 2011, 2012).

Recent developments of imaging techniques and microfluidic fabrication technologies (Karadimitriou and Hassanizadeh 2012; Waheed et al. 2016; Ishutov et al. 2018; Jahanbakhsh et al. 2020) enable better determination of fluid flow and solute transport in reproducible, transparent porous media, in comparison to the experiments conducted in opaque media, for instance, in unconsolidated packed beads (Scheven et al. 2005; Bijeljic et al. 2013b) and in geological rocks such as sandstones (Klise et al. 2008; Gjetvaj et al. 2015) and carbonate rocks (Scheven et al. 2005; Bijeljic et al. 2013a, b), which are associated with large uncertainties regarding measurement interpretations (Yang and Wang 2019). Among the non-invasive imaging methods, laser-induced fluorescence (LIF) has been employed for pore-scale studies of solute transport (e.g., Rashidi et al. 1996; Rashidi 1997; Fontenot and Vigil 2002; Stöhr et al. 2003; Kree and Villermaux 2017; Roth et al. 2021). During an LIF experiment, fluorescent dyes (such as rhodamine B) serve as solute tracers and are injected along with the fluid flow. The fluorescent dyes are then excited by a laser light with a wavelength within the absorption band of the dyes. The dyes then emit light at another wavelength at various intensities as a function of dye concentration. The emitted light is captured by cameras to produce images with which the distribution of dye concentrations can be quantified, based on the fluorescent light intensity (Van Cruyningen et al. 1990; Lozano et al. 1994; Borg et al. 2001; Pietro de et al. 2014). Although published numerical (e.g., Bijeljic et al. 2013b; Oostrom et al. 2016; Dou et al. 2018; Ahkami et al. 2020) and experimental studies have greatly contributed to our understanding of solute transport in porous media, measurements in heterogeneous, in particular fractured, porous media are still sparse. It is thus crucial to acquire quantitative measurements especially of solute concentration fields, that result from solute transport in fractured porous media, which are ubiquitous in geological formations. However, determining solute concentration fields in nature is typically difficult to impossible.

In this work, we report on solute transport in a quasi-two-dimensional (quasi-2D) fractured porous medium, which was fabricated using 3D-printing technology. The medium incorporates distinct heterogeneous features: two porous matrices with different permeabilities, two flow-through fractures, and two dead-end fractures. A fluorescent dye (rhodamine B) was injected as a pulse input into this 3D-printed fractured porous medium, to characterize the role of high-permeability inclusions on solute transport. To assist the interpretation of solute transport, pore-scale fluid velocity fields were also measured, employing particle image velocimetry (PIV) techniques. In the following, we describe in Sect. 2 the employed methods, which includes a detailed description of the 3D-printed fractured porous medium, the LIF experiment setup, the PIV experiment, and the two sets of indicators (i.e. temporal/spatial moments and mixing metrics). Section 3 presents the results and a discussion of the breakthrough curves (as well as temporal moments), mass fractions, spatial moments, and mixing metrics, to elucidate the role of high-permeability inclusions on solute transport in the medium. The conclusions are presented in Sect. 4.

2 Methodology

2.1 Fractured Porous Medium

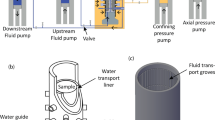
The 3D-printed fractured porous medium for the LIF experiments was fabricated by 3D-LABS GmbH with the MultiJet Modeling technology (3D-LABS 2021). The medium is clear-transparent with an inner dimension of 100 mm in length, 85 mm in width, and 0.3 mm in height. By placing (i.e. printing) square, impermeable, pillars with a dimension of 0.8 \(\times\) 0.8 \(\times\) 0.3 mm\(^3\) inside, we constructed the medium with two porous matrices and four fractures. The two matrices are a low-permeability matrix and a high-permeability matrix with spacings of 0.2 and 0.3 mm, respectively, between the 3D-printed pillars. The permeabilities of the two matrices are numerically calculated to be \(\sim 4.2\times 10^{-10}\) m\(^2\) and \(\sim 9.4\times 10^{-10}\) m\(^2\), respectively, using lattice-Boltzmann methods (Ahkami et al. 2019). In each matrix, we embedded one flow-through fracture and one dead-end fracture (Fig. 1). The flow-through fractures are parallel to the main flow direction, directly connecting the fluid inlet to the fluid outlet of the medium. In contrast, the dead-end fractures are angled with respect to the main flow direction, directing the fluid from the inlet to the left and right, impermeable, boundaries (Fig. 1). The widths of fractures are 2.5 mm in the high-permeability matrix and 2.4 mm in the low-permeability matrix. The fracture permeability is theoretically estimated to be \(7.5\times 10^{-9}\) m\(^2\), using the so-called cubic law with an aperture of 0.3 mm. This fractured porous medium enables us to identify and quantify the effects of different geometrical features, such as rock fractures and matrices, on solute transport. This porous medium geometry has been used previously during Particle Image Velocimetry (PIV) experiments (Ahkami et al. 2019) and during numerical simulations using lattice-Boltzmann methods to investigate single-species mineral precipitation (Ahkami et al. 2020).

Fig. 1
figure 1

The schematic setup of the LIF experiments, where the deionized water and the dye tracers are injected with a high-precision pump into the horizontally placed fractured porous medium. The beam from a pulsed green laser is expanded by a volume expander and is reflected downwards by a mirror to form a light volume, which enters the medium from its top and induces the excitation of the dye. The emitted light is then captured by a camera from the top. The medium consists of a high- and a low-permeability matrix, two dead-end fractures, and two flow-through fractures as described in the main text. The 3D-printed porous matrices are rendered yellow

Full size image

2.2 Setup of the LIF Experiments

During the LIF experiments, the fractured porous medium is placed horizontally. The medium is illuminated from its top by an expanded laser beam with a wavelength of 527 nm, emitted from a pulse laser with a pulse width of 300 ns (Fig. 1). The radiations from the excited fluorescent dyes are captured using a monochrome, 50 MP (6004\(\times\)5291 pixels) CMOS camera at an imaging frequency of 2 FPS (300 ns exposure time) from the top. A 540 nm long-pass filter is attached to the front of the camera lens to filter out the green laser light, only allowing the transmission of the radiated fluorescent light signals. Our imaging system produces single-exposure images with an areal resolution of \(\sim\)21.1 \(\upmu\)m per pixel for the LIF measurements. In this study, the pixel brightness of the captured images is assumed to be proportional to the dye concentration (Hidrovo and Hart 2001; Crimaldi 2008). Compared to the typical LIF measurements in open water without reflection surfaces, surface reflection in porous media does induce extra light, which could be interpreted as solute concentration. In our experiments, this reflection light was observed at the inlet end, where the dye concentration is high. However, the intensity of this reflection light is much smaller compared to the self-emitted light, and only last less than a few seconds after the starting of the experiment. Thus the reflection light could introduce offset in mass balance calculation, but will not change the overall findings of our study.

The fluorescent (rhodamine B) dye is seeded into deionized water and injected into the fractured porous medium as a pulse input (Fig. 1) when the fluid (here deionized water) flow reaches steady-state conditions inside the medium. During the LIF experiments, the fluid flow and the pulse injection of dyes is maintained at a constant rate of Q = 0.03 ml/s using a high-precision pulsation-free pump (neMESYS 2600N, Cetoni) together with a set of valves (Burkert Type 6144-3/2-way flipper solenoid valve), enabling a smooth and pulsation-free transition between the injection of deionized water and the pulse injection of dyes. To be precise, the LIF experiments consist of two stages: (1) during Stage I, the deionized water is circulated to establish a steady-state, saturated (single-phase) flow through the medium; and (2) during Stage II, once the steady-state flow of deionized water is reached, the injection of the deionized water is switched to the injection of the deionized water with the fluorescent dye, yielding a flooding of the dye in a pulsed manner through the medium.

During the experiments, the transient displacements of dyes are registered in a time series of images. The registered images contain not only signals (i.e. the fluorescent light intensity), but also the noise originated by, for example, light distortion and light refraction at the edges of the pillars. In order to improve the signal-to-noise ratio, we subtract from the captured images a reference image to yield the dye concentration. Here, the reference image is the averaged image from the last 5 frames. The reference image captures the background solute concentration of the medium when the fractured medium has been flooded with deionized water for more than 450 s. The subtraction of the reference image suppresses the background noise, uniformity of the expanded laser beam, and the light distortion at the edges of the square pillars (Ahkami et al. 2019).

2.3 Fluid Velocity Measurement with PIV

In this study, we determine the fluid velocities from PIV measurements, following the approach described in our previous paper (Ahkami et al. 2019). Analogous to the approach followed during the LIF experiments, the fractured porous medium is placed horizontally during the PIV experiments. The deionized water is circulated through the medium at the same flow rate of Q = 0.03 ml/s to reach steady-state conditions. The seeding particles used in the PIV measurements are spherical, PMMA, rhodamine B, fluorescent particles with a particle size of 15–20 \(\upmu\)m and a density of \(\rho =1.5\) g/cm\(^{3}\). Unlike the LIF experiments, the medium is perpendicularly illuminated by an upward-diffused laser beam with a wavelength of 532 ± 0.25 nm. The seeding particles are then excited by the illumination, emitting radiation with a wavelength of 590 nm. This emitted light is captured by the same camera as the LIF one, which faces downwards, perpendicularly to the fractured porous medium. A high-pass filter is attached to the front of the camera lens to filter out the laser light, transmitting only the radiation from fluorescent particles. During the PIV experiments, our imaging system produces single-exposure images at 30 FPS with an areal resolution of \(\sim\)17.7 \(\upmu\)m per pixel. To determine the fluid velocity, we follow the Temporo-ensemble PIV method we developed (Ahkami et al. 2019). In the present study, we employ an interrogation window of 5\(\times\)5 pixels, yielding a fluid flow velocity field with an areal resolution of \(\sim\) 30 \(\upmu\)m per velocity vector. The measured fluid velocity field is shown in Fig. 2, and the longitudinally averaged fluid velocity, \(\bar{u}_y=(1/L)\int _0^L u(y) \mathrm{d}y\), is shown in Fig. 11, where L is the length of the fractured domain. The PIV-measured velocity is used to compare with the solute velocity, and more importantly to calculate the flux-related dilution index, described in Sect. 2.6.

2.4 Spatial Moments

In this study, the transport of dyes is characterized using the n-th spatial moment, \(\mathbf {M}_{n}\), of normalized dye concentration fields, including the zeroth, \(M_{0}\), first, \(\mathbf {M}_{1}\), and second, \(\mathbf {M}_{2}\), moments (Horn 1971; Brenner 1980; Adams and Gelhar 1992; Amaral Souto and Moyne 1997; Ahkami et al. 2020; Grimm Lima et al. 2020) for a domain, \(\Omega\),

$$\begin{aligned} \begin{aligned} \mathbf {M}_n&= \int _\Omega C(\mathbf {r},t)\mathbf {r}^n \mathrm{d}\Omega ,\\ C(\mathbf {r},t)&= \frac{1}{255}\big (g(\mathbf {r},t)-g(\mathbf {r},t=0)\big ), \end{aligned} \end{aligned}$$
(1)

where t is time, \(\mathbf {r}=(x,y)\) is the normalized pixel coordinate with \(x=x_p/L\) and \(y=y_p/L\), \(x_p\) and \(y_p\) are lateral (perpendicular to the main flow) and longitudinal (parallel to the main flow) coordinates of pixels, respectively, and L is the medium size in the longitudinal direction (Fig. 2). Here, \(C(\mathbf {r},t)\) represents the normalized solute concentration with respect to the initial concentration at t=0, \(g(\mathbf {r},t)\) is the pixel-wise gray value at location \(\mathbf {r}\) and time t, and 255 is the maximum/saturated gray value. The moments of normalized concentrations, including the center of mass of the normalized concentration field, \(\mathbf {r}_{c}=(x_c,y_c)\), and the variance, \({\sigma }^{2}\), are calculated by (Adams and Gelhar 1992)

$$\begin{aligned} \left. \begin{aligned}&\mathbf {r}_{c}=\mathbf {M}_{1}/M_{0},&\\&{\sigma }^{2} = \mathbf {M}_{2}/M_0-\mathbf {r}_{c}^{2}.&\end{aligned} \right. \end{aligned}$$
(2)

The solute travel velocity can then be determined by the velocity of the gravity center of the solute plume in the domain, \(\mathbf {u}_s=\mathrm{d}\mathbf {r}_{c}/\mathrm{d}t\). The solute dispersion coefficient can then be quantified by \(\mathbf {D}=0.5\mathrm{d}{\sigma }^2/\mathrm{d}t\) (Adams and Gelhar 1992).

2.5 Temporal Moments

Similar to tracer tests in nature, we examine the heterogeneity of the fluid flow field in this analogue-material fractured porous medium conducting a tracer breakthrough curve analysis. Following Kittilä et al. (2019, 2020a, 2020b), the n-th temporal moment, \(M_{t,n}\), of the breakthrough curve can be defined by

$$\begin{aligned} M_{t,n} = \int ^\infty _0 t^n E(t) \mathrm{d}t, \end{aligned}$$
(3)

where \(E=\rho Q \bar{C}_\mathrm{out}/m_\mathrm{inj}\) is the so-called age distribution function, \(\bar{C}_\mathrm{out}\) is the average outlet concentration of the solute, Q is the volumetric flow rate, \(\rho\) is the fluid density, and \(m_\mathrm{inj}\) is the injected solute mass. The solute recovery, R, at the outlet is described by the zeroth temporal moment, \(R=M_{t,0}\), and the mean residence time, \(t_m\), can be calculated using the first and zeroth temporal moments, \(t_m=M_{t,1}/M_{t,0}\). The variance, \(\sigma ^2_t=M_{t,2}/M_{t,0}-t_m^2\), provides a measure of solute spreading (Yu et al. 1999). The longitudinal solute traveling velocity can be calculated as \(u_{t,y}=L/t_m\), and the longitudinal macro-dispersion coefficient can be determined as \(D_{yy}^\mathrm{macro}=0.5 u_{t,y}^3 \sigma ^2_t/L\) (Yu et al. 1999).

2.6 Mixing Metrics

Mixing behaviors of solutes can be described by using the evolution of the scalar dissipation rate (Le Borgne et al. 2010; Engdahl et al. 2013; Boon et al. 2017), \(R_d\) [M\(^2\)/(TL\(^3\))], and the volumetric dilution index (Kitanidis 1994; Bolster et al. 2011a), \(I_d\) [L\(^3\)],

$$\begin{aligned} \left. \begin{aligned}&R_{d}(t)=\int _\Omega D_m \nabla C(\mathbf {r},t)\cdot \nabla C(\mathbf {r},t) \mathrm{d}\Omega ,&\\&I_d(t) = \mathrm {Exp}\left( -\int _\Omega p(\mathbf {r},t) \mathrm {ln} p(\mathbf {r},t) \mathrm{d}\Omega \right) ,&\\&p(\mathbf {r},t)=\frac{C(\mathbf {r},t)}{\int _\Omega C(\mathbf {r},t) \mathrm{d}\Omega },&\end{aligned} \right. \end{aligned}$$
(4)

where \(D_m\) [L\(^2\)/T] is the molecular diffusion coefficient of the solute, \(\Omega\) indicates the domain, where solute mixing occurs, and p [1/L\(^3\)] is the concentration probability function of the solute. Note that in Eq. 4, p is normalized to the total mass of Domain \(\Omega\). The scalar dissipation rate quantifies the rate of mixing and the volumetric dilution index presents the uniformity degree of the solute concentration in the domain of interest.

In contrast to the volumetric dilution index, the flux-related dilution index, \(E_q\) [L\(^3\)/T], describes the mixing of solute along its travel distance when the injection of the solute is continuous (Rolle et al. 2009; Chiogna et al. 2011; Rolle and Kitanidis 2014),

$$\begin{aligned} \left. \begin{aligned}&E_q(y,t) = \mathrm {Exp}\left( -\int _A u_y(\mathbf {r}) p_q(\mathbf {r},t) \mathrm {ln} p_q(\mathbf {r},t) \mathrm{d}A \right) ,&\\&p_q(\mathbf {r},t)=\frac{C(\mathbf {r},t)}{F(\mathbf {r},t)},&\\&F(\mathbf {r},t)=\int _A u_y(\mathbf {r}) C(\mathbf {r},t) \mathrm{d}A,&\end{aligned} \right. \end{aligned}$$
(5)

where \(F(\mathbf {r},t)\) [M/T] is the total solute mass over the transversal cross-sectional area at the location, \(\mathbf {r}\), along the longitudinal axis (here y), \(p_q\) [T/L\(^3\)] is the flux-related probability density function of the solute, A [L\(^2\)] is the cross-sectional area perpendicular to the longitudinal axis, and \(u_y\) [L/T] is the pore-water velocity in the y direction.

3 Results and Discussion

Fluid flow is generally characterized by the dimensionless Reynolds number, Re \(=l u/\nu\), where u is the characteristic fluid velocity, l is a characteristic length, and \(\nu\) is the fluid kinematic viscosity. In our study, Re is estimated to be around 0.7 for the flow in the matrix (with l = 0.3 mm being the medium height and u = 2.35\(\times\)10\(^{-3}\) ms\(^{-1}\) being the mean fluid velocity in the medium) and around 2.4 for the flow in the flow-through fractures (with l = 0.3 mm being the medium height and u = 8.0\(\times\)10\(^{-3}\) ms\(^{-1}\) being the mean fluid velocity in the flow-through fractures (Figs. 2 and 11 ). Note that the PIV-measured fluid velocities in the flow-through fractures match well with the velocity values estimated with the mean solute travel time (\(\sim\)12 s) along the flow-through fractures. Here, the water kinematic viscosity is taken as \(\nu\) = 1.0\(\times\)10\(^{-6}\) m\(^{2}\)s\(^{-1}\) (at 20 \(^\circ\)C).

The transport of solutes is typically characterized by the dimensionless Peclet number, which compares the degree of advective (associated with pore-fluid velocity) to diffusive (associated with solute diffusivity) solute transport. The pore-scale Peclet number, Pe  \(=u l/D_m\), for this study is calculated to be \(\sim\)2000, where the diffusion coefficient of rhodamine B is taken as \(D_m\) = 3.6\(\times\)10\(^{-10}\) m\(^{2}\)s\(^{-1}\) (Gendron et al. 2008), and the characteristic velocity is taken as the mean fluid velocity in the medium, given as u = 2.35\(\times\)10\(^{-3}\) ms\(^{-1}\). This high Peclet number value strongly suggests an advection-dominated transport of the dye (rhodamine B) during our LIF experiments (Ahkami et al. 2020). Alternatively, the above Peclet number can be given as the ratio of a diffusive time scale, \(\tau _\mathrm{diff}=l^2/D_m\), and an advective timescale, \(\tau _\mathrm{adv}=l/u\). Taking u = 2.35\(\times\)10\(^{-3}\) ms\(^{-1}\) and l = 0.3 mm, we can determine \(\tau _\mathrm{adv}\) = 0.13 s and \(\tau _\mathrm{dif}\) = 250 s, for the transport of solute through the medium. Bolster et al. (2011b) suggests that any time earlier than \(\tau _\mathrm{adv}\) is defined as the early time and any time between \(\tau _\mathrm{adv}\) and \(\tau _\mathrm{dif}\) refers to the intermediate pre-asymptotic time. Our study focuses on the transport behavior from the very early to intermediate pre-asymptotic times. In the rest of the paper, we use the dimensionless time, \(t^*=t/\tau _\mathrm{diff}\), to characterize the transport process.

Fig. 2
figure 2

(Left) Sub-domain definitions: \(\Omega ^{Hk}\) and \(\Omega ^{Lk}\) are the regions of high- and low-permeability matrices, respectively. Enlargement of the actual 3D-printed pillars is shown as an inset. The coordinate system origin x-y is set at the center of the medium inlet. (Right) The fluid velocity field of the longitudinal fluid flow direction, measured with the PIV method. The colorbar indicates values in mm/s

Full size image

To examine the effect of high-permeability inclusions (i.e. fractures) on solute transport, two sub-domains are defined, namely \(\Omega ^{Hk}\) and \(\Omega ^{Lk}\), with respect to the high-permeability and low-permeability regions (Fig. 2). Depending on the analysis necessity, the calculations of quantities (e.g. spatial moments and mixing metrics) are conducted on individual sub-domains or on the whole domain. Analyses and explanations will be given in detail when and where the calculated quantities are displayed. The division of the domain also facilitates the assessment of the solute progression and depletion processes associated with the medium heterogeneity. As described in Sect. 2.2, the fractured porous medium is initially saturated and flooded with deionized water at a constant volumetric flow rate of Q = 0.03 ml/s. The injection of solute (rhodamine B) starts after the flow of deionized water reaches steady-state conditions, involving

  1. (1)

    The progression of solute for an injection period of \(t^*= \sim\)0.158 to replace the initial deionized water, and

  2. (2)

    The depletion of solute by the subsequent injection of deionized water for the remainder of the experiment.

Here, solute progression and depletion are separated at the time (\(t^*=\sim\)0.158) when the total mass of the solute reaches its maximum in the fractured medium (see Sect. 3.2).

3.1 Progression and Depletion of Solute

Figure 3 shows the snapshots of the solute concentration fields, \(C(\mathbf {r},t)\), during solute progression and depletion at \(t^*\)=0.056, 0.118, 0.158, and 0.298. These four time instances sequentially correspond to the times, when the total solute mass change rate reaches its maximum (also the mean inlet solute concentration reaches its maximum) at \(t_\mathrm{inlet}^p\)=0.056, when the mean outlet solute concentration reaches its maximum at \(t_\mathrm{outlet}^p\)=0.118, when the total solute mass reaches its maximum at \(t_\mathrm{mass}^p\)=0.158, and when the total solute mass change rate reaches its minimum at \(t_\mathrm{mass}^v\)=0.298 (Fig. 4). The snapshot at \(t_\mathrm{inlet}^p\)=0.056 (top-left in Fig. 3) shows the early time of the progression, when the solute penetrates into the high-permeability matrix and its embedded dead-end fracture and flow-through fractures. In particular, the solute has advanced much further towards the outlet via the flow-through fractures, due to the much higher fluid velocities along them, compared to the fluid velocities in the matrices.

Fig. 3
figure 3

Snapshots of the normalized concentration fields, \(C(\mathbf {r},t)\), during the transport of solute at \(t^*\)=0.056, 0.118, 0.158, and 0.298

Full size image

Further progression of solute, as shown in the snapshot at \(t_\mathrm{outlet}^p\)=0.118, promotes the spreading of solute from the inlet end towards the outlet end. The snapshot clearly indicates that the spreading of solute is faster in the high-permeability matrix, largely driven by the advective transport in the matrix and the strong mass exchange between fractures and matrix resulting in an off-center distribution of solute (i.e. more solute is in the high-permeability region, \(\Omega ^{Hk}\)). In addition, a concentration discontinuity can be observed between the high- and the low-permeability regions. The high-permeability region, \(\Omega ^{Hk}\)), has almost been swept by the solute, while the downstream end of the low-permeability region, \(\Omega ^{Lk}\)), is still free of solute. This emphasizes and confirms that, during advection-dominated transport processes, the preferential flow paths (e.g. fractures, or high-permeability inclusions) strongly dominate the transport of solutes, particularly during the early progression time. The observed effect of preferential flow paths for the displacement of tracers, in an advection-dominated systems, is numerically confirmed by our lattice-Boltzmann simulations (Ahkami et al. 2020).

The depletion of solute commences right after the total solute mass reaches its maximum at \(t_\mathrm{mass}^p\)=0.158. Figure 3 illustrates the snapshots of the solute concentration fields, \(C(\mathbf {r},t)\), during the depletion of solute at \(t_\mathrm{mass}^v\)=0.298, where the subsequent injection of the deionized water dilutes the solute in the high-permeability region, \(\Omega ^{Hk}\), and its embedded flow-through and the dead-end fractures, near the inlet of the medium. With further injection of deionized water, the displacement of solute commences in the low-permeability region, \(\Omega ^{Lk}\), whilst the solute spreads further into the downstream and lateral regions. Similar to the progression process, the solute is preferably removed along the preferential flow paths or high-permeability inclusions within the medium.

3.2 Breakthrough Curve and Solute Mass

Fig. 4
figure 4

Normalized total solute mass, \(M_0^*\) (blue line), normalized solute mass change rate, \(\frac{\mathrm{d}M_0^*}{\mathrm{d}t}\) (red-dashed line), the averaged inlet solute concentration (green line), and the solute breakthrough curve (purple line) at the outlet, against the dimensionless time, \(t^*\). Here, all quantities are normalized to their individual maxima

Full size image

Figure 4 shows the normalized zeroth moment (Eq. 1), \(M_0^*\), of the whole medium domain, the normalized change rate of solute mass, \(\frac{\mathrm{d}M_0^*}{dt}\), the normalized average solute concentration, \(\bar{C}_\mathrm{in}^*\), at the fluid inlet (\(y=0\)), and the normalized average solute concentration, \(\bar{C}_\mathrm{out}^*\), at the fluid outlet (\(y=y_\mathrm{max}\)), i.e. the solute breakthrough curve, against the injected PVs. Here, \(M_0^*=M_0/\max (M_0)\), \(\frac{\mathrm{d}M_0^*}{\mathrm{d}t}=\frac{\mathrm{d}M_0}{\mathrm{d}t}/\max (\frac{\mathrm{d}M_0}{\mathrm{d}t})\), \(\bar{C}_\mathrm{in}^*=\bar{C}_{in}/\max (\bar{C}_\mathrm{in})\), where \(\bar{C}_\mathrm{in}=\frac{1}{w_f}\int C(x,y_\mathrm{max})\mathrm{d}x\), and \(\bar{C}_\mathrm{out}^*=\bar{C}_\mathrm{out}/\max (\bar{C}_\mathrm{out})\), where \(\bar{C}_\mathrm{out}=\frac{1}{w_f}\int C(x,y_\mathrm{max})\mathrm{d}x\), and \(w_f\)=85 mm is the width of the domain. In other words, the normalization is subjected to their corresponding maximum values during the whole experiment. Note that \(t^*\)=0 corresponds to the time when the solute enters the medium inlet.

During the progression process, \(\frac{\mathrm{d}M_0^*}{\mathrm{d}t}\) first largely follows the evolution of the mean inlet concentration until \(t^*=t_\mathrm{inlet}^p\). Afterwards, \(\frac{\mathrm{d}M_0^*}{\mathrm{d}t}\) starts to decrease, and reaches zero when \(M_0^*\) is at its maximum at \(t^*=t_\mathrm{mass}^p\). Figure 4 also indicates that the peak arrival time of the solute (i.e. \(\bar{C}_\mathrm{out}^*\)) is earlier than the peak  arrival time (i.e. \(t_\mathrm{mass}^p\)) of total solute mass in the medium. As shown in Fig. 3, the solute mass is largely transported through the flow-through fractures before \(t^*=t_\mathrm{mass}^p\). This means that the peaks in the solute breakthrough curves are mainly controlled by the solute transport in the flow-through fractures (also see the breakthrough curves in Fig. 5). Interestingly, a relative higher peak is observed in the breakthrough curve for the low-permeability region (\(\Omega ^{Lk}\)), compared to the one for the high-permeability region (\(\Omega ^{Hk}\)). This observation seems counter intuitive at first glance, because much more solute mass enters \(\Omega ^{Hk}\), as shown by the solute mass fraction in Figs. 5 and 10. However, because of the high permeability contrast between the fracture and the matrix in \(\Omega ^{Lk}\), much more mass is transported through the flow-through fracture in \(\Omega ^{Lk}\) before \(t^*=t_\mathrm{outlet}^p\), compared to the matrix of \(\Omega ^{Lk}\). In contrast, because of the low permeability contrast between the fracture and matrix in \(\Omega ^{Hk}\), solute mass can relatively easily enter the matrix of \(\Omega ^{Hk}\), leading to a “dilution" effect in the outlet solute concentration of \(\Omega ^{Hk}\), thus slightly flatting the outlet solute concentration profile over time.

The depletion of solute starts at \(t^*=t_\mathrm{mass}^p\), when \(M_0^*\) reaches its maximum (Fig. 4). Between \(t^*\)=\(\sim\)0.21\(-\)0.3, the solute breakthrough curve of the whole medium shows nearly constant mean outlet solute concentrations, due to the competition between the rebound of the outlet solute concentration of \(\Omega ^{Hk}\) and the continuous decline of the outlet solute concentration of \(\Omega ^{Lk}\) (Fig. 5), because the inlet solute concentrations of the whole medium, of \(\Omega ^{Hk}\), and of \(\Omega ^{Lk}\) are continuously declining (Figs. 4 and 10 ). As shown in Fig. 3, the rebound of the outlet solute concentration of \(\Omega ^{Hk}\) is supported by the arrival of the solute plume in the matrix of \(\Omega ^{Hk}\) (specifically at the right edge of \(\Omega ^{Hk}\)). However, no such secondary solute plume can be observed in \(\Omega ^{Lk}\), thus no rebound can be seen in the solute outlet concentration.

Fig. 5
figure 5

Solute mass fraction, \(m_f\), and mean solute outlet concentration, \(\bar{C}_\mathrm{out}^*\), of Regions \(\Omega ^{Hk}\) and \(\Omega ^{Lk}\), against the dimensionless time, \(t^*\). Here the regional mean outlet concentration is normalized to the maximum of the mean outlet concentration of the whole domain

Full size image

Figure 5 shows the evolution of solute mass fraction, \(m_f^i=M_{0}^i/M_{0}^\mathrm{tot}\), of the two sub-domains (\(\Omega ^{Hk}\) and \(\Omega ^{Lk}\)). Here, \(M_{0}^i\) and \(M_{0}^\mathrm{tot}\) are the zeroth moments in the i-region and the whole domain, respectively. Thus, the evolution of the solute mass fraction describes the solute mass retention evolution during the experiment. The high-permeability region retains up to \(\sim\)70% of the total injected solute mass after the start of solute injection, but slowly reaches a continuous decline in solute mass fraction and stabilizes at a bit more than 50% until the end of the experiment is reached. This high solute mass retention is mainly caused by the high advective solute mass flux into \(\Omega ^{Hk}\) (Figs. 10 and 11 ). The unevenly distributed mass flux also introduces a discontinuity in solute concentration between \(\Omega ^{Hk}\) and \(\Omega ^{Lk}\), resulting in an asymmetrical solute plume around the longitudinal axis, observed during the solute progression process (Fig. 3).

The aforementioned observations on solute breakthrough curves and solute mass distribution suggest that the high-permeability inclusions (here fractures) and their permeability contrast play an important role on solute transport processes. Our experimental results confirm that the high-permeability inclusions do serve as preferential flow paths for solute transport, and the higher the matrix permeability, the more solute mass will enter into this matrix. However, depending on the fluid velocity contrast (or permeability contrast) between the included high-permeability features and the hosting porous medium matrix, solute breakthrough curves can behave quite differently, as shown in Fig. 5. A smaller permeability contrast could yield multiple peaks in the solute breakthrough curves, illustrated by the breakthrough curve of \(\Omega ^{Hk}\). In contrast, a higher permeability contrast can elevate the peak magnitude of the solute breakthrough curve, illustrated by the breakthrough curve of \(\Omega ^{Lk}\). The evolution of the three solute breakthrough curves also indicates that Region \(\Omega ^{Hk}\) influences more significantly the overall solute transport in the medium, due to its higher permeability, than Region \(\Omega ^{Lk}\).

3.3 Solute Velocity and Dispersion Coefficient

Fig. 6
figure 6

a Normalized longitudinal solute velocity of the center of the solute mass. b Normalized longitudinal solute dispersion coefficient. Here the inset shows the relative positions of the center of the solute mass. c Normalized transversal solute dispersion coefficient, against the dimensionless time, \(t^*\). The superscripts Hk and Lk label the variables for Regions \(\Omega ^{Hk}\) and \(\Omega ^{Lk}\), respectively, and \(\Omega\) stands for the whole medium

Full size image

Figure 6a shows the normalized longitudinal solute velocities, namely \(u_y^*\), \(u_y^{*,Hk}\), and \(u_y^{*,Lk}\), of the centers of solute mass, in \(\Omega\) (the whole medium), Region \(\Omega ^{Hk}\), and Region \(\Omega ^{Lk}\), respectively. We decide not to examine the transversal solute velocities due to the strong influence of the solute inlet on a limited domain size. In the current setup, \(y_c\)=0.5 implies that the center of solute mass sits at the center of the medium, and \(y_c<\)0.5 or \(y_c>\)0.5 describes an eccentric position of the solute plume towards the inlet or the outlet of the medium, respectively. Positive and negative values of \(x_c\) imply an eccentric position of the solute plume in \(\Omega ^{Lk}\) and \(\Omega ^{Hk}\), respectively. Note that here \(x_c\) and \(y_c\) are relative coordinates, which are normalized to the longitudinal length of the medium (see Sect. 2.4). The evolution of the center of solute mass confirms the preferential entry of solute into \(\Omega ^{Hk}\) during the solute progression process and the preferential flooding of solute in \(\Omega ^{Hk}\) during the depletion process. The center of mass of the solute plume in both \(\Omega ^{Lk}\) and \(\Omega ^{Hk}\) moves slowly towards the sidewall of the medium. This movement is largely caused by the spreading of solute along the dead-end fractures and later flooding of deionized water during the solute depletion process, which drives the solute mass to regions of low fluid velocities. The center of solute mass eventually stays at the halfway point along the longitudinal direction, indicating equally weighted spatial distributions of solute mass in the medium.

Figure 6a shows that \(u_y^*\), \(u_y^{*,Hk}\), and \(u_y^{*,Lk}\) reach their maxima shortly after \(t^*=t_\mathrm{inlet}^p\). Because of the limited domain size in comparison to the relatively “long" duration of the solute injection pulse (Fig. 4), thereby preventing steady-state dispersion, \(u_y^*\) and \(u_y^{*,Hk}\) can only reach about half of the mean fluid velocity and, interestingly, \(u_y^{*,Lk}\) can reach more than 60% of the mean fluid velocity. Taking the breakthrough curves in Figs. 4 and 5 with their temporal moments, one can calculate the mean solute residence times, 84.0 s, 90 s, and 68.7 s for \(\Omega\) (the whole medium), \(\Omega ^{Hk}\), and \(\Omega ^{Lk}\), respectively. These residence times yield the normalized solute velocity, \(u_{t,y}^*=u_{t,y}/u\), as 0.51, 0.47, and 0.62, for \(\Omega\), \(\Omega ^{Hk}\), and \(\Omega ^{Lk}\), respectively. These numbers match well with the peak longitudinal velocities (\(u_y^*\), \(u_y^{*,Hk}\), and \(u_y^{*,Lk}\)), shown in Fig. 6a. These results again confirm the influence of the permeability contrast between the high-permeability inclusions and the hosting porous medium matrix on solute transport. A higher contrast prevents the entering of solute into the matrix but promotes the fast transport of solute along the high-permeability inclusions, leading to a higher apparent solute migration speed.

The spreading of solutes can be characterized by their dispersion coefficient. Here, we only examine the longitudinal and transversal components of \(\mathbf {D}\), i.e. \(D_{yy}\) and \(D_{xx}\), as shown in Figs. 6b, d. Instead of presenting the actual values, we plot the normalized longitudinal and transversal solute dispersion coefficients, \(D_{xx}^*=D_{xx}/D_m\) and \(D_{yy}^*=D_{yy}/D_m\), for the whole medium, \(D_{xx}^{*,Hk}=D_{xx}^{Hk}/D_m\) and \(D_{yy}^{*,Hk}=D_{yy}^{Hk}/D_m\), for \(\Omega ^{Hk}\), and \(D_{xx}^{*,Lk}=D_{xx}^{Lk}/D_m\) and \(D_{yy}^{*,Lk}=D_{yy}^{Lk}/D_m\), for \(\Omega ^{Lk}\). Similar to the longitudinal solute velocity, \(D_{yy}^*\), \(D_{yy}^{*,Hk}\), and \(D_{yy}^{*,Lk}\) reach their peak values shortly after \(t^*=t_\mathrm{inlet}^p\). Furthermore, the peak of \(D_{yy}^{*,Lk}\) is about twice the peak of both \(D_{yy}^*\) and of \(D_{yy}^{*,Hk}\), and \(D_{yy}^{*,Lk}\) shows a much faster drop from its peak value and becomes negative between \(t^*\)= 0.11\(-\)0.21 (right after \(t_\mathrm{outlet}^p\) and before \(t_\mathrm{mass}^v\)). The negative \(D_{yy}^{*,Lk}\) is largely due to the quick depletion of the solute mass in the high-permeability inclusion (in particular in the flow-though fracture), leading to the longitudinal “shrinking" of the solute plume in \(\Omega ^{Lk}\). The rebound of \(D_{yy}^{*,Lk}\) is caused by the release of solute mass from the dead-end fracture into the down-stream matrix, as shown in Fig. 3. Using the temporal moments from the breakthrough curves, the normalized macro-dispersion coefficient, \(D_\mathrm{macro}^*=D_\mathrm{macro}/D_m\), can be calculated to be 1.32\(\times\)10\(^5\), 1.19\(\times\)10\(^5\), and 1.37\(\times\)10\(^5\), for \(\Omega\) (the whole medium), \(\Omega ^{Hk}\), and \(\Omega ^{Lk}\), respectively. Aside from having about twice the peak values of \(D_{yy}^*\), \(D_{yy}^{*,Hk}\), and \(D_{yy}^{*,Lk}\), the temporal moments yield the same sequential order for dispersion coefficients of \(\Omega\) (the whole medium), \(\Omega ^{Hk}\), and \(\Omega ^{Lk}\), as the one obtained from the spatial moments. In contrast to the longitudinal dispersion coefficient, the transversal dispersion coefficient is strongly controlled by the lateral spreading of solute at the inlet (e.g. the first peaks of \(D_{xx}^*\) and \(D_{xx}^{*,Hk}\)) and later the transport of solute along the dead-end fractures (e.g. the second peak of \(D_{xx}^*\) and the first peak of \(D_{xx}^{*,Lk}\)). Because of the low permeability contrast between the fractures and the matrix in \(\Omega ^{Hk}\), the solute front moves faster than the one in the dead-end fracture, so that the solute spreading in the dead-end fracture in \(\Omega ^{Hk}\) is not showing a second peak in \(D_{xx}^{*,Hk}\). These results further validate the influence of the permeability contrast between the high-permeability inclusions and the hosting matrix on solute transport.

3.4 Solute Mixing

The above discussion on temporal and spatial moments indicate that permeability contrasts between fractures and their hosting matrices play an important role in the spreading of solute and in the solute retention capacity. In this section, we investigate the influence of permeability contrasts on the solute mixing behavior, using the mixing metrics defined in Sect. 2.6. Strictly speaking, both the scalar dissipation rate and the volumetric dilution index (Eq. 4) are typically defined for a “closed” or “unbounded" system, where the total mass is considered to be conservative in the region of interest (Kitanidis 1994; Rolle et al. 2009; Bolster et al. 2011a; Chiogna et al. 2011, 2012; Engdahl et al. 2013). For our limited open region, the values of the calculated scalar dissipation rate and volumetric dilution index is apparently associated with the solute mass in the region. For the same reason, the flux-related dilution index (Eq. 5) appears to be a more appropriate measure (Rolle et al. 2009).

Fig. 7
figure 7

a Dissipation rate for \(\Omega\) (the whole medium), \(\Omega ^{Hk}\), and \(\Omega ^{Lk}\), against the dimensionless time, \(t^*\). The inset displays the dissipation rate against the mass change rate for \(\Omega\) (the whole medium), \(\Omega ^{Hk}\), and \(\Omega ^{Lk}\). b Dissipation rate, normalized by the maximum mass of the respective region, against \(t^*\). The inset displays the dissipation rate, normalized by the maximum mass of the respective region, against the mass change rate, normalized by the maximum mass of the respective region

Full size image

Figure 7 shows the evolution of the scalar dissipation rates, namely \(R_d\), \(R_d^{Hk}\), and \(R_d^{Lk}\), in Regions \(\Omega\) (the whole medium), \(\Omega ^{Hk}\), and \(\Omega ^{Lk}\), respectively. The increase and decrease in the magnitude of the dissipation rate suggest an enhancement (by shearing of the fluid) and a degradation (by dispersion and diffusion of the solute) of the concentration contrast in the domain under consideration, respectively. In open systems, as shown in Eq. 4, besides the redistribution of solute mass in the system, the dissipation rate is strongly influenced by the mass change rate: the dissipation rate first increases when the total solute mass increases, and reaches its peak value after the peak arrival of the total solute mass (indicated by \(dM_0^i/dt\)=0), followed by a decrease as the total solute mass decreases (insets in Fig. 7). As expected, solute progression enhances solute concentration contrasts in all regions (Fig. 3), resulting in an increase in the mixing rates (the magnitude of the dissipation rate increases). Region \(\Omega ^{Lk}\) clearly exhibits the lowest mixing rate, caused by having the highest contrast between the fracture permeability and the matrix permeability. To be able to interpret the influence of high-permeability inclusion on solute mixing, we propose a normalization of the scalar dissipation rate with respect to the maximum total mass in the region of interest, as shown in Fig. 7b. This normalization clearly differentiates the role of permeability contrast on solute mixing: because of the slower migration of solute mass into the matrix of the Region \(\Omega ^{Lk}\) than the one in the Region \(\Omega ^{Hk}\), the Region \(\Omega ^{Lk}\) yields the lowest and the highest concentration contrast during the progression and depletion of solute, respectively. The highly advective solute transport in the matrix of the Region \(\Omega ^{Hk}\) induces strong solute dispersion, which brings down the concentration contrast during the depletion of solute. Figure 7b shows a similar scaling of \(R_d/\mathrm{max}(M_0)\propto (t^*)^{-6.5}\) at \(t^*\)=0.5\(-\)1.1, which eventually evolves into \(R_d/\mathrm{max}(M_0)\propto (t^*)^{-4.0}\) when \(t^*\) is over 1.30, for all regions (i.e. Regions \(\Omega\), \(\Omega ^{Hk}\), and \(\Omega ^{Lk}\)) during the depletion of solute, indicating a non-Fickian transport (Le Borgne et al. 2010, 2013; Engdahl et al. 2013).

Fig. 8
figure 8

Volumetric dilution indices (a) and the rate of increase of the volumetric dilution index (b) for \(\Omega\) (the whole medium), \(\Omega ^{Hk}\), and \(\Omega ^{Lk}\), against the dimensionless time, \(t^*\). The inset in (a) shows the volumetric dilution index normalized by the maximum mass in the respective region

Full size image

To distinguish the occupation of pore volume due to solute dilution from due to solute spreading (e.g. plume deformation and stretching due to advective transport), Kitanidis (1994) introduced the volumetric dilution index to describe the pore volume occupied by solute dilution. Figure 8a shows the evolution of the volumetric dilution indices (\(I_d\), \(I_d^{Hk}\) and \(I_d^{Lk}\)) and the rate of increase of the volumetric dilution index (\(\mathrm{d}ln(I_d)/\mathrm{d}t\), \(\mathrm{d}ln(I_d^{Hk})/\mathrm{d}t\), and \(\mathrm{d}ln(I_\mathrm{d}^{Lk})/\mathrm{d}t\)) in Regions \(\Omega\) (the whole medium), \(\Omega ^{Hk}\), and \(\Omega ^{Lk}\). In our experiment, the volumetric dilution indices first increase to their maxima (slightly after the peak arrival of the regional total mass), and then slowly drop back to zero, due to the leaving of solute mass which eventually leads to the decrease in the pore volume occupied by solute dilution and the dilution index. The inset in Fig. 8a shows a consistent scaling of \(I_d/\mathrm{max}(M_0)\propto (t^*)^{-2.5}\) for all regions (i.e. Regions \(\Omega\), \(\Omega ^{Hk}\), and \(\Omega ^{Lk}\)), when \(t^*\) is over 0.5 (during the depletion of solute). Except for the first few measurements (which are strongly influenced by image noise due to the low solute mass), the rate of increase shows a monotonic decrease towards zero. Figure 8 shows a higher pore volume occupation and a higher rate of increase in \(\Omega ^{Hk}\), compared to \(\Omega ^{Lk}\). As argued by Kitanidis (1994), although purely advective solute transport has no direct effect on the solute dilution rate, advective transport stretches the plume shape and enlarges the regions with steep concentration gradients, resulting in significant increases in solute dilution in the long run. Compared to \(\Omega ^{Lk}\), \(\Omega ^{Hk}\) has larger pores and a larger permeability, therefore logically displaying a more striated plume shape (Fig. 3), resulting in higher solute dilution rates (Fig. 8). One must also keep in mind that \(\Omega ^{Lk}\) and \(\Omega ^{Hk}\) have extremely close rates of increase, which are proportional to the local dispersion coefficients (Kitanidis 1994), caused by their similarity in transversal fluid velocities and pore structures.

Fig. 9
figure 9

Flux-related dilution index in (a) \(\Omega\) (the whole medium), (b) \(\Omega ^{Hk}\), and (c) \(\Omega ^{Lk}\). Shown are only up to t*=0.5, because the indices are constant for the remainder of the experiment

Full size image

Because of the relatively “long" injection pulse, with respect to the limited domain size, we further examine the solute mixing behaviors in the fractured medium, using the flux-related dilution index (Eq. 5). Physically, the flux-related dilution index describes the dilution of a solute through the distribution of a given solute mass flux over a larger fluid flux (Rolle et al. 2009), thereby presenting the effective volumetric fluid flux transferring the solute mass flux across a given cross-section perpendicular to the longitudinal axis (here y). Figure 9 shows the evolution of the flux-related dilution indices, namely \(E_q\), \(E_q^{Hk}\), and \(E_q^{Lk}\), in \(\Omega\) (the whole medium), \(\Omega ^{Hk}\), and \(\Omega ^{Lk}\), respectively. The corresponding mass flux evolutions are plotted in Fig. 12. Because we have different spatial resolutions of the solute concentration and fluid velocity fields (see Sects. 2.2 and 2.3 ), the flux-related dilution index is calculated with pore-averaged solute concentrations and longitudinal fluid velocities. Figure 9 shows that at a given longitudinal position y, \(E_q\), \(E_q^{Hk}\), and \(E_q^{Lk}\) monotonically increase and level off during later injected pore volumes. That the flux-related dilution index levels off indicates a homogeneously distributed mass flux across the cross-section at a later time. Along the longitudinal axis, at a given time instance, the flux-related dilution index displays first a decreasing trend, up to \(y=\sim\)0.9 (slightly behind where the dead-end fractures end), and then a rebound until the outlet of the medium is reached. The decrease of the flux-related dilution index suggests a “converging" mass flux, where the convergence of the mass flux first occurs along the high-permeability inclusions (i.e. fractures) during early times of solute injection and later in the matrix, after the flooding of fractures with deionized water. This is different from typical applications of the flux-related dilution index, where continuous solute injection occurs (Rolle et al. 2009, 2013; Rolle and Kitanidis 2014; Chiogna et al. 2011, 2012). As shown in Fig. 3, relatively highly striated plume tails can be see along the streamlines of dead-end fractures and in the center of the medium (around the interface between \(\Omega ^{Hk}\) and \(\Omega ^{Lk}\)) during later times. Compared to \(\Omega ^{Hk}\), \(\Omega ^{Lk}\) shows relatively low solute dilution indices due to its smaller pore size and high permeability contrast with respect to its high-permeability inclusions.

4 Conclusion

In this contribution, laser-induced fluorescence (LIF) and particle image velocimetry (PIV) experiments were conducted to address the transport of solutes in a 3D-printed, fractured porous medium. A fluorescent (rhodamine B) dye solute (with deionized water) was injected into the medium as a pulse input at a constant flow rate. The dye (i.e. solute) concentration is linearly interpreted from the brightness of the radiated fluorescent emissions. We address the role of permeability contrast between the high-permeability inclusions (here fractures) and their hosting porous medium matrix on the transport of solutes, analyzing solute breakthrough curves and their temporal moments, and spatial moments, mass fractions, and mixing metrics of concentration fields. With the same high-permeability inclusions, compared to a high-permeability matrix, the low-permeability matrix (together with its inclusions) displays a higher concentration peak in its breakthrough curve, but hosts less solute mass, due to the existence of flow-through fractures. Moreover, compared to a high-permeability matrix, the low-permeability matrix (together with its inclusions) displays a larger peak solute velocity (determined using first temporal and spatial moments) and a higher peak longitudinal dispersion coefficient. As shown by the calculated dissipation rate, the high-permeability inclusions strongly influence the mixing rate, and a high-permeability matrix (together with its inclusions) offers higher mixing rates, compared to a low-permeability matrix. The normalization of the scalar dissipation rate with respect to the maximum regional solute mass offers a general examination of solute mixing in an open, limited region, where the total solute mass varies over time, and suggests a similar scaling of the scalar dissipation rate against time for all regions. Similarly, a high-permeability matrix (together with its inclusions) results in more pore volumes being occupied by the solute, compared to the low-permeability matrix, as indicated by the volumetric dilution index. The normalization of the volumetric dilution index with respect to the maximum regional solute mass also yields a consistent scaling of the volumetric dilution index against time for all investigated regions. The rate of increase in the volumetric dilution index also clearly captures the similarity between the local transversal solute dispersion in the high- and low-permeability matrices, due to their similar transversal fluid velocities and pore structures. The consistency in the scaling of the scalar dissipation rate and the volumetric dilution index against time is largely due to the similar fluid velocity field between the regions, as demonstrated by the fluid velocity measurement. Our integrated LIF–PIV measurements allow calculating the flux-related dilution index using pore-scale fluid velocities. The flux-related dilution index clearly captures the striated tails along the streamlines in dead-end fractures and around the interface between the high- and low-permeability matrices. Our study provides insights into the interplay between the geometric features of the fractured porous medium and solute transport behaviors.