The Co-Moving Velocity in Immiscible Two-Phase Flow in Porous Media

Abstract

We present a continuum (i.e., an effective) description of immiscible two-phase flow in porous media characterized by two fields, the pressure and the saturation. Gradients in these two fields are the driving forces that move the immiscible fluids around. The fluids are characterized by two seepage velocity fields, one for each fluid. Following Hansen et al. (Transport in Porous Media, 125, 565 (2018)), we construct a two-way transformation between the velocity couple consisting of the seepage velocity of each fluid, to a velocity couple consisting of the average seepage velocity of both fluids and a new velocity parameter, the co-moving velocity. The co-moving velocity is related but not equal to velocity difference between the two immiscible fluids. The two-way mapping, the mass conservation equation and the constitutive equations for the average seepage velocity and the co-moving velocity form a closed set of equations that determine the flow. There is growing experimental, computational and theoretical evidence that constitutive equation for the average seepage velocity has the form of a power law in the pressure gradient over a wide range of capillary numbers. Through the transformation between the two velocity couples, this constitutive equation may be taken directly into account in the equations describing the flow of each fluid. This is, e.g., not possible using relative permeability theory. By reverse engineering relative permeability data from the literature, we construct the constitutive equation for the co-moving velocity. We also calculate the co-moving constitutive equation using a dynamic pore network model over a wide range of parameters, from where the flow is viscosity dominated to where the capillary and viscous forces compete. Both the relative permeability data from the literature and the dynamic pore network model give the same very simple functional form for the constitutive equation over the whole range of parameters.

1 Introduction

When two immiscible fluids compete for the same pore space, we are dealing with immiscible two-phase flow in porous media (Bear 1988). A holy grail in porous media research is to find a proper description of immiscible two-phase flow at the continuum level, i.e., at scales where the porous medium may be treated as a continuum. Our understanding of immiscible two-phase flow at the pore level is increasing at a very high rate due to advances in experimental techniques combined with an explosive growth in computer power (Blunt 2017). Still, the gap in scales between the physics at the pore level and a continuum description remains huge and the bridges that have been built so far across this gap are either complicated to cross or rather rickety. To the latter class, we find the still dominating theory, first proposed by Wyckoff and Botset in 1936 (Wyckoff and Botset 1936) and with an essential amendment by Leverett in 1940 (Leverett 1940), namely relative permeability theory. The basic idea behind this theory is the following: Put yourself in the place of one of the two immiscible fluids. What does this fluid see? It sees a space in which it can flow limited by the solid matrix of the porous medium, but also by the other fluid. This reduces its mobility in the porous medium by a factor known as the relative permeability for that fluid. And here is the rickety part: this reduction of available space — expressed through the saturation — is assumed to be the only parameter affecting the reduction factor or relative permeability. This is a very strong statement and clearly does not take into account that the distribution and shape of the immiscible fluid clusters will depend on how fast the fluids are flowing, and that these two factors affect the reduction of the permeability. Still, in the range of flow rates relevant for many industrial applications, this assumption works pretty well. It therefore remains the essential work horse for practical applications.

Thermodynamically Constrained Averaging Theory (TCAT) (Hassanizadeh and Gray 1990, 1993a, b; Niessner et al. 2011; Gray and Miller 2014) is a very different approach to immiscible two-phase flow problem. The TCAT approach is generic and not particular to two-fluid flow problems. It is based on thermodynamically consistent definitions made at the macro-scale based on volume averages of pore-scale thermodynamic quantities. Closure relations are then formulated at the macro-scale along the lines of the homogenization approach of Whitaker (1986). A key advantage of TCAT is that all quantities are explicitly defined in terms of pore-scale quantities. For example, the pressure that appears in Darcy’s law would be formally defined as a volume average of the pore-scale pressure field. A key disadvantage of TCAT is that very many averaged variables are produced, and many complicated assumptions are needed to derive useful results.

Another development somewhat along the same lines, based on non-equilibrium thermodynamics uses Euler homogeneity to define the up-scaled pressure. From this, Kjelstrup et al. derive constitutive equations for the flow (Kjelstrup et al. 2018, 2019).

Another class of theories is based on detailed and specific assumptions concerning the physics involved. An example is Local Porosity Theory (Hilfer and Besserer 2000; Hilfer 2006a, b, c; Hilfer and Döster 2010; Döster et al. 2012). A very different approach is DeProf (Decomposition in Prototype Flow) theory which is a fluid mechanical model combined with non-equilibrium statistical mechanics based on a classification scheme of fluid configurations at the pore level (Valavanides et al. 1998; Valavanides 2012, 2018).

Recent work (Hansen et al. 2018; Roy et al. 2020) has explored a new approach to immiscible two-phase flow in porous media based on Euler homogeneity. It provides a transformation from the seepage velocity of each fluid to another pair of fluid velocities, the average seepage velocity and the co-moving velocity. The co-moving velocity, as we shall see, is a velocity parameter that appears as a result of the Euler scaling assumption, which is not associated with any material transport. The transformation is reversible: knowing the average seepage velocity and the co-moving velocity, one can determine the seepage velocity of each fluid. It is the aim of the present work to develop this approach further, especially with respect to the co-moving velocity.

A little more than a decade ago, Tallakstad et al. (2009a, b) injected simultaneously air and a glycerol-water mixture into a glass-bead filled Hele–Shaw cell measuring the pressure drop across it as a function of the combined flow rate of the two fluids, finding a power law relation between them. Aursjø et al. (2014) repeated the Tallakstad et al. experiment, but this time with two incompressible fluids, finding the same power law dependency, but with a somewhat different power law exponent. The power law relation between pressure difference and flow rate, which corresponds to the local average seepage velocity depending on the local pressure gradient to a power when gradients in the saturation are negligible, has since been reported by other groups (Sinha et al. 2017; Gao et al. 2020; Zhang et al. 2021). This includes finding that the power law regime exists only in a finite range of pressure gradients; at smaller or larger gradients the relation is linear. Computational and theoretical approaches to understanding this behavior have followed the experimental findings, see (Sinha and Hansen 2012; Sinha et al. 2013; Xu and Wang 2014; Yiotis et al. 2019; Roy et al. 2019; Lanza et al. 2021; Fyhn et al. 2021).

This nonlinear constitutive law for the average seepage velocity is a reflection of the behavior of each of the two immiscible fluids. The Euler approach of Hansen et al. (2018); Roy et al. (2020) makes it possible to transform this constitutive law describing the local average seepage velocity as a function of the local driving forces into constitutive laws for each of the two fluids. However, this hinges on providing a constitutive law for the co-moving velocity.

We will in this paper develop a constitutive equation for the co-moving velocity under the assumption that gradients in the saturation may be neglected. Together with the constitutive equation for the average velocity, we then have a complete description of the flow as long as there are no saturation gradients.

Generalizing our results to when there are saturation gradients will be the subject of future investigations.

We investigate the constitutive equation for the co-moving velocity using two approaches. The first one is to use experimental relative permeability data from the literature to construct the constitutive equation for the co-moving velocity. Since the relative permeability approach obeys the Euler homogeneity assumption, it is possible to express the co-moving velocity in terms of the relative permeabilities. This opens up for reverse engineering the experimental data which have been cast in terms of relative permeability curves in order to construct the co-moving velocity.

It should be noted here that this reverse engineering of the data does not rely on the relative permeability constitutive equations being accurate or even correct. It simply consists of translating the data that have been cast in the form of relative permeability data into seepage velocity data that in turn allow us to construct the co-moving velocity.

The second approach is based on a dynamic pore network model (Joekar-Niasar and Hassanizadeh 2012) first introduced by Aker et al. (1998) and then later refined (Gjennestad et al. 2018, 2020). A review of the model was recently published by Sinha et al. (2020). It allows us to emulate closely the experiments of Tallakstad et al. (2009a, b), e.g., reproducing the power law dependence of the flow rate on the pressure drop (Sinha and Hansen 2012).

The constitutive law for the co-moving velocity turns out to be surprisingly simple, see Eq. (52). The reason for this remains an open question.

The main body of the paper is divided into three sections. The first one, Sect. 2, reviews the Euler homogeneity approach to immiscible two-phase flow in porous media (Hansen et al. 2018; Roy et al. 2020). The section starts by laying the groundwork for the theory by defining central variables.

In Sect. 2.1, we address central questions concerning these variables: Are they at all possible to define or will they be swamped by fluctuations? Is it possible to see them as state variables, that is, variables that describe the flow there and then without depending on the history of the system? Can we still deal with these variables when there is hysteresis? After this discussion, we go on to describe in Sect. 2.2 the consequences of the volumetric flow rate being an Euler homogeneous function in the area over which the volume is measured. We then go on in Sect. 2.3 describe how the equations of the previous subsection together with constitutive equations for the local average seepage velocity and the local co-moving velocity form a closed set of equations that determine the local seepage velocities of the fluids, the local saturation and the local pressure field. In Sect. 2.4 we give a physical interpretation of the meaning of the co-moving velocity. In Sect. 3, we turn to analyzing experimental data from the literature that allow us to reconstruct the co-moving velocity. We start this section by describing (Sect. 3.1) how relative permeability theory may be cast in the language of the Euler scaling approach of Sect. 2. In this way, we relate the relative permeabilities to the co-moving velocity. We emphasize yet again that this does not imply that relative permeability theory is correct. Rather, the assumption is: If we assume the central equations of relative permeability theory, then the co-moving velocity could be expressed in terms of relative permeability curves, see Eqs. (45) or (46). Section 3.2 present our analysis of different relative permeability data sets including the reconstructed co-moving velocity, see Eq. (52). This is the main result in this paper. Section 4 focuses on using a dynamic pore network model to calculate the co-moving velocity. Sect. 4.1 details how we extract the average seepage velocity and then the co-moving velocity from the numerical data generated by the model. We then fit the data to the form (52) in Sect. 4.2, finding excellent agreement. Hansen et al. (2018) presented the co-moving velocity gotten by the dynamic pore network model, but using a different set of variables than we use here. Section 4.3 discusses the relation between the functional form we find for the co-moving velocity here and the one found in Hansen et al. We have earlier in this introduction described the work of Tallakstad et al. (2009a, b) and subsequent workers, where a nonlinear relation between average seepage velocity and pressure gradient was uncovered. In Sect. 4.4, we report on what happens to the co-moving velocity when the flow is in the regime. The interesting answer is it does not change character. We then go on to investigate in Sect. 4.5 what happens to the co-moving velocity when the wetting saturation or the non-wetting saturation falls below the threshold for two-phase flow. We see a change in the coefficients describing the co-moving velocity, but not its functional form when the wetting saturation falls below the two-phase flow threshold. However, no such jump is seen at the other threshold. We note that there is hysteresis associated with the low wetting saturation threshold but not with the low non-wetting saturation threshold (Knudsen and Hansen 2006). Lastly in this section, we discuss the effect of changing the viscosity ratio of the two immiscible fluids on the co-moving velocity, see Sect. 4.6. Finally, we draw our conclusions in Sect. 5.

2 Euler scaling approach

We consider in the following two incompressible and immiscible fluids, one of which more wetting with respect to the pore matrix than the other. We will refer to the first fluid as the wetting fluid and the second one the non-wetting fluid. The viscosity of the wetting fluid is $\mu _w$ and of the non-wetting fluid $\mu _n$.

We consider a porous medium at a scale where it may be viewed as a continuum. This is a scale that is much larger than the pore scale. Whereas at the pore scale concepts such as fluid clusters, interfaces and wetting are central, they are not useful at the continuum scale. Rather, different concepts, and hence variables, should be—and to some degree are—used. This is the viewpoint will retain throughout this section.

This viewpoint has consequences. In this continuum limit, the pores are essentially infinitely small, and so are the fluid interfaces in the pores. Hence, it is no longer fruitful to view the problem as the flow of two immiscible fluids since the key notions that belong to such a description all are closely related to pore-scale concepts. Rather, the two immiscible fluids may be seen acting as a single fluid whose rheological properties—for example the effective viscosity—is controlled by two variables, the pressure P and the wetting saturation $S_w$.

There are two driving forces in the continuum limit description that get this single fluid to move: spatial gradients in the pressure, $\nabla P$ and the saturation, $\nabla S_w$. The latter driving force has its origin at the pore level in capillary forces. We may express this driving force in terms of a field with the dimensions of pressure, $P_c$, which depends on the saturation, so that $\nabla P_c(S_w)=(dP/dS_w)\nabla S_w$. In relative permeability theory, we would call $P_c$ the dynamic capillary pressure field.

It is necessary to describe the single fluid using two velocity fields. This is a reflection of the saturation not being transported at the same velocity as the fluid itself. We name the velocity field that transports the fluid $\mathbf {v}_p$ and the velocity field that transports the wetting saturation $\mathbf {v}_w$,

$$\begin{aligned} \phi \ \frac{\partial S_w}{\partial t}=-\nabla \cdot \mathbf {v}_w \phi S_w\;, \end{aligned}$$

(1)

where $\phi$ is the porosity field and t is time.

We define the porosity field as follows: We may associate with each point in the porous medium a Representative Elementary Volume (REV) which is very large compared to the pore scale, but small compared to continuum scale. The porosity of a given point is then the pore volume of REV divided by the volume of the REV. We note that there might be structure in the porous medium at the continuum scale, so that the porosity field may vary spatially, generating a nonzero gradient $\nabla \phi$.

We also define a Representative Elementary Area (REA) (Bear and Bachmat 2012). We pick a point in the porous medium. There will be a stream line associated with the velocity field $\mathbf {v}_p$ at that point. We place a plane of area A orthogonal to the stream line centered at the point. We assume that the plane is small enough so that the other stream lines passing through the plane all are essentially parallel to the first one. We also assume that the plane is small enough for the porous medium to be homogeneous over the size of the plane with respect to porosity and permeability. This is the REA.

This allows us to define a transverse pore area

$$\begin{aligned} A_p=\phi A\;. \end{aligned}$$

(2)

The transverse pore area is the area of the REA that cuts through the pores.

The transverse pore area $A_p$ may be split into a transverse wetting fluid area $A_w$ and a transverse non-wetting fluid area $A_n$. We mean by $A_w$ the area of the plane covered by the wetting fluid and $A_n$ the area covered by the non-wetting fluid. We have that

$$\begin{aligned} A_p=A_w+A_n\;. \end{aligned}$$

(3)

The wetting and non-wetting saturations $S_w$ and $S_n$ may be expressed as

$$\begin{aligned} S_w=\frac{A_w}{A_p}\;, \end{aligned}$$

(4)

and

$$\begin{aligned} S_n=\frac{A_n}{A_p}\;, \end{aligned}$$

(5)

so that

$$\begin{aligned} S_w+S_n=1\;. \end{aligned}$$

(6)

There is a volumetric flow rate $Q_p$ passing through the plane which may be decomposed into a volumetric flow rate for the wetting fluid, $Q_w$, and a volumetric flow rate for the non-wetting fluid $Q_n$. We have that

$$\begin{aligned} Q_p=Q_{w}+Q_{n}\;. \end{aligned}$$

(7)

This allows us to define three velocities,

$$\begin{aligned} v_w=\frac{Q_w}{A_w}\;, \end{aligned}$$

(8)

and

$$\begin{aligned} v_n=\frac{Q_n}{A_n}\;, \end{aligned}$$

(9)

and

$$\begin{aligned} v_p=\frac{Q_p}{A_p}= \frac{A_w}{A_p}\ \frac{Q_w}{A_w}+\frac{A_n}{A_p}\ \frac{Q_n}{A_n}=S_wv_w+S_nv_n\;. \end{aligned}$$

(10)

These are the seepage velocities. We will refer to $v_p$ as the average seepage velocity in the following.

We may note here that since we are assuming the fluids to be incompressible, it makes no difference whether we define the seepage velocities of each fluid with respect to volume flow or mass flow. However, the average seepage velocity $v_p$, defined in Eq. (10) will be different if averaged with respect to mass rather than volume. The formalism we are about to develop in Sect. 2.2 and onwards, could have been done using this averaging instead. We have, however, decided to stick with volume averaging.

2.1 Fluctuations, State Variables and Hysteresis

We will in the following sections treat the variables we have just defined as functions of each other, even to the point of taking derivatives. In this section, we pose the question of whether this is at all possible. There are three aspects we need to address in this context: The first one concerns fluctuations. If the variables we consider fluctuate strongly, it is not possible to find functional relations between them. The second aspect is the question of whether the variables we measure depend only on the flow there and then or whether they in addition depend on the history of the flow. If the former is true, we are dealing with state variables. The third aspect concerns the possibility of these variables being multi-valued. That is, there is hysteresis. Is the analysis we present still valid when there is hysteresis?

Fluctuations: Self-averaging is an important property of fluctuating systems. A self-averaging system is one where the relative strength of the fluctuations shrinks with increasing size of the system. If this is so, the variables attain well-defined values and functional relations between them may be sought.

To give an example, this is precisely the situation when thermodynamics is used to describe a gas. The more molecules it consists of, the more well defined the macroscopic thermodynamic variables and their relations are. We note, however, that in such systems there is one exception: At critical points, the fluctuations dominate and self-averaging is lost (Aharony and Harris 1996).

An important feature of flooding processes, slow or fast, is that they typically generate fractal injection patterns (Feder et al. 2022). These patterns, like the fluctuations near critical points, are typically not self-averaging. However, there will always be a largest length scale above which the process does not produce fractals. Here, self-averaging sets in. In the continuum limit—which is what we consider here—we are surely above this scale.

It should be noted that there is not a one-to-one correspondence between the fluid configurations and the values of the macroscopic variables. Rather, typically there are many fluid configurations giving rise to the same values for the macroscopic variables. This is not a problem as it is the macroscopic variables that are measured, not the underlying fluid configurations.

One may then ask oneself, does this mean that the theory being developed here is untestable on small systems such as those that can be modeled using computational method such as the lattice Boltzmann method or dynamic pore network models since we can never reach sufficient system sizes for the fluctuations to be small enough? The answer is no as one may use time averaging to emulate size. In fact, Kjelstrup et al. (2018) report that around 100 links are enough to define a REV in the dynamic pore network model (Sinha et al. 2020) we explore further on in this paper.

State variables: Steady-state flow of immiscible fluids in a porous medium needs to be carefully defined. We have settled on the following: It is a flow where the macroscopic variables have values (measured in practice as gliding averages over time) that do not drift in any direction. This does not preclude fluid clusters moving, merging and breaking up. In three-dimensional flow, one may have that both fluid phases percolate. If the flow then is not too fast, the fluid interfaces will not move. However, when there is no percolation of either phase, which is typically easier to obtain in two-dimensional systems, the clusters will exhibit a rich dynamics.

Erpelding et al. (2013) studied experimentally and computationally such a two-dimensional system. Their experimental setup consisted of a two-dimensional (42 cm $\times$ 85 cm) Hele–Shaw cell filled with immobilized 1-mm glass beads. Along one of the short edge, two immiscible fluids (a water-glycerol mixture and air) were injected simultaneously through 15 alternating injection points at constant rates. The opposite edge of the Hele–Shaw cell was left open, and the two orthogonal sides were both sealed. Hence, there would be a flow across the cell from the injection points in the direction of the open edge. Some distance from the injection points in the flow direction, the fluids would mix sufficiently to create a mixture of fluid clusters that when averaged over time would be homogeneous.

This system would be set up at a given flow rate and a number of variables were measured. The flow rate would then be raised and new values for the variables would be measured. Then, the flow rate would revert to the original value and the variables measured anew. The variables would attain the values they had before the flow rate was raised. The flow is history independent in the language of Erpelding et al. (2013), and the macroscopic variables describing it would then be state variables. They would characterize the flow there and then, and not depend on the history of the flow.

Hysteresis: There is the hysteresis caused by the difference between first and secondary flooding (Blunt 2017). Typically at low injection rates, the system will remember its history and the values for the macroscopic variables will be different when the first and second time one floods the system.

There is, however, also another kind of hysteresis which is related to the study of Erpelding et al. (2013). Modeling the Hele–Shaw system, Knudsen and Hansen (2006) studied the wetting fractional flow as a function of wetting saturation under steady-state conditions using a dynamic pore network model. They found that there are two transitions between two-phase flow and single-phase flow when the saturation is the control parameter. The transition between only the non-wetting fluid moving at low saturation to both fluids moving at higher saturation does not show any hysteresis with respect to which way one passes through the transition. However, the other transition between only the wetting fluid moving at high saturation and both fluids moving at lower saturation does show a strong hysteresis. This is depicted in Fig. 2 in Reference (Knudsen and Hansen 2006). This hysteresis, we believe, is caused by this transition being related to a first-order (or spinodal) phase transition.

Hysteretic behavior is a signal that the macroscopic state variables are multi-valued, signaling—of course—that the underlying microscopic physics has more than one stable mode. Hysteresis is far from uncommon in physics. In fact, it is a defining property of first-order phase transitions. There are no principal problems manipulating multi-valued functions, for example taking their derivatives as long as one does not mix up the branches. Staying on a given branch requires small changes of the independent variables, watching for jumps in the dependent variables (Poston and Steward 1978).

2.2 Homogeneity of $Q_p$ and Consequences Thereof

In the following, we review the central arguments in Hansen et al. (2018).

The volumetric flow rate $Q_p$ is a homogeneous function of order one in the areas $A_w$ and $A_n$. This implies that $A_w$ and $A_n$ are independent variables. What this independence means is that we may change the area A of the REA by changing $A_w$, while keeping $A_n$ fixed or changing $A_n$ while keeping $A_w$ fixed. This makes $A_p$, defined in Eq. (3), a dependent variable.

Suppose we scale the two areas $A_w \rightarrow \lambda A_w$ and $A_n\rightarrow \lambda A_n$. This corresponds to enlarging the area A of the REA to $\lambda A$. The scaling $A_w \rightarrow \lambda A_w$ and $A_n\rightarrow \lambda A_n$ affects the volumetric flow rate as follows:

$$\begin{aligned} Q_p(\lambda A_w,\lambda A_n)=\lambda Q_p(A_w,A_n)\;, \end{aligned}$$

(11)

making $Q_p$ a homogeneous function of order one. Since $A_w$ and $A_n$ are independent variables, we may take the derivative of this expression and then setting $\lambda =1$, finding¹

$$\begin{aligned} Q_p(A_w,A_n)=A_w\left( \frac{\partial Q_p}{\partial A_w}\right) _{A_n}+ A_n\left( \frac{\partial Q_p}{\partial A_n}\right) _{A_w}\;. \end{aligned}$$

(12)

Dividing $Q_p$ in this equation by the transverse pore area $A_p$, we get

$$\begin{aligned} v_p = S_w\left( \frac{\partial Q_p}{\partial A_w}\right) _{A_n} + S_n\left( \frac{\partial Q_p}{\partial A_n}\right) _{A_w} =S_w {\hat{v}}_w + S_n{\hat{v}}_n\;. \end{aligned}$$

(13)

where

$$\begin{aligned} {\hat{v}}_w=\left( \frac{\partial Q_p}{\partial A_w}\right) _{A_n}\;, \end{aligned}$$

(14)

and

$$\begin{aligned} {\hat{v}}_n=\left( \frac{\partial Q_p}{\partial A_n}\right) _{A_w}\;, \end{aligned}$$

(15)

are the thermodynamic velocities. They differ from the seepage velocities (8) and (9) as we shall see, this in spite of $v_p$ being given by both (10) and (13).

We may express the two thermodynamic velocities ${\hat{v}}_w$ and ${\hat{v}}_n$ in terms of the average seepage velocity $v_p$. In order to do so, we change our control variables from $(A_w,A_n)$ to $(A_p,S_w)$. We use Eqs. (4) and (5) and the chain rule to derive

$$\begin{aligned} \left( \frac{\partial }{\partial A_w}\right) _{A_n}= & {} \frac{S_n}{A_p}\ \left( \frac{\partial }{\partial S_w}\right) _{A_p} +\left( \frac{\partial }{\partial A_p}\right) _{S_w}\;, \end{aligned}$$

(16)

and

$$\begin{aligned} \left( \frac{\partial }{\partial A_n}\right) _{A_w} =-\frac{S_w}{A_p}\ \left( \frac{\partial }{\partial S_w}\right) _{A_p} +\left( \frac{\partial }{\partial A_p}\right) _{S_w}\;. \end{aligned}$$

(17)

We now combine these two equations with the definitions (14) and (15), and use $Q_p=A_pv_p$, i.e. Eq. (10), to find

$$\begin{aligned} {\hat{v}}_w=v_p+S_n\frac{dv_p}{dS_w}\;, \end{aligned}$$

(18)

and

$$\begin{aligned} {\hat{v}}_n=v_p-S_w\frac{dv_p}{dS_w}\;. \end{aligned}$$

(19)

This is a remarkable result in that ${\hat{v}}_w$ and ${\hat{v}}_n$ are fully determined by $v_p$ and its derivative with respect to $S_w$. In other words, it is enough to know $v_p(S_w)$ to determine both ${\hat{v}}_w$ and ${\hat{v}}_n$.

From Eqs. (10) and (13), we have that

$$\begin{aligned} S_w v_w+S_n v_n =S_w {\hat{v}}_w+S_n{\hat{v}}_n\;. \end{aligned}$$

(20)

The most general relation between between $({\hat{v}}_w,{\hat{v}}_n)$ and $(v_w,v_n)$ is given by the pair of equations

$$\begin{aligned} {\hat{v}}_{w}=v_{w}+S_{n}v_m\;, \end{aligned}$$

(21)

and

$$\begin{aligned} {\hat{v}}_{n}=v_{n}-S_{w}v_m\;, \end{aligned}$$

(22)

where a new velocity function $v_m$ has been introduced. This is the co-moving velocity.

Equations (21) and (22) define the co-moving velocity. The co-moving velocity provides the link between the seepage velocities and the thermodynamic velocities.

We combine the two Eqs. (21) and (22) with Eqs. (18) and (19), to find

$$\begin{aligned} v_w=v_p+S_n\left( \frac{dv_p}{dS_w}-v_m\right) \;, \end{aligned}$$

(23)

and

$$\begin{aligned} v_n=v_p-S_w\left( \frac{dv_p}{dS_w}-v_m\right) \;. \end{aligned}$$

(24)

Thus, we have expressed the seepage velocity for each fluid $v_w$ and $v_n$ in terms of the average seepage velocity $v_p$ and the co-moving velocity $v_m$. This is in contrast to the thermodynamic velocities ${\hat{v}}_w$ and ${\hat{v}}_n$ where only the average seepage velocity $v_p$ was needed, see Eqs. (18) and (19).

We may see Eqs. (18) and (19) as a mapping $(v_p, v_m)\rightarrow (v_w,v_n)$. The couple $(v_p,v_m)$ contains the same information as the couple $(v_w,v_n)$.

The co-moving velocity was defined in Eqs. (21) and (22). We may express it explicitly by solving (23) and (24) with respect to $v_m$, finding

$$\begin{aligned} v_m=\frac{dv_p}{dS_{w}}+\left( v_n-v_w\right) \;. \end{aligned}$$

(25)

If we now take the derivative of Eqs. (10) with respect to $S_w$ and combine the resulting equation with Eqs. (25), we find

$$\begin{aligned} v_m = S_w\frac{dv_w}{dS_w} + S_n\frac{dv_n}{dS_w}\;. \end{aligned}$$

(26)

We may take either of Eqs. (25) and (26) as alternative definitions of the co-moving velocity.

For clarity, we now display Eqs. (10) and (26) together as follows:

$$\begin{aligned} v_p=S_wv_w+S_nv_n\;,\\ v_m=S_wv'w+S_nv'_n\;, \end{aligned}$$

where we have used the notation $v'_w=dv_w/dS_w$ and $v'_n=dv_n/dS_w$. These two Eqs. (10) and (26), give us the reverse transformation $(v_w,v_n)\rightarrow (v_p,v_m)$.

2.3 Closed Set of Equations

We defined the Representative Elementary Area in Sect. 2. Its size was determined by the largest transverse area over which the streamlines could be regarded as parallel. On larger scales, the stream lines form patterns that reflect the structure and boundaries of the porous medium; e.g., a reservoir. In this section, we construct a closed set of equations that determine the flow at these scales based on the formalism constructed in the previous Section, conservation laws and constitute equations.

The plane with area A we introduced in the preceding subsection was oriented orthogonally to the stream line for $v_p$ at the point it sits. We may orient it differently generating the same equations, but with the velocities now being components relative to the axis of the new plane. This makes it possible to express the equations in terms of vectors.

The fluids are incompressive so that

$$\begin{aligned} \nabla \cdot \phi \mathbf {v}_p=0\;. \end{aligned}$$

(27)

We have here assumed that the porosity may not be spatially uniform. The continuity equation for the wetting saturation, $S_w$, Eq. (1), may be combined with the vector version of Eq. (23) to give

$$\begin{aligned} \phi \ \frac{\partial S_w}{\partial t}=\nabla \cdot \left[ \mathbf {v}_p+S_n\left( \frac{d\mathbf {v}_p}{dS_w}-\mathbf {v}_m\right) \right] \phi S_w\;. \end{aligned}$$

(28)

These two continuity equations must be supplied with two constitutive equations

$$\begin{aligned} \mathbf {v}_p=\mathbf {v}_p(S_w,\nabla S_w,\nabla P)\;, \end{aligned}$$

(29)

and

$$\begin{aligned} \mathbf {v}_m=\mathbf {v}_m(S_w,\nabla S_w,\nabla P)\;, \end{aligned}$$

(30)

to produce a closed set of equations that together with the proper boundary and initial values solve the immiscible two-phase flow problem in the continuum limit.

We note that the nonlinear constitutive equation that can be constructed for $\mathbf {v}_p$ from the observations in Tallakstad et al. (2009a, b), Aursjø et al. (2014), Sinha et al. (2017), Gao et al. (2020), Zhang et al. (2021) is easily combined with this approach.

2.4 Interpreting the Co-moving Velocity $v_m$

Let us now pose the question: is $\mathbf {v}_m$ transporting anything? Eqs. (8), (9) and (10) show that there is volumetric transport associated with the velocities $\mathbf {v}_w$, $\mathbf {v}_n$ and $\mathbf {v}_p$. We will in the following show that there is no such transport associated with $\mathbf {v}_m$.

We base the discussion that now follows on Roy et al. (2020). We will consider components rather than vectors. We introduce the differential transverse area distributions $a_p$, $a_w$ and $a_n$. Their meaning is as follows: $a_p(v) dv$ is the area covered by fluid, wetting or non-wetting, that has a velocity in the interval $[v,v+dv]$. Likewise, $a_w(v) dv$ is the area covered by wetting fluid that has a velocity in the interval $[v,v+dv]$ and $a_n(v) dv$ is the area covered by non-wetting fluid that has a velocity in the interval $[v,v+dv]$. Hence, we have that

$$\begin{aligned}&A_p=\int _{-\infty }^\infty dv\ a_p\;, \end{aligned}$$

(31)

$$\begin{aligned}&A_w=\int _{-\infty }^\infty dv\ a_w\;, \end{aligned}$$

(32)

and

$$\begin{aligned} A_n=\int _{-\infty }^\infty dv\ a_n\;. \end{aligned}$$

(33)

The velocities defined in Eqs. (8), (9) and (10) are then given by

$$\begin{aligned}&v_p=\frac{1}{A_p}\int _{-\infty }^\infty vdv\ a_p\;, \end{aligned}$$

(34)

$$\begin{aligned}&v_w=\frac{1}{A_w}\int _{-\infty }^\infty vdv\ a_w\;, \end{aligned}$$

(35)

and

$$\begin{aligned} v_n=\frac{1}{A_n}\int _{-\infty }^\infty vdv\ a_n\;. \end{aligned}$$

(36)

The differential transverse areas are essentially velocity histograms, thus making a connection between the continuum scale and the flow at small scales.

We may now combine these three Eqs. (34), (35) and (36), with Eq. (25) to give

$$\begin{aligned} v_m=\frac{dv_p}{dS_w}-v_w+v_n=\frac{1}{A_p} \int _{-\infty }^\infty vdv\ \left[ \frac{\partial a_p}{\partial S_w}-\frac{a_w}{S_w}+\frac{a_n}{S_n}\right] =\frac{1}{A_p} \int _{-\infty }^\infty vdv\ a_m\;, \end{aligned}$$

(37)

from which we infer

$$\begin{aligned} a_m(v)=\frac{\partial a_p(v)}{\partial S_w}-\frac{a_w(v)}{S_w}+\frac{a_n(v)}{S_n}\;. \end{aligned}$$

(38)

This is the co-moving differential transverse area. We now integrate this over all velocities to find the total co-moving transverse area $A_m$,

$$\begin{aligned} A_m= & {} \int _{-\infty }^\infty dv\ a_m=\frac{d}{dS_w}\int _{-\infty }^\infty dv\ a_p -\frac{1}{S_w}\int _{-\infty }^\infty dv\ a_w+\frac{1}{S_n}\int _{-\infty }^\infty dv\ a_n\nonumber \\= & {} \frac{dA_p}{dS_w}-\frac{A_w}{S_w}+\frac{A_n}{S_n}=0\;. \end{aligned}$$

(39)

There is no area associated with the co-moving velocity. As a consequence, there is no volumetric flux associated with it as

$$\begin{aligned} Q_m=A_m v_m=0\;, \end{aligned}$$

(40)

nor is the co-moving velocity associated with any particular exchange of conserved quantities. Both of these results make sense, since $A_w+A_n=A_p$ (Eq. (3)) and $Q_w+Q_n=Q_p$ (Eq. (7)): There is no room for $v_m$ being associated with any transverse area or with volumetric transport. We may see the transformation $(v_w,v_n)\rightarrow (v_p,v_m)$ as a way of partitioning the flow. $(A_w,A_n)$ and $(Q_w,Q_n)$ constitute one partitioning, $(A_p,A_m)=(A_p,0)$ and $(Q_p,Q_m)=(Q_p,0)$ another.

Equation (25) shows that $v_m$ is related to the relative velocity of the two fluids, $v_n-v_w$. However, the difference velocity, $v_n-v_w$ cannot be given an interpretation as being part of a partitioning of the flow.

Before we now switch to the structure of the co-moving velocity $v_m$, it is now appropriate to remind the reader of why the mapping $(v_w,v_n)\rightleftarrows (v_p,v_m)$, that is Eqs. (10) and (26) for the transformation $(v_w,v_n)\rightarrow (v_p,v_m)$, and Eqs. (23) and (24) for the transformation $(v_w,v_n)\leftarrow (v_p,v_m)$, is important. With the nonlinear constitute law for $v_p$ being uncovered experimentally, computationally and theoretically (Tallakstad et al. 2009a, b; Aursjø et al. 2014; Sinha et al. 2017; Gao et al. 2020; Zhang et al. 2021; Sinha and Hansen 2012; Sinha et al. 2013; Xu and Wang 2014; Yiotis et al. 2019; Roy et al. 2019; Lanza et al. 2021; Fyhn et al. 2021), a theory that can relate this constitutive law to the flow properties of each of the immiscible fluids is necessary. It is precisely such a theory that we are presenting here.

3 Reverse Engineering Relative Permeability Data

Our aim is now to reverse engineer experimental data from the literature that have been presented as relative permeability curves to reconstruct a constitutive equation for the co-moving velocity.

In order to do so, we begin this section by placing relative permeability theory within the framework of the Euler homogeneity approach. This allows us to express the co-moving velocity $v_m$ in terms of the relative permeabilities.

It is important to note here that this approach does not hinge on whether the relative permeability approach is correct or not. Rather, we are simply translating the data back to their origin and from there we construct $v_m$.

Which relative permeability data sets to choose? Since we have no preconceived ideas of the form of $v_m$ or what controls it, we have more or less randomly picked relative permeability data sets. Any other way of picking them would bias the results.

We note that the relative permeability data are hysteretic. There is, however, no problem in taking the derivatives of these curves in order to extract the co-moving velocities. It might be that the co-moving velocities also are hysteretic. At this point, we do not know.

3.1 Relative Permeability Theory in Light of Euler Homogeneity

Relative permeability theory (Wyckoff and Botset 1936) is based on the two constitutive equations,

$$\begin{aligned} \mathbf {v}_w = - \displaystyle \frac{K k_{rw}}{\phi S_w\mu _w} \nabla P\;, \end{aligned}$$

(41)

and

$$\begin{aligned} \mathbf {v}_n = - \displaystyle \frac{K k_{rn}}{\phi S_n\mu _n} \nabla P\;, \end{aligned}$$

(42)

when we assume that there are no saturation gradients so that $\nabla P_c=0$ (Valavanides 2018). Here K is the absolute permeability. The factors $k_{rw}=k_{rw}(S_w)$ and $k_{rn}= k_{rn}(S_w)$ are the wetting and non-wetting relative permeabilities.

We introduce the plate of area A as in Sect. 2.2 and form the volumetric flow rate through it, $Q_p$. From this we get $v_p$ by using Eq. (10). Combining this equation with the the relative permeability constitutive equations, also named the generalized Darcy Eqs. (41) and (42), gives

$$\begin{aligned} v_p=- \mu _w v_0\left[ \frac{k_{rw}}{\mu _w}+\frac{k_{rn}}{\mu _n}\right] \;, \end{aligned}$$

(43)

where we have introduced a velocity scale which is independent of $S_w$,

$$\begin{aligned} v_0=-\frac{K}{\mu _w\phi }|\nabla P|\;. \end{aligned}$$

(44)

We see that this is an Euler homogeneous function of order zero in $A_w$ and $A_n$ implying that $Q_p=(A_w+A_n)v_p$ trivially fulfills Eq. (11). Hence, relative permeability theory obeys all the relations we derive in Sect. 2.2.

We now combine the generalized Darcy Eqs. (41) and (42) with Eq. (26) for the co-moving velocity $v_m$. We find

$$\begin{aligned} v_m = \mu _w v_0\left[ \frac{S_w}{\mu _w}\frac{d}{dS_w} \left( \frac{k_{rw}}{S_w}\right) +\frac{S_n}{\mu _n} \frac{d}{dS_w}\left( \frac{k_{rn}}{S_n}\right) \right] \;. \end{aligned}$$

(45)

We may also write $v_m$ as

$$\begin{aligned} v_m=\frac{dv_p}{dS_w}+\mu _w v_0\left[ \frac{k_{rn}}{\mu _n}-\frac{k_{rw}}{\mu _w}\right] \;, \end{aligned}$$

(46)

using Eq. (25).

3.2 Analysis of Relative Permeability Curves from the Literature

We analyze in the following relative permeability curves from References (Bennion and Bachu 2005; Fulcher et al. 1985; Oak et al. 1990; Virnovsky et al. 1998; Reynolds and Krevor 2015; Leverett 1939) in light of the discussion in Sect. 3.1. Our aim is to determine $v_p$ and $v_m$ as a function of the wetting saturation $S_w$.

The wetting and non-wetting relative permeabilities $k_{rw}(S_w)$ and $k_{rn}(S_w)$ data together with the wetting and non-wetting viscosities $\mu _w$ and $\mu _{n}$ as supplied by the authors are the essential data we use in our analysis. Other parameters such as the surface tension $\gamma$, porosity $\phi$ and absolute permeability K we use to set the velocity scale $v_0$ and to determine a scale for the pressure gradient.

The data points for $k_{rn}$, $k_{rw}$ and $S_w$ were obtained explicitly from tables when available in the cited works. If explicit values were not given, the values were extracted graphically from the plots using the software Webplotdigitizer (Rohatgi 2020).

In all of the experiments, the measurements were performed when the flow reached steady state i.e. when the variation in pressure and saturation attained values within some acceptable threshold interval. The sources have different definitions of when steady state has been reached, but this threshold is usually taken to be fluctuations within $1 - 2 \%$ over the span of minutes to hours depending on the experiment, see (Oak et al. 1990).

The data we use were obtained either during drainage or imbibition processes.

We plot the velocities $v_p$ in Eq. (43) and $v_m$ in Eq. (45) in dimensionless units by dividing by a velocity scale $v_0$ and $\mu _w$. We do this in the following way: We define

$$\begin{aligned} {\tilde{v}}_p(S_w)=\left[ \frac{k_{rw}(S_w)}{\mu _w}+\frac{k_{rn}(S_w)}{\mu _n}\right] \;, \end{aligned}$$

(47)

and

$$\begin{aligned} {\tilde{v}}_m (S_w)= \left[ \frac{S_w}{\mu _w}\frac{d}{dS_w} \left( \frac{k_{rw}(S_w)}{S_w}\right) +\frac{S_n}{\mu _n} \frac{d}{dS_w}\left( \frac{k_{rn}(S_w)}{S_n}\right) \right] \;. \end{aligned}$$

(48)

We then define

$$\begin{aligned} {\tilde{v}}_0={\tilde{v}}_p(S_w=1)\;, \end{aligned}$$

(49)

leading to

$$\begin{aligned} \frac{v_p(S_w)}{v_0}=\frac{{\tilde{v}}_p(S_w)}{{\tilde{v}}_0}\;, \end{aligned}$$

(50)

and

$$\begin{aligned} \frac{v_m(S_w)}{v_0}=\frac{{\tilde{v}}_m(S_w)}{{\tilde{v}}_0}\;. \end{aligned}$$

(51)

It is the right-hand side of these two equations that we plot.

The first and second columns of figures where we present our data analysis 1–7 show plots of $v_p(S_w)/v_0$ and $v_m(S_w)/v_0$, while the third column shows $v_m/v_0$ plotted against $d(v_p/v_0)/dS_w$. We have used both Eqs. (45) and (46) to determine $v_m$. They are of course in principle equivalent, but they demand different numerical differentiations. Both gave the same result. It is the values of $v_m$ calculated from Eq. (46) that are shown in the plots.

The experimental data shown in the plots in this section have not been picked based on any special criteria. However, we have prioritized data sets with a larger number of data points for the plots.

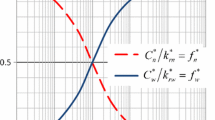
We now turn to the results of our analysis. The third column of Figs. 1–7 shows $v_m/v_0$ as a function of $v'_p/v_0$ where $v'_p=dv_p/dS_w$. The surprising result is that the relation

$$\begin{aligned} v_m=av_0+b\frac{dv_p}{dS_w}\;, \end{aligned}$$

(52)

where a and b are constants with respect to $v'_p$, fits the data excellently. This is our main result.

The parameters a and b in (52) have been determined by finding the visually best straight line for each data set. These best lines are shown in the figures. The quality of the fits vary. The data in Fig. 1 fit the best to a straight line, whereas the data that fit to a straight line the least are found in Fig. 5. This is reflected in the uncertainty of the coefficients a and b. The uncertainty is in general larger in a than in b. Note that the a and b coefficients for drainage and imbibition in Figs. 2 and 3 are slightly different.

In the first two columns of Figs. 1, 2, 3, 4, 5, 6 7 where we have plotted $v_p$ and $v_m$ against $S_w$, we have fitted the data to polynomials; for $v_p$ we have used fourth-order polynomials for the numerical fits, and for $v_m$ we have used third-order polynomials. The reason for this lies in Eq. (52) which indicates that $v_m$ should be modeled with a polynomial of one less order than that of $v_p$. The $v_p$-polynomial is numerically fitted directly to the data. For the $v_m$ fit, one can either I: fit a third-order polynomial directly to the data, or II: calculate the coefficients for the $v_m$ fit using those found for $v_p$ using Eq. (52). In principle, these two methods should give the same results. However, method II is highly sensitive to noise in the data series. Method II was used for all the data set, and the correspondence is good between the fit and the data for the sets with the lowest amount of deviation, Fig. 1 in particular. Here, method II showed only small deviations from method I in the initial and final values of the data series. Method I was used in all of the plots, as the method of fit for $v_p$ and $v_m$ does not affect the rest of the results.

We plot in Fig.  8 the values of the coefficients a and b as a function of the pressure gradient for all the data series. The pressure $\varDelta P$ is rendered dimensionless by dividing it by $\mu _w v_0/K$, $\varDelta P_\lambda =\varDelta P K/\mu _w v_0$.

Fig. 1

Experimental data from Table 3 in Bennion and Bachu (2005). Upper row: Basal Cambrian sandstone, drainage with brine as non-wetting fluid and $\hbox {CO}_2$ as wetting fluid, $\phi = 0.177$, $K = 5.43\times 10^{-16}$ $\hbox {m}^2$. Lower row: Wabamum carbonate, drainage with $\hbox {CO}_2$ as non-wetting fluid and brine as wetting fluid, $\phi = 0.177$, $K = 2.07 \times 10^{-16}$ $\hbox {m}^2$

Fig. 2

Experimental data from Fig. 4 in Oak et al. (1990). The process is primary drainage (upper row) and imbibition (lower row) of a single experimental run. Both rows: Berea sandstone, natural gas as non-wetting fluid and water as wetting fluid, $\phi = 0.193$, $K = 2072.49 \times 10^{-16}$ $\hbox {m}^2$. $\phi$ and $\gamma$ were not supplied by the authors

Fig. 3

Experimental data from Fig. 3 in Oak et al. (1990) The process is primary drainage (upper row) and imbibition (lower row) of a single experimental run. Both rows: Berea sandstone, water as non-wetting fluid and oil as wetting fluid, $\phi = 0.193$, $K = 1973.8\times 10^{-16}$ $\hbox {m}^2$. $\phi$ and $\gamma$ were not supplied by the authors

Fig. 4

Experimental data from runs no. 4 and 5 in Reynolds and Krevor (2015). Upper row: Bentheimer sandstone, drainage with $\hbox {CO}_2$ as non-wetting fluid and water as wetting fluid, $\phi = 0.222$, $K = 17862.89\times 10^{-16}$ $\hbox {m}^2$. Lower row: Bentheimer sandstone, drainage with $\hbox {CO}_2$ as non-wetting fluid and brine as wetting fluid, $\phi = 0.222$, $K = 17862.89 \times 10^{-16}$ $\hbox {m}^2$

Fig. 5

Experimental data extracted graphically using Webplotdigitizer (Rohatgi 2020) from runs no. 18 and 19 in Fulcher et al. (1985). Both rows: Berea sandstone, drainage with oil as non-wetting fluid and water as wetting fluid, $\phi = 0.224$. Upper row has $K = 4109.45\times 10^{-16}$ $\hbox {m}^2$, and lower row $K = 3794.63 \times 10^{-16}$ $\hbox {m}^2$

Fig. 6

Experimental data extracted graphically from Virnovsky et al. (1998), Figs. 4 and 5. Both rows: Berea sandstone, drainage with oil as non-wetting fluid and $\hbox {H}_2$O as wetting fluid, $\phi = 0.561$, $K = 2131.7\times 10^{-16}$ m ²

Fig. 7

Experimental data extracted graphically using Webplotdigitizer (Rohatgi 2020) from Fig. 9 (sand II) in Leverett (1939). Upper row: drainage in sand, with oil as the non-wetting fluid and water as the wetting fluid, $\phi = 0.35$, $K = 17270.75\times 10^{-16}$ $\hbox {m}^2$. Lower row: sand with oil as the non-wetting fluid and water as the wetting fluid, $\phi = 0.45$, $K = 10263.76\times 10^{-16}$ $\hbox {m}^2$

Fig. 8

Calculated coefficients a and b from all experimental data as a function of the scaled pressure gradient $\varDelta P_{\lambda }$. In the left plot, the only data point not shown is $a=-58\pm 20$ from the Oak et al. data set (Oak et al. 1990). In the right plot, the single data point above $b=1$ is obtained from a data set with few data points, see Fig. 5. Values for more data sets than have been plotted in Figs. 1–7 are included: the rest of the data series in Table 3 in Bennion and Bachu (2005), an additional water/oil data series from Fig. 3 in Oak et al. (1990), runs no. 2, 3 and 6 from Reynolds and Krevor (2015), and the two lower flow-rate data series from Figs. 4 and 5 in Virnovsky et al. (1998)

4 The Average Seepage Velocity $v_p$ and the Co-moving Velocity $v_m$ in a Dynamic Pore Network Model

The porous medium is represented by a network of nodes and links in dynamic pore network modeling (Joekar-Niasar and Hassanizadeh 2012). The immiscible fluids are transported through the links which are connected at the nodes. The dynamic pore network model we consider here was introduced by Aker et al. (1998). A recent review describe it in detail, see (Sinha et al. 2020).

The nodes do not contain fluid, only the links do. The nodes only represent the points where the links meet. The flow rate $q_j$ inside any link j of the network at any instant of time is obtained by Sinha et al. (2013), Washburn (1921),

$$\begin{aligned} \displaystyle q_j = -\frac{g_j}{l_j\mu _{av}}\left[ \varDelta p_j - \sum p_{c,j}\right] \;, \end{aligned}$$

(53)

where $l_j$ is the link length, $g_j$ is the link permeability which depends on the cross section of the link and $\varDelta p_j$ is the pressure drop across link. The viscosity term $\mu _{av}$ is the saturation-weighted viscosity of the fluids inside the link given by $\mu _{av} = s_{j,w}\mu _w + s_{j,n}\mu _n$ where $s_{j,w}$ and $s_{j,n}$ are the wetting and non-wetting fluid saturations inside the link. The term $\sum p_{c,j}$ is the total interfacial pressure from the fluid interfaces in the link j. A pore typically consists of two wider pore bodies connected by a narrow pore throat. We model this by using hour-glass shaped links. The variation of the interfacial pressure with the interface position for such a link is modeled by Sinha et al. (2013)

$$\begin{aligned} \displaystyle |p_c\left( x\right) | = \frac{2\gamma \cos \theta }{r_j} \left[ 1-\cos \left( \frac{2\pi x}{l_j}\right) \right] \;, \end{aligned}$$

(54)

where $r_j$ is the average radius of the link and $x \in [0,l_j]$ is the position of the interface inside the link. Here, $\theta$ is the contact angle between the interface and the pore wall and $\gamma$ is the surface tension between the fluids.

These two Eqs. (54) and (53), together with the Kirchhoff relations, i.e., the sum of the net volume flux at every node at each time step will be zero, provide a set of linear equations. In order to calculate the local flow rates, we solve these equations with a conjugate gradient solver (Batrouni and Hansen 1988). All the interfaces are then advanced accordingly using small time steps.

In order to achieve steady-state flow, we apply periodic boundary conditions in the direction of flow.

We use a two-dimensional square lattice with $64 \times 64$ links with link lengths $l_j = 1\,\mathrm{mm}$. Disorder is introduced by choosing the link radii $r_j$ randomly from a uniform distribution in the range $0.1\,\mathrm{mm}$ to $0.4\,\mathrm{mm}$. We use 100 different realizations of such networks for our simulations.

Assuming Poiseuille flow in the links, the average link permeability $r_j^2/8$ will be $7.8\times 10^{-7}$ $\hbox {m}^2$. As it is a square lattice, the length of it compensates for its width, making its permeability equal to the link permeability times $\sqrt{2}$ to account for its $45^\circ$ tilt. This gives an estimate for the average permeability of the lattice around $5.5\times 10^{-7}$ $\hbox {m}^2$.

We will in the following explore $v_p$ and $v_m$ as a function of the wetting saturation $S_w$ defined as the total volume of wetting fluid in the links divided by their total pore volume, and the average pressure gradient defined as $\varDelta P/L$ where $\varDelta P$ is the pressure difference across the network. The viscosity ratio M is defined as the ratio of the viscosity $\mu _n$ of non-wetting fluid to the viscosity $\mu _w$ of the wetting fluid ($M=\mu _n/\mu _w$).

4.1 Fitting the Average Seepage Velocity $v_p$ and the Co-moving Velocity $v_m$ to Polynomials

We discuss here $v_p$ and $v_m$ as a function of the wetting saturation $S_w$ for fixed pressure gradient $\varDelta P/L$. The average seepage velocity $v_p$ is measured directly from the model. The co-moving velocity is inferred from the velocity difference $v_n-v_w$ and the derivative $dv_p/dS_w$ according to Eq. (25). We fit the data to the polynomials

$$\begin{aligned} v_p=\sum _{k=0}^4 C_k S_w^k\;, \end{aligned}$$

(55)

and

$$\begin{aligned} v_m=\sum _{k=0}^3 D_k S_w^k\;. \end{aligned}$$

(56)

We find that the three or fourth-order polynomials form an adequate compromise between accuracy and the wish to keep the number of fitting parameters down.

Figure 9 shows how the seepage velocity $v_p$ behaves as a function of the wetting saturation $S_w$ for four different pressure gradients: $\varDelta P/L$ = 0.22, 0.5, 0.71 and 1.0 MPa/m. The results are obtained for $0.05 \le S_w \le 0.95$ with intervals of 0.05, totaling 20 data points. For now, we use $\mu _w=0.03$ Pa s and $\mu _n=0.01$ Pa s, i.e., $M=\mu _n/\mu _w=1/3$. The effect of a varying viscosity ratio will be explored later in this paper. We observe the quality of the fits to improve with increasing pressure gradient.

Fig. 9

Fitting of the numerical results for $v_p$ vs $S_w$ with Eq. (55) with $\mu _w=0.03$ Pa s and $\mu _n=0.01$ Pa s (i.e., $M=1/3$), and for four different pressure gradients, $\varDelta P/L=$ 0.22, 0.50, 0.71 and 1.0 MPa/m. The fitting parameters are shown in the legends in each figure. The rate of change of $v_p$ ($v_p^{\prime }=dv_p/dS_w$) will be calculated from this figure and will be used to express $v_m$ in terms of $v_p^{\prime }$ in Fig. 10

We use the data in Fig. 9 to approximate $v_p^{\prime }$ by central differencing, which then is used to determine $v_m$ from Eq. (25). We show the result in Fig. 9 where we plot $v_m$ as a function of $S_w$.

Fig. 10

Fitting of the numerical results for $v_m$ vs. $S_w$ using Eq. (56). The parameters M and $\varDelta P/L$ are as in Fig. 9

We plot $v_m$ against $v_p^{\prime }$ in Fig. 11 for fixed $\varDelta P/L=$ 0.22, 0.50, 0.71, 1.0, 1.4 and 2.1 MPa/m. We introduce a velocity scale $v_0=v_p(S_w=1,\varDelta P/L)$ to make the fits comparable to the relative permeability-based fits we discussed in Sect. 3. As is evident, Eq. (52) fits the data well. We note that both a and b vary with the pressure gradient $\varDelta P/L$. Hence, we write Eq. (52) as

$$\begin{aligned} v_m\left( S_w,\frac{\varDelta P}{L}\right) =a\left( \frac{\varDelta P}{L}\right) v_0\left( \frac{\varDelta P}{L}\right) + b\left( \frac{\varDelta P}{L}\right) \ \frac{dv_p}{dS_w}\left( S_w,\frac{\varDelta P}{L}\right) \;. \end{aligned}$$

(57)

We have in this equation written explicitly what parameters each variable depends upon. This will become important in the next section.

Fig. 11

The co-moving velocity as a function of $dv_p/dS_w$ from Eq. (25) for $\mu _w=0.03$ Pa s and $\mu _n=0.01$ Pa s, and $\varDelta P/L=$ 0.22, 0.5, 0.71, 1.0, 1.4 and 2.1 MPa/m

4.2 The Co-moving Velocity when $dv_p/dS_w$ is Treated as an Independent Variable

The co-moving velocity $v_m$ has been calculated using the dynamic network model in both References Hansen et al. (2018) and Sinha et al. (2020). In contrast to our approach here, the derivative $v_p^{\prime }$ was treated as an independent variable in those papers. That is, $v_m$ was plotted against $(S_w,v_p^{\prime })$ producing a plane. In Hansen et al. (2018), a variant of the dynamic pore network model we use here was used (Gjennestad et al. 2018), resulting in the relation

$$\begin{aligned} v_m\left( S_w,\frac{dv_p}{dS_w}\right) =c+d\ S_w+e\ \frac{dv_p}{dS_w}\;, \end{aligned}$$

(58)

where $c\approx -0.095$, $d\approx -0.15$ and $e\approx 0.79$ for data averaged over both square and hexagonal lattices. Sinha et al. considered both a square lattice and a lattice based on a reconstructed Berea sandstone, giving $c=5.00\pm 0.13$, $d=-6.36\pm 0.25$ and $e=0.94\pm 0.01$ for the square lattice and $c=10.10\pm 0.32$, $d=-12.94\pm 0.62$ and $e=0.88\pm 0.01$ for the reconstructed Berea sandstone.

Equation (57) constitutes a cut through the plane $(S_w,v_p^{\prime })$ given by $\varDelta P/L$ constant. It is an open question as to why the explicit $S_w$ dependence disappears in Eq. (57) when making this cut.

4.3 Dependence of Coefficients a and b on the Pressure Gradient

Figure 12 shows the variation of $av_0$ and b defined in Eq. (57), as a function of the pressure gradient $\varDelta P/L$. We observe two different regions as the fluid velocities increase with increasing pressure gradient. We name these regions I and II.

Region I — This is the low pressure gradient region. We find a good fit to the data with the line $av_0=0.7m/s-1.1(\varDelta P/L)m^2/MPa s$. The coefficient b has a value around 0.76. Due to low flow velocity, the $av_0$ and b found in this region can be compared with the relative permeability data in Sect. 3.

Region II — This is the high pressure gradient region. Here $av_0$ saturates to a value near $-0.1$ m/s, whereas b approaches the value 1 asymptotically. This is outside the region where the relative permeability data would be relevant.

The crossover of $av_0$ from positive to negative value and the onset of increment in b is observed to take place around the same pressure gradient.

Fig. 12

a and b, respectively, shows $av_0$ and b defined in Eq. (57) as a function of the pressure gradient $\varDelta P/L$. The viscosities of the fluids were $\mu _w=0.03$ Pa s and $\mu _n=0.01$ Pa s, so that $M=1/3$. We have marked two regions, I and II in both (a) and (b). The straight line in region I in a is $0.7m/s-1.1(\varDelta P/L)m^2/MPa s$

4.4 $v_p$ as a Function of $S_w$ and $\varDelta P/L$

We now turn to the average seepage velocity $v_p$. As described in Introduction, there is a regime over an interval of pressure gradients where the flow rate is proportional to the pressure gradient to a power (Tallakstad et al. 2009a, b; Aursjø et al. 2014; Sinha et al. 2017; Gao et al. 2020; Zhang et al. 2021). This regime is clearly visible in our dynamic pore network model (Sinha and Hansen 2012; Fyhn et al. 2021). Our aim in this section is to map out the $v_p$ over a wide range of saturations $S_w$ and pressure gradients $\varDelta P/L$.

Figure 13a shows how the flow rate Q increases as the pressure gradient $\varDelta P/L$ increases. We observe the following behavior:

$$\begin{aligned} Q\propto \left\{ \begin{array}{ll} 0 &{} {, |\varDelta P| \le P_s\;,}\\ \left( \left| \frac{\varDelta P}{L}\right| -\frac{P_s}{L}\right) ^{\beta } &{} {, |\varDelta P| > P_s\,,}\\ \end{array} \right. \end{aligned}$$

(59)

where $P_s$ is a threshold pressure below which there is no flow. This threshold is a finite-size effect, see (Roy et al. xxxx). Above a pressure difference $|\varDelta P|\gg P_t$, the exponent $\beta =1$ and we observe Darcy-like linear flow. Below this pressure difference, $P_s< |\varDelta P| < P_t$, the exponent $\beta > 1$.

The inset in Figure 13a demonstrates how the threshold pressure $P_s$ and $\beta$ were calculated: For a constant $S_w$, we first set a particular $\beta$ value and fit the numerical results to Eq. (59), finding $P_s$ as well as the error associated with the fit. In this way we get a $P_s$ value and an error value as a function of $\beta$. The curves in the inset show the error as a function of $\beta$ for different saturations. We identify the minimum of the error vs. $\beta$ curve. The value of $\beta$ giving the error minimum and the corresponding $P_s$ value are the values we assign to the system for that saturation $S_w$.

Figure 13b and c shows the variation of exponent $\beta$ and the transition point $P_t$ as functions of the wetting saturation $S_w$. Both $\beta$ and $P_t$ are observed to have a maximum at $S_w=0.5$ to decrease on both sides of it. We have that $\beta =1$ for $S_w=0$ and $S_w=1$ as we are then dealing with single fluid flow.

Fig. 13

a shows Q vs. $\varDelta P$ for wetting saturations $S_w=$ 0.1, 0.3, 0.5, 0.7 and 0.9. The viscosities of the fluids were $\mu _w=0.03$ Pa s and $\mu _n=0.01$ Pa s. The inset shows the fitting error between the data and Eq. (59) as a function of $\beta$ for the different wetting saturations. b and (c) show the dependence of $P_t$ and $\beta$ on $S_w$

Fig. 14

$v_p$ as a function of saturation $S_w$ for $\varDelta P/L=0.22$, 0.40, 0.50 and 0.71 MPa/m, respectively. The viscosities of the fluids were $\mu _w=0.03$ Pa s and $\mu _n=0.01$ Pa s. A red square indicates that the flow is in the nonlinear region for the set of parameters, $\varDelta P/L$ and $S_w$, that produce this data point. A blue circle indicates that the flow is in the linear region

Figure 14 shows the flow rate $Q=v_p A_p$ (Eq. (10)) as a function of the wetting saturation $S_w$ for four different pressure gradients, $\varDelta P/L=0.22$, 0.40, 0.50 and 0.71 MPa/m. The data points shown as red squares indicate that the flow is in the nonlinear regime where $\beta >1$, i.e., $P_s< |\varDelta P| < P_t$. The data points shown as blue circles indicate that the flow is in the linear regime, i.e., $|\varDelta P| > P_t$. Hence, we see that for a range of pressure gradients, e.g., $\varDelta P/L=0.4$ MPa/m, $v_p$ visits both the linear and nonlinear regimes over the range of wetting saturations $S_w$. For pressure gradients larger than 0.5 MPa/m, $v_p$ is always in the linear regime over the entire range of $S_w$.

We now compare Figs. 13 and 14. We note that the transition between the linear and nonlinear regimes in Fig. 14 appears at essentially the same pressure gradient that separates regimes I and II in Fig. 13. This points towards a connection. However, such a connection is yet to be found.

4.5 Limits

The irreducible wetting saturation $S_{w,irr}$ is the minimum wetting saturation possible irrespective of the pressure gradient. The residual non-wetting saturation $S_{n,r}$ is the minimum non-wetting saturation possible irrespective of the pressure gradient. At any finite pressure gradient $\varDelta P/L$ there will be a minimum wetting saturation $S_{w,\min }(\varDelta P/L)$ which approaches $S_{w,irr}$ as the pressure gradient is increased. Likewise, there will be for any finite pressure gradient a minimum non-wetting saturation $S_{n,\min }(\varDelta P/L)$ which approaches $S_{n,r}$ as the pressure gradient in increased. Let us define $S_{w,\max }(\varDelta P/L)=1-S_{n,\min }(\varDelta P/L)$. When $S_w$ reaches $S_{w,\min }(\varDelta P/L)$ or $S_{w,\max }(\varDelta P/L)$, either the wetting or the non-wetting fluid stops moving.

Knudsen and Hansen (2006) demonstrated that there is hysteresis at $S_{w,\min }(\varDelta P/L)$ based on a dynamic pore network model closely related to the one we use here, see their Fig. 2. The way Knudsen and Hansen did this was to increase or decrease the saturation step by step, building on the steady-state configurations that already were established at the previous saturation.

In the numerical work we present here based on the dynamic pore network model, we re-initiate the model every time we change the saturation. This means that the system for each value of the saturation chooses the most stable branch, masking the hysteresis. It is in this spirit we present our results in the following.

Using Eq. (10), we have that either

$$\begin{aligned} v_p=v_n(1-S_w)\;, \quad \text{ for }\ S_w \rightarrow (S_{w,\min })^+\;, \end{aligned}$$

(60)

or

$$\begin{aligned} v_p=v_wS_w \quad \text{ for }\ S_w \rightarrow (S_{w,\max })^-\;, \end{aligned}$$

(61)

Hence, we have

$$\begin{aligned} \frac{dv_p}{dS_w}=-v_n \quad \text{ for }\ S_w \rightarrow (S_{w,\min })^+\;, \end{aligned}$$

(62)

or

$$\begin{aligned} \frac{dv_p}{dS_w}=v_w \quad \text{ for }\ S_w \rightarrow (S_{w,\max })^-\;, \end{aligned}$$

(63)

Combining these two equations with Eq. (25), we find that

$$\begin{aligned} v_m=0 \quad \text{ for }\ S_w\rightarrow (S_{w,\min })^+\ \text{ or }\ S_w\rightarrow (S_{w,\max })^-\;. \end{aligned}$$

(64)

We show in Fig. 15a and b the wetting and non-wetting seepage velocities as a function of $S_w$ for pressure gradients $\varDelta P/L=0.22$, 0.30, 0.40 and 0.50 MPa/m. The viscosities were $\mu _w=0.03$ Pa s and $\mu _n=0.01$ Pa s. Both of the seepage velocities $v_w$ and $v_n$ signal a nonzero $S_{w,\min }(\varDelta P/L)$. However, we find that $S_{w,\max }(\varDelta P/L)=1$.

We denote $v_n=v_n^*$ the non-wetting seepage velocity we find for $S_w < S_{w,\min }(\varDelta P/L)$. It is possible to reach such saturations by initiating the network with a saturation $S_w$ and a pressure difference $\varDelta P_i/L$ making $S_w>S_{w,\min }(\varDelta P_i/L)$, and then reduce the pressure difference to $\varDelta P/L$ such that $S_w < S_{w,\min }(\varDelta P/L)$.

We show in Fig. 15c $v_p/v_n$ as a function of $S_w$. The straight line is the function $1-S_w$. By comparing with Fig. 15b that as soon as $S_w < S_{w,\min }(\varDelta P/L)$, the data for $v_p/v_n$ follows the line $1-S_w$. This is in accordance with Eq. (60).

This teaches us the following: For $v_p=(1-S_w) v_n^*$, i.e., when $S_w < S_{w,\min }(\varDelta P/L)$, we have $dv_p/dS_w=-v_n^*$ and $v_m=0$, see Eq. (64). If we now compare with Fig.  11, we see that the fits to Eq. (57) do not pass through this point, $(dv_p/dS_w,v_m)=(-v_n^*,0)$. The difference is too large to be attributed to the uncertainty of the fits. We note that we are here dealing with single phase flow. If the constitutive law for $v_m$ in Eq. (57) is the result of correlations appearing in two-phase flow, there is no reason for the single fluid case to fall on this curve.

We will in the future present an full analysis of this problem, taking hysteresis fully into account.

Fig. 15

a $v_w$ a function of the wetting saturation $S_w$ for $\varDelta P=0.22, 0.30, 0.40$ and 0.50 MPa/m. The vertical dotted line shows the value of $S_{w,\min }(\varDelta P)$ below which $v_w \approx 0$. b $v_n$ as a function of the wetting saturation $S_w$. The horizontal dotted lines show $v_n^*$ when $S_w<S_{w,\min }$. c shows the comparison of the numerical results with Eq. (60) (see the dotted line) for all 4 pressure gradients. The viscosities of the fluids were $\mu _w=0.03$ Pa s and $\mu _n=0.01$ Pa s

We now turn to the limit where the capillary number is so high that the capillary forces are negligible compared to the viscous forces. We achieve this limit in the dynamic pore network model by setting the surface tension $\gamma$ in Eq. (54) to zero. If the viscosities of the two fluids are equal, there will be no difference between the fluids and $v_w=v_n$. Furthermore, we will have that $v_p$ is independent of the wetting saturation $S_w$, so that $dv_p/dS_w=0$. From Eq. (25) we then have that the co-moving velocity $v_m=0$.

We show in Fig. 16, $v_m$ as a function of $dv_p/dS_w$ in the limit of $\gamma =0$ but with the fluid viscosities being $\mu _w=0.03$ Pa s and $\mu _n=0.01$ Pa s, respectively. We find that $v_m$ follows Eq. (57) with $av_0=-0.06$ and $b=0.99$. From Eqs. (10), (23) and (24), we then have that $v_n=v_w=v_p$.

Fig. 16

The figure shows how $v_m$ varies with $v_p^{\prime } (=dv_p/dS_w)$ in the limit of large capillary numbers when the capillary forces are vanishingly small compared to the viscous forces. We have set the surface tension $\gamma =0$ in the dynamic pore network model, while keeping $\mu _w=0.03$ Pa s and $\mu _n=0.01$ Pa s. For reference, the red solid line represents the equation: $v_m=dv_p/dS_w$

4.6 Viscosity Ratio M

We will here discuss how the viscosity of the two fluids will affect the relation between $v_p$ and $v_m$. We will also discuss how the parameters $av_0$ and b depend on the fluid viscosities $\mu _w$ and $\mu _n$.

Figure 17 shows how co-moving velocity behaves as a function of $dv_p/dS_w(S_w,\varDelta P/L)$ for different values of saturation, see Eq. (57) when the fluid viscosities are changed. We compare $v_m$ as a function of $dv_p/dS_w$ for viscosity ratio $M=3$ ($\mu _w=0.03$ Pa s and $\mu _n=0.01$ Pa s) with viscosity ratio $M=1/3$ ($\mu _w=0.01$ Pa s and $\mu _n=0.03$ Pa s). Figure 17a, b, c and d, respectively, is based on pressure gradients $\varDelta P/L$ = 0.22, 0.5, 1.0 and 1.4 MPa/m. We find that both coefficients $av_0$ and b change considerably when the viscosity ratio is inverted. For both M values, the co-moving velocity follows Eq. (57). For $M= 1/3$, $av_0$ decreases with increasing pressure gradient. The coefficient b remains at value around 0.76 until the pressure gradient exceeds a value around $\varDelta P/L > 0.5$ MPa/m. On the other hand, for $M=3$, $av_0$ and b remain constant around 1.5 and 0.94, respectively, irrespective of the pressure gradients we have considered.

Fig. 17

Variation of $v_m$ with $dv_p/dS_w$ for four different pressure gradient: a 0.22, b 0.50, c 1.0 and d 1.4  MPa/m. Results are shown for two different viscosity ratios: $M=3$ ($\mu _w=0.03$ Pa s and $\mu _n=0.01$ Pa s) shown as blue squares and $M=1/3$ ($\mu _w=0.01$ Pa s and $\mu _n=0.03$ Pa s) as red circles

Fig. 18

Variation of $av_0$ and b with viscosity ratio M for a constant pressure gradient $\varDelta P/L$. The numerical results are repeated for four different pressure gradients, $\varDelta P/L= 0.5$, 1.0, 2.0 and 3.0 MPa/m. For $M=1.0$, we set $\mu _n=0.01$ Pa s and $\mu _w=0.01$ Pa s. For $M>1$, we keep $\mu _w=0.01$ Pa s while $\mu _n$ has a value $M\mu _w$ Pa s. On the other hand, for $M<1$, we keep $\mu _n=0.01$ Pa s while $\mu _w$ has a value $\mu _n/M$ Pa s

We plot in Fig. 18 the coefficients $av_0$ and b as functions of the viscosity ratio M for different values of the pressure gradient $\varDelta P/L$. For the chosen span of parameters, we observe three distinct regions:

Region A ($M \le 1$ ) - In this region, both $av_0$ and b seem independent of M. Moreover, b remains constant around 0.77 for $\varDelta P/L < 0.5$ MPa/m and increases for larger values of the pressure gradient. $av_0$ decreases with increasing pressure gradient as long as $\varDelta P/L < 0.5$ MPa/m. Beyond this limit, $av_0$ saturates at a value close to zero.

Region B ($1 \le M \le 2$ ) - In this region $av_0$ and b are both increasing functions of M.

Region C ($M \ge 2$ ) - In this region, $av_0$ and b neither changes with viscosity ratio M nor with the pressure gradient $\varDelta P/L$.

5 Discussion

The aim of this paper has been to expand on the theory based on Euler homogeneity that was first presented in Hansen et al. (2018). It provides a number of relations between the seepage velocities of each fluid involved which together with constitutive equations for the average fluid velocity and the co-moving velocity form a closed set of equations.

It has recently been discovered that the constitutive equation for the average seepage velocity of the fluids follows a power law in the pressure gradient for a range of parameter values (Tallakstad et al. 2009a, b; Aursjø et al. 2014; Sinha et al. 2017; Gao et al. 2020; Zhang et al. 2021). Relative permeability theory offers the mapping $(v_w,v_n)\rightarrow v_p$. However, the nonlinear constitutive equation for $v_p$ requires the opposite mapping $v_p\rightarrow (v_w,v_n)$, which is indeterminate within relative permeability theory. Euler homogeneity theory, on the other hand, offers the two-way mapping $(v_w,v_n)\leftrightarrows (v_p,v_m)$, which is readily combined with the nonlinear constitutive equation for $v_p$. It is an additional bonus that the constitutive equation for $v_m$, Eq. (52), is as simple as it is.

The co-moving velocity which together with the average seepage velocity of the fluids closes the equation set as described in Sect. 2.3, is related to the seepage velocity difference $v_n-v_w$, but it is not the same, see Eqs. (25) and (26). We discuss in Sect. 2.4 the interpretation of $v_m$. It should be noted that the co-moving velocity is not associated volume transport, see Eq. (40).

We determine the constitutive equation for the co-moving velocity from relative permeability data found in the literature in Sect. 3. We do this by reverse engineer the data which have been cast in the form of relative permeability curves.

Our main result is Eq. (52), which shows that the co-moving velocity is linear in the derivative of the average seepage velocity with respect to the saturation when the pressure gradient is kept fixed, see Figs. 1 to 7. It is an open question as to why this is so.

Since we do not have theory as to why the co-moving velocity takes the simple form it does, we have not applied any particular criterion for which data sets to investigate. Any attempt at this would taint the results by our preconception on what causes the functional form (52). In particular, we have not taken the possibility for hysteresis into account. We discuss why it is still permissible to treat hysteretic data as representatives of analytic functions in Sect. 2.1.

We continue in Sect. 4 to consider the constitutive equation for the co-moving velocity. We find the same constitutive equation as in Eq. (52), see Fig. 11. It is remarkable that this remains true also when the constitutive equation for the average seepage velocity moves into the power-law region, see Sect. 4.4.

We have in this paper only considered systems without a saturation gradient. This has allowed us to ignore capillary pressure effects. A next step is to incorporate such a saturation gradient into the system to observe how the constitutive Eq. (52) for the co-moving velocity changes.